Analytical Solution for Wave Diffraction by a Concentric Three-Cylinder System near a Vertical Wall

Abstract

In this study, a semi-analytical model was developed to study wave diffraction around a concentric three-cylinder system near a wall based on linear potential theory. As a critical element, the target problem is transformed into bidirectional incident wave diffraction around two concentric structures based on the image principle and an analytical solution is obtained through eigenfunction expansion combined with a matching technique and Graf’s addition theorem. The validity of the proposed model was verified by comparing its results to known values. Parametric studies on porosity, annular spacing, incident angle, space between the structure and wall, and water depth were performed. The hydrodynamic loads and free-surface elevations in the system were calculated and compared to those reported in existing works on impermeable and permeable cylinders near a wall. The results indicate that the wave loads and run-ups on the exterior cylinder increase significantly based on the existence of the wall. However, based on the presence of an exterior porous protective structure, a significantly reduced influence of the wall on the interior cylinder can be observed. Considering the widespread use of concentric circular structures in ocean engineering, it is essential to conduct study on the hydrodynamic performance of concentric systems near walls, which can provide useful information for the design of marine structures.

1. Introduction

The interactions between water waves and vertical cylinders passing through a fluid surface have been an active research topic over the past few decades. This is partially because these structures are widely employed in the construction of oil rigs, docks, wave power energy conversion systems, etc. In general, the design of marine facilities requires the accurate prediction of the peak values of hydrodynamic loads and run-ups to ensure adequate strength for offshore platforms and sufficient clearance below decks [1]. Therefore, with an increase in the number of marine platforms and wind power plants constructed for human activities, it is becoming increasingly important to study the hydrodynamic performance of marine facilities.

Some scholars have studied the wave diffraction performances of various permeable structures. The wavemaker theory was first proposed by Chwang [2], who studied the total hydrodynamic pressure distribution on a wavemaker and provided a basis for examining regular wave interactions between porous structures such as porous walls [3] and perforated breakwaters [4]. Since then, several types of porous structures have been studied in terms of wave diffraction performance, among which concentric porous cylindrical structures are an important research object. Wang and Ren [5] investigated the diffraction problem of an Airy wave using a concentric porous cylindrical structure by employing the eigenfunction expansion approach. They determined that the wave loading and elevations exerted on the inner cylinder were significantly reduced by the outer porous cylinder. Teng et al. [6] investigated the interaction between waves and a cylinder with an upper porous outer wall and an inner solid column. Konispoliatis et al. [7] presented a theoretical investigation of the second-order steady horizontal and vertical drift forces acting on a vertical porous cylindrical body which is exposed to the action of regular plane waves propagating in finite depth waters. The typical concentric cylindrical structure was later investigated under different types of incident waves. The interactions between such structures and different types of waves, such as solitary waves [8,9], short-crested waves [10], and cnoidal waves [11,12], have been studied by several researchers. Additionally, many studies have focused on the modification of concentric cylindrical structures to develop a concentric dual-arc structure [13], truncated cylinder with an upper porous cylinder [14], or floating compound porous cylinder [15]. The wave interaction with a group of dual porous cylinders consisting of an outer porous cylinder that protects an impermeable inner cylinder is investigated using the eigenfunction expansion approach by Sankarbabu et al. [16]. Using the 3D numerical analysis method and eigenfunction expansion method, Park et al. [17] evaluated the wave forces acting on the array of dual cylindrical cylinders with partial porous area, which consist of an impermeable inner cylinder and a porous outer cylinder. Dokken et al. [18,19] performed a mathematical analysis of the linear wave diffraction–radiation problem of a porous geometry localized in the surface of a inviscid fluid. Recently, Mackay et al. [20] proposed a boundary element method model for calculating wave forces on structures composed of solid and porous surfaces, where the porous surface can be subject to either a linear or quadratic pressure–velocity relation.

In addition to situations involving one or more cylinders, there are various offshore structures such as pier columns close to ports, for which it is necessary to predict hydrodynamic performance in water near coastlines or docks. The existence of side walls strongly influences the wave diffraction performance of coastal structures and causes their hydrodynamic loads to differ from those in unbounded water [21]. Green’s function mapping method has been used to solve the interactions of waves with structures near a wall. Several scholars have established analytical programs for the boundary element method based on this mapping method [22]. However, the boundary element method is computationally expensive, and there are multiple solutions in the case of high-frequency problems. To avoid the issues associated with the boundary element method, Teng and Ning [23] converted the problem of wave diffraction around an impermeable cylinder near a wall into an issue of two-directional incident wave interaction with two cylinders via image theory. Subsequently, Teng et al. [24] used the same method to analyze wave radiation around a solid cylinder near a wall. Furthermore, Ning et al. [25] extended the work by Teng and Ning [23] by discussing the interactions of waves with a solid cylinder in front of an orthogonal vertical wall and an analytical solution was obtained. A set of truncated cylinders arranged parallel to a plane wall was investigated by Mavrakos et al. [26]. Zheng and Zhang [21,27] solved the diffraction and radiation problems for near-wall truncated cylinders and provided a theoretical solution. Recently, Chatjigeorgiou [28] addressed the issue of water wave diffraction by a cylindrical array in front of a vertical wall. Konispoliatis et al. [29] investigated the phenomenon of regular waves interacting with cylindrical arrays in front of infinite-length and finite-length vertical breakwaters. Cong et al. [30,31] developed a novel analytical model to investigate the interactions between water waves and a permeable single cylinder near a wall, as well as a group of permeable cylinders near a wall. They evaluated both hydrodynamic loads and free-surface wave elevations. Konispoliatis [32] explored the performance of a set of cylindrical oscillating water column devices with a vertical axis of symmetry placed in front of a breakwater. Loukogeorgaki and Chatjigeorgiou [33,34] analyzed the hydrodynamic performance of a linear array of truncated circular cylinders in front of a vertical wall for investigating the effect of the wave reflections combined with the disturbances induced by the bodies themselves. Konispoliatis et al. [35] dealt with the analytical evaluation of the hydrodynamic characteristics of an array of vertical axisymmetric bodies of arbitrary shape, placed in front of a reflecting vertical breakwater, which can be conceived as floaters for wave power absorption. Based on research by many scholars, we have gained a deep understanding of the interactions between waves and structures in front of straight walls. However, research on the hydrodynamic performance of concentric structures in front of walls is still very limited. Considering that concentric structures are widely applied in engineering facilities in ocean engineering, it is necessary to study their performance.

In this study, an analytical method was developed for water wave diffraction around a concentric cylindrical structure near a vertical wall. This problem was transformed into an equivalent issue of bi-directional incident waves’ interaction with two concentric cylindrical structures via image theory. Additionally, an analytical solution was obtained through eigenfunction expansion combined with a matching technique and Graf’s addition theorem. Accordingly, the free-surface wave elevations and hydrodynamic loads under various conditions were analyzed in detail, which can provide information that is useful for the design of coastal porous structures subjected to hydrodynamics.

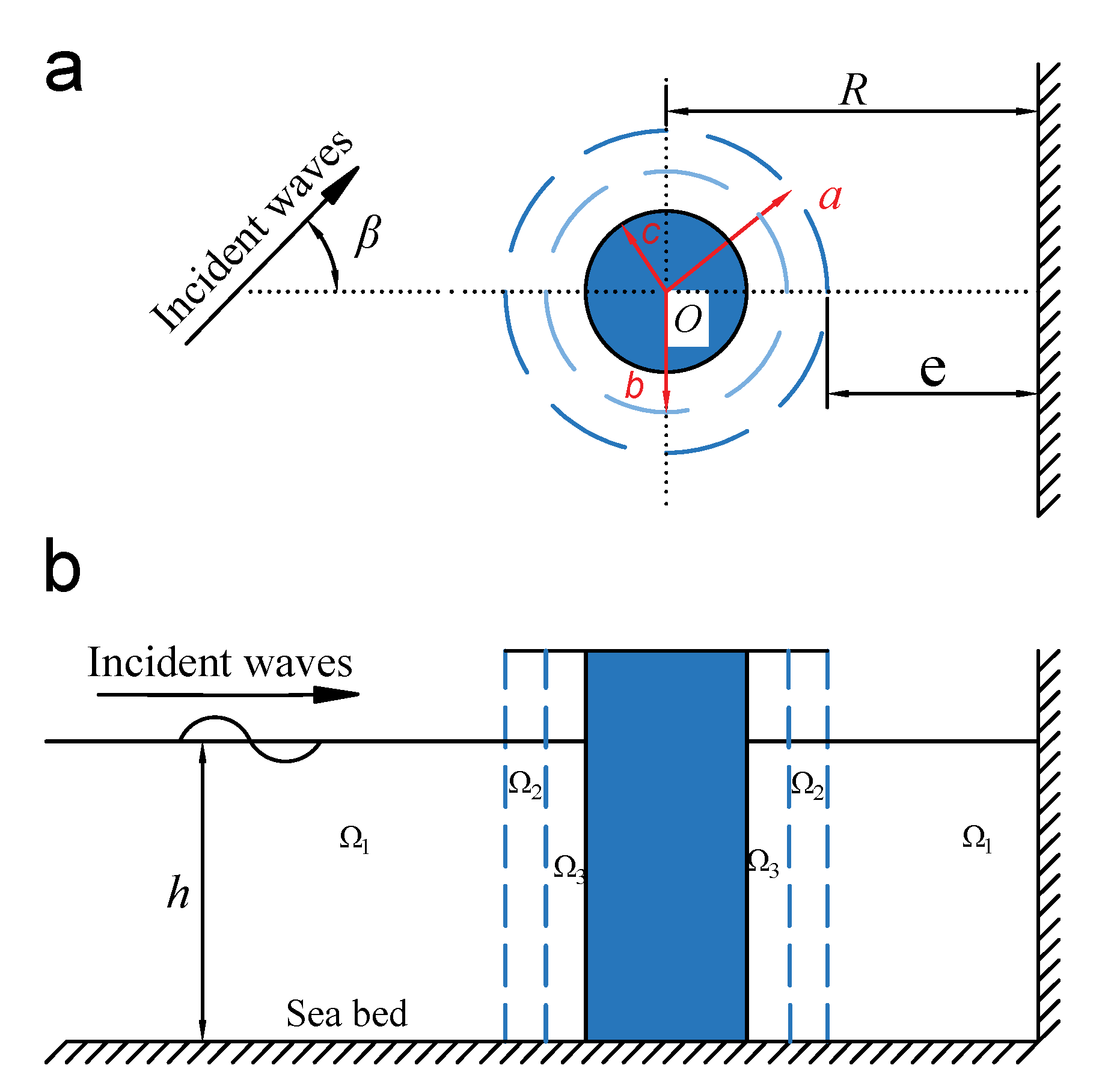
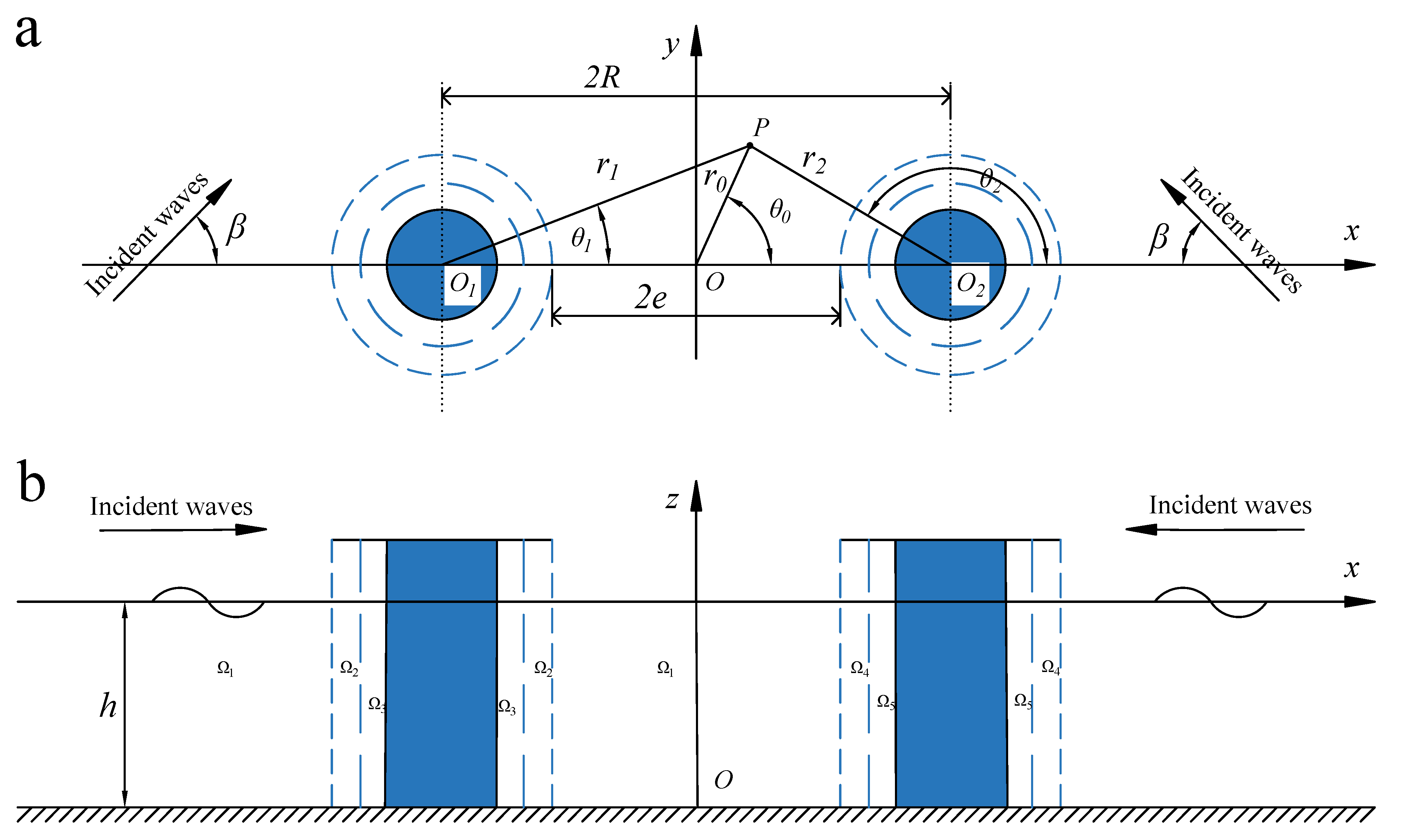
2. Formulation

A concentric porous structure near a wall is considered, as shown in Figure 1. The thickness of the outer cylinder is sufficiently small to be considered as negligible relative to the incident wavelength. A structure formed by three concentric cylinders with radii of a, b and c, is rigidly fixed in water with a depth h. The minimum distance between concentric structure center and wall is R, and $e=R-a$. Assuming that the wall is infinitely long and completely reflective, the present problem can be converted into bi-directional incident wave diffraction around two concentric structures based on the imaging theory [23], as shown in Figure 2. A Cartesian co-ordinate system $O-xyz$ is applied with the origin located at the middle of the two concentric cylindrical systems at the bottom of the water with its z-axis pointing upward. For the two concentric cylindrical systems, the two polar coordinates are $(O_p{r}_p{\theta }_{p}z,p=1,2)$, which are defined by origins located at $(-R,0,0)$ and $(R,0,0)$, respectively. By considering the outer porous cylinders of the two concentric systems as boundaries, the entire fluid domain can be divided into three subdomains, where ${\Omega }_1(r_p>a,0\le z\le h,p=1,2)$ is the region outside of the two structures, and ${\Omega }_2(b\le r_1\le a,0\le z\le h)$ and ${\Omega }_3(b\le r_1\le a,0\le z\le h)$ are the annular regions between the outer and middle cylinders of the left and right concentric cylindrical systems, respectively, ${\Omega }_4(c\le r_2\le b,0\le z\le h)$ and ${\Omega }_5(c\le r_2\le b,0\le z\le h)$ are the interior regions between the middle and inner cylinders of the left and right concentric cylindrical systems, respectively.

In the derivative process, the fluid is assumed to be incompressible and inviscid, and the motion of the fluid is considered irrotational. Then, the velocity potential can be written as $\Phi (x,y,z,t)=\mathrm{Re}\left[\varphi (x,y,z)e^{-iwt}\right]$, in which $\varphi$ is a time-independent velocity potential that satisfies the Laplace equation in every flow regions, $\mathrm{i}=\sqrt{-1}$. The three-dimensional governing equation for fluid motion is

$$\frac{{\partial }^2{\varphi }^{\left(j\right)}}{\partial x^2}+\frac{{\partial }^2{\varphi }^{\left(j\right)}}{\partial y^2}+\frac{{\partial }^2{\varphi }^{\left(j\right)}}{\partial z^2}=0\mathrm{for}j=1,2,3,4,5$$

(1)

The complex velocity potential in each region ${\Omega }_j(j=1,2,3)$ can be written as

$${\varphi }^{\left(j\right)}={\varphi }_I+{\varphi }_S^{\left(j\right)}$$

(2)

where ${\varphi }_I$ and ${\varphi }_S^{\left(j\right)}$ denote the incident velocity potential and scattered velocity potential, respectively, both of which satisfy Equation (1). For two incident waves propagating along the $\beta$ and $\pi -\beta$ directions, the total incident velocity potential ${\varphi }_I$ can be written as [21]:

$${\varphi }_I=f\left(z\right)e^{ikysin\beta }[e^{ikxcos\beta }+e^{-ikxcos\beta }]$$

(3)

where $f\left(z\right)=-i\frac{gH}{2\omega }\frac{cosh\left(kz\right)}{cosh\left(kh\right)}$, g denotes the gravitational acceleration, and k denotes the wave number. The wave number k and the angular frequency $\omega$ keep the dispersion relationship as ${\omega }^2=gktanh\left(kh\right)$. Additionally, to illustrate the ratio of the water depth to the wavelength, the wave parameter $C_w=\frac{g}{{\omega }^{2}h}$ is introduced [2,5,36].

These velocity potentials must also satisfy the free-surface and water-bottom boundary conditions, meaning

$$\frac{\partial {\varphi }^{\left(j\right)}}{\partial z}-\frac{{\omega }^2}{g}{\varphi }^{\left(j\right)}=0\mathrm{for}z=h,j=1,2,3,4,5$$

(4)

$$\frac{\partial {\varphi }^{\left(j\right)}}{\partial z}=0\mathrm{for}z=0,j=1,2,3,4,5$$

(5)

Normal velocity of the impermeable inner column surface is zero yield

$$\frac{\partial {\varphi }^{\left(j\right)}}{\partial r_p}=0\mathrm{for}{r}_p=c,j=3,5,p=1,2$$

(6)

The boundary condition for a permeable outer cylinder can be written as [2,37,38]

$$\frac{\partial {\varphi }^{\left(1\right)}}{\partial r_1}=\frac{\partial {\varphi }^{\left(2\right)}}{\partial r_1}=ik{G}_1({\varphi }^{\left(2\right)}-{\varphi }^{\left(1\right)})\mathrm{for}{r}_1=a$$

(7)

$$\frac{\partial {\varphi }^{\left(1\right)}}{\partial r_2}=\frac{\partial {\varphi }^{\left(4\right)}}{\partial r_2}=ik{G}_2({\varphi }^{\left(4\right)}-{\varphi }^{\left(1\right)})\mathrm{for}{r}_2=a$$

(8)

$$\frac{\partial {\varphi }^{\left(2\right)}}{\partial r_1}=\frac{\partial {\varphi }^{\left(3\right)}}{\partial r_1}=ik{G}_1({\varphi }^{\left(3\right)}-{\varphi }^{\left(2\right)})\mathrm{for}{r}_1=b$$

(9)

$$\frac{\partial {\varphi }^{\left(4\right)}}{\partial r_2}=\frac{\partial {\varphi }^{\left(5\right)}}{\partial r_2}=ik{G}_2({\varphi }^{\left(5\right)}-{\varphi }^{\left(4\right)})\mathrm{for}{r}_2=b$$

(10)

The term of $G_j=\frac{\rho \omega {\gamma }_j}{\mu k}(j=1,2)$ denotes the porous parameter, where $\rho$, $\mu$, and $\gamma$ denote the density of the fluid, constant coefficient of dynamic viscosity, and material constant, respectively. The porous parameter G can also be expressed as $G_r+i{G}_i$, where $G_r$ is the real part and $G_i$ is the imaginary part [39]. In general G is always a complex number except if the resistance to flow plays a dominant role in the inertial effects of the fluid inside the porous material, where G becomes real. Li et al. [40] demonstrated that $G_r$ dominates $G_i$. In this study, $G_i$ is assumed to be equal to zero, as discussed by Wang and Ren [5]. Additionally, the porous cylinder becomes an impermeable cylinder for $G_j=0$, whereas for $G_j\to \infty$, the exterior structure vanishes [41].

Finally, the scattered waves from the exterior region must meet the conditions for radiation at infinity, namely

$$\underset{r_0\to \infty }{lim}\sqrt{r_0}[\frac{\partial {\varphi }_S^{\left(1\right)}}{\partial r_0}-ik{\varphi }_S^{\left(1\right)}]=0$$

(11)

3. Analytical Solutions

The complex velocity potential of each subdomain is represented by an orthogonal series based on the a separation of variables.

In Region $j(j=2,4)$, the complex velocity potentials satisfying Equation (4), (5), (7) and (9) can be written in their respective coordinate systems by using eigenfunction expansion as follows:

$${\varphi }^{\left(j\right)}=f\left(z\right)\sum _{n=-\infty }^{\infty }[B_n^{\left(j\right)}{J}_n\left(k{r}_j\right)+D_n^{\left(j\right)}{H}_n^{\left(1\right)}\left(k{r}_j\right)]e^{in{\theta }_j}\mathrm{for}j=2,4,b_j\le r_j\le a_j$$

(12)

where $B_n^{\left(j\right)}$ and $D_n^{\left(j\right)}$ are the unknown coefficients, $J_n\left(\right)$ is the first kind of Bessel function of order n, and $H_n^{\left(1\right)}\left(\right)$ denotes the Hankel function of the first kind of order n.

In Region $j(j=3,5)$, the complex velocity potentials satisfying Equations (4)–(6), (8) and (10) can be written in their respective coordinate systems by using eigenfunction expansion as follows:

$${\varphi }^{\left(j\right)}=f\left(z\right)\sum _{n=-\infty }^{\infty }\left[E_n^{\left(j\right)}{U}_n\left(k{r}_j\right)\right]e^{in{\theta }_j}\mathrm{for}j=3,5,c_j\le r_j\le b_j$$

(13)

where

$$U_n\left(kr\right)=\left\{\begin{array}{c}{J}_n\left(kr\right)-\frac{J_n^{\prime }\left(kc\right)}{H_n^{\left(1\right)\prime }\left(kc\right)}{H}_n^{\left(1\right)}\left(kr\right)\mathrm{for}c\ne 0\hfill \\ J_n\left(kr\right)\mathrm{for}c=0\hfill \end{array}\right.$$

(14)

and $E_n^{\left(j\right)}$ is the unknown coefficients.

In Region 1, the complex velocity potential satisfying Equations (4), (5), (7) and (8) can be decomposed into a summation of two concentric systems with diffracted velocity potentials in the exterior domain as follows:

$$\begin{array}{c}\hfill {\varphi }^{\left(1\right)}=f\left(z\right)\sum _{n=-\infty }^{\infty }[J_n\left(k{r}_j\right)e^{in({\theta }_j-\beta +\pi /2)}{e}^{ik{r}_{0j}cos({\theta }_{0j}-\beta )}+J_n\left(k{r}_j\right)e^{in({\theta }_j+\beta -\pi /2)}{e}^{ik{r}_{0j}cos({\theta }_{0j}-\pi +\beta )}\\ \hfill +\sum _{f=1}^2{A}_n^{\left(f\right)}{C}_n^{\left(f\right)}{H}_n^{\left(1\right)}\left(k{r}_f\right)e^{in{\theta }_f}]\mathrm{for}f,j=1,2,f\ne j\end{array}$$

(15)

where $A_n^{\left(f\right)}$ denotes the unknown coefficients to be determined, and ${\theta }_{01}=\pi$, ${\theta }_{02}=0$, $C_n^{\left(f\right)}=\frac{J_n^{\prime }\left(k{a}_f\right)}{H_n^{\left(1\right)\prime }\left(k{a}_f\right)}$, $a_f$ is the radius of the corresponding cylinder f.

In Equation (10), the waves stemming from the two concentric cylindrical structures are represented by their own local polar coordinate systems. To express the velocity potentials in these local coordinate systems, the Graf’s addition theorem for Bessel functions is applied as [42] :

$$\begin{array}{c}\hfill H_n^{\left(1\right)}\left(k{r}_f\right)e^{in{\theta }_f}=\sum _{m=-\infty }^{\infty }{H}_{n+m}^{\left(1\right)}\left(k{r}_{jf}\right)J_m\left(k{r}_j\right)e^{im({\theta }_{jf}-{\theta }_j)+in{\theta }_{fj}}\mathrm{for}{a}_j\le r_j<r_{jf}\end{array}$$

(16)

where ${\theta }_{fj}$ (${\theta }_{12}=0$, ${\theta }_{21}=\pi$) is the angle between the x-axis and the vector from the center of the structure f to j.

By substituting Equation $\left(16\right)$ into Equation $\left(15\right)$, ${\varphi }^{\left(1\right)}$ can be rewritten as

$$\begin{array}{c}\hfill {\varphi }^{\left(1\right)}=f\left(z\right)\sum _{n=-\infty }^{\infty }[I^{\left(j\right)}{J}_n\left(k{r}_j\right)e^{in(\pi /2-\beta )}{e}^{in{\theta }_j}+{\widehat{I}}^{\left(j\right)}{J}_n\left(k{r}_j\right)e^{in(\beta -\pi /2)}{e}^{in{\theta }_j}+A_n^{\left(j\right)}{C}_n^{\left(j\right)}{H}_n^{\left(1\right)}\left(k{r}_j\right)e^{in{\theta }_j}\\ \hfill +\sum _{f=1}^2\sum _{m=-\infty }^{\infty }{A}_n^{\left(f\right)}{C}_n^{\left(f\right)}{H}_{n-m}^{\left(1\right)}\left(k{r}_{jf}\right)J_m\left(k{r}_j\right)e^{im{\theta }_j+i(n-m){\theta }_{fj}}]\\ \hfill \mathrm{for}f,j=1,2,f\ne j,a_j\le r_j<2r_{jf}\end{array}$$

(17)

where $I^{\left(j\right)}=e^{ik{r}_{0j}cos({\theta }_{0j}-\beta )}$, ${\widehat{I}}^{\left(j\right)}=e^{ik{r}_{0j}cos({\theta }_{0j}-\pi +\beta )}$ and $C_n^{\left(f\right)}=C_n^{\left(j\right)}=\frac{J_n^{\prime }\left(ka\right)}{H_n^{\prime }\left(ka\right)}$.

Substituting Equations $\left(12\right)$, $\left(13\right)$ and $\left(17\right)$ into the boundary condition of the porous cylinder Equations (7)–(10) yields

$$\begin{array}{c}\hfill A_n^{\left(j\right)}-B_n^{\left(j\right)}-M_n^{\left(j\right)}{D}_n^{\left(j\right)}+\sum _{f=1}^2\sum _{m=-\infty }^{\infty }{A}_m^{\left(f\right)}{C}_m^{\left(f\right)}{H}_{m-n}^{\left(1\right)}\left(k{r}_{jf}\right)e^{i(m-n){\theta }_{fj}}\\ \hfill =-I^{\left(j\right)}{e}^{in(\pi /2-\beta )}-{\widehat{I}}^{\left(j\right)}{e}^{in(\beta -\pi /2)}\end{array}$$

(18)

$$\begin{array}{c}\hfill B_n^{\left(j\right)}[N_n^{\left(j\right)}-\mathrm{i}{G}_1]+D_n^{\left(j\right)}[Q_n^{\left(j\right)}-\mathrm{i}{G}_1{P}_n^{\left(j\right)}]+\mathrm{i}{G}_1{A}_n^{\left(j\right)}{C}_n^{\left(j\right)}{P}_n^{\left(j\right)}\\ \hfill +\sum _{f=1}^2\sum _{m=-\infty }^{\infty }\mathrm{i}{G}_1{A}_m^{\left(f\right)}{C}_m^{\left(f\right)}{H}_{m-n}^{\left(1\right)}\left(k{r}_{jf}\right)e^{i(m-n){\theta }_{fj}}\\ \hfill =-\mathrm{i}{G}_1{I}^{\left(j\right)}{e}^{in(\pi /2-\beta )}-\mathrm{i}{G}_1{\widehat{I}}^{\left(j\right)}{e}^{in(\beta -\pi /2)}\end{array}$$

(19)

$$\begin{array}{c}\hfill B_n^{\left(j\right)}{J}_n^{\prime }\left(k{b}_j\right)+D_n^{\left(j\right)}{H}_n^{\left(1\right)\prime }\left(k{b}_j\right)-E_n^{\left(j\right)}{U}_n^{\prime }\left(k{b}_j\right)=0\end{array}$$

(20)

$$\begin{array}{c}\hfill \mathrm{i}{G}_2{B}_n^{\left(j\right)}{J}_n\left(k{b}_j\right)+\mathrm{i}{G}_2{D}_n^{\left(j\right)}{H}_n^{\left(1\right)}\left(k{b}_j\right)+E_n^{\left(j\right)}[U_n^{\prime }\left(k{b}_j\right)-\mathrm{i}{G}_2{U}_n\left(k{b}_j\right)]=0\end{array}$$

(21)

where $M_n^{\left(j\right)}=H_n^{\left(1\right)\prime }\left(k{a}_j\right)/J_n^{\prime }\left(k{a}_j\right)$, $N_n^{\left(j\right)}=J_n^{\prime }\left(k{a}_j\right)/J_n\left(k{a}_j\right)$, $P_n^{\left(j\right)}=H_n^{\left(1\right)}\left(k{a}_j\right)/J_n\left(k{a}_j\right)$, $Q_n^{\left(j\right)}=H_n^{\left(1\right)\prime }\left(k{a}_j\right)/J_n\left(k{a}_j\right)$.

The Equations (18)–(21) are a complete set of equations with the unknown coefficients $A_n^{\left(1\right)},A_n^{\left(2\right)}$, $B_n^{\left(1\right)},B_n^{\left(2\right)}$, $D_n^{\left(1\right)},D_n^{\left(2\right)}$, $E_n^{\left(1\right)}$ and $E_n^{\left(2\right)}$ for the entire fluid domain. The series are truncated after N terms, and n lies between 0 and N. Previous studies have reported excellent convergence achieved by truncating the expansion series after finite terms (e.g., $N=20$). Therefore, the unknown coefficients can be obtained efficiently by considering only a few truncated terms. The hydrodynamic force, overturning moment, and free-surface elevation can subsequently be determined for engineering applications.

For the real concentric system, the free-surface elevation $\eta$ of water waves can be written as

$$\begin{array}{c}\hfill {\eta }^{\left(j\right)}=-\frac{1}{g}\frac{\partial {\varphi }^{\left(j\right)}}{\partial t}\mathrm{for}z=h,j=1,2,3\end{array}$$

(22)

where ${\eta }^{\left(j\right)}$ represents the wave elevation in region ${\Omega }_j(j=1,2,3)$.

$$\begin{array}{c}\hfill {\eta }^{\left(1\right)}=\frac{H}{2}\sum _{n=-\infty }^{\infty }[I^{\left(j\right)}{J}_n\left(k{r}_j\right)e^{in({\theta }_j-\beta +\pi /2)}+{\widehat{I}}^{\left(j\right)}{J}_n\left(k{r}_j\right)e^{in({\theta }_j+\beta -\pi /2)}\\ \hfill +\sum _{f=1}^2{A}_n^{\left(f\right)}{C}_n^{\left(f\right)}{H}_n^{\left(1\right)}\left(k{r}_f\right)e^{in{\theta }_f}]\end{array}$$

(23)

$$\begin{array}{c}\hfill {\eta }^{\left(2\right)}=\frac{H}{2}\sum _{n=-\infty }^{\infty }[B_n^{\left(1\right)}{J}_n\left(k{r}_1\right)+D_n^{\left(1\right)}{H}_n^{\left(1\right)}\left(k{r}_1\right)]e^{in{\theta }_1}\end{array}$$

(24)

$$\begin{array}{c}\hfill {\eta }^{\left(3\right)}=\frac{H}{2}\sum _{n=-\infty }^{\infty }\left[E_n^{\left(1\right)}{U}_n\left(k{r}_1\right)\right]e^{in{\theta }_1}\end{array}$$

(25)

For the real concentric system, based on the linearized Bernoulli equation, the complex velocity potentials in the three regions ${\varphi }^{\left(j\right)}(j=1,2,3)$ can be substituted into the hydrodynamic pressure formula, and the pressure distribution of the wave field is calculated as

$$P^{\left(j\right)}=-\rho \frac{\partial {\varphi }^{\left(j\right)}}{\partial t}\mathrm{for}j=1,2,3$$

(26)

The hydrodynamic forces acting on the two cylinders along the two orthogonal directions in the horizontal plane $f_{1x},f_{1y},f_{2x}$ and $f_{2y}$ can be obtained by integrating the pressure as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{f}_{1x}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}({\varphi }^{\left(1\right)}-{\varphi }^{\left(2\right)}){\mid }_{r_1=a}acos{\theta }_1\mathrm{d}{\theta }_1\hfill \\ f_{1y}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}({\varphi }^{\left(1\right)}-{\varphi }^{\left(2\right)}){\mid }_{r_1=a}asin{\theta }_1\mathrm{d}{\theta }_1\hfill \\ f_{2x}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}{\varphi }^{\left(2\right)}-{\varphi }^{\left(3\right)}{\mid }_{r_1=b}bcos{\theta }_1\mathrm{d}{\theta }_1\hfill \\ f_{2y}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}{\varphi }^{\left(2\right)}-{\varphi }^{\left(3\right)}{\mid }_{r_1=b}bsin{\theta }_1\mathrm{d}{\theta }_1\hfill \\ f_{3x}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}{\varphi }^{\left(3\right)}{\mid }_{r_1=c}ccos{\theta }_1\mathrm{d}{\theta }_1\hfill \\ f_{3y}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}{\varphi }^{\left(3\right)}{\mid }_{r_1=c}csin{\theta }_1\mathrm{d}{\theta }_1\hfill \end{array}\right.\end{array}$$

(27)

in which,

$$\left\{\begin{array}{c}{f}_{1x}=\left(\rho g\pi (H/2)ah\right)\frac{(-e^{-i\omega t})tanh\left(kh\right)}{kh}\{(A_{-1}^{\left(1\right)}-A_1^{\left(1\right)})J_1\left(ka\right)+(D_1^1-D_{-1}^1)M_1^1{J}_1\left(ka\right)\hfill \\ +(A_1^{\left(1\right)}-A_{-1}^{\left(1\right)})C_1^{\left(1\right))}{H}_1^{\left(1\right)}\left(ka\right)+(D_{-1}^{\left(1\right)}-D_1^{\left(1\right)})H_1^{\left(1\right)}\left(ka\right)\}\hfill \\ f_{1y}=\left(\rho g\pi (H/2)ah\right)\frac{(-i{e}^{-i\omega t})tanh\left(kh\right)}{kh}\{-(A_1^{\left(1\right)}+A_{-1}^{\left(1\right)})J_1\left(ka\right)+(D_1^{\left(1\right)}+D_{-1}^{\left(1\right)})M_1^{\left(1\right)}{J}_1\left(ka\right)\hfill \\ +(A_1^{\left(1\right)}+A_{-1}^{\left(1\right)})C_1^{\left(1\right)}{H}_1^{\left(1\right)}\left(ka\right)-(D_1^{\left(1\right)}+D_{-1}^{\left(1\right)})H_1^{\left(1\right)}\left(ka\right)\}\hfill \\ f_{2x}=\left(\rho g\pi (H/2)bh\right)\frac{(-e^{-i\omega t})tanh\left(kh\right)}{kh}[(B_1^{\left(1\right)}-B_{-1}^{\left(1\right)})J_1\left(kb\right)+(D_1^{\left(1\right)}-D_{-1}^{\left(1\right)})H_1^{\left(1\right)}\left(kb\right)\hfill \\ -(E_1^{\left(1\right)}-E_{-1}^{\left(1\right)})U_1\left(kb\right)]\hfill \\ f_{2y}=\left(\rho g\pi (H/2)bh\right)\frac{(-e^{-i\omega t})tanh\left(kh\right)}{kh}[(B_1^{\left(1\right)}+B_{-1}^{\left(1\right)})J_1\left(kb\right)+(D_1^{\left(1\right)}+D_{-1}^{\left(1\right)})H_1^{\left(1\right)}\left(kb\right)\hfill \\ -(E_1^{\left(1\right)}+E_{-1}^{\left(1\right)})U_1\left(kb\right)]\hfill \\ f_{3x}=\left(\rho g\pi (H/2)ch\right)\frac{(-e^{-i\omega t})tanh\left(kh\right)}{kh}(E_1^{\left(1\right)}-E_{-1}^{\left(1\right)})U_1\left(kc\right)\hfill \\ f_{3y}=\left(\rho g\pi (H/2)ch\right)\frac{(-e^{-i\omega t})tanh\left(kh\right)}{kh}(E_1^{\left(1\right)}+E_{-1}^{\left(1\right)})U_1\left(kc\right)\hfill \end{array}\right.$$

(28)

Similarly, the overturning moments on the two cylinders along the two orthogonal directions in the horizontal plane $m_{1x},m_{1y},m_{2x}$ and $m_{2y}$, can be obtained as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{m}_{1x}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}z\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}({\varphi }^{\left(1\right)}-{\varphi }^{\left(2\right)}){\mid }_{r_1=a}acos{\theta }_1\mathrm{d}{\theta }_1\hfill \\ m_{1y}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}z\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}({\varphi }^{\left(1\right)}-{\varphi }^{\left(2\right)}){\mid }_{r_1=a}asin{\theta }_1\mathrm{d}{\theta }_1\hfill \\ m_{2x}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}z\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}({\varphi }^{\left(2\right)}-{\varphi }^{\left(3\right)}){\mid }_{r_1=b}bcos{\theta }_1\mathrm{d}{\theta }_1\hfill \\ m_{2y}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}z\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}({\varphi }^{\left(2\right)}-{\varphi }^{\left(3\right)}){\mid }_{r_1=b}bsin{\theta }_1\mathrm{d}{\theta }_1\hfill \\ m_{3x}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}z\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}{\varphi }^{\left(3\right)}{\mid }_{r_1=c}ccos{\theta }_1\mathrm{d}{\theta }_1\hfill \\ m_{3y}=-i\rho \omega e^{-i\omega t}\underset{0}{\overset{h}{\int }}z\mathrm{d}z\underset{0}{\overset{2\pi }{\int }}{\varphi }^{\left(3\right)}{\mid }_{r_1=c}csin{\theta }_1\mathrm{d}{\theta }_1\hfill \end{array}\right.\end{array}$$

(29)

in which,

$$\left\{\begin{array}{c}{m}_{1x}=\left(\rho g(H/2)a{h}^2\right)\frac{(-\pi e^{-i\omega t})}{{\left(kh\right)}^2}[khtanh\left(kh\right)-1+\frac{1}{cosh\left(kh\right)}][(A_{-1}^{\left(1\right)}-A_1^{\left(1\right)})J_1\left(ka\right)\hfill \\ +(D_1^1-D_{-1}^1)M_1^1{J}_1\left(ka\right)+(A_1^{\left(1\right)}-A_{-1}^{\left(1\right)})C_1^{\left(1\right))}{H}_1^{\left(1\right)}\left(ka\right)+(D_{-1}^{\left(1\right)}-D_1^{\left(1\right)})H_1^{\left(1\right)}\left(ka\right)]\hfill \\ m_{1y}=\left(\rho g(H/2)a{h}^2\right)\frac{(-i\pi e^{-i\omega t})}{{\left(kh\right)}^2}[khtanh\left(kh\right)-1+\frac{1}{cosh\left(kh\right)}][-(A_1^{\left(1\right)}+A_{-1}^{\left(1\right)})J_1\left(ka\right)\hfill \\ +(D_1^{\left(1\right)}+D_{-1}^{\left(1\right)})M_1^{\left(1\right)}{J}_1\left(ka\right)+(A_1^{\left(1\right)}+A_{-1}^{\left(1\right)})C_1^{\left(1\right)}{H}_1^{\left(1\right)}\left(ka\right)-(D_1^{\left(1\right)}+D_{-1}^{\left(1\right)})H_1^{\left(1\right)}\left(ka\right)]\hfill \\ m_{2x}=\left(\rho g(H/2)b{h}^2\right)\frac{(-2i{e}^{-i\omega t})}{\left(ka\right){\left(kh\right)}^2}[khtanh\left(kh\right)-1+\frac{1}{cosh\left(kh\right)}][(B_1^{\left(1\right)}-B_{-1}^{\left(1\right)})J_1\left(kb\right)\hfill \\ +(D_1^{\left(1\right)}-D_{-1}^{\left(1\right)})H_1^{\left(1\right)}\left(kb\right)-(E_1^{\left(1\right)}-E_{-1}^{\left(1\right)})U_1\left(kb\right)]\hfill \\ m_{2y}=\left(\rho g(H/2)b{h}^2\right)\frac{\left(2e^{-i\omega t}\right)}{\left(ka\right){\left(kh\right)}^2}[khtanh\left(kh\right)-1+\frac{1}{cosh\left(kh\right)}][(B_1^{\left(1\right)}+B_{-1}^{\left(1\right)})J_1\left(kb\right)\hfill \\ +(D_1^{\left(1\right)}+D_{-1}^{\left(1\right)})H_1^{\left(1\right)}\left(kb\right)-(E_1^{\left(1\right)}+E_{-1}^{\left(1\right)})U_1\left(kb\right)]\hfill \\ m_{3x}=\left(\rho g(H/2)b{h}^2\right)\frac{(-2i{e}^{-i\omega t})}{\left(ka\right){\left(kh\right)}^2}[khtanh\left(kh\right)-1+\frac{1}{cosh\left(kh\right)}](E_1^{\left(1\right)}-E_{-1}^{\left(1\right)})U_1\left(kc\right)\hfill \\ m_{3y}=\left(\rho g(H/2)b{h}^2\right)\frac{\left(2e^{-i\omega t}\right)}{\left(ka\right){\left(kh\right)}^2}[khtanh\left(kh\right)-1+\frac{1}{cosh\left(kh\right)}](E_1^{\left(1\right)}+E_{-1}^{\left(1\right)})U_1\left(kc\right)\hfill \end{array}\right.$$

(30)

The total wave forces and overturning moments acting on the outer ($i=1$), middle ($i=2$) and inner ($i=3$) cylinders can be expressed as

$$F_i=\sqrt{{\left(F_{ix}\right)}^2+{\left(F_{iy}\right)}^2},M_i=\sqrt{{\left(M_{ix}\right)}^2+{\left(M_{iy}\right)}^2}\mathrm{for}i=1,2,3$$

(31)

where,

$$F_{ix}=Re\left(f_{ix}\right),F_{iy}=Re\left(f_{iy}\right),M_{ix}=Re\left(m_{ix}\right),M_{iy}=Re\left(m_{iy}\right)\mathrm{for}i=1,2,3$$

(32)

For convenience, the factors $\rho gHah$, $\rho gHbh$ and $\rho gHch$ are used to make the hydrodynamic loads dimensionless. The maximum dimensionless hydrodynamic loads on the outer $F_O$, middle $F_M$ and inter $F_I$ structures are defined as

$$F_O=\frac{|F_1|}{\rho gHah},F_M=\frac{|F_2|}{\rho gHbh},F_I=\frac{|F_3|}{\rho gHch}$$

(33)

4. Results

To study the hydrodynamic characteristics of a concentric system near a vertical wall, a program was written in FORTRAN to implement the analytical solution described in the previous section. The factor H is used to make the wave elevation $\eta$ dimensionless. To gain a deeper understanding, we also considered the case of concentric systems located in unbounded water (UW). For this calculation, the radius of the outer cylinder was set to $a=10$ m and the wave height remained constant at $H=1$ m. This paper gives the mathematical formula of the interaction between waves and a concentric three-cylinder structure. However, the concentric two-cylinder structures are prevalently used in coastal and ocean engineering; for instance, the successful application of a dual cylindrical breakwater in the Nagashima Port, Japan and the Ekofish gravity offshore structure in the North Sea [10]. Thus, this paper mainly uses the following parameters to study the interaction between water waves and the concentric structure, i.e., $G_1=1$, $G_2\to \infty$ (in the practical calculation, $G=1000$ is applied).

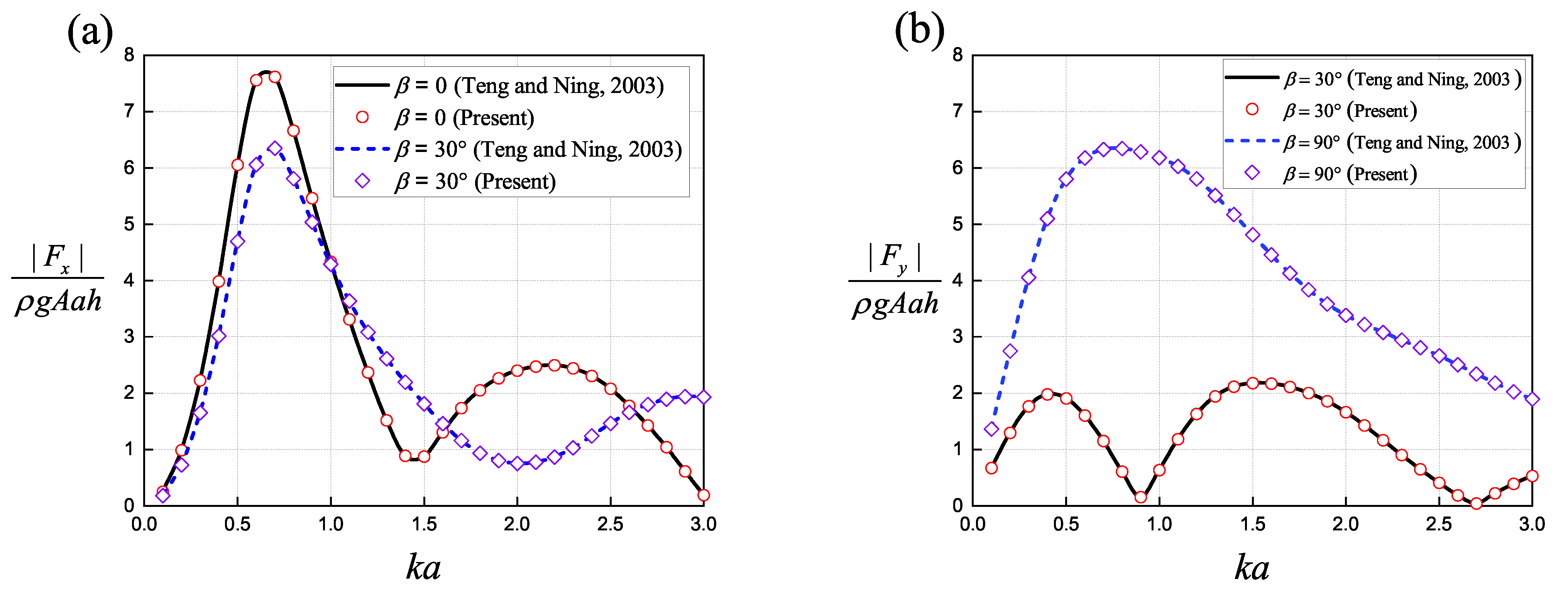
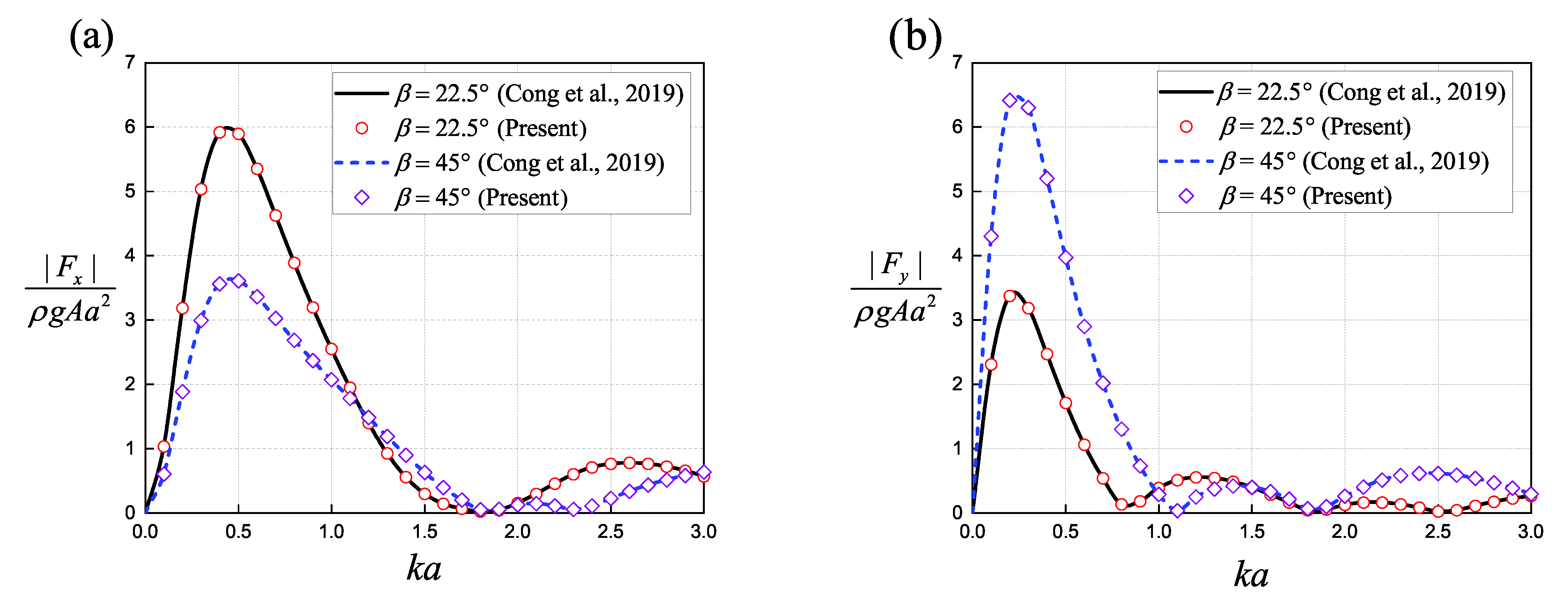
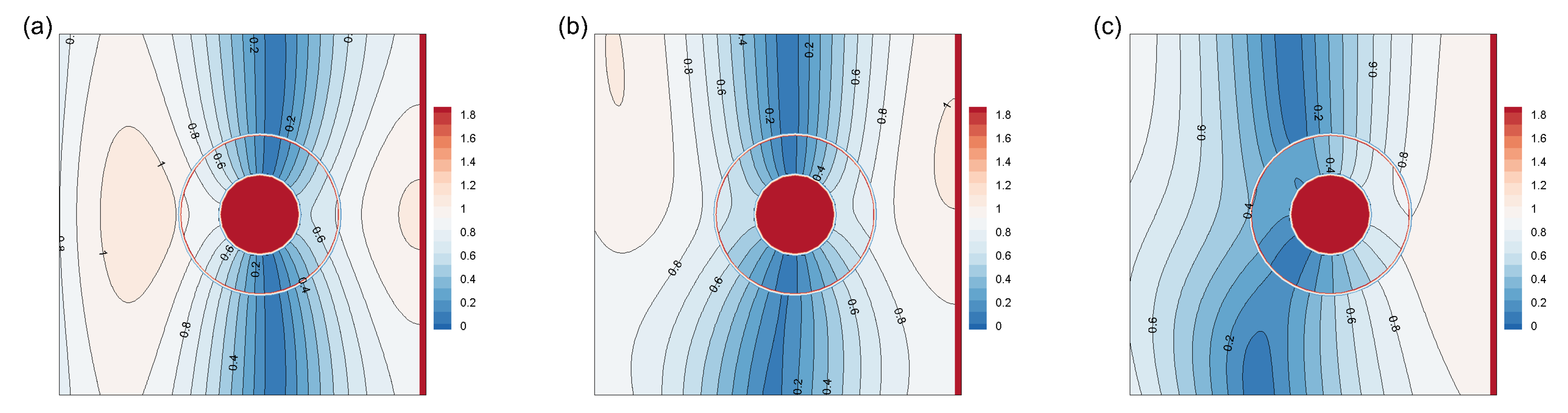
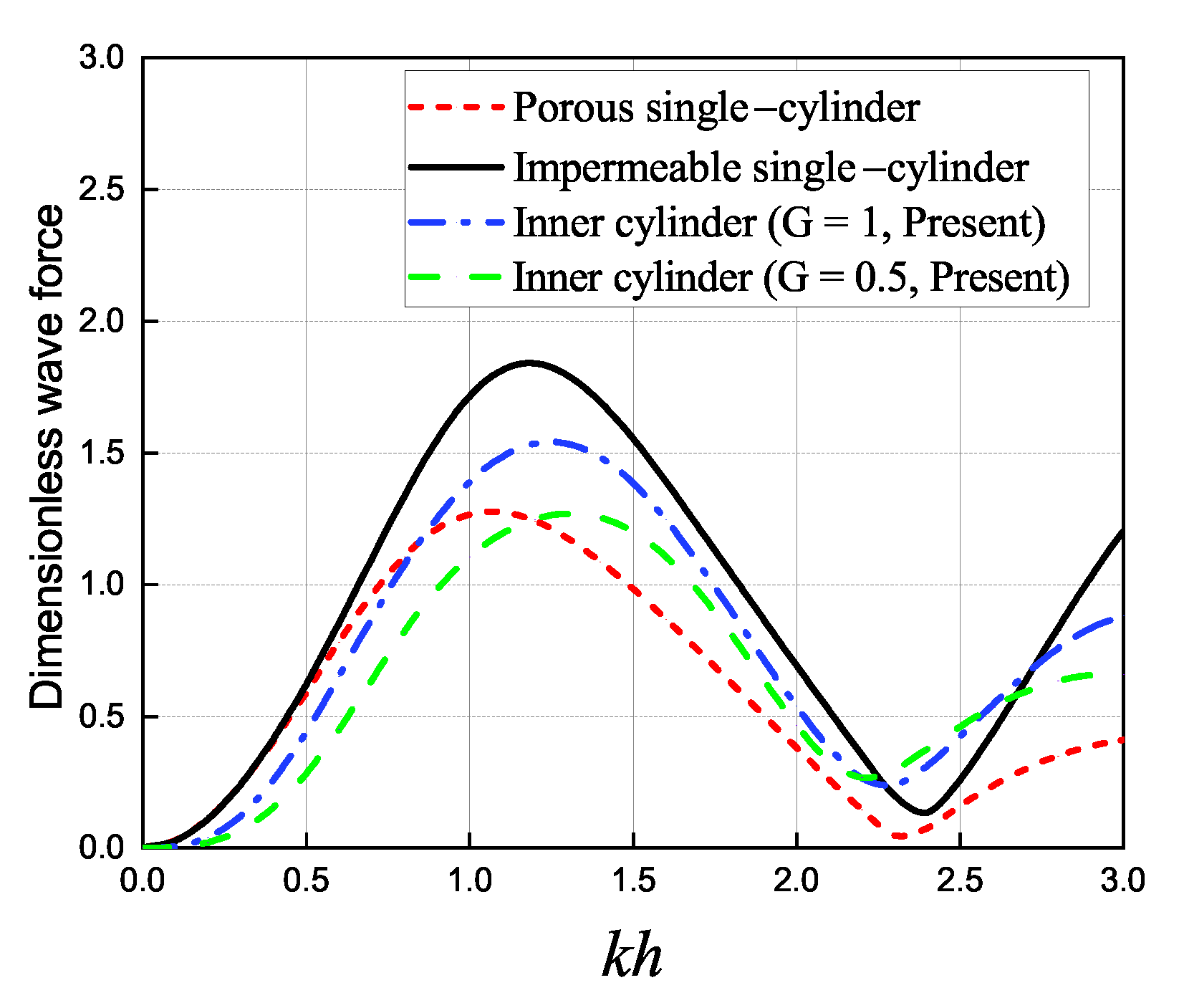
4.1. Model Validation

The validity of the proposed method was verified by comparing our results to the numerical results presented by Teng and Ning [23] and Cong et al. [30]. When the porous parameter $G_1=0$, the concentric system becomes an impermeable cylinder, as discussed by Teng and Ning [23]. Figure 3 presents a comparison of the hydrodynamic loads on a solid cylinder near a wall derived by our method and by Teng and Ning [23] for $h/a=1$, $G_1=0$, and $e/a=1$. One can see good agreement between these results. When $b=c=0$ and the porous-effect parameter $G_1\ne 0$, the structure becomes a porous cylinder, as discussed by Cong et al. [30]. Figure 4 presents a comparison of the hydrodynamic loads on a porous cylinder near a wall derived by our method and by Cong et al. [30] for $b=c=0$, $h/a=5$, $G_1=1$, and $e/a=1$. One can see that the results are consistent, further validating the proposed method.

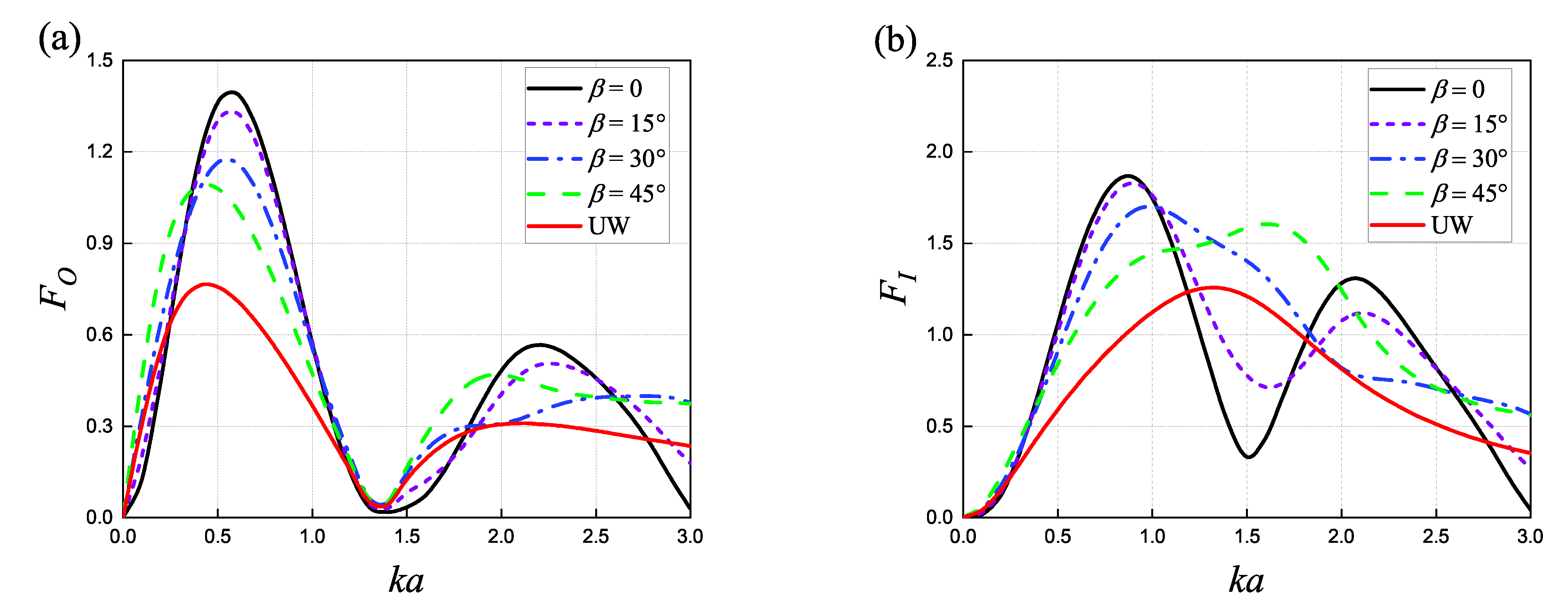
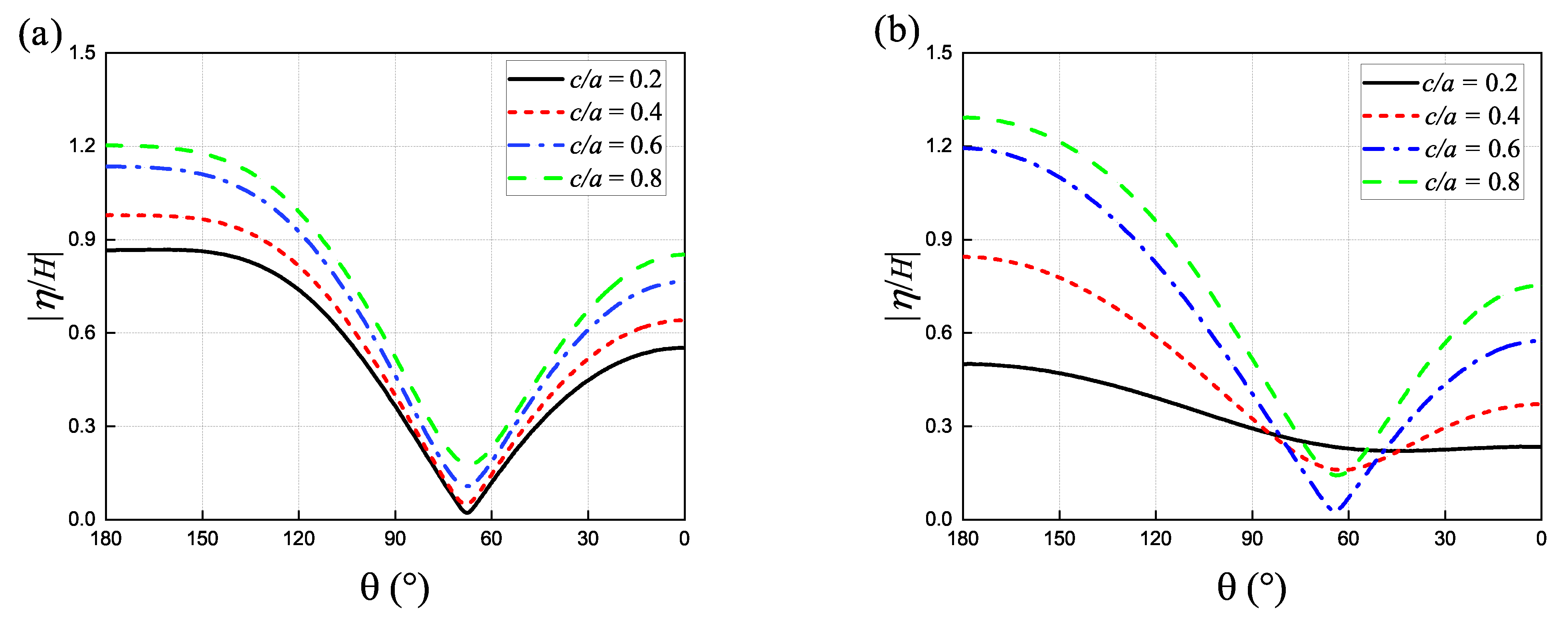
4.2. Influence of the Wave Incident Angle

Because the considered concentric structures are symmetrical, changes in the wave incident angle have no effect on the wave loads in the unbounded water area. However, the wave incident angle has a significant impact on wave forces and elevations in the presence of a vertical wall. Figure 5 presents the effect of the wave incident angle $\beta$ on the hydrodynamic loads on the system for $e/a=1,c/a=0.5$, $h/a=1.5$, and $G_1=1$. The wave incident angle was varied as $\beta =0,{15}^{\circ },{30}^{\circ }$, and ${45}^{\circ }$. One can see that when $ka<0.7$, the wave forces acting on the two cylinders increase as the wave number $ka$ increases and reach peak values in the low-frequency region. Additionally, the hydrodynamic loads on the outer and inner cylinders gradually decrease with an increasing $\beta$. An analogous phenomenon was observed by Teng and Ning [23] and Cong et al. [30] for wave diffraction by impermeable and permeable cylinders near a wall. Additionally, based on the presence of the wall, the wave loads acting on the exterior structure are significantly larger than those in the unbounded water. Based on the combined influence of the vertical wall and exterior porous cylinder, the variation in the forces acting on the interior impermeable structure is relatively complex.

Figure 6 presents the dimensionless wave elevation distribution around the system near the vertical wall for various incident angles $\beta$ with $C_w=0.8$, $G_1=1$, $c/a=0.5$, $e/a=1$, and $h/a=1.5$. When $\beta >0$, the symmetrical characteristics of the wave field are lost. Additionally, a slight increase in the wave run-up around the leeward side of the outer cylinder can be observed when $\beta ={45}^{\circ }$. In general, the porous structure provides a certain level of wave dissipation and reduces wave run-up, but reflected waves increase wave run-up on the leeward side of the outer cylinder. When the waves are obliquely incident, the elevation exhibits relatively complex variations. Additionally, a significant decrease in wave run-up around the windward sides of the two cylinders can be observed as $\beta$ increases. This is because the effects of the reflected waves on the system are weakened when the waves are obliquely incident.

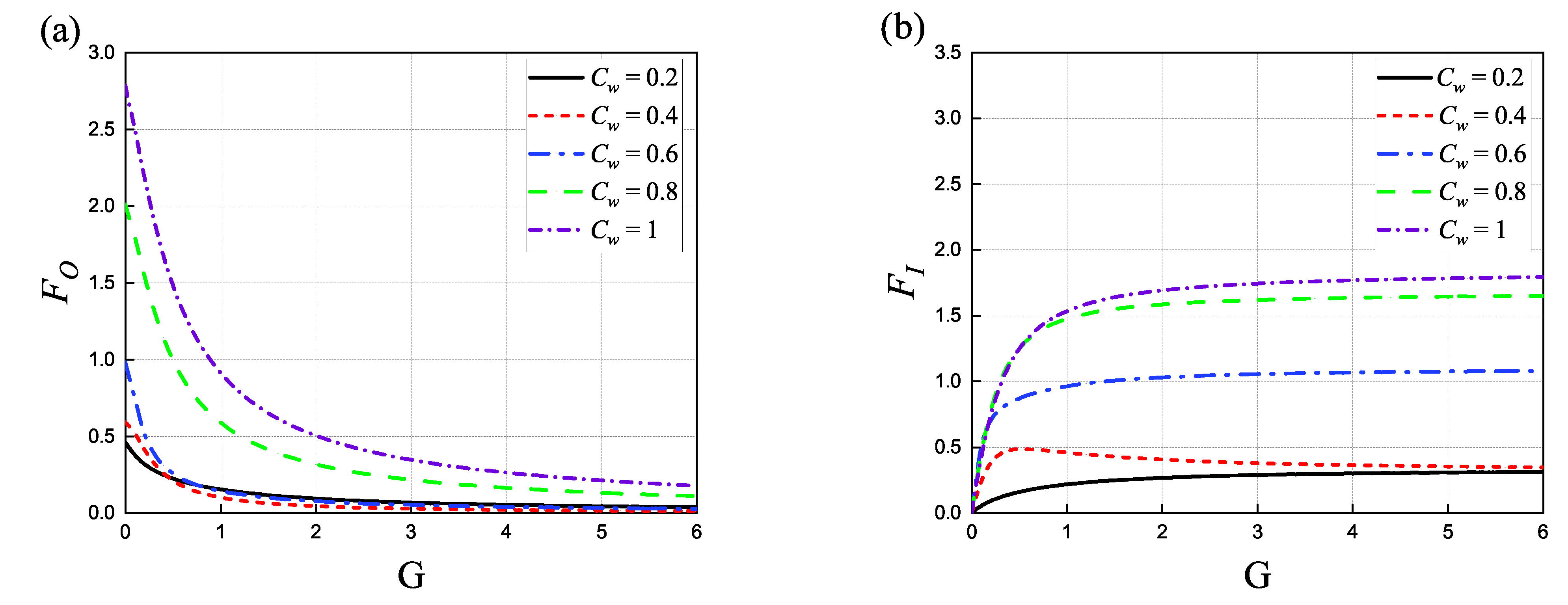
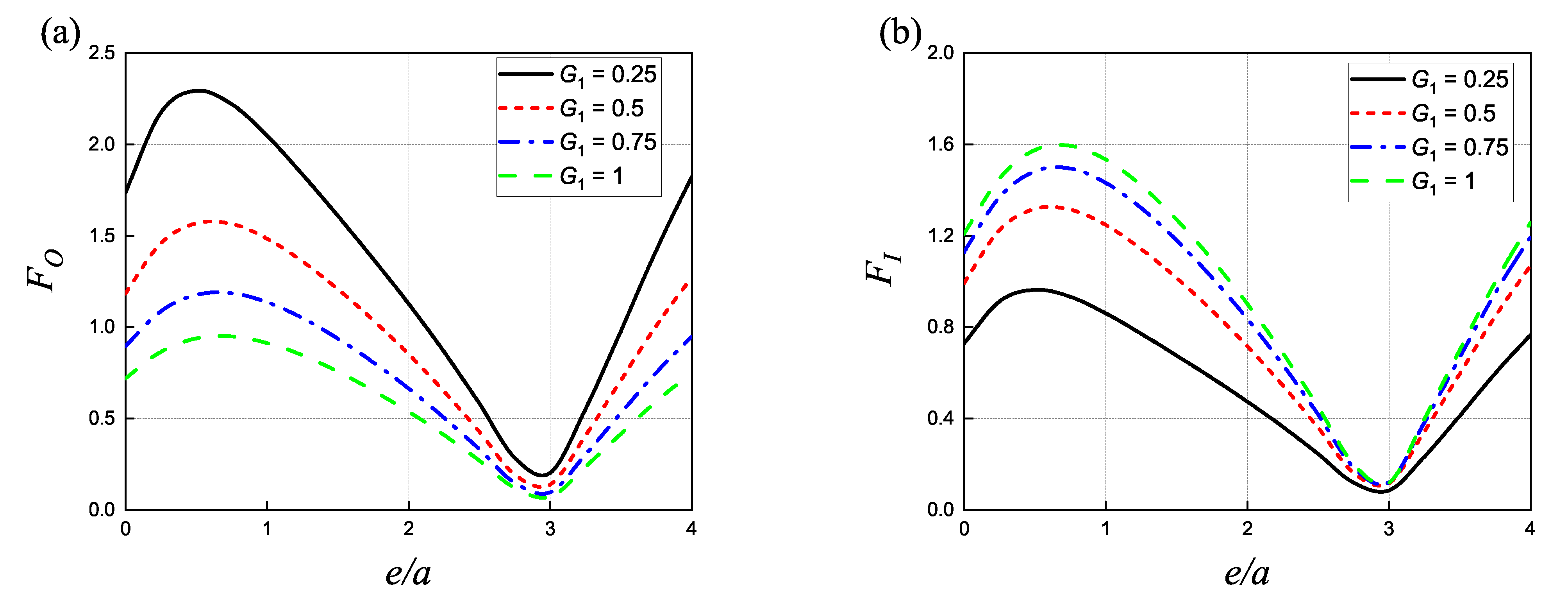
4.3. Influence of the Porous Parameter

The hydrodynamic loads on the two cylinders versus the porous parameter $G_1$ are presented in Figure 7 for different $C_w$ when $e/a=1$, $c/a=0.5$, $\beta =0$, and $h/a=1.5$. The wave forces acting on the outer cylinder decrease monotonically until they reach a minimum value, and then exhibit an almost constant value as G increases further. The loads on the impermeable inner cylinder increase monotonically toward their asymptotic value with an increasing value of $G_1$. Additionally, with an increasing $C_w$, the hydrodynamic loads on the inner layer gradually increase. In Figure 7b, one can also see that when $G_1<1$, the lower-frequency waves have a greater influence on the hydrodynamic loads on the porous outer cylinder compared to the higher-frequency waves.

Figure 8 presents the variations in the maximum wave run-up for different $G_1$ with $C_w=1$, $e/a=1$, $c/a=0.5$, $\beta =0$, and $h/a=1.5$. On the windward and leeward sides, the wave run-ups on the porous outer cylinder decrease, whereas those on the impermeable inner cylinder increase with an increasing $G_1$. This can be attributed to the increased wave propagation from the porous outer cylinder as the $G_1$ value increases, leading to increased direct wave action on the inner cylinder. Overall, the influence of $G_1$ plays a more important role in wave run-up on the impermeable inner cylinder than on the permeable outer cylinder. Additionally, the minimum run-up on the two cylinders occurs at approximately $\theta ={80}^{\circ }$. This may be related to the distance between the structure and the wall. The limitations attributed to the assumption of total wave reflection lead to a more pronounced influence of the incident wave on the structure.

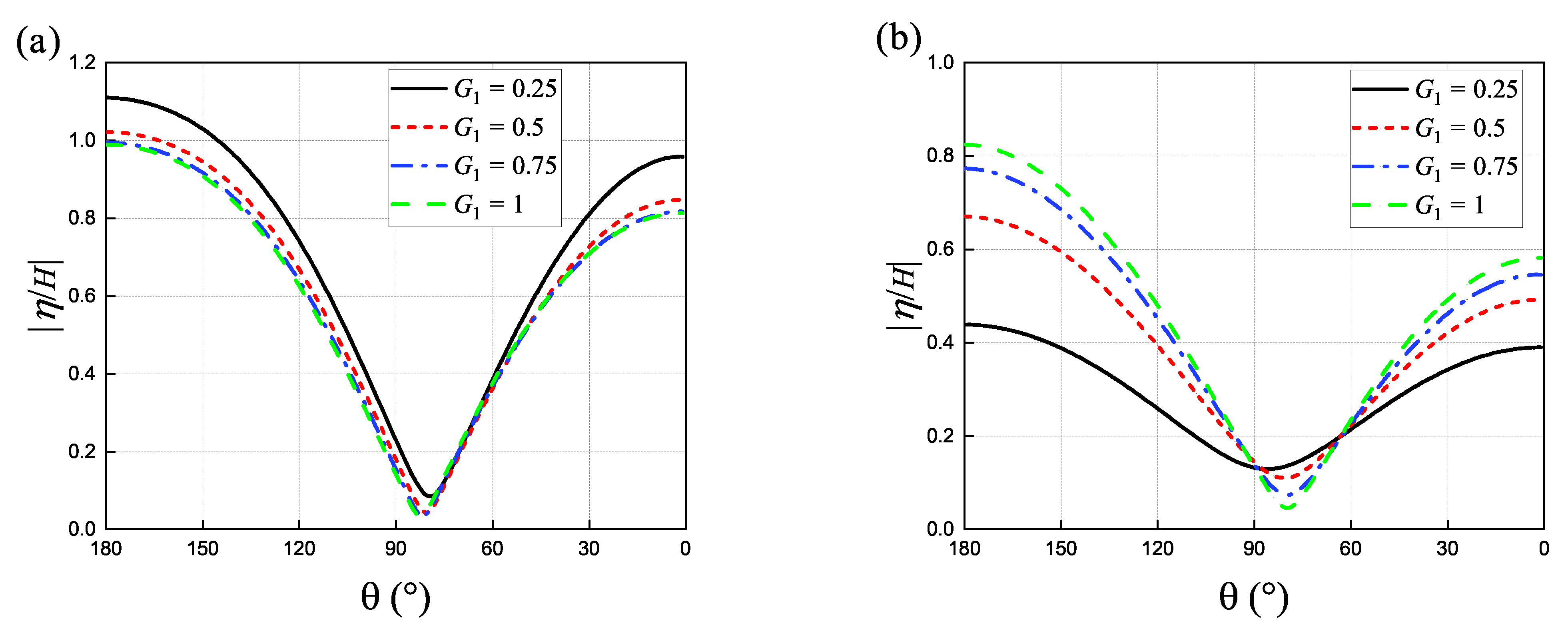
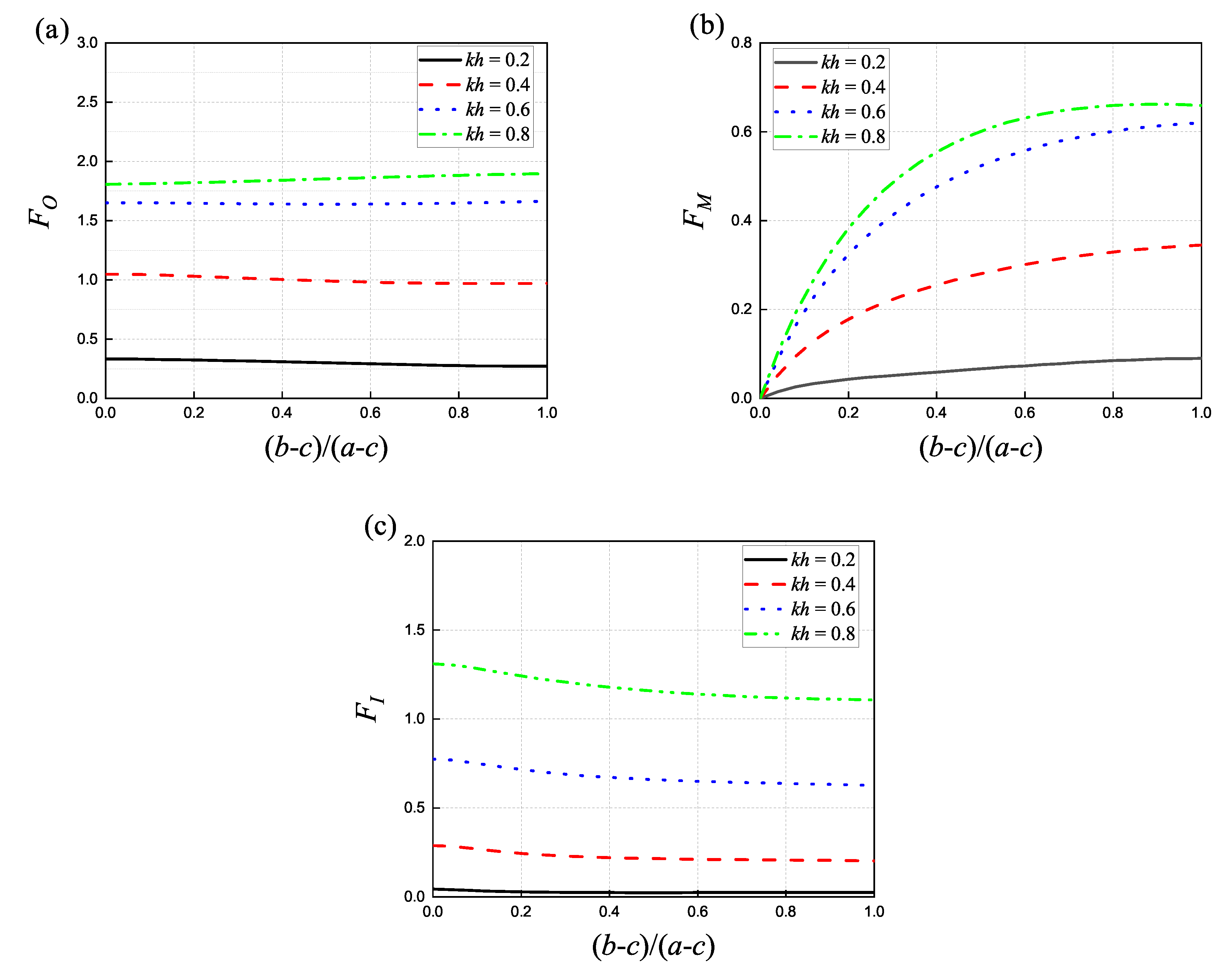
4.4. Influence of Annular Spacing

The hydrodynamic loads on the two cylinders versus the radius ratio $b/a$ are presented in Figure 9 for different $C_w$ when $e/a=1$, $G_1=1$, $\beta =0$, and $h/a=1.5$. In Figure 9b, the hydrodynamic loads on the impermeable inner cylinder increase gradually as $c/a$ increases, whereas the forces increase monotonically with an increasing $C_w$, indicating that long waves have a more significant effect than short waves. Excluding the case of $C_w=0.4$, the hydrodynamic loads on the outer porous cylinder gradually decrease with an increasing $C_w$. A similar phenomenon was observed by Wang and Ren [5] for wave diffraction by a concentric system in unbounded water, meaning that except for the variations in wave amplitude, the vertical wall has a limited effect on the patterns of variation of hydrodynamic loads on the structure.

Figure 10 presents the maximum wave run-up for the concentric system for different $c/a$ when $C_w=0.8$, $e/a=1$, $G_1=1$, $\beta =0$, and $h/a=1.5$. On the windward and leeward sides, the wave run-ups on the two cylinders increase as $b/a$ increases. The influence of $c/a$ on wave run-up is greater around the inner cylinder than around the porous outer cylinder. This is because with an increase in $c/a$, these is reduced space for wave development in the annual spacing, leading to waves directly acting on the inner cylinder after passing through the permeable outer structure. Additionally, the minimum run-up on the two cylinders occurs at approximately $\theta ={70}^{\circ }$, which is similar to the observations in Figure 8.

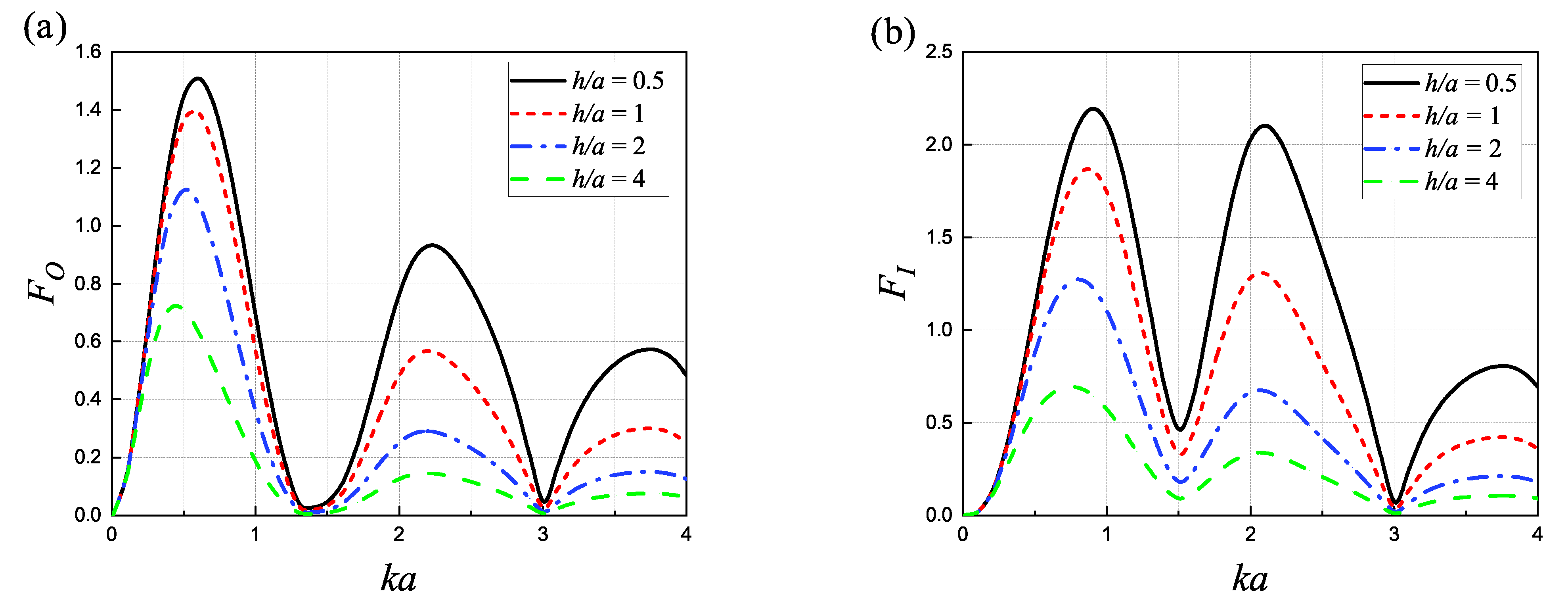
4.5. Influence of Water Depth

The hydrodynamic loads on the two cylinders versus the wave number $ka$ are presented in Figure 11 for different depth radius ratios $h/a$ when $e/a=1$, $G_1=1$, $\beta =0$, and $c/a=0.5$. The force acting on the two cylinders decreases gradually as $h/a$ increases. As shown in Figure 11, the hydrodynamic loads on the two cylinders exhibit an oscillatory nature with an increasing $ka$, and the oscillatory amplitude decreases. This is because the parameter h in Equation (25) exhibits a linear relationship with the hydrodynamic loads, meaning the water depth only affects the amplitude. Furthermore, the force on the porous outer cylinder oscillates between its peak and trough values with an increasing $ka$. The wave forces on the two cylinders exhibit periodic variations as $ka$ increases.

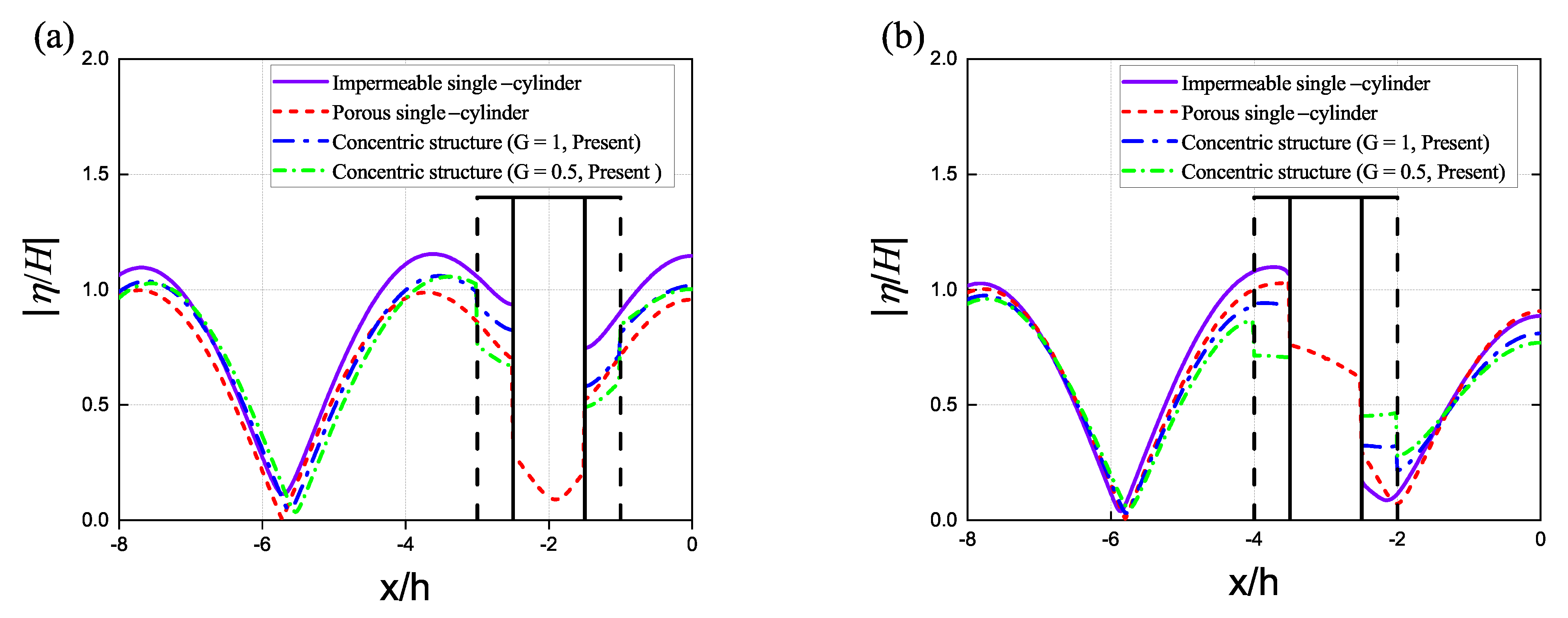
4.6. Influence of the Distance between Structure and Wall

The wave forces on the two cylinders versus $e/a$ are presented in Figure 12 for different G when $C_w=1$, $\beta =0$, $h/a=1.5$ and $c/a=0.5$. Based on the effects of the wall on the wave field, the hydrodynamic forces on the system increase for a particular range of $e/a$ and decrease for other range values of $e/a$, which differs from the force on a concentric system without a wall. One can see that the hydrodynamic loads on the two cylinders decrease initially and then increase until they reach their maximum at approximately $e/a=0.8$, followed by a decrease to their minimum at approximately $e/a=3$. Based on the presence of the wall and the assumption of total reflection, the wave amplitude of the entire wavefield is enhanced. When the structure passes through the peaks and troughs of the wavefield as it moves away from the wall, periodic variations in the hydrodynamic loads can be observed.

4.7. Influence of Location of the Middle Cylinder

Figure 13 shows the influence of the location of the middle cylinder on the wave forces versus $(b-c)/(a-c)$ for different $kh$ when $e/a=1.0$, $\beta =0$, $h/a=1$ and $c/a=0.5$. As expected, the concentric three-cylinder system provides better protection for the inner cylinder than the concentric two-cylinder structure. As indicated in Figure 13, the wave forces on the outer and inner cylinders slightly decreases when the middle cylinder moves from close to the inner cylinder to the outer cylinder. For the middle cylinder, the wave force increases monotonically towards its asymptotic value. This indicates that the presence of the middle cylinder can not significantly influence the inner and outer structures, but requires a higher cost of construction than the concentric two-cylinder system. It may be one reason that the concentric two-cylinder structures are more widely used in practice.

4.8. Comparison of the Wave Loads and Elevations of Three Structures

The radius of the single cylinder is the same as that of the interior structure in the concentric system. Figure 14 and Figure 15 present the variations in wave forces and run-ups for the three different configurations with $\beta =0,c/a=0.5,h/a=1.5$, $G_1=1$, $G_2=0$ and $e/a=1$. As expected, the wave forces and run-ups are the greatest on an impermeable cylinder near a wall, while they are significantly reduced for a porous cylinder. The hydrodynamic loads and wave run-ups on the inner cylinder are between those on the solid and porous cylinders when $G_1=1$. At $G_1=0.5$, the amplitudes of the wave force and run-up on the inner cylinder are very close to those on a porous cylinder, meaning that, with a concentric structure with appropriate porosity, the inner cylinder not only provides sufficient strength, but is also effective at reducing the wave force and run-up.

Figure 16 presents the dimensionless wave elevations distribution around the three different configurations with $C_w=1.5$, $\beta =0,c/a=0.5,h/a=1.5$, and $G_1=1$, and $e/a$ values of $1,2$ and 3. In Figure 16, the alternation of the wave peaks and troughs are clearly visualized. This is related to the total reflection of the wave in front of the wall, which creates a steady, increasing wave amplitude field. One can see that the highest wave run-up occurs on the windward and leeward sides of the impermeable cylinder surface for $e/a=1$ (see Figure 16a,d,g), whereas the wave field variation is relatively limited on the porous cylinder and concentric structure. Additionally, as $e/a$ increases (see Figure 16a–c), the wave run-up gradually decreases on the leeward side. Based on presence of a stable wave field formed by the reflection of waves in front of a wall, the alternative occurrence of peaks and troughs in wave run-up on the windward and the leeward sides of the structure can be observed as $e/a$ increases. Figure 17 presents corresponding wave elevations for the three different configurations along $y=0$ for $e/a=1$ and 2. As $e/a$ increases from one to two, on the leeward side, the wave elevation on the three structures is significantly reduced. This is a very intuitive representation of the influence of $e/a$ on wave run-up. Overall, the porosity and distance are critical influencing factors for concentric structures with internal cylinders. Therefore, these are the key factors to focus on in future research.

5. Conclusions

Based on the linear potential theory and imaging theory, an analytical model was developed to study Airy wave diffraction by a concentric system in front of a vertical wall. Comparing the present numerical results with those published by Teng and Ning [23] and Cong et al. [30], it can be found that the method used by this paper is correct and reliable. The effects of the incident angle, water depth, porosity parameter, radius ratio, and space between the structure and wall on hydrodynamic loads, wave run-ups, and wave elevations were explored in detail. Our main conclusions can be summarized as follows:

(1)

Wave incident angle is an important parameter in influencing the wave force and elevation. As the wave frequency increases, the curve of the wave force acting on the concentric system with $ka$ shows an obvious oscillation characteristic. Additionally, the oscillation frequency and the maximum peak of the wave force acting on the outer and inner cylinder gradually decrease as the wave incidence angle increases.

(2)

The various hydrodynamic loads on a concentric structure caused by changes in the structure itself, such as G, $h/a$, and $c/a$, have little relation to the presence of a vertical wall, except for changes in magnitude.

(3)

The distance between the structure and wall is a critical parameter in terms of the hydrodynamic force and wave elevation experience by the structure. These factors are influenced by the strong reflection of the vertical wall. By comparing the wave elevations on an impermeable cylinder, porous cylinder, and concentric structure, we determined that a permeable structure significantly reduces the influence of the wall presence on the wave domain and on the structure itself while effectively reducing wave loads and run-up, thereby mitigating the occurrence of overtopping waves.

(4)

For the three-cylinder structure in front of a wall, the presence of the middle cylinder cannot significantly influence the inner and outer structures, but requires a higher cost of construction than the concentric two-cylinder system. It may be one reason that the concentric two-cylinder structures are more widely used in practice.