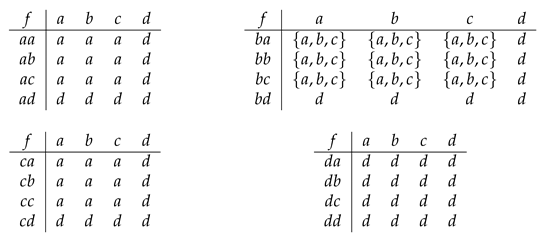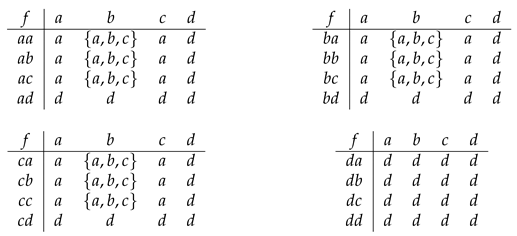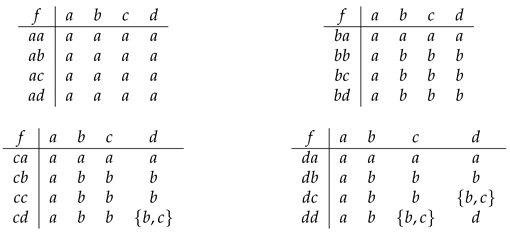Regularities in Ordered n-Ary Semihypergroups

Abstract

This paper deals with a class of hyperstructures called ordered n-ary semihypergroups which are studied by means of j-hyperideals for all positive integers $1\le j\le n$ and $n\ge 3$. We first introduce the notion of (softly) left regularity, (softly) right regularity, (softly) intra-regularity, complete regularity, generalized regularity of ordered n-ary semihypergroups and investigate their related properties. Several characterizations of them in terms of j-hyperideals are provided. Finally, the relationships between various classes of regularities in ordered n-ary semihypergroups are also established.

1. Introduction

The generalization of classical algebraic structures to n-ary structures, where $n\ge 2$, was first proposed by Kasner [1] in 1904. In particular, an n-ary semigroup is the simplest n-ary structure that represents a generalization of ordinary semigroups. It is well known that ideals in semigroups play a significant role for studying the structural properties of regular semigroups. In 1963, Sioson [2] investigated remarkable properties of j-ideals in n-ary semigroups where $1\le j\le n$ and $n\ge 2$. Moreover, the author introduced the concept of regular n-ary semigroups, which is an extension of the concept of regular semigroups, and characterized them in terms of principal j-ideals. We noticed that the notion of j-ideals in n-ary semigroups can be considered as a generalization of (right, left) ideals in classical semigroups. In 1979, Dudek and Groździńska [3] introduced a new concept of regular n-ary semigroups for $n\ge 3$ and discussed its related properties. On the other hand, the concept of j-ideals in n-ary semigroups was extended to considering ordered n-ary semigroups by Simueny et al. [4]. Pornsurat et al. [5] investigated the characterizations of intra-regular ordered n-ary semigroups by means of semiprime j-ideals. For a special case $n=3$, several kinds of regularity of ordered ternary semigroups in terms of entirely ideal-theoretical characterizations have been studied by different authors. For example, the regular ordered ternary semigroup in terms of quasi-ideals and bi-ideals was described by Daddi and Pawar [6]. Some properties of left regular, right regular, completely regular, intra-regular and lightly regular ordered ternary semigroups by means of semiprime ideals were investigated by Pornsurat and Pibaljommee [7] and Kar et al. [8]. Additionally, several types of weak regularity of ordered ternary semigroups in terms of fuzzy ideals were studied by Bashir and Du [9].

The investigation of hyperstructure theory was first initiated by Marty [10] in 1934 when he introduced and studied the concept of hypergroups as a generalization of groups by using a hyperoperation (also called multi-valued operation). Since, the hyperstructure theory has been studied by many mathematicians, see the work of Corsini [11,12], Corsini and Leoreanu [13], Davvaz and Leoreanu [14], Cristea et al. [15,16], Vougiouklis [17] and Heidari et al. [18]. In 2009, Davvaz et al. [19] introduced a special class of hyperstructures called n-ary semihypergroups, which is a natural extension of semigroups, n-ary semigroups and semihypergroups. Such an n-ary hyperstructure and its generalization have been widely studied from the theoretical point of view and for application in many subjects of pure and applied mathematics—for example, applications in biology [20,21] and in chemistry [22,23,24]. In [25], Hila et al. introduced the concept of j-hyperideals of n-ary semihypergroups, which is a generalization of j-ideals of n-ary semigroups, and discussed the related properties. The interesting properties of j-hyperideals in ternary semihypergroups and n-ary semihypergroups can be found in [26,27]. The left regularity, right regularity, intra-regularity, and complete regularity of ternary semihypergroups in terms of various j-hyperideals were characterized by Naka et al. [28,29]. Moreover, several kinds of regularity of ordered ternary semihypergroups have been investigated by Basar et al. [30] and Talee et al. [31]. Motivated by previous works on hyperideal theory in (ordered) ternary semihypergroups, in this paper we attempt to study the regularity of ordered n-ary semihypergroups, where $n\ge 3$. We introduce the concept of (softly) left regularity, (softly) right regularity, (softly) intra-regularity, complete regularity and generalized regularity of ordered n-ary semihypergroups and study their related properties. Several characterizations of them in terms of j-hyperideals are investigated. Finally, the relationships between various classes of regularities in ordered n-ary semihypergroups are also presented. As an application of our results, the corresponding results in (ordered) n-ary semigroups and n-ary semihypergroups are also obtained.

2. Preliminaries

Let S be a nonempty set and let ${\mathcal{P}}^{*}(S)$ be the set of all nonempty subsets of S. A mapping $f:S\times \cdots \times S\to {\mathcal{P}}^{*}(S)$, where S appears $n\ge 2$ times, is called an n-ary hyperoperation. A structure $(S,f)$ is called an n-ary hypergroupoid [32]. For simplicity of notion, we use the abbreviated symbol $a_j^k$ to denote a sequence of elements $a_j,a_{j+1},\dots ,a_k$ of S. For the case $k<j$, $a_j^k$ is the empty symbol. For convenience, we write $f(a_1^n)$ instead of $f(a_1,a_2,\dots ,a_n)$, and write $f(a_1^j,b_{j+1}^k,c_{k+1}^n)$ instead of $f(a_1,\dots ,a_j,b_{j+1},\dots ,b_k,c_{k+1},\dots ,c_n)$. In the case where $a_1=\dots =a_j=a$ and $c_{k+1}=\dots =c_n=c$, we write the second expression in the form $f(a^j,b_{j+1}^k,c^{n-k})$. For any abbreviated symbol of a sequence of subsets of S, we denote analogously. For $A_1,\dots ,A_n\in {\mathcal{P}}^{*}(S)$, we define

$$f(A_1^n)=f(A_1,\dots ,A_n):=\bigcup \{f(a_1^n):a_j\in A_j,j=1,\dots ,n\}.$$

If $A_1=\{a_1\}$, then we write $f(\{a_1\},A_2^n)$ as $f(a_1,A_2^n)$ and analogously in other cases. In the case $A_1=\dots =A_j=Y$ and $A_{j+1}=\dots =A_n=Z$, we write $f(A_1^n)$ as $f(Y^j,Z^{n-j})$.

An n-ary hyperoperation f of an n-ary hypergroupoid $(S,f)$ is called associative [19] if

$$f(a_1^{i-1},f(a_i^{n+i-1}),a_{n+i}^{2n-1})=f(a_1^{j-1},f(a_j^{n+j-1}),a_{n+j}^{2n-1})$$

hold for all $a_1^{2n-1}\in S$ and for all $1\le i\le j\le n$. An n-ary hypergroupoid $(S,f)$ is called an n-ary semihypergroup (also called an n-ary hypersemigroup [19,33]) if f satisfies the associative law. For any positive integer $m=k(n-1)+1$, where $k\ge 2$, the m-ary hyperoperation g of the form

$$g(a_1^{k(n-1)+1})=\underset{f\mathrm{appears}k\mathrm{times}}{\underbrace{f(f(\dots f(f(a_1^n}}),a_{n+1}^{2n-1}),\dots ),a_{(k-1)(n-1)+2}^{k(n-1)+1})$$

is denoted by $f_k$. In this case, $f_k$ is said to be an m-ary hyperoperation derived from f [32].

An ordered n-ary semihypergroup $(S,f,\le )$ (also called a partially ordered n-ary semihypergroup or a po-n-ary semihypergroup) is an n-ary semihypergroup $(S,f)$ and a partially ordered set $(S,\le )$ such that a partial order ≤ is compatible with f. Indeed, for any $a,b\in S$,

$$a\le b\mathrm{implies}f(c_1^{j-1},a,c_{j+1}^n)⪯f(c_1^{j-1},b,c_{j+1}^n)$$

for all $c_1^n\in S$ and for all $1\le j\le n$. Note that, for any $X,Y\in {\mathcal{P}}^{*}(S)$, $X⪯Y$ means for every $x\in X$ there exists $y\in Y$ such that $x\le y$. If H is an n-ary subsemihypergroup of an ordered n-ary semihypergroup $(S,f,\le )$, i.e., $f(H^n)\subseteq H$, then $(H,f,\le )$ is an ordered n-ary semihypergroup.

Throughout this paper, S stands for an ordered n-ary semihypergroup $(S,f,\le )$ with $n\ge 3$, unless specified otherwise. Any $X\in {\mathcal{P}}^{*}(S)$ is denoted as

$$(X]=\{a\in S:a\le b\mathrm{for}\mathrm{some}b\in X\}.$$

Lemma 1 ([5]). 

Let $X,Y,X_1,\dots ,X_n\in {\mathcal{P}}^{*}(S)$. Then, the following statements hold:

(i) 

$X\subseteq (X]$;

(ii) 

$(X]=((X\left]\right]$;

(iii) 

$f((X_1],(X_2],\dots ,(X_n])\subseteq (f(X_1^n)]$;

(iv) 

$(X\cup Y]=(X]\cup (Y]$;

(v) 

$X\subseteq Y$ implies $(X]\subseteq (Y]$.

Definition 1. 

For any positive integer $1\le j\le n$ and $n\ge 2$, a nonempty subset A of S is called a j-hyperideal [25] of S if $f(x_1^{j-1},a,x_{j+1}^n)\subseteq A$ for all $a\in A,x_1^{j-1},x_{j+1}^n\in S$ and $(A]=A$. If A is a j-hyperideal of S, for all $1\le j\le n$, then A is called a hyperideal of S.

For any $A\in {\mathcal{P}}^{*}(S)$ and for any positive integer $1\le j\le n$, we denote by $M^j(A)$ the j-hyperideal of S generated by A. In particular, we write $M^j(a)$ instead of $M^j(\{a\})$ for all $a\in S$.

Lemma 2 ([26]). 

Let $A\in {\mathcal{P}}^{*}(S)$. Then, the following statements hold.

(i) 

$M^1(A)=(f(A,S^{n-1})\cup A]$;

(ii) 

$M^n(A)=(f(S^{n-1},A)\cup A]$;

(iii) 

For any $1<j<n$, $M^j(A)=({\displaystyle \bigcup _{k\ge 1}}{f}_k(S^{k(j-1)},A,S^{k(n-j)})\cup A]$.

Definition 2 ([5]). 

For any positive integer $1\le j\le n$, a j-hyperideal A of S is called prime if, for every $x_1^n\in S$, $f(x_1^n)\subseteq A$ implies $x_i\in A$ for some $1\le i\le n$. A is called semiprime if, for every $a\in S$, $f(a^n)\subseteq A$ implies $a\in A$.

3. Regularities in Ordered n-Ary Semihypergroups

In this section, we introduce different types of regularity of ordered n-ary semihypergroups and investigate the characterization of them in terms of j-hyperideals for $1\le j\le n$ and $n\ge 3$. According to the notion of regular n-ary semigroups (without order), where $n\ge 3$, which was studied by Dudek and Groźdińska [3], the following definition is a generalization of such a notion on ordered n-ary semihypergroups where $n\ge 3$.

Definition 3. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. An element $a\in S$ is called regular if there exist $x_2^{n-1}\in S$ such that $a\in (f(a,x_2^{n-1},a)]$. S is called regular if every elements of S is regular, i.e., S is regular if and only if $a\in (f(a,S^{n-2},a)]$ for all $a\in S$.

Theorem 1. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Then, the following statements are equivalent.

(i) 

S is regular;

(ii) 

${\displaystyle \bigcap _{j=1}^n}{M}_j\subseteq (f(M_1,M_{n-1},M_{n-2},\dots ,M_2,M_n)]$ for all j-hyperideals $M_j$ of S;

(iii) 

${\displaystyle \bigcap _{j=1}^n}{M}^j(a_j)\subseteq (f(M^1(a_1),M^{n-1}(a_2),\dots ,M^2(a_{n-1}),M^n(a_n))]$ for all $a_1^n\in S$;

(iv) 

${\displaystyle \bigcap _{j=1}^n}{M}^j(a)\subseteq (f(M^1(a),M^{n-1}(a),\dots ,M^2(a),M^n(a))]$ for all $a\in S$.

Proof. 

The proof is similar to Theroem 1 in [3]. □

Next, we introduce the concepts of left regular, right regular and intra-regular ordered n-ary semihypergroups, where $n\ge 3$. To introduce the notion of intra-regular ordered n-ary semihypergroups, the following properties are needed.

Lemma 3. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. For any positive integer $1<j<n$, the following statements are equivalent.

(i) 

For each $a\in S$ there exist $x_1^{j-1},x_{j+1}^n\in S$ such that $a\in (f(x_1^{j-1},f(a^n),x_{j+1}^n)]$;

(ii) 

For each $a\in S$ there exist $y_1^{2n-2}\in S$ such that $a\in (f(y_1^{n-1},f(f(a^n),y_n^{2n-2}))]$.

Proof. 

Let $a\in S$ and let j be a fixed positive integer satisfying $1<j<n$ and $n\ge 3$. $(i)⟹(ii)$ Let $a\in (f(x_1^{j-1},f(a^n),x_{j+1}^n)]$ for some $x_1^{j-1},x_{j+1}^n\in S$. Firstly, we show that $a\in (f(z_1,f(a^n),z_3^n)]$ for some $z_1,z_3^n\in S$. For case $j=2$ and $n\ge 3$, we are done. Suppose that $2<j<n$ and $n>3$, by associativity and Lemma 1, we have

$$\begin{array}{ccc}\hfill a& \in & (f(x_1^{j-1},f(a^n),x_{j+1}^n)]\hfill \\ & =& (f(f(x_1^{j-1},a^{n-j+1}),a,a^{j-2},x_{j+1}^n)]\hfill \\ & \subseteq & (f(f(x_1^{j-1},a^{n-j+1}),f(x_1^{j-1},f(a^n),x_{j+1}^n),a^{j-2},x_{j+1}^n)]\hfill \\ & =& (f_2(f{(x_1^{j-1},a^{n-j+1})}^2,a,{\{a^{j-2},x_{j+1}^n\}}^2)]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{(n-j+1)}({\{f(x_1^{j-1},a^{n-j+1})\}}^{n-j+1},a,{\{a^{j-2},x_{j+1}^n\}}^{n-j+1})]\hfill \\ & \subseteq & (f_{(n-j+1)}({\{f(x_1^{j-1},a^{n-j+1})\}}^{n-j+1},f(x_1^{j-1},f(a^n),x_{j+1}^n),{\{a^{j-2},x_{j+1}^n\}}^{n-j+1})]\hfill \\ & =& (f_{(n-j+1)}(f({\{f(x_1^{j-1},a^{n-j+1})\}}^{n-j+1},x_1^{j-1}),f(a^n),x_{j+1}^n,{\{a^{j-2},x_{j+1}^n\}}^{n-j+1})]\hfill \\ & =& (f_{(n-j+1)}(f({\{f(x_1^{j-1},a^{n-j+1})\}}^{n-j+1},x_1^{j-1}),f(a^n),x_{j+1}^n,a^{j-3},\hfill \\ & & a,x_{j+1}^n,{\{a^{j-2},x_{j+1}^n\}}^{n-j})]\hfill \\ & =& (f(f({\{f(x_1^{j-1},a^{n-j+1})\}}^{n-j+1},x_1^{j-1}),f(a^n),x_{j+1}^n,a^{j-3},\hfill \\ & & \underset{f\mathrm{appears}n-j\mathrm{times}}{\underbrace{f(a,x_{j+1}^n,a^{j-2},f(x_{j+1}^n,a^{j-2},x_{j+1},f(\dots f(}}{x}_{n-1}^n,a^{j-2},x_{j+1}^n)\dots ))))]\hfill \\ & =& (f(U,f(a^n),x_{j+1}^n,a^{j-3},V)]\hfill \end{array}$$

where $U:=f({\{f(x_1^{j-1},a^{n-j+1})\}}^{n-j+1},x_1^{j-1})$ and $V:=f(a,x_{j+1}^n,a^{j-2},f(x_{j+1}^n,a^{j-2},x_{j+1}$, $f(\dots f(x_{n-1}^n,a^{j-2},x_{j+1}^n)\dots )))$.

It follows that $a\le b$ for some

$$b\in f(U,f(a^n),x_{j+1}^n,a^{j-3},V):=\bigcup _{c\in U,d\in V}f(c,f(a^n),x_{j+1}^n,a^{j-3},d).$$

Then, there exist $z_1\in U, z_n\in V$ such that $b\in f(z_1,f(a^n),z_3^n)$, where $z_3=x_{j+1},\dots ,z_{n-j+2}=x_n,z_{n-j+3}=a,\dots ,z_{n-1}=a$. Thus, $a\in (f(z_1,f(a^n),z_3^n)]$. Next, we consider

$$\begin{array}{ccc}\hfill a& \in & (f(z_1,f(a^n),z_3^n)]\hfill \\ & =& (f_{(2)}(z_1,a,a^{n-1},z_3^n)]\hfill \\ & \subseteq & (f_{(2)}(z_1,f_{(2)}(z_1,a,a^{n-1},z_3^n),a^{n-1},z_3^n)]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{(2n-2))}({\{z_1\}}^{n-1},a,{\{a^{n-1},z_3^n\}}^{n-1})]\hfill \\ & =& (f({\{z_1\}}^{n-1},f_{(2n-4)}(f(a^n),z_3^n,{\{a^{n-1},z_3^n\}}^{n-2})]\hfill \\ & =& (f({\{z_1\}}^{n-1},f(f(a^n),z_3^n,\underset{f\mathrm{appears}2n-5\mathrm{times}}{\underbrace{f(f(\dots f(f(a^{n-1},z_3),z_4^n,a^2),\dots ),a,z_3^n)}}))].\hfill \end{array}$$

This means that $a\le p$ for some

$$p\in f({\{z_1\}}^{n-1},f(f(a^n),z_3^n,\underset{f\mathrm{appears}2n-5\mathrm{times}}{\underbrace{f(f(\dots f(f(a^{n-1},z_3),z_4^n,a^2),\dots ),a,z_3^n)}})).$$

Then, there exists $y_{2n-2}\in f(f(\dots f(f(a^{n-1},z_3),z_4^n,a^2),\dots ),a,z_3^n)$ such that $p\in f(y_1^{n-1}$, $f(f(a^n),y_n^{2n-2})$, where $y_1=\dots =y_{n-1}=z_1,y_n=z_3,y_{n+1}=z_4,\dots ,y_{2n-3}=z_n.$ Therefore, $a\in (f(y_1^{n-1},f(f(a^n),y_n^{2n-2}))].$

$(ii)⟹(i)$ Let $a\in (f(y_1^{n-1},f(f(a^n),y_n^{2n-2}))]$ for some $y_1^{2n-2}\in S$. By associativity, we have

$$\begin{array}{ccc}\hfill a& \in & (f(y_1^{n-1},f(f(a^n),y_n^{2n-2}))]\hfill \\ & =& (f(f(y_1^{n-1},a),a,a^{n-3},f(a,y_n^{2n-2}))]\hfill \\ & \subseteq & (f(f(y_1^{n-1},a),f(f(y_1^{n-1},a),a,a^{n-3},f(a,y_n^{2n-2})),a^{n-3},f(a,y_n^{2n-2}))]\hfill \\ & =& (f(f(f(y_1^{n-1},a),y_1^{n-1}),f(a^n),y_n^{2n-4},f(y_{2n-3}^{2n-2},a^{n-3},f(a,y_n^{2n-2})))].\hfill \end{array}$$

This means that $a\le b$ for some $b\in f(z_1,f(a^n),z_3^n)$, where $z_1\in f(f(y_1^{n-1},a),y_1^{n-1})$ and $z_n\in f(y_{2n-3}^{2n-2},a^{n-3},f(a,y_n^{2n-2}))$ and $z_3=y_n,z_4=y_{n+1},\dots ,z_{n-1}=y_{2n-4}$. It follows that $a\in (f(z_1,f(a^n),z_3^n)].$ Next, we show that $a\in (f(z_1^{j-1},f(a^n),z_{j+1}^n)]$.

For case $j=2$ and $n\ge 3$, we have $a\in (f(z_1,f(a^n),z_3^n)]=(f(z_1^{j-1},f(a^n),z_{j+1}^n)]$.

For case $2<j<n$ and $n>3$, we have

$$\begin{array}{ccc}\hfill a& \in & (f(z_1,f(a^n),z_3^n)]\hfill \\ & =& \left(f_2(z_1,a^{j-3},a,a^{n-j+2},z_3^n)\right]\hfill \\ & \subseteq & \left(f_2(z_1,a^{j-3},f(z_1,f(a^n),z_3^n),a^{n-j+2},z_3^n)\right]\hfill \\ & =& (f(z_1,a^{j-3},z_1,f(a^n),z_3^{n-j+1},f(z_{n-j+2}^n,a^{n-j},f(a^2,z_3^n)))].\hfill \end{array}$$

Consequently, there exists $c\in f(x_1^{j-1},f(a^n),x_{j+1}^n)$ such that $a\le c$ where $x_1=z_1=x_{j-1},x_2=x_3=\dots =x_{j-2}=a$, $x_{j+1}=z_3, x_{j+2}=z_4,\dots ,x_{n-1}=z_{n-j+1}$ and $x_n\in f(z_{n-j+2}^n,a^{n-j},f(a^2,z_3^n))$. Therefore, $a\in (f(x_1^{j-1},f(a^n),x_{j+1}^n)].$ □

Without loss of generality, we introduce the notion of intra-regular ordered n-ary semihypergroups, where $n\ge 3$, as follows.

Definition 4. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Let $a\in S$.

(i) 

a is called left regular if there exist $x_1^{n-1}\in S$ such that $a\in (f(x_1^{n-1},f(a^n))]$;

(ii) 

a is called right regular if there exist $x_1^{n-1}\in S$ such that $a\in (f(f(a^n),x_1^{n-1})]$;

(iii) 

a is called intra-regular if it satisfies one of the equivalent conditions in Lemma 3.

Furthermore, S is said to be (left regular, right regular) intra-regular if every element of S is (left regular, right regular) intra-regular.

Clearly, the concept of an intra-regular ordered ternary semihypergroup, which was introduced in Definition 2.29 [31], is equal to Definition 4(iii) (for $n=3$) under the condition (i) of Lemma 3. Moreover, if we consider any ordered n-ary semigroup as an ordered n-ary semihypergroup, then Definition 8 in [5] and Definition 4(iii) under the condition (ii) of Lemma 3 coincide.

Remark 1. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Then, the following statements hold.

(i) 

S is left regular if and only if $a\in (f(S,a^{n-1})]$ for all $a\in S$;

(ii) 

S is right regular if and only if $a\in (f(a^{n-1},S)]$ for all $a\in S$;

(iii) 

S is intra-regular if and only if one of the following two conditions holds.

(1) 

For any $1<j<n$, $a\in (f(S^{j-1},f(a^n),S^{n-j})]$ for all $a\in S$.

(2) 

$a\in (f(S^{n-1},f(f(a^n),S^{n-1}))]$ for all $a\in S$.

Example 1. 

Let $S=\{a,b,c,d,e\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(b,a),(b,b),(b,d),(b,e),(c,a),(c,c),(c,d),(c,e),(d,a),(d,d),(e,a),(e,e)\}.$$

Then, $(S,f)$ is a left regular ordered ternary semihypergroup. Moreover, it is not difficult to show that $(S,f)$ is also a right regular ordered ternary semihypergroup.

Example 2. 

Let $S=\{a,b,c,d,e\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(a,c),(b,b),(b,c),(c,c),(d,d),(e,e)\}.$$

Then, $(S,f)$ is an intra-regular ordered ternary semihypergroup.

Theorem 2. 

S is left regular (right regular, respectively) if and only if every n-hyperideal (1-hyperideal, respectively) of S is semiprime.

Proof. 

Let A be an n-hyperideal of S. Let $a\in S$ such that $f(a^n)\subseteq A$. Since S is left regular, there exist $x_1^{n-1}\in S$ such that $a\in (f(x_1^{n-1},f(a^n))]\subseteq (f(x_1^{n-1},A)]\subseteq (A]=A.$ Thus, A is semiprime. Conversely, suppose that every n-hyperideal of S is semiprime: let $a\in S$. Clearly, $(f(S,a^{n-1})]$ is an n-hyperideal of S. Since $f(a^n)\subseteq (f(S,a^{n-1})]$, we have $a\in (f(S,a^{n-1})]$. From Remark 1, we conclude that S is a left regular ordered n-ary semihypergroup. □

Theorem 3. 

S is intra-regular if and only if $A\cap H\cap B\subseteq (f(A,H^{n-2},B)]$ for all n-hyperideals A, 1-hyperideals B of S and $H\in {\mathcal{P}}^{*}(S)$.

Proof. 

Let S be an intra-regular ordered n-ary semihypergroup with $n\ge 3$. Let A be an n-hyperideal, B be a 1-hyperideal of S and $H\in {\mathcal{P}}^{*}(S)$. Suppose that $a\in A\cap H\cap B$: since S is intra-regular, there exist $x_1^{2n-2}\in S$ such that $a\in (f(x_1^{n-1},f(f(a^n),x_n^{2n-2}))]=(f(f(x_1^{n-1},a),a^{n-2},f(a,x_n^{2n-2}))]$. Since $a\in A$, we have $f(x_1^{n-1},a)\subseteq A$. Similarly, since $a\in B$, we obtain $f(a,x_n^{2n-2})\subseteq B$. Since $a\in H$, we have $a\in (f(A,H^{n-2},B)]$ and then $A\cap H\cap B\subseteq (f(A,H^{n-2},B)]$. Conversely, let $a\in S$. From Lemmas 1 and 2, we have

$$\begin{array}{ccc}\hfill a& \in & M^n(a)\cap (a]\cap M^1(a)\hfill \\ & \subseteq & (f(M^n(a),{(a]}^{n-2},M^1(a))]\hfill \\ & \subseteq & (f((\{a\}\cup f(S^{n-1},a)],{(a]}^{n-2},(\{a\}\cup f(a,S^{n-1})])]\hfill \\ & \subseteq & (f(a^n)]\cup (f(a^{n-1},f(a,S^{n-1}))]\cup (f(f(S^{n-1},a),a^{n-2},a)]\cup \hfill \\ & & (f(f(S^{n-1},a),a^{n-2},f(a,S^{n-1}))]\hfill \\ & =& (f(a^n)]\cup (f(f(a^n),S^{n-1})]\cup (f(S^{n-1},f(a^n))]\cup (f(S^{n-1},f(f(a^n),S^{n-1}))].\hfill \end{array}$$

Case 1: $a\in (f(a^n)]$. Then, $a\in (f(a^n)]\subseteq (f(a^{n-1},f(a^n))]\subseteq (f(a^{n-1},f(f(a^n),a^{n-1}))]$$\subseteq (f(S^{n-1},f(f(a^n),S^{n-1}))].$

Case 2: $a\in (f(f(a^n),S^{n-1})]$. Then, $a\in (f(f(a^n),S^{n-1})]\subseteq ((f(a^{n-1},f(f(f(a^n),S^{n-1})$, $S^{n-1}))]=(f(a^{n-1},f(f(a^n),S^{n-2},f(S^n)))]\subseteq (f(S^{n-1},f(f(a^n),S^{n-1}))].$

Case 3: $a\in (f(S^{n-1},f(a^n))]$. Using the similar proof as in Case 2, we obtain $a\in (f(S^{n-1},f(f(a^n),S^{n-1}))].$

From Cases 1 to 3 and Lemma 1(iii), we conclude that S is intra-regular. □

Definition 5. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. S is called completely regular if S is regular, left regular and right regular.

Example 3. 

Let $S=\{a,b,c,d,e\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(a,c),(a,d),(b,b),(b,a),(b,c),(b,d),(c,c),(c,d),(d,d),(e,a),(e,c),(e,d),(e,e)\}.$$

Then, $(S,f)$ is a completely regular ordered ternary semihypergroup.

Lemma 4. 

S is completely regular if and only if $a\in (f(f(a^{n-1},S),a^{n-1})]$ for all $a\in S$.

Proof. 

Let S be a completely regular ordered n-ary semihypergroup and $a\in S$. Since S is regular, we have $a\in (f(a,S^{n-2},a)]$. Since S is left regular and right regular, by Remark 1(i) and (ii), we have $a\in (f(S,a^{n-1})]$ and $a\in (f(a^{n-1},S)]$. It follows that $a\in (f(a,S^{n-2},a)]\subseteq (f(f(a^{n-1},S),S^{n-2},f(S,a^{n-1}))]=(f(f(a^{n-1},f(S^n)),a^{n-1})]\subseteq (f(f(a^{n-1},S),a^{n-1})].$ Conversely, let $a\in S$. Then, $a\in (f(f(a^{n-1},S),a^{n-1})]=(f(a,f(a^{n-2},S,a),a^{n-2})]\subseteq (f(a,S^{n-2},a)]$. So S is regular. Furthermore, we have $a\in (f(f(a^{n-1},S),a^{n-1})]=(f(a^{n-1},f(S,a^{n-1}))]\subseteq (f(a^{n-1},S)]$. From Remark 1(ii), S is right regular. Clearly, $a\in (f(f(a^{n-1},S),a^{n-1})]\subseteq (f(S,a^{n-1})]$. From Remark 1(ii), S is left regular. Therefore, S is completely regular. □

Next, we introduce the concept of softly left, softly right and softly intra-regular ordered n-ary semihypergroups, which are generalizations of left, right and intra-regular ordered n-ary semihypergroups, where $n\ge 3$.

Definition 6. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Let $a\in S$.

(i) 

a is called softly left regular if there exist $x_1^{2n-3}\in S$ such that

$$a\in (f(x_1^{n-1},f(a,x_n^{2n-3},a))].$$

(ii) 

a is called softly right regular if there exist $x_1^{2n-3}\in S$ such that

$$a\in (f(f(a,x_1^{n-2},a),x_{n-1}^{2n-3})].$$

(iii) 

a is called softly intra-regular if there exist $x_1^{3n-4}\in S$ such that

$$a\in (f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4}))].$$

Additionally, S is called (softly left regular, softly right regular) softly intra-regular if each element of S is (softly left regular, softly right regular) softly intra-regular.

Remark 2. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Then, the following statements hold.

(i) 

S is softly left regular if and only if $a\in (f(S^{n-1},f(a,S^{n-2},a))]$ for all $a\in S$;

(ii) 

S is softly right regular if and only if $a\in (f(f(a,S^{n-2},a),S^{n-1})]$ for all $a\in S$;

(iii) 

S is softly intra-regular if and only if $a\in (f(S^{n-1},f(f(a,S^{n-2},a),S^{n-1}))]$ for all $a\in S$.

Example 4. 

Let $S=\{a,b,c,d\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(a,b),(a,c),(b,b),(c,b),(c,c),(d,d)\}.$$

Then, $(S,f)$ is a softly left regular ordered ternary semihypergroup.

Example 5. 

Let $S=\{a,b,c,d,e\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(a,c),(b,b),(b,c),(c,c),(d,d),(e,e)\}.$$

Then, $(S,f)$ is a softly intra-regular ordered ternary semihypergroup.

Theorem 4. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Then, the following statements are equivalent.

(i) 

S is softly left regular.

(ii) 

For any positive integer $1<j\le n$, $M_j\cap M_n\subseteq (f(M_j,S^{n-2},M_n)]$ for all j-hyperideals $M_j$ and all n-hyperideals $M_n$ of S.

(iii) 

$M_n\subseteq (f(M_n,S^{n-2},M_n)]$ for all n-hyperideals $M_n$ of S.

Proof. 

$(i)⟹(ii)$ Let j be a fixed positive integer such that $1<j\le n$ and $n\ge 3$. Let $M_j$ be a j-hyperideal and $M_n$ be an n-hyperideal of S and $a\in M_j\cap M_n$. Since S is softy left regular, there exist $x_1^{2n-3}$ such that $a\in (f(x_1^{n-1},f(a,x_n^{2n-3},a))]$. By associativity, we have

$$\begin{array}{ccc}\hfill a& \in & (f(x_1^{n-1},f(a,x_n^{2n-3},a))]\hfill \\ & \subseteq & (f(x_1^{n-1},f(f(x_1^{n-1},f(a,x_n^{2n-3},a)),x_n^{2n-3},a))]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & \left(f_{2(j-1)}({\{x_1^{n-1}\}}^{j-1},a,{\{x_n^{2n-3},a\}}^{j-1})\right]\hfill \\ & =& \left(f_{2(j-1)}({\{x_1^{n-1}\}}^{j-1},a,x_n^{2n-3},a,{\{x_n^{2n-3},a\}}^{j-2})\right]\hfill \\ & \subseteq & \left(f_{2(j-1)}({\{x_1^{n-1}\}}^{j-1},a,x_n^{2n-3},f(x_1^{n-1},f(a,x_n^{2n-3},a)),{\{x_n^{2n-3},a\}}^{j-2})\right]\hfill \\ & \subseteq & (f_{2(j-1)}({\{x_1^{n-1}\}}^{j-1},a,x_n^{2n-3},f(x_1^{n-1},f(f(x_1^{n-1},f(a,x_n^{2n-3},a)),x_n^{2n-3},a)),\hfill \\ & & {\{x_n^{2n-3},a\}}^{j-2})]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{2(j-1)}({\{x_1^{n-1}\}}^{j-1},a,x_n^{2n-3},f_{2(n-j)}({\{x_1^{n-1}\}}^{n-j},a,{\{x_n^{2n-3},a\}}^{n-j}),\hfill \\ & & {\{x_n^{2n-3},a\}}^{j-2})]\hfill \\ & \subseteq & (f_{2(n-1)}(S^{(n-1)(j-1)},a,S^{n-2},S^{(n-1)(n-j)},S^{(n-1)(n-2)},a)]\hfill \\ & =& (f(\underset{f\mathrm{appears}n-1\mathrm{times}}{\underbrace{f(S^{j-1},f(\dots ,f(S^{j-1}}},a,S^{n-j}),\dots ),S^{n-j}),S^{n-2},\hfill \\ & & \underset{f\mathrm{appears}n-2\mathrm{times}}{\underbrace{f(S^{n-1},f(S^{n-1},\dots f(S^{n-1},f(S^{n-1},a)}})\dots ))],\mathrm{since}a\in M_j\cap M_n,\hfill \\ & \subseteq & (f(M_j,S^{n-2},M_n)].\hfill \end{array}$$

Consequently, $M_j\cap M_n\subseteq (f(M_j,S^{n-2},M_n)]$.

$(ii)⟹(iii)$ It is obvious.

$(iii)⟹(i)$ Let $a\in S$. Then, $a\in M^n(a)\subseteq (f(M^n(a),S^{n-2},M^n(a))]\subseteq (f(\{a\}\cup f(S^{n-1},a),S^{n-2},\{a\}\cup f(S^{n-1},a))]$. We have four cases to be considered as follows.

Case 1: $a\in (f(a,S^{n-2},a)]$. Then, we have $a\in (f(a,S^{n-2},a)]\subseteq (f(a,S^{n-2},f(a,S^{n-2},a))]\subseteq (f(S^{n-1},f(a,S^{n-2},a))]$.

Case 2: $a\in (f(a,S^{n-2},f(S^{n-1},a))]$. Then, we have $a\in (f(a,S^{n-2},f(S^{n-1},a))]\subseteq (f(f(a,S^{n-2},f(S^{n-1},a)),S^{n-2},f(S^{n-1},a))]=(f(f(a,S^{n-1}),S^{n-2},f(a,S^{n-3},f(S^n),a))]\subseteq (f(S^{n-1},f(a,S^{n-2},a))]$.

Case 3: $a\in (f(f(S^{n-1},a),S^{n-2},a)]$. Then, we have $a\in (f(f(S^{n-1},a),S^{n-2},a)]=(f(S^{n-1},f(a,S^{n-2},a))]$.

Case 4: $a\in (f(f(S^{n-1},a),S^{n-2},f(S^{n-1},a))]$. Then, we have $a\in (f(f(S^{n-1},a),S^{n-2}$, $f(S^{n-1},a))]=(f(S^{n-1},f(a,S^{n-3},f(S^n),a))]\subseteq (f(S^{n-1},f(a,S^{n-2},a))]$.

From Cases 1 to 4 and Remark 2(i), S is softly left regular. □

Using the similar proof of Theorem 4, we obtain the following result.

Theorem 5. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Then, the following statements are equivalent.

(i) 

S is softly right regular;

(ii) 

For any positive integer $1\le j<n$, $M_1\cap M_j\subseteq (f(M_1,S^{n-2},M_j)]$ for all 1-hyperideals $M_1$ and all j-hyperideals $M_j$ of S;

(iii) 

$M_1\subseteq (f(M_1,S^{n-2},M_1)]$ for all 1-hyperideals $M_1$ of S.

Theorem 6. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Then, the following statements are equivalent.

(i) 

S is softly intra-regular.

(ii) 

For any positive integer $1<i\le n$ and $1\le j<n$, $M_i\cap M_j\subseteq (f(M_i,S^{n-2},M_j)]$ for all i-hyperideals $M_i$ and all j-hyperideals $M_j$ of S.

(iii) 

For any positive integer $1<k<n$, $M_k\subseteq (f(M_k,S^{n-2},M_k)]$ for all k-hyperideals $M_k$ of S.

Proof. 

$(i)⟹(ii)$ Let $i,j$ be two fixed positive integers such that $1<i\le n$ and $1\le j<n$. Let $M_i$ be an i-hyperideal and $M_j$ be a j-hyperideal of S and $a\in M_i\cap M_j$. Since S is softly intra-regular, there exist $x_1^{3n-4}\in S$ such that $a\in (f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4}))]$. By associativity, we have

$$\begin{array}{ccc}\hfill a& \in & (f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4}))]\hfill \\ & \subseteq & (f(x_1^{n-1},f(f(f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4})),x_n^{2n-3},a),x_{2n-2}^{3n-4}))]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & \left(f_{3(i-1)}({\{x_1^{n-1}\}}^{i-1},a,{\{x_n^{2n-3},a,x_{2n-2}^{3n-4}\}}^{i-1})\right]\hfill \\ & =& \left(f_{3(i-1)}({\{x_1^{n-1}\}}^{i-1},a,x_n^{2n-3},a,x_{2n-2}^{3n-4},{\{x_n^{2n-3},a,x_{2n-2}^{3n-4}\}}^{i-2})\right]\hfill \\ & \subseteq & (f_{3(i-1)}({\{x_1^{n-1}\}}^{i-1},a,x_n^{2n-3},f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4})),\hfill \\ & & x_{2n-2}^{3n-4},{\{x_n^{2n-3},a,x_{2n-2}^{3n-4}\}}^{i-2})]\hfill \\ & \subseteq & (f_{3(i-1)}({\{x_1^{n-1}\}}^{i-1},a,x_n^{2n-3},\hfill \\ & & f(x_1^{n-1},f(f(f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4})),x_n^{2n-3},a),x_{2n-2}^{3n-4})),\hfill \\ & & x_{2n-2}^{3n-4},{\{x_n^{2n-3},a,x_{2n-2}^{3n-4}\}}^{i-2})]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{3(i-1)}({\{x_1^{n-1}\}}^{i-1},a,x_n^{2n-3},f_{3(n-i)}({\{x_1^{n-1}\}}^{n-i},a,{\{x_n^{2n-3},a,x_{2n-2}^{3n-4}\}}^{n-i}),\hfill \\ & & x_{2n-2}^{3n-4},{\{x_n^{2n-3},a,x_{2n-2}^{3n-4}\}}^{i-2})]\hfill \\ & \subseteq & (f_{3(i-1)}(S^{(i-1)(n-1)},a,S^{n-2},f_{3(n-i)}(S^{(n-i)(n-1)},a,S^{(n-i)(2n-2)}),\hfill \\ & & S^{n-1},S^{2(n-1)(i-2)})]\hfill \\ & =& (f_{2(n-1)}(\underset{f\mathrm{appears}n-1\mathrm{times}}{\underbrace{f(S^{i-1},f(\dots ,f(S^{i-1}}},a,S^{n-i}),\dots ),S^{n-i}),S^{n-2},a,S^{(n-i)(2n-2)},\hfill \\ & & S^{(n-1)(2i-3)}],\hfill \\ & & \sin \mathrm{ce}a\in M_i,\hfill \\ & \subseteq & (f_{2(n-1)}(M_i,S^{n-2},a,S^{(n-1)(2n-3)}]\hfill \\ & =& (f_2(M_i,S^{n-2},a,S^{n-2},\underset{f\mathrm{appears}2n-4\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1})\dots ),S^{n-1}}})]\hfill \\ & \subseteq & (f_2(M_i,S^{n-2},a,S^{n-1})].\hfill \end{array}$$

On the other hand, we have

$$\begin{array}{ccc}\hfill a& \in & (f_2(M_i,S^{n-2},a,S^{n-1})]\hfill \\ & \subseteq & (f_2(M_i,S^{n-2},f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4})),S^{n-1})]\hfill \\ & \subseteq & (f_2(M_i,S^{n-2},f(x_1^{n-1},f(f(a,x_n^{2n-3},f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4}))),x_{2n-2}^{3n-4})),\hfill \\ & & S^{n-1})]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_2(M_i,S^{n-2},f_{3(n-j)}({\{x_1^{n-1},a,x_n^{2n-3}\}}^{n-j},a,{\{x_{2n-2}^{3n-4}\}}^{n-j}),S^{n-1})]\hfill \\ & =& (f_{3(n-j)+2}(M_i,S^{n-2},{\{x_1^{n-1},a,x_n^{2n-3}\}}^{n-j},a,{\{x_{2n-2}^{3n-4}\}}^{n-j},S^{n-1})]\hfill \\ & =& (f_{3(n-j)+2}(M_i,S^{n-2},{\{x_1^{n-1},a,x_n^{2n-3}\}}^{n-j-1},x_1^{n-1},a,x_n^{2n-3},a,{\{x_{2n-2}^{3n-4}\}}^{n-j},\hfill \\ & & S^{n-1})]\hfill \\ & \subseteq & (f_{3(n-j)+2}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},a,S^{n-2},a,S^{(n-j)(n-1)},S^{n-1})]\hfill \\ & =& (f_{3(n-j)+1}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},a,S^{n-2},a,S^{(n-j-1)(n-1)},S^{n-2},\hfill \\ & & f(S^n))]\hfill \\ & \subseteq & (f_{3(n-j)+1}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},a,S^{n-2},a,S^{(n-j-1)(n-1)},S^{n-1})]\hfill \\ & =& (f_{3(n-j)+1}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},a,S^{n-2},a,S^{(n-j)(n-1)})]\hfill \\ & \subseteq & (f_{3(n-j)+1}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},\hfill \\ & & f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4})),S^{n-2},a,S^{(n-j)(n-1)})]\hfill \\ & \subseteq & (f_{3(n-j)+1}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},\hfill \\ & & f(x_1^{n-1},f(f(a,x_n^{2n-3},f(x_1^{n-1},f(f(a,x_n^{2n-3},a),x_{2n-2}^{3n-4}))),x_{2n-2}^{3n-4})),S^{n-2},a,\hfill \\ & & S^{(n-j)(n-1)})]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{3(n-j)+1}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},\hfill \\ & & f_{3(j-1)}({\{x_1^{n-1},a,x_n^{2n-3}\}}^{j-1},a,{\{x_{2n-2}^{3n-4}\}}^{j-1}),S^{n-2},a,S^{(n-j)(n-1)})]\hfill \\ & \subseteq & (f_{3(n-1)+1}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},S^{2(n-1)(j-1)},\hfill \\ & & a,S^{(n-1)(j-1)},S^{n-2},a,S^{(n-j)(n-1)})]\hfill \\ & =& (f_{2n-1}(M_i,S^{n-2},S^{(2n-2)(n-j-1)},S^{n-1},S^{2(n-1)(j-1)},\hfill \\ & & a,S^{n-2},\underset{f\mathrm{appears}n-1\mathrm{times}}{\underbrace{f(S^{j-1},f(\dots ,f(S^{j-1}}},a,S^{n-j}),\dots ),S^{n-j}))],\hfill \\ & & \mathrm{since}a\in M_j,\hfill \\ & \subseteq & (f_{2n-1}(M_i,S^{n-3},S^{(n-1)(2n-2)},M_j)]\hfill \\ & =& (f(M_i,S^{n-3},\underset{f\mathrm{appears}2n-2\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1}),\dots ),S^{n-1})}},M_j)]\hfill \\ & \subseteq & (f(M_i,S^{n-2},M_j)].\hfill \end{array}$$

Thus, $M_i\cap M_j\subseteq (f(M_i,S^{n-2},M_j)]$.

$(ii)⟹(iii)$ It is obvious.

$(iii)⟹(iv)$ Let $a\in S$. Then, $a\in M^k(a)\subseteq (f(M^k(a),S^{n-2},M^k(a))]\subseteq (f({\displaystyle \bigcup _{p\ge 1}}{f}_p(S^{p(k-1)},a,S^{p(n-k)})\cup \{a\},S^{n-2},{\displaystyle \bigcup _{q\ge 1}}{f}_q(S^{q(k-1)},a,S^{q(n-k)})\cup \{a\})]$.

We consider the following cases.

Case 1: $a\in (f(f_p(S^{p(k-1)},a,S^{p(n-k)}),S^{n-2},f_q(S^{q(k-1)},a,S^{q(n-k)}))]=(f_{1+p+q}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)})]$ for some $p,q\ge 1$. Then,

$$\begin{array}{ccc}\hfill a& \in & (f_{1+p+q}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)})]\hfill \\ & \subseteq & (f_{1+p+q}(S^{p(k-1)},f_{1+p+q}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)}),\hfill \\ & & S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)})]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{(1+p+q)(n-1)}(S^{p(k-1)(n-1)},a,{\{S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)}\}}^{n-1})]\hfill \\ & =& (f_{n+p(n-k)+q(n-1)}(\underset{f\mathrm{appears}p(k-1)-1\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1}),\dots ),S^{n-1}}}),S^{n-2},a,\hfill \\ & & {\{S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)}\}}^{n-1})]\hfill \\ & \subseteq & (f_{n+p(n-k)+q(n-1)}(S^{n-1},a,{\{S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)}\}}^{n-2},\hfill \\ & & S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)})]\hfill \\ & \subseteq & (f_{n+p(n-k)+q(n-1)}(S^{n-1},a,S^{(p(n-k)+(n-1)(q+1))(n-2)+p(n-k)+(n-2)+q(k-1)},\hfill \\ & & a,S^{q(n-k)})]\hfill \\ & \subseteq & (f_{n+p(n-k)+q(n-1)}(S^{n-1},a,S^{(p(n-k)+(n-1)(q+1))(n-2)+p(n-k)+(n-2)+q(k-1)},\hfill \\ & & f_{1+p+q}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)}),S^{q(n-k)})]\hfill \\ & \subseteq & (f_{n+p(n-k)+q(n-1)}(S^{n-1},a,S^{(p(n-k)+(n-1)(q+1))(n-2)+p(n-k)+(n-2)+q(k-1)},\hfill \\ & & f_{1+p+q}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},S^{q(k-1)},\hfill \\ & & f_{1+p+q}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},S^{q(k-1)},a,S^{q(n-k)}),S^{q(n-k)}),S^{q(n-k)})]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{n+p(n-k)+q(n-1)}(S^{n-1},a,S^{(p(n-k)+(n-1)(q+1))(n-2)+p(n-k)+(n-2)+q(k-1)},\hfill \\ & & f_{(1+p+q)(n-2)}({\{S^{p(k-1)},a,S^{p(n-k)},S^{n-2},S^{q(k-1)}\}}^{(n-2)},a,S^{q(n-k)(n-2)}),S^{q(n-k)})]\hfill \\ & =& (f_{n+p(n-k)+q(n-1)+(n-1)+p(n-2)+q(k-2)}(S^{n-1},a,\hfill \\ & & S^{(p(n-k)+(n-1)(q+1))(n-2)+p(n-k)+(n-2)+q(k-1)},\hfill \\ & & {\{S^{p(k-1)},a,S^{p(n-k)},S^{n-2},S^{q(k-1)}\}}^{(n-2)}\hfill \\ & & ,a,S^{n-2},\underset{f\mathrm{appears}q(n-k)-1\mathrm{times}}{\underbrace{f(S^{n-1},f(\dots ,f(S^{n-1},f(S^n))\dots )}}))]\hfill \\ & \subseteq & (f_{n+p(n-k)+q(n-1)+(n-1)+p(n-2)+q(k-2)}(S^{n-1},a,\hfill \\ & & S^{(p(n-k)+(n-1)(q+1))(n-2)+p(n-k)+(n-2)+q(k-1)},S^{((p+1)(n-1)+q(k-1))(n-2)},a,\hfill \\ & & S^{n-1})]\hfill \\ & =& (f_{n+p(n-k)+q(n-1)+(n-1)+p(n-2)+q(k-2)}(S^{n-1},a,\hfill \\ & & S^{(n-1)(p(n-k)+q(k-1)+(n-2)(p+q+2))+(n-2)},a,S^{n-1})]\hfill \\ & =& (f(S^{n-1},f(f(a,S^{n-3},\underset{f\mathrm{appears}p(n-k)+q(k-1)+(n-2)(p+q+2)\mathrm{times}}{\underbrace{f(S^{n-1},f(\dots ,f(S^{n-1},f(S^n))\dots ))}},a),S^{n-1}))]\hfill \\ & \subseteq & (f(S^{n-1},f(f(a,S^{n-2},a),S^{n-1}))].\hfill \end{array}$$

Case 2: $a\in (f(f_p(S^{p(k-1)},a,S^{p(n-k)}),S^{n-2},a)]=(f_{p+1}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},a)]$ for some $p\ge 1$. Then,

$$\begin{array}{ccc}\hfill a& \in & (f_{p+1}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},a)]\hfill \\ & \subseteq & (f_{p+1}(S^{p(k-1)},f_{(p+1)}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},a),S^{p(n-k)},S^{n-2},a)]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{(p+1)(n-1)}(S^{p(k-1)(n-1)},a,{\{S^{p(n-k)},S^{n-2},a\}}^{(n-3)},S^{p(n-k)},S^{n-2},\hfill \\ & & a,S^{p(n-k)},S^{n-2},a)]\hfill \\ & \subseteq & (f_{(p+1)(n-1)}(S^{p(k-1)(n-1)},a,{\{S^{p(n-k)},S^{n-2},a\}}^{(n-3)},S^{p(n-k)},S^{n-2},\hfill \\ & & f_{p+1}(S^{p(k-1)},a,S^{p(n-k)},S^{n-2},a),S^{p(n-k)},S^{n-2},a)]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{(p+1)(n-1)}(S^{p(k-1)(n-1)},a,{\{S^{p(n-k)},S^{n-2},a\}}^{(n-3)},S^{p(n-k)},S^{n-2},\hfill \\ & & f_{(p+1)(n-2)}(S^{p(k-1)(n-2)},a,{\{S^{p(n-k)},S^{n-2},a\}}^{(n-2)}),S^{p(n-k)},S^{n-2},a)]\hfill \\ & \subseteq & (f_{(p+1)(2n-3)}(S^{p(k-1)(n-1)},a,{\{S^{p(n-k)},S^{n-2},a\}}^{(n-3)},S^{p(n-k)},S^{n-2},\hfill \\ & & S^{p(k-1)(n-2)},a,{\{S^{p(n-k)},S^{n-2},a\}}^{(n-1)})]\hfill \\ & \subseteq & (f_{(p+1)(2n-3)}(S^{p(k-1)(n-1)},a,S^{n-3},S^n,S^{(n-1)((p+1)(n-2)-2)},\hfill \\ & & a,S^{(n-1)(p(n-k)+n-1)})]\hfill \\ & \subseteq & (f(\underset{f\mathrm{appears}p(k-1)-1\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1}),\dots ),S^{n-1})}},S^{n-2},f(f(a,S^{n-3},\hfill \\ & & \underset{f\mathrm{appears}(p+1)(n-2)-1\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1}),\dots ),S^{n-1})}},a),S^{n-2},\underset{f\mathrm{appears}p(n-k)+n-2\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1}),\dots ),S^{n-1})}}))]\hfill \\ & \subseteq & (f(S^{n-1},f(f(a,S^{n-2},a),S^{n-1}))].\hfill \end{array}$$

Case 3: $a\in (f(a,S^{n-2},f_q(S^{q(k-1)},a,S^{q(n-k)}))]$. The proof is similar to Case 2.

Case 4: $a\in (f(a,S^{n-2},a)]$. Then, $a\in (f(a,S^{n-2},a)]\subseteq (f(a,S^{n-2},f(a,S^{n-2},a))]\subseteq (f(a,S^{n-2},f(a,S^{n-2},f(a,S^{n-2},a)))]\subseteq (f(S^{n-1},f(a,S^{n-2},f(a,S^{n-1})))]=(f(S^{n-1},f(f(a,S^{n-2},a),S^{n-1}))]$.

From Cases 1 to 4 and Remark 2(iii), we conclude that S is softly intra-regular. □

Definition 7. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. An element $a\in S$ is called generalized regular if there exist $x_1^{2n-2}\in S$ such that $a\in (f(x_1^{n-1},f(a,x_n^{2n-2}))]$. S is called generalized regular if every element of S is generalized regular, i.e., S is generalized regular if and only if $a\in (f(S^{n-1},f(a,S^{n-1}))]$ for all $a\in S$.

Example 6. 

Let $S=\{a,b,c,d,e\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by $f(x_1,x_2,x_3)=(x_1\circ x_2)\circ x_3$, for all $x_1^3\in S$, where ∘ is defined by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(a,b),(a,c),(a,e),(b,b),(c,c),(c,b),(c,e),(d,d),(e,b),(e,e)\}.$$

Then, $(S,f)$ is a generalized regular ordered ternary semihypergroup.

Theorem 7. 

S is generalized regular if and only if for each $1<j<n$, $M_j\subseteq (f(S^{n-j},M_j,S^{j-1})]$ for all j-hyperideals $M_j$ of S.

Proof. 

Firstly, let j be a fixed positive integer satisfying $1<j<n$. Let $M_j$ be a j-hyperideal of S and $a\in M_j$. Since S is generalized regular, there exist $x_1^{2n-2}\in S$ such that

$$\begin{array}{ccc}\hfill a& \in & (f(x_1^{n-1},f(a,x_n^{2n-2}))]\hfill \\ & =& (f(x_1^{n-j},f(x_{n-j+1}^{n-1},a,x_n^{2n-j-1}),x_{2n-j}^{2n-2})],\mathrm{since}a\in M_j,\hfill \\ & \subseteq & (f(x_1^{n-j},M_j,x_{2n-j}^{2n-2})]\hfill \\ & \subseteq & (f(S^{n-j},M_j,S^{j-1})].\hfill \end{array}$$

Thus, $M_j\subseteq (f(S^{n-j},M_j,S^{j-1})]$. Conversely, let $a\in S$. Then, $a\in M^j(a)\subseteq (f(S^{n-j},M^j(a),S^{j-1})]\subseteq (f(S^{n-j},{\displaystyle \bigcup _{k\ge 1}}{f}_{k}f(S^{k(j-1)},a,S^{k(n-j)})\bigcup \{a\},S^{j-1})]$. We have two cases to be considered, as follows.

Case 1: $a\in (f(S^{n-j},f_k(S^{k(j-1)},a,S^{k(n-j)}),S^{j-1})]$ for some $k\ge 1$.

If $k=1$, then $a\in (f(S^{n-j},f(S^{j-1},a,S^{n-j}),S^{j-1})]=(f(S^{n-1},f(a,S^{n-1}))]$.

If $k\ge 2$, then

$$\begin{array}{ccc}\hfill a& \in & a\in \left(f_{k+1}(S^{n-j},S^{k(j-1)},a,S^{k(n-j)},S^{j-1})\right]\hfill \\ & =& (f_{k+1}(S^{n-j},S^{j-1},S^{j-1},S^{(k-2)(j-1)},a,S^{(k-2)(n-j)},S^{n-j},S^{n-j},S^{j-1})]\hfill \\ & =& (f_{k+1}(f(S^n),S^{j-2},S^{(k-2)(j-1)},a,S^{(k-2)(n-j)},S^{n-j-1},f(S^n))]\hfill \\ & \subseteq & (f_{k-1}(S^{(k-1)(j-1)},a,S^{(k-1)(n-j)})].\hfill \end{array}$$

By associativity, we have

$$\begin{array}{ccc}\hfill a& \in & (f_{k-1}(S^{(k-1)(j-1)},a,S^{(k-1)(n-j)})]\hfill \\ & \subseteq & (f_{k-1}(S^{(k-1)(j-1)},f_{k-1}(S^{(k-1)(j-1)},a,S^{(k-1)(n-j)}),S^{(k-1)(n-j)})]\hfill \\ & \subseteq & \dots \hfill \\ & \subseteq & (f_{(k-1)(n-1)}(S^{(k-1)(j-1)(n-1)},a,S^{(k-1)(n-j)(n-1)})]\hfill \\ & =& (f(\underset{f\mathrm{appears}(k-1)(j-1)-1}{\underbrace{f(f(..f(f(S^n),S^{n-1}),\dots ),S^{n-1}}}),S^{n-2},f(a,S^{n-2},\hfill \\ & & \underset{f\mathrm{appears}(k-1)(n-j)-1}{\underbrace{f(f(..f(f(S^n),S^{n-1}),\dots ),S^{n-1}}})))]\hfill \\ & \subseteq & (f(S^{n-1},f(a,S^{n-1}))].\hfill \end{array}$$

Case 2: $a\in (f(S^{n-j},a,S^{j-1})]$. Then, $a\in (f(S^{n-j},a,S^{j-1})]\subseteq (f(S^{n-j},f(S^{n-j},a,S^{j-1}),S^{j-1})]\subseteq \dots \subseteq (f_{n-1}(S^{(n-j)(n-1)},a,S^{(j-1)(n-1)})].$

Next, we consider the following cases.

If $j=2$ and $n=3$, then we are done.

If $j=2$ and $n>3$, then $a\in (f_{n-1}(S^{(n-2)(n-1)},a,S^{(n-1)})]=(f(\underset{f\mathrm{appears}n-2\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1}),\dots ),S^{n-1})}},S^{n-2},f(a,S^{n-1}))\subseteq (f(S^{n-1},f(a,S^{n-1}))].$

If $j>2$ and $n>3$, then

$$\begin{array}{ccc}\hfill a& \in & (f_{n-1}(S^{(n-2)(n-1)},a,S^{(n-1)})]\hfill \\ & =& (f(\underset{f\mathrm{appears}n-j-1\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1}),\dots ),S^{n-1})}},S^{n-2},f(a,S^{n-2},\hfill \\ & & \underset{f\mathrm{appears}j-2\mathrm{times}}{\underbrace{f(f(\dots f(f(S^n),S^{n-1}),\dots ),S^{n-1})}}))]\hfill \\ & \subseteq & (f(S^{n-1},f(a,S^{n-1}))].\hfill \end{array}$$

Therefore, S is generalized regular. □

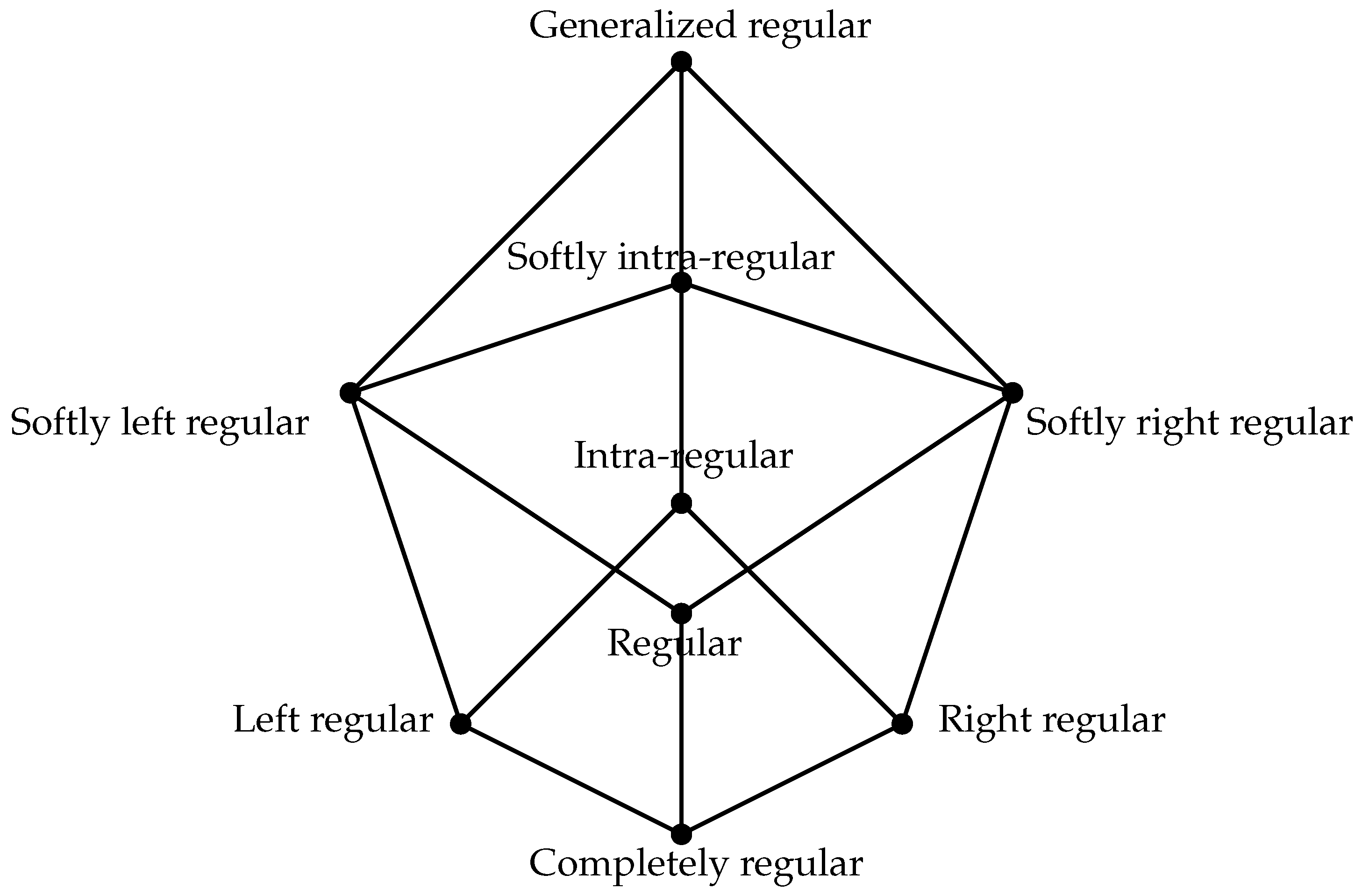
Finally, we establish the relationships between regularities in ordered n-ary semihypergroups, where $n\ge 3$, as follows.

Lemma 5. 

Let S be an ordered n-ary semihypergroup with $n\ge 3$. Then, the following statements hold.

(i) 

Every left (right) regular is intra-regular;

(ii) 

Every regular is softly left (right) regular;

(iii) 

Every left (right) regular is softly left (right) regular;

(iv) 

Every softly left (right) regular is softly intra-regular;

(v) 

Every intra-regular is softly intra-regular;

(vi) 

Every softly intra-regular is generalized regular.

Proof. 

(i) Let S be a left regular ordered n-ary semihypergroup. Then, there exist $x_1^{n-1}\in S$ such that $a\in (f(x_1^{n-1},f(a^n))]\subseteq (f(x_1^{n-1},f(f(x_1^{n-1},f(a^n)),a^{n-1}))]=(f(f(x_1^{n-1},x_1),x_2^{n-1},f(f(a^n),a^{n-1}))]\subseteq (f(S^{n-1},f(f(a^n),S^{n-1}))]$. Consequently, by Remark 1, we conclude that S is intra-regular.

(ii) Let S be a regular ordered n-ary semihypergroup. Then, there exist $x_2^{n-1}\in S$ such that $a\in (f(a,x_2^{n-1},a)]\subseteq (f(a,x_2^{n-1},f(a,x_2^{n-1},a))]\subseteq (f(S^{n-1},f(a,S^{n-2},a))]$. From Remark 2(i), S is softly left regular.

The proofs of (iii)–(vi) are obvious. □

The following examples show that the converse assertions of Lemma 5 do not hold true in general.

Example 7. 

We know that an ordered ternary semihypergroup $(S,f)$, as given in Example 2, is an intra-regular ordered ternary semihypergroup. Since $f(S,a,a)=\{b,e\}$, we have $a\notin (f(S,a,a))]$. From Remark 1, we conclude that $(S,f)$ is not a left regular ordered ternary semihypergroup. This shows that the converse statement of Lemma 5(i) does not hold.

Example 8. 

Let $S=\{a,b,c,d\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(a,b),(a,c),(b,b),(c,b),(c,c),(d,d)\}.$$

Then, $(S,f)$ is an ordered ternary semihypergroup. Clearly, $a\in (f(f(a,a,a),a,a)]$, $b\in \{a,b,c\}=(f(f(b,a,b),a,b)]$, $c\in \{a,b,c\}=(f(f(c,a,c),a,b)]$ and $d\in (f(f(d,d,d),d,d)].$ By Definition 6, $(S,f)$ is a softly right ordered ternary semihypergroup. On the other hand, since $c\notin (f(c,S,c)]$, by Definition 3, we conclude that $(S,f)$ is not a regular ordered ternary semihypergroup. This shows that the reverse assertion of Lemma 5(ii) is not true.

Example 9. 

We know that an ordered ternary semihypergroup $(S,f)$ that has been given in Example 6 is a generalized regular ordered ternary semihypergroup. Clearly, $K=\{a,c,d\}$ is a 3-hyperideal of S. Looking at the table, one can immediately see that $f(K,S,K)=f(a,S,K)\bigcup f(c,S,K)\bigcup f(d,S,K)=\{a,d\}$. It follows that $K⊈f(K,S,K)$. From Theorem 4, we conclude that $(S,f)$ is not a softly left regular ordered ternary semihypergroup.

Example 10. 

We know that an ordered ternary semihypergroup $(S,f)$, which was given in Example 1, is a left regular and right regular ordered ternary semihypergroup. Since $c\notin \{b\}=(f(f(c,c,S),c,c)]$, by Lemma 4, we conclude that $(S,f)$ is not a completely regular ordered ternary semihypergroup.

Example 11. 

Let $S=\{a,b,c,d,e,g\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(a,b),(a,c),(a,d),(a,g),(b,b),(c,c),(d,d),(e,e),(g,g)\}.$$

Then, $(S,f)$ is an ordered ternary semihypergroup. Evidently, $A=\{a,e\},B=\{a,c,d,e\}$ and S are all a 1-hyperideal of S. It is not difficult to show that $A=(f(A,S,A)]$, $B=(f(B,S,B)]$ and $S=(f(S,S,S)]$. From Theorem 5, we conclude that $(S,f)$ is a softly right regular ordered ternary semihypergroup. Since $f(g,g,g)=\{a\}\subseteq A$ but $g\notin A$, we find that A is not a semiprime 1-hyperideal of S. From Theorem 2, $(S,f)$ is not a right regular ordered ternary semihypergroup. This shows that the converse assertion of Lemma 5(iii) is not true in general.

Example 12. 

We know that an ordered ternary semihypergroup $(S,f)$ that has been given in Example 5 is a softly intra-regular ordered ternary semihypergroup. Obviously, $K=\{a,b,e\}$ is a 1-hyperideal of S. Since $K⊈\{b,e\}=(f(K,S,K)]$, by Theorem 5, we conclude that $(S,f)$ is not a softly right regular ordered ternary semihypergroup, which verifies that the converse statement of Lemma 5(iv) does not hold.

Example 13. 

Let $S=\{a,b,c,d,e,g\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(a,b),(a,c),(a,d),(a,g),(b,b),(c,c),(d,d),(e,e),(g,g)\}.$$

Then, $(S,f)$ is an ordered ternary semihypergroup. Clearly, $K=\{a,e\}$ and S are all 2-hyperideals of S. It is easy to show that $K=(f(K,S,K)]$. From Theorem 6, $(S,f)$ is a softly intra-regular ordered ternary semihypergroup. However, $(S,f)$ is not an intra-regular ordered ternary semihypergroup. In fact, there exist a n-hyperideal $A=\{a,b,e,g\}$, an 1-hyperideal $B=\{a,c,e,g\}$ and a nonempty subset $H=\{a,b,c,g\}$ of S such that $A\cap H\cap B=\{a,g\}⊈\{a,e\}=f(A,H,B)$. From Theorem 3, we conclude that $(S,f)$ is not an intra-regular ordered ternary semihypergroup. This shows that the converse statement of Lemma 5(v) does not satisfy.

Example 14. 

Let $S=\{a,b,c,d\}$. Define a ternary hyperoperation $f:S\times S\times S\to {\mathcal{P}}^{*}(S)$ by the following tableand define a partial order on S as follows

$$\le :=\{(a,a),(b,b),(b,c),(c,c),(d,d)\}.$$

Then, $(S,f)$ is an ordered ternary semihypergroup. Clearly, $\{a\},\{a,b\},\{a,b,c\}$ and S are all 2-hyperideals of S. It is not difficult to see that $A=(f(S,A,S)]$ for all 2-hyperideals A of S. From Theorem 7, $(S,f)$ is a generalized regular ordered ternary semihypergroup. On the other hand, S is not a softly intra-regular ordered ternary semihypergroup. In fact, since $K=\{a,b,c\}$ is an 2-hyperideal of S and $A⊈\{a,b\}=(f(A,S,A)]$, by Theorem 6, we conclude that $(S,f)$ is not a softly intra-regular ordered ternary semihypergroup. This shows that the reverse assertion of Lemma 5(vi) does not hold true in general.

4. Conclusions

Similar to the theory of ordered semigroups, left and right hyperideals play an important role for studying the regularity of ordered semihypergroups. In this paper, we investigated the properties of j-hyperideals, which is a generalization of a left and a right hyperideal of an ordered semihypergroup, on ordered n-ary semihypergroups, where a positive integer $1\le j\le n$ and $n\ge 3$. We introduced the notions of (softly) left regularity, (softly) right regularity, (softly) intra-regularity, complete regularity and generalized regularity of ordered n-ary semihypergroups and gave the characterizations of them in terms of j-hyperideals. Finally, we obtained the relationships between various regularities in ordered n-ary semihypergroups which can be expressed by Figure 1.

As an application of the results of this paper, the corresponding results for n-ary semihypergroups can be also obtained because every n-ary semihypergroup endowed with the equality relation is an ordered n-ary semihypergroup.