Approximating Solutions of Non-Linear Troesch’s Problem via an Efficient Quasi-Linearization Bessel Approach
Abstract
:1. Introduction
2. Basic Facts
2.1. Bessel Functions
2.2. Quasi-Linearization Approach
3. Direct Approach
Boundary Conditions in the Matrix Forms
| Algorithm 1 The computation of s-derivative of the vector |
|
4. QLM-Bessel
5. Error Analysis
The Accuracy of Methods
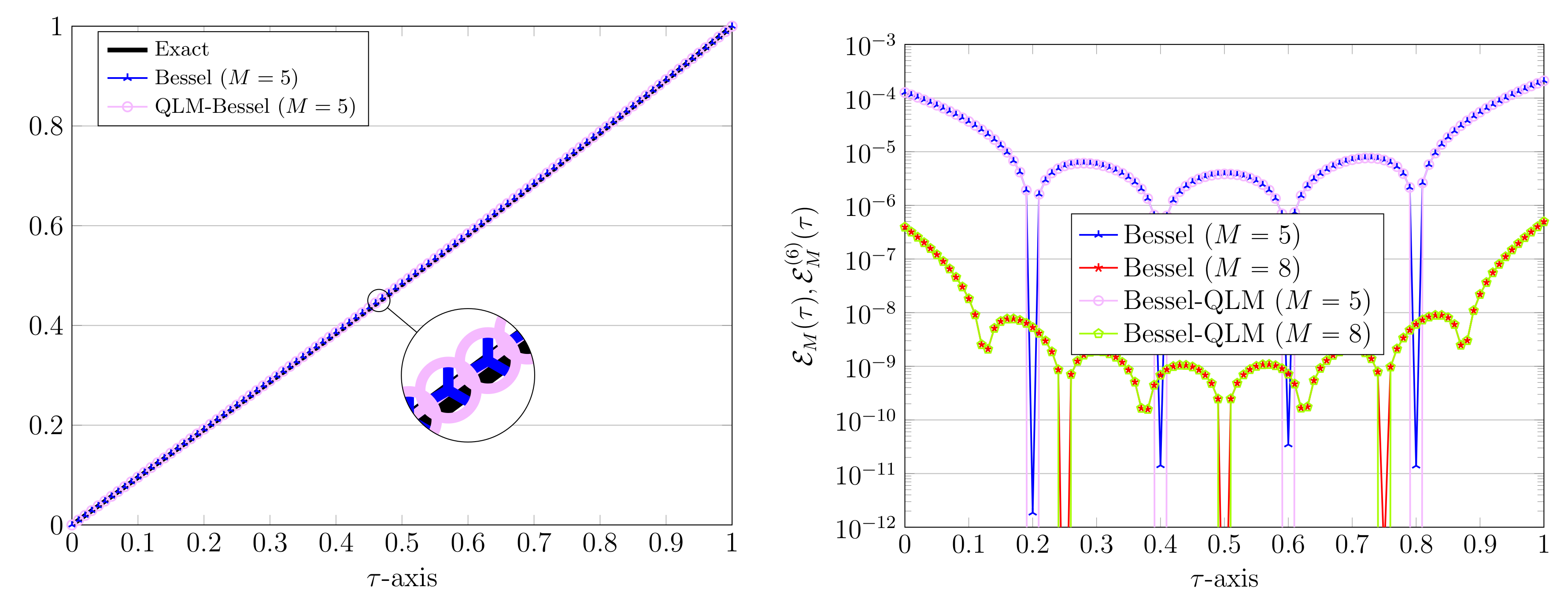
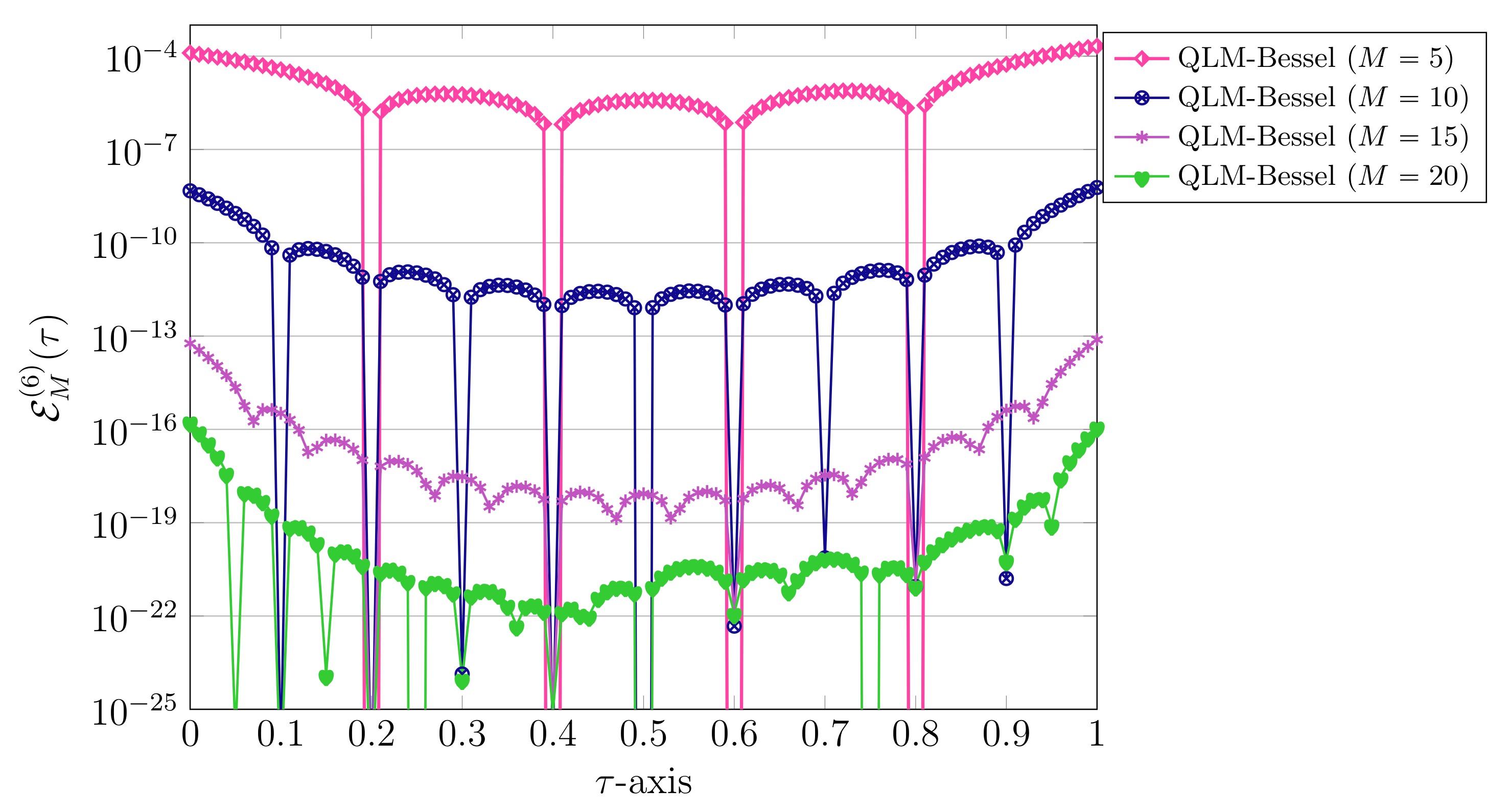
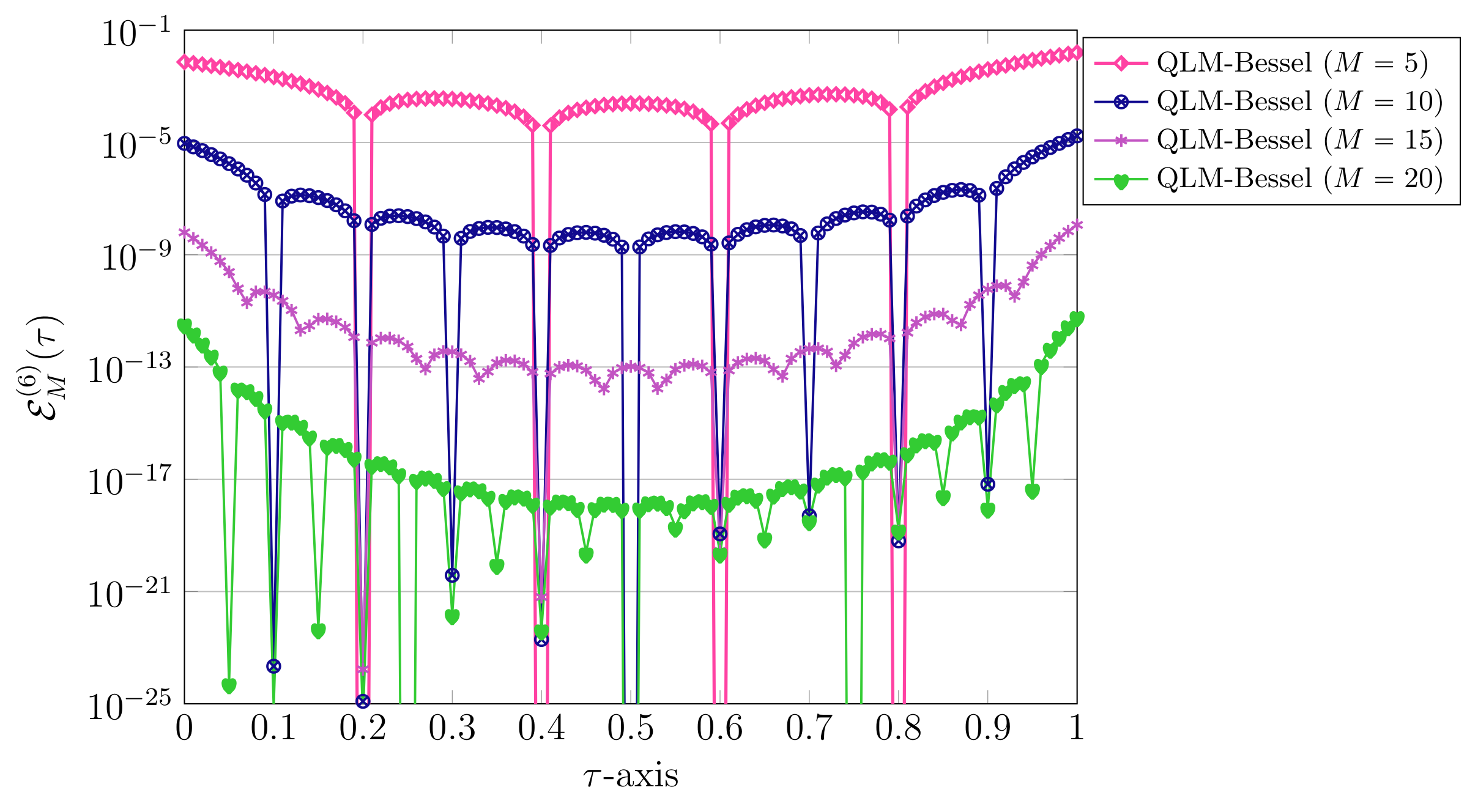
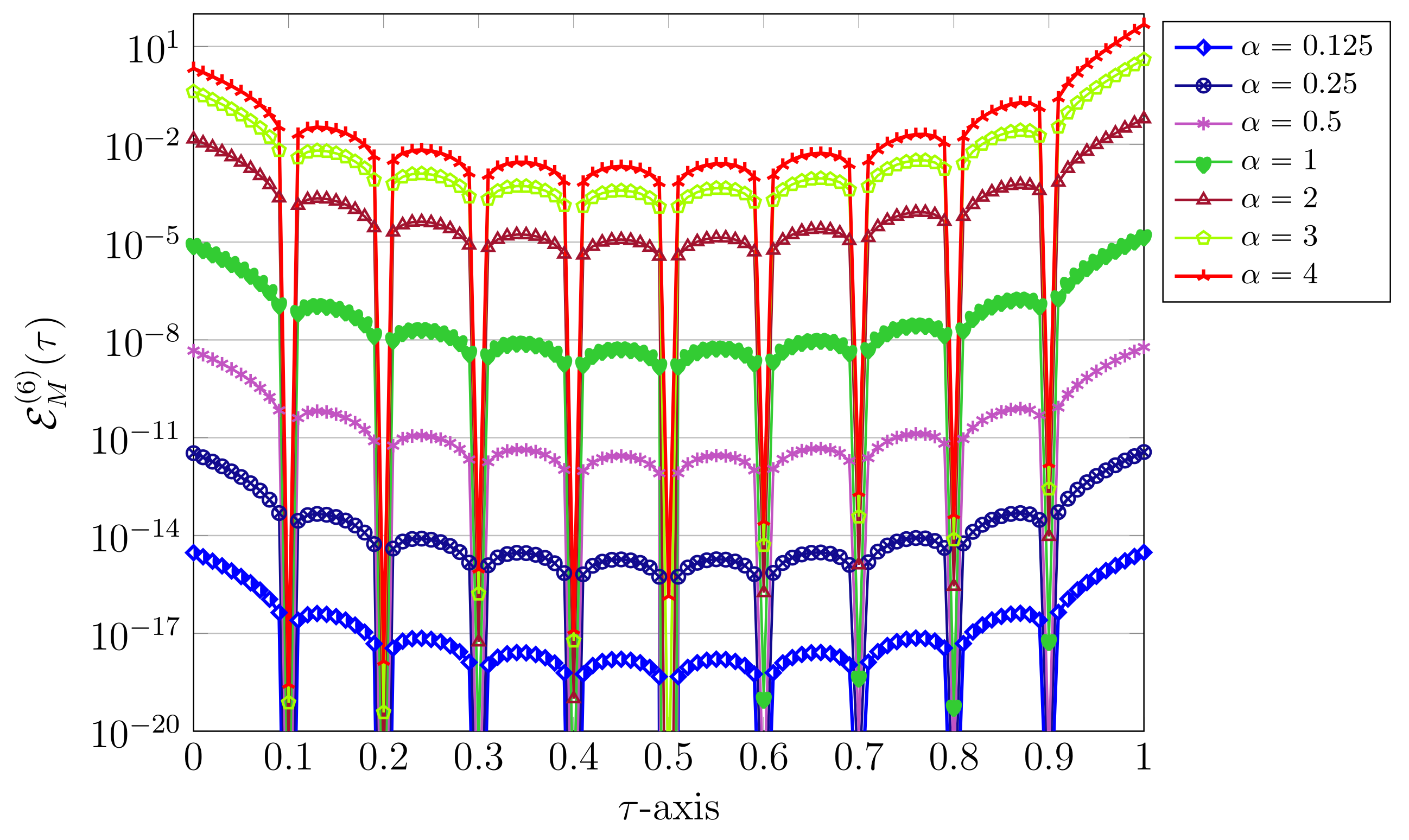
6. Graphical and Computational Results
6.1. Test Case 1:
6.2. Test Case 2:
6.3. Test Case 3:
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Markin, V.S.; Chernenko, A.A.; Chizmadehev, Y.A.; Chirkov, Y.G. Aspects of the theory of gas porous electrodes. In Fuel Cells: Their Electrochemical Kinetics; Bagotskii, V.S., Vasilev, Y.B., Eds.; Consultants Bureau: New York, NY, USA, 1966; pp. 21–33. [Google Scholar]
- Gidaspow, D.; Baker, B.S. A model for discharge of storage batteries. J. Electrochem. Soc. 1973, 120, 1005–1010. [Google Scholar] [CrossRef]
- Weibel, E.S. On the confinement of a plasma by magnetostatic fields. Phys. Fluids 1959, 2, 52–56. [Google Scholar] [CrossRef]
- Troesch, B.A. Intrinsic Difficulties in the Numerical Solution of a Boundary Value Problem; Internal Report NN-142; TRW, Inc.: Redondo Beach, CA, USA, 1960. [Google Scholar]
- Troesch, B.A. A simple approach to a sensitive two-point boundary value problem. J. Comput. Phys. 1976, 21, 279–290. [Google Scholar] [CrossRef]
- Roberts, S.; Shipman, J. On the closed form solution of Troesch’s problem. J. Comput. Phys. 1976, 21, 291–304. [Google Scholar] [CrossRef]
- Jones, D.J. Solution of Troesch’s and other two point boundary value problems by shooting techniques. J. Comput. Phys. 1973, 12, 42–434. [Google Scholar] [CrossRef]
- Chang, S. Numerical solution of Troesch’s problem by simple shooting method. Appl. Math. Comput. 2010, 216, 3303–3306. [Google Scholar] [CrossRef]
- Alias, N.; Manaf, A.; Ali, A.; Habib, M. Solving Troesch’s problem by using modified nonlinear shooting method. J. Teknolog. 2016, 78, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Scott, M. On the conversion of boundary-value problems into stable initial-value problems via several invariant imbedding algorithms. In Numerical Solutions of Boundary-Value Problems for Ordinary Differential Equations; Aziz, A.K., Ed.; Academic Press: New York, NY, USA, 1975; pp. 89–149. [Google Scholar]
- Khuri, S.A. A numerical algorithm for solving the Troesch’s problem. Int. J. Comput. Math. 2003, 80, 493–498. [Google Scholar] [CrossRef]
- Feng, X.; Mei, L.; He, G. An efficient algorithm for solving Troesch’s problem. Appl. Math. Comput. 2007, 189, 500–507. [Google Scholar] [CrossRef]
- Khuri, S.A.; Sayfy, A. Troesch’s problem: A B-Spline collocation approach. Math. Comput. Model. 2011, 54, 1907–1918. [Google Scholar] [CrossRef]
- Zarebnia, M.; Sajjadian, M. The sinc-Galerkin method for solving Troesch’s problem. Math. Comput. Model. 2012, 56, 218–228. [Google Scholar] [CrossRef]
- Nabati, M.; Jalalvand, M. Solution of Troesch’s problem through double exponential Sinc-Galerkin method. Comput. Methods Differ. Equ. 2017, 5, 141–157. [Google Scholar]
- Temimi, H. A discontinuous Galerkin finite element method for solving the Troesch’s problem. Appl. Math. Comput. 2012, 219, 521–529. [Google Scholar] [CrossRef]
- Raja, M.A.Z. Stochastic numerical treatment for solving Troesch’s problem. Infor. Sci. 2014, 279, 860–873. [Google Scholar] [CrossRef]
- Doha, E.H.; Baleanu, D.; Bahrawi, A.H.; Hafez, R.M. A Jacobi collocation method for Troesch’s problem in plasma physics. Proc. Rom. Acad. A 2014, 15, 130–138. [Google Scholar]
- Temimi, H.; Ben-Romdhane, M.; Ansari, A.R.; Shishkin, G.I. Finite difference numerical solution of Troesch’s problem on a piecewise uniform Shishkin mesh. Calcolo 2017, 54, 225–242. [Google Scholar] [CrossRef]
- Parand, K.; Ghaderi, A.; Delkhosh, M.; Pourgholi, R. A matrix formulation of the Tau method for the numerical solution of non-linear problems. arXiv 2017, arXiv:1708.06941. [Google Scholar]
- Singh, R. An iterative technique for solving a class of local and nonlocal elliptic boundary value problems. J. Math. Chem. 2020, 58, 1874–1894. [Google Scholar] [CrossRef]
- Rufai, M.A.; Ramos, H. One-step hybrid block method containing third derivatives and improving strategies for solving Bratu’s and Troesch’s problems. Numer. Math. Theor. Meth. Appl. 2020, 13, 946–972. [Google Scholar]
- Sahlan, M.N.; Afshari, H. Three new approaches for solving a class of strongly nonlinear two-point boundary value problems. Bound. Value Probl. 2021, 1, 1–21. [Google Scholar]
- Krall, H.L.; Frink, O. A new class of orthogonal polynomials: The Bessel polynomials. Trans. Am. Math. Soc. 1949, 65, 100–115. [Google Scholar] [CrossRef]
- Izadi, M.; Cattani, C. Generalized Bessel polynomial for multi-order fractional differential equations. Symmetry 2020, 12, 1260. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. An efficient approximation technique applied to a non-linear Lane-Emden pantograph delay differential model. Appl. Math. Comput. 2021, 401, 1–10. [Google Scholar]
- Izadi, M. Numerical approximation of Hunter-Saxton equation by an efficient accurate approach on long time domains. UPB Sci. Bull. Ser. A 2021, 83, 291–300. [Google Scholar]
- Izadi, M.; Cattani, C. Solution of nonlocal fractional-order boundary value problems by an effective accurate approximation method. Appl. Ana. Optim. 2021, 5, 29–44. [Google Scholar]
- Yüzbaşi, Ş. Numerical solutions of singularly perturbed one-dimensional parabolic convection-diffusion problems by the Bessel collocation method. Appl. Math. Comput. 2013, 220, 305–315. [Google Scholar] [CrossRef]
- Yüzbaşi, Ş. A collocation method based on the Bessel functions of the first kind for singular perturbated differential equations and residual correction. Math. Meth. Appl. Sci. 2015, 38, 3033–3042. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. Numerical approximations to the nonlinear fractional-order Logistic population model with fractional-order Bessel and Legendre bases. Chaos Solitons Fract. 2021, 145, 1–11. [Google Scholar] [CrossRef]
- Yüzbaşi, Ş. A collocation approach for solving two-dimensional second-order linear hyperbolic equations. Appl. Math. Comput. 2018, 338, 101–114. [Google Scholar] [CrossRef]
- Izadi, M. A comparative study of two Legendre-collocation schemes applied to fractional logistic equation. Int. J. Appl. Comput. Math. 2020, 6, 71. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M. A comparative study of the fractional-order clock chemical model. Mathematics 2020, 8, 1436. [Google Scholar] [CrossRef]
- Izadi, M.; Afshar, M. Solving the Basset equation via Chebyshev collocation and LDG methods. J. Math. Model. 2021, 9, 61–79. [Google Scholar]
- Singh, H.; Srivastava, H.M. Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Appl. Sci. 2020, 10, 2850. [Google Scholar] [CrossRef] [Green Version]
- Hashemizadeh, E.; Ebadi, M.A.; Noeiaghdam, S. Matrix method by Genocchi polynomials for solving nonlinear Volterra integral equations with weakly singular kernels. Symmetry 2020, 12, 2105. [Google Scholar] [CrossRef]
- Yüzbaşi, Ş.; Savasaneril, N.B. Hermite polynomial approach for solving singular perturb delay differential equation. J. Sci. Arts 2020, 20, 845–854. [Google Scholar] [CrossRef]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Nonlinear Boundary-Value Problems; Elsevier Publishing Company: New York, NY, USA, 1965. [Google Scholar]
- Mandelzweig, V.B.; Tabakin, F. Quasilinearization approach to nonlinear problems in physics with application to nonlinear ODEs. Comput. Phys. Commun. 2001, 141, 268–281. [Google Scholar] [CrossRef] [Green Version]
- Izadi, M. An approximation technique for first Painlevé equation. TWMS J. App. Eng. Math. 2021, 11, 739–750. [Google Scholar]
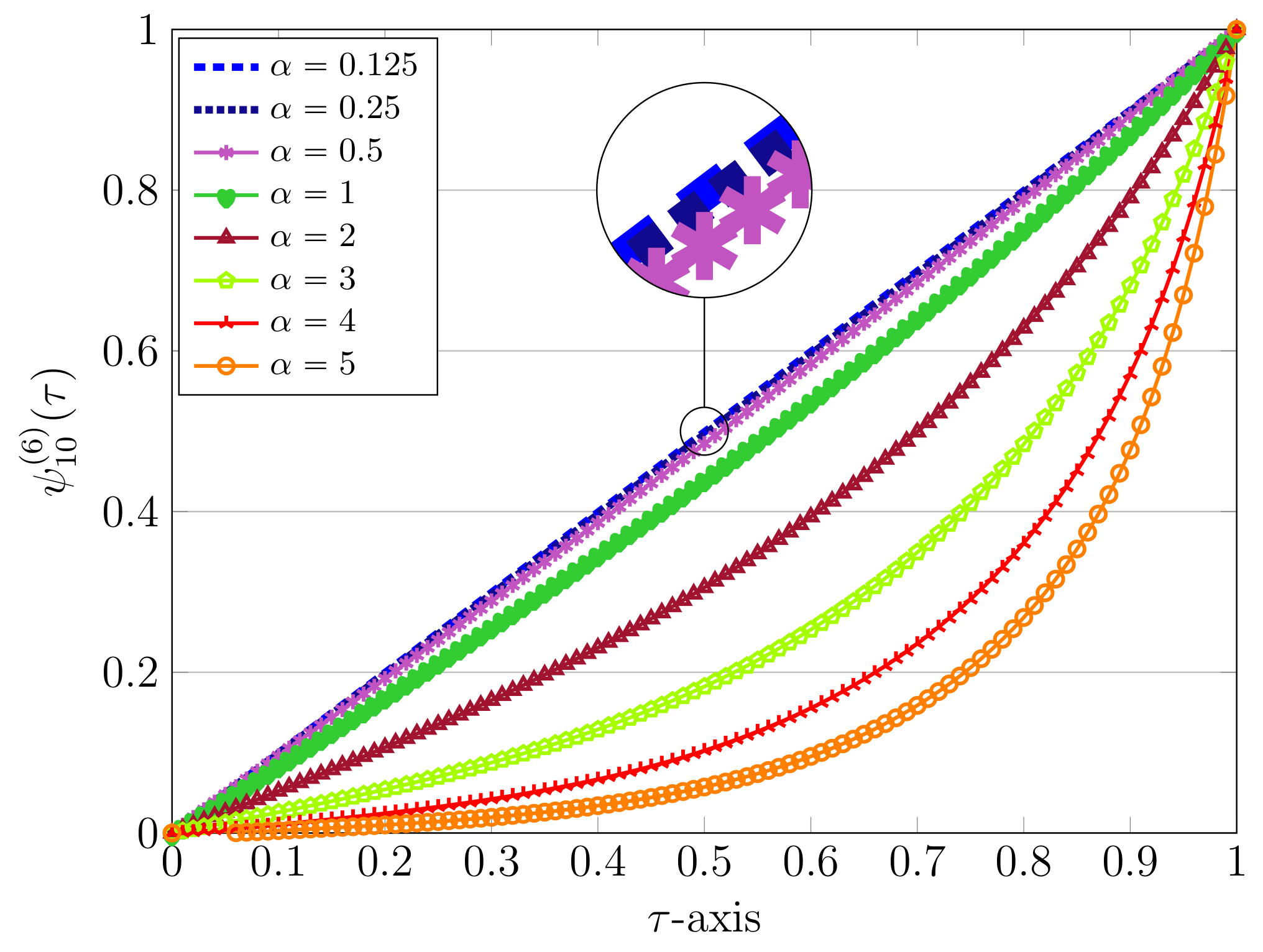
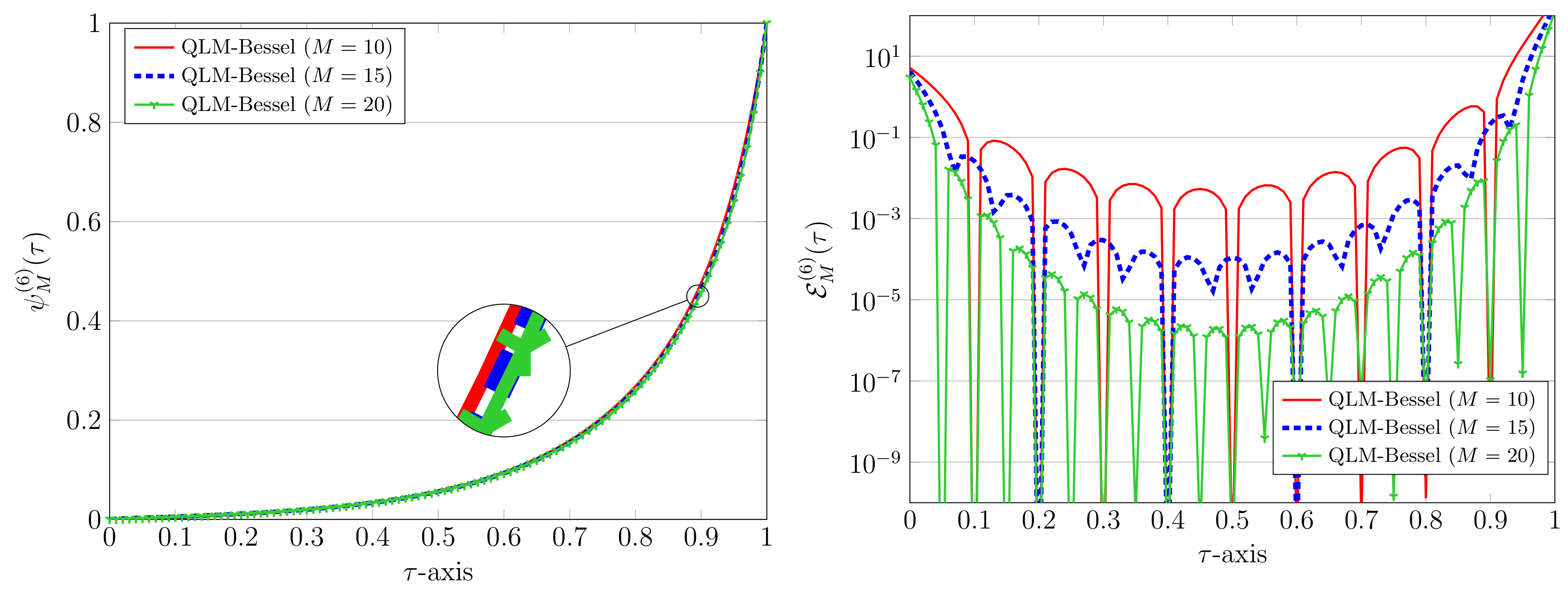
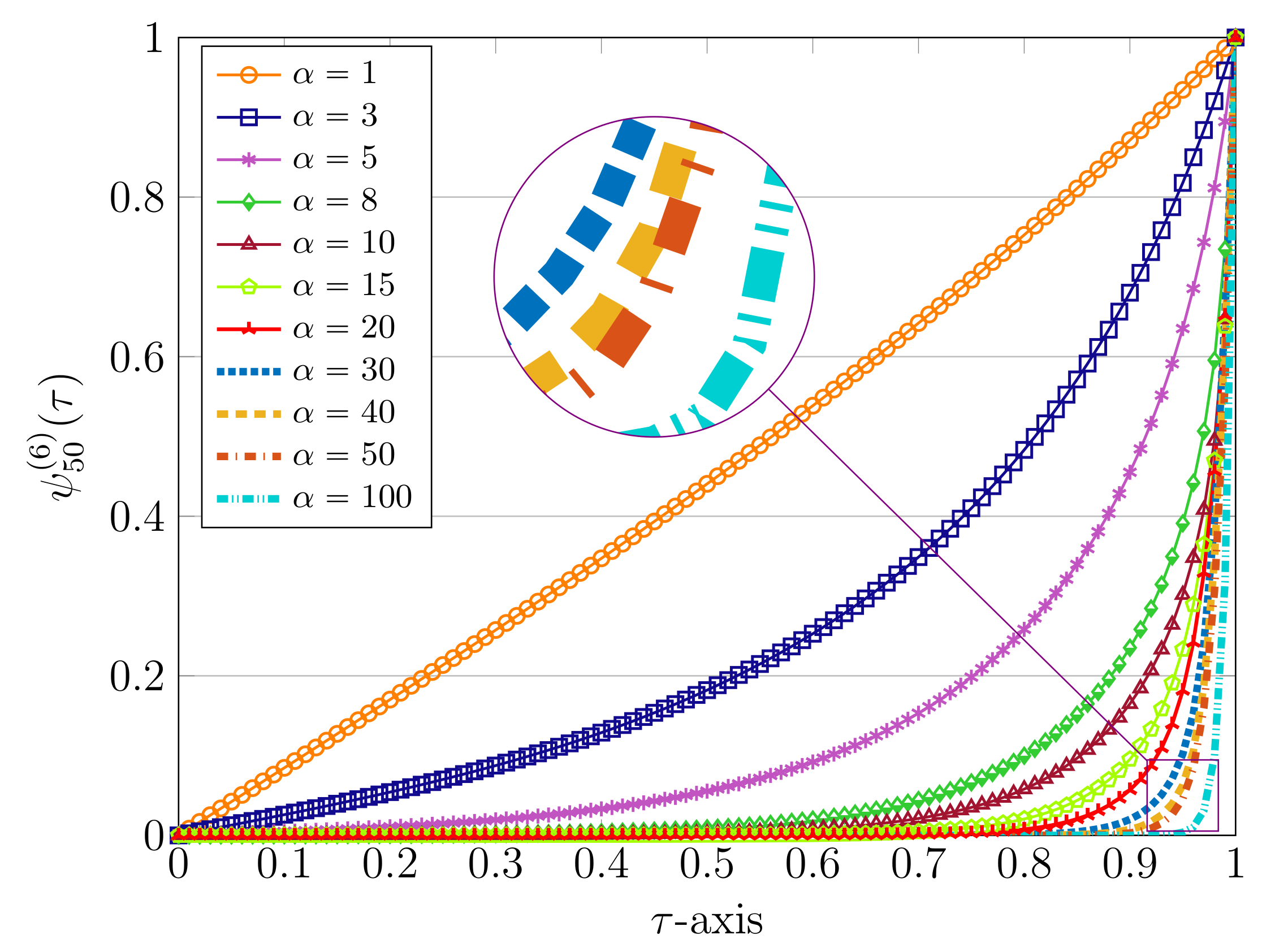
| Bessel | QLM-Bessel | SBT [20] | BSA [13] | DESG [15] | MNLSM [9] | |
|---|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izadi, M.; Yüzbaşi, Ş.; Noeiaghdam, S. Approximating Solutions of Non-Linear Troesch’s Problem via an Efficient Quasi-Linearization Bessel Approach. Mathematics 2021, 9, 1841. https://doi.org/10.3390/math9161841
Izadi M, Yüzbaşi Ş, Noeiaghdam S. Approximating Solutions of Non-Linear Troesch’s Problem via an Efficient Quasi-Linearization Bessel Approach. Mathematics. 2021; 9(16):1841. https://doi.org/10.3390/math9161841
Chicago/Turabian StyleIzadi, Mohammad, Şuayip Yüzbaşi, and Samad Noeiaghdam. 2021. "Approximating Solutions of Non-Linear Troesch’s Problem via an Efficient Quasi-Linearization Bessel Approach" Mathematics 9, no. 16: 1841. https://doi.org/10.3390/math9161841
APA StyleIzadi, M., Yüzbaşi, Ş., & Noeiaghdam, S. (2021). Approximating Solutions of Non-Linear Troesch’s Problem via an Efficient Quasi-Linearization Bessel Approach. Mathematics, 9(16), 1841. https://doi.org/10.3390/math9161841








