A Mass- and Energy-Conserving Numerical Model for a Fractional Gross–Pitaevskii System in Multiple Dimensions
Abstract
1. Introduction
2. Numerical Model
3. Structural Properties
4. Numerical Properties
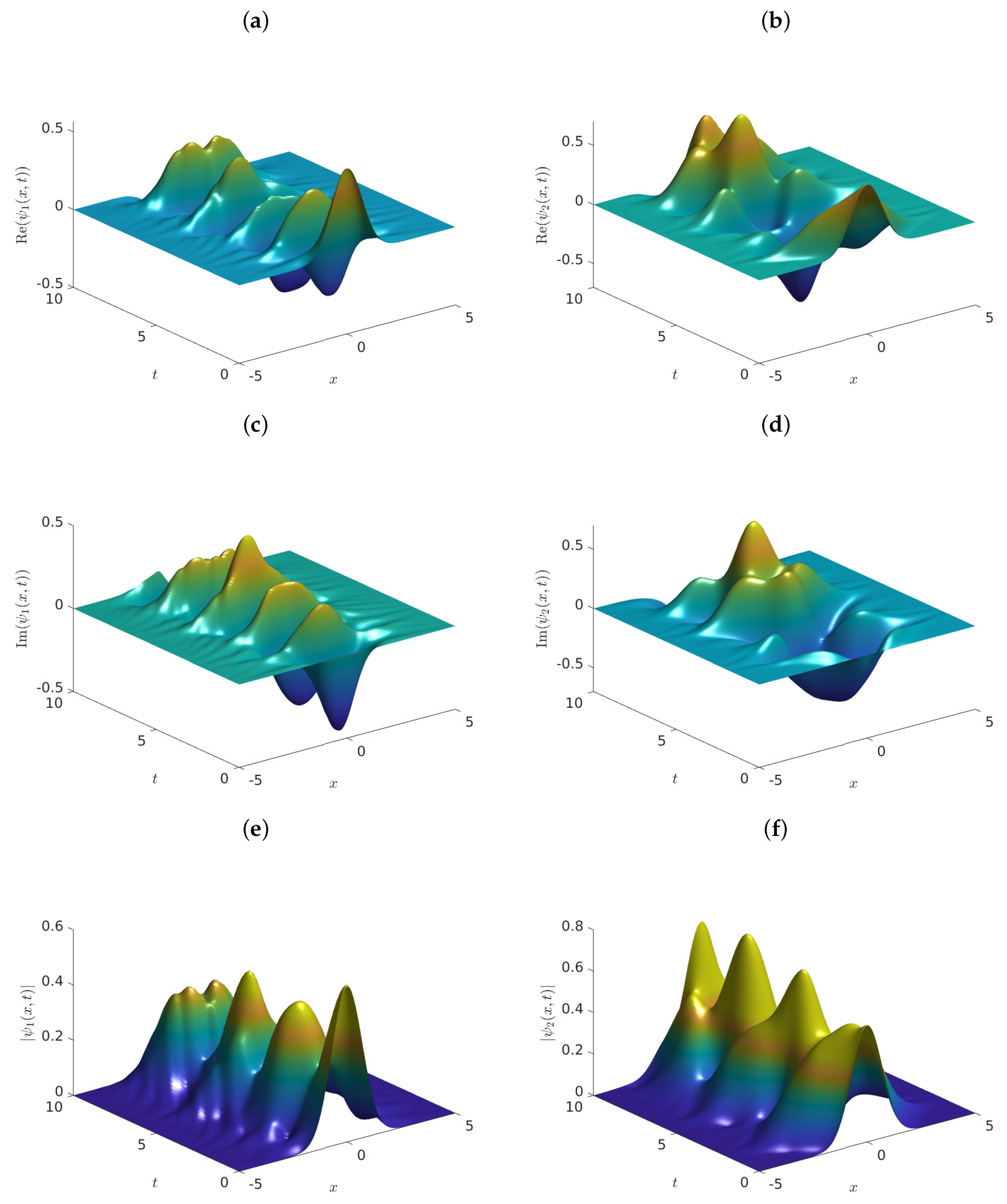
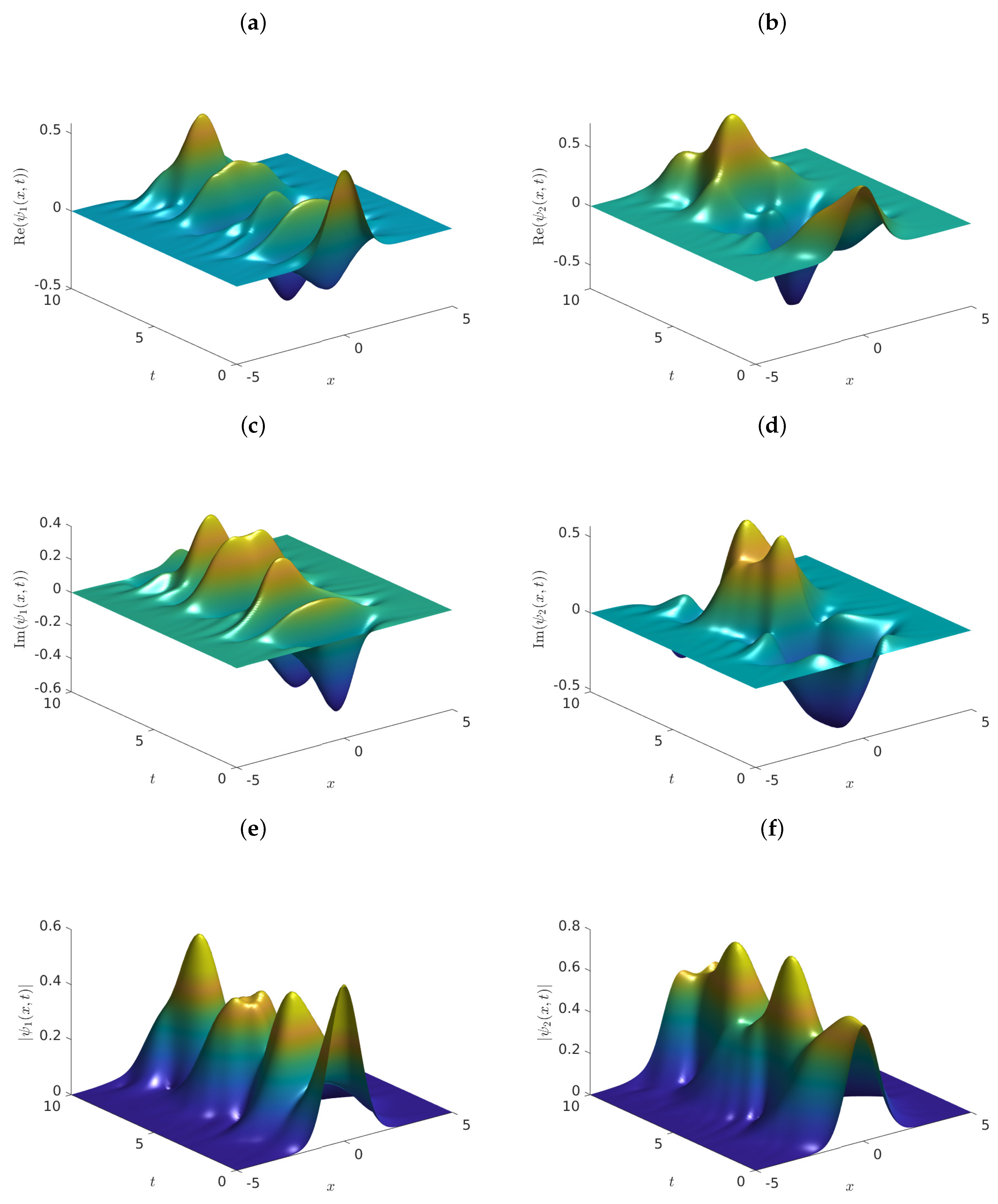
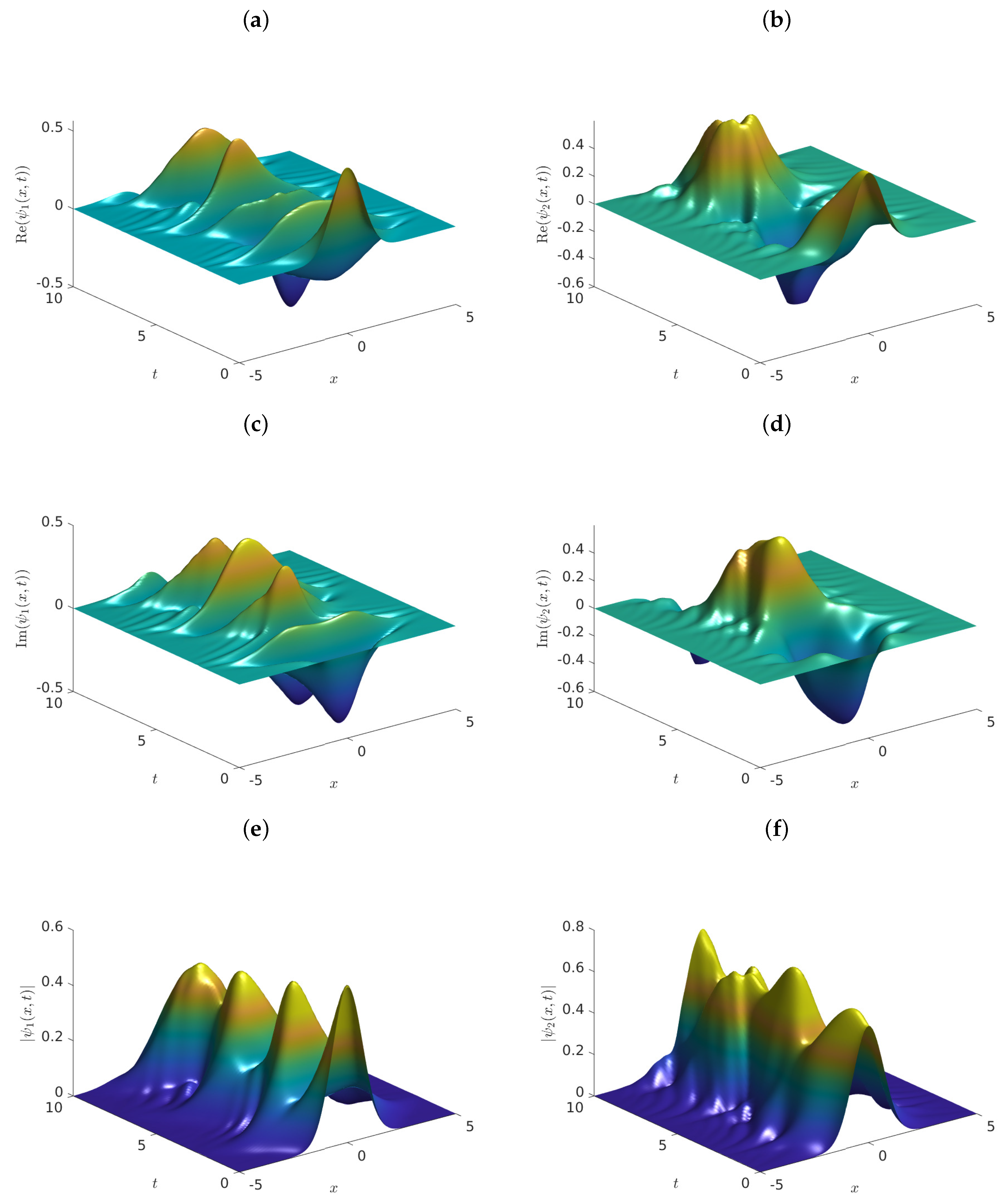
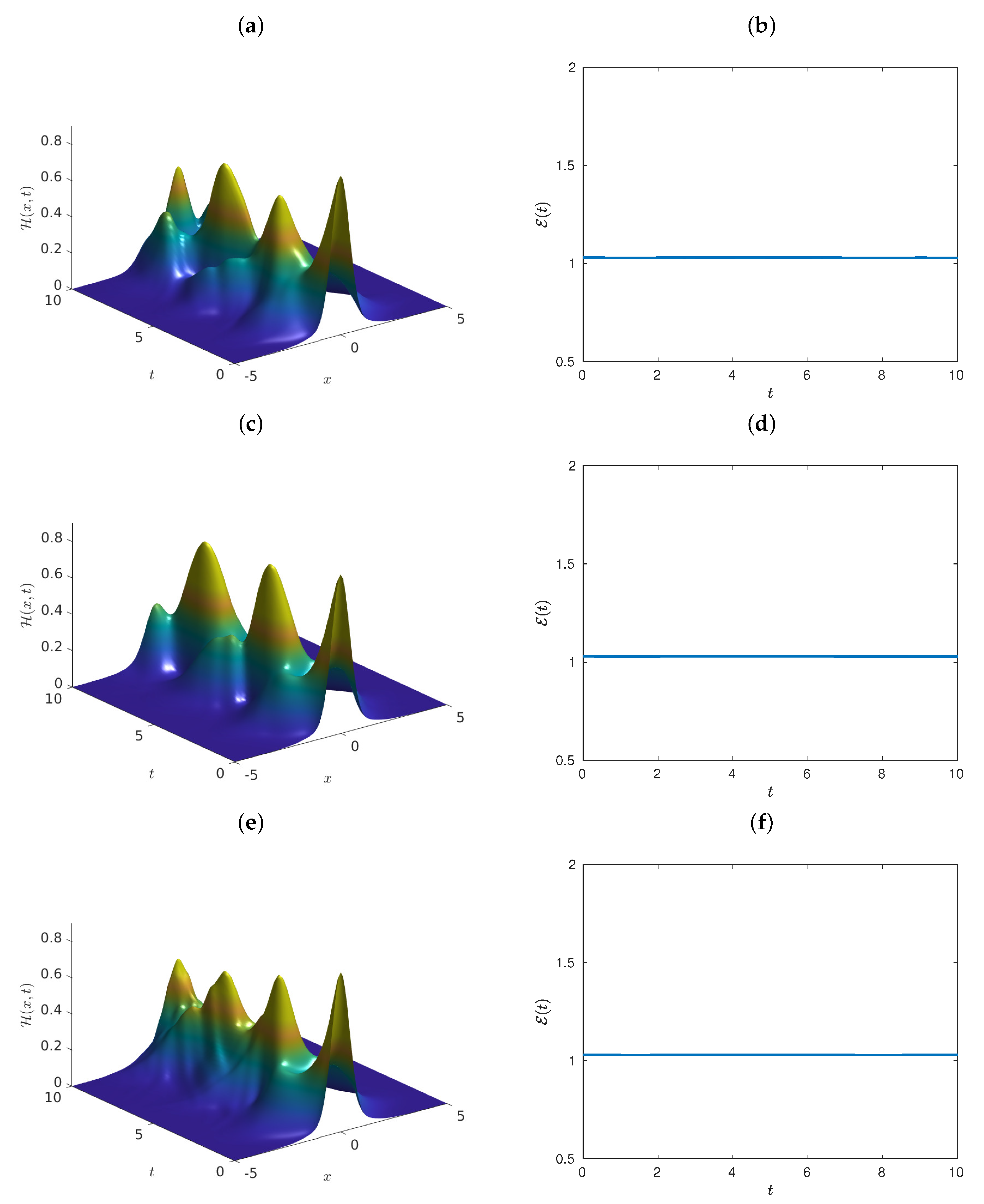
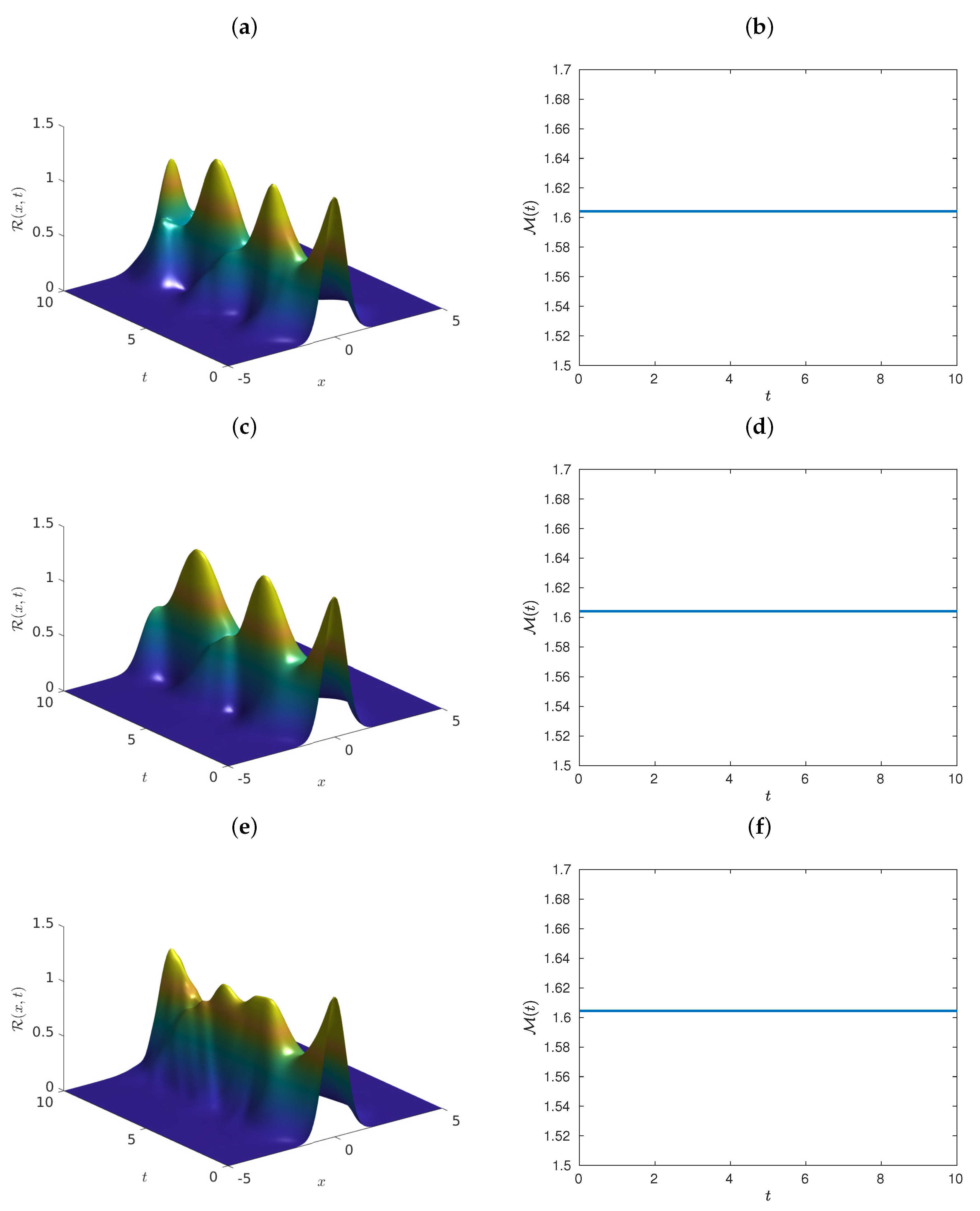
5. Numerical Simulations
- Case 1.
- and .
- Case 2.
- and .
- Case 3.
- and .
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Matlab Code
Appendix B. Fractional Calculus
References
- Adjabi, Y.; Jarad, F.; Baleanu, D.; Abdeljawad, T. On Cauchy problems with Caputo Hadamard fractional derivatives. J. Comput. Anal. Appl. 2016, 21, 661–681. [Google Scholar]
- Tan, W.; Jiang, F.L.; Huang, C.X.; Zhou, L. Synchronization for a class of fractional-order hyperchaotic system and its application. J. Appl. Math. 2012, 2012, 974639. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, C.; Hu, H.; Liu, L. Inequality estimates for the boundedness of multilinear singular and fractional integral operators. J. Inequalities Appl. 2013, 2013, 1–15. [Google Scholar] [CrossRef][Green Version]
- Liu, F.; Feng, L.; Anh, V.; Li, J. Unstructured-mesh Galerkin finite element method for the two-dimensional multi-term time–space fractional Bloch–Torrey equations on irregular convex domains. Comput. Math. Appl. 2019, 78, 1637–1650. [Google Scholar] [CrossRef]
- Hendy, A.S.; Macías-Díaz, J.E. A numerically efficient and conservative model for a Riesz space-fractional Klein–Gordon–Zakharov system. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 22–37. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Cai, Z.; Huang, J.; Huang, L. Periodic orbit analysis for the delayed Filippov system. Proc. Am. Math. Soc. 2018, 146, 4667–4682. [Google Scholar] [CrossRef]
- Chen, T.; Huang, L.; Yu, P.; Huang, W. Bifurcation of limit cycles at infinity in piecewise polynomial systems. Nonlinear Anal. Real World Appl. 2018, 41, 82–106. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Huang, L. The number and stability of limit cycles for planar piecewise linear systems of node—Saddle type. J. Math. Anal. Appl. 2019, 469, 405–427. [Google Scholar] [CrossRef]
- Bai, L.; Liu, F.; Tan, S. A new efficient variational model for multiplicative noise removal. Int. J. Comput. Math. 2020, 97, 1444–1458. [Google Scholar] [CrossRef]
- Yuan, H. Convergence and stability of exponential integrators for semi-linear stochastic variable delay integro-differential equations. Int. J. Comput. Math. 2020, 98, 903–932. [Google Scholar] [CrossRef]
- Aldhaifallah, M.; Tomar, M.; Nisar, K.; Purohit, S. Some new inequalities for (k, s)-fractional integrals. J. Nonlinear Sci. Appl. 2016, 9, 5374–5381. [Google Scholar] [CrossRef]
- Houas, M. Certain Weighted Integral Inequalities Involving the Fractional Hypergeometric Operators. Sci. Ser. A Math. Sci. 2016, 27, 87–97. [Google Scholar]
- Houas, M. On some generalized integral inequalities for Hadamard fractional integrals. Med. J. Model. Simul. 2018, 9, 43–52. [Google Scholar]
- Baleanu, D.; Mohammed, P.O.; Vivas-Cortez, M.; Rangel-Oliveros, Y. Some modifications in conformable fractional integral inequalities. Adv. Differ. Equ. 2020, 2020, 1–25. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Mohammed, P.O.; Kashuri, A. New modified conformable fractional integral inequalities of Hermite–Hadamard type with applications. J. Funct. Spaces 2020, 2020, 4352357. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Abdeljawad, T. Integral inequalities for a fractional operator of a function with respect to another function with nonsingular kernel. Adv. Differ. Equ. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Brevik, I. A new version of the Hermite–Hadamard inequality for Riemann–Liouville fractional integrals. Symmetry 2020, 12, 610. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering; Academic Press: London, UK, 1999. [Google Scholar]
- Serna-Reyes, A.J.; Macías-Díaz, J. Theoretical analysis of a conservative finite-difference scheme to solve a Riesz space-fractional Gross—Pitaevskii system. J. Comput. Appl. Math. 2021, 113413. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Riesz potential operators and inverses via fractional centred derivatives. Int. J. Math. Math. Sci. 2006, 2006, 48391. [Google Scholar] [CrossRef]
- Wang, X.; Liu, F.; Chen, X. Novel second-order accurate implicit numerical methods for the Riesz space distributed-order advection-dispersion equations. Adv. Math. Phys. 2015, 2015, 590435. [Google Scholar] [CrossRef]
- Farmakis, I.; Moskowitz, M. Fixed Point Theorems and Their Applications; World Scientific: Singapore, 2013. [Google Scholar]
- Macías-Díaz, J.E. An explicit dissipation-preserving method for Riesz space-fractional nonlinear wave equations in multiple dimensions. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 67–87. [Google Scholar] [CrossRef]
- Ferreira, R.A. A discrete fractional Gronwall inequality. Proc. Am. Math. Soc. 2012, 140, 1605–1612. [Google Scholar] [CrossRef]
- Serna-Reyes, A.J.; Macías-Díaz, J.E.; Reguera, N. A Convergent Three-Step Numerical Method to Solve a Double-Fractional Two-Component Bose–Einstein Condensate. Mathematics 2021, 9, 1412. [Google Scholar] [CrossRef]
- Macías-Díaz, J.; Medina-Ramírez, I. An implicit four-step computational method in the study on the effects of damping in a modified α-Fermi—Pasta—Ulam medium. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3200–3212. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E.; Puri, A. A numerical method with properties of consistency in the energy domain for a class of dissipative nonlinear wave equations with applications to a Dirichlet boundary-value problem. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. Appl. Math. Mech. 2008, 88, 828–846. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. On the solution of a Riesz space-fractional nonlinear wave equation through an efficient and energy-invariant scheme. Int. J. Comput. Math. 2019, 96, 337–361. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Zaslavsky, G.M. Conservation laws and Hamilton’s equations for systems with long-range interaction and memory. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1860–1878. [Google Scholar] [CrossRef]
- Tang, T.; Yu, H.; Zhou, T. On energy dissipation theory and numerical stability for time-fractional phase-field equations. SIAM J. Sci. Comput. 2019, 41, A3757–A3778. [Google Scholar] [CrossRef]
- Tarasov, V.E. Continuous limit of discrete systems with long-range interaction. J. Phys. A Math. Gen. 2006, 39, 14895. [Google Scholar] [CrossRef]
- Tarasov, V.E. Lattice model of fractional gradient and integral elasticity: Long-range interaction of Grünwald–Letnikov–Riesz type. Mech. Mater. 2014, 70, 106–114. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. A numerically efficient dissipation-preserving implicit method for a nonlinear multidimensional fractional wave equation. J. Sci. Comput. 2018, 77, 1–26. [Google Scholar] [CrossRef]
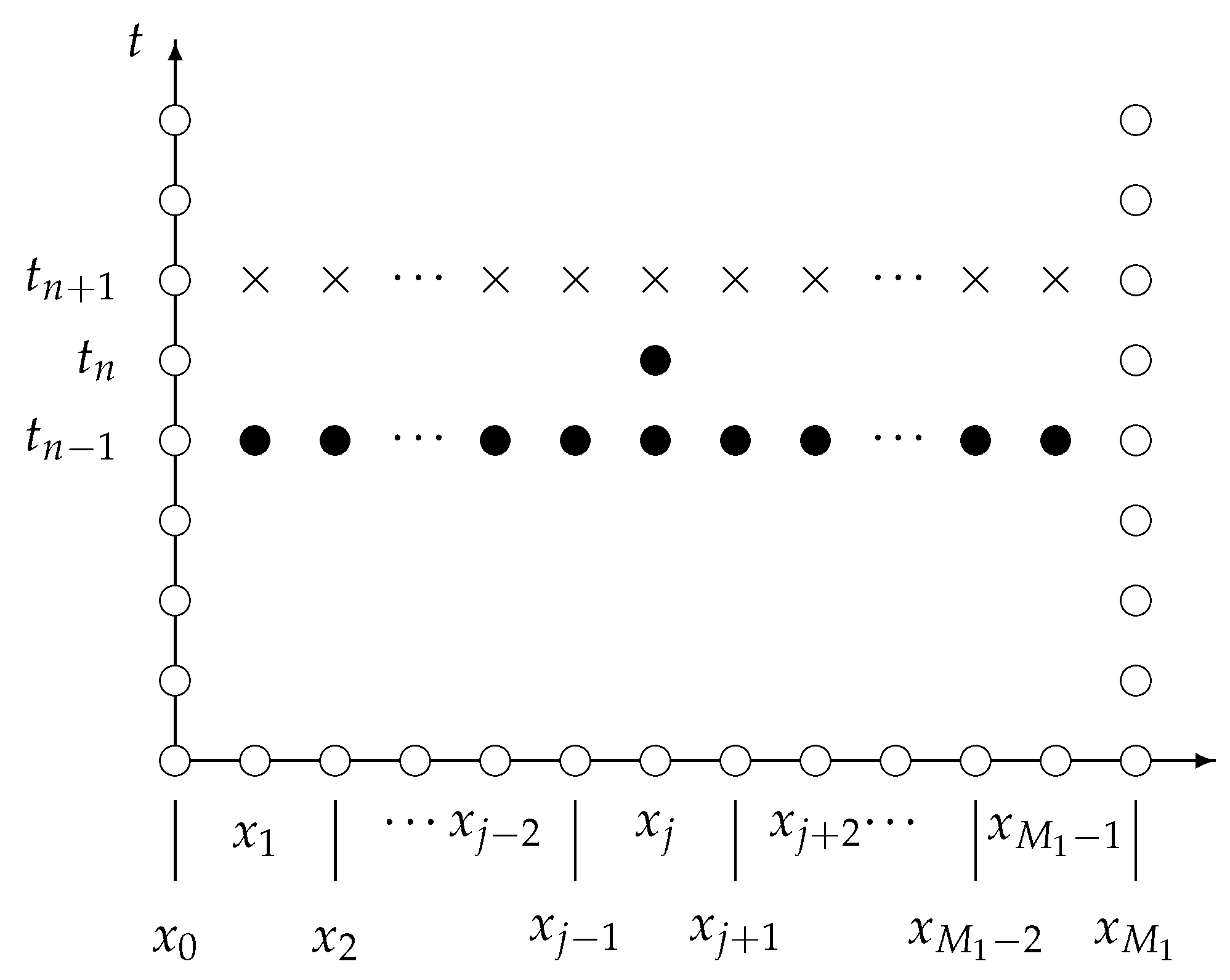
| p | T | D | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 10 | 2 |
| (a) Temporal study of convergence | ||||||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| (b) Spatial study of convergence | ||||||
| h | ||||||
| − | − | − | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serna-Reyes, A.J.; Macías-Díaz, J.E. A Mass- and Energy-Conserving Numerical Model for a Fractional Gross–Pitaevskii System in Multiple Dimensions. Mathematics 2021, 9, 1765. https://doi.org/10.3390/math9151765
Serna-Reyes AJ, Macías-Díaz JE. A Mass- and Energy-Conserving Numerical Model for a Fractional Gross–Pitaevskii System in Multiple Dimensions. Mathematics. 2021; 9(15):1765. https://doi.org/10.3390/math9151765
Chicago/Turabian StyleSerna-Reyes, Adán J., and Jorge E. Macías-Díaz. 2021. "A Mass- and Energy-Conserving Numerical Model for a Fractional Gross–Pitaevskii System in Multiple Dimensions" Mathematics 9, no. 15: 1765. https://doi.org/10.3390/math9151765
APA StyleSerna-Reyes, A. J., & Macías-Díaz, J. E. (2021). A Mass- and Energy-Conserving Numerical Model for a Fractional Gross–Pitaevskii System in Multiple Dimensions. Mathematics, 9(15), 1765. https://doi.org/10.3390/math9151765







