Bounds on the Rate of Convergence for ${\mathit{M}}_{\mathit{t}}^{\mathit{X}}$/${\mathit{M}}_{\mathit{t}}^{\mathit{X}}$/1 Queueing Models

Abstract

We apply the method of differential inequalities for the computation of upper bounds for the rate of convergence to the limiting regime for one specific class of (in)homogeneous continuous-time Markov chains. Such an approach seems very general; the corresponding description and bounds were considered earlier for finite Markov chains with analytical in time intensity functions. Now we generalize this method to locally integrable intensity functions. Special attention is paid to the situation of a countable Markov chain. To obtain these estimates, we investigate the corresponding forward system of Kolmogorov differential equations as a differential equation in the space of sequences $l_1$.

1. Introduction

In this paper we consider the problem of finding the upper bounds for the rate of convergence for some (in)homogeneous continuous-time Markov chains.

To obtain these estimates, we investigate the corresponding forward system of Kolmogorov differential equations.

Consideration is given to classic inhomogeneous birth–death processes and to special inhomogeneous chains with transitions intensities, which do not depend on the current state. Namely, let $\left\{X\right(t),t\ge 0\}$ be an inhomogeneous continuous-time Markov chain with the state space $\mathcal{X}=\{0,1,2,\dots ,\}$. Denote by $p_{ij}(s,t)=P\left\{X\left(t\right)=j\left|X\left(s\right)=i\right.\right\}$, $i,j\ge 0,0\le s\le t$, the transition probabilities of $X\left(t\right)$ and by $p_i\left(t\right)=P\left\{X\left(t\right)=i\right\}$—the probability that $X\left(t\right)$ is in state i at time t. Let $\mathbf{p}\left(t\right)={\left(p_0\left(t\right),p_1\left(t\right),\dots ,\right)}^T$ be probability distribution vector at instant t. Throughout the paper it is assumed that in a small time interval h the possible transitions and their associated probabilities are

$$p_{ij}(t,t+h)=\left\{\begin{array}{cc}{q}_{ij}\left(t\right)h+{\alpha }_{ij}\left(t,h\right),& \mathrm{if}j\ne i,\\ 1-{\displaystyle \sum _{k\in \mathcal{X},k\ne i}}{q}_{ik}\left(t\right)h+{\alpha }_i\left(t,h\right),& \mathrm{if}j=i,\end{array}\right.$$

where ${sup}_{i\ge 0}{\sum }_{j\ge 0}|{\alpha }_{ij}(t,h)|=o\left(h\right)$, for any $t\ge 0$. We also suppose that the transition intensities $q_{ij}\left(t\right)\ge 0$ are arbitrary non-random functions of t, locally integrable on $[0,\infty )$ and, moreover, that there exists a positive number L such that

$$\underset{i\in \mathcal{X}}{sup}\left(\sum _{k\in \mathcal{X},k\ne i}{q}_{ik}\left(t\right)\right)\le L<\infty ,$$

(1)

for almost all $t\ge 0$. Then the probabilistic dynamics of the process $X\left(t\right)$ is given by the forward Kolmogorov system

$$\frac{d}{dt}\mathbf{p}\left(t\right)=A\left(t\right)\mathbf{p}\left(t\right),$$

(2)

where $A\left(t\right)$ is the transposed intensity matrix i.e., $a_{ij}\left(t\right)=q_{ji}\left(t\right)$, $i,j\in \mathcal{X}$.

We can consider (2) as the differential equation with bounded operator function in the space of sequences $l_1$ (see details, for instance in [1]) and apply all results of [2].

Throughout this paper by $\parallel ·\parallel$ (or by ${\parallel ·\parallel }_1$ if ambiguity is possible) we denote the $l_1$-norm, i.e., $\parallel \mathbf{p}\left(t\right)\parallel ={\sum }_{i\in \mathcal{X}}|p_i\left(t\right)|$ and $\parallel A\left(t\right)\parallel ={sup}_{j\in \mathcal{X}}{\sum }_{i\in \mathcal{X}}|a_{ij}\left(t\right)|$. Let $\Omega$ be a set of all stochastic vectors, i.e., $l_1$ vectors with non-negative coordinates and unit norm. Then $\parallel A\left(t\right)\parallel \le 2L$ for almost all $t\ge 0$, and $\mathbf{p}\left(s\right)\in \Omega$ implies $\mathbf{p}\left(t\right)\in \Omega$ for any $0\le s\le t$.

Recall that a Markov chain $X\left(t\right)$ is called weakly ergodic, if $\parallel {\mathbf{p}}^{*}\left(t\right)-{\mathbf{p}}^{**}\left(t\right)\parallel \to 0$ as $t\to \infty$ for any initial conditions ${\mathbf{p}}^{*}\left(0\right)$ and ${\mathbf{p}}^{**}\left(0\right)$, where ${\mathbf{p}}^{*}\left(t\right)$ and ${\mathbf{p}}^{**}\left(t\right)$ are the corresponding solutions of (2).

We consider, as in [3], the four classes of of Markov chains $X\left(t\right)$ with the following transition intensities:

(i) $q_{ij}\left(t\right)=0$ for any $t\ge 0$ if $|i-j|>1$ and both $q_{i,i+1}\left(t\right)={\lambda }_i\left(t\right)$ and $q_{i,i-1}\left(t\right)={\mu }_i\left(t\right)$ may depend on i;

(ii) $q_{i,i-k}\left(t\right)=0$ for $k>1$, $q_{i,i-1}\left(t\right)={\mu }_i\left(t\right)$ may depend on i; and $q_{i,i+k}\left(t\right)$, $k\ge 1$, depend only on k and does not depend on i;

(iii) $q_{i,i+k}\left(t\right)=0$ for $k>1$, $q_{i,i+1}\left(t\right)={\lambda }_i\left(t\right)$ may depend on i; and $q_{i,i-k}\left(t\right)$, $k\ge 1$, depend only on k and does not depend on i;

(iv) both $q_{i,i-k}\left(t\right)$ and $q_{i,i+k}\left(t\right)$, $k\ge 1$, depend only on k and do not depend on i.

Each such process can be considered as the queue-length process for the corresponding queueing system $M_t^X/M_t^X/1$.

Then type (i) transitions describe Markovian queues with possibly state-dependent arrival and service intensities (for example, the classic $M_n\left(t\right)/M_n\left(t\right)/1$ queue); type (ii) transitions allow consideration of Markovian queues with state-independent batch arrivals and state-dependent service intensity; type (iii) transitions lead to Markovian queues with possible state-dependent arrival intensity and state-independent batch service; type (iv) transitions describe Markovian queues with state-independent batch arrivals and batch service. We can refer to them as a $M_t^X/M_t^X/1$ queueing model following the original paper [4], see also [3,5,6].

The paper is organized as follows. Section 2 introduces a description of the problem. Section 3 considers the explicit form of the reduced intensity matrices. In Section 4, we obtain upper bounds for the rate of convergence. Section 5 concludes the paper.

2. Preliminaries

The problem of estimating the rate of convergence, like the very fact of convergence, is very important for studying the long-run (limiting) behavior of continuous time Markov chains with time varying intensities, see detailed discussion, examples and references in [7]. The simplest and most convenient for studying the rate of convergence to the limiting regime is the method of the logarithmic norm, see, for example [1,3,8].

However, there are situations in which this approach does not give good results.

Next, we show the possibility of using a different approach in such cases, namely the method of differential inequalities.

Another (but similar) approach is to use piecewise-line Lyapunov functions, see, for example, [9,10,11,12].

Consider here the two simplest examples of bounding the rate of convergence for differential equations.

Let firstly

$$\frac{d\mathbf{x}}{dt}=P\mathbf{x}$$

be a system of differential equations with $\mathbf{x}={(x_1,x_2)}^T$, and $P=\left(\begin{array}{cc}-5& 8\\ 2& -5\end{array}\right)$. Put $d_1=1,d_2=2$, and $\mathbf{z}=D\mathbf{x}={(d_1{x}_1,d_2{x}_2)}^T$. Then $\frac{d\mathbf{z}}{dt}=DP{D}^{-1}\mathbf{z}$, both column sums for $P^{*}=DP{D}^{-1}$ equal to $-1$. Hence the logarithmic norm $\gamma \left(P^{*}\right)={sup}_i\left(p_{ii}^{*}+{\sum }_{j\ne i}{p}_{ji}^{*}\right)$ equals $-1$, and we obtain a sharp upper bound on the rate of convergence $\parallel \mathbf{z}\left(t\right)\parallel \le e^{-t}\parallel \mathbf{z}\left(0\right)\parallel$. Such a situation is typical if the matrix of the considered system is essentially non-negative (i.e., all off-diagonal elements are non-negative for any $t\ge 0$). Note that the corresponding eigenvalues of P are $-1,-9$.

On the other hand, let $P=\left(\begin{array}{cc}-3& 8\\ -2& -3\end{array}\right)$. Then corresponding eigenvalues of P are $-3\pm 4i$. On the other hand, the “weighting” logarithmic norm P is not less than 1. In principle, here it is also possible to reduce the matrix to the exact value of the logarithmic norm ($-3$), see [2], but the corresponding transformation will be complex and difficult to implement. The best result ($C{e}^{-3t}$) here can be obtained using the Lyapunov function (which does not work well in a countable situation), but the use of differential inequalities gives us an estimate like $C{e}^{-(3+ϵ)t}$ for any positive $ϵ$, see the corresponding description below, in Section 4. This approach deals with the sums of the columns for various combinations of the signs of the coordinates of the solutions of the system; it is described further in Section 4. It was first proposed in our recent papers; see [3] for the case of finite Markov chain with analytical (in t) intensities.

In this paper, it is shown that this method can be applied in a more general situation of locally integrable intensities, and, which is most difficult, for a countable chain that does not lend itself to direct reasoning and requires rather fine approximation estimates.

3. Explicit Forms of the Reduced Intensity Matrices

Due to the normalization condition $p_0\left(t\right)=1-{\sum }_{i\ge 1}{p}_i\left(t\right)$, we can rewrite the system (2) as follows:

$$\frac{d}{dt}\mathbf{z}\left(t\right)=B\left(t\right)\mathbf{z}\left(t\right)+\mathbf{f}\left(t\right),$$

(3)

where

$$\mathbf{f}\left(t\right)={\left(a_{10}\left(t\right),a_{20}\left(t\right),\dots \right)}^T,\mathbf{z}\left(t\right)={\left(p_1\left(t\right),p_2\left(t\right),\dots \right)}^T,$$

$$B\left(t\right)=\left(\begin{array}{ccccc}{a}_{11}-a_{10}& a_{12}-a_{10}& \cdots & a_{1r}-a_{10}& \cdots \\ a_{21}-a_{20}& a_{22}-a_{20}& \cdots & a_{2r}-a_{20}& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{r1}-a_{r0}& a_{r2}-a_{r0}& \cdots & a_{rr}-a_{r0}& \cdots \\ ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right).$$

(4)

Let $\mathbf{y}\left(t\right)={\mathbf{z}}^{*}\left(t\right)-{\mathbf{z}}^{**}\left(t\right)$ be the difference of two solutions of system (3), and $\mathbf{y}\left(t\right)={\left(y_1\left(t\right),y_2\left(t\right),\dots ,\right)}^T$. Then, in contrast to the coordinates of the vector $\mathbf{p}\left(t\right)$, the coordinates of the vector $\mathbf{y}\left(t\right)$ have arbitrary signs.

Consider now the ‘homogeneous’ system

$$\frac{d}{dt}\mathbf{y}\left(t\right)=B\left(t\right)\mathbf{y}\left(t\right),$$

(5)

corresponding to (3). As was firstly noticed in [13], it is more convenient to study the rate of convergence using the transformed version $B^{*}\left(t\right)$ of $B\left(t\right)$ given by $B^{*}\left(t\right)=TB\left(t\right)T^{-1}$, where T is the upper triangular matrix of the form

$$T=\left(\begin{array}{cccccc}1& 1& 1& \cdots & 1& \cdots \\ 0& 1& 1& \cdots & 1& \cdots \\ 0& 0& 1& \cdots & 1& \cdots \\ ⋮& ⋮& ⋮& \ddots & \cdots \\ 0& 0& 0& \cdots & 1& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right).$$

(6)

Let $\mathbf{u}\left(t\right)=T\mathbf{y}\left(t\right)$. Then the system (5) can be rewritten in the form

$$\frac{d}{dt}\mathbf{u}\left(t\right)=B^{*}\left(t\right)\mathbf{u}\left(t\right),$$

(7)

where $\mathbf{u}\left(t\right)={\left(u_1\left(t\right),u_2\left(t\right),\dots \right)}^T$ is the vector with the coordinates of arbitrary signs. If one of the two matrices $B^{*}\left(t\right)$ or $B\left(t\right)$ is known, the other is also (uniquely) defined.

The approach based on the differential inequalities (see [3]) seems to be the most general. On the other hand, if $B^{*}\left(t\right)$ is essentially non-negative (i.e., all off-diagonal elements are non-negative for any $t\ge 0$), then the method based on the logarithmic norm gives the same results, but in a much more visual form, see [3].

Let us write out the form of the matrix $B^{*}\left(t\right)$ for each class of chains; in more detail, the corresponding transformations can be seen in [3].

For $X\left(t\right)$ belonging to class $\left(\mathrm{i}\right)$ (inhomogeneous birth–death process) one has

$$B^{*}\left(t\right)=TB\left(t\right)T^{-1}=$$

$$\left(\begin{array}{ccccccc}-\left({\lambda }_0+{\mu }_1\right)& {\mu }_1& 0& \cdots & 0& \cdots & \cdots \\ {\lambda }_1& -\left({\lambda }_1+{\mu }_2\right)& {\mu }_2& \cdots & 0& \cdots & \cdots \\ \ddots & \ddots & \ddots & \ddots & \ddots & \cdots \\ 0& \cdots & \cdots & {\lambda }_{r-1}& -\left({\lambda }_{r-1}+{\mu }_r\right)& {\mu }_r& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right).$$

(8)

For $X\left(t\right)$ belonging to class $\left(\mathrm{ii}\right)$ (which corresponds to the queueing system with batch arrivals and single services), one has

$$B^{*}\left(t\right)=TB\left(t\right)T^{-1}=\left(\begin{array}{ccccc}{a}_{11}& {\mu }_1& 0& \cdots & 0\\ a_1& a_{22}& {\mu }_2& \cdots & 0\\ a_2& a_1& a_{33}& {\mu }_3& \cdots & \\ \ddots & \ddots & \ddots & \ddots & \ddots \\ \ddots & \ddots & \ddots & \ddots & \ddots \end{array}\right).$$

(9)

For $X\left(t\right)$ belonging to class $\left(\mathrm{iii}\right)$ (which corresponds to the queueing system with single arrivals and group services), one has $B^{*}\left(t\right)=TB\left(t\right)T^{-1}=$

$$\left(\begin{array}{ccccc}-\left({\lambda }_0+b_1\right)& b_1-b_2& b_2-b_3& \cdots & \cdots \\ {\lambda }_1& -\left({\lambda }_1+\sum _{i\le 2}{b}_i\right)& b_1-b_3& \cdots & \cdots \\ \ddots & \ddots & \ddots & \ddots & \ddots \\ 0& \cdots & \cdots & {\lambda }_{r-1}& -\left({\lambda }_{r-1}+{\displaystyle \sum _{i\le r}}{b}_i\right)\cdots \\ \ddots & \ddots & \ddots & \ddots & \ddots \end{array}\right).$$

(10)

Finally, for $X\left(t\right)$ belonging to class $\left(\mathrm{iv}\right)$ (which corresponds to the queueing system with state-independent batch arrivals and group services), one has

$$B^{*}=TB\left(t\right)T^{-1}=\left(\begin{array}{ccccc}{a}_{11}& b_1-b_2& b_2-b_3& \cdots & \cdots \\ a_1& a_{22}& b_1-b_3& \cdots & \cdots \\ \\ \ddots & \ddots & \ddots & \ddots & \ddots \\ a_{r-1}& \cdots & \cdots & a_1& a_{rr}& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right),$$

(11)

where

$$T^{-1}=\left(\begin{array}{cccccc}1& -1& 0& \cdots & 0& \cdots \\ 0& 1& -1& \cdots & 0& \cdots \\ 0& 0& 1& \cdots & 0& \cdots \\ ⋮& ⋮& ⋮& \ddots & \cdots \\ 0& 0& 0& \cdots & 1& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right).$$

Remark 1.

Generally speaking, for models of the first and second classes, the matrix $B^{*}\left(t\right)$ is always essentially non-negative; at the same time, for models of the third and fourth classes, this requires some additional assumptions. Under essential non-negativity of $B^{*}\left(t\right)$ all bounds on the rate of convergence can be obtained via logarithmic norm, see [3]. However, in the general case, this approach may not work, and the method of differential inequalities described in our previous papers, see [3,14], would be more effective.

Thus, in this paper we will consider chains of the third and fourth classes with a countable state space. For simplicity of calculations, we will additionally assume that the size of the simultaneously arriving and/or servicing group of customers does not exceed some fixed number, say R, i.e., that all $q_{ij}\left(t\right)=0$ for $|i-j|>R$ and any $t\ge 0$.

Let $\{d_i,i\ge 1\}$ be a sequence of non-zero numbers such that ${inf}_k|d_k|=d>0$. Denote by $D=diag(d_1,d_2,\dots )$ the corresponding diagonal matrix, with the off-diagonal elements equal to zero. Let $\mathbf{w}\left(t\right)=D\mathbf{u}\left(t\right)$ in (7), then we obtain the following equation

$$\frac{d}{dt}\mathbf{w}\left(t\right)=B^{**}\left(t\right)\mathbf{w}\left(t\right),$$

(12)

where

$$B^{**}\left(t\right)=D{B}^{*}\left(t\right)D^{-1}={\left(b_{ij}^{**}\left(t\right)\right)}_{i,j\ge 1}.$$

(13)

If we write out $B^{*}\left(t\right)={\left(b_{ij}^{*}\left(t\right)\right)}_{i,j\ge 1}$, then

$$b_{ij}^{**}\left(t\right)=\frac{d_i}{d_j}{b}_{ij}^{*}\left(t\right),|i-j|\le R,$$

(14)

and our assumption implies $b_{ij}^{**}\left(t\right)=b_{ij}^{*}\left(t\right)=0$ for any $t\ge 0$ if $|i-j|>R$.

4. Upper Bounds on the Rate of Convergence

Let us first consider a general finite system of linear differential equations, which we will write in the form

$$\frac{d}{dt}\mathbf{x}\left(t\right)=B^{*}\left(t\right)\mathbf{x}\left(t\right),t\ge 0,$$

(15)

where $\mathbf{x}\left(t\right)={\left(x_1\left(t\right),\dots ,x_S\left(t\right)\right)}^T$, and let D now be the corresponding finite diagonal matrix.

The simplest situation with analytical (in t) coefficients $b_{ij}^{*}\left(t\right)$ has been studied in [3,14,15]. The method of estimating under such assumption is based on the fact that, in this case, on any finite interval, each coordinate has a finite number of sign changes, which means that the semiaxis can be divided into intervals, on each of which the signs of the coordinates are constant. Consider such an $(t_1,t_2)$. Choose the signs of $d_k$-s so that all $d_k{x}_k\left(t\right)>0$. Hence $\parallel \mathbf{w}\left(t\right)\parallel ={\parallel \mathbf{x}\left(t\right)\parallel }_D={\sum }_{k=1}^S{d}_k{x}_k\left(t\right)\ge d{\parallel \mathbf{x}\left(t\right)\parallel }_1$ can be considered as the corresponding norm.

Let ${\sum }_{i=1}^S{b}_{ij}^{**}\left(t\right)\le -{\alpha }_D\left(t\right)$, for any j, then

$$\frac{d}{dt}\parallel \mathbf{w}\left(t\right)\parallel =\frac{d\left({\sum }_k{w}_k\right)}{dt}=\sum _{i,j}{b}_{ij}^{**}\left(t\right)w_j\left(t\right)\le -{\alpha }_D\left(t\right)\parallel \mathbf{w}\left(t\right)\parallel .$$

(16)

Then

$$\parallel \mathbf{w}\left(t\right)\parallel =\parallel D\mathbf{x}\left(t\right){\parallel }_1\le e^{-{\int }_s^t{\alpha }_D\left(\tau \right)d\tau }{\parallel D\mathbf{x}\left(s\right)\parallel }_1,t_1<s<t<t_2,$$

(17)

for the corresponding matrix D and corresponding function ${\alpha }_D\left(t\right)$. Hence, we have

$$\parallel \mathbf{x}\left(t\right){\parallel }_1\le \frac{max|d_k|}{min|d_m|}{e}^{-{\int }_s^t{\alpha }_D\left(\tau \right)d\tau }{\parallel \mathbf{x}\left(s\right)\parallel }_1,$$

(18)

for any $t_1<s<t<t_2$, and by continuity, for all $t_1\le s<t\le t_2$.

Let now $s,t$ be arbitrary, $0\le s\le t<\infty$. Then for any interval with fixed signs of coordinates we have bound (18) with the corresponding D and ${\alpha }_D\left(t\right)$. Let now ${\alpha }^{*}\left(t\right)=min{\alpha }_D\left(t\right)$, and $d^{*}\left(S\right)=d^{*}=max\frac{|d_k|}{|d_m|}$, where the minimum and maximum are taken over all possible combinations of coordinate signs of the solution $\mathbf{x}\left(t\right)$, for any $0\le s\le t$. Then we obtain the following general estimate

$$\parallel \mathbf{x}\left(t\right){\parallel }_1\le d^{*}\left(S\right)e^{-{\int }_s^t{\alpha }^{*}\left(\tau \right)d\tau }{\parallel \mathbf{x}\left(s\right)\parallel }_1,$$

(19)

Let there exist positive numbers $M,\beta$ such that

$$e^{-{\int }_s^t{\alpha }^{*}\left(\tau \right)d\tau }\le M{e}^{-\beta (t-s)},0\le s\le t.$$

(20)

Consider now an arbitrary interval $[0,t^{*}]$; if our original coefficients are locally integrable, they can be approximated arbitrarily accurately by a continuous functions. In turn, a continuous function can be approximated arbitrarily accurately by an analytic function. As a result, instead of the integrable $B^{*}\left(t\right)$, we obtain an analytic ${\overline{B}}^{*}\left(t\right)$, such that

$$\begin{array}{c}\hfill {\int }_0^{t^{*}}\parallel B^{*}\left(\tau \right)-{\overline{B}}^{*}\left(\tau \right)\parallel d\tau \le \epsilon .\end{array}$$

(21)

Denote now by $W(t,s)$ and $\overline{W}(t,s)$ the Cauchy operators for (15) and the respective system with matrix ${\overline{B}}^{*}\left(t\right)$. Then, if (20) holds, in accordance with Lemma 3.2.3 [2] (see [2], pp. 110–111) we obtain

$$\begin{array}{c}\hfill \parallel W(t,s)-\overline{W}(t,s)\parallel \le M{d}^{*}{e}^{-\beta (t-s)}\left(e^{M{d}^{*}{\int }_s^t\parallel B^{*}\left(\tau \right)-{\overline{B}}^{*}\left(\tau \right)\parallel d\tau }-1\right)\\ \hfill \le M{d}^{*}{e}^{-\beta (t-s)}\left(e^{M{d}^{*}\epsilon }-1\right).\end{array}$$

(22)

Hence we have the following statement.

Lemma 1.

Let all $b_{ij}^{*}\left(t\right)$ be locally integrable on $[0,\infty )$. Let inequality (20) hold. Then

$$\begin{array}{c}\hfill \parallel \mathbf{x}\left(t\right){\parallel }_1\le d^{*}\left(S\right)M{e}^{-\beta (t-s)}{\parallel \mathbf{x}\left(s\right)\parallel }_1,\end{array}$$

(23)

for any solution of (15) and any $0\le s\le t$.

Let us now return to a countable system (7) and consider the corresponding truncated system

$$\frac{d}{dt}\mathbf{u}(n,t)=B^{*}(n,t)\mathbf{u}(n,t),$$

(24)

where $B^{*}(n,t)={\left(b_{ij}^{*}\left(t\right)\right)}_{i,j=1}^n$.

Below we will identify the finite vector with entries $(a_1,\dots ,a_n)$ and the infinite vector with the same first n coordinates and the others equal to zero.

Rewrite system (24) as

$$\frac{d}{dt}\mathbf{u}(n,t)=B^{*}\left(t\right)\mathbf{u}(n,t)+\left(B^{*}(n,t)-B^{*}\left(t\right)\right)\mathbf{u}(n,t).$$

(25)

Denote by $V(t,s)$ and $V(n,t,s)$ the Cauchy operators for (7) and (24), respectively.

Suppose that $n>S$, and that, in addition

$$\mathbf{u}\left(0\right)=\mathbf{u}(n,0)={\mathbf{u}(S,0),\parallel \mathbf{u}\left(0\right)\parallel }_1\le 1.$$

(26)

Then one has from (7)

$$\mathbf{u}\left(t\right)=V\left(t\right)\mathbf{u}\left(0\right)=V\left(t\right)\mathbf{u}(n,0).$$

(27)

On the other hand, from (25) we have

$$\mathbf{u}(n,t)=V\left(t\right)\mathbf{u}(n,0)+{\int }_0^{t}V(t,\tau )\left(B^{*}(n,\tau )-B^{*}\left(\tau \right)\right)\mathbf{u}(n,\tau )d\tau .$$

(28)

Hence in any norm we obtain the bound

$$\parallel \mathbf{u}\left(t\right)-\mathbf{u}(n,t)\parallel \le {\int }_0^t\parallel V(t,\tau )\parallel \parallel \left(B^{*}(n,\tau )-B^{*}\left(\tau \right)\right)\mathbf{u}(n,\tau )\parallel d\tau .$$

(29)

Denote $sup\frac{|d_k|}{|d_m|}=\widehat{d}<\infty$, where supremum is taken over all possible combinations of coordinate signs of the solution $\mathbf{u}\left(t\right)$ of (7), under assumption $|k-m|=1$.

Put now $D^{*}=diag\left(d^{*}\left(1\right),d^{*}\left(2\right),\dots \right)$.

Note that according to (14) the matrix $B^{**}\left(t\right)$ has nonzero entries only on the main diagonal and at most R diagonals above and below it. Then

$$\parallel B^{*}{\left(t\right)\parallel }_{1D^{*}}={\parallel B^{**}\left(t\right)\parallel }_1\le K=2L{\widehat{d}}^R,$$

(30)

for almost all $t\ge 0$. Then

$${\parallel V(t,s)\parallel }_{1D^{*}}\le e^{K(t-s)}\le e^{K{t}^{*}}.$$

(31)

On the other hand, all elements of the first $n-R$ columns of the matrix $\left(B^{*}(n,\tau )-B^{*}\left(\tau \right)\right)$ are zeros for any $\tau \ge 0$. Hence, all the first $n-R$ coordinates of the corresponding vector $\left(B^{*}(n,\tau )-B^{*}\left(\tau \right)\right)\mathbf{u}(n,\tau )$ are also zeros too, and

$$\parallel \left(B^{*}(n,\tau )-B^{*}\left(\tau \right)\right){\mathbf{u}(n,\tau )\parallel }_{1D^{*}}\le K\sum _{k=n-R}^n{\widehat{d}}^k|u_k\left(t\right)|.$$

(32)

Put $D^{**}=diag({\widehat{d}}^2,{\widehat{d}}^4,\dots )$ and ${\mathbf{w}}^{*}\left(t\right)=D^{**}\mathbf{u}\left(t\right)$.

Then, instead of (30) and (31) we have

$$\parallel B^{*}{\left(t\right)\parallel }_{1D^{**}}={\parallel D^{**}{B}^{*}{D}^{{**}^{-1}}\left(t\right)\parallel }_1\le K^{*}=2L{\widehat{d}}^{2R},$$

(33)

and

$${\parallel V(t,s)\parallel }_{1D^{**}}\le e^{K^{*}(t-s)}\le e^{K^{*}{t}^{*}},$$

(34)

respectively.

Then

$$\begin{array}{c}\hfill \parallel \mathbf{u}\left(n,t\right){\parallel }_{1D^{**}}=\sum _{k=1}^n{\widehat{d}}^{2k}|u_k(n,t)|\le e^{K^{*}{t}^{*}}\sum _{k=1}^S{\widehat{d}}^{2k}|u_k(n,0)|\le e^{K^{*}{t}^{*}}{\widehat{d}}^{2S}\sum _{k=1}^S|u_k(n,0)|.\end{array}$$

(35)

Then (35) and (26) imply the bound

$$\begin{array}{c}\hfill {\widehat{d}}^{2n-2R}\sum _{k=n-R}^n|u_k(n,t)|\le \sum _{k=1}^n{\widehat{d}}^{2k}|u_k(n,t)|\le e^{K^{*}{t}^{*}}{\widehat{d}}^{2S}.\end{array}$$

(36)

Then

$$\begin{array}{c}\hfill \sum _{k=n-R}^n{\widehat{d}}^k|u_k(n,t)|\le {\widehat{d}}^n\sum _{k=n-R}^n|u_k(n,t)|\le e^{K^{*}{t}^{*}}{\widehat{d}}^{2S+2R-n}.\end{array}$$

(37)

Finally, for the right-hand side of (29) we have the bound

$${\int }_0^t{\parallel V(t,\tau )\parallel }_{1D^{*}}{\parallel \left(B^{*}(n,\tau )-B^{*}\left(\tau \right)\right)\mathbf{u}(n,\tau )\parallel }_{1D^{*}}d\tau \le e^{K{t}^{*}}K{t}^{*}{e}^{K^{*}{t}^{*}}{\widehat{d}}^{2S+2R-n},$$

(38)

which tends to be zero at $n\to \infty$.

Hence we have the following statement.

Lemma 2.

Let assumptions of Lemma 1 be fulfilled for any S. Then, under assumption (26), and for any fixed $\epsilon >0$, $t^{*}>0$, we obtain ${\parallel \mathbf{u}\left(t\right)-\mathbf{u}(n,t)\parallel }_{1D^{*}}<\epsilon$ for sufficiently large n, for any $t\in [0,t^{*}]$.

As a result, Lemmas 1 and 2 guarantee an estimate of the form

$$\begin{array}{c}\hfill \parallel \mathbf{u}\left(t\right){\parallel }_1\le M{e}^{-\beta t}{\parallel \mathbf{u}\left(0\right)\parallel }_{1D^{*}}.\end{array}$$

(39)

Consider now two arbitrary solutions ${\mathbf{p}}^{*}\left(t\right)$ and ${\mathbf{p}}^{**}\left(t\right)$ of the forward Kolmogorov system (2) with the corresponding initial conditions ${\mathbf{p}}^{*}\left(0\right)$ and ${\mathbf{p}}^{**}\left(0\right)$. Denote by ${\mathbf{p}}_0^{*}\left(t\right)$ and ${\mathbf{p}}_0^{**}\left(t\right)$ the respective vector functions with coordinates $1,2,\dots$ (i.e., without zero coordinates).

One can write $\mathbf{u}\left(t\right)=T\left({\mathbf{p}}_0^{*}\left(t\right)-{\mathbf{p}}_0^{**}\left(t\right)\right)$. Then (see for instance [8]), the following inequality holds: $\parallel {\mathbf{p}}^{*}\left(t\right)-{\mathbf{p}}^{**}{\left(t\right)\parallel }_1\le \frac{2}{d}{\parallel \mathbf{u}\left(t\right)\parallel }_1$.

Finally we obtain the following statement.

Theorem 1.

Let the assumptions of Lemma 1 hold for any natural S. Then $X\left(t\right)$ is weakly ergodic and the following bound on the rate of convergence holds:

$$\begin{array}{c}\hfill \parallel {\mathbf{p}}^{*}\left(t\right)-{\mathbf{p}}^{**}{\left(t\right)\parallel }_1\le \frac{2M}{d}{e}^{-\beta t}{\parallel {\mathbf{p}}_0^{*}\left(0\right)-{\mathbf{p}}_0^{**}\left(0\right)\parallel }_{1D^{*}}.\end{array}$$

(40)

Remark 2.

A specific model (which belongs to both classes $\left(\mathrm{iii}\right)$ and $\left(\mathrm{iv}\right)$) was investigated in [16] by the method described here.

Namely, in this paper, the queueing model with possible transitions and respective intensities of single arrival $\lambda \left(t\right)$ and service of group of two customers $\mu \left(t\right)$ was considered. Hence

$$B^{*}\left(t\right)=$$

$$\begin{array}{c}\hfill =\left(\begin{array}{ccccccc}-\lambda \left(t\right)& -\mu \left(t\right)& \mu \left(t\right)& 0& 0& 0& \cdots \\ \lambda \left(t\right)& -\left(\lambda \left(t\right)+\mu \left(t\right)\right)& 0& \mu \left(t\right)& 0& 0& \cdots \\ 0& \lambda \left(t\right)& -\left(\lambda \left(t\right)+\mu \left(t\right)\right)& 0& \mu \left(t\right)& 0& \cdots \\ 0& 0& \lambda \left(t\right)& -\left(\lambda \left(t\right)+\mu \left(t\right)\right)& 0& \mu \left(t\right)& \cdots \\ 0& 0& 0& \lambda \left(t\right)& -\left(\lambda \left(t\right)+\mu \left(t\right)\right)& 0& \cdots \\ \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right).\end{array}$$

Let $\delta >1$ be a positive number. Put

$d_1=1$, $d_2=1/\delta$, $d_k={\delta }^{k-2}$, $k\ge 3$ if all coordinates of solutions are positive;

$|d_k|={\delta }^{k-1}$, $k\ge 1$ otherwise.

Then one has,

$$\begin{array}{c}\hfill {\alpha }^{*}\left(t\right)\ge min\left[\lambda \left(t\right)\left(1-{\delta }^{-1}\right),\mu \left(t\right)\left(1+\delta \right)-\right.\\ \hfill \left.\lambda \left(t\right)\left({\delta }^2-1\right),\mu \left(t\right)\left(1-{\delta }^{-1}\right)-\lambda \left(t\right)\left(\delta -1\right)\right].\end{array}$$

(41)

Moreover, $d={\delta }^{-1}$, $\widehat{d}=\delta$, $d_k^{*}={\delta }^{k-1}$, for $k\ge 1$.

In particular, if the process $X\left(t\right)$ is homogeneous i.e., $\lambda \left(t\right)=\lambda$ and $\mu \left(t\right)=\mu$ are positive numbers, then ${\int }_0^{\infty }{\alpha }^{*}\left(t\right)dt=+\infty$ is equivalent to ${\alpha }^{*}>0$ and this is equivalent to $0<\lambda <\mu$. Put $\delta =\sqrt{\frac{\mu }{\lambda }}$. Hence,

$${\alpha }^{*}=min\left[{\left(\sqrt{\mu }-\sqrt{\lambda }\right)}^2,\lambda \left(1-\sqrt{\frac{\lambda }{\mu }}\right)\right].$$

(42)

In the paper [16] the specific example with periodic intensities was considered. Namely, let $\lambda \left(t\right)=2+sin2\pi t$ and $\mu \left(t\right)=4-cos2\pi t$. Put $\delta =\frac{11}{10}$. Then, ${\int }_0^1{\alpha }^{*}\left(t\right)dt\ge \frac{1}{22}>0$, $X\left(t\right)$ is exponentially weakly ergodic and has the 1-periodic limiting mean (a Markov chain has the limiting mean $m\left(t\right)$, if ${lim}_{t\to \infty }\left(m\left(t\right)-E(t,k)\right)=0$ for any k, $E(t,k)$ is the mathematical expectation of $X\left(t\right)$ under initial condition $X\left(0\right)=k$ ). Now, applying the known truncation technique (see the detailed discussion and bounds in [8]), one can compute all probability characteristics of the queue-length process $X\left(t\right)$. Some of the corresponding graphs are shown in Figure 1, Figure 2, Figure 3 and Figure 4; see detailed discussion in [16].

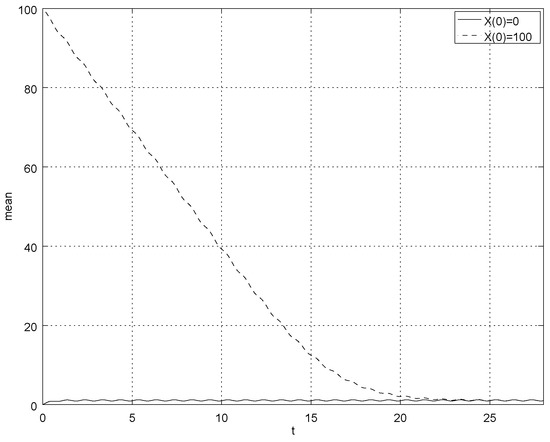
Figure 1. The mean $E(t,0)$ and $E(t,100)$ for $t\in [0,28]$, this figure shows the rate of convergence.

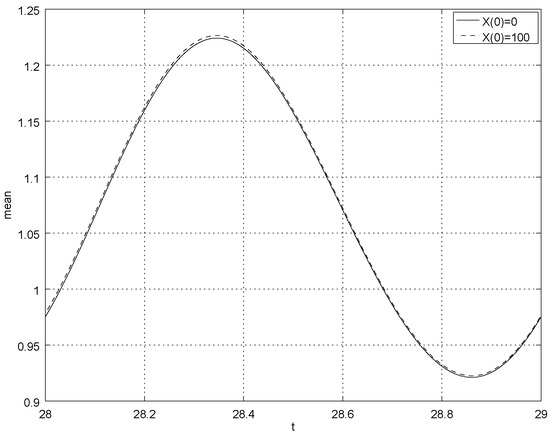
Figure 2. The mean $E(t,0)$ and $E(t,100)$ for $t\in [28,29]$, this figure shows approximation of the limiting mean.

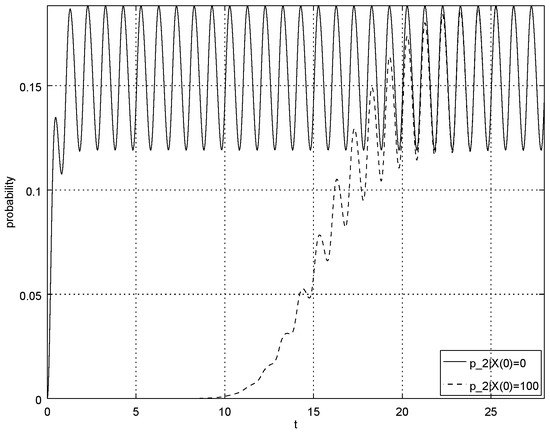
Figure 3. Probability $p_2\left(t\right)$ for $t\in [0,28]$ and initial conditions $X\left(0\right)=0$ and $X\left(0\right)=100$; this figure shows the rate of convergence.

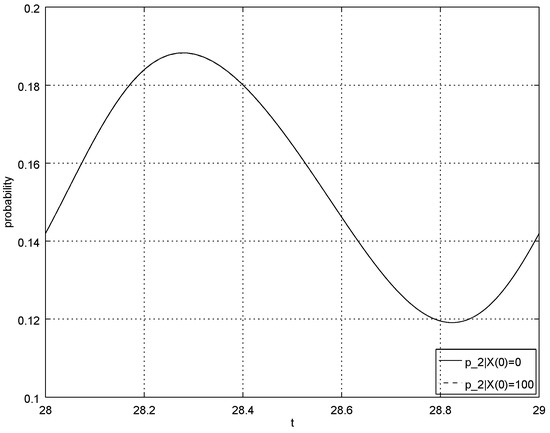
Figure 4. Probability $p_2\left(t\right)$ for $t\in [28,29]$ and initial conditions $X\left(0\right)=0$ and $X\left(0\right)=100$; this figure shows approximation of the limiting probability $p_2\left(t\right)$.

5. Conclusions

In this paper, we have substantiated one of the most general methods for studying the rate of convergence to limit characteristics for weakly ergodic Markov chains with continuous time. Namely, the applicability of the method of differential inequalities for countable inhomogeneous processes in the case of a nonsmooth dependence of intensities as functions of time is shown. Thus, studying models with continuous time from the theory of queues, biology, physics and other sciences, and obtaining guaranteed estimates of the rate of convergence, we can both make sure that the influence of the initial conditions of the system disappears with increasing time, and build the main characteristics of the system to control them.