On the Loop Homology of a Certain Complex of RNA Structures

Abstract

In this paper, we establish a topological framework of $\tau$-structures to quantify the evolutionary transitions between two RNA sequence–structure pairs. $\tau$-structures developed here consist of a pair of RNA secondary structures together with a non-crossing partial matching between the two backbones. The loop complex of a $\tau$-structure captures the intersections of loops in both secondary structures. We compute the loop homology of $\tau$-structures. We show that only the zeroth, first and second homology groups are free. In particular, we prove that the rank of the second homology group equals the number $\gamma$ of certain arc-components in a $\tau$-structure and that the rank of the first homology is given by $\gamma -\chi +1$, where $\chi$ is the Euler characteristic of the loop complex.

1. Introduction

Ribonucleic acid (RNA) is a biomolecule that folds into a helical configuration of its primary sequence by forming hydrogen bonds between pairs of nucleotides. The most prominent class of coarse-grained structures are the RNA secondary structures [1,2]. These are contact structures that can be represented as diagrams where vertices are nucleotides and arcs are base pairs drawn in the upper half-plane. As a secondary structure can be uniquely decomposed into loops, the free energy of a structure is calculated as the sum of the energy of its individual loops [3]. The loop-based energy models for RNA secondary structure prediction have played an important role in unveiling the various regulatory functions of RNA [4].

RNA molecules evolve under selection pressures on both sequence and structure. One prominent example are RNA riboswitches [5], which is a class of RNA molecules that can express two alternative secondary structures, each of which appears in a specific biophysical context. In order to analyze riboswitch sequences, Huang et al. developed a Boltzmann sampler of sequences that are simultaneously compatible with a pair of structures, i.e., a bi-secondary structure, based on the loop energy model [6]. The time complexity of computing such bi-compatible sequences turns out be intimately related to the number of so called exposed nucleotides, i.e., the number of vertices shared by multiple loops appearing in the algorithm. In some sense, finding bi-compatible sequences is easy if the intersection of such loops is small and becomes difficult when the intersection is large. In order to address the complexity problem, Bura et al. studied the simplicial homology of the loop complex (derived from the intersections of loops) of a bi-secondary structure [7,8]. Subsequently, they introduced the weighted homology of bi-structures, in which simplices are endowed with specific weights allowing the expression of the size of the loop intersections [9].

The aforementioned work focuses on the structural transition without changing the underlying sequence. However, selection pressures act on both sequence and structure, resulting in the simultaneous change of genotypes and phenotypes. This motivates the study of the evolutionary transition between two distinct sequence–structure pairs. In what follows, we take the first step by, analogous to [7,8], computing the simplicial homology of their loop complex.

In this paper we study triples, $(S,T,\varphi )$, consisting of an ordered pair of RNA secondary structures, $(S,T)$, [1,2,10,11,12,13] together with a non-crossing partial matching, $\varphi$, between the two backbones. We shall denote such a triple a transition structure or τ-structure and note that the mapping $\varphi$ relates homologous bases between two underlying RNA sequences.

The topological framework of $\tau$-structures developed here is designed to quantify the probability of evolutionary transitions between RNA sequence-structure pairs subject to specific sequence constraints. In an algorithmic guise, $\tau$-structures play a central role in solving the following computational problem: Given two arbitrary RNA secondary structures, determine a pair of specifically related sequences that minimizes the total free energies of the two sequence–structure pairs. Our main objective is to compute the simplicial homology of the loop complex of a $\tau$-structure. In order to state our main theorem, we next introduce the notions of $\varphi$-crossing and arc-component.

Two arcs $(i_1,i_2)$ and $(j_1,j_2)$ are $\varphi$-crossing, i.e., if either one of the following is the case:

(1)

Both $i_1$ and $i_2$ are incident to $\varphi$-arcs such that $\varphi \left(i_1\right)<j_1<\varphi \left(i_2\right)<j_2$ or $j_1<\varphi \left(i_1\right)<j_2<\varphi \left(i_2\right)$, or;

(2)

Both $j_1$ and $j_2$ are incident to $\varphi$-arcs such that $i_1<{\varphi }^{-1}\left(j_1\right)<i_2<{\varphi }^{-1}\left(j_2\right)$ or ${\varphi }^{-1}\left(j_1\right)<i_1<{\varphi }^{-1}\left(j_2\right)<i_2$.

$\varphi$-crossing induces an equivalence relation for which nontrivial equivalence classes are called arc-components. An arc-component is of type 1 if both endpoints of any arc are incident to $\varphi$-arcs.

We shall prove the following main result.

Main Theorem.

Let $I=(S,T,\varphi )$ be a τ-structure and $H_n\left(I\right)$ the n-th homology group of its loop complex, $K\left(I\right)$. Then, the following is the case:

$$\begin{array}{cc}\hfill H_3\left(I\right)& =0,\hfill \\ \hfill H_2\left(I\right)& \cong \underset{k=1}{\overset{\gamma }{⨁}}\mathbb{Z},\hfill \\ \hfill H_1\left(I\right)& \cong \underset{k=1}{\overset{\gamma -\chi +1}{⨁}}\mathbb{Z},\hfill \end{array}$$

where γ denotes the number of arc-components of type 1 and χ the Euler characteristic of $K\left(I\right)$.

Our framework generalizes the work of [7,8] on bi-structures. Bi-structures can be viewed as particular $\tau$-structures, namely those over two identical sequences. The loop complex of a bi-structure exhibits only a nontrivial zeroth and second homology, the latter being freely generated by crossing components [7,8]. On the algorithmic side, $\tau$-structures play a similar role as bi-structures in [6] where a Boltzmann sampler of sequences that are simultaneously compatible with two structures is presented.

The loop complex of $\tau$-structures exhibits a variety of new features. First it has in general a nontrivial first homology group. Secondly, it features two types of arc-components: Those of type 1, which correspond to spheres, and arc-components of type 2, which correspond to surfaces with a nontrivial boundary (see Section 7).

In order to prove the main theorem, we first establish basic properties of the loop complex $X=K\left(I\right)$. Secondly, we manipulate X by means of simplicial collapses and then dissect $K_1$, which is a certain sub-complex of dimension one. As a result, we derive ${\tilde{X}}_2$, which is a specific X-sub-complex, and we organize it into its crossing components. We note that ${\tilde{X}}_2$ is not unique, as its construction depends on certain choices. We then proceed with a combinatorial analysis of ${\tilde{X}}_2$-crossing components, which lays the foundation for proving that their geometric realizations are either spheres or surfaces with boundary.

The combinatorics of crossing components, specifically Lemma 6, further controls the manner crossing components are glued and this observation facilitates to prove the main result in two stages. First, by computing the homology of components in isolation and, secondly, by computing the homology of the loop complex by Mayer–Vietoris sequences. Several of our arguments are reminiscent of ideas of classical facts, for instance the Jordan curve theorem in the proof of Lemma 7.

The paper is organized as follows: In Section 2, we recall the definitions of RNA secondary structures, bi-structures and their loop complexes. In Section 3, we introduce $\tau$-structures and present some basic facts of their loop complexes. In Section 4, we simplify the loop complex in multiple rounds via simplicial collapses and topological stratification. In Section 5, we investigate the combinatorics of crossing components in the simplified complex. We then compute the homology of components in Section 6 and integrate this information in order to obtain the homology of $\tau$-structures in Section 7. Finally we discuss our results in Section 8.

2. Secondary Structures, Bi-Structures and the Loop Complex

An RNA secondary structure encapsulates the nucleotide interactions within a single RNA sequence. It can be represented as a diagram, which consists of a labeled graph over the vertex set $\left[n\right]:=\{1,\cdots ,n\}$ for which the vertices are arranged in a horizontal line and arcs are drawn in the upper half-plane. Each vertex corresponds to a nucleotide in the primary sequence and each arc, which is denoted by $(i,j)$, represents the base pairing between the i-th and j-th nucleotides in the RNA structure. Two arcs $(i_1,j_1)$ and $(i_2,j_2)$ are crossing if $i_1<i_2<j_1<j_2$. An RNA secondary structure is defined as a diagram satisfying the following three conditions [1,2]: (1) if $(i,j)$ is an arc, then $j-i\ge 2$; (2) any two arcs do not have a common vertex; (3) any two arcs are non-crossing.

Given a secondary structure S, the set $[1,n]:=\{1,\cdots ,n\}$ is called the backbone and an interval $[i,j]\subset [1,n]$ denotes the set of consecutive vertices $\{i,i+1,\dots ,j-1,j\}$. A vertex k is covered by an arc $(i,j)$ if $i\le k\le j$ and there exists no other arc $(p,q)$ such that $i<p<k<q<j$. The set of vertices covered by an arc $(i,j)$ is called a loop, s, and we refer to $(i,j)$ as the covering arc of s. We shall equip each diagram with two “formal” vertices at positions 0 and $n+1$ together with the arc $(0,n+1)$, which we call the rainbow. Its associated distinguished loop is called the exterior loop. Each loop, s, can be represented as a disjoint union of intervals on the backbone of S, $s={\bigcup }_{k=1}^l[i_k,j_k]$, such that $(i_1,j_l)$ and $(j_k,i_{k+1})$ for $1\le k\le l-1$ form arcs and any other vertices in s are unpaired. By construction, a diagram S is in one-to-one correspondence with its set of arcs as well as its set of loops ${\left\{s_i\right\}}_i$.

Let $\mathcal{X}$ be a collection of finite sets. A subset $\{X_0,X_1,\dots ,X_d\}\subset \mathcal{X}$ is defined to be a d-simplex of $\mathcal{X}$ if the set intersection ${\cap }_{k=0}^d{X}_k\ne ⌀$. Let $K_d\left(\mathcal{X}\right)$ be the set of all d-simplices of $\mathcal{X}$. The nerve of $\mathcal{X}$ is a simplicial complex given by $K\left(\mathcal{X}\right)={\bigcup }_{d=0}^{\infty }{K}_d\left(\mathcal{X}\right)\subseteq 2^{\mathcal{X}}$.

The nerve formed by the collection ${\left\{s_i\right\}}_i$ of S-loops is referred to as the loop complex $K\left(S\right)$ of a secondary structure S. The fact that secondary structures correspond to non-crossing diagrams immediately implies that the loop complex of a secondary structure is a tree.

Let S and T be two secondary structures. The pair of secondary structures S and T over $\left[n\right]$, $R=(S,T)$, is called a bi-structure. We represent a bi-structure as a diagram on a horizontal backbone with the S-arcs drawn in the upper and the T-arcs drawn in the lower half plane. The nerve formed by S-loops and T-loops of a bi-structure, R, is called the loop complex, $K\left(R\right)$.

In bi-structures [7], two arcs $\alpha ,{\alpha }^{\prime }$ are equivalent if there exists a sequence of arcs ${\alpha }_1=\alpha ,{\alpha }_2,\dots ,{\alpha }_l={\alpha }^{\prime }$ such that two consecutive arcs ${\alpha }_k$ and ${\alpha }_{k+1}$ are crossing for $1\le k\le l-1$. A crossing component of $R=(S,T)$ is an equivalence class that contains at least two crossing arcs.

The loop complex of a bi-structure has a nontrivial zeroth and second homology group. In particular, the first homology $H_1\left(R\right)$ is zero and the second homology $H_2\left(R\right)$ is free and its rank equals the number of crossing components of the bi-structure R [8].

3. Some Basic Facts

Let S and T be two secondary structures over $\left[n\right]$ and $\left[m\right]$, respectively. We shall refer to their backbones as ${\left[n\right]}_S=\{1_S,2_S,\dots ,n_S\}$ and ${\left[m\right]}_T=\{1_T,2_T,\dots ,m_T\}$. We refer to the pair $(i,\varphi (i\left)\right)$ as a ϕ-arc between $i\in {\left[n\right]}_S$ and $\varphi \left(i\right)\in {\left[m\right]}_T$. Two $\varphi$-arcs $(i_1,\varphi \left(i_1\right))$ and $(i_2,\varphi \left(i_2\right))$ are crossing if $i_1<i_2$ and $\varphi \left(i_1\right)>\varphi \left(i_2\right)$.

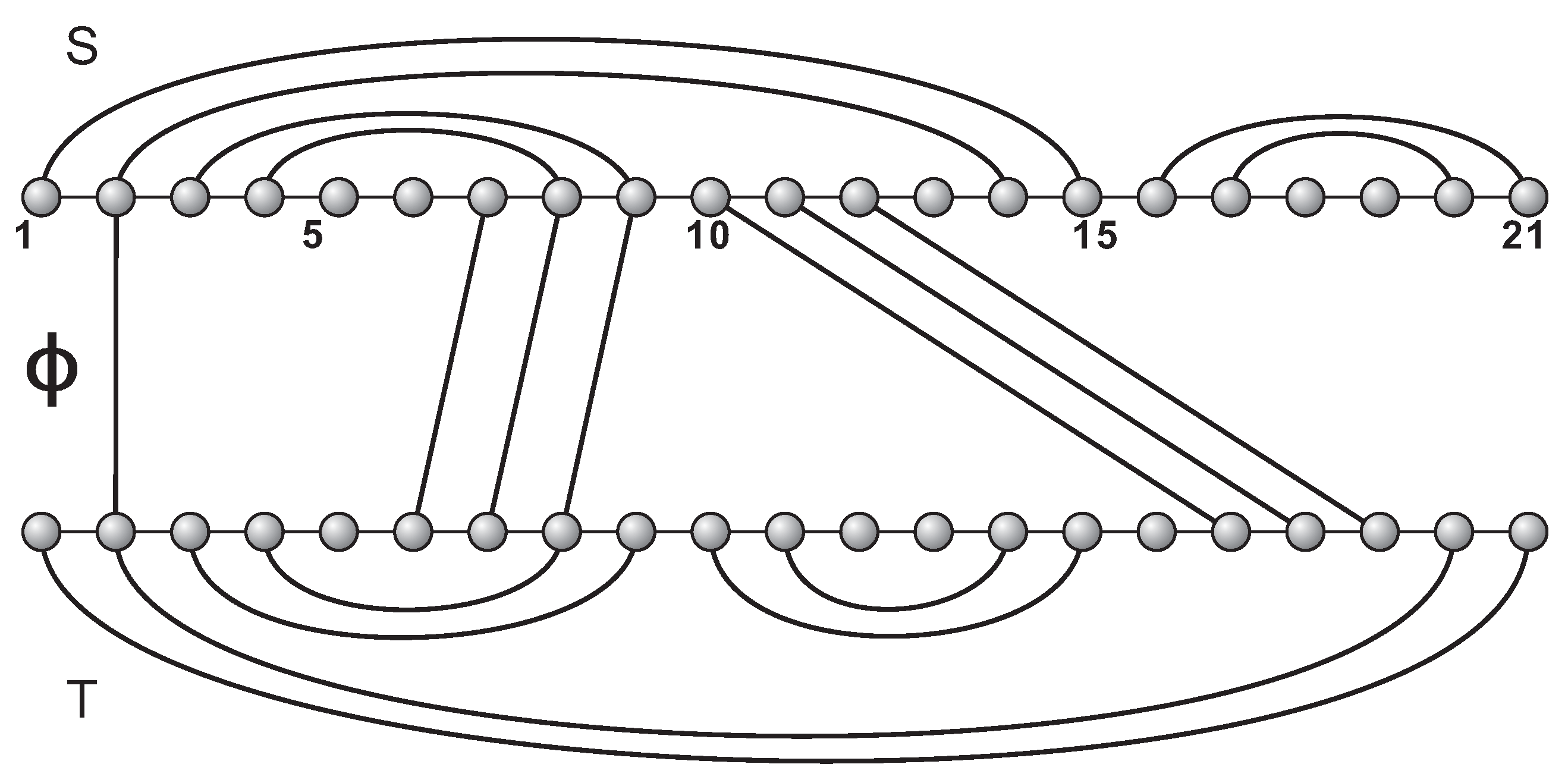
Definition 1.

A$\tau$-structure I is a triple $(S,T,\varphi )$ consisting of an ordered pair of secondary structures, $(S,T)$, together with a partial matching ϕ between their vertex sets ${\left[n\right]}_S$ and ${\left[m\right]}_T$ such that any two ϕ-arcs are non-crossing.

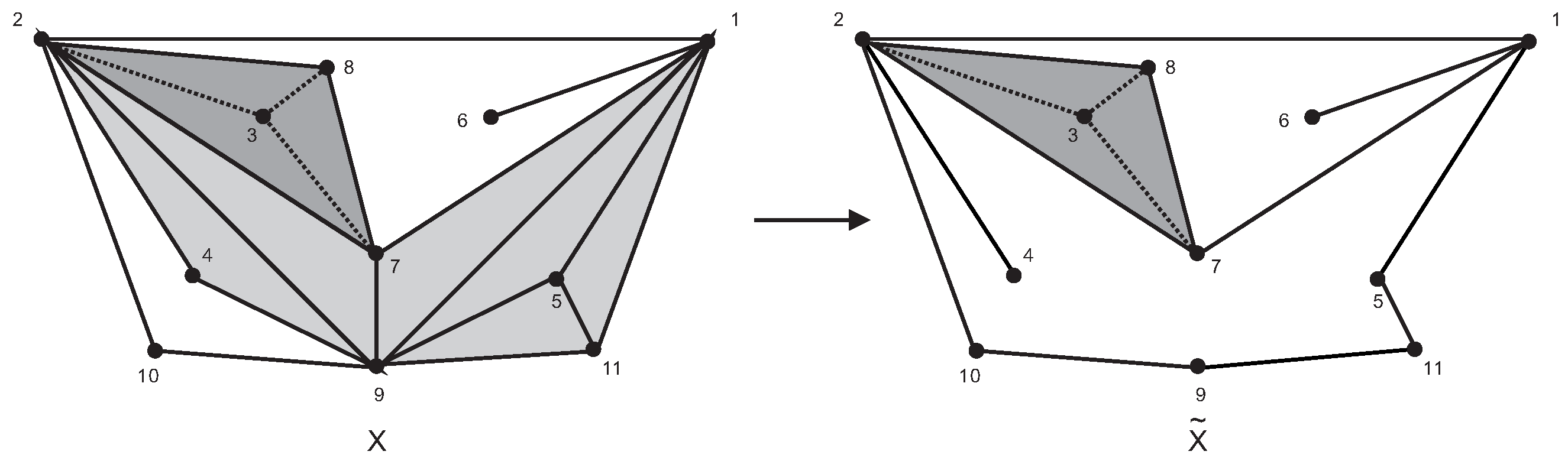
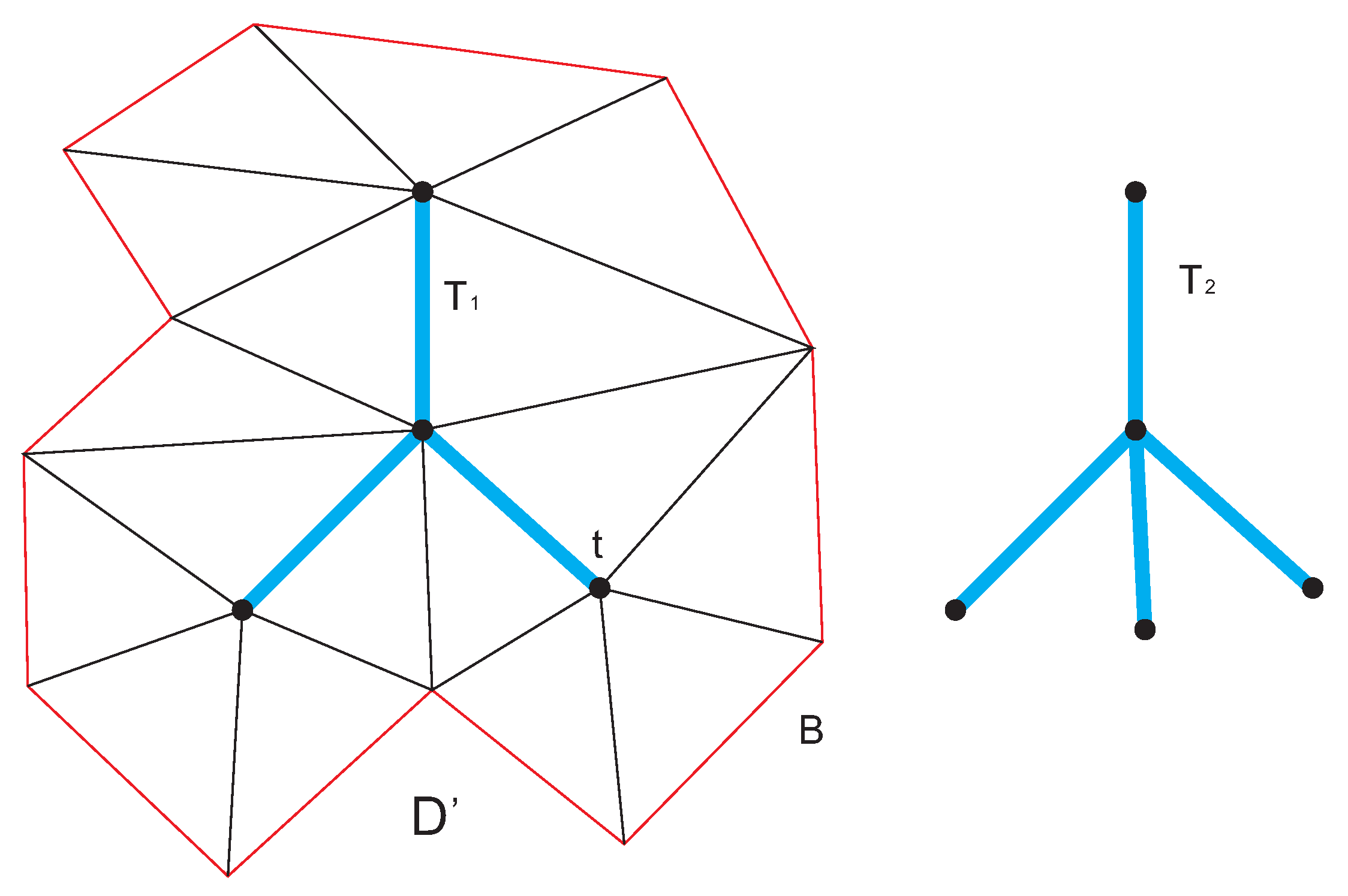
In analogy to the case of bi-structures, we shall represent the diagram of a $\tau$-structure as a labeled graph over two horizontal backbones in which S-arcs are drawn in the upper halfplane and T-arcs are drawn in the lower halfplane with the edges drawn in between the two backbones representing $\varphi$ (see Figure 1).

A bi-structure corresponds to a particular $\tau$-structure having two backbones of the same length and $\varphi$ being the identity map.

The partial matching $\varphi$ induces an equivalence relation ∼ on the set of vertices of the two backbones by identifying for each pair $(i,\varphi (i\left)\right)$ the vertices i and $\varphi \left(i\right)$. The $\varphi$-arcs then correspond one-to-one to nontrivial equivalence classes of size two. This equivalence relation gives rise to the definition of a loop in a $\tau$-structure.

Definition 2.

Given a S-vertex or T-vertex $v\in {\left[n\right]}_S\cup {\left[m\right]}_T$, anI-vertex, $\overline{v}$, is an equivalence class induced by v, i.e., $\overline{v}\in {\left[n\right]}_S\cup {\left[m\right]}_T/\sim$. Given an S-loop s, the $\overline{S}$-loop $\overline{s}$ is the set of equivalence classes induced by the set of s-vertices. Similarly, we define the $\overline{T}$-loop. AnI-loopis defined to be either an $\overline{S}$-loop or a $\overline{T}$-loop.

Now we are in position to introduce the loop complex of a $\tau$-structure.

Definition 3.

The nerve formed by I-loops is called the loop complex$K\left(I\right)={\bigcup }_{d=0}^{\infty }{K}_d\left(I\right)$, where $K_d\left(I\right)$ denotes the set of d-simplices, i.e., the non-empty intersections of d distinct loops. $H_n\left(I\right)$ shall denote the n-th homology group of the loop complex of I.

Let us proceed by collecting some basic properties of the loop complex.

Proposition 1.

Let $I=(S,T,\varphi )$ be a τ-structure and $v_1,v_2$ be two distinct S-vertices. Then ${\overline{v}}_1\ne {\overline{v}}_2$. In particular there exists a bijection between vertices in an S-loop s and vertices in the corresponding $\overline{S}$-loop $\overline{s}$.

Proof. 

By definition, any two $\varphi$-arcs in the partial matching $\varphi$ do not share common endpoints. Thus, $\varphi$ maps $v_1$ and $v_2$ to different T-vertices. Therefore the equivalence classes ${\overline{v}}_1$ and ${\overline{v}}_2$ are different. □

Proposition 2.

Let $I=(S,T,\varphi )$ be a τ-structure and ${\overline{s}}_1$, ${\overline{s}}_2,{\overline{s}}_3$ be three different $\overline{S}$-loops. Then, it follows that:

(1)

either ${\overline{s}}_1\cap {\overline{s}}_2=⌀$ or $|{\overline{s}}_1\cap {\overline{s}}_2|=2$;

(2)

${\overline{s}}_1\cap {\overline{s}}_2\cap {\overline{s}}_3=⌀$.

Proof. 

For the secondary structure S, any two S-loops $s_1$ and $s_2$ either have trivial intersection or intersect at two endpoints of one arc, i.e., either $s_1\cap s_2=⌀$ or $|s_1\cap s_2|=2$. Proposition 1 guarantees that $|{\overline{s}}_1\cap {\overline{s}}_2|=|s_1\cap s_2|$, whence assertion $\left(1\right)$. Any S-vertex is contained in at most two distinct S-loops. Thus $s_1\cap s_2\cap s_3=⌀$. By Proposition 1, ${\overline{s}}_1\cap {\overline{s}}_2\cap {\overline{s}}_3=⌀$. □

By abuse of notation, we refer to $\overline{S}$-loops and $\overline{T}$-loops $\overline{s},\overline{t}$ simply as S-loops and T-loops $s,t$, respectively.

Proposition 3.

Let I be a τ-structure with loop complex $K\left(I\right)$. Then, any 2-simplex $\sigma \in K_2\left(I\right)$ has the form $\{s_1,s_2,t_1\}$ or $\{t_1,t_2,s_1\}$, where $s_1,s_2$ are S-loops and $t_1,t_2$ are T-loops.

Proof. 

By construction, the three loops in a 2-simplex $\sigma$ have a non-empty intersection. In view of Proposition 2, not all three loops are from the same secondary structure. Therefore, $\sigma$ is of the form $\{s_1,s_2,t_1\}$ or $\{t_1,t_2,s_1\}$. □

A 1-simplex $\sigma =\{r_1,r_2\}\in K\left(I\right)$ is called pure if both $r_1$ and $r_2$ belong to the same secondary structure and mixed. Proposition 3 shows that any 2-simplex contains exactly one pure edge and two mixed edges.

Proposition 4.

Let I be a τ-structure with loop complex $K\left(I\right)$. Then, any 3-simplex $\sigma \in K_3\left(I\right)$ has the form $\{s_1,s_2,t_1,t_2\}$, where $s_1,s_2$ are S-loops and $t_1,t_2$ are T-loops.

Proof. 

Suppose that $\sigma =\{r_1,r_2,r_3,r_4\}$. As a face of $\sigma$, $\{r_1,r_2,r_3\}\in K_2\left(I\right)$. By Proposition 3, we can w.l.o.g. set that $r_1=s_1$, $r_2=s_2$ and $r_3=t_1$. Similarly, the face $\{r_1,r_2,r_4\}\in K_2\left(I\right)$ implies that $r_4$ is necessarily a T-loop, i.e., $r_4=t_2$. □

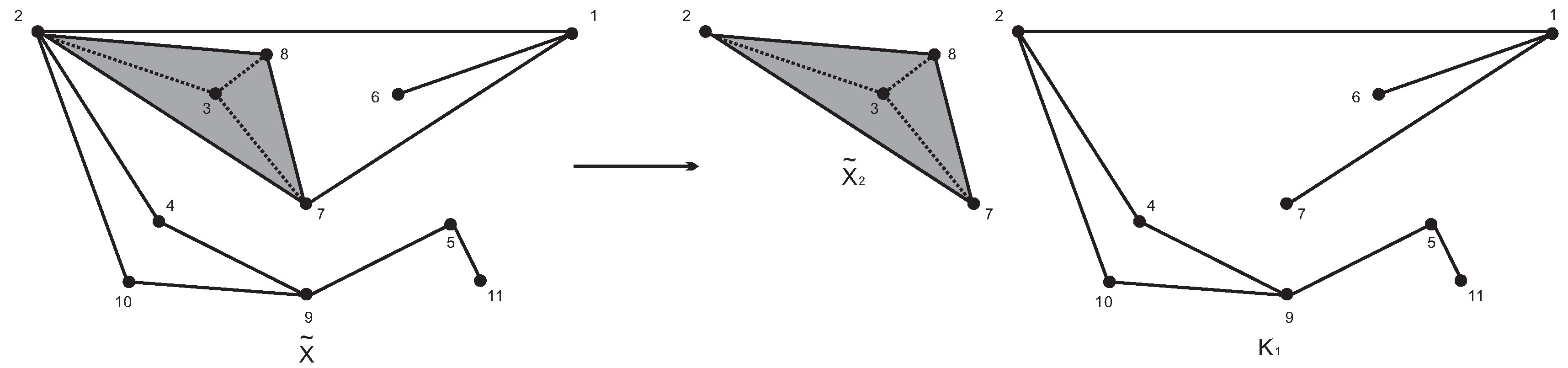
Definition 4.

Given a simplex $\sigma \in K\left(I\right)$, a face $\omega \subset \sigma$ is called$\sigma$-free if, for any simplex ${\sigma }_1\in K\left(I\right)$ containing ω, ${\sigma }_1$ is a face of σ. Clearly, σ is maximal in $K\left(I\right)$. Moreover, σ is the unique maximal simplex that contains ω.

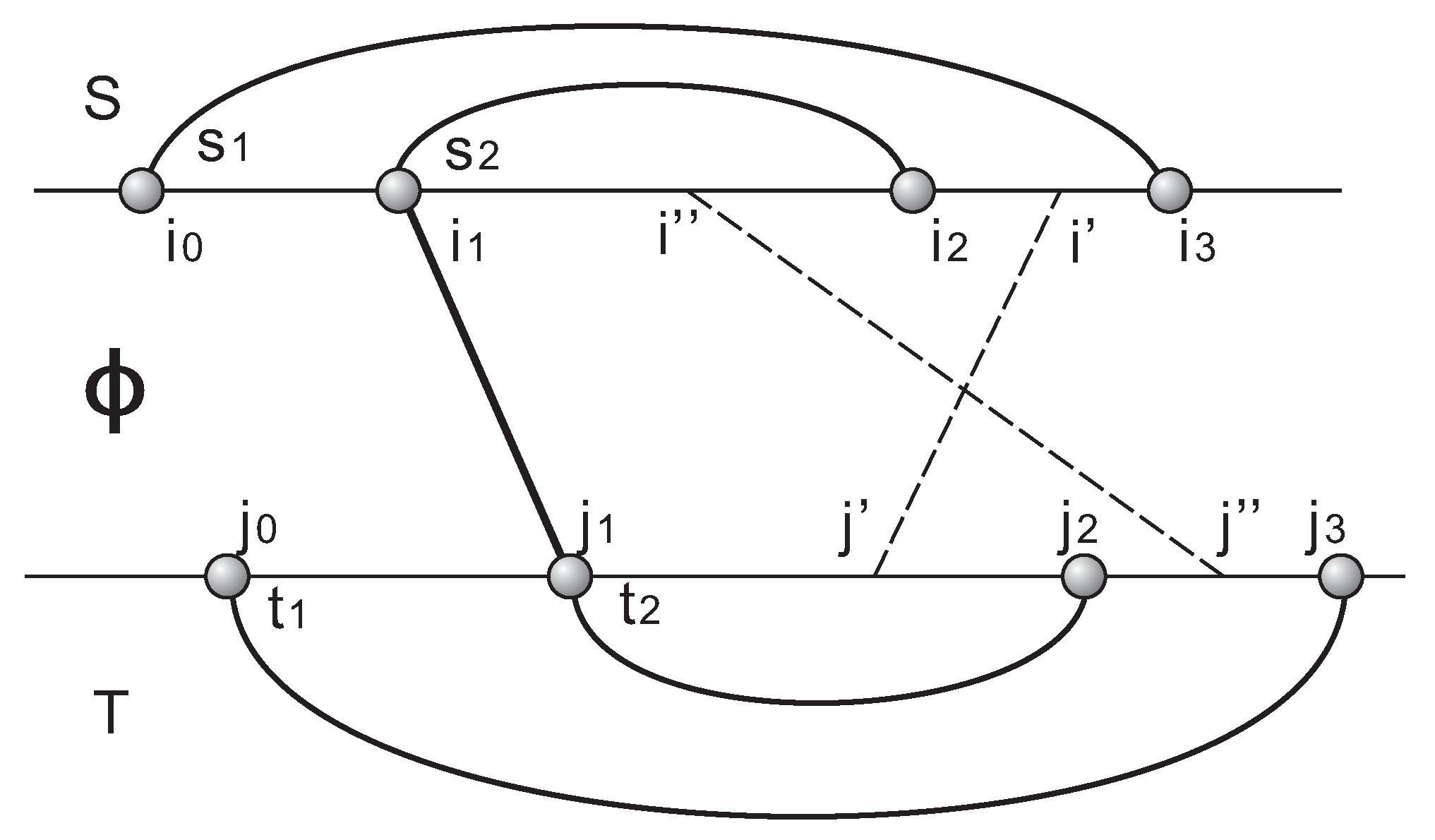
Proposition 5.

Let I be a τ-structure with loop complex $K\left(I\right)$. Then, any 3-simplex $\sigma \in K_3\left(I\right)$ contains a σ-free, mixed 1-face ω.

Proof. 

Let $\sigma =\{s_1,s_2,t_1,t_2\}$. Suppose that the covering arcs of the loops $s_1,s_2,t_1,t_2$ are $(i_0,i_3)$, $(i_1,i_2)$, $(j_0,j_3)$ and $(j_1,j_2)$, respectively, and that we have the distinguished $\varphi$-arc $(i_1,j_1)$ with $\varphi \left(i_1\right)=j_1$. Then, the loops $s_1,s_2,t_1,t_2$ intersect at the equivalence class of $\overline{i_1}=\overline{j_1}$ and by w.l.o.g. we may assume $i_0<i_1<i_2<i_3$ and $j_0<j_1<j_2<j_3$ (see Figure 2).

We shall prove the proposition by contradiction. Suppose that none of the mixed 1-faces of $\sigma$ are free, we consider the two particular mixed edges ${\omega }_1=\{s_1,t_2\}$ and ${\omega }_2=\{s_2,t_1\}$. By assumption, there exist 2-simplices ${\Delta }_1$ and ${\Delta }_2$, such that ${\omega }_1\subset {\Delta }_1$ and ${\omega }_2\subset {\Delta }_2$, neither of which are faces of $\sigma$.

In view of $\{s_1,t_2\}\subset {\Delta }_1$, it follows from Proposition 3 that ${\Delta }_1$ is of the form $\{s_1,t_2,s^{\prime }\}$ or $\{s_1,t_2,t^{\prime }\}$. By w.l.o.g. we set ${\Delta }_1=\{s_1,t_2,t^{\prime }\}$. Since ${\Delta }_1\neg \subset \sigma$, we have $t^{\prime }\ne t_1$. By construction, $s_1\cap t_2\cap t^{\prime }\ne ⌀$. It implies that there exists an I-vertex ${\overline{i}}^{\prime }={\overline{j}}^{\prime }\in s_1\cap t_2\cap t^{\prime }$, which corresponds to a $\varphi$-arc $(i^{\prime },j^{\prime })$. As $\overline{i_1}\in s_1\cap s_2\cap t_1\cap t_2$ and ${\overline{i}}^{\prime }\in s_1\cap t_2\cap t^{\prime }$, the $\varphi$-arc $(i^{\prime },j^{\prime })$ is distinct from $(i_1,j_1)$. Since ${\omega }_1=\{s_1,t_2\}\subset {\Delta }_1$, the $\varphi$-arc $(i^{\prime },j^{\prime })$ connects two intervals ${[i_0,i_1)}_S\cup {[i_2,i_3]}_S$ and ${(j_1,j_2]}_T$, i.e., $i^{\prime }\in {[i_0,i_1)}_S\cup {[i_2,i_3]}_S$ and $j^{\prime }\in {(j_1,j_2]}_T$. Note that if $i^{\prime }\in {[i_0,i_1)}_S$, then $i^{\prime }<i_1$ and $j^{\prime }>j_1$, i.e., the $\varphi$-arcs $(i^{\prime },j^{\prime })$ and $(i_1,j_1)$ are crossing, which is a contradiction. Hence, we derive that the $\varphi$-arc $(i^{\prime },j^{\prime })$ connects ${[i_2,i_3]}_S$ and ${(j_1,j_2]}_T$ (see Figure 2).

Similarly, ${\Delta }_2$ corresponds to a $\varphi$-arc $(i^{″},j^{″})$ distinct from $(i_1,j_1)$. Since ${\omega }_2\subset {\Delta }_2$, it follows that the $\varphi$-arc $(i^{″},j^{″})$ connects two intervals ${(i_1,i_2]}_S$ and ${[j_2,j_3]}_T$ (see Figure 2). In view of $i^{″}<i^{\prime }$ and $j^{″}>j^{\prime }$, the $\varphi$-arcs $(i^{\prime },j^{\prime })$ and $(i^{″},j^{″})$ are crossing, which contradicts the fact that $\varphi$-arcs are non-crossing.

Accordingly, the non-crossing property of $\varphi$-arcs implies that either one, $\{s_1,t_2\}$ or $\{s_2,t_1\}$, is $\sigma$-free. □

Proposition 6.

Given a loop complex $K\left(I\right)$, then any 3-simplex $\sigma \in K_3\left(I\right)$ contains at least two σ-free 2-faces.

Proof. 

By Proposition 5, $\sigma$ contains at least one $\sigma$-free mixed edge $\omega$. Let ${\Delta }_1$ and ${\Delta }_2$ denote the 2-faces of $\sigma$ containing $\omega$. Suppose that there exists a simplex ${\sigma }_1$ satisfying ${\Delta }_1\subset {\sigma }_1$ and ${\sigma }_1\neg \subset \sigma$. Then ${\sigma }_1$ also contains $\omega$, which contradicts $\omega$ being $\sigma$-free. Therefore, ${\Delta }_1$ is $\sigma$-free and, analogously, we derive that ${\Delta }_2$ is $\sigma$-free. □

Proposition 7.

Let I be a τ-structure with loop complex $K\left(I\right)$. Then $H_0\left(I\right)\cong \mathbb{Z}$ and $H_d\left(I\right)=0$ for $d\ge 4$.

Proof. 

By assumption, $\varphi$ induces at least one $\varphi$-arc, which in turn gives rise to at least a 1-simplex connecting an S-loop and a T-loop. Therefore, $K\left(I\right)$ is path-connected and $H_0\left(I\right)\cong \mathbb{Z}$. By the pigeonhole principle, for any set of $d+1$I-loops with $d\ge 4$, at least three belong to the same secondary structure. By Proposition 2, these three loops intersect trivially. Thus, for $d\ge 4$, the intersection of any $d+1$ loops is trivial. As a result, $K\left(I\right)$ does not contain simplices of dimension four or higher. Therefore, $K_d\left(I\right)=⌀$ and $H_d\left(I\right)=0$ for $d\ge 4$. □

4. From $\mathit{X}$ to ${\tilde{\mathit{X}}}_{\mathbf{2}}$

We now begin computing the homology of the loop complex of a $\tau$-structure. Directly constructing its discrete Morse function [14,15] or gradient vector field seems rather involved. We shall take a slightly different approach along the lines of discrete Morse theory. We shall simplify the loop complex in multiple rounds and render it amendable to its homological analysis. One of these simplifications is obtained via elementary collapses, which is a reduction introduced by J.H.C. Whitehead [16]. These collapses can be understood in terms of non-critical points of the Morse function.

4.1. Simplicial Collapses

The notion of elementary collapse is closely related to the freeness of a simplex. Given a complex K, let $\sigma$ be a maximal simplex and $\Delta$ be a $\sigma$-free face with codimension 1. The removal of $\sigma$ and $\Delta$ constitutes elementary collapse [16,17] and gives rise to a new complex $K\setminus \{\sigma ,\Delta \}$. We say that K simplicial collapses to a sub-complex $K^{\prime }$, which is denoted by $K\searrow K^{\prime }$ if there is a sequence of complexes $K_0=K,K_1,\dots ,K_q=K^{\prime }$ such that $K_i$ is obtained from $K_{i-1}$ via an elementary collapse. Clearly, K and $K^{\prime }$ are homotopy equivalent.

In the following, we shall employ simplicial collapses in order to reduce the loop complex in two steps: first, eliminating all tetrahedra and then removing triangles possessing a free edge.

Step 1: Given a 3-simplex ${\sigma }_1=\{s_1,s_2,t_1,t_2\}$, Proposition 5 guarantees that ${\sigma }_1$ always has a free mixed edge $\omega$ and two free triangles ${\Delta }_1,{\Delta }_1^{\prime }$ containing $\omega$. The triple $(\omega ,{\Delta }_1,{\Delta }_1^{\prime })$ is called a ${\sigma }_1$-butterfly. In analogy to the analysis in case of bi-structures [7], we perform the butterfly removal on the loop complex. Specifically, the simplicial collapse consists of two elementary collapses with respect to $({\sigma }_1,{\Delta }_1)$ and $({\Delta }_1^{\prime },\omega )$ and provides us a sub-complex $K_1=K\left(I\right)\setminus \{{\sigma }_1,{\Delta }_1,{\Delta }_1^{\prime },\omega \}$, which is homotopy equivalent to $K\left(I\right)$.

We observe that $K_1$ is again the loop complex of a $\tau$-structure $I_1=(S_1,T_1,{\varphi }_1)$ obtained by splicing vertices in I as follows: For any I-vertex $q\in s_1\cap s_2\cap t_1\cap t_2$, suppose that q is the equivalence class of an S-vertex i and a T-vertex j. Then, there is a $\varphi$-arc connecting i and j, i.e., $\varphi \left(i\right)=j$. We now splice i into two consecutive vertices $i_1,i_2$ and splice j into two consecutive vertices $j_1,j_2$. The $\varphi$-arc $\varphi \left(i\right)=j$ is replaced with two new $\varphi$-arcs ${\varphi }_1\left(i_1\right)=j_1$ and ${\varphi }_1\left(i_2\right)=j_2$. The arcs are connected in a manner such that the mixed edge $\omega$ is not formed in $K_1$. In the case of $\omega =\{s_1,t_2\}$, we depict the resulting $\tau$-structure $I_1$ in Figure 3 and note that all other cases are treated similarly. Furthermore, we remove any other $\varphi$-arcs that give rise to ${\Delta }_1$, ${\Delta }_1^{\prime }$ or $\omega$. It is straightforward to verify that the loop complex of $I_1$ is exactly $K_1$.

By iteratively eliminating all 3-simplices, $\sigma$ and the associated $\sigma$-butterflies, we derive a sequence of sub-complexes $K_0=K\left(I\right),K_1,\dots ,K_q=X$ such that X does not contain any 3-simplices. Accordingly, we obtain a sequence of $\tau$-structures $I_0=I,I_1,\dots ,I_q=I^{\prime }$ by splicing the corresponding vertices of $\sigma$ such that the loop complex of $I_j$ is given by $K_j$. It is clear that the sub-complex X satisfies the following property.

Lemma 1.

Let $K\left(I\right)$ be the loop complex of a τ-structure I and X be the complex obtained by removing from $K\left(I\right)$ all 3-simplices σ and the associated σ-butterflies. Then the following is the case:

(1) 

X is the complex of a τ-structure $I^{\prime }$ such that each ϕ-arc is incident to at most one arc;

(2) 

X is a sub-complex of $K\left(I\right)$ such that the 0-th skeleton $X^{\left(0\right)}=K{\left(I\right)}^{\left(0\right)}$ and X does not contain any 3-simplices;

(3) 

$H_n\left(X\right)\cong H_n\left(I\right)$, for $n\ge 0$.

A complex possessing the properties of Lemma 1 is called lean. As an immediate consequence we obtain the following.

Corollary 1.

Let I be a τ-structure, then $H_3\left(I\right)=0$.

Proof. 

In view of Proposition 1, as a sub-complex of $K\left(I\right)$, X does not contain any 3-simplices. For X holds $ker{\partial }_3=0$, whence $H_3\left(I\right)\cong H_3\left(X\right)=0$. □

Step 2: Suppose that ${\Delta }_1$ is a 2-simplex in X having a free 1-face ${\omega }_1$. By collapsing $({\Delta }_1,{\omega }_1)$, we obtain a sub-complex $X_1=X\setminus \{{\Delta }_1,{\omega }_1\}$. By successively deleting 2-simplices $\omega$ together with $\tau$-free edges, we derive a sequence of sub-complexes $X_0=X,X_1,\dots ,X_m=\tilde{X}$ such that each 2-simplex of $\tilde{X}$ does not contain any free 1-face.

Proposition 8.

Let $\tilde{X}$ be a complex obtained from X by iteratively removing all 2-simplices ω together with τ-free 1-face. Then, the following is the case:

(1)

$\tilde{X}$ is a sub-complex of X such that the 0-th skeleton ${\tilde{X}}^{\left(0\right)}=X^{\left(0\right)}$ and each 2-simplex of $\tilde{X}$ does not have a free 1-face;

(2)

For $n\ge 0$, we have $H_n\left(\tilde{X}\right)\cong H_n\left(X\right)$.

Figure 4 displays the simplicial collapse from X to $\tilde{X}$.

Remark 1.

The sub-complex $\tilde{X}$ is not unique. By construction, $\tilde{X}$ depends on the particular sequence of the simplicial collapses, as well as which free face of a simplex is being removed (see Figure 5)

Lemma 1 guarantees that $\tilde{X}$ is derived from a lean complex.

Lemma 2.

Let $\tilde{X}$ be the sub-complex derived from a lean complex, then the following is the case:

(1)

For any 2-simplex $\Delta =\{s_1,s_2,t_1\}\in \tilde{X}$, holds $s_1\cap s_2\cap t_1=\left\{\overline{i}\right\}$, i.e., any 2-simplex Δ corresponds to the ϕ-arc, $(i,\varphi (i\left)\right)$;

(2)

Any pure 1-simplex ω of $\tilde{X}$ is either maximal or contained in exactly two 2- simplices $\Delta ,{\Delta }^{\prime }$. In the latter case, ω is associated with an arc $(i,i^{\prime })$ in I, such that vertices $i,i^{\prime }$ are incident to ϕ-arcs $(i,j)$ and $(i^{\prime },j^{\prime })$, respectively.

Proof. 

For any $\Delta =\{s_1,s_2,t_1\}\in \tilde{X}$, we have $|s_1\cap s_2\cap t_1|\le |s_1\cap s_2|=2$. By construction, in $\tilde{X}$, $\omega$ is not $\Delta$-free, whence there exists another 2-simplex ${\Delta }^{\prime }=\{s_1,s_2,t_1^{\prime }\}\ne \Delta$ containing $\omega$. Lemma 1 guarantees that $\tilde{X}$ does not contain any 3-simplices, i.e., we have the following.

$$(s_1\cap s_2\cap t_1)\cap (s_1\cap s_2\cap t_1^{\prime })=s_1\cap s_2\cap t_1\cap t_1^{\prime }=⌀.$$

Therefore, sets $s_1\cap s_2\cap t_1$ and $s_1\cap s_2\cap t_1^{\prime }$ are disjoint and both have cardinality 1, whence assertion (1) follows. Let $s_1\cap s_2\cap t_1=\left\{\overline{i}\right\}$, then $\Delta$ is in one-to-one correspondence with the vertex i as well as its induced $\varphi$-arc $(i,\varphi (i\left)\right)$ in I.

Suppose the pure 1-simplex $\omega$ is not maximal, then there exists at least one 2-simplex $\Delta$ having $\omega$ as a face. Since we work in the complex $\tilde{X}$, $\omega$ cannot be $\Delta$-free, whence there exists another 2-simplex ${\Delta }^{\prime }$ containing $\omega$. Assertion (1) then implies that $\Delta$ and ${\Delta }^{\prime }$ are the only such 2-simplices, which completes the proof. □

4.2. Topological Stratification

We shall next show that the complex $\tilde{X}$ is topologically stratified and decomposes into two sub-complexes ${\tilde{X}}_2$ and $K_1$, where ${\tilde{X}}_2$ is induced by all $\tilde{X}$-2-simplices and $K_1$ by all 1-simplices of $\tilde{X}\setminus {\tilde{X}}_2$ (see Figure 6)

Proposition 9.

We have $H_2\left(\tilde{X}\right)\cong H_2\left({\tilde{X}}_2\right)$ and $H_1\left(\tilde{X}\right)\cong H_1\left({\tilde{X}}_2\right)⨁{\oplus }_{i=1}^k\mathbb{Z}$, where the non-negative integer k depends on $K_1$ and ${\tilde{X}}_2\cap K_1$.

Proof. 

By construction, ${\tilde{X}}_2$ is a sub-complex of $\tilde{X}$. We have the short exact sequence of chain complexes $0\stackrel{}{\to }{C}_{*}\left({\tilde{X}}_2\right)\stackrel{i}{\to }{C}_{*}\left(\tilde{X}\right)\stackrel{j}{\to }{C}_{*}(\tilde{X},{\tilde{X}}_2)\stackrel{}{\to }0$, which induces the long exact sequence.

$$\begin{array}{cccccc}\hfill \cdots \stackrel{}{\to }& H_{n+1}(\tilde{X},{\tilde{X}}_2)\stackrel{\partial }{\to }\hfill & \hfill H_n\left({\tilde{X}}_2\right)\stackrel{i_{*}}{\to }& H_n\left(\tilde{X}\right)\stackrel{j_{*}}{\to }\hfill & \hfill H_n(\tilde{X},{\tilde{X}}_2)\stackrel{}{\to }& \cdots .\hfill \end{array}$$

By construction, $\tilde{X}$ does not have any 3-simplices, which implies that $C_3(\tilde{X},{\tilde{X}}_2)=0$. Since ${\tilde{X}}_2$ contains all 2-simplices in $\tilde{X}$, we have $C_2(\tilde{X},{\tilde{X}}_2)=0$. Then we derive $H_3(\tilde{X},{\tilde{X}}_2)=H_2(\tilde{X},{\tilde{X}}_2)=0$. In view of the long exact sequence, we have the following:

$$\begin{array}{cccc}\hfill 0=H_3(\tilde{X},{\tilde{X}}_2)\stackrel{\partial }{\to }& H_2\left({\tilde{X}}_2\right)\stackrel{i_{*}}{\to }& H_2\left(\tilde{X}\right)\stackrel{j_{*}}{\to }\hfill & H_2(\tilde{X},{\tilde{X}}_2)=0,\end{array}$$

in other words, $H_2\left(\tilde{X}\right)\cong H_2\left({\tilde{X}}_2\right)$. For $n=1$, the long exact sequence reads as follows:

$$\begin{array}{cccc}\hfill 0=H_2(\tilde{X},{\tilde{X}}_2)\stackrel{\partial }{\to }& H_1\left({\tilde{X}}_2\right)\stackrel{i_{*}}{\to }& H_1\left(\tilde{X}\right)\stackrel{j_{*}}{\to }\hfill & H_1(\tilde{X},{\tilde{X}}_2),\end{array}$$

which induces the following exact sequence.

$$\begin{array}{ccccc}\hfill 0\stackrel{\partial }{\to }& H_1\left({\tilde{X}}_2\right)\stackrel{i_{*}}{\to }& H_1\left(\tilde{X}\right)\stackrel{j_{*}}{\to }\hfill & Im{j}_{*}r& 0.\end{array}$$

The relative homology $C_1(\tilde{X},{\tilde{X}}_2)$ is freely generated by the 1-simplices in $\tilde{X}\setminus {\tilde{X}}_2$. By definition, we have $H_1(\tilde{X},{\tilde{X}}_2)=ker\left({\overline{\partial }}_1\right)/Im\left({\overline{\partial }}_2\right)$, where $C_2(\tilde{X},{\tilde{X}}_2)\stackrel{{\overline{\partial }}_2}{\to }{C}_1(\tilde{X},{\tilde{X}}_2)\stackrel{{\overline{\partial }}_1}{\to }{C}_0(\tilde{X},{\tilde{X}}_2)$. In view of $Im\left({\overline{\partial }}_2\right)=0$, $H_1(\tilde{X},{\tilde{X}}_2)\cong ker\left({\overline{\partial }}_1\right)$ and $H_1(\tilde{X},{\tilde{X}}_2)$ is free. As a subgroup of the free group $H_1(\tilde{X},{\tilde{X}}_2)$, $Im{j}_{*}$ is free and thus projective. Then, the short exact sequence is split exact and the following is the case:

$$H_1\left(\tilde{X}\right)\cong H_1\left({\tilde{X}}_2\right)\oplus Im{j}_{*}\cong H_1\left({\tilde{X}}_2\right)⨁{\oplus }_{i=1}^k\mathbb{Z},$$

where the non-negative integer $k=rnk(Im{j}_{*})$ depends on $K_1$ and ${\tilde{X}}_2\cap K_1$. □

Proposition 9 shows that the sub-complex $K_1$ gives rise to only free generators in the first homology of $\tilde{X}$.

5. Some Combinatorics of Crossing Components

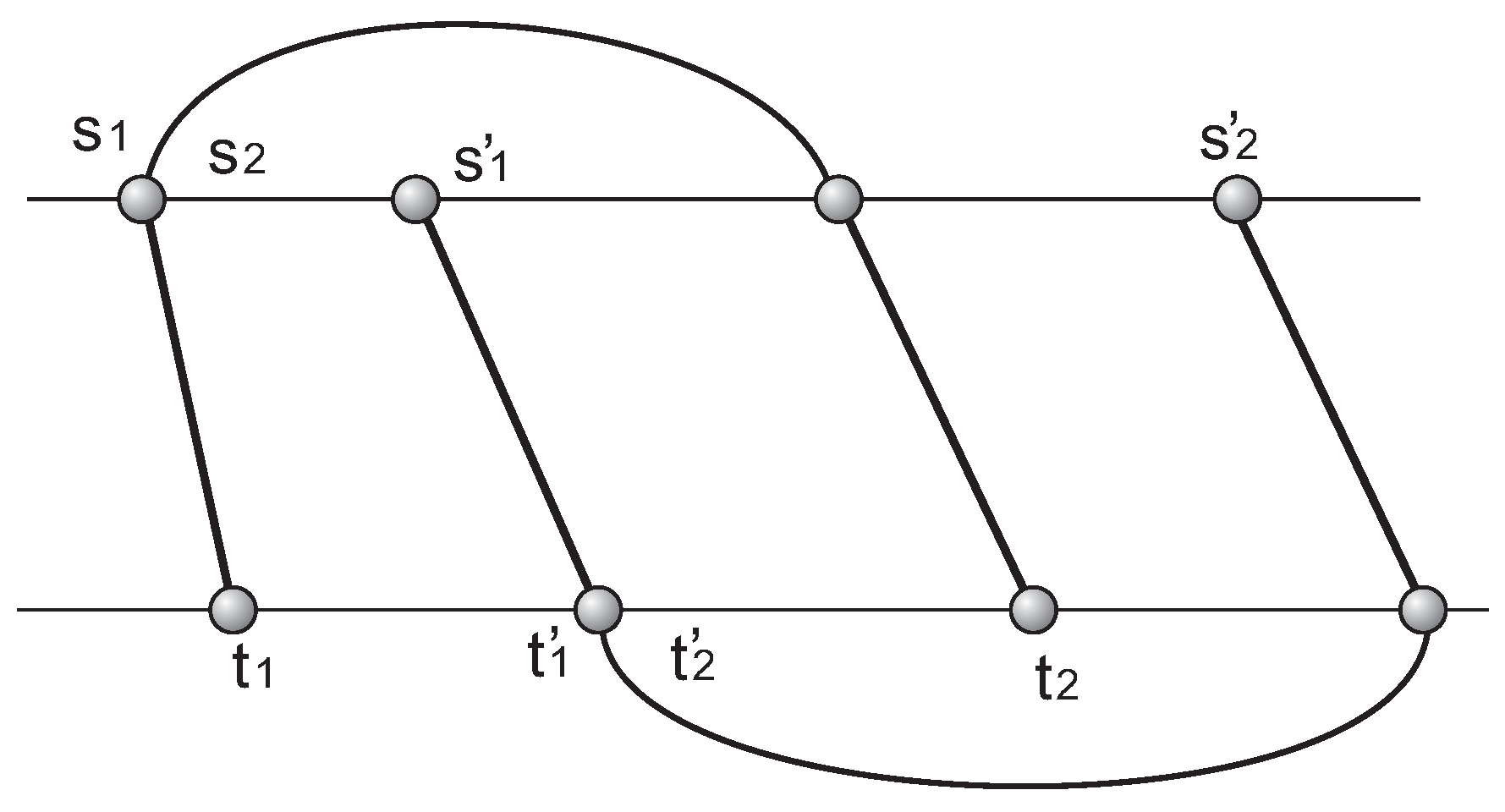
In order to compute the homology of $\tilde{X}$, we introduce an equivalence relation partitioning the set of 2-simplices. To this end, we observe that 2-simplices of $\tilde{X}$ appear in pairs: Given a 2-simplex $\Delta$ with pure edge, $\omega$, Lemma 2 guarantees that there exists a unique 2-simplex ${\Delta }^{\prime }$ such that $\Delta \cap {\Delta }^{\prime }=\omega$. Each pair $(\Delta ,{\Delta }^{\prime })$ is associated with a unique arc $(i_1,i_2)$ and $i_1$ and $i_2$ are incident to the $\varphi$-arcs, $(i_1,\varphi \left(i_1\right))$ and $(i_2,\varphi \left(i_2\right))$. We refer to $(\Delta ,{\Delta }^{\prime })$ together with their pure and $\varphi$-arcs as a couple.

Two couples $({\Delta }_1,{\Delta }_1^{\prime })$ and $({\Delta }_2,{\Delta }_2^{\prime })$ are ϕ-crossing if their corresponding arcs $(i_1,i_2)$ and $(j_1,j_2)$ are $\varphi$-crossing, i.e., if either the following is the case:

(1)

Both $i_1$ and $i_2$ are incident to $\varphi$-arcs such that $\varphi \left(i_1\right)<j_1<\varphi \left(i_2\right)<j_2$ or $j_1<\varphi \left(i_1\right)<j_2<\varphi \left(i_2\right)$, or;

(2)

Both $j_1$ and $j_2$ are incident to $\varphi$-arcs such that $i_1<{\varphi }^{-1}\left(j_1\right)<i_2<{\varphi }^{-1}\left(j_2\right)$ or ${\varphi }^{-1}\left(j_1\right)<i_1<{\varphi }^{-1}\left(j_2\right)<i_2$.

This notion induces an equivalence relation ${\sim }_{\varphi }$ on all $\tilde{X}$-couples to be the transitive closure with respect to $\varphi$-crossing. Two couples $({\Delta }_1,{\Delta }_1^{\prime })$ and $({\Delta }_k,{\Delta }_k^{\prime })$ are $\varphi$-equivalent, denoted by $({\Delta }_1,{\Delta }_1^{\prime }){\sim }_{\varphi }({\Delta }_k,{\Delta }_k^{\prime })$, if there exists a sequence of pairs $({\Delta }_1,{\Delta }_1^{\prime }),({\Delta }_2,{\Delta }_2^{\prime }),\dots ,$$({\Delta }_k,{\Delta }_k^{\prime })$, such that $({\Delta }_i,{\Delta }_i^{\prime })$ and $({\Delta }_{i+1},{\Delta }_{i+1}^{\prime })$ are $\varphi$-crossing for $1\le i\le k-1$. The relation ${\sim }_{\varphi }$ partitions the set of $\tilde{X}$-pairs into equivalence classes, $\left[({\Delta }_1,{\Delta }_1^{\prime })\right]$. A ϕ-crossing component or component, C, of $\tilde{X}$ is the set of 2-simplices contained in an equivalence class $\left[(\Delta ,{\Delta }^{\prime })\right]$. By construction, the set of all 2-simplices in $\tilde{X}$ is partitioned into components, C, and each component C induces a $\tilde{X}$-sub-complex. By the abuse of notation, we shall denote a component as well as its induced $\tilde{X}$-sub-complex by C. We refer to the $\varphi$-arcs of a component C as C-ϕ-arcs.

Suppose that $(i_1,j_1),(i_2,j_2),\dots ,(i_l,j_l)$, where $i_1<i_2<\cdots <i_l$ and $\varphi \left(i_k\right)=j_k$ are C-$\varphi$-arcs. These partition the two backbones into blocks, the outer block ${\beta }_1={[1,i_1)}_S\cup {(i_l,n]}_S\cup {[1,j_1)}_T\cup {(j_l,m]}_T$ and the inner blocks ${\beta }_r={(i_{r-1},i_r)}_S\cup {(j_{r-1},j_r)}_T$, $2\le r\le l$. A block, $\beta$, contains a couple $(\Delta ,{\Delta }^{\prime })$ if all endpoints of $\varphi$-arcs associated with $(\Delta ,{\Delta }^{\prime })$ are contained in $\beta$ and the component $C_1$ if $\beta$ contains all $C_1$-couples.

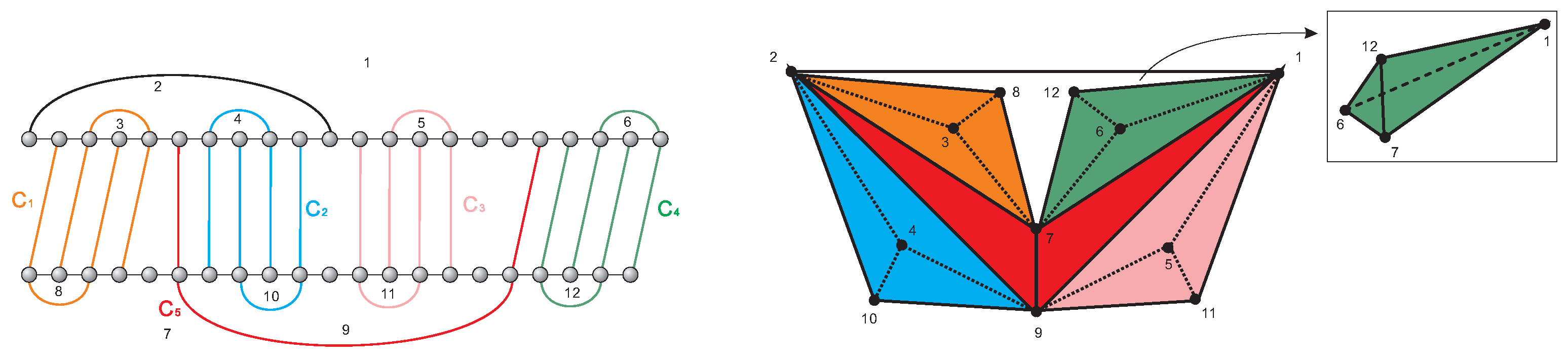
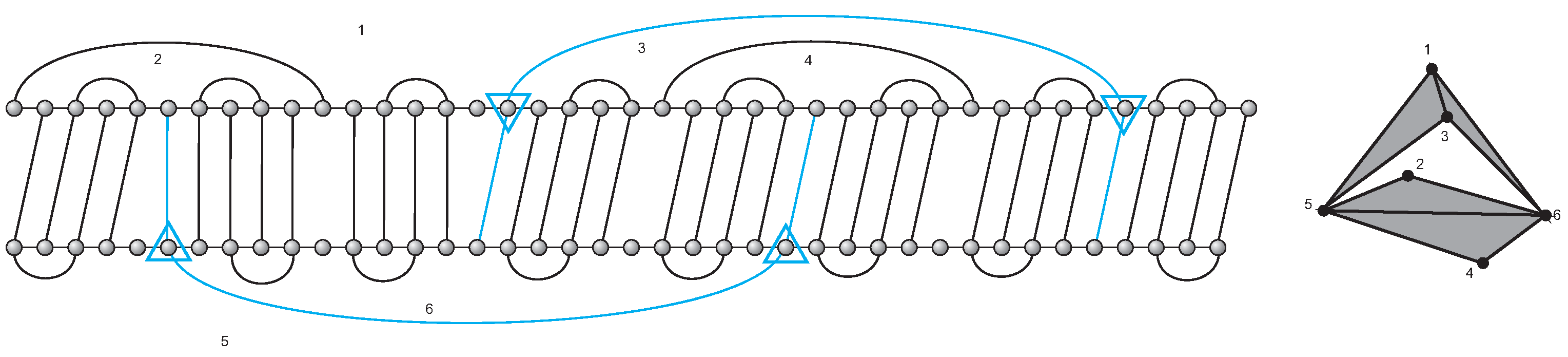
Figure 7 demonstrates a decomposition of $\tilde{X}$ into components. In this example, the complex $K\left(I^{\prime }\right)$ does not a priori contain any free 1-face, whence $K\left(I^{\prime }\right)=\tilde{X}$. It is straightforward to verify that $\tilde{X}$ features the five components:

$$\begin{array}{cc}\hfill C_1=& \left\{\right\{2,3,8\},\{2,3,7\},\{2,7,8\},\{3,7,8\left\}\right\},\hfill \\ \hfill C_2=& \left\{\right\{2,4,9\},\{2,4,10\},\{2,9,10\},\{4,9,10\left\}\right\},\hfill \\ \hfill C_3=& \left\{\right\{1,5,9\},\{1,5,11\},\{1,9,11\},\{5,9,11\left\}\right\},\hfill \\ \hfill C_4=& \left\{\right\{1,6,7\},\{1,6,12\},\{1,7,12\},\{6,7,12\left\}\right\},\hfill \\ \hfill C_5=& \left\{\right\{2,7,9\},\{1,7,9\left\}\right\}.\hfill \end{array}$$

The $\varphi$-arcs of $C_5$ induce the outer block ${[1,5)}_S\cup {(19,22]}_S\cup {[1,5)}_T\cup {(18,21]}_T$ and the inner block ${(7,17)}_S\cup {(7,16)}_T$. The components $C_1,C_4$ are contained in the outer and $C_2,C_3$ in the inner block, respectively.

Lemma 3.

Let C be a $\tilde{X}$-component with blocks ${\beta }_1,{\beta }_2,\dots ,{\beta }_l$. Then, for any other component $C_1\ne C$, there exists a unique block, ${\beta }_k$, that contains $C_1$.

Proof. 

Suppose that C-$\varphi$-arcs are given by $(i_1,j_1),(i_2,j_2),\dots ,(i_l,j_l)$, where $i_1<i_2<\cdots <i_l$ and $\varphi \left(i_k\right)=j_k$.

Claim: Given a $C_1$-couple $(\Delta ,{\Delta }^{\prime })$ with $\varphi$-arcs $(i,j)$ and $(i^{\prime },j^{\prime })$, then there exists a block ${\beta }_k$ that contains both $(i,j)$ and $(i^{\prime },j^{\prime })$.

Firstly, both endpoints $i,j$ are contained in the same C-block otherwise $(i,j)$ would cross a C-$\varphi$-arc. Suppose $(i,j)$ and $(i^{\prime },j^{\prime })$ are contained in different C-blocks. Since C and $C_1$ are distinct components, C-couples and $C_1$-couples are mutually non-crossing. As a result, $C_1$ partitions the C-couples into to two non-empty subsets, one contained in ${(i,i^{\prime })}_S\cup {(j,j^{\prime })}_T$ and the other in ${[1,i)}_S\cup {(i^{\prime },n]}_S\cup {[1,j)}_T\cup {(j^{\prime },m]}_T$. By construction, any couple contained in the former subset and any pair in the latter are non-crossing, which is impossible since C is a component.

It follows that there exists a C-block ${\beta }_k$ that contains both $(i,j)$ and $(i^{\prime },j^{\prime })$.

Any $C_1$-couple $({\Delta }_1,{\Delta }_1^{\prime })$ that crosses $(\Delta ,{\Delta }^{\prime })$ has at least one $\varphi$-arc contained in ${\beta }_k$. By the above argument, both of its $\varphi$-arcs are then contained in ${\beta }_k$, i.e., ${\beta }_k$ contains $({\Delta }_1,{\Delta }_1^{\prime })$. Since $C_1$ is a component this implies that any $C_1$-couple is contained in ${\beta }_k$. □

Lemma 3 gives rise to a relation over the set of $\tilde{X}$-components as follows: $C_1\prec C_2$ if all $C_1$-$\varphi$-arcs are contained in an inner block of $C_2$. In view of Lemma 3, we can verify that the relation ≺ is a well-defined partial order. In Figure 7, $C_2\prec C_5$, $C_3\prec C_5$ and $C_1,C_4,C_5$ are maximal.

We next identify how two 2-simplices that share a mixed edge affect the location of couples along the two backbones. This reflects the planarity of $\tau$-structures and has important consequences for how components are glued in the loop complex.

Lemma 4.

Let Δ and ${\Delta }_1$ be $\tilde{X}$-2-simplices that share the mixed edge, ω, and that correspond to the ϕ-arcs $(i,j)$ and $(i_1,j_1)$, where $i<i_1$. Then any couple $({\Delta }_2,{\Delta }_2^{\prime })$ where $\{{\Delta }_2,{\Delta }_2^{\prime }\}\cap \{\Delta ,{\Delta }_1\}=⌀$ is contained in either

$${(i,i_1)}_S\cup {(j,j_1)}_T\mathrm{or}{[1,i)}_S\cup {(i_1,n]}_S\cup {[1,j)}_T\cup {(j_1,m]}_T.$$

Proof. 

Without loss of generality we may assume that $({\Delta }_2,{\Delta }_2^{\prime })$ features the S-arc $(i_2,i_2^{\prime })$. Let $\omega =\{s,t\}$, since $\Delta \cap {\Delta }_1=\omega$, by construction $i,i_1\in s$ and $j,j_1\in t$. In case one of the vertices, $i_2,i_2^{\prime }$ is contained in ${(i,i_1)}_S$ and the other is contained in ${[1,i)}_S\cup {(i_1,n]}_S$, the arc $(i_2,i_2^{\prime })$ organizes $i,i_1$ into distinct S-loops (see Figure 8), which is a contradiction. Thus, $i_2,i_2^{\prime }$ are contained in ${(i,i_1)}_S$ or ${[1,i)}_S\cup {(i_1,n]}_S$, i.e., the $\varphi$-arcs associated with $({\Delta }_2,{\Delta }_2^{\prime })$ are contained in ${(i,i_1)}_S\cup {(j,j_1)}_T$ or ${[1,i)}_S\cup {(i_1,n]}_S\cup {[1,j)}_T\cup {(j_1,m]}_T$. □

Lemma 5.

Let C be a $\tilde{X}$-component. Then for any 2-simplex $\Delta \in C$ and any 1-face ω, there exists at most one 2-simplex ${\Delta }_1\in C$ such that $\Delta \cap {\Delta }_1=\omega$.

Proof. 

Clearly, the statement holds when $\omega$ is pure. For mixed $\omega$, by w.l.o.g. let $\Delta =\{s_1,s_2,t\}$ $\omega =\{s_2,t\}$ and assume the S-loop $s_2$ corresponds to the arc $(i,i^{\prime })$ where $i<i^{\prime }$.

Suppose there exist distinct 2-simplices ${\Delta }_1,{\Delta }_2\in C$ having $\omega$ as a 1-face. We shall denote the $\Delta$, ${\Delta }_1$ and ${\Delta }_2$-$\varphi$-arcs by $(i,j)$, $(i_1,j_1)$, $(i_2,j_2)$, respectively. Without loss of generality, we may assume that $i<i_1<i_2$. Since any $\varphi$-arcs are non-crossing, we have $j<j_1<j_2$.

We now apply Lemma 4: Since $\Delta \cap {\Delta }_2=\omega$, the couple $({\Delta }_1,{\Delta }_1^{\prime })$ is contained in ${(i,i_2)}_S\cup {(j,j_2)}_T$ or ${[1,i)}_S\cup {(i_2,n]}_S\cup {[1,j)}_T\cup {(j_2,m]}_T$. Since $i<i_1<i_2$, $({\Delta }_1,{\Delta }_1^{\prime })$ is contained in ${(i,i_2)}_S\cup {(j,j_2)}_T$.

In view of $(\Delta ,{\Delta }^{\prime })$ and $({\Delta }_1,{\Delta }_1^{\prime })$ belonging to C, there exists a sequence of pairs $({\alpha }_1,{\alpha }_1^{\prime })=({\Delta }_1,{\Delta }_1^{\prime }),({\alpha }_2,{\alpha }_2^{\prime }),\dots ,({\alpha }_k,{\alpha }_k^{\prime })=(\Delta ,{\Delta }^{\prime })$ such that $({\alpha }_i,{\alpha }_i^{\prime })$ and $({\alpha }_{i+1},{\alpha }_{i+1}^{\prime })$ are crossing.

Lemma 4 applies to any couple $({\alpha }_i,{\alpha }_i^{\prime })$, locating it in ${(i,i_2)}_S\cup {(j,j_2)}_T$ or ${[1,i)}_S\cup {(i_2,n]}_S\cup {[1,j)}_T\cup {(j_2,m]}_T$. In addition, since $({\alpha }_2,{\alpha }_2^{\prime })$ and $({\Delta }_1,{\Delta }_1^{\prime })$ are crossing, $({\alpha }_2,{\alpha }_2^{\prime })$ is contained in ${(i,i_2)}_S\cup {(j,j_2)}_T$, as is $({\alpha }_1,{\alpha }_1^{\prime })=({\Delta }_1,{\Delta }_1^{\prime })$. Analogously, it follows that $({\alpha }_k,{\alpha }_k^{\prime })=(\Delta ,{\Delta }^{\prime })$ is contained in ${(i,i_2)}_S\cup {(j,j_2)}_T$, which is, by construction, impossible.

Accordingly, there exists at most one 2-simplex ${\Delta }_1\in C$ such that $\Delta \cap {\Delta }_1=\omega$. □

Let C be a component and $\omega$ a C-1-face. Lemma 5 implies that $\omega$ is contained in either one or two C-2-simplices. We call a 1-face $\omega$ that is contained in a unique C-2-simplex C-free. Furthermore we call a component C complete if, for any of its 1-faces $\omega$, there exist exactly two 2-simplices $\Delta ,{\Delta }^{\prime }\in C$ such that $\Delta \cap {\Delta }^{\prime }=\omega$ and incomplete, otherwise.

Let C be a component with $\varphi$-arcs $(i_1,j_1),(i_2,j_2),\dots ,(i_l,j_l)$, where $i_1<i_2<\cdots <i_l$ and $\varphi \left(i_k\right)=j_k$. Let ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l$ denote the 2-simplices associated with the $\varphi$-arcs $(i_1,j_1),(i_2,j_2),\dots ,(i_l,j_l)$, respectively. Suppose that C-$\varphi$-arcs partition the two backbones into the sequence of blocks ${\beta }_1,{\beta }_2,\dots ,{\beta }_l$ ordered from left to right and where ${\beta }_1={[1,i_1)}_S\cup {(i_l,n]}_S\cup {[1,j_1)}_T\cup {(j_l,m]}_T={(i_l,i_1)}_S\cup {(j_l,j_1)}_T$ denotes the outer-block. Let ${\omega }_k$ and ${\omega }_k^{\prime }$ denote the mixed 1-faces of ${\Delta }_k$ that are associated with ${\beta }_k$ and ${\beta }_{k+1}$, respectively. We call the mixed edges ${\omega }_1$ and ${\omega }_l^{\prime }$ associated with the outer block the C-boundary. Note that ${\omega }_1$ and ${\omega }_l^{\prime }$ coincide if and only if ${\Delta }_1$ and ${\Delta }_l$ share a common mixed edge.

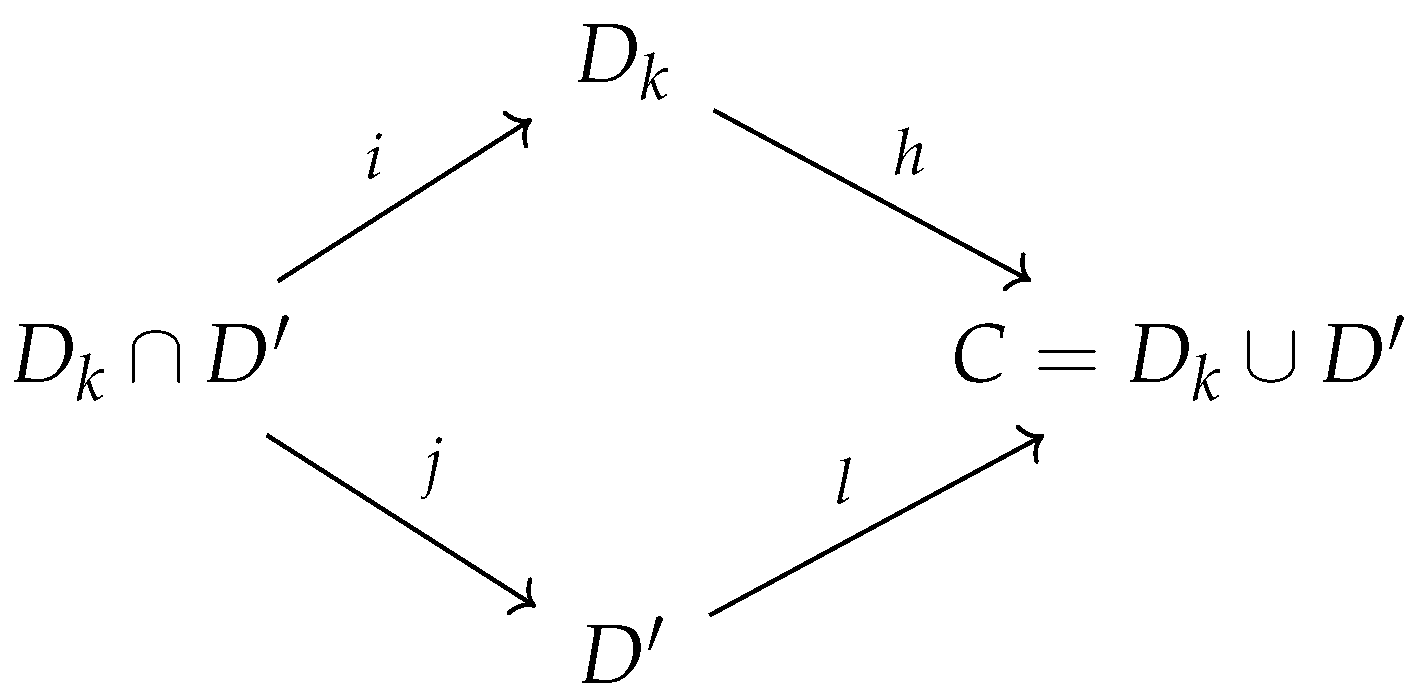
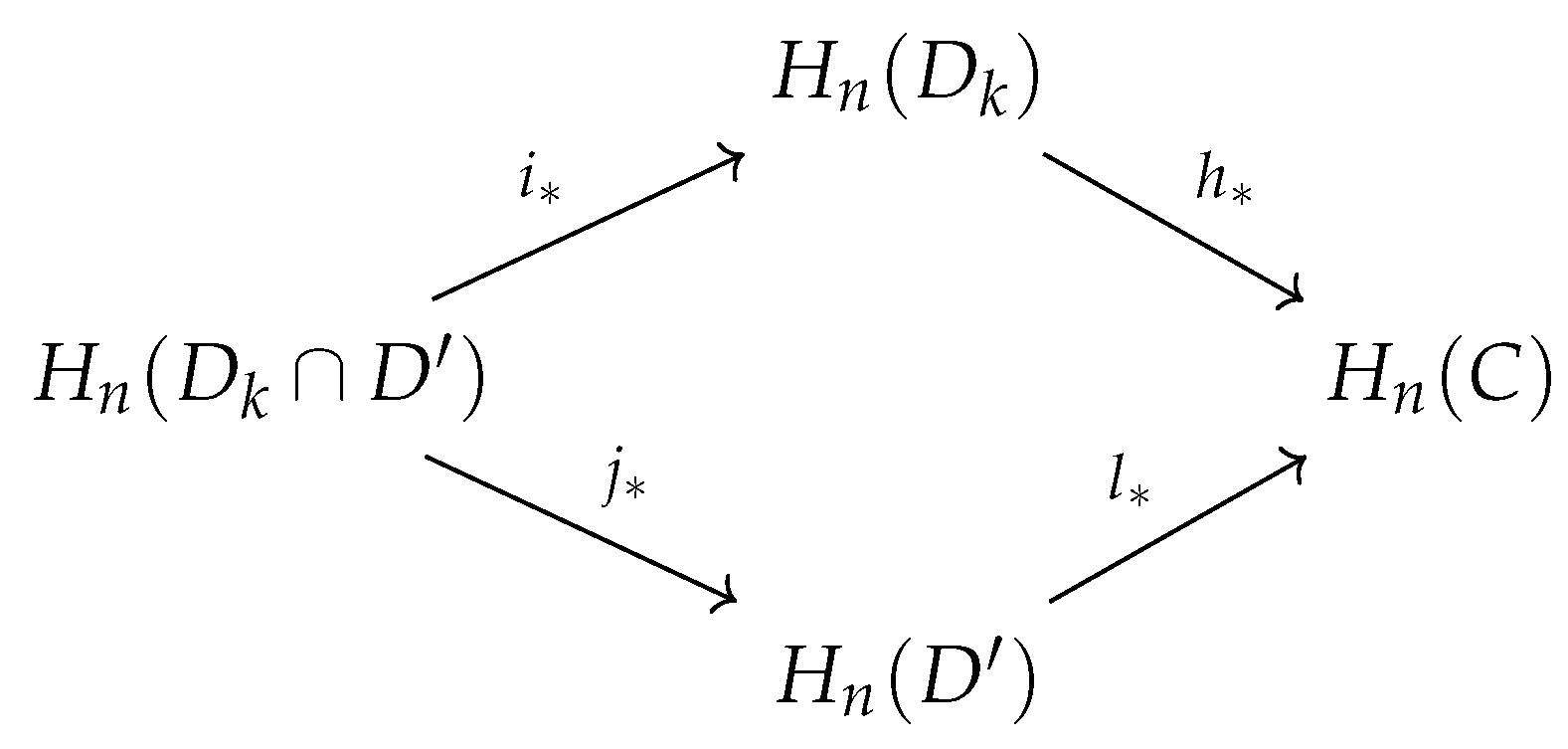
The next lemma constitutes a key observation which facilitates the computation of the homology of $\tau$-structures via the Mayer–Vietoris sequence, see Theorem 2.

Lemma 6.

Let C be an $\tilde{X}$-component having boundary ${\omega }_1$ and ${\omega }_l^{\prime }$, and let $C_1$ be an $\tilde{X}$-component with the property $C_1\nprec C$. Suppose that ω is a 1-simplex shared by C and $C_1$, then $\omega ={\omega }_1$ or $\omega ={\omega }_l^{\prime }$.

Proof. 

Let ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l$ denote the 2-simplices of C associated with the $\varphi$-arcs $(i_1,j_1),(i_2,j_2),$$\dots ,(i_l,j_l)$, ordered from left to right. Suppose that ${\Delta }_0\in C_1$ and ${\Delta }_k\in C$ share a common mixed edge $\omega$ and have the $\varphi$-arcs $(i_0,j_0)$ and $(i_k,j_k)$, respectively. In view of $C_1\nprec C$, $C_1$ is contained in the outer C-block and we may by w.l.o.g. assume that $i_0<i_1$.

The fact ${\Delta }_0\cap {\Delta }_k=\omega$, now organizes C relative to ${\Delta }_k$ in a particular fashion, see Figure 9. Employing Lemma 4 we obtain that, except of $({\Delta }_k,{\Delta }_k^{\prime })$, all C-couples partition into the following.

$$A_1\subset {(i_0,i_k)}_S\cup {(j_0,j_k)}_T\mathrm{and}{A}_2\subset {[1,i_0)}_S\cup {(i_k,n]}_S\cup {[1,j_0)}_T\cup {(j_k,m]}_T.$$

Now we use the fact that that C is a component: Firstly, any $A_1$-couple and any $A_2$-couple are by construction non-crossing. Secondly, by construction, $({\Delta }_k,{\Delta }_k^{\prime })$ is crossing into either only one $A_1$ or $A_2$, which implies that either one, $A_1$ or $A_2$, is trivial.

Suppose $A_1=⌀$. Then all C-$\varphi$-arcs are contained in $[i_k,n]$ which implies ${\Delta }_k={\Delta }_1$. In case $A_2=⌀$, all C-$\varphi$-arcs are contained in $(i_0,i_k]$ which implies ${\Delta }_k={\Delta }_l$. Therefore, for the shared 1-edge, $\omega$, holds $\omega ={\omega }_1$ or $\omega ={\omega }_l^{\prime }$. □

6. The Homology of Components

In order to compute the homology of $\tau$-structures, we shall first compute the homology of components separately and then integrate this information via the Mayer–Vietoris sequence [18,19]. To this end we adopt a topological perspective of crossing components, taking a closer look at the manifold formed by 2-simplices of a component obtained via gluing along their edges.

Given a component C, two couples $({\Delta }_1,{\Delta }_1^{\prime }){\sim }_1({\Delta }_k,{\Delta }_k^{\prime })$ if there exists a sequence of pairs $({\Delta }_1,{\Delta }_1^{\prime }),({\Delta }_2,{\Delta }_2^{\prime }),\dots ,({\Delta }_k,{\Delta }_k^{\prime })$ such that $({\Delta }_i,{\Delta }_i^{\prime })$ and $({\Delta }_{i+1},{\Delta }_{i+1}^{\prime })$ share at least one 1-face for $1\le i\le k-1$. Clearly, ${\sim }_1$ is an equivalence relation and partitions all pairs in C into equivalence classes $D_1,D_2,\dots ,D_k$, which we refer to as C-ribbons.

Lemma 7.

The geometric realization of a complete $\tilde{X}$-component, C is a sphere.

Proof. 

Suppose that ${\sim }_1$ partitions all C-pairs into the ribbons $D_1,D_2,\dots ,D_k$.

Claim 1: The geometric realization of a ribbon, $D_i$, is a surface without boundary.

Since C is complete, for each 2-simplex $\Delta \in D_i$ and its 1-face $\omega$, there exists a unique 2-simplex ${\Delta }_1\in C$ such that $\Delta \cap {\Delta }_1=\omega$. By construction, ${\Delta }_1$ is further contained in $D_i$. This implies that the geometric realization of $D_i$ is a compact and connected 2-manifold, i.e., a surface without boundary.

Let $T_{D_i}$ denote the $D_i$-sub-complex consisting of all pure edges for which its loops are T-loops. We shall employ $T_{D_i}$ in order to relate the crossing relation with ${\sim }_1$.

Claim 2:$T_{D_i}$ is connected, i.e., $T_{D_i}$ is a subtree of T.

Suppose that $T_{D_i}$ contains at least two connected components $T_1$ and $T_2$. Let $D^{\prime }$ denote the subset of 2-simplices of $D_i$ containing at least one $T_1$-vertex. Since all 2-simplices of $D^{\prime }$ are incident to the connected component $T_1$, the complex formed by $D^{\prime }$ is connected. $D^{\prime }$ does not contain any $T_2$-vertices, since otherwise there would, by construction of $D^{\prime }$, exist a pure edge connecting a $T_1$-vertex and a $T_2$-vertex, which contradicts the assumption that $T_{D_i}$ is disconnected. Thus, $D^{\prime }$ is a connected, which is a proper subset of $D_i$, and its geometric realization is a surface having boundary B, see Figure 10.

The set of 2-simplices containing a fixed $T_1$-vertex, t, forms a neighborhood of t in the $D_i$-induced surface, whence any $T_1$-vertex is contained in the interior of $D^{\prime }$. Consequently, the boundary does not contain any $T_1$-vertex. From this, we conclude that the boundary, being a cycle, consists of only S-loops. This, however, is impossible since the complex of a secondary structure S is a tree.

Claim 3:C consists of a unique ribbon.

Suppose that C contains at least two ribbons $D_1$ and $D_2$. Since C is a component, there exists a couple $(\Delta ,{\Delta }^{\prime })$ in $D_1$ and $({\Delta }_0,{\Delta }_0^{\prime })$ not contained in $D_1$, such that $(\Delta ,{\Delta }^{\prime })$ and $({\Delta }_0,{\Delta }_0^{\prime })$ are crossing.

Without loss of generality, we may consider $\Delta =\{s_1,s_2,t_1\}$, ${\Delta }^{\prime }=\{s_1,s_2,t_2\}$, ${\Delta }_0=\{t_1^{\prime },t_2^{\prime },s_1^{\prime }\}$ and ${\Delta }_0^{\prime }=\{t_1^{\prime },t_2^{\prime },s_2^{\prime }\}$, see Figure 11. Since $(\Delta ,{\Delta }^{\prime })$ and $({\Delta }_0,{\Delta }_0^{\prime })$ are crossing, the T-loops $t_1^{\prime },t_2^{\prime }$ are on the path connecting T-loops $t_1$ and $t_2$ in the complex of the secondary structure T.

By Claim 2, $T_{D_1}$ is connected and thus $t_1,t_2\in T_{D_1}$ implies that $\{t_1^{\prime },t_2^{\prime }\}\in T_{D_1}$. Claim 1 guarantees that each 1-face of $D_1$ is not $D_1$-free, whence there exist two $D_1$-2-simplices having the face $\{t_1^{\prime },t_2^{\prime }\}$. However, $({\Delta }_0,{\Delta }_0^{\prime })$ is the unique couple, for which the 2-simplices ${\Delta }_0,{\Delta }_0^{\prime }$ both contain the pure 1-simplex $\{t_1^{\prime },t_2^{\prime }\}$. As a result the fact that $D_1$ is a surface without boundary guarantees that $({\Delta }_0,{\Delta }_0^{\prime })$ is contained in $D_1$, which is a contradiction.

Therefore C is organized as a single ribbon, for which its geometric realization is a surface without boundary. We shall proceed by computing its Euler characteristic $\chi$.

Suppose that C contains n pairs $(\Delta ,{\Delta }^{\prime })$. Then the complex C features $2n$ 2-simplices and $3n$ 1-simplices. Claim 2 stipulates the connectivity of $S_C$ and $T_C$, whence both $S_C$ and $T_C$ are connected subsets of trees and as such trees themselves. We shall use this in order to count 0-simplices as follows: each pair $(\Delta ,{\Delta }^{\prime })$ corresponds to one pure 1-simplex in $S_C$ or $T_C$. Thus $S_C$ and $T_C$ contain n 1-simplices, which implies that C contains $n+(1+1)$ 0-simplices. From this, it follows $\chi =2$ and C is homeomorphic to a sphere. □

Remark 2.

The key in the proof is to show that the projection of $D_i$ onto each secondary structure, $T_{D_i}$, is connected. If $T_{D_i}$ is disconnected, then we can construct a cycle separating different connected components and consisting of only S-loops, resulting in a contradiction. The proof is reminiscent of the Jordan curve theorem in the plane [20,21].

While any complete component is organized as a distinguished ribbon, an incomplete component can consist of multiple ribbons. In Figure 12, the two couples $\left(\right\{2,5,6\},\{4,5,6\left\}\right)$ and $\left(\right\{1,3,5\},\{1,3,6\left\}\right)$ form an incomplete component, which contains two ribbons and each of which are a couple.

Lemma 8.

Given an incomplete $\tilde{X}$-component C, having the ribbons $D_1,D_2,\dots ,D_k$. Then, for each $D_i$, there exists some 1-face $\omega \in D_i$ that is $D_i$-free.

Proof. 

Suppose there exists a ribbon $D_i$, in which each 1-face $\omega \in D_i$ is not $D_i$-free. Lemma 5 guarantees that there exist exactly two 2-simplices $\Delta ,{\Delta }^{\prime }\in D_i$ such that $\Delta \cap {\Delta }^{\prime }=\omega$. Using the argument of Claim 2 of Lemma 7, we can conclude that $T_{D_i}$ is connected.

C consists of at least two distinct ribbons since otherwise $C=D_i$ contains no C-free 1-face, which contradicts the assumption that C is incomplete. Thus there exist a couple $(\Delta ,{\Delta }^{\prime })\in D_i$ and $({\Delta }_0,{\Delta }_0^{\prime })\notin D_i$, such that $(\Delta ,{\Delta }^{\prime })$ and $({\Delta }_0,{\Delta }_0^{\prime })$ are crossing. In analogy to Claim 3 of Lemma 7, we can conclude that both ${\Delta }_0$ and ${\Delta }_0^{\prime }$ are contained in $D_i$, which is impossible.

Therefore there exists a 1-face $\omega \in D_i$ that is $D_i$-free. □

Theorem 1.

Let C be a component of $\tilde{X}$. Then the following is the case:

$$H_2\left(C\right)\cong \left\{\begin{array}{cc}\mathbb{Z}\hfill & ifCiscomplete\hfill \\ 0\hfill & ifCisincomplete\hfill \end{array}\right.$$

(1)

and the following is also the case:

$$H_1\left(C\right)\cong \left\{\begin{array}{cc}0\hfill & ifCiscomplete\hfill \\ {\oplus }_{k=1}^r\mathbb{Z}\hfill & ifCisincomplete,\hfill \end{array}\right.$$

(2)

where the non-negative integer r depends on C. Furthermore, a complete component, $H_2\left(C\right)$ is freely generated by the sum of all C-2-simplices.

Proof. 

In case C is complete, by Lemma 7, C is homeomorphic to a sphere, whence $H_2\left(C\right)\cong \mathbb{Z}$ and $H_1\left(C\right)\cong 0$. Clearly, $H_2\left(C\right)$ is freely generated by the sum of 2-simplices of C.

In case C is incomplete, suppose that $D_1,D_2,\dots ,D_k$ are the C-ribbons. In the following, we prove Equations (1) and (2) by induction on the number k of ribbons.

For $k=1$, C is a ribbon and, as such, is connected. Since C is incomplete, it contains by Lemma 8 at least one C-free 1-face. This implies that the geometric realization of C is a surface with boundary. Therefore $H_2\left(C\right)\cong 0$ and $H_1\left(C\right)$ is free.

For the induction step, we shall combine ribbons in order to compute the homology of an incomplete component. In view of the fact that C is the union of the sub-complexes $D_k$ and $D^{\prime }={\cup }_{j<k}{D}_j$, we have the following inclusion maps:

Each inclusion map induces a chain map on the corresponding simplicial chain groups and a homomorphism between the corresponding homology groups.

Accordingly, we obtain the Mayer–Vietoris sequence

$$\begin{array}{cccccc}\hfill \cdots \stackrel{}{\to }& H_n(D_k\cap D^{\prime })\stackrel{\Phi }{\to }\hfill & \hfill H_n\left(D_k\right)\oplus H_n\left(D^{\prime }\right)\stackrel{\Psi }{\to }& H_n\left(C\right)\stackrel{\partial }{\to }\hfill & \hfill H_{n-1}(D_k\cap D^{\prime })\stackrel{}{\to }& \cdots \hfill \end{array}$$

where $\Phi =i_{*}\oplus j_{*}$, $\Psi =h_{*}-l_{*}$ and ∂ is the connecting homomorphism given by the zig-zag lemma (see [22,23] for more details).

By Lemma 8, $D_k$ contains at least one $D_k$-free 1-face, whence its geometric realization of $D_k$ is a surface with boundary. As a result, $H_2\left(D_k\right)\cong 0$ and $H_1\left(D_k\right)$ is free.

From the definition of ribbon follows, that the intersection $D_k\cap D_j$ of any two ribbons cannot contain any 2-simplices. Furthermore, $D_k\cap D_j$ does not contain any 1-simplices, whence $D_k\cap D_j$ contains only 0-simplices.

In view of $D_k\cap \left({\cup }_{j<k}{D}_j\right)={\cup }_{j<k}(D_k\cap D_j)$, we conclude that $D_k\cap D^{\prime }$ consists of only 0-simplices. Therefore, $H_2(D_k\cap D^{\prime })\cong H_1(D_k\cap D^{\prime })\cong 0$ and $H_0(D_k\cap D^{\prime })$ are free.

In case of $n=2$, the Mayer–Vietoris sequence reads as follows.

$$\begin{array}{cccc}\hfill 0=H_2(D_k\cap D^{\prime })\stackrel{\Phi }{\to }& H_2\left(D_k\right)\oplus H_2\left(D^{\prime }\right)\stackrel{\Psi }{\to }& H_2\left(C\right)\stackrel{\partial }{\to }\hfill & H_1(D_k\cap D^{\prime })=0.\end{array}$$

Thus, $\Psi$ is an isomorphism.

$$H_2\left(C\right)\cong H_2\left(D_k\right)\oplus H_2\left(D^{\prime }\right).$$

By induction hypothesis, we have $H_2\left(D^{\prime }\right)\cong 0$ and due to the fact that $D_k$ contains a free $D_k$-1-face, $H_2\left(D_k\right)\cong 0$. Accordingly, we obtain $H_2\left(C\right)\cong 0$.

In case of $n=1$, we observe the following:

$$\begin{array}{cccc}\hfill 0=H_1(D_k\cap D^{\prime })\stackrel{\Phi }{\to }& H_1\left(D_k\right)\oplus H_1\left(D^{\prime }\right)\stackrel{\Psi }{\to }& H_1\left(C\right)\stackrel{\partial }{\to }\hfill & H_0(D_k\cap D^{\prime })\end{array}$$

which gives rise to the following exact sequence.

$$\begin{array}{ccccc}\hfill 0\stackrel{\Phi }{\to }& H_1\left(D_k\right)\oplus H_1\left(D^{\prime }\right)\stackrel{\Psi }{\to }& H_1\left(C\right)\stackrel{\partial }{\to }\hfill & Im\partial r& 0.\end{array}$$

As a subgroup of the free group $H_0(D_k\cap D^{\prime })$, $Im\partial$ is free and thus projective. As a result, the short exact sequence is split exact and the following:

$$H_1\left(C\right)\cong H_1\left(D_k\right)\oplus H_1\left(D^{\prime }\right)\oplus Im\partial$$

holds. Since both $H_1\left(D_k\right)$ and $H_1\left(D^{\prime }\right)$ are free, we conclude that $H_1\left(C\right)$ is free, which completes the proof. □

Theorem 1 shows that, while the complete components contribute only to the second homology, the incomplete components provide generators of the first homology. In terms of discrete Morse theory, each complete component contains a critical point of dimension 2 and each incomplete component can feature multiple critical points of dimension 1.

7. The Main Theorem

In this section, we compute the homology of a $\tau$-structure. The key tool here is the Mayer–Vietoris sequence, which allows us to connect and compose the homology data of the sub-complexes.

A certain ordering by which the components are glued in combination with Lemma 6 are critical for the application of the Mayer–Vietoris sequence, since they constitute the determinants of how components intersect.

Theorem 2.

Let $\tilde{X}$ be the complex obtained from the loop complex of a τ-structure I. Then, $H_1\left(\tilde{X}\right)$ is free and the following is the case:

$$H_2\left(\tilde{X}\right)\cong {\oplus }_{i=1}^M\mathbb{Z},$$

where M denotes the number of complete $\tilde{X}$-components. Furthermore, $H_2\left(\tilde{X}\right)$ is freely generated by ${\left\{c_i\right\}}_i^M$, where $c_i$ denotes the sum of 2-simplices contained in a complete component, $C_i$.

Proof. 

Let ${\tilde{X}}_2$ be the $\tilde{X}$-sub-complex induced by the $\tilde{X}$-2-simplices. Suppose that ${\tilde{X}}_2$ is partitioned into j components $C_1,\dots ,C_j$. The set $\left\{C_i\right\}$ and any of its subsets are partially ordered and, by recursively removing maximal components, we can obtain a “descending” sequence $(C_{i_1},\cdots ,C_{i_j})$ such that the following obtains.

$$C_{i_h}\nprec C_{i_k}\mathrm{for}h<k.$$

This sequence gives rise to a sequence of sub-complexes, $(Y_0,Y_1,\dots ,Y_j)$ obtained by recursively adding a component as follows: $Y_0=⌀$ and $Y_k=Y_{k-1}\cup C_{i_k}$. By construction, we have $Y_j={\tilde{X}}_2={\cup }_{i=1}^j{C}_i$.

We next prove by induction on the number of components, k, that $H_1\left(Y_k\right)$ is free and $H_2\left(Y_k\right)\cong {\oplus }_{i=1}^{M_k}\mathbb{Z}$, where $M_k$ denotes the number of complete components in $C_{i_1},\dots ,C_{i_k}$.

For the induction basis $k=1$, $Y_1=C_{i_1}$ itself is a component and its homology has been computed in Theorem 1. Clearly, when $C_{i_1}$ is complete, $H_2\left(Y_1\right)$ is freely generated by the sum of 2-simplices of $C_{i_1}$.

For the induction step we consider $Y_k$ as the union of two sub-complexes $C_{i_k}$ and $Y_{k-1}$ and shall combine $C_{i_k}$ and $Y_{k-1}$ by means of the Mayer–Vietoris sequence as follows.

$$\cdots \to H_n(C_{i_k}\cap Y_{k-1})\to H_n\left(C_{i_k}\right)\oplus H_n\left(Y_{k-1}\right)\to H_n\left(Y_k\right)\to H_{n-1}(C_{i_k}\cap Y_{k-1})\to \cdots$$

By construction, $C_{i_h}\nprec C_{i_k}$ for any $h<k$, which enables the application of Lemma 6. We accordingly conclude that the 1-skeleton of $C_{i_k}\cap C_{i_h}$ is contained in $\{{\omega }_1,{\omega }_l^{\prime }\}$.

In view of $C_j\cap \left({\cup }_{i<j}{C}_i\right)={\cup }_{i<j}(C_i\cap C_j)$, for any i and j, we derive that the 1-skeleton of $C_{i_k}\cap Y_{k-1}$ is contained in $\{{\omega }_1,{\omega }_l^{\prime }\}$. This severely constrains $C_{i_k}\cap Y_{k-1}$, which consists of 0-simplices and at most two 1-simplices.

As a result, $H_2(C_{i_k}\cap Y_{k-1})\cong H_1(C_{i_k}\cap Y_{k-1})\cong 0$ and $H_0(C_{i_k}\cap Y_{k-1})$ are free.

In case $n=2$, we have the following.

$$\begin{array}{cccc}\hfill 0=H_2(C_{i_k}\cap Y_{k-1})\stackrel{\Phi }{\to }& H_2\left(C_{i_k}\right)\oplus H_2\left(Y_{k-1}\right)\stackrel{\Phi }{\to }& H_2\left(Y_k\right)\stackrel{\partial }{\to }\hfill & H_1(C_{i_k}\cap Y_{k-1})=0.\end{array}$$

Thus, $\Psi$ is an isomorphism and $H_2\left(Y_k\right)\cong H_2\left(C_{i_k}\right)\oplus H_2\left(Y_{k-1}\right)$. By induction hypothesis, $H_2\left(Y_{k-1}\right)\cong {\oplus }_{k=1}^{M_{k-1}}\mathbb{Z}$, where $M_{k-1}$ denotes the number of complete components in $C_{i_1},\dots ,C_{i_{k-1}}$. Due to Theorem 1, $H_2\left(C_{i_k}\right)\cong \mathbb{Z}$ in case of $C_{i_k}$ being complete and $H_2\left(C_{i_k}\right)\cong 0$ in case of $C_{i_k}$ being incomplete. Thus, we can conclude by induction

$$H_2\left(Y_k\right)\cong {\oplus }_{i=1}^{M_k}\mathbb{Z}.$$

Clearly, $H_2\left(Y_k\right)$ is freely generated by ${\left\{c_{i_h}\right\}}_h^{M_k}$, where $c_{i_h}$ is given by the sum of 2-simplices of the $i_h$-th complete component.

In case $n=1$, we have the following.

$$\begin{array}{cccc}\hfill 0=H_1(C_{i_k}\cap Y_{k-1})\stackrel{\Phi }{\to }& H_1\left(C_{i_k}\right)\oplus H_1\left(Y_{k-1}\right)\stackrel{\Psi }{\to }& H_1\left(Y_k\right)\stackrel{\partial }{\to }\hfill & H_0(C_{i_k}\cap Y_{k-1})\end{array}$$

and the following short exact sequence follows.

$$\begin{array}{ccccc}\hfill 0\stackrel{\Phi }{\to }& H_1\left(C_{i_k}\right)\oplus H_1\left(Y_{k-1}\right)\stackrel{\Psi }{\to }& H_1\left(Y_k\right)\stackrel{\partial }{\to }\hfill & Im\partial \to & 0.\end{array}$$

As a subgroup of the free group $H_0(C_{i_k}\cap Y_{k-1})$, $Im\partial$ is free and thus projective. Then the short exact sequence is split exact and the following is the case.

$$H_1\left(Y_k\right)\cong H_1\left(C_{i_k}\right)\oplus H_1\left(Y_{k-1}\right)\oplus Im\partial .$$

Since both $H_1\left(C_{i_k}\right)$ and $H_1\left(Y_{k-1}\right)$ are free, we can conclude that $H_1\left(Y_k\right)$ is free.

Therefore it follows by induction that $H_1\left({\tilde{X}}_2\right)=H_1\left(Y_j\right)$ is free and $H_2\left({\tilde{X}}_2\right)=H_2\left(Y_j\right)\cong {\oplus }_{i=1}^M\mathbb{Z}$, where M denotes the number of complete components in $C_1,\dots ,C_j$.

In view of Proposition 9, we have the following:

$$H_2\left(\tilde{X}\right)\cong H_2\left({\tilde{X}}_2\right)\cong {\oplus }_{i=1}^M\mathbb{Z}$$

and $H_1\left(\tilde{X}\right)\cong H_1\left({\tilde{X}}_2\right)⨁{\oplus }_{i=1}^k\mathbb{Z}$ is free, which completes the proof. □

The transitive closure with respect to $\varphi$-crossing produces an equivalence relation, i.e., $(i_1,i_2){\sim }_{\varphi }(j_1,j_2)$, if there exists a sequence of arcs such as the following:

$${\alpha }_1=(i_1,i_2),{\alpha }_2,\dots ,{\alpha }_l=(j_1,j_2)$$

such that two consecutive arcs ${\alpha }_k$ and ${\alpha }_{k+1}$ are $\varphi$-crossing for $1\le k\le l-1$.

An arc-component, A, is an ${\sim }_{\varphi }$-equivalence class of arcs such that A contains at least two arcs. A is of type 1 if both endpoints of any of its arcs are incident to $\varphi$-arcs and of type 2, otherwise.

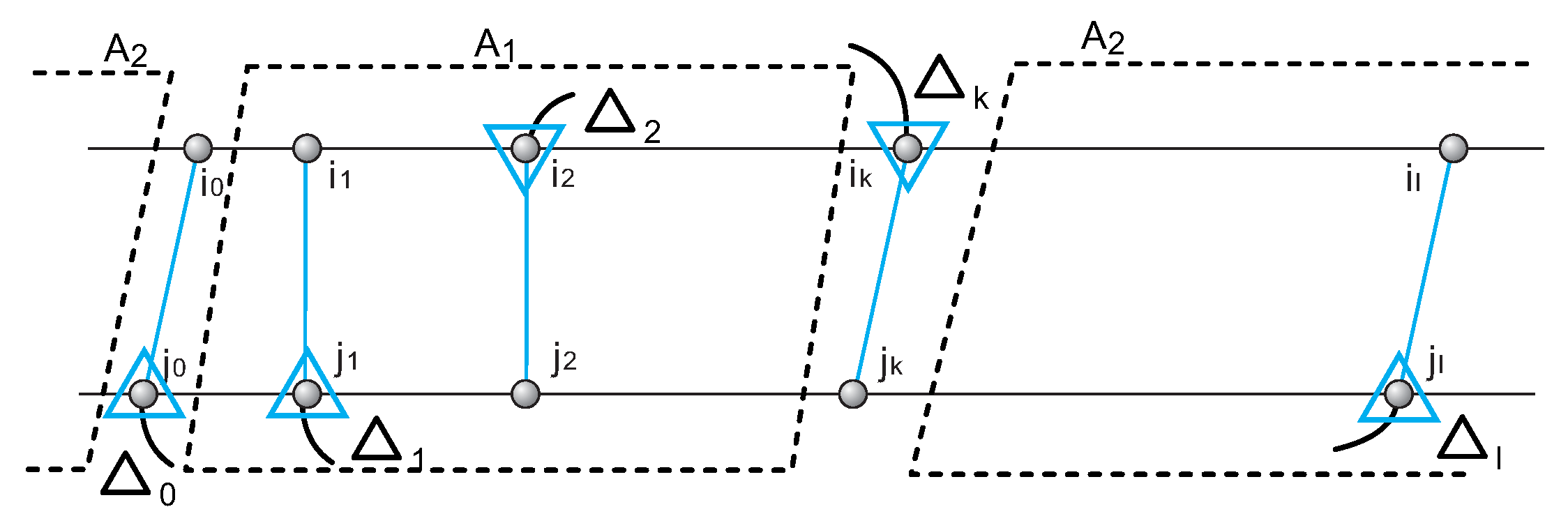
Suppose that $(i_1,j_1),(i_2,j_2),\dots ,(i_l,j_l)$, where $i_1<i_2<\cdots <i_l$ and $\varphi \left(i_k\right)=j_k$ are $\varphi$-arcs associated with A. These partition the two backbones into blocks: the outer block ${\beta }_1={[1,i_1)}_S\cup {(i_l,n]}_S\cup {[1,j_1)}_T\cup {(j_l,m]}_T={(i_l,i_1)}_S\cup {(j_l,j_1)}_T$ and the inner blocks ${\beta }_r={(i_{r-1},i_r)}_S\cup {(j_{r-1},j_r)}_T$, $2\le r\le l$.

Lemma 9.

In $I^{\prime }$, let A be an arc-component of type 1 with blocks ${\beta }_1,{\beta }_2,\dots ,{\beta }_l$. Then, for any arc $(i,i^{\prime })\notin A$, there exists a unique block, ${\beta }_k$, that contains i and $i^{\prime }$.

Proof. 

Without loss of generality, we may assume that $(i,i^{\prime })$ is an S-arc. Since each $\varphi$-arc is incident to at most one arc due to Lemma 1, $(i,i^{\prime })$ is not incident to any $\varphi$-arc associated with A and thus its endpoints are contained in A-blocks.

By construction, any T-arc of A, $(j_p,j_q)$ and $(i,i^{\prime })$ are non-crossing, since otherwise $(i,i^{\prime })$ would belong to the arc-component A. Accordingly, ${\varphi }^{-1}\left(j_p\right)$ and ${\varphi }^{-1}\left(j_q\right)$ are either contained in the interval ${(i,i^{\prime })}_S$ or ${[1,i)}_S\cup {(i^{\prime },n]}_S$ and we can conclude that A-arcs contained in either $Y_0\subset {(i,i^{\prime })}_S$ or $Y_1\subset {[1,i)}_S\cup {(i^{\prime },n]}_S$.

Suppose that i and $i^{\prime }$ are contained in different blocks, then $Y_0$ and $Y_1$ are nontrivial. By construction, any $Y_0$-arc and any $Y_1$-arc are non-crossing, which is impossible since A is an arc-component. As a result i and $i^{\prime }$ are contained in a single A-block. □

Remark 3.

Lemma 9 is the “arc”-analogue of Lemma 3 for arc-components of type 1. Note that the statement does not hold for arc-components of type 2.

Given an arc-component A of type 1 in the interaction structure $I^{\prime }$, each $\varphi$-arc is associated with exactly one 2-simplex, as Lemma 1 guarantees that each $\varphi$-arc is incident to at most one arc. Let ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l$ denote the 2-simplices associated with the $\varphi$-arcs $(i_1,j_1),(i_2,j_2),\dots ,(i_l,j_l)$, respectively. Let ${\omega }_k$ and ${\omega }_k^{\prime }$ denote the mixed 1-faces of ${\Delta }_k$ that are associated with ${\beta }_k$ and ${\beta }_{k+1}$, respectively.

Lemma 10.

Let A be an $I^{\prime }$-arc-component of type 1 with blocks ${\beta }_1,{\beta }_2,\dots ,{\beta }_l$. Let ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l$ denote the 2-simplices associated with A and ${\omega }_k$ and ${\omega }_k^{\prime }$ be the mixed 1-faces of ${\Delta }_k$ that are associated with ${\beta }_k$ and ${\beta }_{k+1}$, respectively. Then ${\omega }_k^{\prime }={\omega }_{k+1}$ for $1\le k\le l-1$ and ${\omega }_l^{\prime }={\omega }_1$.

Proof. 

Let $(i_1,j_1),(i_2,j_2),\dots ,(i_l,j_l)$ denote the $\varphi$-arcs associated with A ordered from left to right. It suffices to prove ${\omega }_1^{\prime }={\omega }_2$. Set ${\omega }_1^{\prime }=\{s,t\}$, where s and t are S-loops and T-loops associated with ${\beta }_2$. Clearly, $i_1\in s$ and $j_1\in t$.

By Lemma 9, any $I^{\prime }$-arc is either contained in ${\beta }_2$ or its complement. This guarantees that $i_1$ and $i_2$ belong to the same S-loop s and, furthermore, that $j_1$ and $j_2$ belong to the same T-loop t.

As a result the 2-simplex ${\Delta }_2$ associated with $(i_2,j_2)$ contains $\{s,t\}$ as a mixed face, i.e., ${\omega }_1^{\prime }={\omega }_2$. □

Now we are in position to prove the Main Theorem.

Proof of the Main Theorem. 

The triviality of the third homology group, $H_3\left(I\right)$, follows from Corollary 1. In view of Lemma 1, Proposition 8 and Theorem 2, we have the following:

$$H_2\left(I\right)\cong H_2\left(\tilde{X}\right)\cong {\oplus }_{k=1}^M\mathbb{Z},$$

where M denotes the number of complete $\tilde{X}$-components.

First we observe that any $\sigma$-butterfly removal does not change the crossing status of any two arcs. Thus, there is a natural bijection between the set of I-arc-components and that of $I^{\prime }$-arc-components. Moreover, each I-arc-component of type 1 corresponds to an $I^{\prime }$-arc-component of type 1.

It suffices to show that when passing from the complex $X=K\left(I^{\prime }\right)$ to $\tilde{X}$, the number of $I^{\prime }$-arc-components of type 1 equals the number M of complete $\tilde{X}$-components.

Claim: there exists a bijection between the set of $I^{\prime }$-arc-components of type 1 and that of complete components of $\tilde{X}$.

Given an $I^{\prime }$-arc-component of type 1, A, let C denote the set of couples $(\Delta ,{\Delta }^{\prime })$ associated with arcs of A. In view of Lemma 10, any 1-simplex that appears as a face in C-couples is shared by at least two 2-simplices. As a result, C does not contain any free 1-simplex and passing from X to $\tilde{X}$, simplicial collapses do not affect C-2-simplices.

Consequently, all C-couples in $I^{\prime }$ simply persist when passing to $\tilde{X}$, where C itself becomes a $\tilde{X}$-component. Lemma 10 further guarantees that C does not contain any free 1-face, whence Lemma 8 implies that C is complete.

Accordingly, the Ansatz $\Phi \left(A\right)=C$ produces a well-defined mapping between $I^{\prime }$ arc-components of type 1 and complete $\tilde{X}$-components.

$\Phi$ is, by construction, injective since the mapping constitutes a mere reinterpretation of an arc-component of type 1.

In order to establish surjectivity, let $C_1$ be a complete $\tilde{X}$-component. $C_1$ induces a distinguished, unique set of $I^{\prime }$-arcs, $A_1$. By construction, any two $A_1$-arcs ${\alpha }_1,{\alpha }_2\in A_1$ satisfy ${\alpha }_1{\sim }_{\varphi }{\alpha }_2$, whence $A_1$ is contained in a nontrivial and distinguished arc-component $A^{\prime }$.

We proceed by proving that $A_1=A^{\prime }$ is an arc-component of type 1. Suppose $A_1⊊A^{\prime }$, then there exist an arc $(i,i^{\prime })\in A^{\prime }\setminus A_1$ and $(j,j^{\prime })\in A_1$ such that $(i,i^{\prime })$ and $(j,j^{\prime })$ are $\varphi$-crossing. Note that $(j,j^{\prime })$ is associated to a $C_1$-couple $({\Delta }_j,{\Delta }_{j^{\prime }})$. Let $\{s,s^{\prime }\}$ be the pure edge associated with $(i,i^{\prime })$. We showed in the proof of Lemma 7, that $S_{C_1}$ is connected.

Since $(i,i^{\prime })$ and $(j,j^{\prime })$ are $\varphi$-crossing, the S-loops $s_1,s_2$ are vertices of ${\Delta }_j,{\Delta }_{j^{\prime }}$ from which follows that both s and $s^{\prime }$ are on a path of two S-loops in $C_1$. Accordingly $\{s,s^{\prime }\}$ is contained in $S_{C_1}$. Lemma 7 guarantees that $C_1$ is a sphere, whence there exists a $C_1$-couple $({\Delta }_0,{\Delta }_0^{\prime })$ for which $\{s,s^{\prime }\}$ is a pure face. As a result we obtain $(i,i^{\prime })\in A_1$, which is a contradiction from which $A^{\prime }=A_1$ follows.

By Lemma 2, both endpoints of an $A_1$-arc are incident to $\varphi$-arcs, whence $A_1$ is an arc-component of type 1 and $\Phi \left(A_1\right)=C_1$, whence $\Phi$ is surjective and, thus, bijective.

Therefore $\gamma =M$ and $H_2\left(I\right)\cong {\oplus }_{k=1}^{\gamma }\mathbb{Z}$.

The Euler characteristic $\chi$ of $K\left(I\right)$ can be expressed as the alternating sum of ranks of its homology groups, i.e., $\chi =rnk\left(H_0\left(I\right)\right)-rnk\left(H_1\left(I\right)\right)+rnk\left(H_2\left(I\right)\right)-rnk\left(H_3\left(I\right)\right)$, whence $rnk\left(H_1\left(I\right)\right)=\gamma -\chi +1$. Theorem 2 shows that $H_1\left(I\right)\cong H_1\left(\tilde{X}\right)$ is free, from which we can conclude $H_1\left(I\right)\cong {\oplus }_{k=1}^{\gamma -\chi +1}\mathbb{Z}$. □

8. Discussion

In this paper we computed the simplicial homology of $\tau$-structures. $\tau$-structures represent a meaningful generalization of bi-structures [7,8] as they allow us to study transitions between sequence–structure pairs where the underlying sequences differ in specific manners. Bi-structures would only facilitate the analysis of such pairs, where the underlying sequences are equal. Intuitively, the free energy of such sequence–structure pairs, which is a quantity that is straightforward to compute, characterizes the probability of finding such a pair of sequences in the course of evolution.

We are currently extending the results of this paper by computing the weighted homology of $\tau$-structures over a discrete valuation ring, R. This entails the study of weighted complexes in which simplices are endowed with weights [9,24,25]. These weighted complexes feature a new boundary map, ${\partial }_n^v:C_{n,R}\left(X\right)\to C_{n-1,R}\left(X\right)$, where $C_{n,R}\left(X\right)$ denotes the free R-module generated by all n-simplices contained in X. ${\partial }_n^v$ is given by the following.

$${\partial }_n^v\left(\sigma \right)=\sum _{i=0}^n\frac{v\left({\widehat{\sigma }}_i\right)}{v\left(\sigma \right)}·{(-1)}^i{\widehat{\sigma }}_i.$$

As it is the case for bi-structures [9], the weighted homology plays a crucial role in the Boltzmann sampling of sequence–structure pairs that minimize the free energy of the $\tau$-structure.

Our approach differs from the purely algebraic proofs for the simplicial loop homology of bi-structures [8]. In the case of bi-structures, the computation for the second homology employs the fact that their first homology group is trivial. This allows us to understand the second homology group via a long exact sequence of relative homology groups. However, for $\tau$-structures, the first homology is, in general, nontrivial and therefore requires a different approach.

We first reduce the loop complex $K\left(I\right)$ to the sub-complex $\tilde{X}$ via simplicial collapses, retaining the homology of the original space. We then dissect a certain 1-dimensional sub-complex in Proposition 9 and then decompose $\tilde{X}$ into components based on the $\varphi$-crossing of couples. This decomposition allows us to identify different generators of the homology, with incomplete and complete components contributing to the first and second homologies, respectively. Finally, we compute the homology of $\tilde{X}$ by gluing components in a particular manner. This makes use of the planarity of $\tau$-structures in Lemma 6 and assures that we encounter particularly simple intersections, when applying the Mayer–Vietoris sequence. It is worth pointing out that in the proof of Theorem 2 the particular ordering in which the components are glued is crucial.

In view of Proposition 9, Theorems 1 and 2, the generators of the first homology of the loop complex originate from the combining of the sub-complex $K_1$, incomplete components and the gluing of different components. The detailed descriptions of all these generators are a work in progress and here we restrict ourselves to using the Euler characteristic to express the rank of the first homology group. Only complete crossing components contribute to the second homology and their geometric realizations are spheres. We provide a combinatorial characterization of the generators in I in terms of arc-components of type 1.

As for applications of this framework, we currently employ $\tau$-structures to investigate the evolutionary trajectories of viruses, such as flus and the Coronavirus. Specifically, we compute the loop homology of evolutionary transitions to gain deeper insight into sequence-structure-function relationships of the virus.