Abstract
This paper presents a study on the complexity of cargo arrangements in the pallet loading problem. Due to the diversity of perspectives that have been presented in the literature, complexity is one of the least studied practical constraints. In this work, we aim to refine and propose a new set of metrics to measure the complexity of an arrangement of cargo in a pallet. The parameters are validated using statistical methods, such as principal component analysis and multiple linear regression, using data retrieved from the company logistics. Our tests show that the number of boxes was the main variable responsible for explaining complexity in the pallet loading problem.
1. Introduction
With globalization, supply chains have expanded largely in number of partners, making synchronization essential for their performance. A key issue in performance is the unitization measure of products used—the pallet—allowing flows between and out of the distribution centres in the supply chain [1] (storage, cross docking, and transportation of product distribution). The pallet-loading problem, also known as the manufacturer’s pallet loading problem, consists in placing a maximum number of identical rectangular boxes in a single rectangular palette [2]. Further research development has emerged in the last few years regarding different variants of the problem, e.g., non-identical geometrical forms. Cutting and packing (C&P) problems are hard combinatorial problems, which arise in the context of many real-world applications, both in industry and in services [3,4].
In the pallet loading problem, order picking is one of the most important activities since it is generally difficult and costly. Picking represents about 55% of all warehouse-related expenses. As such, optimizing the order of picking works should be a priority for any company [5].
Picking can be either automatic or manual. The former requires an automatized system of machines as well as a good warehouse organization to optimize the packing flow. The latter requires at least one picker to manually load a container or a pallet. The location of the items to be loaded in the pallet can have a significant impact on the loading/unloading operations. Quantifying how impactful the box/items’ arrangements can be for human and machine labour is essential to rearrange and optimize the timing and costs of the operations, both for the client and for ground workers.
The novelty of this paper is the study of the complexity of cargo arrangements in the pallet loading problem. Due to the diversity of perspectives that have been presented in the literature, complexity is one of the least studied practical constraints.
To better understand this topic, we studied how the complexity constraint fits within the pallet loading problem. A first analysis was performed to characterise this topic and what concepts were related to it. As there are diverging perspectives about this problem, we needed to study the multiple approaches that were taken by various authors to handle the complexity constraint. By knowing the theory behind this problem, it became clear what type of actions should be taken regarding this constraint. After gathering all the information needed about both the pallet loading problem and the complexity constraint, a second phase was started by collecting and analysing data. A set of parameters were created to attempt to quantify the complexity of each loading process. Using these parameters, logistics data were collected from a third-party company. Mathematical methods appropriate to this type of data were used to break it down and give us a better understanding of what creates more complexity during the loading process of a pallet. This type of research approach is applied to solve an organizational problem and can be classified as action research [6].
This paper is structured as follows: a literature review and analysis of the approaches described by other authors on the complexity of the pallet loading problem; Materials and Methods, where a characterization is given of the problem regarding what might be deemed complex in pallet cargo arrangements, constraints, and objectives based on the previous analysis, and definition of metrics to quantify the complexity of each arrangement; the results of the application of the metrics to samples for data gathering and data validation through computational tests; finally, we present the conclusions and future directions.
2. Literature Review
2.1. The Role of the Complexity Constraint in the Pallet Loading Problem
The pallet loading problem (PLP), known as the manufacturer’s problem, consists in arranging products in boxes onto a rectangular pallet to optimize its utilization [7,8]. It is assumed that the boxes, available in large quantities, should be arranged orthogonally.
This problem has been addressed using several different methods, such as Linear Programming 0–1 [8,9,10] for the two-dimensional non-guillotine cutting problem. Additionally, heuristics and metaheuristics have been applied to this problem with good results, such as simulated annealing [11], genetic algorithm [12], tabu search, [8], and block heuristics [13,14,15].
In the PLP, the complexity constraint (which measures how complex the pattern required to be loaded is) is one of the hardest to address because manual pallet loading may not be adequate, e.g., due to the possibility of the patterns being misunderstood by loading personnel, thus making the operation take longer to perform. In addition, the usage of automatized mechanisms for packing may not be the most suitable to make complex cargo arrangements. The financial aspects are also to be considered. These situations highlight the existing limitations of human and technological resources. The increase in complexity in packing patterns usually translates into greater material handling effort. That effort is more significant if the complexity of the pattern causes changes in the way the box loading is carried out. Instead of being able to load the boxes with clamps or forklift trucks, the complexity of the pattern may force a manual loading of the boxes, which makes the process much more difficult. In case there are no alternative box loading methods that optimize the process, the pattern must conform with the limitations of the technology used [7].
In the literature, when studying complexity constraints, the concepts of guillotine patterns and robot packable pattern are often mentioned. A loading pattern is said to be guillotineable if, for example, a parallelepiped is being transported and that object is subjected to multiple cuts parallel to its faces. By doing so, smaller parallelepipeds are obtained, which represent the numerous stacked boxes. Although this arrangement is easy to pack and describe, it is not always the proper option for loading pallets due to the instability of the cargo during transportation. This situation is more critical in pallets when other operations are needed to restrain the boxes and make transportation safe—such as shrink-wrapping or interlocking [16].
The other pattern—the robot packable pattern—is calculated by placing the first box in the bottom left behind corner of the container and then placing the remaining boxes either on the right, front, or on top of the first one [17,18,19]. A guillotineable pattern is also a robot packable pattern due to the way the boxes’ faces coincide with each other and with the container or pallet, but the opposite situation does not occur. The boxes are packed by a robot equipped with an elevating mechanism parallel to the base of the container or pallet. Each box is lifted and released in the correct position using vacuum cells. Due to the nature of this pattern, robots used to pack boxes possess extra constraints so that there are no collisions between previously packed boxes and the boxes to follow. Hence, there cannot be any boxes packed in front of, to the right of, or above the destination of the boxes the robot is currently placing. Boxes can also be placed manually in the pallet, although that operation is likely to take longer to perform than completing the same task with an automatized system.
To handle these constraints, multiple authors have presented different solutions. Morabito and Arenalest [20] proposed an AND/OR graph approach, which consists of an algorithm combining two basic strategies: backtracking, which chooses all available non-final paths to be explored, and hill-climbing, which chooses the optimal path and keeps discarding remaining ones. Hifi [21] used an approximate algorithm containing additional constraints, such as stability constraints. Egeblad and Pisinger [19] proposed a local search algorithm that searches for potential solutions by making local changes to the current solution until an optimal solution is found or when a time limit is elapsed. The authors report that this solution performs better in medium-sized instances [19].
In the end, the robot packable pattern can be considered as an automatized variation of the guillotineable pattern, due to its usage in robotic systems, while the guillotineable pattern is more adequate in manual loading because it is easy to understand and pack from the picker’s perspective.
2.2. A Typology for C&P Problems by Wäscher
Considering that the pallet-loading problem is a C&P problem, it is possible to apply the typology of Wäscher et al. [22] to characterise it, which is a revised and improved version of the one created by Dyckhoff [23]. The version we are using here is composed of five different categories:
- Dimensionality (one, two, three, and as a problem variation, more than three dimensions);
- Type of assignment (output value maximization, where a set of large items is insufficient to accommodate a set of small items ready to be packed, forcing the usage of all large objects while removing the need for any selection, and input value minimization, where a set of large objects can fully accommodate all smaller ones, which changes the goal towards minimizing the value of large items to be used);
- The shape of small items (regular items, such as rectangular or circular shaped items, and irregular items, which do not have a well-known geometrical shape);
- The assortment of large objects (a single element, where this scenario can have two variations: (1) when the extension of the large object may be fixed in all dimensions; (2) when at least one dimension is variable in its extension, and several large objects);
- The assortment of small items (identical small items of similar shape and size, weakly heterogeneous assortment, where the small items can be grouped into a low number of classes when compared to the total number of items, and strongly heterogeneous assortment, where nearly all items are treated as an individual entity).
In weakly heterogeneous assortments, items with identical shape and size that are placed with different orientations are treated as different kinds of items. C&P problems contain two sets of elements: small and large items. Small items need to be placed inside larger items so that all small items in a subset can lie entirely on the large items preventing small items from overlapping [18].
Applying Wäscher’s Typology to the Pallet Loading Problem
Though the pallet-loading problem might be considered a 2D problem by some authors, here, it will be treated as a 3D problem. Packing boxes into a pallet may not be viewed as a 3D problem if the arrangement does not involve the placement of boxes on top of other boxes. That does not usually happen because companies want to use the least possible number of pallets to transport cargo, therefore filling the pallets with boxes is the good approach.
In the pallet loading problem, both scenarios (output value maximization and input value minimization) classified by Wäscher et al. [22] suit this problem because in real life, there are situations where there could be a limited number of available pallets or there are functionally an infinite number of available pallets.
The first situation requires a maximization of the “value” of small objects. If that number represents the packing of boxes per pallet, then that should be the case to consider for this problem, since the larger the number of boxes packed in one pallet, the more complex the arrangement of the packing can be. That also occurs when having an elevated heterogeneous assortment, because it makes the act of packing less linear due to the increase in available options on sorting the items. This type of assortment is rather common in companies that deal with multiple types of items, such as Amazon, and it is the one considered in this pallet loading problem.
The large object to consider for this problem is the pallet. This object is very commonly used worldwide to transport cargo in warehouses and can be made of many materials, such as wood, metal, and plastic. Multiple worldwide organizations have created standards for the dimensions of their pallets, such as ISO (International Organization for Standardization). This means that there is a diversity of pallets when it comes to size, although some have similar dimensions. For this problem, one should consider the existence of multiple large objects (with either a heterogeneous or homogeneous assortment of large objects) since in a large warehouse environment, there is usually a mass unloading or loading of boxes from different destinations, each using different sized pallets.
The smallest items to consider in this problem will be rectangular boxes, which is the most common box format, and it is the best one to use when attempting to minimize trim-loss, which refers to the patterns formed by the empty space after the small objects are placed on the large object.
Although a significant number of papers have addressed the PLP using exact and heuristics mathematical models, the complexity of the pallet loading will be addressed here from the perspective of the picking personnel. Furthermore, as far as we know, multivariate analysis has not been described in the literature addressing this problem, hence the novelty of this research.
3. Materials and Methods
Upon analysing what literature refers to as being complex in the pallet loading problem, one question arises: does the perspective of the authors match the perspective of the picking personnel? To assess that analysis, a third-party logistics company was visited to hold discussions with the workers who load pallets daily and establish what they consider to be complex in the pallet loading process, and a case study was conducted [24]. The company—Luis Simões—operating in the Iberian Peninsula, was available to help us understand how the processes related to the loading of pallets work and what are the most meaningful difficulties during picking operations. The company facilitated a tour of one of their warehouses where some of the working staff were invited to explain procedures while colleagues would simultaneously execute the operations being described. Upon hearing the pickers’ opinion on the complexity of their tasks, a set of metrics was created to replicate that complexity in the pallet loading process. A new visit to that same warehouse allowed us to obtain samples to be measured according to the metrics created. Each worker was asked to rate the loading process using those same metrics. Some ratings could be directly obtained by observing the packed pile. Other parameters were extracted from an Excel file generated from the input provided by pickers after concluding the task of loading all the boxes to the pallet. The metrics were then adjusted according to the information gathered via the Excel input file and direct observation of the pile. A measurement scale was used to qualify and/or quantify the data variables in statistics and different kinds of techniques was used for statistical analysis.
In the analysis of this information, we applied a principal components analysis to determine the most important parameters within the complexity of the pallet loading problem. Ultimately, a multiple linear regression was used to determine a mathematical model that can predict the complexity of any given loaded pallet.
3.1. Metrics to Analyse Complexity
Packing a pallet manually—although it may seem linear—involves more variables than might be expected. Each parameter will be evaluated by using a Likert scale ranging from 1 to 10, where 1/10 is a parameter that does not add much complexity into the loading operation or is not applicable to the respective scenario, and 10/10 would be a parameter adding greater complexity. These metrics only consider situations where one person is singlehandedly loading a single pallet. The following paragraphs will explain each of the nine parameters created to evaluate the complexity of the pallet loading problem.
The first parameter is the number of boxes. Regardless of the size and weight of each box, the higher the number of boxes being packed, the more time consuming it is to arrange them properly in the stack. This parameter is rated 10/10 when there are 80 or more boxes since it is rare to have this many boxes being packed into a single pallet.
The second parameter refers to the average box weight. This parameter measures the accumulated fatigue inflicted on the worker by the weight of the boxes. This parameter is rated 10/10 for weights of 15 kg or higher. This weight is used as the maximum rate of the scale because a worker should not carry weight volumes over 23 kg due to a high risk of injury (stress/damage to the back, knees, or arms) [25]. Therefore, to maintain a safety margin, the weight of 15 kg was considered instead of 23 kg.
The third parameter is the percentage of fragile boxes to pack. Some boxes have a specific orientation to be carried/placed or are too frail to have boxes placed on top of them. Therefore, these boxes require special attention when carrying and loading them onto the pallet. It is considered as a maximum rating when the pallet packs contain a percentage over 50% of fragile boxes.
The next parameter is the average maximum width. Some boxes with a large disparity of measurements, such as a box with 160 × 160 × 20 cm, may struggle to be packed due to increased length. The centre of gravity will tend to be far from the picker, which may cause the box to fall. The maximum rate for this parameter is 180 cm, which is a size close to an adult person’s height. That is because the arm span of an individual, when compared to its height, has a ratio of approximately 1 [26].
The fifth parameter created is the number of box types to label. The company uses a label system with a unique barcode for each type of box being packed. When the packed pallet reaches its destination, the clients can scan the code to check what was received. Although it does not add much complexity to the process, it can be very time consuming—according to the workers—should they need to label many types of boxes.
The sixth parameter is the number of boxes to separate within a pile, or number of boxes to pack in columns. Though required by only a few clients, this parameter is considered by the working personnel at Luis Simões SA as one of the most complex constraints as it requires not packing different types of boxes in the same stack. For example, a product X can only be piled with other products X, never in stacks of products Y or Z. What makes this parameter so complex is that, depending on the quantities and sizes of each type of box, the height of each subpile may have a greater variation, which may force the pickers to reload the boxes to achieve a final stack with a balanced size.
The seventh parameter is the number of upper boxes required to make a surface for another packed pallet. To maximize the space of a truck’s container, it is possible to stack small, loaded pallets. For that, the boxes in the upper surface must be stable enough and properly rearranged to make sure the stacked pallet does not fall. Rearranging the boxes may take some time and increase the complexity of the loading operation.
The eighth parameter is the height difference between worker and pile. One of the major struggles of the manual pallet loading process is the maximum reach of the worker to the top of the pile. If the worker is short and the pile is high, he/she will struggle to place the final boxes in the upper layer of the pile. This scenario represents one with the highest difficulty. Numerically, this parameter is measured by the difference of heights between the worker and the pile. The maximum difficulty is represented by a difference of at least 35 cm between the worker and the pile.
The final parameter to measure is the number of heavy boxes to pack. For this metric, a heavy box is considered as weighing at least 8 kg. Once again, having a special focus on particularly heavy boxes is crucial, as they may cause physical damage to workers when not following security directives while moving boxes. Recommendations advise bending the knees, and keeping boxes around waist level when lifting to minimize the risk of injury. Bending the back while attempting to pick up the box, holding it without placing the hands firmly in its base and extremities, and lifting weight above shoulder level are must-avoid situations for any worker involved [25]. It is sometimes necessary to place heavy boxes in a very low or very high spot. Under those circumstances, it may be better to request assistance from other workers to help to decrease the effort applied. A 10/10 score will be given to this parameter if the pallet is packed with 18 or more heavy boxes. If the pallet is not packed with boxes weighing at least 8 kg, then this variable is classified with 1 out of 10.
3.2. Sample Retrieval
Having defined the metrics, the next step is to apply it in real-life situations to gather enough data weighing each metric and increase the metric system’s accuracy. The Luís Simões SA corporation was once again available to enable this procedure. The data gathering process is as follows:
- Each worker, upon completing the loading process of a pallet, will print and a label with (a) a barcode and (b) other necessary numerical information to be stuck to the packed pallet prior to shipping. Two of such numbers will help to differentiate each packed pallet and each order.
- At the end of the day, the software system will create an Excel file with all the data collected by the workers.
- During the box loading process, each box is scanned so that the Excel file contains information such as the time the box was picked, the quantity, and its dimensions.
- After compiling data from the two numbers affixed to each pallet from multiple packed pallets, each picker would rate the complexity of the pallet he/she packed from 1 to 10.
Although most of the data needed to extract and measure according to the developed metrics can be easily obtained from that Excel file, some of the data could only be attained via indirect methods, and some could not be obtained at all. Having come to this conclusion, it was deemed necessary to introduce changes to the metrics’ system.
After obtaining the file, the next step was to extract the data of the samples retrieved according to each previously described parameter. As the information had been previously parametrised and organised, it was possible to quickly extract the values for the number of boxes, average box weight, average maximum box width, number of box types to separate within the pile, and number of heavy boxes to pack.
When it comes to box fragility, such information is not obtainable directly. To distinguish fragile boxes from non-fragile boxes, each box had to be analysed one by one according to certain characteristics inherent to the materials of the product and the box itself. Four different ratings were given to each box. For a box to be considered non-fragile, both the product and the box had to be consistent and resistant. If the box itself had signs that it could rupture without damaging the goods, then it would be rated differently from the previous ones. For example, in some cardboard boxes, there is a part where the cardboard is taped. If a significant area of the tape is not attached to the cardboard itself, then it could be a fragile point from where the tape could be ripped off by an edge of a heavy box and slightly damage the package. Although this can be a problem under certain circumstances, it is not significant enough compared to the other two scale units where boxes are considered fragile. In products where there is no cardboard wrapping the product, if the upper area of contact is too small or is made of non-resistant materials, they can be considered as fragile.
Not all products are contained inside cardboard boxes. When the product is in direct contact with other boxes, the object must be resistant enough at all points of contact to avoid causing any damage. The end of the fragility scale is when both the box and the product can be easily destroyed if a heavy box is placed on top of them. In this analysis of the fragility of the boxes, it was always taken into consideration how the analysed boxes would fare with heavy boxes. This was because some packages considered as fragile could take many boxes on top of them without causing damage since the cumulative weight could be low enough. Some boxes display a symbol indicative of how many similar boxes can be handled in a single stack—which should always be considered during the loading process.
After analysing the number of box types to label, it was decided to fine-tune this metric to evaluate the homogeneity of boxes—this metric now rates the number of box types. This change was made because it is more important to focus on the homogeneity of boxes than on the labelling process since the latter only occurs in specific circumstances and is only required by certain clients.
Given that the information input for the parameter that measures the number of upper boxes that will serve as a base to stack another packed pallet is not collected directly by the company and is also dependent on the methods applied by each worker to pile the boxes, we have decided to dismiss this metric. We have set a new metric that measures the time spent packing a full pallet, considering the significance of this variable in the assessment of the time allocated to the loading process takes. The time registered for the first and the last layer of boxes loaded were subtracted to obtain the time spent loading the pallet.
Finally, to measure the height difference between the worker and the packed pallet, each worker would register his/her height. As the Excel file has no automatic record on how high the packed pallet is that data were obtained by inputting the area of the pallet and of each box. These were successively subtracted until the pallet area remaining was approximate to 0. Another layer would then be calculated.
Before the application of this method, the measurement was conducted by sorting the boxes by weight—heavier boxes are usually placed in the base of the pallet—and, when all the boxes were packed, the tallest box of each layer would be added, with the result being the total height of the packed pallet. With this method, the more boxes the pallet had, the less accurate it proved to be. Despite this problem, this latter method was accurate enough for the purpose. After obtaining the height of the pallet and loaded boxes, the value obtained was subtracted to the height of the worker who loaded the boxes.
After explaining each parameter and how they were extracted, Table 1 will show the final set of metrics and respective scaling and units according to the following example: parameter: rating (range of values). To simplify the representation of the variables, each will be represented by a number. The parameter representing the evaluation of the loading process that was performed by each worker is represented by the number 0.

Table 1.
Parameters and respective scaling, rating (range of values) and units.
4. Results
After extracting the samples, the data were analysed using IBM SPSS Statistics for Windows, version 26.0. In Table A1 and Table A2, it is possible to see the absolute and scaled values for each variable in each sample. Please refer to Table 1 for correspondence between the variable number and respective designation.
Factor analysis, specifically the principal component analysis (PCA) with varimax rotation (using Kaiser Normalization), was applied. The principal component analysis is a factorial analysis technique that transforms a set of correlated variables into a smaller number of independent variables, which correspond to a combination of the original ones. These new variables are known as principal components [27]. This technique is often seen as a data reduction method. Another main characteristic of this method is the reduction of the presented information into a smaller number of variables, the principal components, which represent the most relevant information contained in the original variables. The principal components will be sorted by highest to lowest in terms of importance. That importance is translated into a higher variance rate of the collected data. The first component explains the highest variance rate. The second explains a rate not explained by the previous one, etc. The most irrelevant component is the one that contributes the least to the total variance of the data [28].
To validate the usage of the PCA in a set of variables, some authors propose different rules for data validation. MacCallum et al. [29] applied a rule that suggested a minimum of five observations per variable.
To check how consistent the number of observations is, one technique that can be used is Cronbach’s Alpha value [30]. This value has a range from 0 to 1 and evaluates the reliability of the data obtained. Although, in the literature, most authors only consider as acceptable a value above 0.7, only a value below 0.5 can be considered as unacceptable. Values between 0.5 and 0.7 are considered as questionable, requiring further analysis to determine if the data are adequate. It is worth noting that this value is sensitive to the correlation and number of variables tested. Having few variables may cause a low alpha score, as well as a low correlation between the variables. One cause for low correlation is having variables that measure irrelevant data. These issues can cause a test to be wrongly discarded, therefore, Cronbach’s Alpha must be carefully used [30,31].
The Cronbach’s Alpha obtained for the nine independent variables is 0.701, which is rated as acceptable [32]. The next step is to run the PCA analysis. One of the possible outputs while performing the PCA in SPSS is the KMO and Bartlett’s test of sphericity. This test checks how adequate each individual variable is as well as considering the whole grouping of variables together. Similar to Cronbach’s Alpha, the output of this test ranges from 0 to 1. Values above 0.8 are considered adequate for factor analysis, while values below 0.6 show that the samples used are not good enough [30]. The intermediate values indicate that the set of variables has average quality in terms of factor analysis usage.
The KMO value of 0.636 is classified as reasonable, which means the data tested are good enough for a PCA, although that value should ideally be a bit higher. The sigma value of Bartlett’s test of sphericity is below 0.05, which means the tested set of variables is adequate for a PCA by demonstrating that the correlations’ matrix, shown in Table A3, possesses significant correlations between the nine variables, rejecting the hypothesis that the correlations matrix is an identity matrix.
Table 2 indicates the descriptive statistics for all variables. It is worth highlighting the mean of the variable 1, the number of boxes, which is much higher than other variables. Additionally, the standard deviation of variable 6, the number of column piles, indicates there is a large amount of data variation in the observation retrieved for this variable. The values used in Table 2 are scaled and are not the original measurements. The correspondence column shows the range of values that matches the values in the mean column. For example, a mean of 8.39 for the Number Boxes of variable translates into 51 to 60 boxes, according to the scale shown in Table 1.

Table 2.
Descriptive statistics.
Table 3 shows the eigenvalues and total variance of the principal components and only the principal components with eigenvalues above 1 should be extracted [33]. In this case, there are three components to be extracted. Together, they explain almost 75% of the total variance of the data collected.

Table 3.
Eigenvalues and total variance.
Finally, the principal components are seen below, in Table 4. Component 1, which explains 41% of the total variance, contains the number of column piles, number of box types, time spent packing, and percentage of fragile boxes. This component can be called Box Quantities. The second component explains 22% of the total variance and is affected by the number of heavy boxes packed, the average weight of the packed boxes and the average maximum width. This component can be named Box Dimensions. The final principal component only covers 12% of the total variance and possesses the remaining two variables, the height difference between worker and pile and the number of boxes. This component can be called Complexity.

Table 4.
Rotated component matrix.
To see if the percentage of total variance explained by the principal components increases, a new test was performed with a variation of the PCA, the categorical PCA, which is a test suited for categorical variables. After running the test to force the extraction of three components, the percentage increased to 79%. The three components possess the set of variables seen in Table 3. Considering that the third component explains a low percentage of the total variance, and its eigenvalue is very close to the rejection border, it is possible to force SPSS to redo the test while creating only two components. The results of that second test are shown in Table 5 and Table 6.

Table 5.
Rotated data extraction for categorical PCA with 2 dimensions.

Table 6.
Rotated component loadings for 2 dimensions.
Table 5 shows that the two dimensions have acceptable Cronbach’s Alpha values, and together they explain around 69% of the total variance of the original variables. Table 6 displays the two principal components, with the respective variables in bold (only variables with a non-negative component loading of at least 0.5 are determinants for that component). The first one possesses five variables (Number of Box Types, Time Spent Packing, Number of Column Piles, Number of Boxes, Percentage of Fragile Boxes) and can be called Box Quantities. The second one possesses four variables (Average maximum width, Number of Heavy Boxes Packed, Average Weight of Packed Boxes and Height Difference Between Worker and Pile) and is known as Box Dimensions.
After using the PCA with the nine collected independent variables, a multiple linear regression was carried out with the principal components extracted in the previous section. The multiple linear regression is a mathematical analysis method using a given a set of data with independent variables (known as predictors) and one dependent variable (known as a criterion). The independent variables are used to predict the value of the dependent variable [34]. This method results in an equation. The values obtained are adjusted to the set of variables that was used; therefore, after applying the equation, values close to the dependent variable are expected. This relation between both types of variables can be seen in Equation (1):
where βi‘s are the slope between y and the appropriate xi. To refine the model, there is also the β0, the y-intercept, and ε, the error term that captures errors in measurement of y and the effect on y of any variables missing from the equation that would contribute to explaining variations in y [35].
First, a regression was conducted using the two principal components previously extracted and the dependant variable—the Packed Pallet Evaluation variable. To perform this multiple linear regression, the method chosen is called Stepwise. There are multiple iterations, starting with a model possessing only one variable and then progressively adding a new variable and removing others if they are not significant enough to the model [36].
The adjusted R square obtained has a value of 0.202, meaning that this linear regression explains 20.2% of the variance in the data, which is a small value but adequate for the data. It is expected to see the R values increase with the increase in the number of variables inserted into the model, the F-test, which tests the null hypothesis that the model explains zero variance in the dependent variable. The p-value is below the usual significance level of 0.05, which means the null hypothesis is rejected, meaning that this model explains a significant amount of the variance of the dependent variable.
The β values indicate the predictability for each variable. The Stepwise method only selected one of the two components obtained, considering the Box Quantities component the only relevant component for the model. The constant has a β of 5.026 while the Box Quantities component has a value of 1.009. The t values show that the Box Quantities component has decent predictability power over the dependent value, although its coefficient is small when compared to the constant (16.042 to 3.219).
To validate a multiple linear regression, some assumptions must be checked to see if the test is reliable. These assumptions are the normality, homogeneity, error independency, and multicollinearity [36]. First, there is a graphical overview of the normality of the residuals, with a Predicted Probability plot. The dots in Figure 1, although they have some slight deviations from the line, follow the line’s tendency overall, which corroborates the normality of the regression. Figure 2 is used to check homogeneity. The dots representing the residuals seem widely dispersed and not concentrated in a specific zone, which means the homogeneity exists here. Finally, to confirm error independency, there is the Durbin–Watson value. The value obtained should be higher than 1.5 and below 2.5. The ones obtained in the two regressions executed with the principal components are approximately 2.1, which means there is error independency. Finally, the multicollinearity should have a value below 10. The ones obtained are equal to 1, meaning there is no multicollinearity between variables.
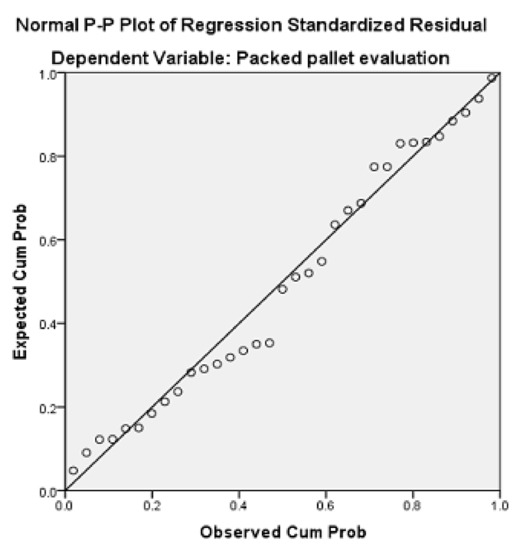
Figure 1.
Predicted probability plot (for 2 principal components).
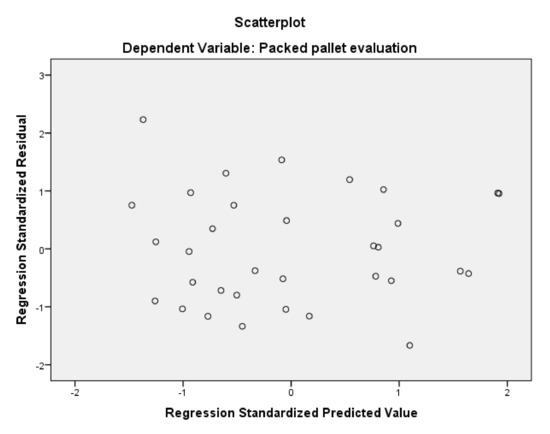
Figure 2.
Scatterplot to test residuals homogeneity (for 2 principal components).
Equation (2), as seen below,
represents the predictability of the model, where x1 represents the Box Quantities component. In the end, this regression allowed us to conclude that the component Box Quantities, which contains the variables Number of Column Piles, Number of Box Types, Number of Boxes, Time Spent Packing and Percentage of Fragile Boxes, is the component that explains the variance of the Evaluation variable better, while the Box Dimensions component is not very relevant towards explaining the dependant variable.
Next, another multiple linear regression was performed, but this time with the original nine variables and not with the principal components. This was undertaken to see if the variables contained by the Box Quantities component are considered relevant by the multiple linear regression.
The new test shows that the Adjusted R Square is higher than the ones in previous tests, having the model explain 33.1% of the variance of the Evaluation variable, and the Durbin–Watson value is also good (2.376). The F value is high (19.285) while the sigma value of Bartlett’s test of sphericity is below 0.05, which means that the model obtained is relevant, although only 1 out of 9 variables were kept in the model using the stepwise method. That variable is the Number of Column Piles, which is contained by the Box Quantities component. In Figure 3 it can be seen that the residuals follow the line with no odd deviations, meaning that there is data normality. In Figure 4 the dots are spread in the graphic area, meaning there is data homogeneity. Equation (3)
sums up the model, where the x1 represents the variable “Number of Column Piles” and the β is 3.637. The variable that affects the complexity of the pallet loading problem, according to this model, is the Number of Column Piles. This multiple linear regression matches what was seen in the principal components analysis: the Box Quantities component was the most significant. This test showed that, statistically, only one variable is responsible for explaining the Evaluation variable. However, the latter variable is subjective, which means that other parameters can affect this variable, depending on the perceptions of the different workers.
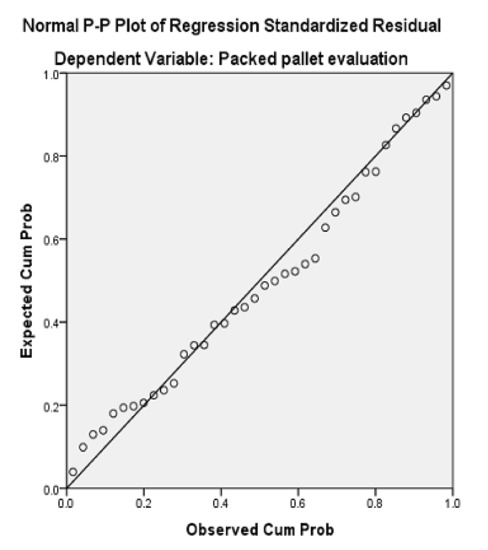
Figure 3.
Predicted probability plot (for 9 variables).
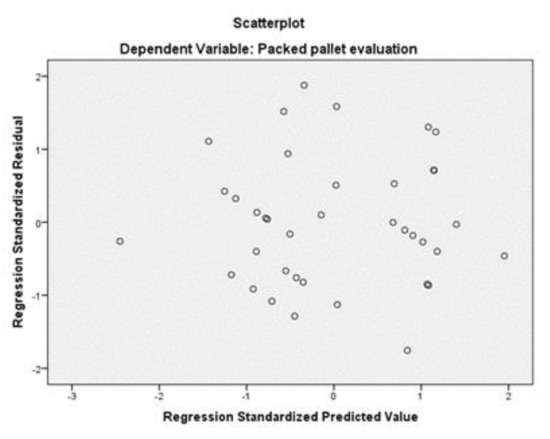
Figure 4.
Scatterplot to test residuals homogeneity (for 9 variables).
5. Discussion
This paper studied the complexity of the pallet loading problem through principal component analysis based on the literature review and the outcome of the audit of the loading workers/picking personnel of a third-party logistics company.
We defined the factors relevant to that complexity (Table 1) and a set of metrics along with the range of the scale of values to be considered. Our approach was based on a review of the literature and the outcome of the audit of the loading workers/picking personnel of a third-party logistics company.
After testing the principal components analysis and the multiple linear regression with both the two principal components and the nine original variables, it is possible to conclude that the Box Quantities component is what explains the complexity of the pallet loading process. The Box Dimensions component was not deemed impactful on the complexity of the pallet loading problem. In the regression with the nine original variables, only the variable Number of Column Piles was retained in the model when using the Stepwise method, meaning that the significances of the other variances were too low. It is worth noting that the variable Number of Column Piles belongs to the Box Quantities component, matching the results from the regression with the components. To consider a variable that measures something that is subjective can generate discrepancies of opinions that will reflect on the results. For a box picker, a variable responsible for much of the complexity may not be as significant for a different category of worker. Though perspectives may clash, in this situation, the results showed that one of the parameters that most workers deem as complex was indeed proven to be complex. This does not mean other parameters do not affect the complexity, but only that regarding this specific parameter there is statistical evidence that it increased the complexity. As it belongs to the Box Quantities component, the Number of Boxes proved not to be significant in the regression, although it was more relevant than most other parameters.
6. Conclusions
We conclude that only a few variables, which are included in a single main component, are significant enough to explain the complexity of the pallet loading problem—mainly the Number of Column Piles variable. From a practical standpoint, having multiple piles in a pallet, paired with other constraints, such as forcing homogeneous piles, can greatly disturb the workers who oversee that load. Failing to organize the boxes in a way that minimizes trim-loss and maximizes the space occupied in the pallet, while keeping the whole stack uniform and stable can cause the picker to reorganize everything. Even if the worker has years of experience loading pallets, it can be very hard to complete the whole process smoothly in one try.
When undertaking this analysis on a principal component level, the Box Quantities component contains the Number of Column Piles variable and also contains other variables that are directly related to how impactful the Number of Column Piles is. Assuming they cannot be mixed in the same pile, if there are multiple types of boxes to load, they must be properly distributed on the surface of the pallet. This situation is more impactful the higher the number of boxes is. If there are fragile boxes to be loaded, they must be as close to the top of the stack as possible to avoid damage, constraining the loading process even more. All these factors affect or are affected by the Number of Column Piles variable. This raises some questions. Could the limited number and diversity of samples collected be a factor in these results? Would they be different if a larger number of samples from different companies was collected?
Regarding the metrics created, in theory they seemed to be impactful in the complexity constraint, but most did not show any statistical evidence that they affected the complexity of the pallet loading process. Perhaps for someone who does this process daily for years, certain parameters do not affect his/her performance. However, from the perspective of a researcher, someone who does not have practical experience in that job, all these parameters seem important. It is worth noting that not all workers have the same experience. The more experienced the picker is, the more likely it is that less parameters will affect the complexity of a loading process, in his/her perspective. Would the results be different if certain metrics were removed? Although the parameters measure different aspects between themselves, they may have certain characteristics in common that can affect the result measured. This was seen above when breaking down the behaviour of certain variables inherent to the Box Quantities component.
For future research it would be interesting to increase the dimension and diversity of the samples collected to verify results and acquire additional data for the further testing of other parameters. Being aware of the difficulties that each pattern can cause during the loading is important, so that the person in charge of the process can create a more suitable loading strategy. Having solid data about which variables have a higher impact in the complexity of a pattern greatly helps in that purpose, especially because most companies have specific requirements about how the loaded pallet should look in the end. When loading pallets with complex patterns, one should analyse the most restraining aspects of it and start the process with those in mind to minimize the impact and maximize the efficiency.
Author Contributions
Conceptualization, H.B. and T.P.; methodology, H.B. and A.G.R.; validation T.P. and F.A.F.; formal analysis, F.A.F.; writing—original draft preparation, H.B. and T.P. All authors revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Portuguese national funds through FCT—Fundação para a Ciência e Tecnologia, I.P., under the project UIDB/04752/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Application of the created metrics in the collected set of samples.
Table A1.
Application of the created metrics in the collected set of samples.
| Sample\Parameter | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Evaluation |
| Units | Kg | % | m | mins | m | |||||
| 1 | 55 | 2.38 | 20.0 | 0.170 | 5 | 0 | 4 | −1.087 | 0 | 4 |
| 2 | 121 | 3.09 | 54.5 | 0.310 | 11 | 0 | 9 | 1.340 | 0 | 4 |
| 3 | 99 | 2.05 | 77.8 | 0.210 | 9 | 0 | 6 | −0.652 | 0 | 4 |
| 4 | 174 | 2.36 | 2.3 | 0.170 | 4 | 0 | 15 | −0.617 | 0 | 2 |
| 5 | 5 | 2.61 | 0 | 0.153 | 1 | 0 | 1 | −1.294 | 0 | 1 |
| 6 | 87 | 3.61 | 36.8 | 0.361 | 25 | >9 | 42 | 1.310 | 11 | 9 |
| 7 | 199 | 3.79 | 38.7 | 0.290 | 18 | 0 | 8 | 1.340 | 11 | 4 |
| 8 | 450 | 2.48 | 13.3 | 0.150 | 8 | 0 | 31 | 1.340 | 0 | 3 |
| 9 | 16 | 23.40 | 0 | 0.570 | 2 | 0 | 16 | −0.756 | 16 | 2 |
| 10 | 50 | 5.86 | 0 | 0.530 | 1 | 0 | 2 | 1.340 | 0 | 4 |
| 11 | 176 | 2.57 | 24.4 | 0.220 | 54 | >9 | 48 | 1.220 | 11 | 9 |
| 12 | 32 | 12.25 | 0 | 0.290 | 9 | 9 | 9 | −0.566 | 22 | 6 |
| 13 | 97 | 9.14 | 1.0 | 0.310 | 10 | >9 | 22 | 1.220 | 32 | 7 |
| 14 | 78 | 2.41 | 3.8 | 0.390 | 13 | >9 | 24 | 0.323 | 0 | 5 |
| 15 | 153 | 2.61 | 0 | 0.150 | 1 | 0 | 8 | −0.774 | 0 | 8 |
| 16 | 375 | 2.91 | 0 | 0.410 | 3 | 0 | 13 | 1.340 | 0 | 3 |
| 17 | 31 | 23.40 | 0 | 0.560 | 2 | 0 | 6 | 0.106 | 31 | 7 |
| 18 | 86 | 7.96 | 0 | 0.270 | 3 | 0 | 8 | 0.140 | 6 | 5 |
| 19 | 33 | 5.31 | 0 | 0.330 | 2 | 0 | 4 | −1.126 | 18 | 2 |
| 20 | 25 | 10.60 | 100 | 0.280 | 1 | 0 | 3 | −0.888 | 25 | 2 |
| 21 | 52 | 2.43 | 61.5 | 0.270 | 14 | >9 | 19 | −0.839 | 0 | 6 |
| 22 | 143 | 1.90 | 21 | 0.160 | 10 | >9 | 13 | −0.885 | 0 | 7 |
| 23 | 108 | 2.28 | 27.8 | 0.170 | 24 | >9 | 21 | −0.930 | 0 | 7 |
| 24 | 91 | 1.83 | 49.5 | 0.220 | 15 | >9 | 15 | −0.924 | 0 | 8 |
| 25 | 106 | 1.60 | 12.3 | 0.190 | 13 | >9 | 17 | −0.865 | 0 | 6 |
| 26 | 24 | 5.86 | 0 | 0.530 | 1 | 0 | 3 | −0.096 | 0 | 5 |
| 27 | 32 | 17.72 | 0 | 0.340 | 1 | 0 | 7 | −0.258 | 32 | 6 |
| 28 | 24 | 14.07 | 0 | 0.390 | 1 | 0 | 9 | −0.726 | 24 | 3 |
| 29 | 90 | 1.63 | 52.2 | 0.200 | 16 | >9 | 16 | −0.770 | 0 | 5 |
| 30 | 162 | 2.23 | 100 | 0.270 | 1 | 0 | 12 | 0.051 | 0 | 6 |
| 31 | 130 | 1.89 | 53.8 | 0.160 | 22 | >9 | 25 | −0.832 | 0 | 3 |
| 32 | 99 | 10 | 0 | 0.600 | 1 | 0 | 5 | 1.220 | 99 | 3 |
| 33 | 95 | 3.88 | 10.5 | 0.240 | 16 | > 9 | 27 | 1.220 | 17 | 6 |
| 34 | 115 | 2.31 | 87.8 | 0.320 | 7 | 7 | 20 | 1.340 | 16 | 8 |
| 35 | 34 | 4.37 | 17.6 | 0.390 | 4 | 4 | 10 | −0.672 | 14 | 3 |
| 36 | 1550 | 2.62 | 41.9 | 0.200 | 14 | 0 | 90 | 1.340 | 120 | 4 |
| 37 | 49 | 4.95 | 14.3 | 0.260 | 6 | 6 | 5 | −0.713 | 12 | 8 |
| 38 | 77 | 5.92 | 15.6 | 0.390 | 18 | >9 | 19 | 1.220 | 38 | 6 |

Table A2.
Scaling of the parameters measured according to the collected set of samples.
Table A2.
Scaling of the parameters measured according to the collected set of samples.
| Sample\Parameter | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Evaluation |
| 1 | 8 | 2 | 4 | 1 | 3 | 1 | 1 | 1 | 1 | 4 |
| 2 | 10 | 3 | 10 | 2 | 6 | 1 | 2 | 10 | 1 | 4 |
| 3 | 10 | 2 | 10 | 2 | 5 | 1 | 2 | 2 | 1 | 4 |
| 4 | 10 | 2 | 1 | 1 | 2 | 1 | 3 | 2 | 1 | 2 |
| 5 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 10 | 3 | 8 | 3 | 10 | 10 | 9 | 10 | 6 | 9 |
| 7 | 10 | 3 | 8 | 2 | 8 | 1 | 1 | 10 | 6 | 4 |
| 8 | 10 | 2 | 3 | 1 | 4 | 1 | 7 | 10 | 1 | 3 |
| 9 | 4 | 10 | 1 | 4 | 1 | 1 | 4 | 2 | 8 | 2 |
| 10 | 7 | 4 | 1 | 3 | 1 | 1 | 1 | 10 | 1 | 4 |
| 11 | 10 | 2 | 5 | 2 | 10 | 10 | 10 | 10 | 6 | 9 |
| 12 | 6 | 9 | 1 | 2 | 5 | 9 | 2 | 2 | 10 | 6 |
| 13 | 10 | 7 | 1 | 2 | 5 | 10 | 5 | 10 | 10 | 7 |
| 14 | 10 | 2 | 1 | 3 | 7 | 10 | 5 | 9 | 1 | 5 |
| 15 | 10 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 8 |
| 16 | 10 | 2 | 1 | 3 | 2 | 1 | 3 | 10 | 1 | 3 |
| 17 | 6 | 10 | 1 | 4 | 1 | 1 | 2 | 5 | 10 | 7 |
| 18 | 10 | 6 | 1 | 2 | 2 | 1 | 2 | 5 | 3 | 5 |
| 19 | 6 | 4 | 1 | 2 | 1 | 1 | 1 | 1 | 9 | 2 |
| 20 | 5 | 8 | 10 | 2 | 1 | 1 | 1 | 1 | 10 | 2 |
| 21 | 8 | 2 | 10 | 2 | 7 | 10 | 4 | 2 | 1 | 6 |
| 22 | 10 | 2 | 5 | 1 | 5 | 10 | 3 | 1 | 1 | 7 |
| 23 | 10 | 2 | 6 | 1 | 10 | 10 | 5 | 1 | 1 | 7 |
| 24 | 10 | 2 | 9 | 2 | 7 | 10 | 3 | 1 | 1 | 8 |
| 25 | 10 | 2 | 3 | 2 | 7 | 10 | 4 | 2 | 1 | 6 |
| 26 | 5 | 4 | 1 | 3 | 1 | 1 | 1 | 2 | 1 | 5 |
| 27 | 6 | 10 | 1 | 2 | 1 | 1 | 2 | 2 | 10 | 6 |
| 28 | 5 | 9 | 1 | 3 | 1 | 1 | 2 | 2 | 10 | 3 |
| 29 | 10 | 2 | 10 | 2 | 8 | 10 | 4 | 2 | 1 | 5 |
| 30 | 10 | 2 | 10 | 2 | 1 | 1 | 3 | 4 | 1 | 6 |
| 31 | 10 | 2 | 10 | 1 | 10 | 10 | 5 | 2 | 1 | 3 |
| 32 | 10 | 7 | 1 | 4 | 1 | 1 | 1 | 10 | 10 | 3 |
| 33 | 10 | 3 | 3 | 2 | 8 | 10 | 6 | 10 | 9 | 6 |
| 34 | 10 | 2 | 10 | 2 | 4 | 7 | 4 | 10 | 8 | 8 |
| 35 | 6 | 3 | 4 | 3 | 2 | 4 | 2 | 2 | 7 | 3 |
| 36 | 10 | 2 | 9 | 2 | 7 | 1 | 10 | 10 | 10 | 4 |
| 37 | 7 | 4 | 3 | 2 | 3 | 6 | 1 | 2 | 6 | 8 |
| 38 | 9 | 4 | 4 | 3 | 8 | 10 | 4 | 10 | 10 | 6 |

Table A3.
Correlations matrix (values in bold represent high correlation between variables).
Table A3.
Correlations matrix (values in bold represent high correlation between variables).
| Variable Code | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 1.000 | |||||||||
| 2 | −0.525 | 1.000 | ||||||||
| 3 | 0.379 | −0.428 | 1.000 | |||||||
| 4 | 0.571 | −0.458 | 0.516 | 1.000 | ||||||
| 5 | −0.235 | 0.526 | −0.261 | −0.240 | 1.000 | |||||
| 6 | 0.371 | −0.270 | 0.251 | 0.771 | −0.140 | 1.000 | ||||
| 7 | 0.458 | −0.299 | 0.262 | 0.663 | −0.080 | 0.480 | 1.000 | |||
| 8 | 0.456 | −0.108 | 0.015 | 0.280 | 0.314 | 0.055 | 0.460 | 1.000 | ||
| 9 | −0.282 | 0.692 | −0.192 | −0.133 | 0.453 | −0.044 | 0.072 | 0.230 | 1.000 | |
| 0 | 0.416 | −0.118 | 0.166 | −0.046 | 0.431 | 0.591 | 0.356 | 0.155 | 0.029 | 1.000 |
References
- Accorsi, R.; Baruffaldi, G.; Manzini, R.; Pini, C. Environmental Impacts of Reusable Transport Items: A Case Study of Pallet Pooling in a Retailer Supply Chain. Sustainability 2019, 11, 3147. [Google Scholar] [CrossRef]
- Silva, E.; Oliveira, J.F.; Wäscher, G. The pallet loading problem: A review of solution methods and computational experiments. Int. Trans. Oper. Res. 2016, 23, 147–172. [Google Scholar] [CrossRef]
- Gomes, A.M.; Gonçalves, J.F.; Alvarez-Valdés, R.; de Carvalho, V. Special issue on “Cutting and Packing”. Int. Trans. Oper. Res. 2013, 20, 441–442. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Hwang, F.J.; Lu, H.-C. An effective placement method for the single container loading problem. Comput. Ind. Eng. 2016, 97, 212–221. [Google Scholar] [CrossRef]
- Order Picking in The Warehouse—Supply Chain/Logistics. Available online: https://www.thebalance.com/order-picking-in-the-warehouse-2221190 (accessed on 18 July 2018).
- Dresch, A.; Lacerda, D.P.; Miguel, P.A.C. A distinctive analysis of case study, action research and design science research. Rev. Bras. Gestão Negócios 2015, 17, 1116–1133. [Google Scholar] [CrossRef]
- Bischoff, E.E.; Ratcliff, M. Issues in the development of approaches to container loading. Omega 1995, 23, 377–390. [Google Scholar] [CrossRef]
- Pureza, V.; Morabito, R. Some experiments with a simple tabu search algorithm for the manufacturer’s pallet loading problem. Comput. Oper. Res. 2006, 33, 804–819. [Google Scholar] [CrossRef]
- Alvarez-Valdes, R.; Parreño, F.; Tamarit, J.M. A branch-and-cut algorithm for the pallet loading problem. Comput. Oper. Res. 2005, 32, 3007–3029. [Google Scholar] [CrossRef]
- Kocjan, W.; Holmström, K. Computing stable loads for pallets. Eur. J. Oper. Res. 2010, 207, 980–985. [Google Scholar] [CrossRef]
- Dowsland, K. Some experiments with simulated annealing techniques for packing problems. Eur. J. Oper. Res. 1993, 68, 389–399. [Google Scholar] [CrossRef]
- Herbert, A.; Dowsland, K. A family of genetic algorithms for the pallet loading problem. Ann. Oper. Res. 1996, 63, 415–436. [Google Scholar] [CrossRef]
- Scheithauer, G.; Terno, J. The G4-heuristic for the pallet loading problem. J. Oper. Res. Soc. 1996, 47, 511–522. [Google Scholar] [CrossRef]
- Morabito, R.; Morales, S.A. Simple and effective recursive procedure for the manufacturer’s pallet loading problem. J. Oper. Res. Soc. 1998, 49, 819–828. [Google Scholar] [CrossRef]
- Martins, G.H.A.; Dell, R.F. Solving the pallet loading problem. Eur. J. Oper. Res. 2008, 184, 429–440. [Google Scholar] [CrossRef]
- Bortfeldt, A.; Wäscher, G. Constraints in container loading-A state-of-the-art review. Eur. J. Oper. Res. 2013, 229, 1–20. [Google Scholar] [CrossRef]
- Amossen, R.R.; Pisinger, D. Multi-dimensional bin packing problems with guillotine constraints. Comput. Ind. Eng. 2010, 37, 1999–2006. [Google Scholar] [CrossRef][Green Version]
- Martello, S.; Pisinger, D.; Vigo, D.; Boef, E.; Korst, J. Algorithm 864: General and robot-packable variants of the three-dimensional bin packing problem. ACM Trans. Math. Softw. 2007, 33, 7. [Google Scholar] [CrossRef]
- Egeblad, J.; Pisinger, D. Heuristic approaches for the two- and three-dimensional knapsack packing problem. Comput. Oper. Res. 2009, 36, 1026–1049. [Google Scholar] [CrossRef]
- Morabito, R.; Arenalest, M. An AND/OR-Graph Approach to the Container Loading Problem. Int. Trans. Oper. Res. 1994, 1, 59–73. [Google Scholar]
- Hifi, M. Approximate algorithms for the container loading problem. Int. Trans. Oper. Res. 2002, 9, 747–774. [Google Scholar] [CrossRef]
- Wäscher, G.; Haussner, H.; Schumann, H. An improved typology of cutting and packing problems. Eur. J. Oper. Res. 2006, 183, 1109–1130. [Google Scholar] [CrossRef]
- Dyckhoff, H. A typology of cutting and packing problems. Eur. J. Oper. Res. 1990, 44, 145–159. [Google Scholar] [CrossRef]
- Barros, H. Complexity Analysis in the Distributor Pallet Loading Problem. Master’s Thesis, Polytechnic Institute of Porto, Porto, Portugal, 2018. [Google Scholar]
- Back Injury Prevention for the Landscaping and Hiorticultural Services Industry. Available online: https://www.osha.gov/dte/grant_materials/fy06/46g6-ht22/back_injury_prevention.pdf (accessed on 21 July 2018).
- Size of A Human: Body Proportions. Available online: https://hypertextbook.com/facts/2006/bodyproportions.shtml (accessed on 25 July 2018).
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Pereira, T.; Rocha, J.; Telhada, J.; Carvalho, M.S. Characterization of the Portuguese SSS into the Europe: A contribution. Lect. Notes Comput. Sci. 2015, 9335, 252–266. [Google Scholar] [CrossRef]
- MacCallum, R.C.; Widaman, K.F.; Preacher, K.J.; Hong, S. Sample Size in Factor Analysis: The Role of Model Error. Multivar. Behav. Res. 2001, 36, 611–637. [Google Scholar] [CrossRef] [PubMed]
- Hair, .J.F., Jr.; Black, W.C.; Babin, B.J.; Anderson, R.E.; Tatham, R.L. Multivariate Data Analysis, 8th ed.; Cengage: Hampshire, UK, 2018. [Google Scholar]
- Woollins, J.D. The Preparation and Structure of Metalla-Sulphur/Selenium Nitrogen Complexes and Cages. Stud. Inorg. Chem. 1992, 14, 349–372. [Google Scholar] [CrossRef]
- George, D.; Mallery, P. SPSS for Windows Step by Step: A Simple Guide and Reference. 11.0 Update, 4th ed.; Allyn & Bacon: Boston, MA, USA, 2003. [Google Scholar]
- Pituch, K.A.; Stevens, J.P. Applied Multivariate Statistics for the Social Sciences: Analyses with SAS and IBM’s SPSS., 6th ed.; Routledge: Oxfordshire, UK, 2015. [Google Scholar]
- Griffith, A. SPSS for Dummies, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Eberly, L.E. Multiple Linear Regression. In Topics in Biostatistics, 1st ed.; Ambrosius, W.T., Ed.; Humana Press: Totowa, NJ, USA, 2007; Volume 404. [Google Scholar] [CrossRef]
- Lewis, M. Stepwise Versus Hierarchical Regression: Pros and Cons; Annual Meeting of the Southwest Educational Research Association: San Antonio, TX, USA, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).