Lithium-Ion Battery SOC Estimation Based on Adaptive Forgetting Factor Least Squares Online Identification and Unscented Kalman Filter

Abstract

In order to improve the estimation accuracy of the battery state of charge (SOC) based on the equivalent circuit model, a lithium-ion battery SOC estimation method based on adaptive forgetting factor least squares and unscented Kalman filtering is proposed. The Thevenin equivalent circuit model of the battery is established. Through the simulated annealing optimization algorithm, the forgetting factor is adaptively changed in real-time according to the model demand, and the SOC estimation is realized by combining the least-squares online identification of the adaptive forgetting factor and the unscented Kalman filter. The results show that the terminal voltage error identified by the adaptive forgetting factor least-squares online identification is extremely small; that is, the model parameter identification accuracy is high, and the joint algorithm with the unscented Kalman filter can also achieve a high-precision estimation of SOC.

1. Introduction

The state of charge (SOC) of the power battery of an electric vehicle is the basis of the energy management of the battery and the vehicle. The accuracy of the estimation result directly affects the performance and safety of the battery and the vehicle.

Currently, battery SOC estimation methods include ampere-hour integration method, open-circuit voltage method, data-driven algorithm, and equivalent circuit model observation method, etc. [1]. The ampere-hour integral method is simple to calculate, but it has high requirements for the accuracy of the initial value, and it is easy to produce cumulative errors during the estimation process and cannot be self-corrected. The open-circuit voltage of the open-circuit voltage method needs to be obtained by fully standing the battery, which is not suitable for direct application in real vehicles and is generally used in conjunction with the ampere-hour integration method [2,3,4,5]. Data-driven algorithms do not need to consider the internal model of the system but have high data requirements, and data training is more difficult. The equivalent circuit model observation method is based on the circuit model, using charge and discharge data to first identify the model parameters and then combine various filtering algorithms to estimate the battery SOC.

Model parameters affect the accuracy of the model, which in turn affects the accuracy of battery SOC estimation. Parameter identification can be divided into two types, offline and online. The simpler least-squares fitting method in the offline identification method generally requires appropriate initial parameters, which is inconvenient to apply. Luo et al. [6] used a simulated annealing algorithm that does not require initial parameters, has a fast convergence rate, and can obtain a global optimum to identify parameters. However, as the battery usage environment and the number of cycles change, its offline identification results are difficult to adapt to the battery environment changes.

Therefore, some scholars have proposed online identification to update the equivalent circuit model parameters in real-time to ensure the accuracy of the model. Wang et al. [7] proposed a recursive least squares-extended Kalman filter (RLS-EKF) algorithm, which uses the recursive least squares method to achieve online parameter identification and then combined with the extended Kalman filter to estimate the battery SOC. The battery is a time-varying system. After the equivalent circuit model is established, different voltages, currents, and SOCs will affect the changes of model parameters. Using offline-identified model parameters to estimate the real-time changing SOC itself is a helpless compromise. Partovibakhsh et al. [8] used adaptive extended Kalman filter (AEKF) and recursive least square method to estimate the open-circuit voltage (OCV), and then estimates the battery SOC through the SOC–OCV relationship. The experimental results show that this method has a certain improvement effect. However, recursive least squares is more suitable for systems with constant unknown parameters, while battery parameters are slow time-varying systems, and recursive least squares are prone to “data saturation” [9]. In order to overcome the problem of “data saturation” in parameter identification, Zheng et al. [10] adopted the combined algorithm of recursive least squares and AEKF with forgetting factor to improve the tracking effect of the algorithm. Xu et al. [11] used a combined algorithm of recursive least squares with forgetting factor and unscented Kalman filter (UKF). However, the fixed forgetting factor must not meet the requirements of the model in real-time, and there is a lack of dynamic research on the forgetting factor. Verbrugge et al. [12] studied the effects of fixed forgetting factors and optimized variable forgetting factors on recognition results. Wang et al. [13] found that the recursive algorithm based on the battery model used by Verbrugge will become unstable when the sampling frequency is high.

Based on the above analysis, this paper proposes real-time optimization of recursive least squares forgetting factor through particle swarm algorithm, combined with unscented Kalman filter to achieve lithium-ion battery SOC estimation, aiming to further improve the accuracy of battery SOC estimation. Accurate estimation of model parameters is very important for SOC estimation based on equivalent circuit models. Accurate estimation of model parameters is equivalent to improving the modeling accuracy of the model. This paper takes into account the real-time changes of the battery state and introduces the adaptive forgetting factor optimized by the simulated annealing algorithm to more accurately identify the real-time parameters of the battery. The obtained adaptive forgetting factor is used to adjust the trust of new and old test data, effectively avoiding the “data saturation” problem of the traditional recursive least squares. Finally, combined with the unscented Kalman filter algorithm to achieve the ultimate goal of accurate estimation of battery SOC.

2. Establishment of Equivalent Circuit and Open Circuit Voltage Model

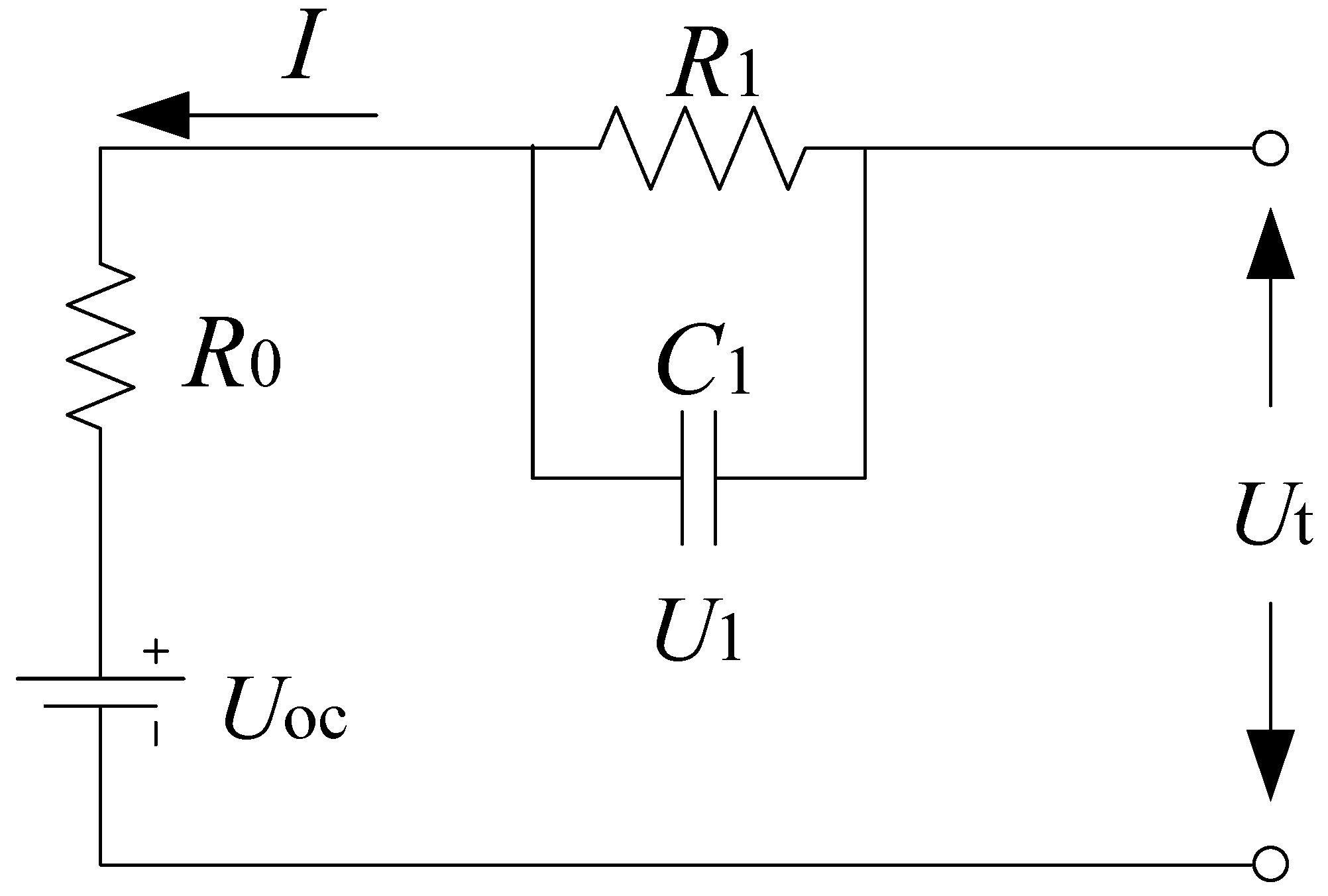
2.1. Equivalent Circuit Model

The battery model is the premise of the Kalman filter algorithm to estimate the battery state. Commonly used equivalent circuit models include the Rint model, Thevenin model, and PNGV (the Partnership for a New Generation of Vehicles) model, etc. [14,15,16]. For the ternary lithium battery, the Thevenin equivalent circuit model can ensure high accuracy and reduce the complexity of the model. Therefore, this article selects the Thevenin equivalent circuit model. The model structure is shown in Figure 1.

In the above Figure: U_oc is the open-circuit voltage; R₀ is the ohmic internal resistance; I is the operating current, and the charging direction is the positive direction of the current; R₁ is the polarization internal resistance; C₁ is the polarization capacitance [17]; U₁ is the polarization ring terminal voltage; and U_t is the battery terminal voltage.

According to Kirchhoff’s voltage law and Kirchhoff’s current law, the electrical relationship of the equivalent circuit model can be obtained as:

$$\{\begin{array}{l}{\dot{U}}_1=\frac{-U_1}{R_1{C}_1}+\frac{I}{C_1}\\ U_t=U_{\mathrm{oc}}-U_1-I\cdot R_0\end{array}$$

(1)

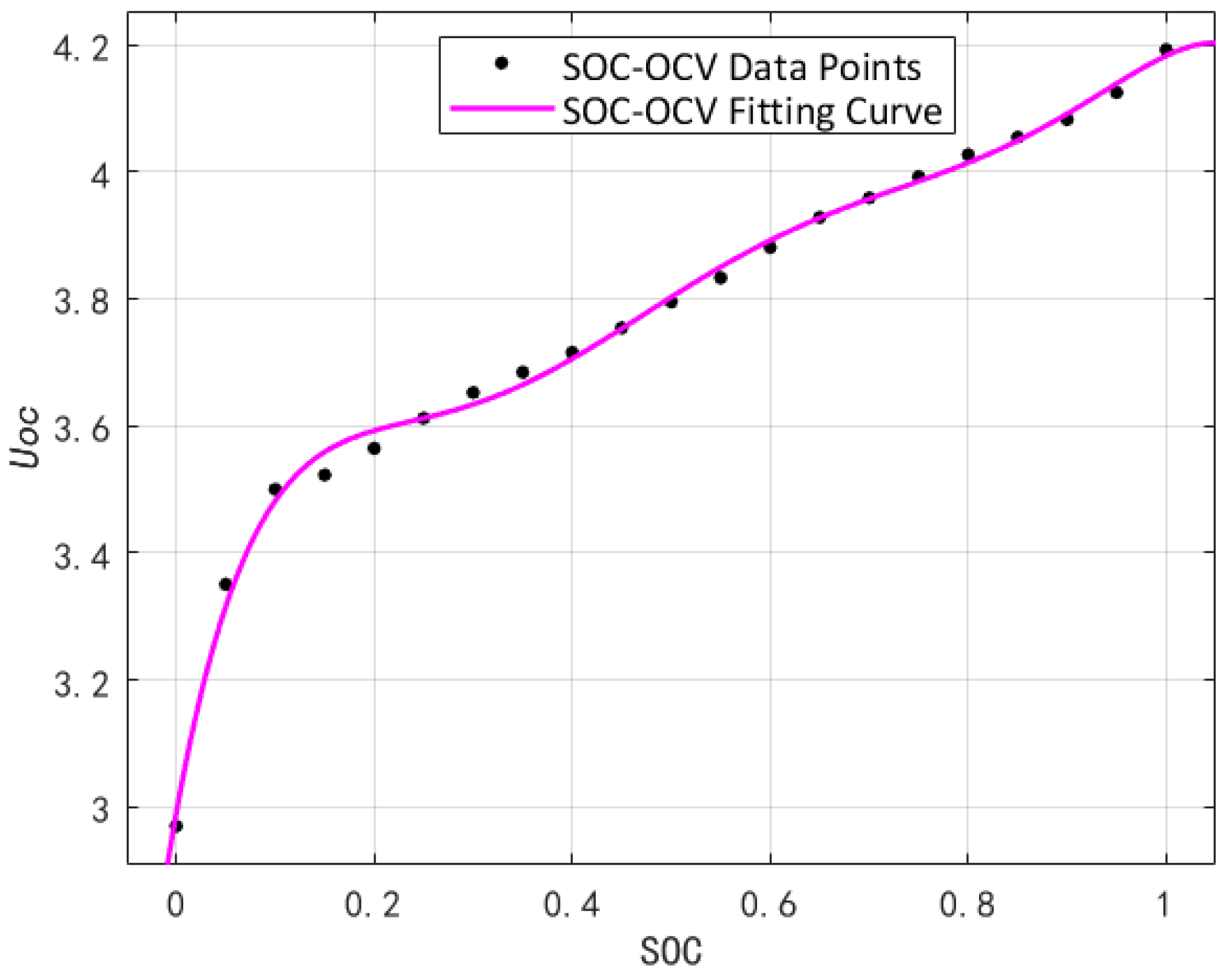
2.2. Open Circuit Voltage Model

There is a one-to-one mapping relationship between the open-circuit voltage and the state of charge of lithium-ion batteries, which provides a possible way for SOC estimation and correction, but the open-circuit voltage cannot be directly measured in real-time. It can be determined by the terminal voltage value after fully standing still. Therefore, it cannot be directly used for real-time SOC estimation on real vehicles. The SOC–OCV relationship of lithium-ion batteries is obtained through experiments, and combined with the filtering algorithm of SOC estimation, the estimation and correction of the SOC of lithium-ion batteries can be realized. The test plan for obtaining the SOC–OCV relationship under a normal temperature environment is as follows:

• The temperature control box controls the test environment temperature at 25 °C. After charging with a constant current at a rate of 1/3 C to a cut-off voltage of 4.2 V, charging at a constant voltage until the current is less than 0.02 C, and then standing for 1 h. It is considered fully charged at this time, SOC = 100%;
• Discharge 5% of the battery capacity at a rate of 1/3 C, and record the terminal voltage value at this moment after standing for 1 h;
• Repeat the previous step operation 20 times, that is, discharge the battery to SOC = 0.

The terminal voltage value at each SOC after standing for 1 h can be equivalent to the OCV value at each SOC. Perform polynomial fitting on the obtained SOC–OCV data to obtain the SOC–OCV curve relationship over the full SOC range. After comparing different fitting orders and considering the influence of over-fitting and under-fitting, it was finally decided to use a 6-order polynomial to fit the SOC–OCV data points obtained from the above experiment. U_oc represents the open-circuit voltage and Z represents the SOC, the 6-order polynomial fitting Equation is:

$$U_{\mathrm{oc}}=a_1{Z}^6+a_2{Z}^5+a_3{Z}^4+a_4{Z}^3+a_5{Z}^2+a_{6}Z+a_7$$

(2)

With the help of Matlab fitting toolbox, the 6-order polynomial fitting effect of discharge SOC–OCV can be obtained, as shown in Figure 2.

The fitted polynomial coefficients are shown in

Table 1. Curve fitting coefficient.

Parameter	a1	a2	a3	a4	a5	a6	a7
Value	−43.56	155.4	−215.7	146.6	−50.16	8.674	2.991

.

3. Model Parameter Online Identification

3.1. Forgetting Factor Recursive Least Squares

Before identifying the parameters of forgetting factor recursive least squares (FFRLS), the equivalent circuit model should be discretized into the basic form of the least-squares method. Convert Equation (1) into the expression of s-domain by Laplace transform:

$$U_{\mathrm{t}}(s)-U_{\mathrm{oc}}(s)=I(s)\left(R_0+\frac{R_1}{1+s{R}_1{C}_1}\right)$$

(3)

In the above formula, s is the Laplacian in the s domain.

The bilinear transformation formula is:

$$s=\frac{2}{T}\cdot \frac{1-z^{-1}}{1+z^{-1}}$$

(4)

In the formula, z is the corresponding operator in the discrete z domain. Bilinear transformation realizes the conversion between continuous-time system and discrete-time system.

Use Equation (4) to map Equation (3) from s domain to z domain to obtain the transfer function of the system in the z domain, and simplify it to obtain:

$$G\left(z^{-1}\right)=\frac{U_{\mathrm{t}}\left(z^{-1}\right)-U_{\mathrm{oc}}\left(z^{-1}\right)}{I\left(z^{-1}\right)}=\frac{{\theta }_{2,k}+{\theta }_{3,k}{z}^{-1}}{1-{\theta }_{1,k}{z}^{-1}}$$

(5)

In the above Equation, T is the sampling period; θ_1,k, θ_2,k, θ_3,k are the simplified representations of the time coefficients of k. The specific expression is:

$$\{\begin{array}{l}{\theta }_{1,k}=\frac{2\tau - T}{2\tau + T}\\ {\theta }_{2,k}=\frac{R_{0}T + R_{1}T + 2\tau R_0}{2\tau + T}\\ {\theta }_{3,k}=\frac{R_{0}T + R_{1}T - 2\tau R_0}{2\tau + T}\end{array}$$

(6)

In the Equation, τ = R₁C₁.

Discretization of Equation (5) can be obtained:

$$U_{\mathrm{t}}(k)-U_{\mathrm{oc}}\left(k\right)={\theta }_{1,k}(U_{\mathrm{t}}(k-1)-U_{\mathrm{oc}}(k-1))+{\theta }_{2,k}I(k)+{\theta }_{3,k}I(k-1)$$

(7)

The Equation (7) is further transformed:

$$U_{\mathrm{t}}(k)={\theta }_{1,k}{U}_{\mathrm{t}}(k-1)+U_{\mathrm{oc}}\left(k\right)-{\theta }_{1,k}{U}_{\mathrm{oc}}(k-1)+{\theta }_{2,k}I(k)+{\theta }_{3,k}I(k-1)$$

(8)

T is the sampling period, the value is 1. Hence, U_oc(k) is approximately equal to U_oc(k − 1). Let θ_4,k = U_oc(k) − θ_1,kU_oc(k − 1),ie θ_4,k = (1 − θ_1,k)U_oc(k − 1). The formula conforms to the basic form of the least squares method. The parameter vector of least squares is θ(k) = [θ_1,k,θ_2,k,θ_3,k,θ_4,k]^T, and the data vector is φ(k) = [U_t(k − 1),I(k),I(k − 1),1]. The parameter vector θ(k) can be identified in real time with the aid of the least squares recursive formula.

After identifying θ(k), the model parameters of the equivalent circuit can be obtained by Equation (6):

$$\{\begin{array}{l}{R}_0(k)=\frac{{\theta }_{2,k} - {\theta }_{3,k}}{1 + {\theta }_{1,k}}\\ R_1(k)=\frac{2({\theta }_{1,k} + {\theta }_{2,k} + {\theta }_{3,k})}{1 - {({\theta }_{1,k})}^2}\\ C_1(k)=\frac{1 + {({\theta }_{1,k})}^2}{4({\theta }_{1,k}{\theta }_{2,k} + {\theta }_{3,k})}\\ U_{\mathrm{oc}}(k-1)=\frac{{\theta }_{4,k}}{1 - {\theta }_{1,k}}\end{array}$$

(9)

The forgetting factor recursive least-squares introduces the forgetting factor λ to adjust the weight of new and old data. λ generally takes 0.95–1.00 [9]. Let the gain coefficient be K_e(k), the estimated parameter value is θ(k), and the covariance matrix is P_e(k). The forgetting factor least-squares recursive Equation is:

$$\{\begin{array}{l}{K}_e(k)=\frac{P_e(k - 1)\phi (k)}{\lambda + \phi {(k)}^{\mathrm{T}}{P}_e(k - 1)\phi (k)}\\ P_e(k)=\frac{1}{\lambda }\left[I(k) - K_e(k)\phi {(k)}^{\mathrm{T}}\right]P_e(k - 1)\\ \theta (k)=\theta (k - 1)+\\ K_e(k)\left[U_{\mathrm{t}}(k) - U_{\mathrm{oc}}(k - 1) - \theta {(k - 1)}^{\mathrm{T}}\phi (k)\right]\end{array}$$

(10)

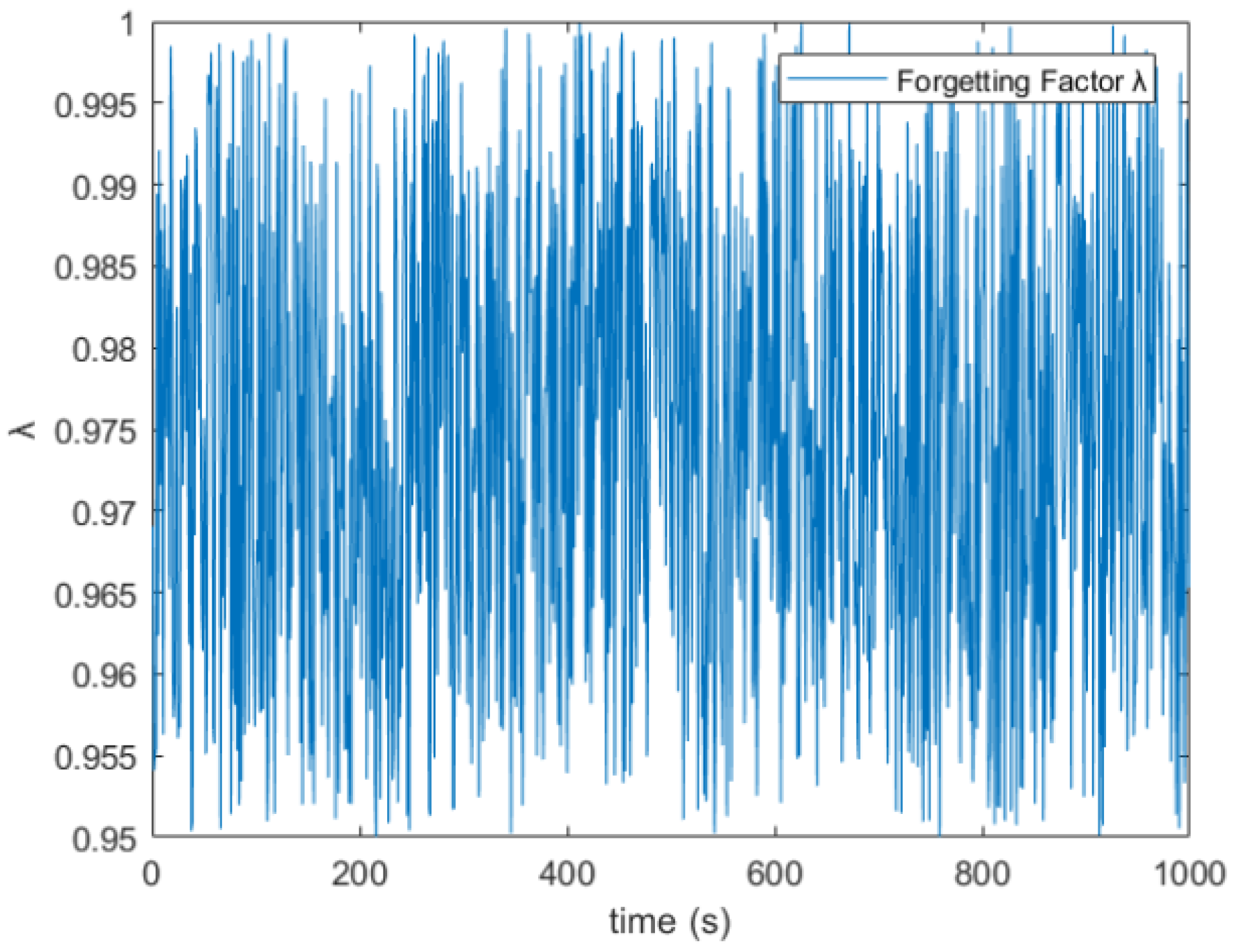
3.2. Simulated Annealing Algorithm Optimizes Forgetting Factor

The simulated annealing (SA) algorithm, as an evolutionary intelligent optimization algorithm, is widely used in the field of optimization. This paper introduces the SA algorithm on the forgetting factor recursive least square algorithm. With the minimum terminal voltage error as the optimization goal, within the optional range of the set forgetting factor, real-time adaptive dynamic optimization of the suitable forgetting factor, avoiding the problem of “data saturation” caused by poor forgetting factor selection, thereby improving the online parameter identification accuracy.

The objective function is:

J = |U_t(k) − φ(k)θ(k − 1)|

(11)

In the formula, U_t(k) is the measured value of the terminal voltage, φ(k)θ(k − 1) is the terminal voltage value estimated by the recursive least square method, and the objective function is the absolute value of the terminal voltage error.

Taking the forgetting factor λ as the optimization variable, iterative optimization is carried out with the goal of minimizing J, and then the optimal estimation of the parameters is made.

The adaptive changes of partial forgetting factors optimized by simulated annealing are shown in Figure 3.

It can be seen from Figure 3 that as the experiment progresses, the forgetting factor will adaptively change with the model demand, while the traditional fixed forgetting factor cannot achieve the effect of adaptive change; that is, it cannot adapt to the demand of the model change in real-time.

4. Joint Estimation of Battery SOC

4.1. Principle of Battery SOC Estimation Based on UKF

The battery model system is nonlinear, and it is impossible to directly use the Kalman filter to provide the filtering method under linear and Gaussian conditions. Therefore, some scholars have proposed the extended Kalman filter method [18], but this method only applies the first-order Taylor formula to the system Expansion ignores high-order terms and inevitably introduces large linearization errors. Unscented Kalman filter abandons the traditional method of linearizing nonlinear functions, adopts the Kalman filter framework, and uses unscented transformation for one-step prediction equations to deal with the transfer of mean and covariance [19,20,21].

The UKF algorithm approximates the probability density distribution of a nonlinear function, and uses a series of samples to approximate the posterior probability density of the state, without ignoring high-order terms, and has high calculation accuracy. The process of estimating battery SOC based on the unscented Kalman filter based on the Thevenin equivalent circuit model is as follows:

• Suppose the system state equation discretized from Section 3.1 is:

  $$\{\begin{array}{l}{x}_{k+1}=f\left(x_k,u_k\right)+{\omega }_k\\ h_k=g\left(x_k,u_k\right)+{\nu }_k\end{array}$$

  (12)

In the formula, Subscript k represents discrete moment k. x is the system state variable, x = [SOC, U₁]. u is the system input, u = I. h is the system output, h = U_t. ω is the state noise, and its covariance matrix is Q. ν is the noise, its covariance matrix is R.

SOC expression:

$${SOC}_{k+1}={SOC}_k+I_k/Q_c$$

(13)

In the formula, Q_c is the battery capacity.

Then the specific expression of the discretized system state Equation is:

$$\{\begin{array}{l}\left[\begin{array}{c}{U}_{1,k+1}\\ {SOC}_{k+1}\end{array}\right]=\left[\begin{array}{c}\exp \left(-1/\left(R_{1,k}{C}_{1,k}\right)\right)U_{1,k}+R_{1,k}\left(1-\exp \left(-1/\left(R_{1,k}{C}_{1,k}\right)\right)\right)I_k\\ {SOC}_k+I_k/Q_c\end{array}\right]+{\omega }_k\hfill \\ U_{t,k}=U_{1,k}+R_{0,k}{I}_k+U_{\mathrm{oc}}\left({SOC}_k\right)+v_k\hfill \end{array}$$

(14)

2.

Initialization of state variables $\widehat{x}$ and covariance P:

$$\{\begin{array}{l}\widehat{x}=E[x]\\ P=E[(x-\widehat{x}){(x-\widehat{x})}^{\mathrm{T}}]\end{array}$$

(15)

Obtain 2n + 1 Sigma points by unscented transformation:

$$\{\begin{array}{l}{x}_0=\widehat{x},i=0\hfill \\ x_i=\widehat{x}+{(\sqrt{(n+\lambda )P})}_i,i=1\sim n\hfill \\ x_i=\widehat{x}-{(\sqrt{(n+\lambda )P})}_{i-n},i=n+1\sim 2n\hfill \end{array}$$

(16)

In the Equation, n is the dimension of the state vector, n = 2, λ = 3 − n.

Calculate the corresponding weights of the sampling points:

$$\{\begin{array}{l}{\omega }_0^m=\frac{\lambda }{(n + \lambda )}\hfill \\ {\omega }_0^m=\frac{\lambda }{(n + \lambda )}+\left(1-{\alpha }^2+\beta \right)\hfill \\ {\omega }_i^c={\omega }_i^m=\frac{\lambda }{2(n + \lambda )},i=1\sim 2n\hfill \end{array}$$

(17)

In the Equation, α is the factor of controlling the distribution state of sampling points, and the value is 1; β is the non-negative weight coefficient, and the value is 2; ω^m_i is the mean weight of the i-th sampling point, and ω^c_i is the i-th sampling point The weight of the covariance.

3.

Update state one-step predicted value and covariance:

$$\{\begin{array}{l}{x}_{i,k\mid k-1}=f\left(x_{i,k-1},i_{k-1}\right)\hfill \\ x_{k\mid k-1}={\displaystyle \sum _{i=0}^{2n}}{\omega }_i^m{x}_{i,k\mid k-1}\hfill \\ {\mathit{P}}_{k\mid k-1}={\displaystyle \sum _{i=0}^{2n}}{\omega }_i^c\left(x_{i,k-1}-x_{k\mid k-1}\right){\left(x_{i,k-1}-x_{k\mid k-1}\right)}^{\mathrm{T}}+Q\hfill \end{array}$$

(18)

4.

Observation and Sigma point set observations mean prediction:

$$\{\begin{array}{l}{h}_{i,k\mid k-1}=g\left(x_{i,k\mid k-1},i_{k-1}\right)\hfill \\ h_{k\mid k-1}={\displaystyle \sum _{i=0}^{2n}{\omega }_i^m{y}_{i,k\mid k-1}}\hfill \end{array}$$

(19)

5.

Observation covariance update:

$$\{\begin{array}{c}{\mathit{P}}_{hh,k}={\displaystyle {\displaystyle \sum }_{i=0}^{2n}}{\omega }_i^c\left(h_{i,k\mid k-1}-h_{k\mid k-1}\right){\left(h_{i,k\mid k-1}-h_{k\mid k-1}\right)}^{\mathrm{T}}+\mathit{R}\\ {\mathit{P}}_{xh,k}={\displaystyle {\displaystyle \sum }_{i=0}^{2n}}{\omega }_i^c\left(x_{i,k\mid k-1}-x_{k\mid k-1}\right){\left(h_{i,k\mid k-1}-h_{k\mid k-1}\right)}^{\mathrm{T}}\end{array}$$

(20)

In the formula, P_hh is the covariance of the system predictive quantity, and P_xh is the covariance of the state quantity and the predictive quantity.

6.

Calculate Kalman gain:

$${\mathit{K}}_{k+1}={\mathit{P}}_{xh,k}{\mathit{P}}_{hh,k}^{-1}$$

(21)

7.

State matrix and covariance measurement update:

$$\{\begin{array}{r}\hfill x_{k+1\mid k+1}=x_{k+1|k+1}+K_{k+1}\left(h_{k+1}-h_{k+1|k}\right)\\ \hfill {\mathit{P}}_{x,k+1\mid k+1}={\mathit{P}}_{x,k+1\mid k}-K_{k+1}{\mathit{P}}_{xy,k+1}{K}_{k+1}^{\mathrm{T}}\end{array}$$

(22)

4.2. SA-FFRLS Combined with UKF to Estimate SOC

The forgetting factor is introduced in the least-squares method, and its purpose is to assign a certain weight to the historical data application, which can effectively improve the “data saturation” problem of slow time-varying systems such as equivalent circuit model parameters. However, a fixed forgetting factor cannot meet the requirements of dynamic allocation of historical data weights for different batteries and different environments.

In this paper, the simulated annealing algorithm is used to adaptively screen the appropriate forgetting factor in real-time to meet the dynamic requirements of the forgetting factor under the influence of different batteries and different use environments. The unscented Kalman filter algorithm can be combined to achieve an accurate estimation of model parameters and battery SOC. The technical route of joint estimation is shown in Figure 4.

5. Algorithm Verification

5.1. Introduction to Test and Simulation

The technical parameters of the lithium iron phosphate battery selected in this paper are: rated capacity 27 A·h, rated cell voltage 3.7 V, charge cut-off voltage 4.2 V, discharge cut-off voltage 2.75 V, charge and discharge efficiency η = 0.95, T = 1 s.

Refer to the electric vehicle battery test manual to perform the dynamic stress test (DST) on the battery. The cycle of DST working condition is 360 s, and 70 DST cycles are set to discharge the battery capacity from 100% to about 10%. Figure 5 shows the current and voltage data of 1 DST cycle in the actual test.

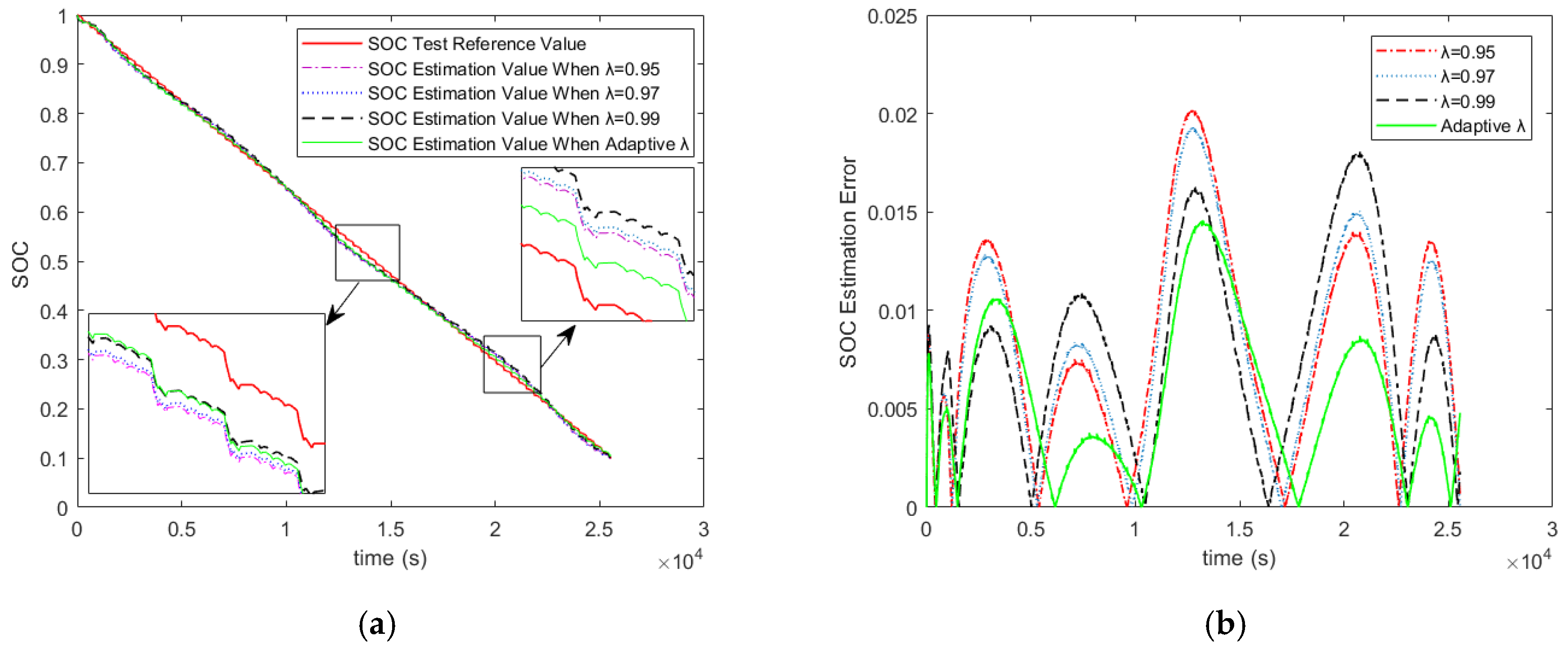
5.2. Comparison of Simulation Results

M language programming based on MATLAB realizes the simulation of the proposed online identification and SOC estimation algorithm. The DST test data is simultaneously subjected to adaptive forgetting factor least square identification and ordinary forgetting factor least square identification, and the adaptive range of forgetting factor λ is set to 0.95–1.00. For ordinary FFRLS, choose the forgetting factor to be 0.95, 0.97, and 0.99, respectively, for comparison. The comparison of the absolute value of the voltage error at the online identification terminal is shown in Figure 6.

It can be seen from Figure 6 that the terminal voltage error of each algorithm is very small, and the terminal voltage follows better. But overall, the terminal voltage error corresponding to the adaptive forgetting factor λ is smaller than those of λ = 0.95, λ = 0.97, and λ = 0.99. The maximum error of the dynamic λ terminal voltage is 9.46 mV and the average terminal voltage error is 0.156 mV; the maximum error of the terminal voltage of λ = 0.95 is 20.4 mV, and the average terminal voltage error is 0.477 mV; the maximum error of the terminal voltage of λ = 0.97 is 16.2 mV, The average terminal voltage error is 0.303 mV; the maximum error of the terminal voltage with λ = 0.99 is 13.6 mV, and the average terminal voltage error is 0.178 mV.

From the comparison of the terminal voltage error, the terminal voltage error of the adaptive forgetting factor λ is always at a very low level, and when a fixed λ is selected, the difference in the terminal voltage error is relatively large. Therefore, for different batteries or test conditions, choosing a suitable λ will have a greater impact on the terminal voltage simulation results, while the dynamic λ will adaptively maintain a low error level.

The above-mentioned online identification algorithm of different forgetting factors is combined with the unscented Kalman filter to estimate the battery SOC value. The estimation result and error comparison are shown in Figure 7.

It can be seen from Figure 7 that the overall estimation error level of the battery SOC using the adaptive forgetting factor λ is the lowest. The estimation errors of the three in the early stage of the working condition are very close, but after 5 000 s, the algorithm using the adaptive forgetting factor λ is obviously better than the other fixed forgetting factor algorithms. As the experiment progresses, it can effectively eliminate long-term accumulated errors and keep the estimated errors at a low level. The maximum absolute error of battery SOC estimation with λ = 0.95 is 2.02%, and the average absolute error is 0.84%; the maximum absolute error of battery SOC estimation with λ = 0.97 is 1.93%, and the average absolute error is 0.81%; the battery with λ = 0.99 is used The maximum absolute error of SOC estimation is 1.81%, and the average absolute error is 0.79%; the maximum absolute error of battery SOC estimation using adaptive forgetting factor λ is 1.45%, and the average absolute error is 0.56%.

Compared with similar studies done in documents [7,8], etc., the estimation algorithm proposed in this paper can not only achieve a smaller overall estimation error, but also control the estimation results not to diverge more with the accumulation of errors over time. That is to say, the ability to correct errors is stronger, which benefits from the combination of the online identification method of the adaptive forgetting factor and the unscented Kalman filter estimation.

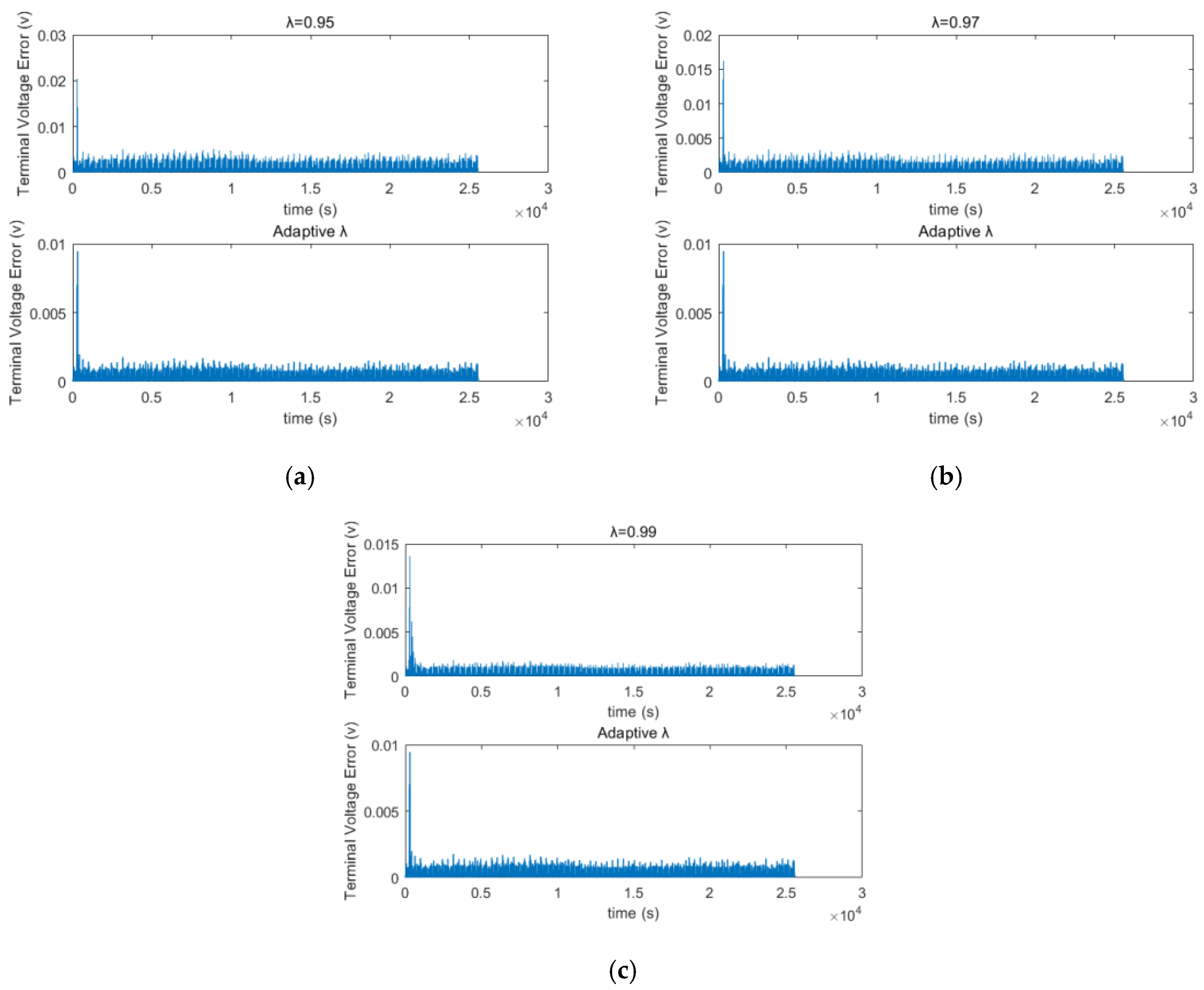
5.3. Algorithm Robustness Verification

In the actual power battery SOC estimation, it is often difficult to obtain an accurate initial SOC value, and a wrong initial SOC value may cause a large SOC estimation error. In order to verify the robustness of the algorithm proposed in this paper, when the true initial value of SOC is 1, the initial value of SOC is deliberately set to error values of 0.5, 0.7, and 0.9 to observe the ability of the algorithm to converge to the true value. The convergence of the algorithm is shown in Figure 8.

It can be seen from Figure 8 that even if the initial value of SOC has an error of 50%, the algorithm can still converge the estimated SOC value to near the true value in a short time, and the algorithm has better robustness.

6. Conclusions

This paper builds the Thevenin equivalent circuit model based on a certain ternary lithium battery and uses the simulated annealing optimization algorithm to adaptively update the forgetting factor. The research results show that, compared with the traditional fixed forgetting factor algorithm, the terminal voltage error of the adaptive forgetting factor recursive least square algorithm identification is lower; that is, the model identification accuracy is high. The accuracy of estimating the battery SOC combined with the unscented Kalman filter is also higher than that of the fixed forgetting factor.

Compared with the traditional fixed forgetting factor least-square algorithm, the adaptive forgetting factor recursive least squares and unscented Kalman filtering algorithm proposed in this paper can jointly estimate the battery SOC, which can realize real-time self-selection of the best forgetting factor, so as to satisfy dynamic requirements for forgetting factors under different batteries or different use environments.