A Surrogate Model-Based Hybrid Approach for Stochastic Robust Double Row Layout Problem
Abstract
1. Introduction
2. Related Literature
3. Problem Description
4. Proposed Approach
4.1. Local Search Algorithm
4.1.1. Encoding and Decoding
4.1.2. Local Search Algorithm
| Algorithm 1. The pseudo-code of local search algorithm. |
| Input: The maximum number of iterations, MaxIter; the number of machines, m; the maximum value of breakpoint, maxB; the maximum value of the offset, maxO. |
| Begin: Randomly initialize a solution y = (π, m/2, 0); Evaluate the solution y by Equation (1), obtaining f(y); Let miny = y; For b = to maxB do o = 0; While o <=maxO do Let the breakpoint and the extra clearance of the leftmost machine on row 1 in y be b and o, respectively; For iter = 0 to MaxIter do = Inversion (y);//inversion operation (Algorithm 2) = 2-Top_FI();//2-top local search (Algorithm 3) If f(y) > f() then y = ; End End If f(miny) > f(y)then miny = y; End o = o + 0.5; End End Return miny. |
4.1.3. The Inversion Operation
| Algorithm 2. Inversion operation, Inversion (y). |
| Input: A solution y = (π, b, o); the number of machines, m. Begin: Generate uniformly distributed random integers i and num in [1, m] and , respectively; If m< 20 then num is set as a random integer in [3, 4]; End j = i + num − 1; If j >m then j = j − m; End For k = 1 to num/2 do Swap the two machines at positions i and j of π; i = i + 1; if i > m then i = 1; End j = j − 1; If j < 1 then j = m; End End Return y = (π, b, o). |
4.1.4. The 2-Top Local Search with the First Improvement Search Strategy
| Algorithm 3. The 2-top local search with the first improvement search strategy, 2-Top_FI (y). |
| Input: A solution y = (π, b, o), and the number of machines, m. Begin: Repeat Let N(y) = ;//The neighbourhood of solution y. For i = 1 to m−1 then For j = i + 1 to m then Swap the machines at positions i and j of π to produce a new machine sequence and a new solution , and add into N(y); End End Randomly shuffle the order of the solutions in N(y); = y; For each in N(y) do If f(y) > f() then y = ; break; End End Until f(y) >= f(); Return y. |
4.2. Exact Approach
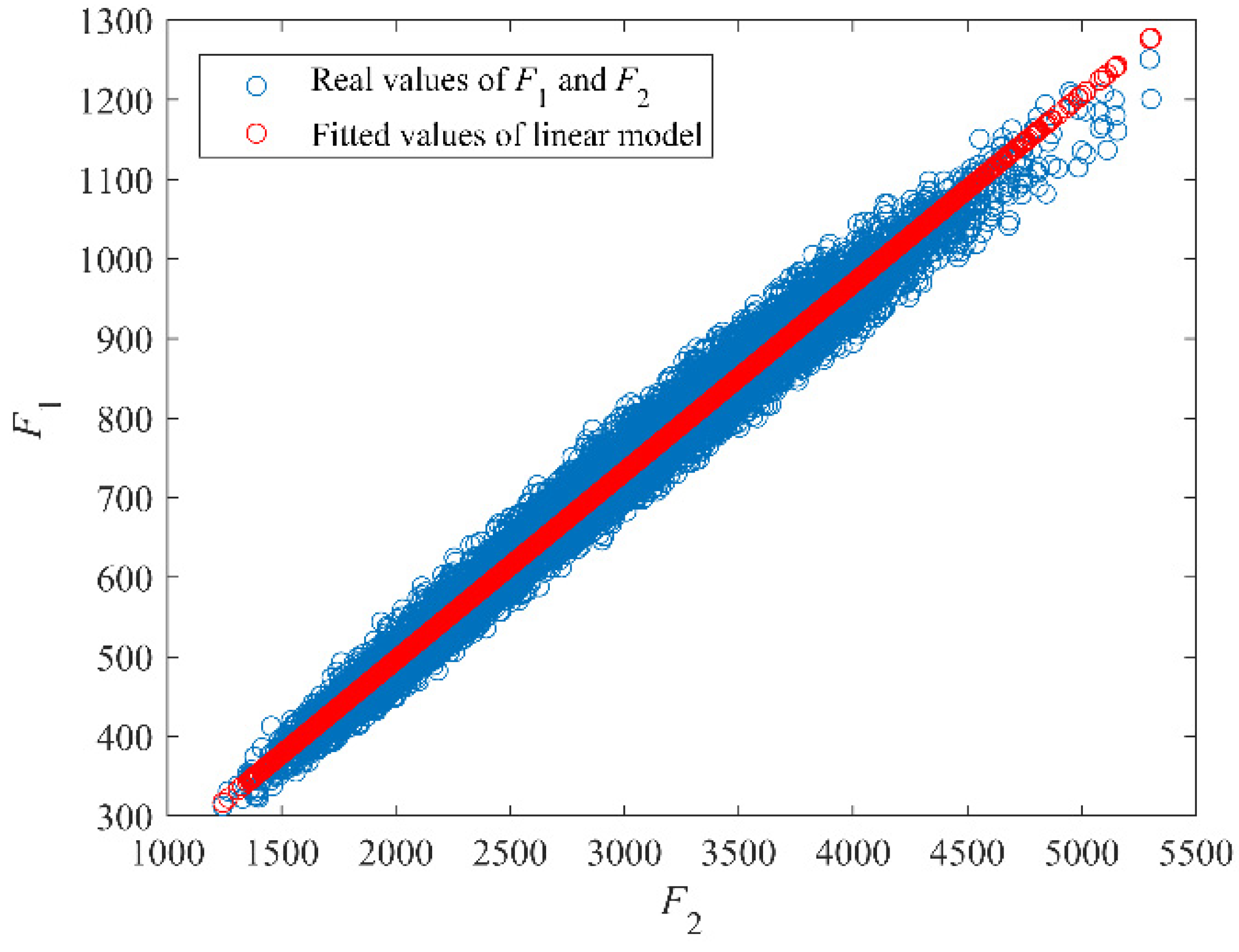
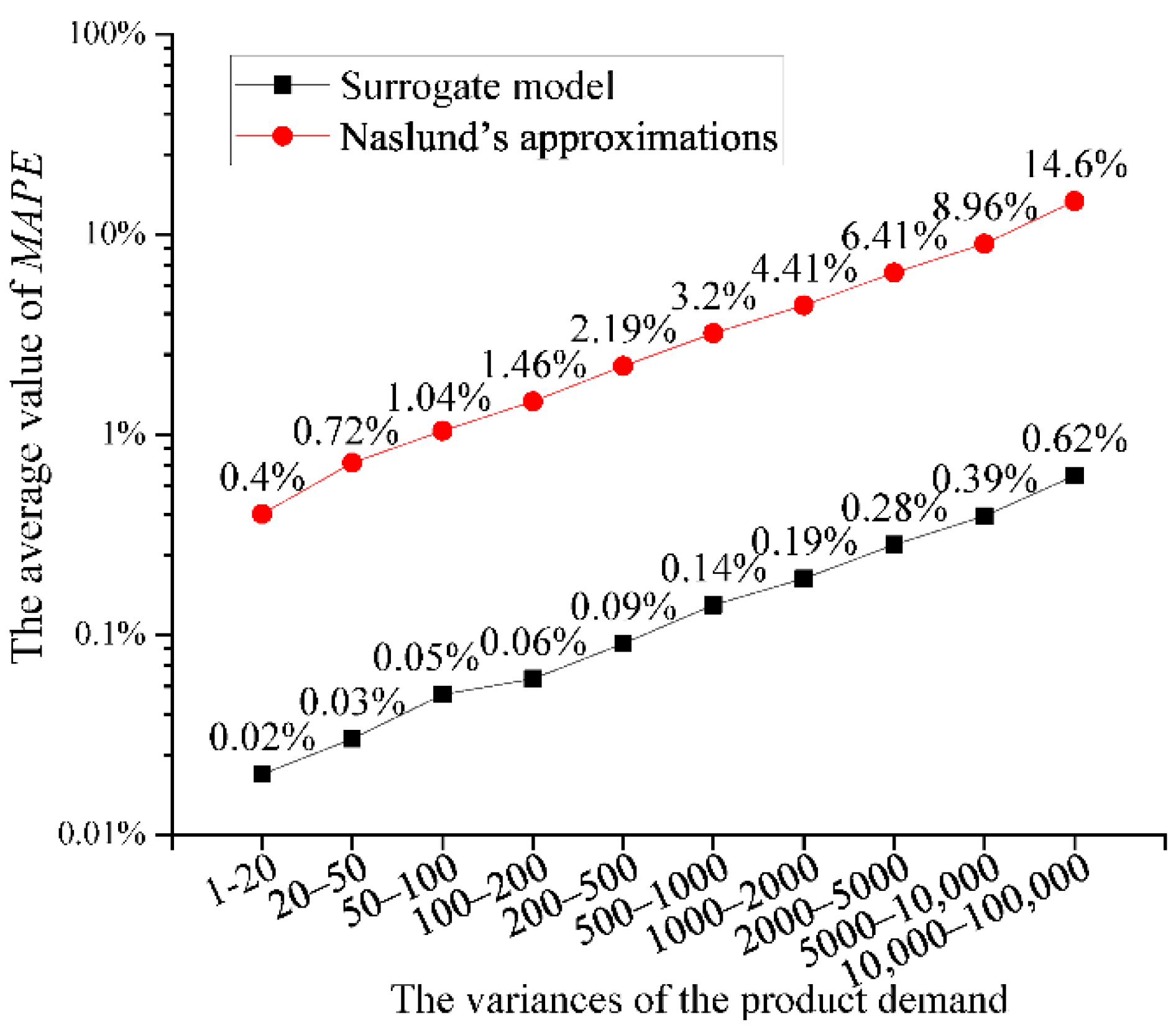
4.2.1. Surrogate Model
4.2.2. Optimize the Exact Location of Each Machine by Exact Approach
| Algorithm 4. Optimize the exact location of each machine by exact approach. |
| Input: A solution y = (π, b, o). Begin: Utilizing π and b of y to fix the binary variables in the model in Section 3, a linear programming model (LP1) is obtained, where objective function Equation (1) is replaced with the linear formula in Equation (17); LP1 is solve by CPLEX and a solution, = (π, b, ), is produced; Equation (1) is used to calculate the material handling cost of , f(); If f() < f(y) then y = ; End Return y. |
5. Experimental Results
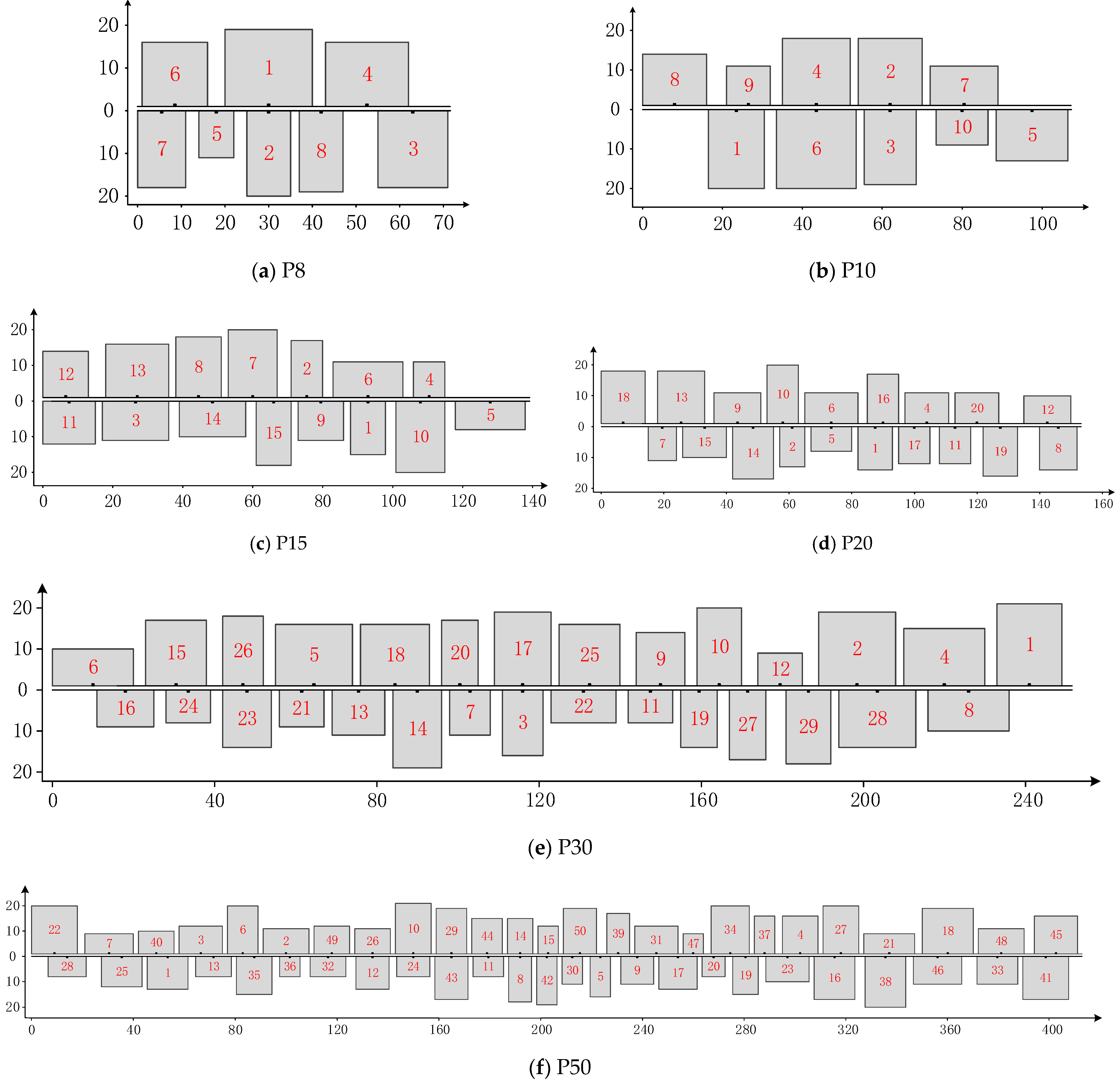
5.1. Problem Instances
5.2. Algorithm Parameters and Comparative Approaches
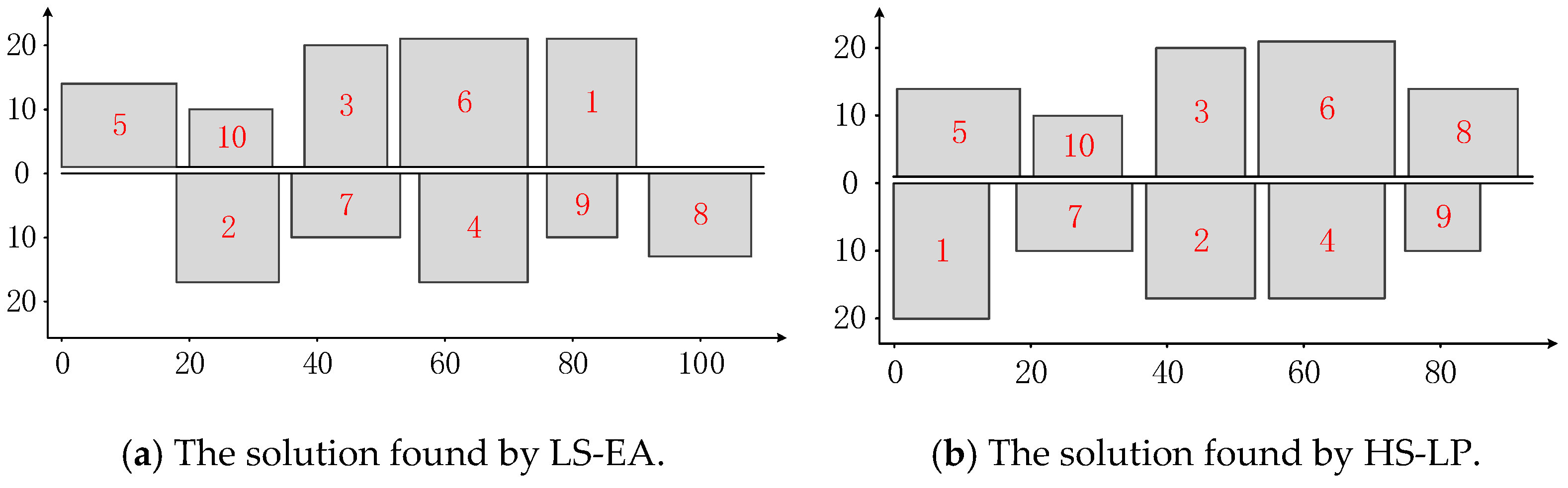
5.3. Experimental Results and Analysis
5.4. Statistical Significance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Palubeckis, G. An approach integrating simulated annealing and variable neighborhood search for the bidirectional loop layout problem. Mathematics 2021, 9, 5. [Google Scholar] [CrossRef]
- Akturk, M.; Gultekin, H.; Karasan, O.E. Robotic cell scheduling with operational flexibility. Discret. Appl. Math. 2005, 145, 334–348. [Google Scholar] [CrossRef][Green Version]
- Anjos, M.F.; Vieira, M.V.C. Mathematical optimization approach for facility layout on several rows. Optim. Lett. 2021, 15, 9–23. [Google Scholar] [CrossRef]
- Zuo, X.; Murray, C.C.; Smith, A.E. Solving an extended double row layout problem using multiobjective tabu search and linear programming. IEEE Trans. Autom. Sci. Eng. 2014, 11, 1122–1132. [Google Scholar] [CrossRef]
- Chung, J.; Tanchoco, J. The double row layout problem. Int. J. Prod. Res. 2010, 48, 709–727. [Google Scholar] [CrossRef]
- Wang, S.; Zuo, X.; Liu, X.; Zhao, X.; Li, J. Solving dynamic double row layout problem via combining simulated annealing and mathematical programming. Appl. Soft Comput. 2015, 37, 303–310. [Google Scholar] [CrossRef]
- Tang, L.; Zuo, X.; Wang, C.; Zhao, X. A MOEA/D based approach for solving robust double row layout problem. In IEEE Congress on Evolutionary Computation (CEC); IEEE: Sendai, Japan, 2015; pp. 1966–1973. [Google Scholar]
- Asl, A.D.; Wong, K.Y.; Tiwari, M.K. Unequal-area stochastic facility layout problems: Solutions using improved covariance matrix adaptation evolution strategy, particle swarm optimisation, and genetic algorithm. Int. J. Prod. Res. 2016, 54, 799–823. [Google Scholar]
- Tayal, A.; Gunasekaran, A.; Singh, S.P.; Dubey, R.; Papadopoulos, T. Formulating and solving sustainable stochastic dynamic facility layout problem: A key to sustainable operations. Ann. Oper. Res. 2017, 253, 621–655. [Google Scholar] [CrossRef]
- Kim, M.; Chae, J. Monarch butterfly optimization for facility layout design based on a single loop material handling path. Mathematics 2019, 7, 154. [Google Scholar] [CrossRef]
- Drira, A.; Pierreval, H.; Hajri-Gabouj, S. Facility layout problems: A survey. Annu. Rev. Control. 2007, 31, 255–267. [Google Scholar] [CrossRef]
- Hosseini-Nasab, H.; Fereidouni, S.; Fatemi Ghomi, S.M.T.; Fakhrzad, M.B. Classification of facility layout problems: A review study. Int. J. Adv. Manuf. Technol. 2018, 94, 957–977. [Google Scholar] [CrossRef]
- Zhang, Z.; Murray, C.C. A corrected formulation for the double row layout problem. Int. J. Prod. Res. 2012, 50, 4220–4223. [Google Scholar] [CrossRef]
- Amaral, A.R.S. Optimal solutions for the double row layout problem. Optim. Lett. 2013, 7, 407–413. [Google Scholar] [CrossRef]
- Secchin, L.D.; Amaral, A.R.S. An improved mixed-integer programming model for the double row layout of facilities. Optim. Lett. 2019, 13, 193–199. [Google Scholar] [CrossRef]
- Chae, J.; Regan, A.C. A mixed integer programming model for a double row layout problem. Comput. Ind. Eng. 2020, 140, 106244. [Google Scholar] [CrossRef]
- Amaral, A.R.S. A mixed-integer programming formulation for the double row layout of machines in manufacturing systems. Int. J. Prod. Res. 2019, 57, 34–47. [Google Scholar] [CrossRef]
- Dahlbeck, M.; Fischer, A.; Fischer, F. Decorous combinatorial lower bounds for row layout problems. Eur. J. Oper. Res. 2020, 286, 929–944. [Google Scholar] [CrossRef]
- Amaral, A.R.S. A mixed-integer programming formulation of the double row layout problem based on a linear extension of a partial order. Optim. Lett. 2021, 15, 1407–1423. [Google Scholar] [CrossRef]
- Güļsen, M.; Murray, C.C.; Smith, A.E. Double-row facility layout with replicate machines and split flows. Comput. Oper. Res. 2019, 108, 20–32. [Google Scholar] [CrossRef]
- Guan, J.; Lin, G.; Feng, H.B.; Ruan, Z.Q. A decomposition-based algorithm for the double row layout problem. Appl. Math. Model. 2020, 77, 963–979. [Google Scholar] [CrossRef]
- Murray, C.C.; Smith, A.E.; Zhang, Z. An efficient local search heuristic for the double row layout problem with asymmetric material flow. Int. J. Prod. Res. 2013, 51, 6129–6139. [Google Scholar] [CrossRef]
- Amaral, A.R.S. A heuristic approach for the double row layout problem. Ann. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Amaral, A.R.S. A parallel ordering problem in facilities layout. Comput. Oper. Res. 2013, 40, 2930–2939. [Google Scholar] [CrossRef]
- Yang, X.; Cheng, W.; Smith, A.E.; Amaral, A.R.S. An improved model for the parallel row ordering problem. J. Oper. Res. Soc. 2020, 71, 475–490. [Google Scholar] [CrossRef]
- Gong, J.; Zhang, Z.; Liu, J.; Guan, C.; Liu, S. Hybrid algorithm of harmony search for dynamic parallel row ordering problem. J. Manuf. Syst. 2021, 58, 159–175. [Google Scholar] [CrossRef]
- Amaral, A.R.S. The corridor allocation problem. Comput. Oper. Res. 2012, 39, 3325–3330. [Google Scholar] [CrossRef]
- Ahonen, H.; de Alvarenga, A.; Amaral, A.R.S. Simulated annealing and tabu search approaches for the Corridor Allocation Problem. Eur. J. Oper. Res. 2014, 232, 221–233. [Google Scholar] [CrossRef]
- Kalita, Z.; Datta, D. Solving the bi-objective corridor allocation problem using a permutation-based genetic algorithm. Comput. Oper. Res. 2014, 52, 123–134. [Google Scholar]
- Kalita, Z.; Datta, D.; Palubeckis, G. Bi-objective corridor allocation problem using a permutation-based genetic algorithm hybridized with a local search technique. Soft Comput. 2019, 23, 961–986. [Google Scholar] [CrossRef]
- Zhang, Z.; Mao, L.; Guan, C.; Zhu, L.; Wang, Y. An improved scatter search algorithm for the corridor allocation problem considering corridor width. Soft Comput. 2020, 24, 461–481. [Google Scholar] [CrossRef]
- Fischer, A.; Fischer, F.; Hungerländer, P. A new exact approach to the space-free double row layout problem. In Operations Research Proceedings 2015; Springer International Publishing: Cham, Denmark, 2017; pp. 125–130. [Google Scholar]
- Palubeckis, G. Fast local search for single row facility layout. Eur. J. Oper. Res. 2015, 246, 800–814. [Google Scholar] [CrossRef]
- Allahyari, M.Z.; Azab, A. Mathematical modeling and multi-start search simulated annealing for unequal-area facility layout problem. Expert Syst. Appl. 2018, 91, 46–62. [Google Scholar] [CrossRef]
- Bozorgi, N.; Abedzadeh, M.; Zeinali, M. Tabu search heuristic for efficiency of dynamic facility layout problem. Int. J. Adv. Manuf. Technol. 2015, 77, 689–703. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Javadian, N.; Javadi, B.; Safaei, N. Design of a facility layout problem in cellular manufacturing systems with stochastic demands. Appl. Math. Comput. 2007, 184, 721–728. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Lin, K.P. Short-term traffic flow forecasting based on data-driven model. Mathematics 2020, 8, 152. [Google Scholar] [CrossRef]
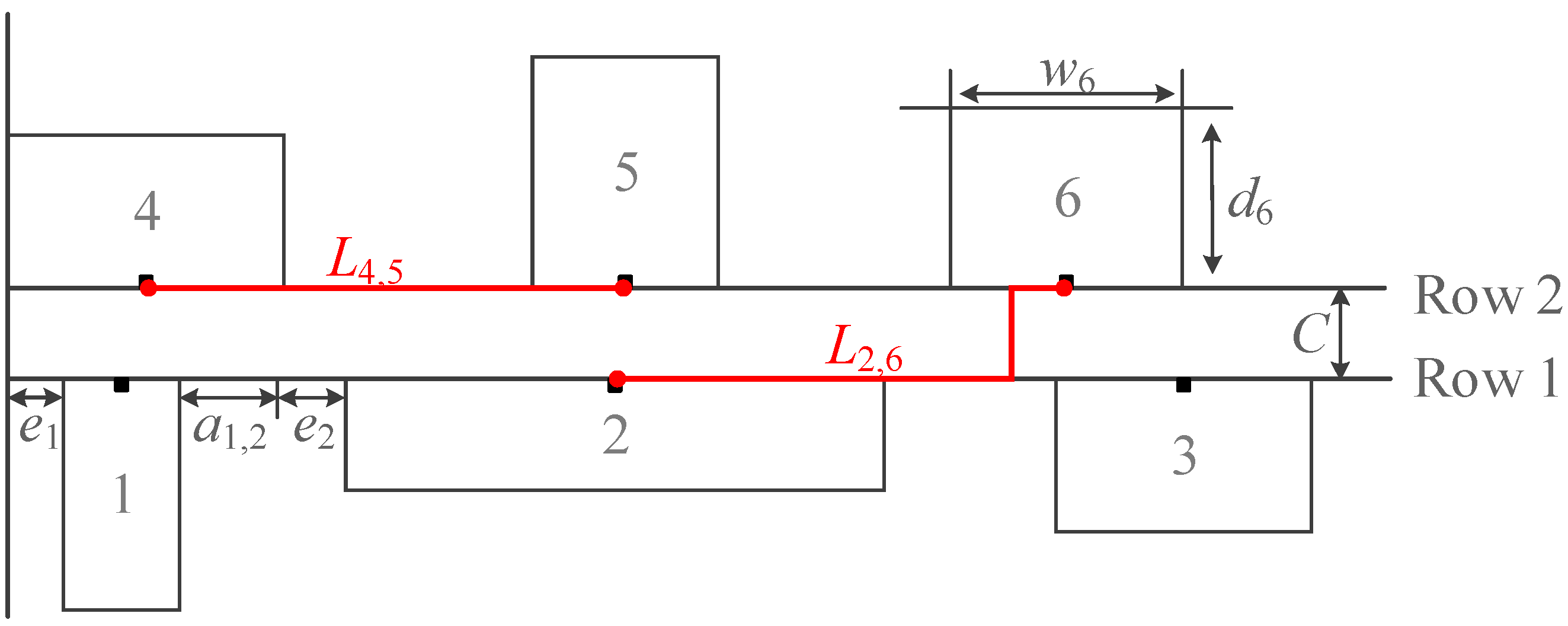
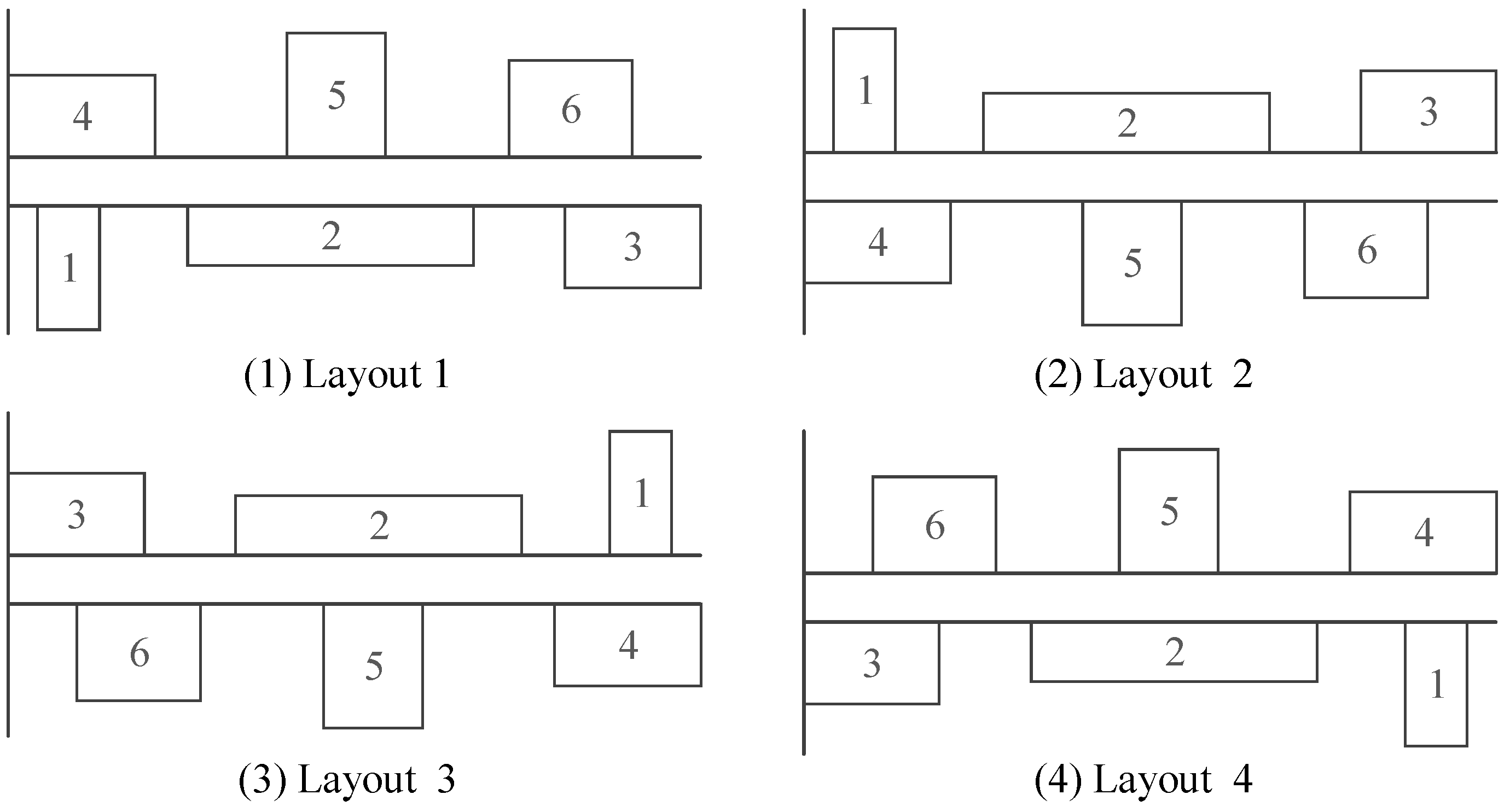
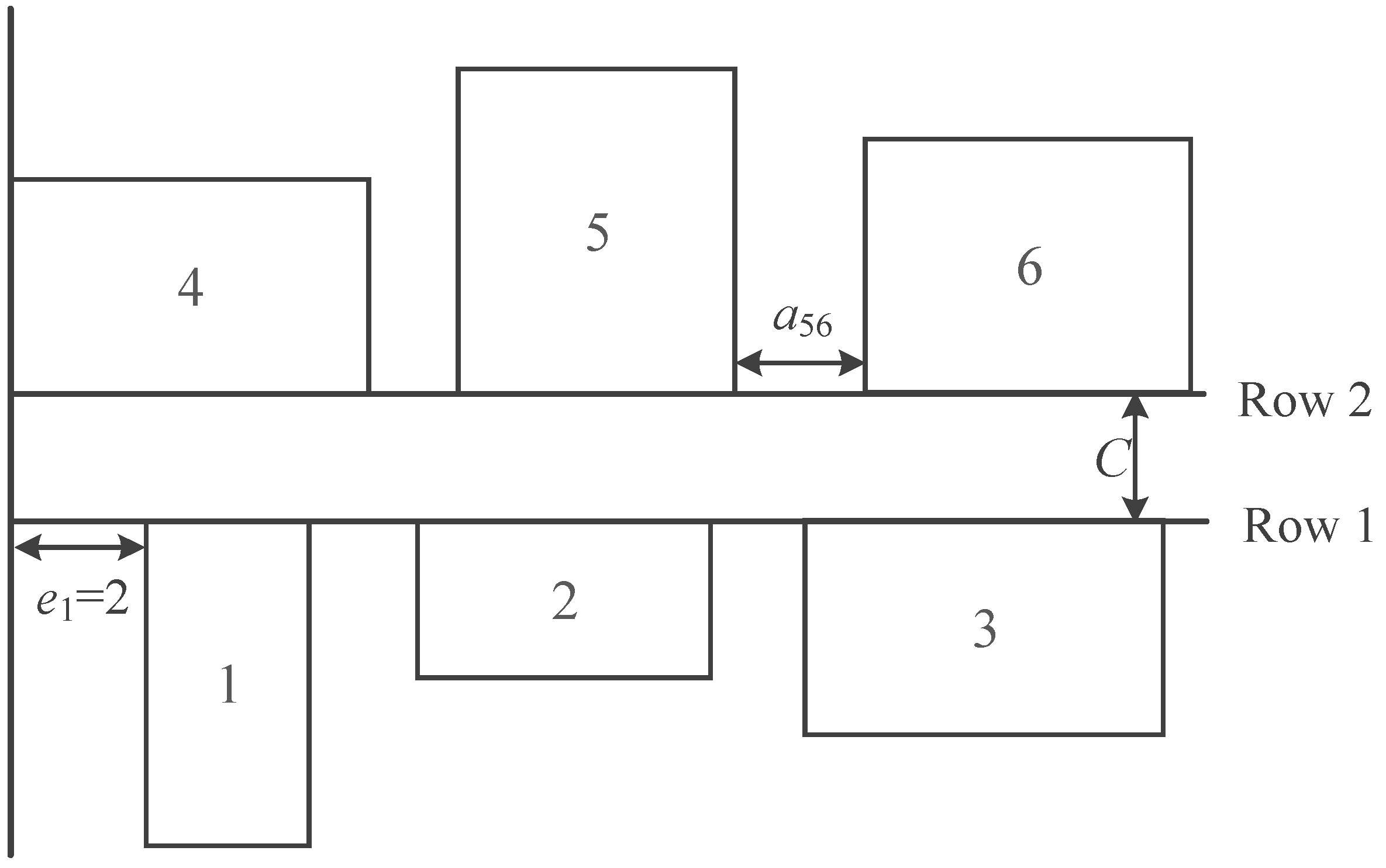
| Decision Variables | Variable Descriptions |
|---|---|
| xi | Continuous decision variable denotes the abscissa of machine . |
| Auxiliary continuous decision variables are utilized to determine the distance between machines and . | |
| qir | Binary variable, such that qir = 1 if machines is placed on the row r, otherwise qir = 0. |
| sij | Binary variable, such that sij = 1 if both machines and are placed on the same row, otherwise sij = 0. |
| zijr | Binary variable, such that zijr = 1 if both machines and are placed on the same row and i is placed to the left of j, otherwise zijr = 0. |
| Problem Instances | E(Dcp) | Var(Dcp) | m | t | l |
|---|---|---|---|---|---|
| P8 | (30–60) | (1–20) | 8 | 4 | 6 |
| P10 | (50–80) | (50–100) | 10 | 5 | 7 |
| P15 | (60–100) | (100–1000) | 15 | 6 | 9 |
| P20 | (100–200) | (500–1000) | 20 | 8 | 12 |
| P30 | (200–500) | (1000–5000) | 30 | 12 | 20 |
| P50 | (500–1000) | (5000–10,000) | 50 | 15 | 30 |
| Problem Instances | P8 | P10 | P15 | P20 | P30 | P50 | |
|---|---|---|---|---|---|---|---|
| HS-LP | Min cost | 6.824 × 104 | 1.608 × 105 | 9.817 × 105 | 5.167 × 106 | 7.790 × 107 | 7.188 × 108 |
| Aver cost | 6.824 × 104 | 1.608 × 105 | 9.913 × 105 | 5.239 × 106 | 7.888 × 107 | 7.299 × 108 | |
| Time (s) | 0.55 | 1.33 | 5.02 | 15.42 | 79.74 | 519.58 | |
| LS-EA | Min cost | 6.824 × 104 | 1.558 × 105 | 9.817 × 105 | 5.164 × 106 | 7.747 × 107 | 7.096 × 108 |
| Aver cost | 6.824 × 104 | 1.593 × 105 | 9.851 × 105 | 5.208 × 106 | 7.864 × 107 | 7.256 × 108 | |
| Time (s) | 0.52 | 1.15 | 4.98 | 15.17 | 76.75 | 495.58 | |
| EM | Cost | 6.824 × 104 | 1.483 × 105 | 9.878 × 105 | 5.668 × 106 | 9.144 × 107 | 9.578 × 108 |
| Time (s) | 0.63 | 3.28 | 3600.00 | 3600.00 | 3600.00 | 3600.00 | |
| Optimality gap (%) | 0.00 | 0.00 | 50.67 | 78.05 | 91.25 | 98.34 | |
| Problem Instance | LS-EA | HS-LP | EM | |||||
|---|---|---|---|---|---|---|---|---|
| Min Cost | Aver Cost | Time (s) | Min Cost | Aver Cost | Time (s) | Cost | Time (s) | |
| P10 | 1.483 × 105 | 1.483 × 105 | 6.88 | 1.608 × 105 | 1.608 × 105 | 7.13 | 1.483 × 105 | 3.28 |
| Problem Instances | P8 | P10 | P15 | P20 | P30 | P50 |
|---|---|---|---|---|---|---|
| Max reduction | 0.69% | 6.18% | 0.19% | 0.42% | 0.55% | 0.14% |
| Aver reduction | 0.29% | 2.07% | 0.05% | 0.12% | 0.11% | 0.04% |
| Time (s) | 0.004 | 0.004 | 0.013 | 0.030 | 0.159 | 0.837 |
| LS-EA versus HS-LP | Sign Test (p-Value) | Wilcoxon Signed Ranks Test (p-Value) | ||
|---|---|---|---|---|
| Wins | Equals | Loses | ||
| 56 | 39 | 25 | 0.008 | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Zuo, X.-Q.; Zhao, X.-C. A Surrogate Model-Based Hybrid Approach for Stochastic Robust Double Row Layout Problem. Mathematics 2021, 9, 1711. https://doi.org/10.3390/math9151711
Wan X, Zuo X-Q, Zhao X-C. A Surrogate Model-Based Hybrid Approach for Stochastic Robust Double Row Layout Problem. Mathematics. 2021; 9(15):1711. https://doi.org/10.3390/math9151711
Chicago/Turabian StyleWan, Xing, Xing-Quan Zuo, and Xin-Chao Zhao. 2021. "A Surrogate Model-Based Hybrid Approach for Stochastic Robust Double Row Layout Problem" Mathematics 9, no. 15: 1711. https://doi.org/10.3390/math9151711
APA StyleWan, X., Zuo, X.-Q., & Zhao, X.-C. (2021). A Surrogate Model-Based Hybrid Approach for Stochastic Robust Double Row Layout Problem. Mathematics, 9(15), 1711. https://doi.org/10.3390/math9151711







