Potential-Growth Indicators Revisited: Higher Generality and Wider Merit of Indication
Abstract
:1. Introduction
2. Razzhevaikin-Tyrtyshnikov’s Algorithm to Construct a PGI
- (1)
- The next > 1. In this case, ρ(Ak) > 1, hence we have ρ(An) > 1 by virtue of Theorem 1.
- (2)
- The next = 1 and ≠ 1 for some i < k. In this case, a proper renumbering in matrix Ak relocates to the lower right angle and, if < 1, we can continue the chain, but if > 1, we come to point 1) above.
- (3)
- All = 1, i ≤ k. Two subcases are possible here.
- (3.1)
- There is an irreducible principal submatrix B of Ak having dimension greater than one. In this subcase, ρ(Ak) ≥ ρ(B) > 1, so that ρ(An) > 1 by virtue of Theorem 1.
- (3.2)
- There exists a renumbering in Ak that brings it to a triangular form with units on the principal diagonal. In this case, ρ(Ak) = 1, so that ρ(An) = 1 by virtue of Theorem 1.
3. Calamagrostis Epigeios Case Study
3.1. Material and Method
3.2. Calibration of the C. epigeios PPMs
3.3. Calibration from the Above-Ground Data Alone
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Matlab Expressions for PGIs
a/43 + (23*b)/301 + (10*d)/129 + (2*e)/129 + (7*g)/36 + h/36 − (7*a*g)/1548 − (a*h)/1548 − (23*b*g)/1548 + (c*f)/516 − (23*b*h)/10,836 + (5*c*g)/774 + (7*d*f)/1548 + (c*h)/774 + (e*f)/1548 + (d*h)/1161 − (e*g)/1161;
a/61 + (3*b)/8 + (7*d)/183 + (8*f)/183 + h/6 + k/9 + o/6 − (a*h)/366 − (b*h)/16 + (c*g)/366 + (d*g)/549 − (a*k)/549 − (7*d*h)/1098 − (b*k)/24 + (7*c*k)/1098 − (4*f*h)/549 − (a*o)/366 + (4*c*m)/549 − (b*o)/16 + (8*d*m)/1647 − (8*f*k)/1647 − (7*d*o)/1098 + (e*n)/61 + (8*e*o)/183 + (f*n)/366 − (h*o)/36 − (k*o)/54 + (a*h*o)/2196 + (b*h*o)/96 − (c*g*o)/2196 − (d*g*o)/3294 + (a*k*o)/3294 + (7*d*h*o)/6588 − (e*h*n)/366 + (b*k*o)/144 − (4*e*h*o)/549 − (f*h*n)/2196 − (7*c*k*o)/6588 + (c*l*n)/366 + (4*c*l*o)/549 + (c*m*n)/2196 + (d*l*n)/549 − (e*k*n)/549 + (8*d*l*o)/1647 + (d*m*n)/3294 − (8*e*k*o)/1647 − (f*k*n)/3294.
ans = 0
0
0
a/86 + (23*b)/602 + (5*d)/129 + e/129 + (7*g)/72 + h/72 − (a^2/1849 + (46*a*b)/12,943 + (20*a*d)/5547 + (4*a*e)/5547 − (7*a*g)/774 − (a*h)/774 + (529*b^2)/90,601 + (460*b*d)/38,829 + (92*b*e)/38,829 − (23*b*g)/774 − (23*b*h)/5418 + (100*d^2)/16,641 + (40*d*e)/16,641 + (35*d*g)/1161 + (d*h)/129 + (7*f*d)/387 + (4*e^2)/16,641 + (e*g)/387 + (e*h)/1161 + (f*e)/387 + (49*g^2)/1296 + (7*g*h)/648 + (10*c*g)/387 + h^2/1296 + (2*c*h)/387 + (c*f)/129)^(1/2)/2
References
- Caswell, H. Matrix Population Models: Construction, Analysis and Interpretation, 2nd ed.; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Logofet, D.O. Projection Matrices Revisited: A Potential-Growth Indicator and the Merit of Indication. J. Math. Sci. 2013, 193, 671–686. [Google Scholar] [CrossRef]
- Harary, F.; Norman, R.Z.; Cartwright, D. Structural Models: An Introduction to the Theory of Directed Graphs; John Wiley: New York, NY, USA, 1965. [Google Scholar]
- Gantmacher, F.R. Matrix Theory; Chelsea Publ.: New York, NY, USA, 1959. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Logofet, D.O. Matrices and Graphs: Stability Problems in Mathematical Ecology; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Logofet, D.O.; Kazantseva, E.S.; Belova, I.N.; Onipchenko, V.G. Backward Prediction Confirms the Conclusion on Local Plant Population Viability. Zhurnal Obs. Biol. (J. Gen. Biol.) 2020, 81, 257–271. (In Russian) [Google Scholar] [CrossRef]
- Cushing, J.M.; Yicang, Z. The Net Reproductive Value and Stability in Matrix Population Models. Nat. Res. Model. 1994, 8, 297–333. [Google Scholar] [CrossRef]
- Li, C.-K.; Schneider, H. Application of Perron–Frobenius Theory to Population Dynamics. J. Math. Biol. 2002, 44, 450–462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Logofet, D.O.; Belova, I.N. Nonnegative Matrices as a Tool to Model Population Dynamics: Classical Models and Contemporary Expansions. J. Math. Sci. 2008, 155, 894–907. [Google Scholar] [CrossRef]
- Protasov, V.Y.; Logofet, D.O. Rank-One Corrections of Nonnegative Matrices, with an Application to Matrix Population Models. SIAM J. Matrix Anal. Appl. 2014, 35, 749–764. [Google Scholar] [CrossRef]
- Logofet, D.O.; Kazantseva, E.S.; Belova, I.N.; Onipchenko, V.G. How Long Does a Short-Lived Perennial Live? A Modelling Approach. Biol. Bul. Rev. 2018, 8, 406–420. [Google Scholar] [CrossRef]
- Logofet, D.O.; Golubyatnikov, L.L.; Ulanova, N.G. Realistic Choice of Annual Matrices Contracts the Range of λs Estimates. Mathematics 2020, 8, 2252. [Google Scholar] [CrossRef]
- Razzhevaikin, V.N.; Tyrtyshnikov, E.E. On Stability Indicators of Nonnegative Matrices. Dokl. Math. 2020, 101, 43–45. [Google Scholar] [CrossRef]
- Razzhevaikin, V.N.; Tyrtyshnikov, E.E. On the Construction of Stability Indicators for Nonnegative Matrices. Math. Notes 2021, 109, 407–418. [Google Scholar] [CrossRef]
- Logofet, D.O.; Ulanova, N.G.; Belova, I.N. From Uncertainty to an Exact Number: Developing a Method to Estimate the Fitness of a Clonal Species with Polyvariant Ontogeny. Biol. Bull. Rev. 2017, 7, 387–402. [Google Scholar] [CrossRef]
- Ulanova, N.G. Plant Age Stages during Succession in Woodland Clearings in Central Russia. In Vegetation Science in Retrospect and Perspective, Proceedings of the IAVS Symposium; Opulus: Uppsala, Sweden, 2000; pp. 80–83. [Google Scholar]
- Ulanova, N.G.; Klochkova, I.N.; Demidova, A.N. Modeling the Population Dynamics of Calamagrostis epigeios (L.) Roth during Reforestation in a Mixed Spruce Forest Clearcut. Sib. Bot. Vestn. 2007, 2, 91–96. Available online: www.csbg.nsc.ru/uploads/journal.csbg.ru/pdfs/i3.pdf (accessed on 5 July 2021). (In Russian, with English summary).
- Logofet, D.O.; Ulanova, N.G.; Belova, I.N. Polyvariant Ontogeny in Woodreeds: Novel Models and New Discoveries. Biol. Bull. Rev. 2016, 6, 365–385. [Google Scholar] [CrossRef]
- Smirnova, O.V.; Chistyakova, A.A.; Zaugolnova, L.B.; Evstigneev, O.I.; Popadiouk, R.V.; Romanovsky, A.M. Ontogeny of a Tree. Bot. J. 1999, 84, 8–20. [Google Scholar]
- Logofet, D.O. Polyvariant Ontogeny in Plants: When the Second Eigenvalue Plays a Primary Role. In Advanced Mathematical Methods in Biosciences and Applications; Berezovskaya, F., Toni, B., Eds.; STEAM-H Science, Technology, Engineering, Agriculture, Mathematics & Health; Springer: Cham, Switzerland, 2019; pp. 111–130. [Google Scholar] [CrossRef]
- Logofet, D.O.; Ulanova, N.G.; Belova, I.N. Adaptation on the Ground and Beneath: Does the Local Population Maximize Its λ1? Ecol. Complex. 2014, 20, 176–184. [Google Scholar] [CrossRef]
- Logofet, D.O. Convexity in Projection Matrices: Projection to a Calibration Problem. Ecol. Model. 2008, 216, 217–228. [Google Scholar] [CrossRef]
- Serebryakova, T.I. Shoot Morphogenesis and the Evolution of Life Forms in Graminoids; Nauka: Moscow, Russia, 1971; p. 360. [Google Scholar]
- Logofet, D.O. Complexity in Matrix Population Models: Polyvariant Ontogeny and Reproductive Uncertainty. Ecol. Complex. 2013, 15, 43–51. [Google Scholar] [CrossRef]
- Logofet, D.O.; Kazantseva, E.S.; Belova, I.N.; Onipchenko, V.G. Local Population of Eritrichium caucasicum as an Object of Mathematical Modelling. I. Life Cycle Graph and a Nonautonomous Matrix Model. Biol. Bul. Rev. 2017, 7, 415–427. [Google Scholar] [CrossRef]
- Logofet, D.O. Aggregation may or may not eliminate reproductive uncertainty. Ecol. Model. 2017, 363, 187–191. [Google Scholar] [CrossRef]
- Metz, J.A.J.; Mylius, S.D.; Diekmann, O. When Does Evolution Optimize? Evol. Ecol. Res. 2008, 10, 629–654. [Google Scholar]
- Gyllenberg, M.; Service, R. Necessary and Sufficient Conditions for the Existence of an Optimisation Principle in Evolution. J. Math. Biol. 2011, 62, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Razzhevaikin, V.N. Selection Functionals in Autonomous Models of Biological Systems with Continuous Age and Spatial Structure. Comput. Math. Math. Phys. 2010, 50, 322–329. [Google Scholar] [CrossRef]
- Razzhevaikin, V.N. Stability Indicators for Highly Sparse Non-Negative Matrices. Issled. Oper. Modeli Sist. Resheniya 2020, 6, 3–14. (In Russian) [Google Scholar]
- Leslie, P.H. On the Use of Matrices in Certain Populations Mathematics. Biometrika 1945, 33, 183–212. [Google Scholar] [CrossRef]
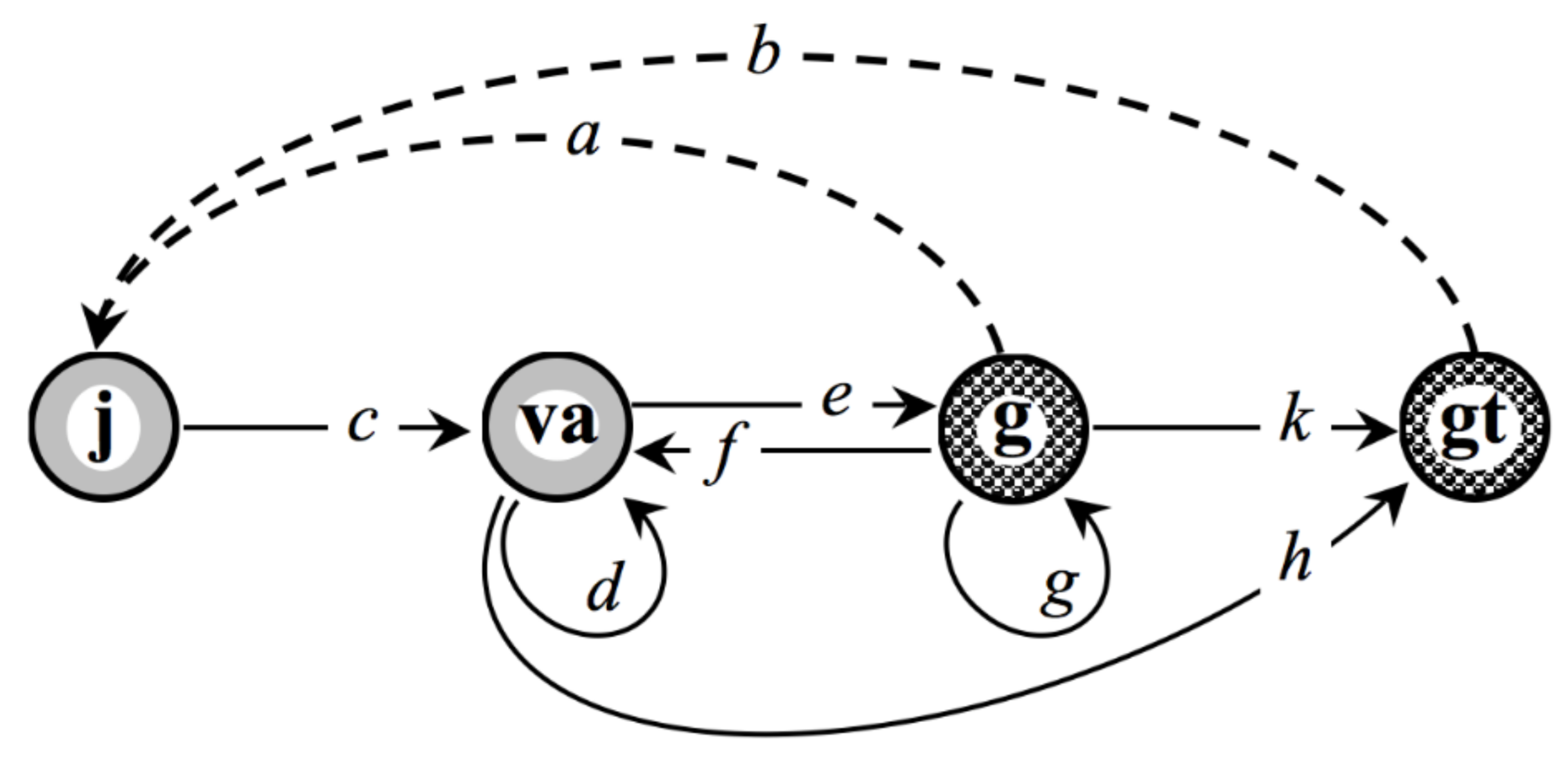
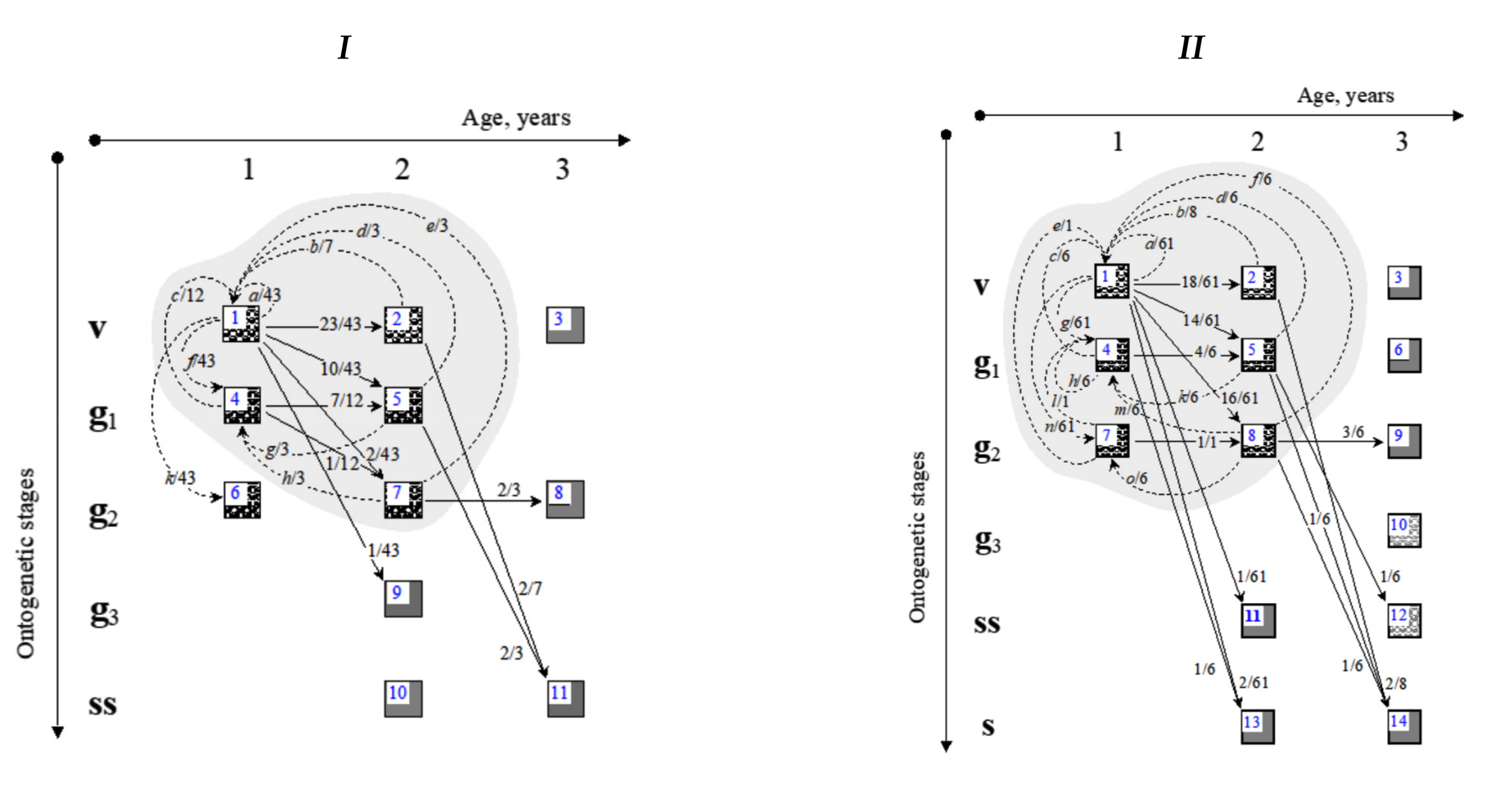
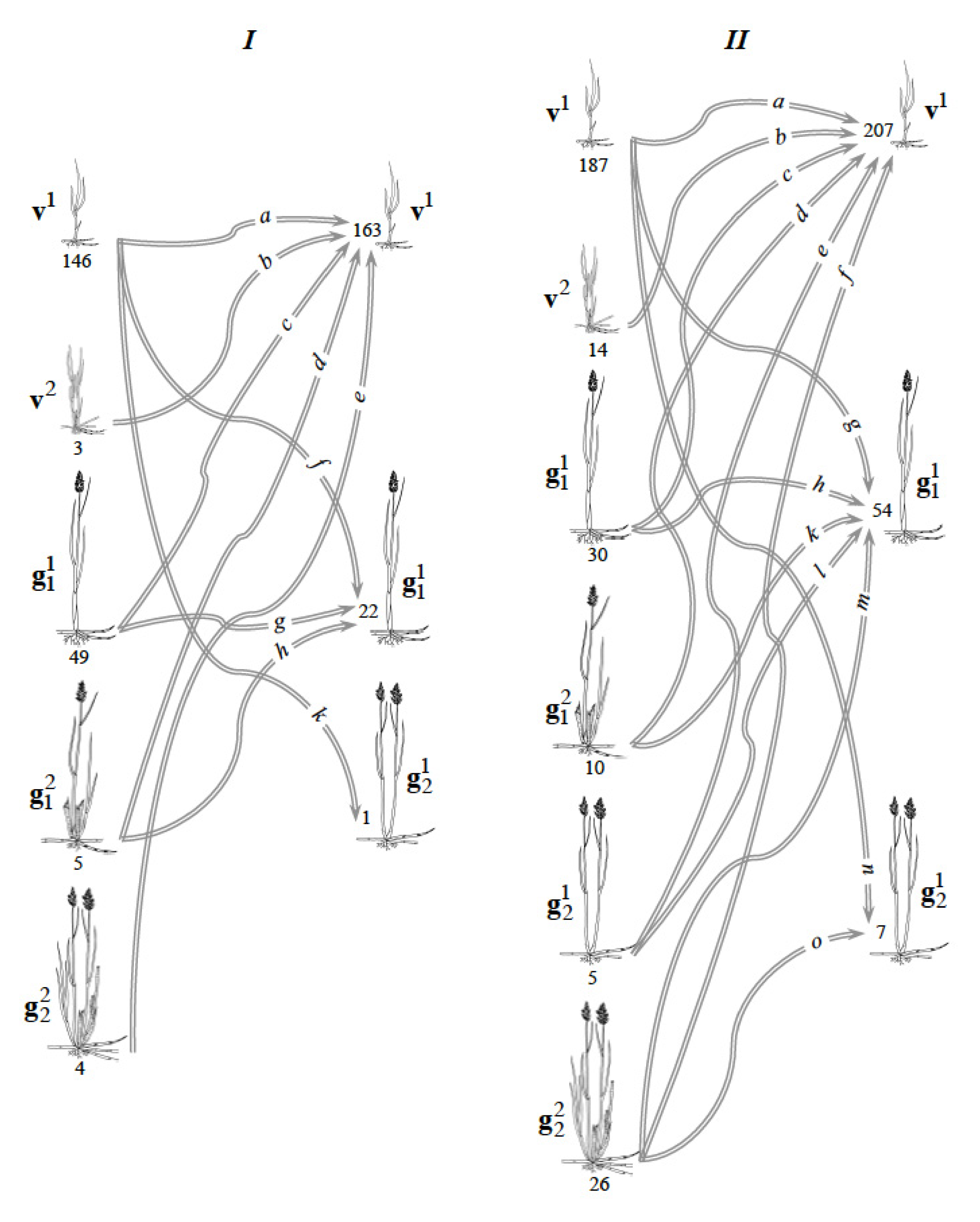
| Parent Status in 2014 | Number of Daughter Tufts, 2015 | Daughter Tuft Status, 2015 | Parameter Value | Matrix L and Its Reproductive-Core Submatrix | λ1(L) (S0/S1)λ1 µ(L) RRT(L) |
|---|---|---|---|---|---|
| Colony I | |||||
| v1 | a | v1 | 117 |  | 3.4266 2.4361 2.4525 1.9690 |
| v2 | b | v1 | 3 | ||
| g11 | c | v1 | 38 | ||
| g12 | d | v1 | 3 | ||
| g22 | e | v1 | 2 | ||
| v1 | f | g11 | 12 | ||
| g11 | g | g11 | 9 | ||
| g12 | h | g11 | 1 | ||
| v1 | k | g21 | 1 | ||
| Colony II | |||||
| v1 | a | v1 | 138 |  | 3.9066 2.7773 n/a 5.0870 |
| v2 | b | v1 | 14 | ||
| g11 | c | v1 | 24 | ||
| g12 | d | v1 | 9 | ||
| g21 | e | v1 | 4 | ||
| g22 | f | v1 | 18 | ||
| v1 | g | g11 | 43 | ||
| g11 | h | g11 | 5 | ||
| g12 | k | g11 | 1 | ||
| g21 | l | g11 | 1 | ||
| g22 | m | g11 | 4 | ||
| v1 | n | g21 | 3 | ||
| g22 | o | g21 | 4 | ||
| Parameter | Additional Constraints (21)/(22) | Parameters a,…, o for | R(Lrec): minR maxR | Parameters for | |||
|---|---|---|---|---|---|---|---|
| Reproductive-Core Submatrix Lrec and its [minλ1, maxλ1] 1 | |||||||
| minλ1 | maxλ1 | minRRT | maxRRT | ||||
| Colony I, System (17), (19) | |||||||
| a | a + f + k ≥ c + g | (S0/S1)λ1(L) ∈ [2.0480, 2.6247] | 108 | 144 | 3.5032 2 5.5645 3 3.2238 4 –4.7321 5 3.2238 6,7 3.5994 8 2.7470 9 5.2905 10 | 111 | 105 |
| b | b ≥ e | 3 | 3 | 1 | 3 | ||
| c | c + g ≥ d + h | 48 | 11 | 46 | 48 | ||
| d | d + h ≥ b | 1 | 4 | 4 | 4 | ||
| e | e ≤ b | 3 | 1 | 1 | 3 | ||
| f | 1 | 1 | 1 | 20 | |||
| g | Number of solutions: | 1 | 20 | 17 | 1 | ||
| h | 179 102 | 20 | 1 | 4 | 1 | ||
| Colony II, System (18), (20) | |||||||
| a | a + g + n ≥ c + h | (S0/S1)λ1(L) ∈ [2.4502, 3.9647] | 177 | 168 | 4.5063 2 6.6161 3 –2.7975 4 –8.6342 5 3.3074 7 2.9385 8 2.5164 9 12.9744 10 | 131 | 131 |
| b | b ≥ d + k | 11 | 5 | 10 | 14 | ||
| c | c + h ≥ f + m + o | 1 | 29 | 29 | 29 | ||
| d | d + k ≥ e + l | 8 | 1 | 9 | 9 | ||
| e | e + l ≤ d + k | 1 | 1 | 4 | 4 | ||
| f | f + m + o ≥ b | 9 | 3 | 24 | 20 | ||
| g | 41 | 16 | 1 | 39 | |||
| h | 10 | 29 | 24 | 1 | |||
| k | 1 | 4 | 1 | 1 | |||
| l | 1 | 4 | 4 | 4 | |||
| m | 1 | 1 | 24 | 9 | |||
| n | Number of solutions: | 6 | 6 | 5 | 6 | ||
| o | 5 616 093 932 | 1 | 1 | 2 | 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Logofet, D.O.; Razzhevaikin, V.N. Potential-Growth Indicators Revisited: Higher Generality and Wider Merit of Indication. Mathematics 2021, 9, 1649. https://doi.org/10.3390/math9141649
Logofet DO, Razzhevaikin VN. Potential-Growth Indicators Revisited: Higher Generality and Wider Merit of Indication. Mathematics. 2021; 9(14):1649. https://doi.org/10.3390/math9141649
Chicago/Turabian StyleLogofet, Dmitrii O., and Valerii N. Razzhevaikin. 2021. "Potential-Growth Indicators Revisited: Higher Generality and Wider Merit of Indication" Mathematics 9, no. 14: 1649. https://doi.org/10.3390/math9141649
APA StyleLogofet, D. O., & Razzhevaikin, V. N. (2021). Potential-Growth Indicators Revisited: Higher Generality and Wider Merit of Indication. Mathematics, 9(14), 1649. https://doi.org/10.3390/math9141649







