One Concave-Convex Inequality and Its Consequences

Abstract

Our starting point is an integral inequality that involves convex, concave and monotonically increasing functions. We provide some interpretations of the inequality, in terms of both probability and terms of linear functionals, from which we further generate completely monotone functions and means. The latter application is seen from the perspective of monotonicity and convexity.

1. Integral Inequality

The following Lemma originates from unsolved Problem 8, Jósef Wildt International Mathematical Competition (see [1]).

Lemma 1.

Let $f,g:[a,b]\to {\mathbb{R}}_{+},f\left(a\right)=g\left(a\right)=0$ two continuous functions, such that f is convex, and g concave. If $h:[a,b]\to \mathbb{R}$ is an increasing function, then

$${\int }_a^{b}h\left(x\right)g\left(x\right)dx{\int }_a^{b}f\left(x\right)dx\le {\int }_a^{b}g\left(x\right)dx{\int }_a^{b}h\left(x\right)f\left(x\right)dx.$$

(1)

Proof.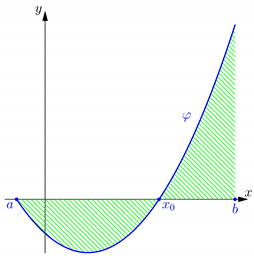 

Define

$$\phi \left(x\right)=f\left(x\right){\int }_a^{b}g\left(t\right)dt-g\left(x\right){\int }_a^{b}f\left(t\right)dt.$$

It follows that $\phi$ is a continuous convex function, such that $\phi \left(a\right)=0,{\int }_a^b\phi \left(x\right)dx=0.$ If $\phi \equiv 0$, then we have equality in (1).

Otherwise, there is a unique $x_0\in (a,b)$ such that $\phi \left(x_0\right)=0,\phi \left(t\right)<0,t<x_0;\phi \left(t\right)>0,t>x_0.$ An easy proof of this fact can be obtained using Proposition 1.3.5 from [2], and below is the geometric illustration of this fact.

Since h is increasing, we can define a measure $\mu$ with

$$\mu (c,d]=h\left(d\right)-h\left(c\right),a\le c<d\le b,$$

and then extend it on the Borel sigma algebra $\mathcal{B}(a,b)$ as described in [3].

Now we calculate

$$\begin{array}{cc}\hfill & {\int }_a^{b}h\left(x\right)\phi \left(x\right)dx={\int }_a^b(h\left(x\right)-h\left(a\right))\phi \left(x\right)dx+h\left(a\right)\underset{=0}{\underbrace{{\int }_a^b\phi \left(x\right)dx}}\hfill \\ \hfill & ={\int }_a^b\phi \left(x\right){\int }_a^{x}d\mu \left(t\right)dx=\left(Fubini\right)\hfill \\ \hfill & ={\int }_a^b\left({\int }_t^b\phi \left(x\right)dx\right)d\mu \left(t\right)\hfill \\ \hfill & ={\int }_a^{x_0}\left({\int }_t^b\phi \left(x\right)dx\right)d\mu \left(t\right)+{\int }_{x_0}^b\left({\int }_t^b\phi \left(x\right)dx\right)d\mu \left(t\right)\hfill \\ \hfill & ={\int }_a^{x_0}\left({\int }_a^b-{\int }_a^t\right)\phi \left(x\right)dxd\mu \left(t\right)+{\int }_{x_0}^b\left({\int }_t^b\phi \left(x\right)dx\right)d\mu \left(t\right)\hfill \\ \hfill & ={\int }_a^{x_0}\left(-{\int }_a^t\phi \left(x\right)dx\right)d\mu \left(t\right)+{\int }_{x_0}^b\left({\int }_t^b\phi \left(x\right)dx\right)d\mu \left(t\right).\hfill \end{array}$$

(2)

Both summands in (2) are greater than zero, from which one can conclude that

$${\int }_a^{b}h\left(x\right)\phi \left(x\right)dx\ge 0$$

i.e., (1).  □

2. Probabilistic Point of View

The Lemma result 1 can be interpreted in probability terms. First, suppose that we have a probability space $(\Omega ,\mathcal{F},\mu )$ and a random variable $Z:\Omega \to \mathbb{R},$ with the Borel sigma algebra on $\mathbb{R},$ such that $P(a\le Z\le b)=1.$ If we consider the increasing function $h\left(t\right)=P(a\le Z\le t)$ in Lemma 1, then we have the following inequality in terms of mathematical expectations

$${\int }_a^{b}f\left(x\right)dxE\left[\underset{Z}{\overset{b}{\int }}g\left(t\right)dt\right]\le {\int }_a^{b}g\left(x\right)dxE\left[\underset{Z}{\overset{b}{\int }}f\left(t\right)dt\right],$$

(3)

since we can use an analogous technique from line (2).

There is another probability interpretation of (1). Let us divide both sides of (1) by ${\int }_a^{b}f\left(x\right)dx·{\int }_a^{b}g\left(x\right)dx,$ hence

$$\frac{{\int }_a^{b}h\left(x\right)g\left(x\right)dx}{{\int }_a^{b}g\left(x\right)dx}\le \frac{{\int }_a^{b}h\left(x\right)f\left(x\right)dx}{{\int }_a^{b}f\left(x\right)dx}.$$

This inequality enables us to deduce a second inequality between mathematical expectations, viz.

$$E\left[h\right(X\left)\right]\le E\left[h\right(Y\left)\right],$$

(4)

where the random variable X has a concave density function $g:[a,b]\to {\mathbb{R}}_{+},$ random variable Y has convex density function $f:[a,b]\to {\mathbb{R}}_{+}$ such that $g\left(a\right)=f\left(a\right)=0$ and $h:[a,b]\to \mathbb{R}$ is an increasing function, as before.

3. Applications to Complete Monotone Functions and Means

In this section, we will offer some applications of Lemma 1, in terms of completely monotone functions and means.

Recall that a function f is said to be completely monotone on an open interval $I\subset (0,\infty )$ if it has derivatives of all orders there and satisfies

$${(-1)}^n{f}^{\left(n\right)}\left(x\right)\ge 0\mathrm{for}\mathrm{all}x\in I\mathrm{and}n=0,1,2,\dots .$$

(5)

The class of all completely monotone functions on I is denoted by $CM\left(I\right).$ We can observe here that completely monotone functions are log-convex and, therefore, convex functions (see [4]).

Let us consider two linear functionals, respectively defined by

$$AH={\int }_a^{b}g\left(x\right)dx{\int }_a^{b}H\left(x\right)f\left(x\right)dx-{\int }_a^{b}H\left(x\right)g\left(x\right)dx{\int }_a^{b}f\left(x\right)dx,$$

(6)

where f and g are functions as in Lemma 1, and

$$BF={\int }_a^{b}g\left(x\right)dx{\int }_a^{b}h\left(x\right)F\left(x\right)dx-{\int }_a^{b}h\left(x\right)g\left(x\right)dx{\int }_a^{b}F\left(x\right)dx,$$

(7)

where g and h are functions as in Lemma 1.

From the conclusion of that lemma, we know $AH\ge 0,$ for any increasing function H on $[a,b]$, and $BF\ge 0,$ for any convex function F on $[a,b]$, such that $F\left(a\right)=0.$

Theorem 1.

$\left(\mathrm{i}\right)$

Let $H\in C^1[a,b]$ and let $A:C[a,b]\to \mathbb{R}$ be a linear functional defined with (6). Then, there exists $\xi \in [a,b]$, such that

$$AH=H^{\prime }\left(\xi \right)A{e}_1,$$

(8)

where $e_1\left(x\right)=x.$

$\left(\mathrm{ii}\right)$

Let $F\in C^2[0,b],F\left(0\right)=0,$ and let $B:C[0,b]\to \mathbb{R}$ be a linear functional defined with (7). Then, there exists $\eta \in [0,b]$, such that

$$BF=F^{″}\left(\eta \right)B{e}_2,$$

(9)

where $e_2\left(x\right)=x^2/2.$

Proof. 

$\left(\mathrm{i}\right)$ Let

$$m=\underset{x\in [a,b]}{min}{H}^{\prime }\left(x\right),M=\underset{x\in [a,b]}{max}{H}^{\prime }\left(x\right).$$

Let us observe that the function $\phi \left(x\right)=Mx-H\left(x\right)=M{e}_1\left(x\right)-H\left(x\right)$ is increasing since ${\phi }^{\prime }\left(x\right)=M-H^{\prime }\left(x\right)\ge 0.$ Hence, $A\phi \ge 0$, and we conclude

$$AH\le M·A{e}_1.$$

Similarly,

$$mA{e}_1\le AH\le MA{e}_1.$$

Now, we have (8) using Bolzano’s Intermediate Value Theorem.

$\left(\mathrm{ii}\right)$ Let

$$m=\underset{x\in [0,b]}{min}{F}^{″}\left(x\right),M=\underset{x\in [0,b]}{max}{F}^{″}\left(x\right).$$

Define $\psi \left(x\right)=M{x}^2/2-F\left(x\right)=M{e}_2\left(x\right)-F\left(x\right).$ Then $\psi \left(0\right)=0$ and $\psi$ is convex, since ${\psi }^{″}\left(x\right)=M-F^{″}\left(x\right)\ge 0$ concluding $BF\le M·B{e}_2.$ Similarly, $mB{e}_1\le BF$ and, therefore, we have (9) using Bolzano’s Intermediate Value Theorem.  □

Corollary 1.

$\left(\mathrm{i}\right)$

If $H_1,H_2\in C^1[a,b]$,; then, there exists $\xi \in [a,b]$, such that

$$\frac{H_1^{\prime }\left(\xi \right)}{H_2^{\prime }\left(\xi \right)}=\frac{A{H}_1}{A{H}_2}.$$

(10)

$\left(\mathrm{ii}\right)$

If $F_1,F_2\in C^2[0,b]$,; then, there exists $\eta \in [0,b]$, such that

$$\frac{F_1^{″}\left(\eta \right)}{F_2^{″}\left(\eta \right)}=\frac{B{F}_1}{B{F}_2}.$$

(11)

$\left(\mathrm{iii}\right)$

Let I be any open interval in $(0,\infty ).$ Assume that $\mathcal{H}=\{H_t:t\in I\}$ is the family of differentiable functions on $[a,b],$ such that $t\mapsto d{H}_t\left(x\right)/dx$ is in $CM\left(I\right)$, for any $x\in [a,b].$ Then $t\mapsto A{H}_t$ also belongs to $CM\left(I\right);$

$\left(\mathrm{iv}\right)$

Let I be any open interval in $(0,\infty ).$ Assume that $\mathcal{F}=\{F_t:t\in I\}$ is the family of differentiable functions on $[a,b],$ such that $t\mapsto d^2{F}_t\left(x\right)/d{x}^2$ is in $CM\left(I\right)$, for any $x\in [a,b].$ Then, $t\mapsto A{F}_t$ also belongs to $CM\left(I\right);$

$\left(\mathrm{v}\right)$

for any $r<s<t,r,s,t\in I$ we have

$${\left(A{H}_s\right)}^{t-r}\le {\left(A{H}_r\right)}^{t-s}{\left(A{H}_t\right)}^{s-r}$$

(12)

and

$${\left(B{F}_s\right)}^{t-r}\le {\left(B{F}_r\right)}^{t-s}{\left(B{F}_t\right)}^{s-r}$$

(13)

$\left(\mathrm{vi}\right)$

for any $p\le u,q\le v,p,q,u,v\in I,$ we have

$$M_{p,q}(A,\mathcal{H})\le M_{u,v}(A,\mathcal{H})$$

(14)

where

$$M_{p,q}(A,\mathcal{H})=\left\{\begin{array}{cc}{\left(\frac{A{H}_p}{A{H}_q}\right)}^{\frac{1}{p-q}},\hfill & p\ne q;\hfill \\ \exp \left(\frac{\frac{d}{dp}\left(A{H}_p\right)}{A{H}_p}\right),\hfill & p=q;\hfill \end{array}\right.$$

(15)

also

$$M_{p,q}(B,\mathcal{F})\le M_{u,v}(B,\mathcal{F})$$

(16)

where

$$M_{p,q}(B,\mathcal{F})=\left\{\begin{array}{cc}{\left(\frac{B{F}_p}{B{F}_q}\right)}^{\frac{1}{p-q}},\hfill & p\ne q;\hfill \\ \exp \left(\frac{\frac{d}{dp}\left(B{F}_p\right)}{B{F}_p}\right),\hfill & p=q.\hfill \end{array}\right.$$

(17)

Proof. 

$\left(\mathrm{i}\right)$ We introduce an auxiliary function $\varphi \left(x\right)=H_1\left(x\right)A{H}_2-H_2\left(t\right)A{H}_1.$ By part (i) of Theorem 1, there exists $\xi \in [a,b]$, such that

$$A\varphi ={\varphi }^{\prime }\left(\xi \right)A{e}_1.$$

Since $A\varphi =0,$ the result follows after we check $A{e}_1\ne 0$ (see Remark below).

$\left(\mathrm{ii}\right)$ Let us define $\psi \left(x\right)=F_1\left(x\right)B{F}_2-F_2\left(t\right)B{F}_1.$ By part (ii) of Theorem 1, there exists $\xi \in [0,b]$, such that

$$B\psi ={\psi }^{″}\left(\eta \right)B{e}_2.$$

Since $B\psi =0,$ we have our result after we check that $B{e}_2\ne 0.$

$\left(\mathrm{iii}\right)-\left(\mathrm{iv}\right)$ Since $A{H}_t=H_t^{\prime }\left(\xi \right)A{e}_1$ and $A{F}_t=F_t^{″}\left(\xi \right)A{e}_2$, we conclude that $t\mapsto A{H}_t$ and $t\mapsto A{H}_t$ are completely monotone functions on $I.$

$\left(\mathrm{iii}\right)-\left(\mathrm{iv}\right)$ Since $A{H}_t=H_t^{\prime }\left(\xi \right)A{e}_1$ and $A{F}_t=F_t^{″}\left(\xi \right)A{e}_2$, we conclude that $t\mapsto A{H}_t$ and $t\mapsto A{H}_t$ are completely monotone functions on $I.$

$\left(\mathrm{v}\right)$ First, it is known, see [2] (p. 21) or [5] (p. 4), that a function $\varphi$ is convex on an interval I if, and only if,

$$\varphi \left(s_1\right)\left(s_3-s_2\right)+\varphi \left(s_2\right)\left(s_1-s_3\right)+\varphi \left(s_3\right)\left(s_2-s_1\right)\ge 0$$

for $s_1<s_2<s_3,s_1,s_2,s_3\in I.$ Now, since $t\mapsto A{H}_t$ and $t\mapsto B{F}_t$ are log-convex functions, we have our claims.

$\left(\mathrm{vi}\right)$ Again from the log-convexity of the function $t\mapsto A{H}_t$, we have (see [2] ([p. 23]))

$$\frac{logA{H}_q-logA{H}_p}{q-p}\le \frac{logA{H}_v-logA{H}_u}{v-u},$$

(18)

for $p\le u,q\le v;p\ne q,u\ne v,$ that is, in fact, (14). The case $p=q$ in (14) we obtain after we pass the limit $p\le u$ in (18).  □

Remark 1.

There is one important issue with the possible zeros in denominators in the above fractions. As we pointed out at the beginning of this section, completely monotone functions are also log-convex (see [4] (p. 885)) so if, say, $A{H}_{t_0}=0$ for some $t_0\in I,$ then $A{H}_t=0$ for all $t\in I.$

Let us now illustrate Corollary 1 on a concrete family of functions.

Example 1.

Let $0<a<b,I=(0,1),\mathcal{H}=\{H_t:t\in I\},H_t\left(x\right)=\frac{x^{1-t}}{1-t},t\in I.$ Then $t\mapsto d{H}_t\left(x\right)/dt=x^{-t}>0$ is completely monotone function on I and from Corollary 1 we know that the function

$$t\mapsto A{H}_t=\frac{1}{1-t}{\int }_a^{b}g\left(x\right)dx{\int }_a^b{x}^{1-t}f\left(x\right)dx-\frac{1}{1-t}{\int }_a^b{x}^{1-t}g\left(x\right)dx{\int }_a^{b}f\left(x\right)dx$$

is also completely monotone on I for any concave function $g:[a,b]\to {\mathbb{R}}_{+}$ and any convex function $f:[a,b]\to {\mathbb{R}}_{+},$ and this function satisfies Lyapunov inequality (12) and means (15) can be produced.

Example 2.

Let $0=a<b=1,I=(0,1),\mathcal{F}=\{F_t:t\in I\},$

$F_t\left(x\right)=\frac{x^{2-t}}{(t-1)(t-2)}-\frac{x}{(t-1)(t-2)},t\in I.$

Then, $t\mapsto d^2{F}_t\left(x\right)/d{x}^2=x^{-t}>0$ is completely monotone function on I and, from Corollary 1, we know that the function $t\mapsto B{F}_t,$

$$B{F}_t=\frac{1}{(t-1)(t-2)}{\int }_0^{b}g\left(x\right)dx{\int }_0^b{x}^{2-t}h\left(x\right)dx+\frac{b^{3-t}}{(t-1)(t-2)(t-3)}{\int }_0^{b}g\left(x\right)h\left(x\right)dx,$$

is completely monotone on I for any concave function $g:[0,b]\to {\mathbb{R}}_{+}$ and any increasing function $h:[0,b]\to {\mathbb{R}}_{+}.$ Additionally, using function $t\mapsto B{F}_t$, we can produce means (17).

Examples 1 and 2 used some adapted examples of generating families from [4] because of the specific requirements on the functions f and h in Lemma 1.

Example 3.

Let $-\infty <a<b<\infty ,I=(0,\infty )$ and a family $\mathbf{H}=\{H_t:t\in I\}$ of functions on $[a,b]$ defined by

$$H_t\left(x\right)=-\frac{e^{-tx}}{t}.$$

(19)

Since $t\mapsto \frac{d}{dx}{H}_t\left(x\right)=e^{-tx}>0$ is from $CM\left(I\right)$ then $t\mapsto A{H}_t,$ with

$$A{H}_t=-\frac{1}{t}{\int }_a^{b}g\left(x\right)dx{\int }_a^b{e}^{-tx}f\left(x\right)dx+\frac{1}{t}{\int }_a^b{e}^{-tx}g\left(x\right)dx{\int }_a^{b}f\left(x\right)dx,$$

is also completely monotone on I for any concave function $g:[a,b]\to {\mathbb{R}}_{+}$ and any convex function $f:[a,b]\to {\mathbb{R}}_{+}$, and this function satisfies Lyapunov inequality (12) and means (15) can be produced.

Example 4.

Let $0=a<b<\infty ,I=(0,\infty )$ and a family $\mathbf{F}=\{F_t:t\in I\}$ of functions on $[0,b]$ defined by

$$F_t\left(x\right)=\frac{e^{-tx}-1}{t^2}.$$

(20)

Since $t\mapsto d^2{F}_t\left(x\right)/d{x}^2=e^{-tx}>0$ is from $CM\left(I\right)$, then $t\mapsto B{F}_t,$

$$B{F}_t={\int }_0^{b}g\left(x\right)dx{\int }_0^b\frac{e^{-tx}-1}{t^2}h\left(x\right)dx+\frac{e^{-tb}-b-1}{t^3}{\int }_0^{b}g\left(x\right)h\left(x\right)dx,$$

is completely monotone on I for any concave function $g:[0,b]\to {\mathbb{R}}_{+}$ and any increasing function $h:[0,b]\to {\mathbb{R}}_{+}.$ Additionally, using function $t\mapsto B{F}_t$, we can produce means (17).