An Oscillation Test for Solutions of Second-Order Neutral Differential Equations of Mixed Type

Abstract

It is easy to notice the great recent development in the oscillation theory of neutral differential equations. The primary aim of this work is to extend this development to neutral differential equations of mixed type (including both delay and advanced terms). In this work, we consider the second-order non-canonical neutral differential equations of mixed type and establish a new single-condition criterion for the oscillation of all solutions. By using a different approach and many techniques, we obtain improved oscillation criteria that are easy to apply on different models of equations.

1. Introduction

This paper discusses the oscillatory behavior of solutions of second-order neutral differential equations of mixed type:

$$\begin{array}{ccc}& & {\left(r\left(s\right){\left({\left(x\left(s\right) + p_1\left(s\right)x\left({\varrho }_1\left(s\right)\right) + p_2\left(s\right)x\left({\varrho }_2\left(s\right)\right)\right)}^{\prime }\right)}^{\alpha }\right)}^{\prime }\hfill \\ & & + q_1\left(s\right)x^{\alpha }\left({\theta }_1\left(s\right)\right) + q_2\left(s\right)x^{\alpha }\left({\theta }_2\left(s\right)\right) =0,\hfill \end{array}$$

(1)

where $s\ge s_0$. Throughout this paper, we assume the following:

(C1) 

$\alpha \in Q_{odd}^{+}:= \left\{a/b:a,b\in {\mathbb{Z}}^{+}\mathrm{are}\mathrm{odd}\right\};$

(C2) 

$r\in C\left(\left[s_0,\infty \right),\left(0,\infty \right)\right)$$r^{\prime }\left(s\right) >0$, and ${\int }_{s_0}^{\infty }{r}^{-1/\alpha }\left(\xi \right)\mathrm{d}\xi <\infty ,$ where $C\left(I,J\right)$ is the set of all continuous real-valued functions $F:I\to J;$

(C3) 

${\varrho }_1,{\varrho }_2,{\theta }_1,{\theta }_2\in C\left(\left[s_0,\infty \right),\mathbb{R}\right)$, ${\varrho }_1\left(s\right) \le s,$ ${\varrho }_2\left(s\right) \ge s,$ ${\theta }_1\left(s\right) \le s,$ ${\theta }_2\left(s\right) \ge s$, and ${\varrho }_1\left(s\right),{\varrho }_2\left(s\right),{\theta }_1\left(s\right),{\theta }_2\left(s\right) \to \infty$ as $s\to \infty ;$

(C4) 

$p_1,p_2,q_1,q_2\in C\left(\left[s_0,\infty \right),\left[0,\infty \right)\right)$ and $q_1,$$q_2$ are not identically zero for large s.

Let x be a real-valued function defined for all s in a real interval $[s_x,\infty ),s_x\ge s_0,$ which has the properties

$$x+p_1·x\circ {\varrho }_1+p_2·x\circ {\varrho }_2\in C^1\left(\left[s_x,\infty \right),\mathbb{R}\right)$$

and

$$r·{\left(x+p_1·x\circ {\varrho }_1+p_2·x\circ {\varrho }_2\right)}^{\prime }\in C^1\left(\left[s_x,\infty \right),\mathbb{R}\right).$$

Then, x is called a solution of (1) on $[s_x,\infty )$ if x satisfies (1) for all $s\ge s_x$. We will consider only the solutions of (1) that exist on some half-line $\left[s_x,\infty \right)$ for $s_x\ge s_0$ and satisfy the condition

$$sup\left\{\left|x\left(s\right)\right|:s_c\le s<\infty \right\} >0\mathrm{for}\mathrm{any}{s}_c\ge s_x.$$

A nontrivial solution x of any differential equation is said to be oscillatory if it has arbitrary large zeros; otherwise, it is said to be non-oscillatory.

The oscillation and asymptotic behavior of solutions to various classes of delay and advanced differential equations have been widely discussed in the literature. For second-order delay equations, the studies found in [1,2,3,4,5] were concerned with studying the oscillatory behavior of the equation:

$${\left(r\left(s\right){\left({\left(x\left(s\right) + p_1\left(s\right)x\left({\varrho }_1\left(s\right)\right)\right)}^{\prime }\right)}^{\alpha }\right)}^{\prime }+q_1\left(s\right)x^{\alpha }\left({\theta }_1\left(s\right)\right) =0,$$

(2)

with the canonical operator $\pi \left(s_0\right) =\infty$, where

$$\pi \left(s\right):={\int }_{s_0}^s{r}^{-1/\alpha }\left(\xi \right)\mathrm{d}\xi .$$

One can find developments and comparisons of the oscillation criteria of (2) in the recently published paper by Moaaz et al. [4] for a non-canonical case, that is,

$${\int }_{s_0}^{\infty }{r}^{-1/\alpha }\left(\xi \right)\mathrm{d}\xi <\infty .$$

Bohner et al. [6] simplified and improved the previous results found by Agarwal et al. [7] and Han et al. [8]. For more general equations and more accurate results, see [9,10].

For second-order advanced equations, Chatzarakis et al. [11,12] studied the asymptotic behavior of the equation:

$${\left(r\left(s\right){\left(x{\left(s\right)}^{\prime }\right)}^{\alpha }\right)}^{\prime }+q_2\left(s\right)x^{\alpha }\left({\theta }_2\left(s\right)\right) =0,$$

in the non-canonical case, and improved a number of pre-existing results.

Although there are many results of studies of the oscillation of solutions of delay differential equations, the results that concern the study of mixed equations are few—see, for example [13,14,15,16,17,18,19,20,21,22,23,24]. By using the Riccati transformation technique, Arul and Shobha [13] obtained some sufficient conditions for oscillation of the equation:

$${\left(r\left(s\right){\left(x\left(s\right)+a\left(s\right)x(s-\varrho )+b\left(s\right)x(s+\delta )\right)}^{\prime }\right)}^{\prime }+q\left(s\right)f\left(x\left(\theta \left(s\right)\right)\right) =0,$$

where $0\le a\left(s\right) \le a<\infty ,$$0\le b\left(s\right)\le b<\infty ,$ and $f\left(u\right)/u\ge k>0$. Dzurina et al. [22] established some criteria for the oscillation of the equation

$${\left(x\left(s\right)+p_{1}x(s-{\varrho }_1)+p_{2}x(s+{\varrho }_2)\right)}^{\prime \prime }=q_1\left(s\right)x(s-{\theta }_1)+q_2\left(s\right)x(s+{\theta }_2),$$

where ${\varrho }_i,{\theta }_i\ge 0$ are constants, $q_i$ is nonnegative, and $i=1,2$. Tunc et al. [24] studied the oscillatory behavior of solutions of the equation:

$${\left(r\left(s\right){\left({\left(x\left(s\right)+p_1\left(s\right)x\left({\varrho }_1\left(s\right)\right)+p_2\left(s\right)x\left({\varrho }_2\left(s\right)\right)\right)}^{\prime }\right)}^{\alpha }\right)}^{\prime }+q\left(s\right)x^{\alpha }\left(\theta \left(s\right)\right) =0,$$

in the canonical case $\pi \left(s_0\right) =\infty$, and considered the cases:

$$\left(\mathrm{i}\right)p_1\left(s\right)\ge 0,p_2\left(s\right)\ge 1\mathrm{and}{p}_2\left(s\right) \ne 1\mathrm{eventually}$$

and

$$\left(\mathrm{ii}\right)p_2\left(s\right)\ge 0,p_1\left(s\right)\ge 1\mathrm{and}{p}_2\left(s\right) \ne 1\mathrm{eventually}.$$

Thandapani et al. [23] considered the equation

$${\left({\left(x\left(s\right)+p_{1}x(s-{\varrho }_1)+p_{2}x(s+{\varrho }_2)\right)}^{\alpha }\right)}^{\prime \prime }+q_1\left(s\right)x^{\beta }(s-{\theta }_1)+q_2\left(s\right)x^{\gamma }(s+{\theta }_2)=0,$$

where $\alpha$, $\beta$, and $\gamma$ are the ratios of odd positive integers, and established some sufficient conditions for the oscillation of all of the solutions. For more results, techniques, and approaches that deal with the oscillation of delay differential equations of higher orders, see [25,26,27,28,29,30,31,32,33].

The objective of this paper is to study the oscillatory and asymptotic properties of a class of delay differential equations of mixed neutral type with the non-canonical operator. The oscillation criteria are obtained via only one condition, and hence, they are easy to apply. Moreover, by using generalized Riccati substitution, we get new criteria that improve some of the results reported in the literature. An example is provided to illustrate the significance of the main results.

2. Preliminary Results

In the following, we present the notations used in this study:

-

For the continuous function r, we define the integral operator $\kappa \left(u,v\right)$ for $u<v$ as

$$\kappa \left(u,v\right) :={\int }_u^v{r}^{-1/\alpha }\left(\delta \right)\mathrm{d}\delta ;$$

-

For any solution x of (1), we define the corresponding function $\upsilon$ as

$$\upsilon \left(s\right) :=x\left(s\right) + p_1\left(s\right)x\left({\varrho }_1\left(s\right)\right) + p_2\left(s\right)x\left({\varrho }_2\left(s\right)\right),\mathrm{for}s\ge s_0.$$

-

Briefly, we use the notations

$$\begin{array}{ccc}\hfill B_1\left(s\right)& :& =1-p_1\left(s\right)\frac{\kappa \left({\varrho }_1\left(s\right),\infty \right)}{\kappa \left(s,\infty \right)}-p_2\left(s\right),\hfill \\ \hfill H\left(s\right)& :& =q_1\left(s\right)B_2^{\alpha }\left({\theta }_1\left(s\right)\right) + q_2\left(s\right)B_2^{\alpha }\left({\theta }_2\left(s\right)\right),\hfill \\ \hfill G\left(s\right)& :& =q_1\left(s\right)B_1^{\alpha }\left({\theta }_1\left(s\right)\right) + q_2\left(s\right)B_1^{\alpha }\left({\theta }_2\left(s\right)\right)\hfill \end{array}$$

and

$$B_2\left(s\right) :=1-p_1\left(s\right)-p_2\left(s\right)\frac{\kappa \left(s_1,{\varrho }_2\left(s\right)\right)}{\kappa \left(s_1,s\right)},\mathrm{for}s\ge s_1\ge s_0.$$

Lemma 1

([6], Lemma 2.6). Assume that $\Theta \left(v\right) :=Av-B{\left(v-C\right)}^{\left(\alpha +1\right)/\alpha }$, where $A,$ B, and C are real constants, $B>0$, and $\alpha \in Q_{odd}^{+}$. Then, the maximum value of Θ on $\mathbb{R}$ at $v^{\ast }=C+{\left(\alpha A/\left(\left(\alpha +1\right)B\right)\right)}^{\alpha }$ is

$$\Theta \left(v^{\ast }\right) \le \underset{v\in \mathbb{R}}{max}\Theta \left(v\right) =AC+\frac{{\alpha }^{\alpha }}{{\left(\alpha +1\right)}^{\alpha +1}}{A}^{\alpha +1}{B}^{-\alpha }.$$

Lemma 2.

Let x be a positive solution of (1). If υ is decreasing, then

$${\left(\frac{\upsilon \left(s\right)}{\kappa \left(s,\infty \right)}\right)}^{\prime }\ge 0,$$

(3)

eventually. Further, if υ is increasing, then

$${\left(\frac{\upsilon \left(s\right)}{\kappa \left(s_1,s\right)}\right)}^{\prime }\le 0,$$

(4)

for all $s\ge s_1\ge s_0.$

Proof. 

Suppose that (1) has a positive solution x on $\left[s_0,\infty \right)$. Obviously, $\upsilon \left(s\right) \ge x\left(s\right) >0$ for all $s\ge s_1\ge s_0$. Thus, from (1), we get

$${\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }=-q_1\left(s\right)x^{\alpha }\left({\theta }_1\left(s\right)\right)-q_2\left(s\right)x^{\alpha }\left({\theta }_2\left(s\right)\right) \le 0.$$

Hence, $r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }$ is non-increasing, and so ${\upsilon }^{\prime }\left(s\right)$ has a constant sign for $s\ge s_1$.

Assume that ${\upsilon }^{\prime }\left(s\right) <0$ on $\left[s_1,\infty \right).$ Then,

$$\upsilon \left(s\right) \ge -{\int }_s^{\infty }{r}^{-1/\alpha }\left(\xi \right)r^{1/\alpha }\left(\xi \right){\upsilon }^{\prime }\left(\xi \right)\mathrm{d}\xi \ge -\kappa \left(s,\infty \right)r^{1/\alpha }\left(s\right){\upsilon }^{\prime }\left(s\right),$$

(5)

and so,

$${\left(\frac{\upsilon \left(s\right)}{\kappa \left(s,\infty \right)}\right)}^{\prime }=\frac{\kappa \left(s,\infty \right){\upsilon }^{\prime }\left(s\right)+r^{-1/\alpha }\left(s\right)\upsilon \left(s\right)}{{\left(\kappa \left(s,\infty \right)\right)}^2}\ge 0.$$

Next, assume that ${\upsilon }^{\prime }\left(s\right) >0$ on $\left[s_1,\infty \right)$. Hence, we obtain

$$\upsilon \left(s\right)\ge {\int }_{s_1}^s{r}^{-1/\alpha }\left(\xi \right)r^{1/\alpha }\left(\xi \right){\upsilon }^{\prime }\left(\xi \right)\mathrm{d}\xi \ge \kappa \left(s_1,s\right)r^{1/\alpha }\left(s\right){\upsilon }^{\prime }\left(s\right),$$

and it follows that

$${\left(\frac{\upsilon \left(s\right)}{\kappa \left(s_1,s\right)}\right)}^{\prime }=\frac{\kappa \left(s_1,s\right){\upsilon }^{\prime }\left(s\right) - r^{-1/\alpha }\left(s\right)\upsilon \left(s\right)}{{\kappa }^2\left(s_1,s\right)}\le 0.$$

Thus, the proof is complete. □

3. Main Results

Theorem 1.

Assume that $H\left(s\right) \ge G\left(s\right) >0$. If

$$\underset{s\to \infty }{limsup}{\int }_{s_1}^s\frac{1}{r^{1/\alpha }\left(u\right)}{\left({\int }_{s_1}^{u}G\left(\xi \right){\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)\mathrm{d}\xi \right)}^{1/\alpha }\mathrm{d}u=\infty ,$$

(6)

for $s_1\ge s_0$, then all solutions of (1) are oscillatory.

Proof. 

Assume the contrary: that (1) has a non-oscillatory solution x on $\left[s_0,\infty \right)$. Without loss of generality (since the substitution $y=-x$ transforms (1) into an equation of the same form), we suppose that x is an eventually positive solution. Then, there exists $s_1\ge s_0$ such that $x\left({\varrho }_1\left(s\right)\right)$, $x\left({\varrho }_2\left(s\right)\right),$$x\left({\theta }_1\left(s\right)\right)$, and $x\left({\theta }_2\left(s\right)\right)$ are positive for all $s\ge s_1$. Thus, from (1) and the definition of $\upsilon$, we note that $\upsilon \left(s\right)\ge x\left(s\right)>0$ and $r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }$ is non-increasing. Hence, ${\upsilon }^{\prime }>0$ or ${\upsilon }^{\prime }<0$ eventually.

Assume that ${\upsilon }^{\prime }\left(s\right) <0$ on $\left[s_1,\infty \right)$. By using Lemma 2, we have

$$\upsilon \left({\varrho }_1\left(s\right)\right) \le \frac{\kappa \left({\varrho }_1\left(s\right),\infty \right)}{\kappa \left(s,\infty \right)}\upsilon \left(s\right),$$

based on the fact that ${\varrho }_1\left(s\right) \le s$. Therefore,

$$\begin{array}{ccc}\hfill x\left(s\right)& =& \upsilon \left(s\right) - p_1\left(s\right)x\left({\varrho }_1\left(s\right)\right) - p_2\left(s\right)x\left({\varrho }_2\left(s\right)\right)\hfill \\ & \ge & \upsilon \left(s\right) - p_1\left(s\right)\upsilon \left({\varrho }_1\left(s\right)\right) - p_2\left(s\right)\upsilon \left({\varrho }_2\left(s\right)\right)\hfill \\ & \ge & \left(1-p_1\left(s\right)\frac{\kappa \left({\varrho }_1\left(s\right),\infty \right)}{\kappa \left(s,\infty \right)}-p_2\left(s\right)\right)\upsilon \left(s\right)\hfill \\ & =& B_1\left(s\right)\upsilon \left(s\right).\hfill \end{array}$$

Hence, (1) becomes

$${\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }\le -q_1\left(s\right)B_1^{\alpha }\left({\theta }_1\left(s\right)\right){\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right) - q_2\left(s\right)B_1^{\alpha }\left({\theta }_2\left(s\right)\right){\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right),$$

and since ${\theta }_1\left(s\right) \le {\theta }_2\left(s\right)$, we have

$$\begin{array}{ccc}\hfill {\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }& \le & -q_1\left(s\right)B_1^{\alpha }\left({\theta }_1\left(s\right)\right){\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right) - q_2\left(s\right)B_1^{\alpha }\left({\theta }_2\left(s\right)\right){\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right)\hfill \\ & \le & -\left(q_1\left(s\right)B_1^{\alpha }\left({\theta }_1\left(s\right)\right) + q_2\left(s\right)B_1^{\alpha }\left({\theta }_2\left(s\right)\right)\right){\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right)\hfill \\ & =& -G\left(s\right){\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right).\hfill \end{array}$$

(7)

Since ${\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }\le 0$, we have

$$r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\le r\left(s_1\right){\left({\upsilon }^{\prime }\left(s_1\right)\right)}^{\alpha }:=-L<0,$$

(8)

for all $s\ge s_1,$ and from (5) and (8), we have

$${\upsilon }^{\alpha }\left(s\right) \ge L{\kappa }^{\alpha }\left(s,\infty \right)\mathrm{for}\mathrm{all}s\ge s_1.$$

(9)

Combining (7) with (9) yields

$${\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }\le -G\left(s\right)L{\kappa }^{\alpha }\left({\theta }_2\left(s\right),\infty \right),$$

(10)

for all $s\ge s_1$. Integrating (10) from $s_1$ to s, we obtain

$$\begin{array}{ccc}\hfill r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }& \le & r\left(s_1\right){\left({\upsilon }^{\prime }\left(s_1\right)\right)}^{\alpha }-L{\int }_{s_1}^{s}G\left(\xi \right){\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)\mathrm{d}\xi \hfill \\ & \le & -L{\int }_{s_1}^{s}G\left(\xi \right){\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)\mathrm{d}\xi .\hfill \end{array}$$

Integrating the last inequality from $s_1$ to s, we get

$$\upsilon \left(s\right) \le \upsilon \left(s_1\right)-L^{1/\alpha }{\int }_{s_1}^s\frac{1}{r^{1/\alpha }\left(u\right)}{\left({\int }_{s_1}^{u}G\left(\xi \right){\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)\mathrm{d}\xi \right)}^{1/\alpha }\mathrm{d}u.$$

Passing to the limit as $s\to \infty$, we arrive at a contradiction with (6). Now, assume that ${\upsilon }^{\prime }\left(s\right)>0$ on $\left[s_1,\infty \right).$ From Lemma 2, we arrive at

$$\upsilon \left({\varrho }_2\left(s\right)\right)\le \frac{\kappa \left(s_1,{\varrho }_2\left(s\right)\right)}{\kappa \left(s_1,s\right)}\upsilon \left(s\right).$$

(11)

From the definition of $\upsilon$, we obtain

$$\begin{array}{ccc}\hfill x\left(s\right)& =& \upsilon \left(s\right)-p_1\left(s\right)x\left({\varrho }_1\left(s\right)\right)-p_2\left(s\right)x\left({\varrho }_2\left(s\right)\right)\hfill \\ & \ge & \upsilon \left(s\right)-p_1\left(s\right)\upsilon \left({\varrho }_1\left(s\right)\right)-p_2\left(s\right)\upsilon \left({\varrho }_2\left(s\right)\right).\hfill \end{array}$$

(12)

Using that (11) and $\upsilon \left({\varrho }_1\left(s\right)\right)\le \upsilon \left(s\right)$, where ${\varrho }_1\left(s\right)<s$ in (12), we obtain

$$\begin{array}{ccc}\hfill x\left(s\right)& \ge & \upsilon \left(s\right)\left(1-p_1\left(s\right)-p_2\left(s\right)\frac{\kappa \left(s_1,{\varrho }_2\left(s\right)\right)}{\kappa \left(s_1,s\right)}\right)\hfill \\ & \ge & B_2\left(s\right)\upsilon \left(s\right).\hfill \end{array}$$

(13)

Hence, (1) becomes

$${\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }\le -q_1\left(s\right)B_2^{\alpha }\left({\theta }_1\left(s\right)\right){\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right)-q_2\left(s\right)B_2^{\alpha }\left({\theta }_2\left(s\right)\right){\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right),$$

and since ${\theta }_1\left(s\right)\le {\theta }_2\left(s\right)$, we have

$$\begin{array}{ccc}\hfill {\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }& \le & -q_1\left(s\right)B_2^{\alpha }\left({\theta }_1\left(s\right)\right){\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right)-q_2\left(s\right)B_2^{\alpha }\left({\theta }_2\left(s\right)\right){\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right)\hfill \\ & \le & -\left(q_1\left(s\right)B_2^{\alpha }\left({\theta }_1\left(s\right)\right)+q_2\left(s\right)B_2^{\alpha }\left({\theta }_2\left(s\right)\right)\right){\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right)\hfill \\ & =& -H\left(s\right){\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right).\hfill \end{array}$$

(14)

On the other hand, it follows from (6) and (C2) that ${\int }_{s_1}^{s}G\left(\xi \right){\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)\mathrm{d}\xi$ must be unbounded. Further, since ${\kappa }^{\prime }\left(s,\infty \right)<0$, it is easy to see that

$${\int }_{s_1}^{s}G\left(\xi \right)\mathrm{d}\xi \to \infty \mathrm{as}s\to \infty .$$

(15)

Integrating (14) from $s_2$ to s, we get

$$\begin{array}{ccc}\hfill r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }& \le & r\left(s_2\right){\left({\upsilon }^{\prime }\left(s_2\right)\right)}^{\alpha }-{\int }_{s_2}^{s}H\left(\xi \right){\upsilon }^{\alpha }\left({\theta }_1\left(\xi \right)\right)\mathrm{d}\xi \hfill \\ & \le & r\left(s_2\right){\left({\upsilon }^{\prime }\left(s_2\right)\right)}^{\alpha }-{\upsilon }^{\alpha }\left({\theta }_1\left(s_2\right)\right){\int }_{s_2}^{s}H\left(\xi \right)\mathrm{d}\xi .\hfill \end{array}$$

Since $H\left(s\right)>G\left(s\right)$, we get

$$r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\le r\left(s_2\right){\left({\upsilon }^{\prime }\left(s_2\right)\right)}^{\alpha }-{\upsilon }^{\alpha }\left({\theta }_1\left(s_2\right)\right){\int }_{s_2}^{s}G\left(\xi \right)\mathrm{d}\xi ,$$

(16)

which, with (15), contradicts the fact that ${\upsilon }^{\prime }\left(s\right) >0$. The proof is complete. □

Theorem 2.

Assume that $H\left(s\right) \ge G\left(s\right) >0$. If

$$\underset{s\to \infty }{limsup}{\kappa }^{\alpha }\left({\theta }_2\left(s\right),\infty \right){\int }_{s_1}^{s}G\left(\xi \right)\mathrm{d}\xi >1,$$

(17)

then all solutions of (1) are oscillatory.

Proof. 

Assume the contrary: that (1) has a non-oscillatory solution x on $\left[s_0,\infty \right)$. Without loss of generality (since the substitution $y=-x$ transforms (1) into an equation of the same form), we suppose that x is an eventually positive solution. Then, there exists $s_1 \ge s_0$ such that $x\left({\varrho }_1\left(s\right)\right) >0$, $x\left({\varrho }_2\left(s\right)\right) >0,$$x\left({\theta }_1\left(s\right)\right) >0$, and $x\left({\theta }_2\left(s\right)\right) >0$ for all $s\ge s_1.$ As in the proof of Theorem 1, ${\upsilon }^{\prime }>0$ or ${\upsilon }^{\prime }<0$ eventually.

Assume that ${\upsilon }^{\prime }<0$ on $\left[s_1,\infty \right)$. Integrating (7) from $s_1$ to s, we get

$$\begin{array}{ccc}\hfill r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }& \le & r\left(s_1\right){\left({\upsilon }^{\prime }\left(s_1\right)\right)}^{\alpha }-{\int }_{s_1}^{s}G\left(\xi \right){\upsilon }^{\alpha }\left({\theta }_2\left(\xi \right)\right)\mathrm{d}\xi \hfill \\ & \le & -{\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right){\int }_{s_1}^{s}G\left(\xi \right)\mathrm{d}\xi .\hfill \end{array}$$

(18)

Since ${\theta }_2\left(s\right)\ge s,$ then from (3), we have

$$\upsilon \left({\theta }_2\left(s\right)\right) \ge \frac{\kappa \left({\theta }_2\left(s\right),\infty \right)}{\kappa \left(s,\infty \right)}\upsilon \left(s\right),$$

(19)

and using (19) and (5) in (18), we obtain

$$r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\le r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }{\kappa }^{\alpha }\left({\theta }_2\left(s\right),\infty \right){\int }_{s_1}^{s}G\left(\xi \right)\mathrm{d}\xi .$$

(20)

Dividing both sides of inequality (20) by $r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }$ and taking the $limsup$, we get

$$\underset{s\to \infty }{limsup}{\kappa }^{\alpha }\left({\theta }_2\left(s\right),\infty \right){\int }_{s_1}^{s}G\left(\xi \right)\mathrm{d}\xi \le 1,$$

we obtain a contradiction with the condition (17).

Now, assume that ${\upsilon }^{\prime }>0$ on $\left[s_1,\infty \right).$ From (17) and the fact that $\kappa \left({\theta }_2\left(s\right),\infty \right) <\infty$, we have that (15) holds. Then, this part of the proof is similar to that of Theorem 1. Therefore, the proof is complete. □

Theorem 3.

Assume that $H\left(s\right) \ge G\left(s\right) >0$ and (15) hold. Further, if the differential equation

$${\upsilon }^{\prime }\left(s\right) + \frac{1}{r^{1/\alpha }\left(s\right)}\frac{\kappa \left({\theta }_2\left(s\right),\infty \right)}{\kappa \left({\theta }_1\left(s\right),\infty \right)}{\left({\int }_{s_1}^{s}G\left(\xi \right)\mathrm{d}\xi \right)}^{1/\alpha }\upsilon \left({\theta }_1\left(s\right)\right) =0$$

(21)

is oscillatory, then all solutions of (1) are oscillatory.

Proof. 

Assume the contrary: that (1) has a non-oscillatory solution x on $\left[s_0,\infty \right)$. Without loss of generality (since the substitution $y=-x$ transforms (1) into an equation of the same form), we suppose that x is an eventually positive solution. Then, there exists $s_1\ge s_0$ such that $x\left({\varrho }_1\left(s\right)\right) >0$, $x\left({\varrho }_2\left(s\right)\right) >0,$$x\left({\theta }_1\left(s\right)\right) >0$, and $x\left({\theta }_2\left(s\right)\right) >0$ for all $s\ge s_1.$ As in the proof of Theorem 1, ${\upsilon }^{\prime }>0$ or ${\upsilon }^{\prime }<0$ eventually.

Assume that ${\upsilon }^{\prime }<0$ on $\left[s_1,\infty \right)$. Since ${\theta }_2\left(s\right) \ge {\theta }_1\left(s\right),$ we get, from (3), that

$$\upsilon \left({\theta }_2\left(s\right)\right) \ge \frac{\kappa \left({\theta }_2\left(s\right),\infty \right)}{\kappa \left({\theta }_1\left(s\right),\infty \right)}\upsilon \left({\theta }_1\left(s\right)\right),$$

which, with (18), gives

$$r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\le \frac{{\kappa }^{\alpha }\left({\theta }_2\left(s\right),\infty \right)}{{\kappa }^{\alpha }\left({\theta }_1\left(s\right),\infty \right)}{\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right){\int }_{s_1}^{s}G\left(\xi \right)\mathrm{d}\xi .$$

Now, we see that $\upsilon >0$ is a solution of the inequality

$${\upsilon }^{\prime }\left(s\right) + \frac{1}{r^{1/\alpha }\left(s\right)}\frac{\kappa \left({\theta }_2\left(s\right),\infty \right)}{\kappa \left({\theta }_1\left(s\right),\infty \right)}{\left({\int }_{s_1}^{s}G\left(\xi \right)\mathrm{d}\xi \right)}^{1/\alpha }\upsilon \left({\theta }_1\left(s\right)\right) \le 0.$$

Using [34], we find that (21) also has a positive solution—a contradiction.

By proceeding as in the proof of Theorem 1, the proof of this theory is completed. □

Corollary 1.

Assume that $H\left(s\right) \ge G\left(s\right) >0$ and (15) hold. If

$$\underset{s\to \infty }{liminf}{\int }_{{\theta }_1\left(s\right)}^s\frac{1}{r^{1/\alpha }\left(u\right)}\frac{\kappa \left({\theta }_2\left(u\right),\infty \right)}{\kappa \left({\theta }_1\left(u\right),\infty \right)}{\left({\int }_{s_1}^{u}G\left(\xi \right)\mathrm{d}\xi \right)}^{1/\alpha }\mathrm{d}u>\frac{1}{\mathrm{e}},$$

(22)

then all solutions of (1) are oscillatory.

Proof. 

Using ([35], Theorem 2), we have that (22) implies the oscillation of (21). From Theorem 3, we have that (1) is oscillatory. □

Theorem 4.

Assume that $H\left(s\right)>0,$$G\left(s\right)>0$. If there exist functions $\psi ,\delta \in C^1\left(\left[s_0,\infty \right),\left(0,\infty \right)\right)$, and $s_1\in \left[s_0,\infty \right)$ such that

$$\underset{s\to \infty }{limsup}\left\{\frac{{\kappa }^{\alpha }\left(s,\infty \right)}{\delta \left(s\right)}{\int }_{s_1}^s\left(\delta \left(\xi \right)G\left(\xi \right)\frac{{\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)}{{\kappa }^{\alpha }\left(\xi ,\infty \right)}-\frac{r\left(\xi \right){\left({\delta }^{\prime }\left(\xi \right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{\left(\delta \left(\xi \right)\right)}^{\alpha }}\right)\mathrm{d}\xi \right\} >1$$

(23)

and

$$\underset{s\to \infty }{limsup}{\int }_{s_1}^s\left(\psi \left(\xi \right)H\left(\xi \right) -\frac{1}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{r\left(\xi \right){\left({\psi }^{\prime }\left(\xi \right)\right)}^{\alpha +1}}{{\psi }^{\alpha }\left(\xi \right){\left({\theta }_1^{\prime }\left(\xi \right)\right)}^{\alpha }}\right)\mathrm{d}\xi =\infty ,$$

(24)

then all solutions of (1) are oscillatory.

Proof. 

Assume the contrary: that (1) has a non-oscillatory solution x on $\left[s_0,\infty \right)$. Without loss of generality (since the substitution $y=-x$ transforms (1) into an equation of the same form), we suppose that x is an eventually positive solution. Then, there exists $s_1\ge s_0$ such that $x\left({\varrho }_1\left(s\right)\right) >0$, $x\left({\varrho }_2\left(s\right)\right) >0,$$x\left({\theta }_1\left(s\right)\right) >0$, and $x\left({\theta }_2\left(s\right)\right) >0$ for all $s\ge s_1.$ From Theorem 1, ${\upsilon }^{\prime }>0$ or ${\upsilon }^{\prime }<0$ eventually.

Assume that ${\upsilon }^{\prime }<0$ on $\left[s_1,\infty \right).$ As in the proof of Theorem 1, we arrive at (7). Now, we define the function

$$\omega \left(s\right) =\delta \left(s\right)\left(\frac{r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }}{{\upsilon }^{\alpha }\left(s\right)}+\frac{1}{{\kappa }^{\alpha }\left(s,\infty \right)}\right)\mathrm{on}\left[s_1,\infty \right).$$

(25)

From (5), we get that $\omega \ge 0$ on $\left[s_1,\infty \right).$ Differentiating (25), we obtain

$$\begin{array}{ccc}\hfill {\omega }^{\prime }\left(s\right)& =& \frac{{\delta }^{\prime }\left(s\right)}{\delta \left(s\right)}\omega \left(s\right) + \delta \left(s\right)\frac{{\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }}{{\upsilon }^{\alpha }\left(s\right)}-\alpha \delta \left(s\right)r\left(s\right){\left(\frac{{\upsilon }^{\prime }\left(s\right)}{\upsilon \left(s\right)}\right)}^{\alpha +1}\hfill \\ & & +\frac{\alpha \delta \left(s\right)}{r^{1/\alpha }\left(s\right){\kappa }^{\alpha +1}\left(s,\infty \right)}\hfill \\ & \le & \frac{{\delta }^{\prime }\left(s\right)}{\delta \left(s\right)}\omega \left(s\right) + \delta \left(s\right)\frac{{\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }}{{\upsilon }^{\alpha }\left(s\right)}-\frac{\alpha }{{\left(\delta \left(s\right)r\left(s\right)\right)}^{1/\alpha }}{\left(\omega \left(s\right)-\frac{\delta \left(s\right)}{{\kappa }^{\alpha }\left(s,\infty \right)}\right)}^{\left(\alpha +1\right)/\alpha }\hfill \\ & & +\frac{\alpha \delta \left(s\right)}{r^{1/\alpha }\left(s\right){\kappa }^{\alpha +1}\left(s,\infty \right)}.\hfill \end{array}$$

(26)

Combining (7) and (26), we have

$$\begin{array}{ccc}\hfill {\omega }^{\prime }\left(s\right)& \le & -\frac{\alpha }{{\left(\delta \left(s\right)r\left(s\right)\right)}^{1/\alpha }}{\left(\omega \left(s\right)-\frac{\delta \left(s\right)}{{\kappa }^{\alpha }\left(s,\infty \right)}\right)}^{\left(\alpha +1\right)/\alpha }-\delta \left(s\right)G\left(s\right)\frac{{\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right)}{{\upsilon }^{\alpha }\left(s\right)}\hfill \\ & & +\frac{\alpha \delta \left(s\right)}{r^{1/\alpha }\left(s\right){\kappa }^{\alpha +1}\left(s,\infty \right)}+\frac{{\delta }^{\prime }\left(s\right)}{\delta \left(s\right)}\omega \left(s\right).\hfill \end{array}$$

(27)

Using Lemma 1 with $A:={\delta }^{\prime }\left(s\right)/\delta \left(s\right),$ $B:=\alpha {\left(\delta \left(s\right)r\left(s\right)\right)}^{-1/\alpha },$ $C:=\delta \left(s\right)/{\kappa }^{\alpha }\left(s,\infty \right)$ and $\xi :=\omega$, we get

$$\begin{array}{ccc}\hfill \frac{{\delta }^{\prime }\left(s\right)}{\delta \left(s\right)}\omega \left(s\right)-\frac{\alpha }{{\left(\delta \left(s\right)r\left(s\right)\right)}^{1/\alpha }}{\left(\omega \left(s\right)-\frac{\delta \left(s\right)}{{\kappa }^{\alpha }\left(s,\infty \right)}\right)}^{\left(\alpha +1\right)/\alpha }& \le & \frac{r\left(s\right)}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{{\left({\delta }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\left(\delta \left(s\right)\right)}^{\alpha }}\hfill \\ & & +\frac{{\delta }^{\prime }\left(s\right)}{{\kappa }^{\alpha }\left(s,\infty \right)},\hfill \end{array}$$

(28)

and since $s\le {\theta }_2\left(s\right)$, we arrive at

$$\upsilon \left({\theta }_2\left(s\right)\right) \ge \frac{\kappa \left({\theta }_2\left(s\right),\infty \right)}{\kappa \left(s,\infty \right)}\upsilon \left(s\right),$$

(29)

which, in view of (27), (28), and (29), gives

$$\begin{array}{ccc}\hfill {\omega }^{\prime }\left(s\right)& \le & \frac{{\delta }^{\prime }\left(s\right)}{{\kappa }^{\alpha }\left(s,\infty \right)}+\frac{1}{{\left(\alpha +1\right)}^{\alpha +1}}r\left(s\right)\frac{{\left({\delta }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\left(\delta \left(s\right)\right)}^{\alpha }}-\delta \left(s\right)G\left(s\right)\frac{{\upsilon }^{\alpha }\left({\theta }_2\left(s\right)\right)}{{\upsilon }^{\alpha }\left(s\right)}\hfill \\ & & +\frac{\alpha \delta \left(s\right)}{r^{1/\alpha }\left(s\right){\kappa }^{\alpha +1}\left(s,\infty \right)}\hfill \\ & \le & -\delta \left(s\right)G\left(s\right)\frac{{\kappa }^{\alpha }\left({\theta }_2\left(s\right),\infty \right)}{{\kappa }^{\alpha }\left(s,\infty \right)}+{\left(\frac{\delta \left(s\right)}{{\kappa }^{\alpha }\left(s,\infty \right)}\right)}^{\prime }+\frac{r\left(s\right){\left({\delta }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{\left(\delta \left(s\right)\right)}^{\alpha }}.\hfill \end{array}$$

(30)

Integrating (30) from $s_2$ to $s,$ we arrive at

$$\begin{array}{ccc}\hfill {\int }_{s_2}^s\left(\delta \left(\xi \right)G\left(\xi \right)\frac{{\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)}{{\kappa }^{\alpha }\left(\xi ,\infty \right)}-\frac{r\left(\xi \right){\left({\delta }^{\prime }\left(\xi \right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{\left(\delta \left(\xi \right)\right)}^{\alpha }}\right)\mathrm{d}\xi & \le & {\left.\left(\frac{\delta \left(s\right)}{{\kappa }^{\alpha }\left(s,\infty \right)}-\omega \left(s\right)\right)\right|}_{s_2}^s\hfill \\ & \le & -{\left.\left(\delta \left(s\right)\frac{r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }}{{\upsilon }^{\alpha }\left(s\right)}\right)\right|}_{s_2}^s.\hfill \end{array}$$

(31)

From (5), we have

$$-\frac{r^{1/\alpha }\left(s\right){\upsilon }^{\prime }\left(s\right)}{\upsilon \left(s\right)}\le \frac{1}{\kappa \left(s,\infty \right)},$$

which, in view of (31), implies

$$\frac{{\kappa }^{\alpha }\left(s,\infty \right)}{\delta \left(s\right)}{\int }_{s_2}^s\left(\delta \left(\xi \right)G\left(\xi \right)\frac{{\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)}{{\kappa }^{\alpha }\left(\xi ,\infty \right)}-\frac{r\left(\xi \right){\left({\delta }^{\prime }\left(\xi \right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{\left(\delta \left(\xi \right)\right)}^{\alpha }}\right)\mathrm{d}\xi \le 1.$$

Thus, we get a contradiction with (23).

Now, assume that ${\upsilon }^{\prime }\left(s\right) >0$ on $\left[s_1,\infty \right).$ Let us define the Riccati function

$$\phi \left(s\right) =\psi \left(s\right)\frac{r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }}{{\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right)},\mathrm{on}\left[s_1,\infty \right).$$

(32)

We find that $\phi \ge 0$ on $\left[s_1,\infty \right).$ Differentiating (32), we get

$${\phi }^{\prime }\left(s\right) =\frac{{\psi }^{\prime }\left(s\right)}{\psi \left(s\right)}\phi \left(s\right) + \psi \left(s\right)\frac{{\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }}{{\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right)}-\alpha \psi \left(s\right)r\left(s\right)\frac{{\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }{\upsilon }^{\prime }\left({\theta }_1\left(s\right)\right){\theta }_1^{\prime }\left(s\right)}{{\upsilon }^{\alpha +1}\left({\theta }_1\left(s\right)\right)}.$$

(33)

Combining (14) and (33), we have

$${\phi }^{\prime }\left(s\right) \le \frac{{\psi }^{\prime }\left(s\right)}{\psi \left(s\right)}\phi \left(s\right) - \psi \left(s\right)H\left(s\right) - \alpha \psi \left(s\right)r\left(s\right)\frac{{\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }{\upsilon }^{\prime }\left({\theta }_1\left(s\right)\right){\theta }_1^{\prime }\left(s\right)}{{\upsilon }^{\alpha +1}\left({\theta }_1\left(s\right)\right)}.$$

Since ${\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }<0$ and ${\theta }_1\left(s\right) \le s,$ we arrive at

$${\phi }^{\prime }\left(s\right) \le \frac{{\psi }^{\prime }\left(s\right)}{\psi \left(s\right)}\phi \left(s\right) - \psi \left(s\right)H\left(s\right) - \alpha \psi \left(s\right)r\left(s\right){\theta }_1^{\prime }\left(s\right)\frac{{\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\upsilon }^{\alpha +1}\left({\theta }_1\left(s\right)\right)},$$

and from (32), we have

$${\phi }^{\prime }\left(s\right)\le \frac{{\psi }^{\prime }\left(s\right)}{\psi \left(s\right)}\phi \left(s\right)-\psi \left(s\right)H\left(s\right)-\frac{\alpha {\theta }_1^{\prime }\left(s\right)}{{\psi }^{1/\alpha }\left(s\right)r^{1/\alpha }\left(s\right)}{\varphi }^{\left(\alpha +1\right)/\alpha }\left(s\right).$$

Using the inequality

$$Kv-s{v}^{{}^{\left(\alpha +1\right)/\alpha }}\le \frac{{\alpha }^{\alpha }}{{(\alpha +1)}^{\alpha +1}}\frac{K^{\alpha +1}}{s^{\alpha }},s>0,$$

(34)

with $K={\psi }^{\prime }\left(s\right)/\psi \left(s\right),$ $s=\alpha {\theta }_1^{\prime }\left(s\right)/{\psi }^{1/\alpha }\left(s\right)r^{1/\alpha }\left(s\right),$ and $v=\phi ,$ we have

$${\phi }^{\prime }\left(s\right) \le -\psi \left(s\right)H\left(s\right) + \frac{1}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{r\left(s\right){\left({\psi }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\psi }^{\alpha }\left(s\right){\left({\theta }_1^{\prime }\left(s\right)\right)}^{\alpha }}.$$

(35)

Integrating (35) from $s_2$ to $s,$ we arrive at

$${\int }_{s_2}^s\left(\psi \left(\xi \right)H\left(\xi \right)-\frac{1}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{r\left(\xi \right){\left({\psi }^{\prime }\left(\xi \right)\right)}^{\alpha +1}}{{\psi }^{\alpha }\left(\xi \right){\left({\theta }_1^{\prime }\left(\xi \right)\right)}^{\alpha }}\right)\mathrm{d}\xi \le \phi \left(s_2\right).$$

Taking the limsup on both sides of this inequality, we have a contradiction with (24). The proof of the theorem is complete. □

Theorem 5.

Assume that $H\left(s\right) >0$ and $G\left(s\right) >0$. If there exist the functions $\delta \in C^1\left(\left[s_0,\infty \right),\left(0,\infty \right)\right)$ and $s_1\in \left[s_0,\infty \right)$ such that (23) and

$$\underset{s\to \infty }{liminf}\frac{\alpha }{\Psi \left(s\right)}{\int }_s^{\infty }\frac{{\theta }_1^{\prime }\left(\xi \right)}{r^{1/\alpha }\left(\xi \right)}{\Psi }^{\left(\alpha +1\right)/\alpha }\left(\xi \right)\mathrm{d}\xi >\frac{\alpha }{{\left(\alpha +1\right)}^{\left(\alpha +1\right)/\alpha }}$$

(36)

hold, where

$$\Psi \left(s\right) ={\int }_s^{\infty }H\left(\xi \right)\mathrm{d}\xi ,$$

then all solutions of (1) are oscillatory.

Proof. 

Assume the contrary: that (1) has a non-oscillatory solution x on $\left[s_0,\infty \right)$. Without loss of generality (since the substitution $y=-x$ transforms (1) into an equation of the same form), we suppose that x is an eventually positive solution. Then, there exists $s_1\ge s_0$ such that $x\left({\varrho }_1\left(s\right)\right) >0$, $x\left({\varrho }_2\left(s\right)\right) >0,$$x\left({\theta }_1\left(s\right)\right) >0$, and $x\left({\theta }_2\left(s\right)\right) >0$ for all $s\ge s_1.$ Theorem 1 yields that ${\upsilon }^{\prime }$ eventually has one sign.

Assume that ${\upsilon }^{\prime }\left(s\right)<0$ on $\left[s_1,\infty \right).$ The proof is similar to that of Theorem 4.

Now, assume that ${\upsilon }^{\prime }\left(s\right)>0$ on $\left[s_1,\infty \right).$ Let us define the Riccati function

$$\phi \left(s\right) =\frac{r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }}{{\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right)}.$$

(37)

We see that $\phi \ge 0$ on $\left[s_1,\infty \right).$ Differentiating (37), we arrive at

$${\phi }^{\prime }\left(s\right) =\frac{{\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }}{{\upsilon }^{\alpha }\left({\theta }_1\left(s\right)\right)}-\alpha r\left(s\right)\frac{{\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }{\upsilon }^{\prime }\left({\theta }_1\left(s\right)\right){\theta }_1^{\prime }\left(s\right)}{{\upsilon }^{\alpha +1}\left({\theta }_1\left(s\right)\right)}.$$

(38)

Combining (14) and (38), we have

$${\phi }^{\prime }\left(s\right) \le -H\left(s\right)-\alpha r\left(s\right)\frac{{\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }{\upsilon }^{\prime }\left({\theta }_1\left(s\right)\right){\theta }_1^{\prime }\left(s\right)}{{\upsilon }^{\alpha +1}\left({\theta }_1\left(s\right)\right)}.$$

Since ${\left(r\left(s\right){\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha }\right)}^{\prime }<0$ and ${\theta }_1\left(s\right)\le s,$ we arrive at

$${\phi }^{\prime }\left(s\right) \le -H\left(s\right) - \alpha r\left(s\right){\theta }_1^{\prime }\left(s\right)\frac{{\left({\upsilon }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\upsilon }^{\alpha +1}\left({\theta }_1\left(s\right)\right)},$$

which, with (37), gives

$${\phi }^{\prime }\left(s\right)\le -H\left(s\right)-\frac{\alpha {\theta }_1^{\prime }\left(s\right)}{r^{1/\alpha }\left(s\right)}{\phi }^{\left(\alpha +1\right)/\alpha }\left(s\right).$$

(39)

Integrating (39) from s to ∞, and using the fact that $\phi \left(s\right) >0$ and ${\phi }^{\prime }\left(s\right) <0$, we get

$$-\phi \left(s\right) \le -{\int }_s^{\infty }H\left(\xi \right)\mathrm{d}\xi -{\int }_s^{\infty }\frac{\alpha {\theta }_1^{\prime }\left(\xi \right)}{r^{1/\alpha }\left(\xi \right)}{\phi }^{\left(\alpha +1\right)/\alpha }\left(\xi \right)\mathrm{d}\xi .$$

Hence, we have

$$\frac{\phi \left(s\right)}{\Psi \left(s\right)}\ge 1+\frac{1}{\Psi \left(s\right)}{\int }_s^{\infty }\frac{\alpha {\theta }_1^{\prime }\left(\xi \right)}{r^{1/\alpha }\left(\xi \right)}{\Psi }^{\left(\alpha +1\right)/\alpha }\left(\xi \right){\left(\frac{\phi \left(\xi \right)}{\Psi \left(\xi \right)}\right)}^{\left(\alpha +1\right)/\alpha }\mathrm{d}\xi .$$

(40)

Let $\vartheta ={inf}_{s\ge s}\phi \left(s\right)/\Psi \left(s\right)$;then, obviously, $\vartheta \ge 1$. Hence, it follows from (40) and (36) that

$$\vartheta \ge 1+\alpha {\left(\frac{\vartheta }{\alpha +1}\right)}^{\left(\alpha +1\right)/\alpha }$$

or

$$\frac{\vartheta }{\alpha +1}\ge \frac{1}{\alpha +1}+\frac{\alpha }{\alpha +1}{\left(\frac{\vartheta }{\alpha +1}\right)}^{\left(\alpha +1\right)/\alpha },$$

which contradicts the admissible value of $\vartheta$ and $\alpha$. Therefore, the proof is complete. □

Corollary 2.

Assume that $H\left(s\right) >0$ and $G\left(s\right) >0.$ If (36) and either

$$\underset{s\to \infty }{limsup}{\int }_s^s\left(G\left(\xi \right){\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)-\frac{{\alpha }^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{r}^{1/\alpha }\left(\xi \right)\kappa \left(\xi ,\infty \right)}\right)\mathrm{d}\xi >1,$$

(41)

$$\underset{s\to \infty }{limsup}{\kappa }^{\alpha -1}\left(s,\infty \right){\int }_s^s\left(G\left(\xi \right)\frac{{\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)}{{\kappa }^{\alpha -1}\left(\xi ,\infty \right)}-\frac{1}{{\left(\alpha +1\right)}^{\alpha +1}{r}^{1/\alpha }\left(\xi \right){\kappa }^{\alpha }\left(\xi ,\infty \right)}\right)\mathrm{d}\xi >1,$$

(42)

or

$$\underset{s\to \infty }{limsup}{\kappa }^{\alpha }\left(s,\infty \right){\int }_s^{s}G\left(\xi \right)\frac{{\kappa }^{\alpha }\left({\theta }_2\left(\xi \right),\infty \right)}{{\kappa }^{\alpha }\left(\xi ,\infty \right)}\mathrm{d}\xi >1,$$

(43)

hold, then all solutions of (1) are oscillatory.

Proof. 

By choosing $\delta \left(s\right) ={\kappa }^{\alpha }\left(s,\infty \right),$$\delta \left(s\right) =\kappa \left(s,\infty \right),$ or $\delta \left(s\right) =1$, the condition (23) reduces to one of the conditions (41)–(43), respectively. □

Example 1.

Consider the second-order neutral differential equation

$${\left(s^2{\left(x\left(s\right) + p_1^{\ast }x\left(\frac{s}{\lambda }\right) + p_2^{\ast }x\left(\lambda s\right)\right)}^{\prime }\right)}^{\prime }+q_1^{\ast }x\left(\frac{s}{\mu }\right) + q_2^{\ast }x\left(\mu s\right) =0,$$

(44)

where $s\ge 1,$ $\lambda \ge 1,$ $\mu \ge 1,$ $p_1^{\ast }>p_2^{\ast }$, and $\lambda \left(p_1^{\ast }+p_2^{\ast }\right) \in \left(0,1\right)$. Now, we note that $r\left(s\right) =s^2,$$p_1\left(s\right) =p_1^{\ast },$$p_2\left(s\right) =p_2^{\ast },$${\varrho }_1\left(s\right) =s/\lambda ,$${\varrho }_2\left(s\right) =\lambda s,$$q_1\left(s\right) =q_1^{\ast },$$q_2\left(s\right) =q_2^{\ast },$ ${\theta }_1\left(s\right) =s/\mu ,$ and ${\theta }_2\left(s\right) =\mu s$. Thus, we have that

$$B_1\left(s\right) =1-\lambda p_1^{\ast }-p_2^{\ast },B_2\left(s\right) =1-p_1^{\ast }-p_2^{\ast }\left(\frac{s-\frac{1}{\lambda }}{s-1}\right)$$

and

$$G\left(s\right) = \left(q_1^{\ast }+q_2^{\ast }\right)\left(1-\lambda p_1^{\ast }-p_2^{\ast }\right).$$

Set $W\left(s\right) = \left(s-\frac{1}{\lambda }\right)/\left(s-1\right)$. Since ${lim}_{s\to \infty }W\left(s\right)=1$, there exists $s_{ϵ}>s_0$ such that $W\left(s\right)<1+ϵ$ for all $ϵ>0$ and every $s\ge s_{ϵ}$. By choosing $ϵ=\lambda -1,$ we obtain $W\left(s\right)<\lambda$ for all $s\ge s_{\ast }$. Thus, and taking into account the fact that $p_1^{\ast }>p_2^{\ast }$ and $\lambda p_1^{\ast }+p_2^{\ast }\in \left(0,1\right)$, we get that $B_2\ge B_1>0$. Now, from Theorem 2, we have that equation (44) is oscillatory if

$$q_1^{\ast }+q_2^{\ast }>\frac{\mu }{1-\lambda p_1^{\ast }-p_2^{\ast }}.$$

(C1)

On the other hand, using Corollary 1, we see that (44) is oscillatory if

$$q_1^{\ast }+q_2^{\ast }>\frac{\mu }{\left(1-\lambda p_1^{\ast }-p_2^{\ast }\right)}\frac{\mu }{\mathrm{e}ln\mu }.$$

(C2)

Next, since $W\left(s\right) <\lambda$ for all $s\ge s_{\ast }$, we find that $B_2\left(s\right) >1-\left(p_1^{\ast }+\lambda p_2^{\ast }\right)$, and so, $H\left(s\right) > \left(q_1^{\ast }+q_2^{\ast }\right)\left(1-\left(p_1^{\ast }+\lambda p_2^{\ast }\right)\right)$. Hence, by choosing $\psi \left(s\right) =1$, condition (24) holds, directly. Using Theorem 4, we see that (44) is oscillatory if

$$q_1^{\ast }+q_2^{\ast }>\frac{1}{4}\frac{\mu }{\left(1-\lambda p_1^{\ast }-p_2^{\ast }\right)}.$$

(C3)

Remark 1.

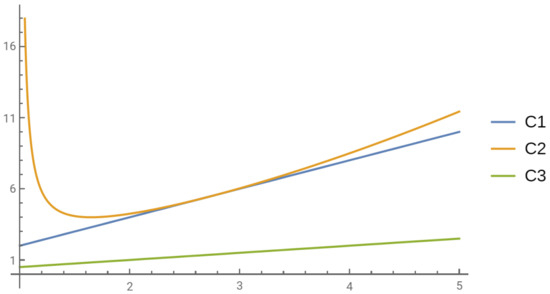
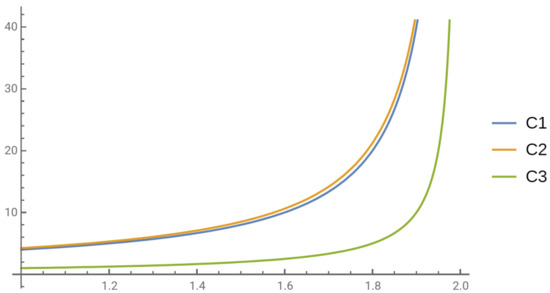
Taking the fact that $\mu >eln\mu$ into account, it is easy to notice that condition (C3) supports the most efficient condition for oscillation of (44). Figure 1 and Figure 2 display a comparison of the criteria (C1)–(C3).

Figure 1. Comparison of the criteria (C1)–(C3) when $\lambda =2,$ $p_1^{\ast }=0.25$, and $p_2^{\ast }=0$.

Figure 2. Comparison of the criteria (C1)–(C3) when $\mu =2,$ $p_1^{\ast }=0.5$, and $p_2^{\ast }=0$.

Remark 2.

In the special case of (44), $p_2^{\ast }=q_2^{\ast }=0$, that is,

$${\left(s^2{\left(x\left(s\right) + p_1^{\ast }x\left(\frac{s}{\lambda }\right)\right)}^{\prime }\right)}^{\prime }+q_1^{\ast }x\left(\frac{s}{\mu }\right) =0.$$

The oscillation criterion (C3) reduces to

$$q_1^{\ast }>\frac{1}{4}\frac{\mu }{\left(1-\lambda p_1^{\ast }\right)},$$

(45)

which is the exact criterion that was obtained in Example 3.1 in [7]. Moreover, if $p_1^{\ast }=0$ and $\mu =1$, then condition (45) reduces so that $q_1^{\ast }>1/4$, which is a sharp condition for oscillation of the second-order Euler equation.

4. Conclusions

Most works that studied the oscillatory behavior of mixed equations regarded the canonical case $\pi \left(l_0\right) =\infty$. Likewise, works that were concerned with the non-canonical case of neutral equations obtained two conditions for testing the oscillation. In this paper, we focused on studying the non-canonical case, and we created criteria with only one condition that is easy to verify. Therefore, our results are an extension, complement, and improvement to previous results in the literature. It is interesting to extend the results of this paper to higher-order equations.