Solution of Exterior Quasilinear Problems Using Elliptical Arc Artificial Boundary
Abstract
1. Introduction
2. Exact Quasilinear Elliptical Arc Artificial Boundary Condition
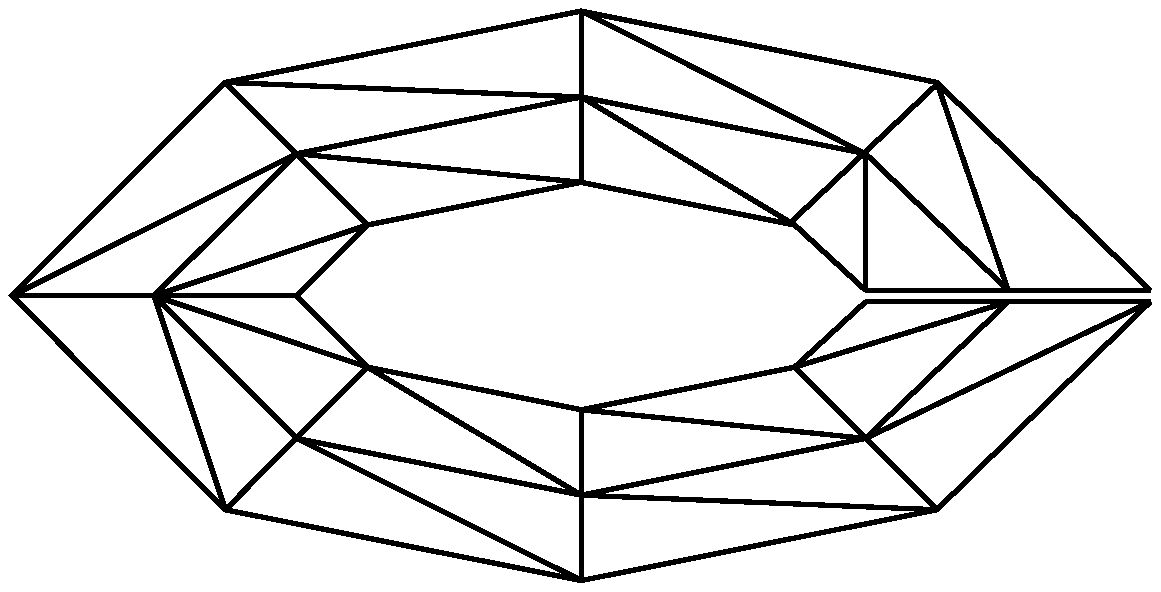
3. Finite Element Approximation
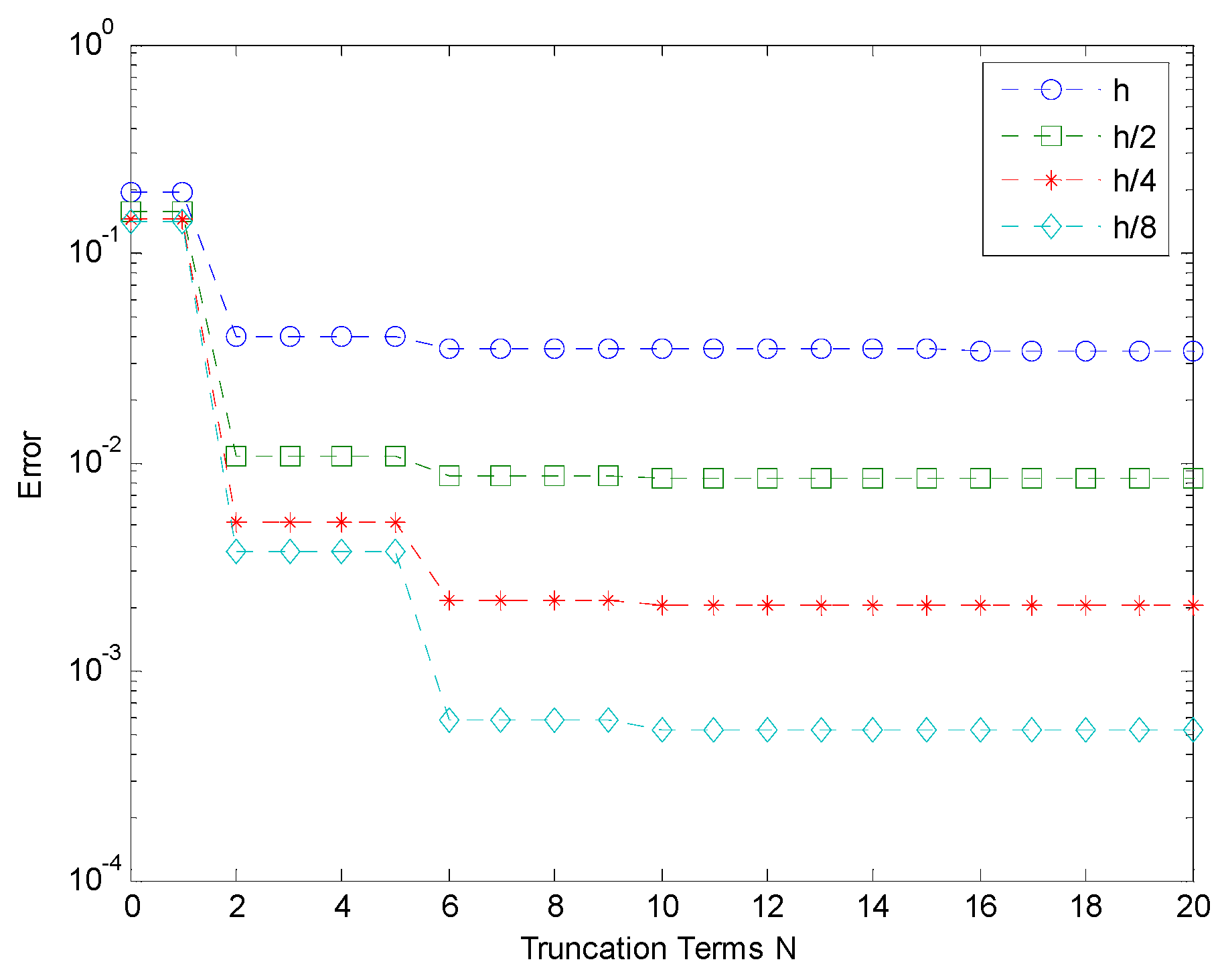
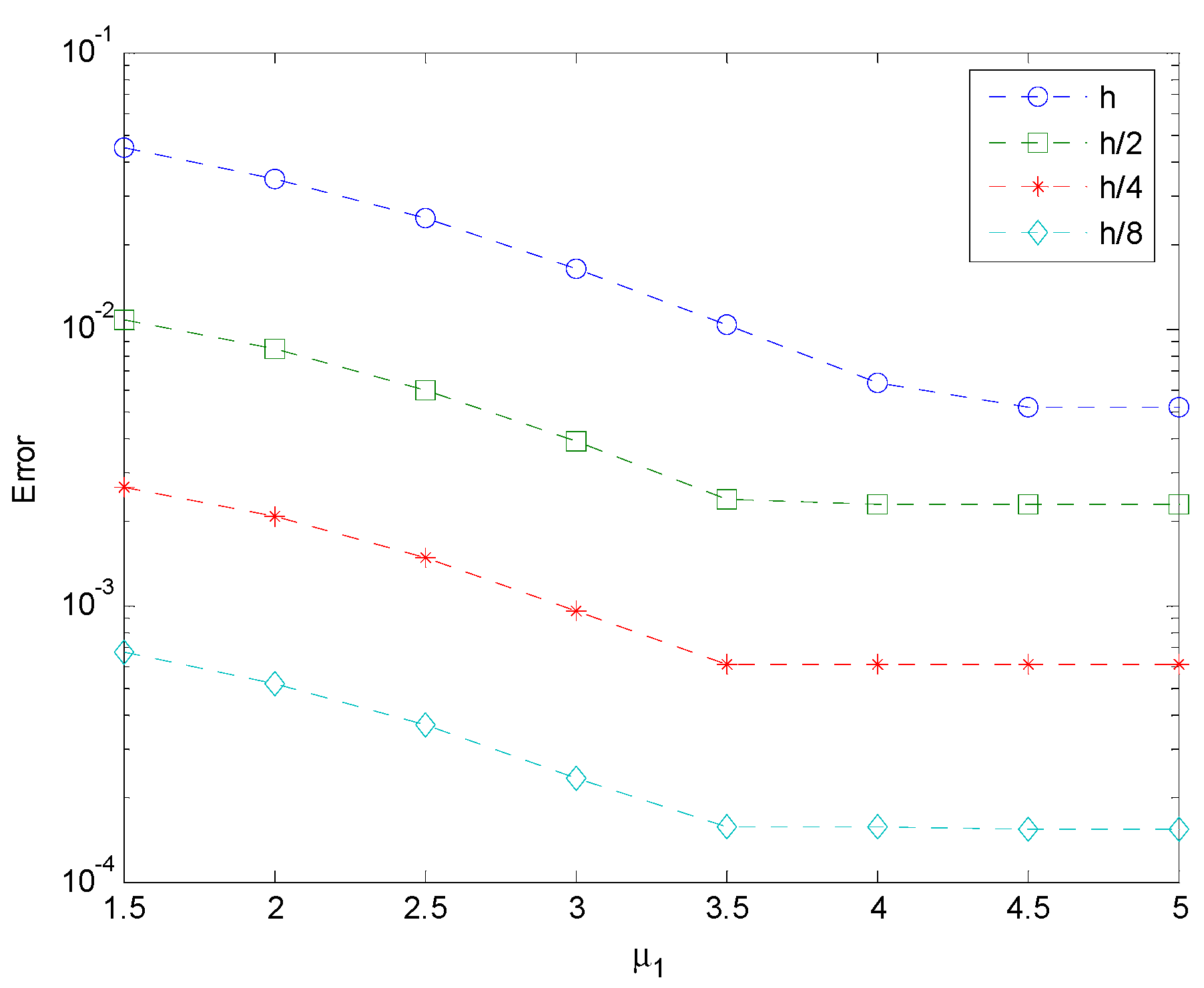
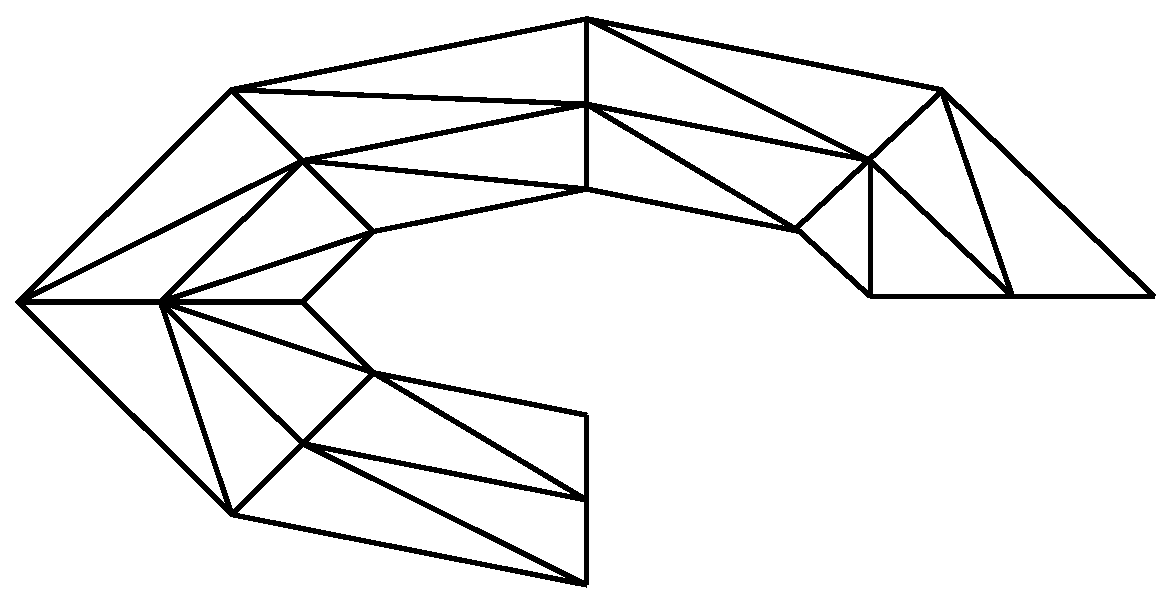
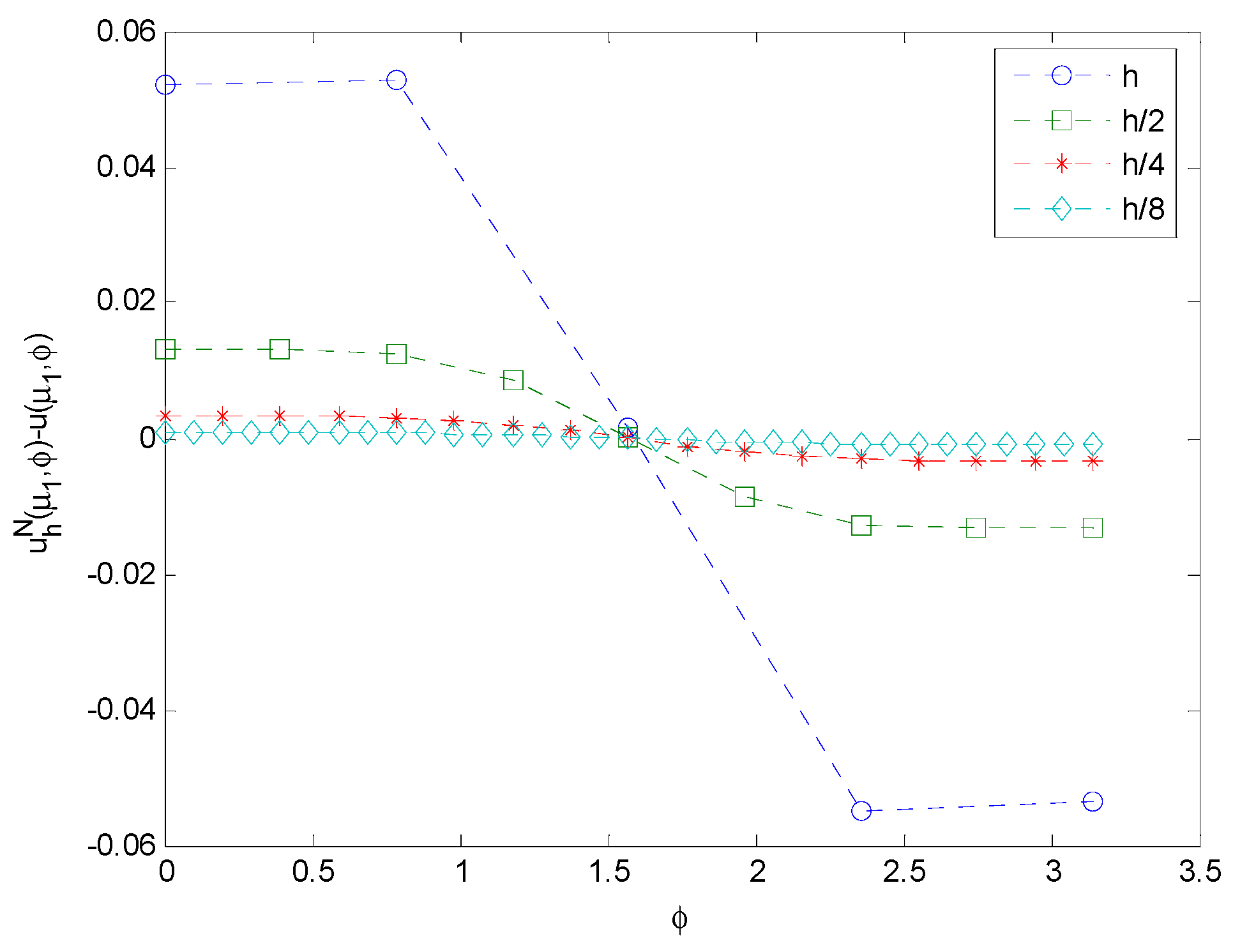
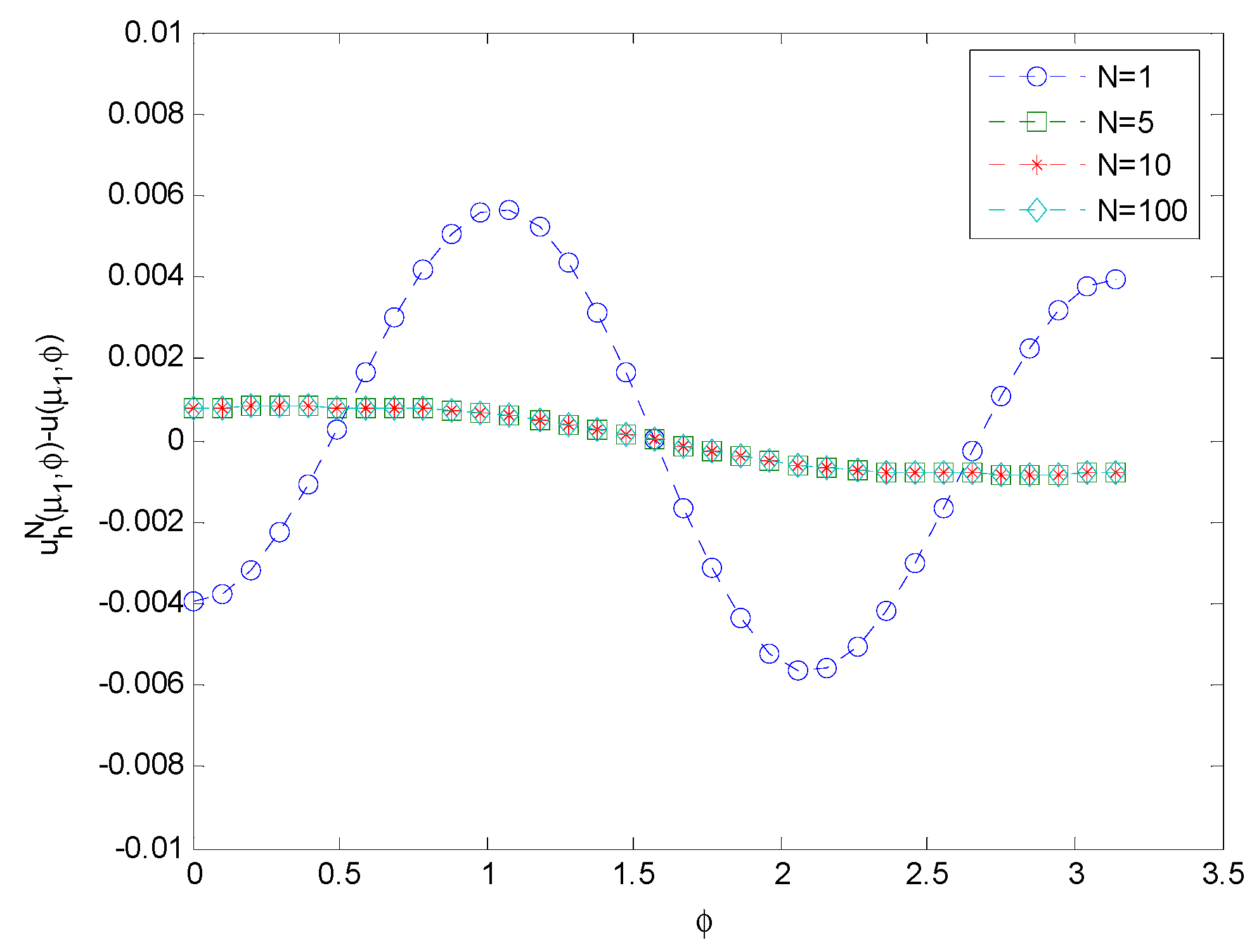
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, H.; Wu, X. Approximation of infinite boundary condition and its application to finite element methods. J. Comput. Math. 1985, 3, 179–192. [Google Scholar]
- Han, H.; Wu, X. The Artificial Boundary Method—Numerical Solutions of Partial Differential Equations on Unbounded Domains; Tsinghua University Press: Beijing, China, 2009. [Google Scholar]
- Feng, K. Finite element method and natural boundary reduction. In Proceedings of International Congress Mathematicians; Polish Academy Press: Warszawa, Poland, 1983. [Google Scholar]
- Feng, K.; Yu, D. Canonical integral equations of elliptic boundary value problems and their numerical solutions. In Proceedings of China-France Symposium on the Finite Element Methods; Science Press: Beijing, China, 1983. [Google Scholar]
- Yu, D. Natural Boundary Integral Method and Its Applications; Kluwer Academic Publishers: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Keller, J.B.; Givoli, D. Exact non-reflecting boundary conditions. J. Comput. Phys. 1989, 82, 172–192. [Google Scholar] [CrossRef]
- Grote, M.J.; Keller, J.B. On non-reflecting boundary conditions. J. Comput. Phys. 1995, 122, 231–243. [Google Scholar] [CrossRef]
- Hlavacek, I.; Krizek, M.; Maly, J. On Galerkin approximations of a quasi-linear nonpotential elliptic problem of a nonmonotone type. J. Math. Anal. Appl. 1994, 184, 168–189. [Google Scholar] [CrossRef]
- Hlavacek, I. A note on the Neumann problem for a quasilinear elliptic problem of a nonmonotone type. J. Math. Anal. Appl. 1997, 211, 365–369. [Google Scholar] [CrossRef][Green Version]
- Chow, S. Finite element error estimates for non-linear elliptic equations of monotone type. Numer. Math. 1989, 54, 373–393. [Google Scholar] [CrossRef]
- Liu, W. Finite element approximations of a nonlinear elliptic equation arising from biomaterial problems in elastic-plastic mechanics. Numer. Math. 2000, 86, 491–506. [Google Scholar] [CrossRef]
- Korotov, S.; Křížek, M. Finite element analysis of varitional crimes for a quasilinear elliptic problem in 3D. Numer. Math. 2000, 84, 549–576. [Google Scholar] [CrossRef]
- Milner, F.A. Mixed finite element methods for quasilinear second-order elliptic problems. Math. Comput. 1985, 44, 303–320. [Google Scholar] [CrossRef]
- Meddahi, S. On a mixed finite element formulation of a second-order quasilinear problem in the plane. Numer. Methods Part. Differ. Equ. 2004, 20, 90–103. [Google Scholar] [CrossRef]
- Karchevsky, M.; Fedotov, A. Error estimates and iterative procedure for mixed finite element solution of second-order quasi-linear elliptic problems. Comput. Methods Appl. Math. 2004, 4, 445–463. [Google Scholar] [CrossRef]
- Houston, P.; Robson, J.; Suli, E. Discontinuous Galerkin finite element approximation of quasilinear elliptic boundary value problems I: The scalar case. IMA J. Numer. Anal. 2005, 25, 726–749. [Google Scholar] [CrossRef]
- Houston, P.; Suli, E.; Wihler, T.P. A posteriori error analysis of hp-version discontinuous Galerkin finite-element methods for second-order quasi-linear elliptic PDEs. IMA J. Numer. Anal. 2008, 28, 245–273. [Google Scholar] [CrossRef]
- Bi, C.; Ginting, V. A posteriori error estimates of discontinuous Galerkin method for nonmonotone quasi-linear elliptic problems. J. Sci. Comput. 2013, 55, 659–687. [Google Scholar] [CrossRef]
- Sun, S.; Huang, Z.; Wang, C. Weak galerkin finite element method for a class of quasilinear elliptic problems. Appl. Math. Lett. 2018, 79, 67–72. [Google Scholar] [CrossRef]
- Garau, E.M.; Morin, P.; Zuppa, C. Convergence of an adaptive Kačanov FEM for quasi-linear problems. Appl. Numer. Math. 2011, 61, 512–529. [Google Scholar] [CrossRef]
- Guo, L.; Bi, C. Adaptive finite element method for nonmonotone quasi-linear elliptic problems. Comput. Math. Appl. 2021, 93, 94–105. [Google Scholar] [CrossRef]
- Han, H.; Huang, Z.; Yin, D. Exact artificial boundary conditions for quasilinear elliptic equations in unbounded domains. Commun. Math. Sci. 2008, 6, 71–83. [Google Scholar] [CrossRef]
- Liu, D.; Yu, D. A FEM-BEM formulation for an exterior quasilinear elliptic problem in the plane. J. Comput. Math. 2008, 26, 378–389. [Google Scholar]
- Liu, B.; Du, Q. On the coupled of NBEM and FEM for an anisotropic quasilinear problem in elongated domains. Am. J. Comput. Math. 2012, 2, 143–155. [Google Scholar] [CrossRef]
- Liu, B.; Du, Q. The Coupling of NBEM and FEM for quasilinear problems in a bounded or unbounded domain with a concave angle. J. Comput. Math. 2013, 31, 308–325. [Google Scholar]
- Ingham, D.B.; Kelmanson, M.A. Boundary Integral Equation Analyses of Singular, Potential, and Biharmonic Problems; Springer: Beilin/Heidelberg, Germany, 1984. [Google Scholar]
- Chen, Y.; Du, Q. Solution of exterior problems using elliptical arc artificial boundary. Eng. Lett. 2016, 24, 202–206. [Google Scholar]
- Chen, C.; Zhou, J. Boundary Element Methods; Academic Press: London, UK, 1992. [Google Scholar]
- Meddahi, S.; Gonzalez, M.; Perez, P. On a FEM-BEM formulation for an exterior quasilinear problem in the plane. SIAM J. Numer. Anal. 2000, 37, 1820–1837. [Google Scholar] [CrossRef][Green Version]
- Xu, J. Theory of Multilevel Methods. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1989. [Google Scholar]

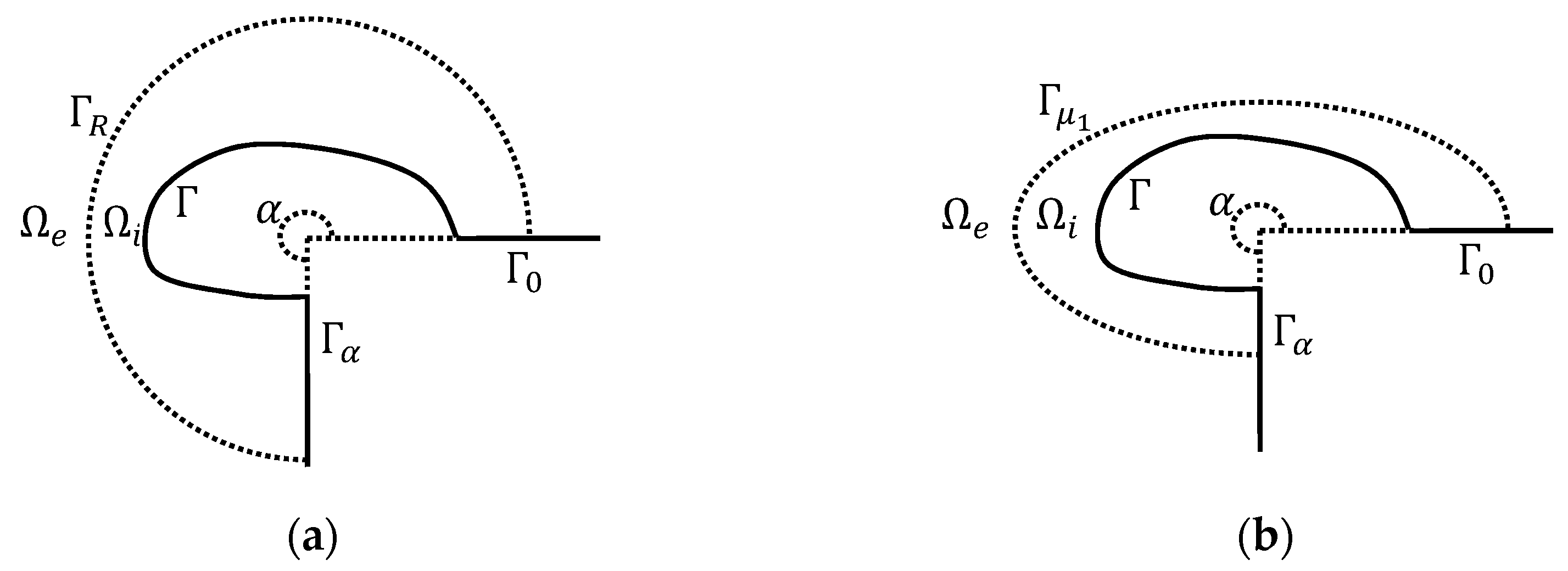



| Mesh | Error | Error |
|---|---|---|
| 0.078260 | 0.034508 | |
| 0.015860 | 0.008414 | |
| 0.003546 | 0.002088 | |
| 0.000840 | 0.000521 |
| Mesh | Error | Error |
|---|---|---|
| h | 0.064870 | 0.033738 |
| h/2 | 0.011609 | 0.007163 |
| h/4 | 0.002651 | 0.001776 |
| h/8 | 0.000636 | 0.000444 |
| Mesh | Error | Error |
|---|---|---|
| 0.091740 | 0.054584 | |
| 0.018287 | 0.013246 | |
| 0.004044 | 0.003287 | |
| 0.000950 | 0.000820 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Du, Q. Solution of Exterior Quasilinear Problems Using Elliptical Arc Artificial Boundary. Mathematics 2021, 9, 1598. https://doi.org/10.3390/math9141598
Chen Y, Du Q. Solution of Exterior Quasilinear Problems Using Elliptical Arc Artificial Boundary. Mathematics. 2021; 9(14):1598. https://doi.org/10.3390/math9141598
Chicago/Turabian StyleChen, Yajun, and Qikui Du. 2021. "Solution of Exterior Quasilinear Problems Using Elliptical Arc Artificial Boundary" Mathematics 9, no. 14: 1598. https://doi.org/10.3390/math9141598
APA StyleChen, Y., & Du, Q. (2021). Solution of Exterior Quasilinear Problems Using Elliptical Arc Artificial Boundary. Mathematics, 9(14), 1598. https://doi.org/10.3390/math9141598






