Abstract
The math modeling challenge CoSIAM is a competition based on interdisciplinary collaborative work challenges. This research seeks to demonstrate the value of this type of challenge-based competition as a learning strategy outside the classroom. Based on data, we conducted a qualitative study on the perception of the participants in the last three versions of the mathematical modeling challenge, in terms of the learning achieved, the benefits of their participation, the knowledge and skills they brought into play, and the change in their conception of modeling. The participants were undergraduate and graduate students in mathematics and other areas, from several Colombian and Mexican universities. The research yielded results in three directions. The first is related to the advantages and limitations of teamwork, the second explores the learning that arises from this experience, and the third is oriented to the disciplinary knowledge mobilized for the solution of this type of problematic situation. The study allowed concluding, among other issues, that learning based on interdisciplinary problem solving, formulated from a global perspective, enhances the acquisition of valuable skills for the participants.
1. Introduction
The math modeling challenge (MMC) is one of the annual events held by the Colombian section of the Society of Industrial and Applied Mathematics (CoSIAM), since 2017. During this event, teams of students from diverse universities and programs (not only mathematics) solve problems under restricted conditions of time and resources, using mathematics and computer science, promoting interdisciplinary work and giving rise to sketches of solutions to real problems of current national interest.
The teams, made up of four people in the undergraduate or graduate categories, are summoned to an event of ten continuous hours duration, at which they are presented with the problem to be solved and for which they are to sketch a solution, which is to be presented through a written document, a presentation, and annexes with demonstrations and prototypes. A group of professors from various universities evaluate and comment on the works received, in such a way that all the participants get feedback on their performance. The evaluation rubric of the submitted works considers the relevance of the proposed solution to the challenge, originality, modeling, simulation and functionality. The teams with the five best-rated solution sketches make a presentation the following day, in front of juries from the real sector, obtaining a new rating for their skills in presenting the work done. The work with the highest mark in each of the categories receives the award.
The first event started with universities in Bogotá (Colombia), but it quickly spread throughout the country, to the point that at the last two events the applied and industrial mathematics community of Mexico (MexSIAM) also participated actively.
In the four contests held so far, the specific challenges were chosen so that the participants could solve problems under an interdisciplinary approach. This choice of problems was related to the management that the organizing committee carried out with the industry, in such a way that the formulation of the challenges responded to a real need in the sectors of the national scope, and demanded an approach of complex systems on the part of the solution sketches. The problems are structured in a general way, considering central aspects related to the framework of the problem (theoretical and normative framework) and a research question that can be specifically contextualized by the participants, according to their disciplinary training.
The research questions for each of the themes of the four versions of the MMC were (1) early warning systems: “How can applied mathematics be implemented in early warning systems? Sketch a solution for a specific sector”, (2) sustainable development in rural landscapes: “How do we develop a social, economic, and environmental commitment for Colombian rural landscapes so that their sustainability is guaranteed? Sketch a solution for a specific landscape”, (3) the blue economy: “How to evaluate the articulation of different opportunities within the framework of the blue economy? Sketch a multidimensional solution for a specific territory”, and (4) management of situations related to the COVID-19 pandemic: “What is the importance and impact of individual and governmental actions to control the pandemic in Colombia?”
This paper shows the results of qualitative research aimed at characterizing the perception of the participants in the math modeling challenge in the period 2018–2020, regarding the learning they achieved, the benefits that their participation represented for their education, the previous knowledge and skills they brought into play, and the change in their conception of modeling before and after the contest.
To begin with, in the theoretical framework, the following four conceptual categories are developed that are the basis of the subsequent analysis of the results: hackathon; interdisciplinarity and collaborative work; modeling; and global perspective. Then, the results obtained from the application of written instruments to the participants are presented and discussed. At the end, conclusions are drawn that demonstrate the value of the math modeling challenge as a learning strategy based on interdisciplinary collaborative work challenges.
2. Theoretical Framework
Professionals are required to be managers of technological and scientific advances in the social environment in which they live, particularly in developing countries such as Colombia.
Given its ubiquity, mathematics is and will be present in the achievement of these advances; therefore, it is necessary that mathematics education includes spaces in which students face real problems and contexts, for which it is necessary to generate or update didactic strategies to develop skills that allow them to address real-world problems using theoretical knowledge and soft skills through computational tools, so that when they are professionals they can be a functional part of multidisciplinary teams.
The second modeling across the curriculum workshop, conducted by the Society for Industrial and Applied Mathematics in 2014 with the support of the National Science Foundation, is an example of the interest that this topic arouses in the social actors in charge of strengthening applied mathematics for the training of students before their application in the professional field. In Turner et al. [1] (p. 20), it is stated that “virtual experimentation is replacing many aspects of real-world application and the demand for modelers is increasing rapidly. This demand translates into jobs (…) we need to study and understand the STEM pipeline and the role modeling plays, or can play, in stimulating growth and vitality in quantitative disciplines.”
From mathematics education, the need arises to generate or update didactic strategies for the students to develop the skills that allow them to tackle real-world problems, from theoretical knowledge to soft skills through computational tools, so that when they are professionals, they can be a functional part of multidisciplinary teams [2,3,4].
Problem solving and knowledge production face the following three particular challenges: the complexity of real-world problems, fairness when using expert knowledge in decision making, and ensuring the relevance, assertiveness and timeliness of the knowledge generated for decision making, obtaining interdisciplinarity as a necessary strategy [5].
Interdisciplinarity generally refers to the appropriate synergy among the knowledge of different disciplines to produce knowledge that is more interesting than the sum of the individual contributions of the specialties, so that a complex problem can be addressed [6]. It is often compared to multidisciplinarity, which refers to the parallel involvement of a number of disciplines that do not mix, and to transdisciplinarity, which is the concept that breaks down boundaries due to the commitment between parties to transcend disciplines and co-produce knowledge. The evident conflict between the definitions has led to interpreting transdisciplinarity as interdisciplinarity in multiple contexts, so in this paper, following [6], we will speak of interdisciplinarity.
Regarding the complexity of real-world problems, it should be noted that their occurrence comes from the existence of non-linear and non-smooth relationships between the different elements of the systems about which we make decisions, together with the uncertainties of different areas of knowledge and practice [7], giving rise to the properties of emergence, dynamics, self-organization and adaptation of systems, which leads to the necessary requirement to implement interdisciplinary teamwork that studies the multiple variables that intersect in so-called complex systems [8].
Currently, teams that defy disciplinary boundaries and collaboratively address problems in complex systems have been shown to lead the agile transformations necessary for discoveries to be translated into implementations [9], facilitating the resolution of difficult-to-address problems [10] that a single discipline would not have the means to solve [11]. They have also generated spaces of mutual respect, adaptability and conflict resolution [12], and have made it possible for research work to become more efficient [5].
Interdisciplinary training for problem solving, particularly from mathematical modeling, coincides with the much-studied consideration of the importance of migrating from a learning model, where the protagonist of teaching (and learning) is the teacher and the relationship with the students does not go beyond transmission. The pedagogical trends point to meaningful learning, which is centered on the student and places the teacher no longer as a transmitter, but as a facilitator or mediator in the construction of knowledge.
Collaborative work especially benefits this important action in learning by grouping teaching strategies that engage the students with common goals. Again, the teacher becomes the guide of the teaching and learning process, rather than its protagonist [13].
In this context, the hackathon becomes an interesting educational strategy, based mainly on empathetic and collaborative work. “The term ‘hackathon’ combines ‘hack’—a solution achieved through intense innovation—and ‘marathon’—an event of defined duration and concentrated effort” [14] (p. 37). Its goal is the development of a gathering of students to design creative and innovative solutions to real-world scientific/social problems. With this aim, scientific and technological knowledge, imagination, collaborative work and entrepreneurial ‘spirit’ will be brought into play. On the other hand, the pedagogical/didactic aspiration has as its “objectives to raise awareness of technical talent […] and to foster a competitive but cooperative culture for talents to showcase their knowledge. It also allows participants to connect with faculty, labs, campus centers and, most importantly, with each other” [15] (p. 347).
This type of (informal) educational event is organized by sharing a challenge (usually ‘real’) with the participants (groups of students, preferably diverse insofar as being open to different readings of the world reinforces the scope of the innovation to be proposed) and inviting them to generate efficient solutions to the problem proposed. The work required to develop this solution is framed in a system of restricted resources (tools and time) and requires intense work under pressure [16].
Some benefits of hackathons for learning are the mobilization of skills for the solution of close and easily appropriated situations, continuous learning and learning from experience [17], connection with the productive sector (since in many cases the challenges to be solved are proposed by entities of the productive sector, whether private or public) and the starring role of collaborative action.
Another feature of hackathons, and in particular the math modeling challenge, is the inclusion of a global perspective. Authors, such as [18,19,20,21] and others, argue the growing importance of forming a global perspective in students and place it as one of the key objectives of education today.
This is not a new concept; it has been proposed since the 1920s by the World Education Fellowship, with its journal The New Era [20]. Especially in the last 40 years, “important work has been carried out in the United Kingdom and North America that is directly related to the development of a global dimension in the curriculum” (p. 270).
The global perspective is a way of perceiving and tapping into the world around us, and it also encompasses an understanding of globalization, and how each region of the world is interconnected economically, politically, and socially.
According to [19], a highly accepted approach to the subject, global perspective is a concept composed of the following five dimensions: perspective awareness, “state of the planet” awareness, cross-cultural awareness, knowledge of global dynamics, and awareness of human choices.
The definitions of each of these dimensions, as proposed by [19], are presented below:
- Perspective awareness: the recognition or awareness by the individual that he or she has a worldview that is not universally shared, that this worldview has been and continues to be shaped by influences that often escape conscious detection, and that others have worldviews that are profoundly different from one’s own (p. 162);
- State of the planet awareness: awareness of prevailing world conditions and developments, including emerging conditions and trends, e.g., population growth, migration, economic conditions, resources and physical environment, political developments, science and technology, law, health, conflicts between and within nations, etc. (p. 163);
- Cross-cultural awareness: awareness of the diversity of ideas and practices found in human societies around the world, how such ideas and practices compare, and including a limited recognition of how one’s own society’s ideas and forms may be viewed from other points of view (p. 164);
- Knowledge of global dynamics: some modest understanding of the key features and mechanisms of the world system, with emphasis on theories and concepts that can enhance intelligent awareness of global change (p. 165);
- Awareness of human choices: Some awareness of the choice issues facing individuals, nations, and the human species, as awareness and knowledge of the world system increases (p. 165).
The global perspective is one of the characteristic elements of the MMC, both as a means and as an end. As a means, it provides a reference to frame the problems proposed to the participants in global dynamics; as an end, it seeks those participants to develop the five dimensions of consciousness that it proposes [19].
These dimensions frame the development of the global perspective for the interdisciplinary approach to problems through mathematical modeling.
3. Methods
In order to analyze the information collected in the math modeling challenge event provided by the participants who attended in 2018, 2019 and 2020, qualitative information was analyzed using the Atlas TI 9 software based on grounded theory.
With respect to the sample, an appeal was made to the participating students in the previously named editions. A total of 55 participants agreed to participate in this study. Some of them participated in more than one competition, giving us a balanced panorama for each of the years, as follows: 23 participants in 2018, 25 in 2019 and 20 in 2020. These 55 students came from 14 different universities (12 Colombian and 2 Mexican), of 13 different undergraduate degrees and 2 different postgraduate degrees.
Considering the chosen research approach, due to its interpretive nature, this sample size was sufficient and guaranteed the theoretical saturation, proper and necessary when looking for emerging theories (in this case the taxonomic structure that explains the experience) typical of the research design based on grounded theory.
For the qualitative analysis of data, as stated above, we chose the grounded theory [22] because the objective of this research was, mainly, to let the data “speak” and to find taxonomic structures or emerging theories that could account for the phenomenon, that is, of the understanding that the participants had around the MMC.
For data collection, an online questionnaire with two sections was designed. The first section consisted of 5 questions that characterized the sample; Aspects such as name, university, career and year in which they participated in the event were included here. The second section consisted of 10 questions, some of them open and others with Likert-type scales. This questionnaire was triangulated to guarantee its credibility [23], consulting three different experts in mathematics education and applied mathematics, obtaining observations that allowed the improvement of the instrument.
For the qualitative analysis of the data (computer assisted—Atlas TI), it was decided to have an inductive, not deductive, coding scheme, that is, as the reading was carried out, the codes used emerged from the same analysis. Thus, we started with 55 primary documents (one for each participant) and after obtaining a theoretical saturation, it was possible to obtain 57 subcategories that described the findings. It is important to consider that, given the encoding process, the same code can appear multiple times in each primary document.
On the other hand, considering the purpose of this research, 5 items have been selected from the 10 questions included in the second section of the questionnaire. In this study, the results of the qualitative analysis of the 5 selected items will be presented, as they refer to the students’ feelings about certain characteristics of the competition. These questions (items) are as follows:
- What did you learn from the math modeling challenge experience?
- What knowledge or skills learned in your career were you able to implement in this activity to solve the challenge?
- State the benefits of working in an interdisciplinary team to solve the problem.
- State the challenges that working in an interdisciplinary team imposed on you to solve the problem.
- Write the three words that best represent for you the concept of mathematical modeling.
4. Results and Discussion
We present the results obtained from the analysis of the aforementioned questions, which were organized into three sections. The first referred to teamwork, particularly to challenges and their benefits; the second focused on the learning that emerges from this experience; and, lastly, the third focused on the disciplinary knowledge mobilized for the solution of this type of problem situation.
Regarding the challenges imposed by working in an interdisciplinary team to solve problems, the participants stated that the most significant challenges they had to face during the event were to transmit ideas and to be able to understand them, to manage to articulate ideas, to have assertive communication, to respond to the complexity of the problem they had to solve, and to work as a team. Students find important value in teamwork, as we can see in Table 1. Note that the frequency allows identification of the number of times that each subcategory appears in the analysis of the corresponding question, for all the primary documents analyzed, and that the percentage corresponds to the proportion of the appearance of that subcategory with respect to the totality of all the subcategories in that question.

Table 1.
Challenges in team work.
In turn, the participants consider that the most important benefits of working in an interdisciplinary team focus on having a holistic perspective of the phenomena, achieving skills and strengths working as a team, consolidating bases for the application of methodological tools to solve a problem, effectively solving a problem, and to be able to be aware of the specialized knowledge of each participant (see Table 2).

Table 2.
Benefits of team work.
Moreover, 71% of the students were part of a team made up of students with different disciplinary backgrounds, and 81% of those who were not on an interdisciplinary team considered that it would have been important or necessary to have one or more members of the different disciplines.
On the other hand, when we asked them about the learning that emerged in this innovative experience, the students stated that they came even closer to solving real-world problems, applying and knowing methodological tools, being creative and looking for alternative solutions to problems, solving a problem in a limited time or with limited resources through efficiency, and being able to articulate ideas from multiple knowledge bases (see Table 3).

Table 3.
MMC learnings.
According to the participants, the knowledge or skills learned in their respective study programs that were useful to them for solving the challenge were mathematics, mathematical modeling, programming, analysis, and differential equations (see Table 4).

Table 4.
Skills students used during the MMC.
The students were asked to define the concept of mathematical modeling using three words. As can be seen in the word cloud in Figure 1, for MMC participants, mathematical modeling is synonymous with representation, abstraction, simulation, prediction and equation, in that order of importance, although other synonyms were also associated.

Figure 1.
The main words that students associate with mathematical modeling.
It is of interest that among the main words that students associate with mathematical modeling are the words simulation and prediction. On the one hand, it is understood that mathematical modeling is a representation with mathematical symbols that uses simulation to obtain a specific result, in which specific data are required; however, the participants show that they do not know the difference between the two concepts. On the other hand, associating mathematical modeling with prediction shows that other purposes of modeling are unknown, such as diagnosis, explanation, and prescription, each of which answers different questions that define its purpose. The complete list of words related to modeling concept and their frequencies are presented in Table 5. A word cloud showing these results is presented in Figure 1.

Table 5.
Words related to modeling concept and their frequency.
Regarding the change in their concept of mathematical modeling, 44% of the participants considered that they did not change their concept after having participated in the MMC. It should be noted that 17% of them considered that their participation in the MMC strengthened their understanding of the concept.
Among the students who considered that there was a change in their concept of mathematical modeling after participating in the event, 29% claimed to have discovered the close connection of the concept with real problems and contexts, while 19% attributed the change in their conception to now having a clearer idea of the thought processes involved in mathematical modeling. We also identified justifications related to the awareness of the need for creativity, teamwork and interdisciplinarity, the functionality of the models and the complexity of real problems.
Of the fifty-seven emerging subcategories, which account for the perception that students have about the MMC, we have chosen those that correspond to the benefits that they could have in terms of learning, collaboration and empowerment. A Sankey diagram is shown in Figure 2, which makes the relationship between these ten aspects explicit. It is interesting to observe the different interconnections, especially in aspects such as teamwork, the holistic perspective and working under pressure.
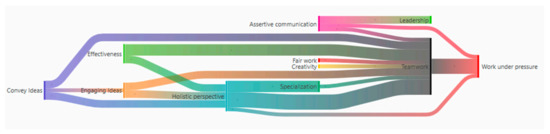
Figure 2.
Sankey diagram for emerging categories.
Those categories make sense because this type of meaningful learning guarantees, in students, the acquisition of new skills and competencies based on previous concepts, but restructuring and rearranging them based on an essentially active exercise of construction and tending towards a meaning of what has been learned (perhaps thought as a mobilization of competencies in context). This important action in learning especially benefits from collaborative work. The collaborative model groups teach strategies that commit the students to working collaboratively to achieve common goals. Once again, the teacher becomes a guide in the teaching and learning process, rather than the protagonist of it [13].
As described in the math modeling challenge, the problems proposed have a global perspective. According to what the students state in the surveys, they notice this perspective and value it positively (61% report a gain in holistic perspective among the benefits of participating in the event). In this sense, the need to solve these problems allows students to think beyond the local.
Indeed, among the possible dimensions of awareness that students can gain [19] the following stand out: awareness of perspective, by recognizing that their point of view on the understanding and solution of the problem is not the only one and that the other participants in their team may have completely different visions of their own; awareness of the state of the planet, given that the problems are global in nature and present current and relevant issues; awareness of global dynamics, because from the above awareness, they gain understanding of the ways in which the world works, especially through the feedback on each solution given by the jurors; and, of course, awareness of human choices, since with limited time and resources they must make choices, even if they do not always consider them optimal, which is a reflection of the real world.
Based on the above, it can be stated that the CoSIAM math modeling challenge is an educational strategy that strengthens the global perspective in its participants, through the simulation of problems with global characteristics that engage the students in taking into consideration these characteristics for their solution through interdisciplinary interactions.
In regard to the challenges proposed in the three events, 72.7% of the students considered that the problem assigned in the math modeling challenge was very important. However, only 25.5% considered that their proposed solution, with respect to the current needs of humanity, was very pertinent.
It is worth highlighting that a professional in mathematics faces the following reality: the quality of their results is measured not only by their good theoretical foundation, but also by their contribution to the solution of the proposed problem; the result is not meaningful if it is not coherent with the actual situation that has arisen. So, it is absolutely necessary to expose students, particularly those in STEAM programs, to real problems for which the solution process is not restricted to the mere application of problem solving, but rather for which mathematical modeling is necessary.
The math modeling challenge CoSIAM, as an educational strategy, allows participants to make the need to commit to the study and the discovery of new knowledge across the borders of the various disciplinary fields visible, in order to contribute to the technological, scientific and social development of their environment.
5. Conclusions
The data for this research were taken from the application of the instruments to the participants in three editions of the MMC. This is a limitation of the study, since there are only a few involved students; however, the information collected reveals emerging trends.
Another limitation of the study is that no information was included regarding the perceptions of the tutors, i.e., the teachers who train and present the teams to the challenge. This is a limitation that can be overcome in future versions of the MMC.
A mathematics professional is faced with the following reality: the quality of his results is measured not only by their good theoretical foundation, but also by their contribution to the solution of the problem posed; the result is meaningless if it is not coherent with the real situation that has been posed. So, it is absolutely necessary that students approach real problems by doing the whole process of mathematical modeling, which includes problem solving. In this sense, MMC becomes a propitious scenario to strengthen mathematical modeling skills, which will allow other students to enjoy the following benefits reported by the surveyed participants: having a holistic perspective of the phenomena, achieving skills and strengths working in a team, consolidating bases for the application of methodological tools for the solution of a problem, solving a problem efficiently, and being aware of the specialized knowledge of each participant.
Although skills in mathematics are the basis of a discussion in applied mathematics, it should be considered that interpersonal skills, such as communication, sympathy and empathy, are also essential for interdisciplinary work. Therefore, simulating real-life situations outside the classroom should be an essential part of the professional education process of applicants for work in applied mathematics.
The proposal of ideas that could be interesting for another discipline in an interdisciplinary environment demands the ability to disseminate knowledge that is unknown to the other discipline, or that requires another structure of thought.
Problem solving empowers the participant with the skills and knowledge acquired during their training process, which is observed in the level of purposeful participation they show during the MMC.
It is significant to understand that learning transcends the classroom, and that it can happen and be strengthened in settings other than those that occur in educational institutions. Having activities that allow students to mobilize skills and knowledge to solve real and close problems, in some controversial cases and under restricted conditions (time, resources), strengthens the student experience. Thus, hackathons, such as the MMC, have a significant impact on student learning, particularly in aspects or competencies that traditionally do not reside in the curriculum. Here, teamwork, openness to a holistic perspective, and work under pressure, for example, play a fundamental role. Other competencies or characteristics that benefit the learning experience are, for example, creativity and assertive communication.
Since the problems proposed in the different versions of the CMM are framed within the concept of global perspective, they motivated the participants to acquire, to a greater or lesser extent, dimensions of global awareness. For example, in the interdisciplinary work, participants acquired perspective awareness by realizing that their position, marked by their cognitive, personal and professional choices, is not the only one, and that it must be reconciled with those of their team members. Awareness of the state of the planet and of global dynamics was obtained from the problematization of situations, for example, the conditions of the blue economy or the situation of COVID-19 allowed them to situate themselves in the real state of the world. Moreover, of course, awareness of human choices was obtained from the socialization of the solution to the problem situations; this socialization allowed them to see that each solution has its own implications and is far from perfect. Indeed, among the possible dimensions of awareness that students can gain [19], the following stand out: awareness of perspective, by recognizing that their point of view on the understanding and solution of the problem is not the only one, and that the other participants in their team may have completely different visions of their own; awareness of the state of the planet, given that the problems are global in nature, and present current and relevant issues; awareness of global dynamics, because from the above awareness they gain understanding of the ways in which the world works, especially through the feedback on each solution given by the jurors; and, of course, awareness of human choices, since with limited time and resources they must make choices, even if they do not always consider them optimal, which is a reflection of the real world.
Author Contributions
Conceptualization, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; methodology, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; software, R.A.M.-R.; validation, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; formal analysis, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; investigation, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; resources, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; data curation, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; writing—original draft preparation, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; writing—review and editing, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; visualization, R.A.M.-R.; supervision, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R.; project administration, R.A.M.-R., D.H.B.-C., C.D.-F. and J.M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Turner, P.; Crowley, J.; Humpherys, J.; Levy, R.; Socha, K.; Ron, W. SIAM Modeling across the Curriculum: Report on a SIAM-NSF Workshop; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2014. [Google Scholar]
- Fowler, K.R.; Galluzzo, B.J.; Bliss, K.M. Math Modeling: Getting Started and Getting Solutions (First); Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2014. [Google Scholar]
- Hill-Cunningham, P.R.; Mott, M.S.; Hunt, A.-B. Facilitating an Elementary Engineering Design Process Module. Sch. Sci. Math. 2018, 118, 53–60. [Google Scholar] [CrossRef]
- Thuneberg, H.; Salmi, H.; Fenyvesi, K. Hands-On Math and Art Exhibition Promoting Science Attitudes and Educational Plans. Educ. Res. Int. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Kueffer, C.; Underwood, E.; Hadorn, G.H.; Holderegger, R.; Lehning, M.; Pohl, C.; Schirmer, M.; Schwarzenbach, R.; Stauffacher, M.; Wuelser, G.; et al. Enabling Effective Problem-oriented Research for Sustainable Development. Ecol. Soc. 2012, 17. [Google Scholar] [CrossRef] [Green Version]
- Brewer, G.D. The challenges of interdisciplinarity. Policy Sci. 1999, 32, 327–337. [Google Scholar] [CrossRef]
- Larson, K.L.; White, D.D.; Gober, P.; Wutich, A. Decision-Making under Uncertainty for Water Sustainability and Urban Climate Change Adaptation. Sustainability 2015, 7, 14761–14784. [Google Scholar] [CrossRef] [Green Version]
- Ostrom, E. A diagnostic approach for going beyond panaceas. Proc. Natl. Acad. Sci. USA 2007, 104, 15181–15187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ameredes, B.T.; Hellmich, M.R.; Cestone, C.M.; Wooten, K.C.; Ottenbacher, K.J.; Chonmaitree, T.; Anderson, K.; Brasier, A.R. The Multidisciplinary Translational Team (MTT) Model for Training and Development of Translational Research Investigators. Clin. Transl. Sci. 2015, 8, 533–541. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cantor, A.; DeLauer, V.; Martin, D.; Rogan, J. Training interdisciplinary “wicked problem” solvers: Applying lessons from HERO in community-based research experiences for undergraduates. J. Geogr. High. Educ. 2015, 39, 407–419. [Google Scholar] [CrossRef]
- Fuller, D.; Hobin, E.P.; Hystad, P.; Shareck, M. Challenges to interdisciplinary training for junior space, place and health researchers. Crit. Public Heal. 2012, 22, 1–7. [Google Scholar] [CrossRef]
- Hart, D.D.; Bell, K.P.; Lindenfeld, L.A.; Jain, S.; Johnson, T.R.; Ranco, D.; McGill, B. Strengthening the role of universities in addressing sustainability challenges: The Mitchell Center for Sustainability Solutions as an institutional experiment. Ecol. Soc. 2015, 20. [Google Scholar] [CrossRef] [Green Version]
- Bell, T.; Urhahne, D.; Schanze, S.; Ploetzner, R. Collaborative Inquiry Learning: Models, tools, and challenges. Int. J. Sci. Educ. 2010, 32, 349–377. [Google Scholar] [CrossRef] [Green Version]
- Olson, K.R.; Walsh, M.; Garg, P.; Steel, A.; Mehta, S.; Data, S.; Petersen, R.; Guarino, A.J.; Bailey, E.; Bangsberg, D.R. Health hackathons: Theatre or substance? A survey assessment of outcomes from healthcare-focused hackathons in three countries. BMJ Innov. 2017, 3, 37–44. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nandi, A.; Mandernach, M. Hackathons as an Informal Learning Platform. In Proceedings of the 47th ACM Technical Symposium on Computing Science Education, SIGCSE 16, ACM, New York, NY, USA, 2–5 March 2016; pp. 346–351. [Google Scholar]
- Lodato, T.J.; Disalvo, C. Issue-oriented hackathons as material participation. New Media Soc. 2016, 18, 539–557. [Google Scholar] [CrossRef]
- Boyd, E.M.; Fales, A.W. Reflective Learning. J. Humanist. Psychol. 1983, 23, 99–117. [Google Scholar] [CrossRef]
- Case, R. Key elements of a global perspective. Soc. Educ. 1993, 57, 318–325. [Google Scholar]
- Hanvey, R.G. An attainable global perspective. Theory Pract. 1982, 21, 162–167. [Google Scholar] [CrossRef]
- Hicks, D. Thirty Years of Global Education: A reminder of key principles and precedents. Educ. Rev. 2003, 55, 265–275. [Google Scholar] [CrossRef]
- Kirkwood, T.F. Our Global Age Requires Global Education: Clarifying Definitional Ambiguities. Soc. Stud. 2001, 92, 10–15. [Google Scholar] [CrossRef]
- McCann, T.; Polacsek, M. Understanding, choosing and applying grounded theory: Part 1. Nurse Res. 2018, 26, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Méndez-Romero, R.A. El Concepto de Excelencia Docente: Una Aproximación Multidimensional Inductivo-Deductiva Desde la Teoría Fundamentada, el Mapeo de la Ciencia y el Análisis Cualitativo de Contenido. Ph.D. Thesis, Universidad de Valladolid, Valladolid, Spain, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).