Generalised Proportional Integral Control for Magnetic Levitation Systems Using a Tangent Linearisation Approach
Abstract
1. Introduction
2. The Magnetic Levitation System and Problem Formulation
2.1. The Nonlinear Model
2.2. Tangent Linearisation
2.3. Flatness of the Linearised Magnetic Levitation System
2.4. Problem Formulation
3. Generalised Proportional Integral Controller Design
3.1. A Flatness-Based Pole Placement Approach for Stabilisation
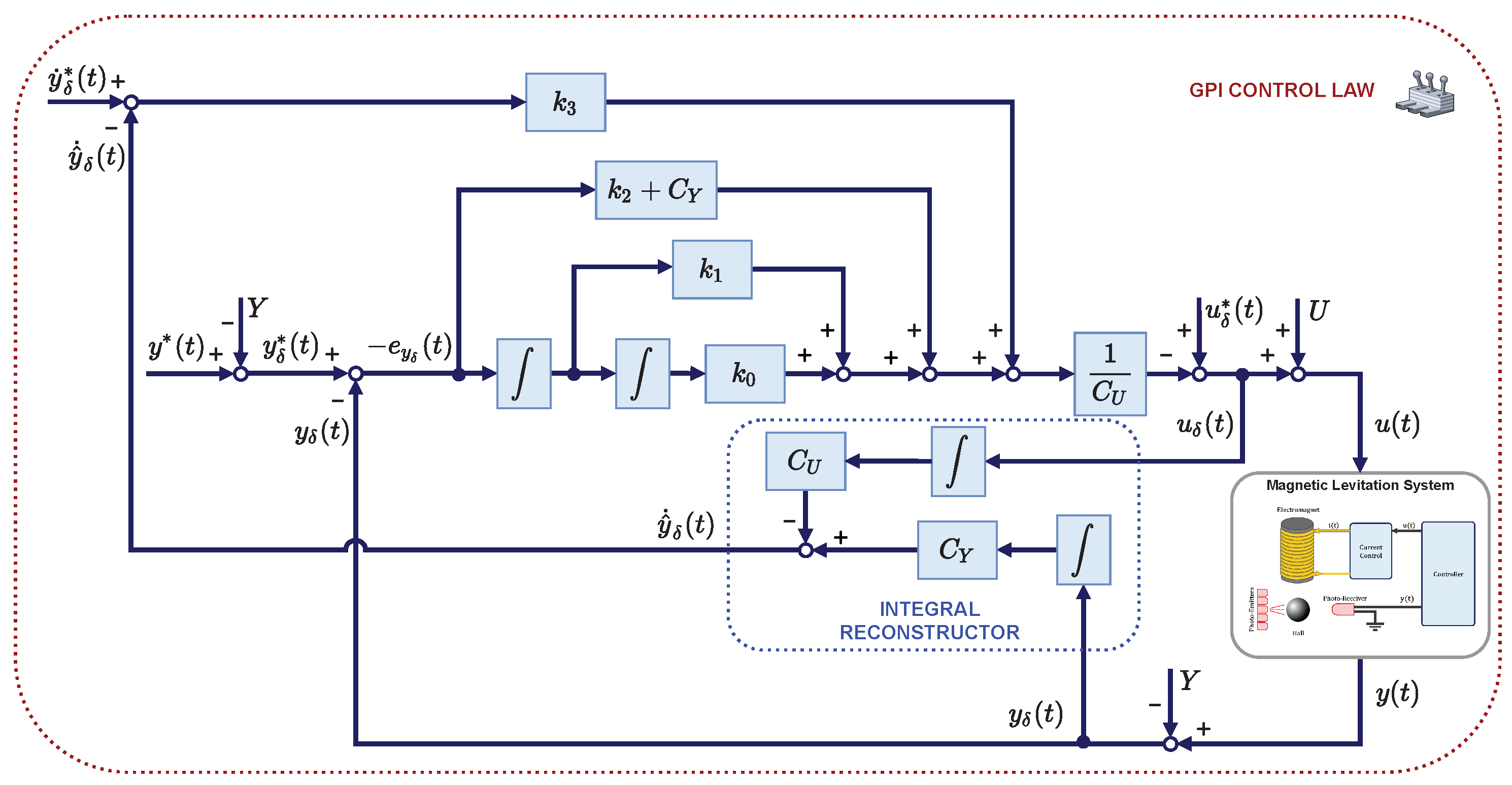
3.2. Using GPI to Locally Control the Magnetic Levitation System
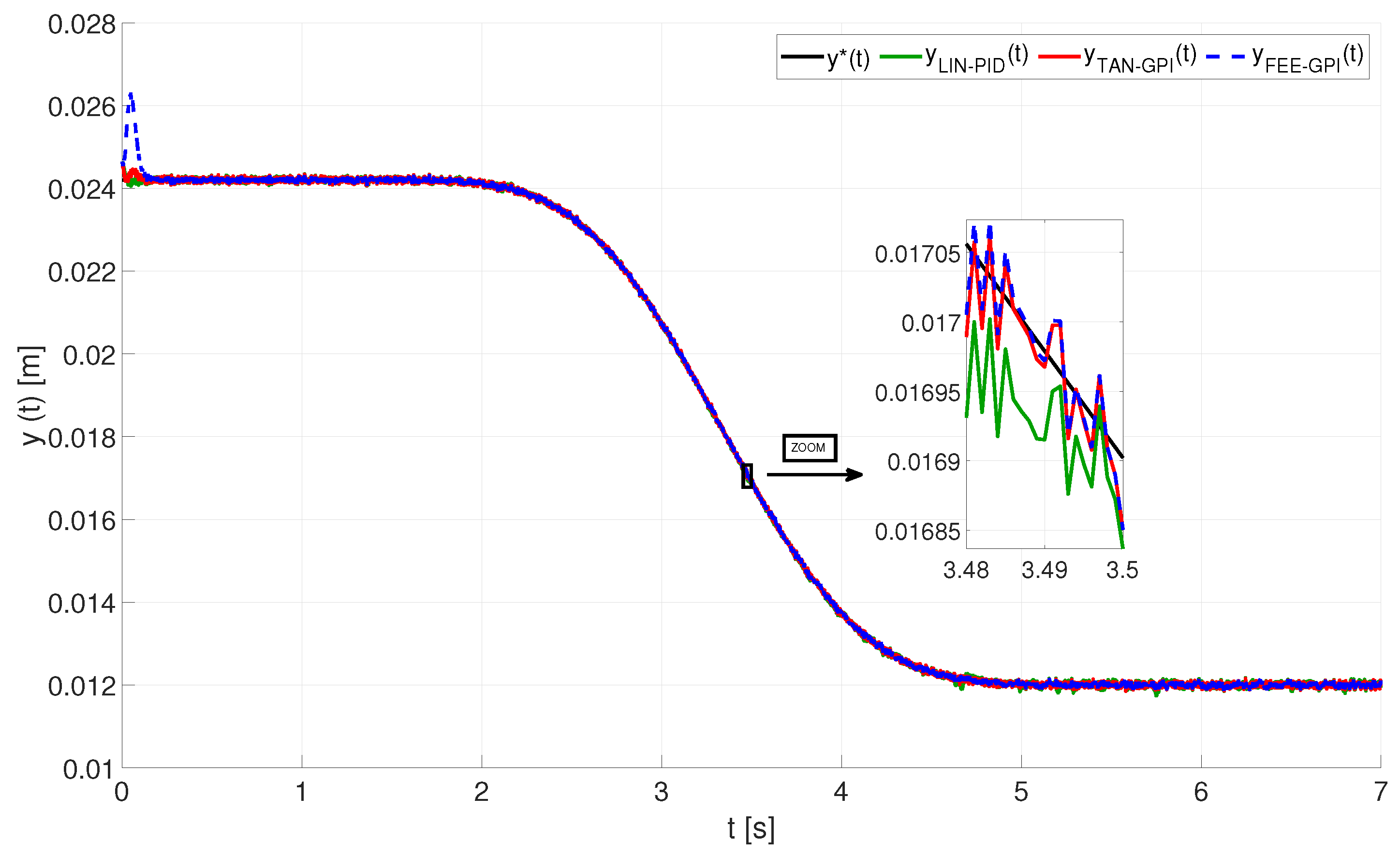
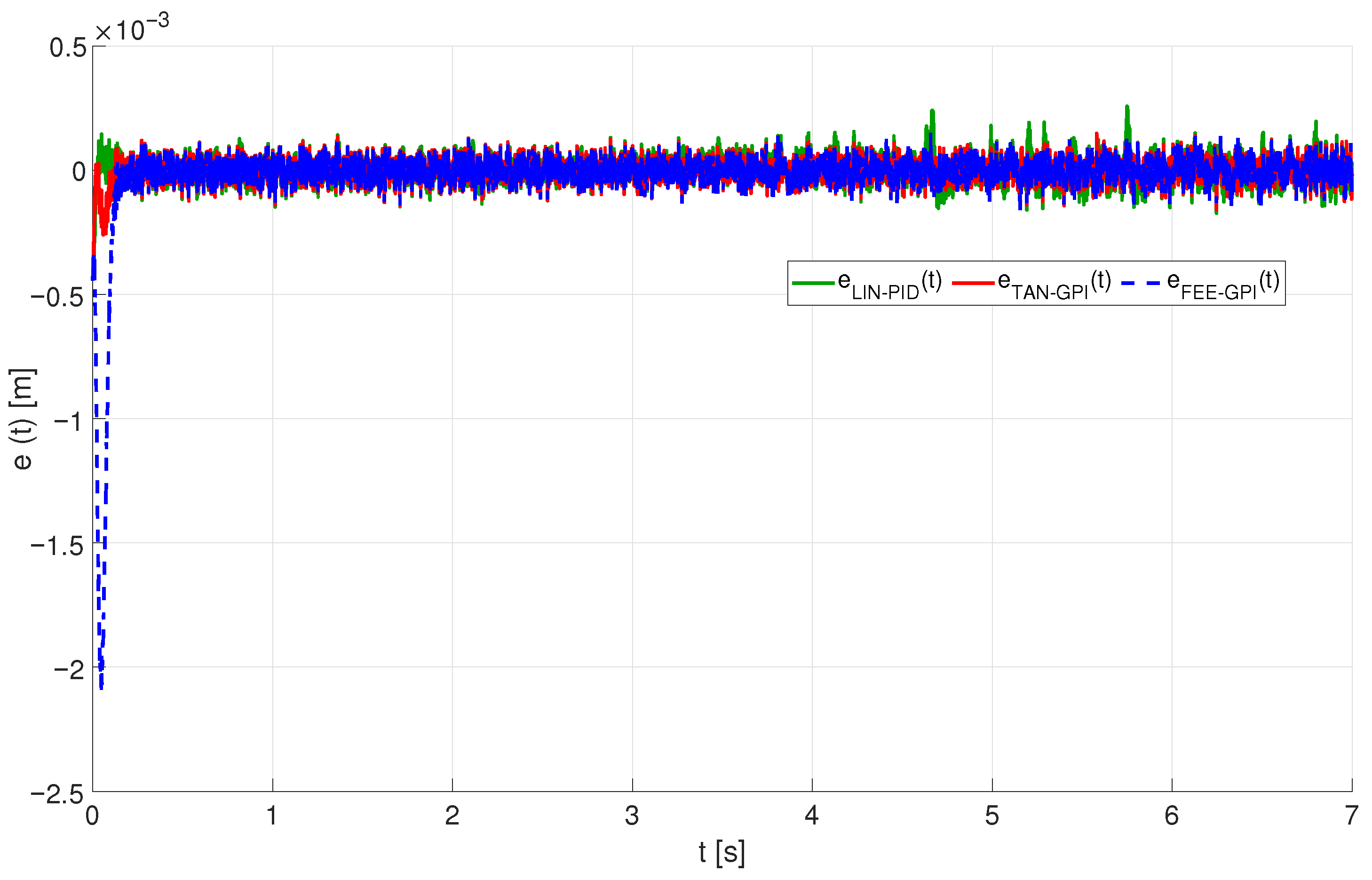
4. Computer Simulations
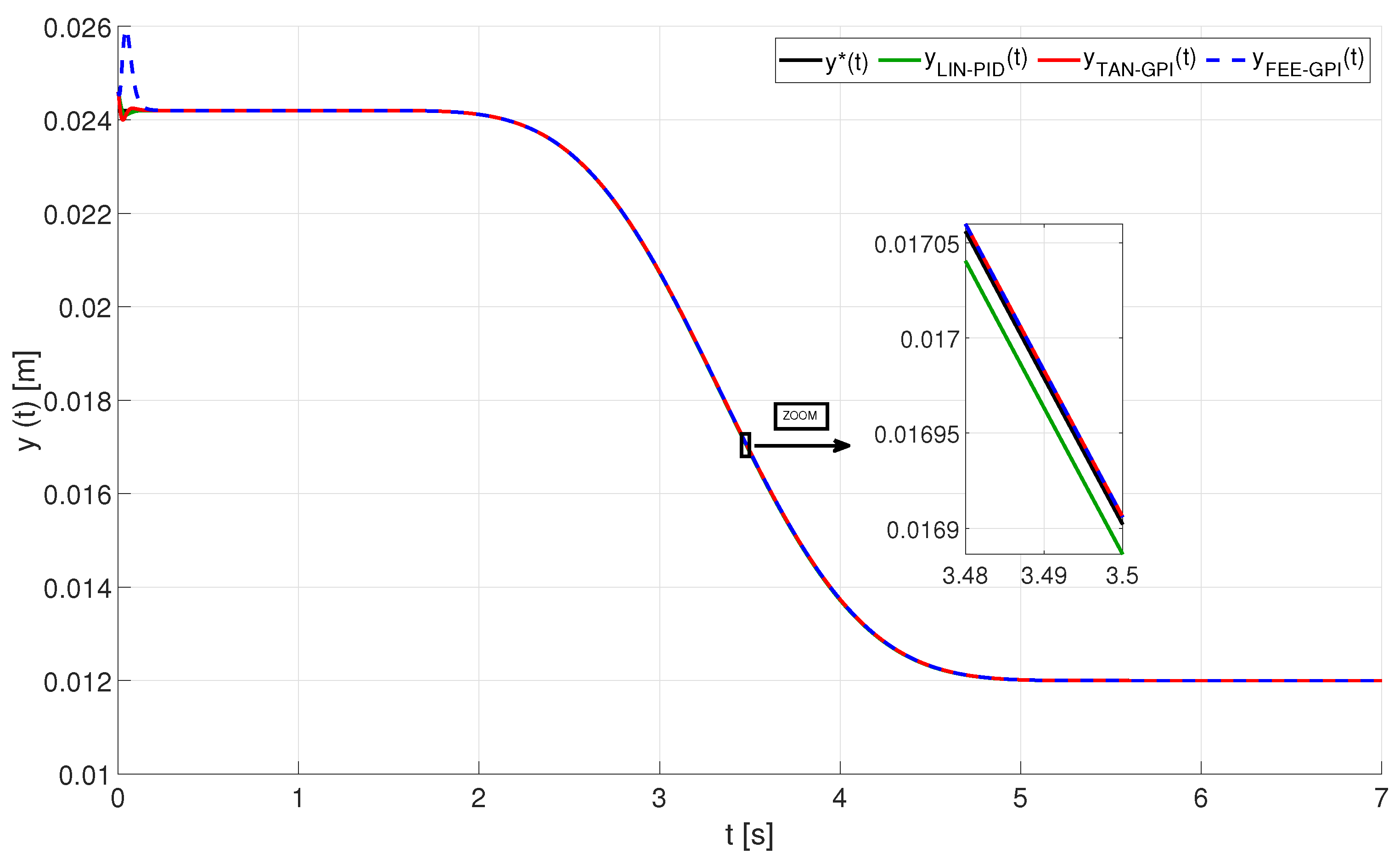
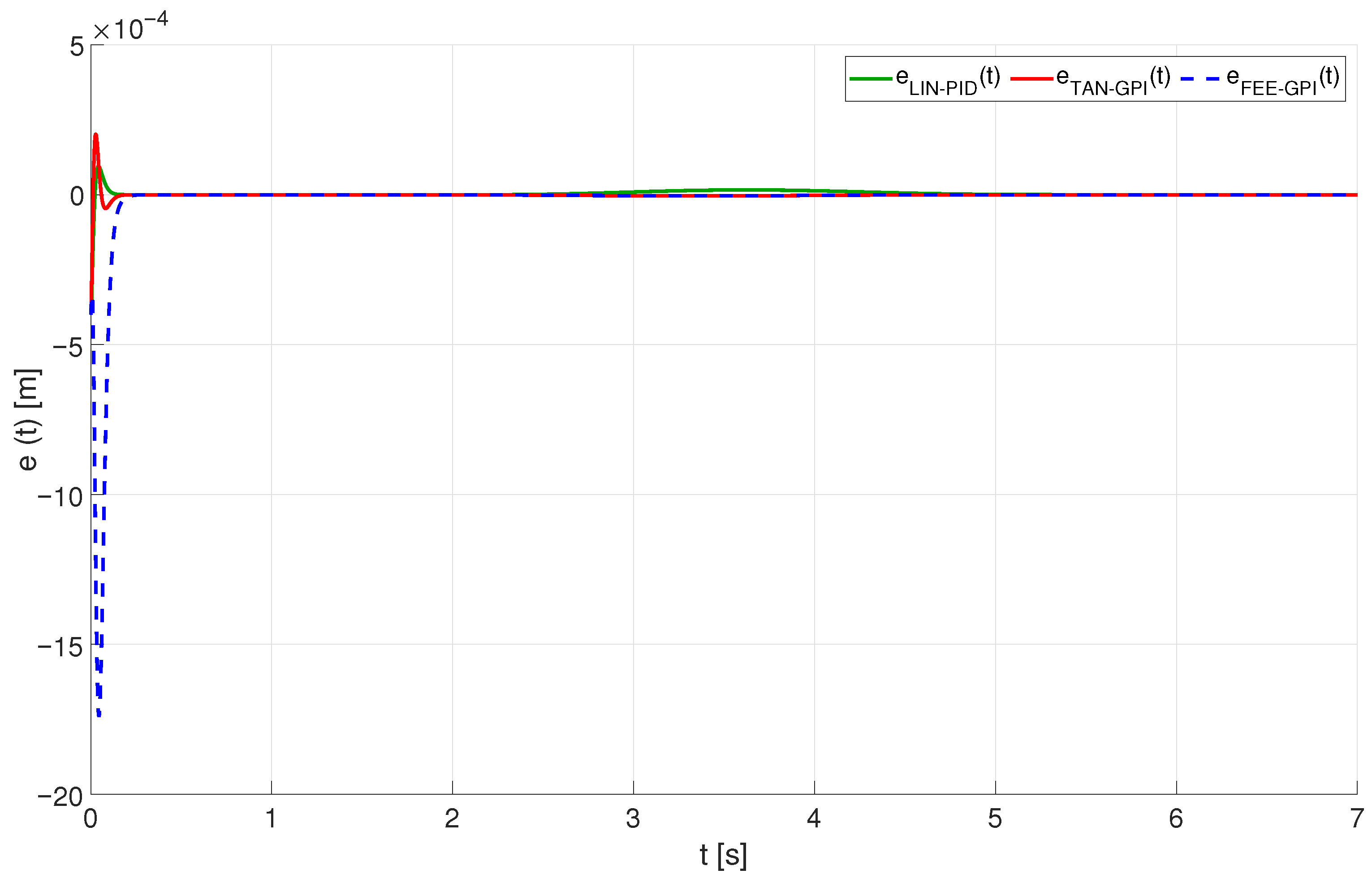
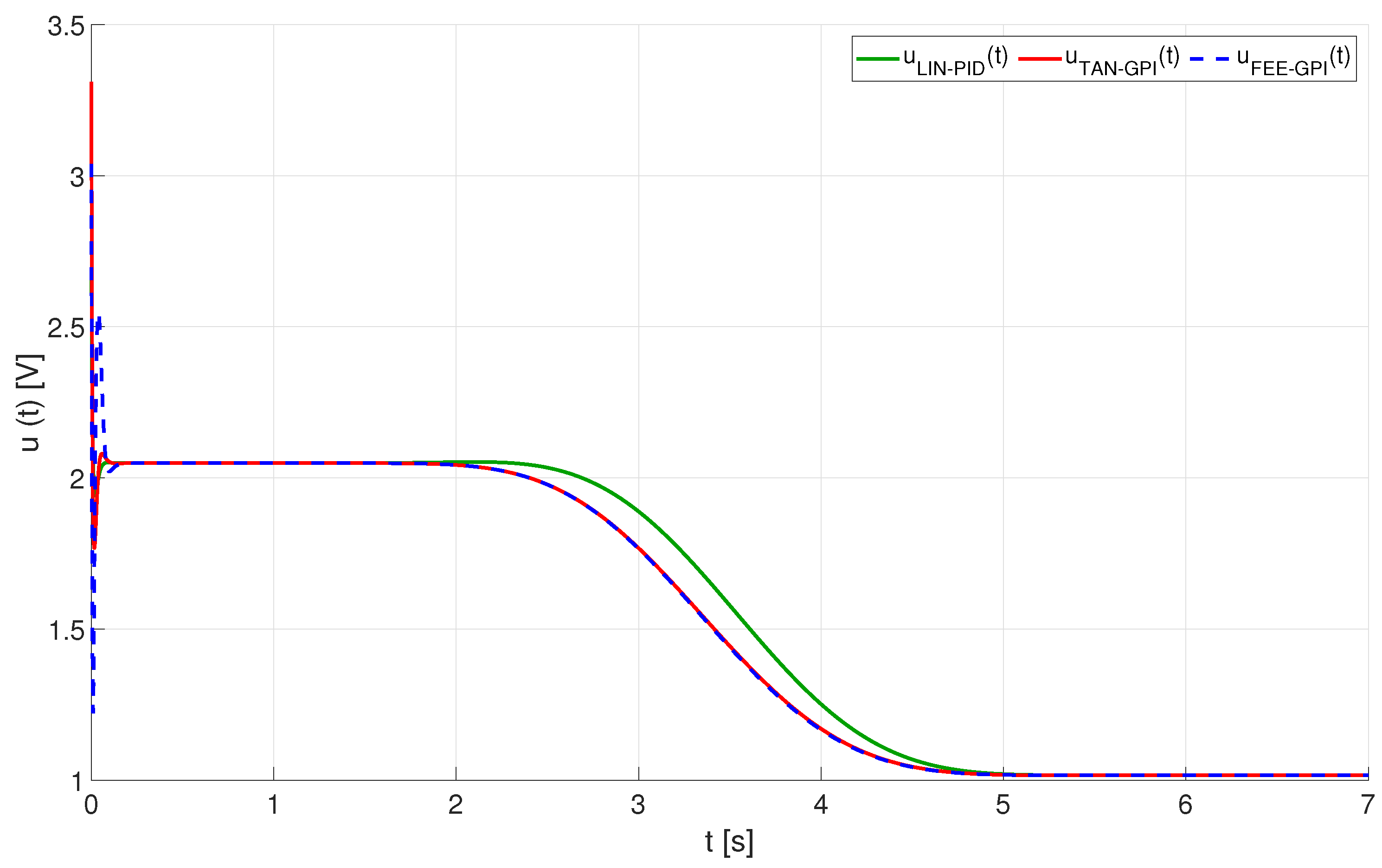
4.1. Tracking a Smooth Rest-to-Rest Trajectory
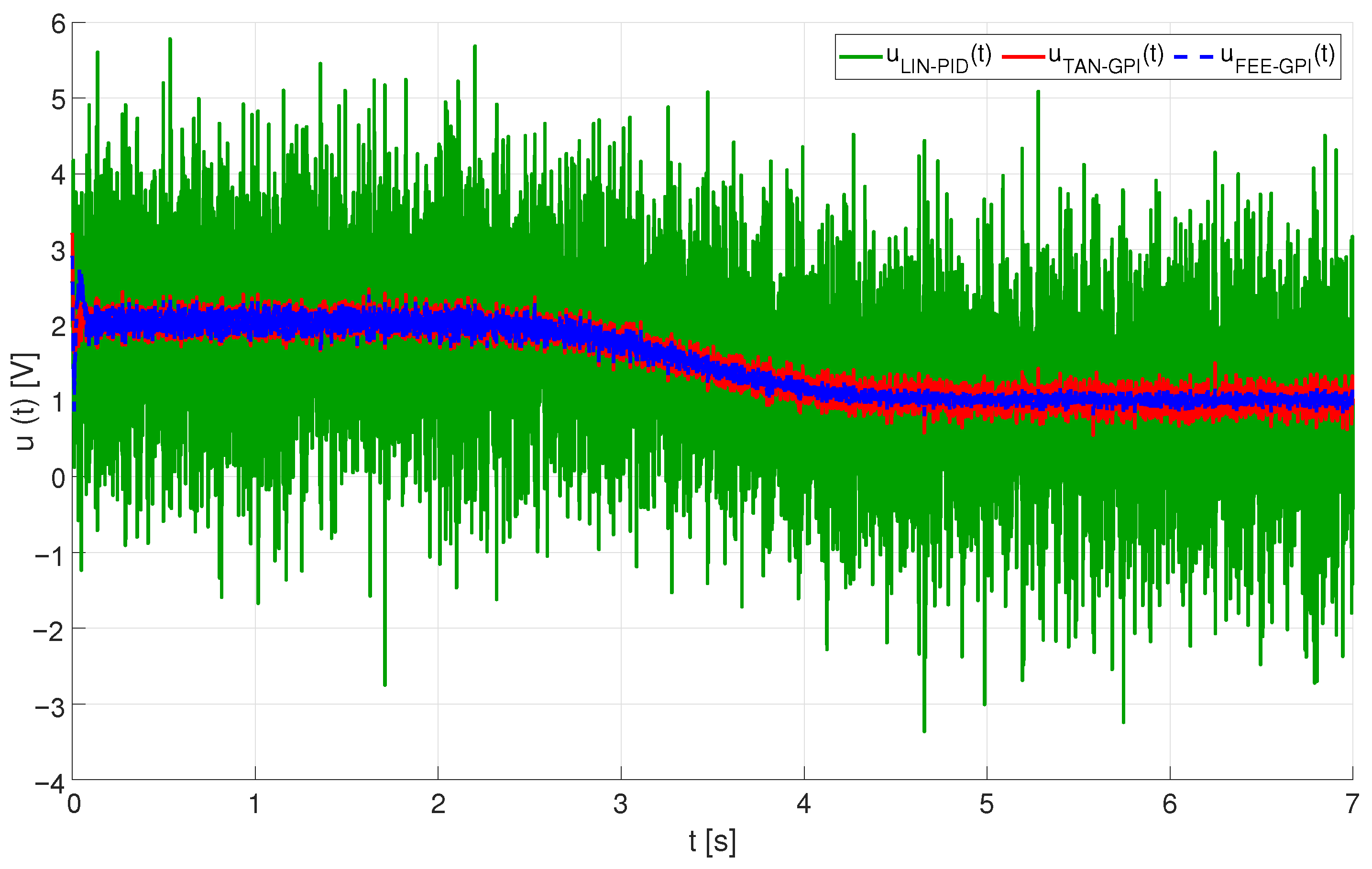
4.2. Robustness with Regard to Measurement Noises
4.3. Robustness with Regard to Controller Gain Mismatches
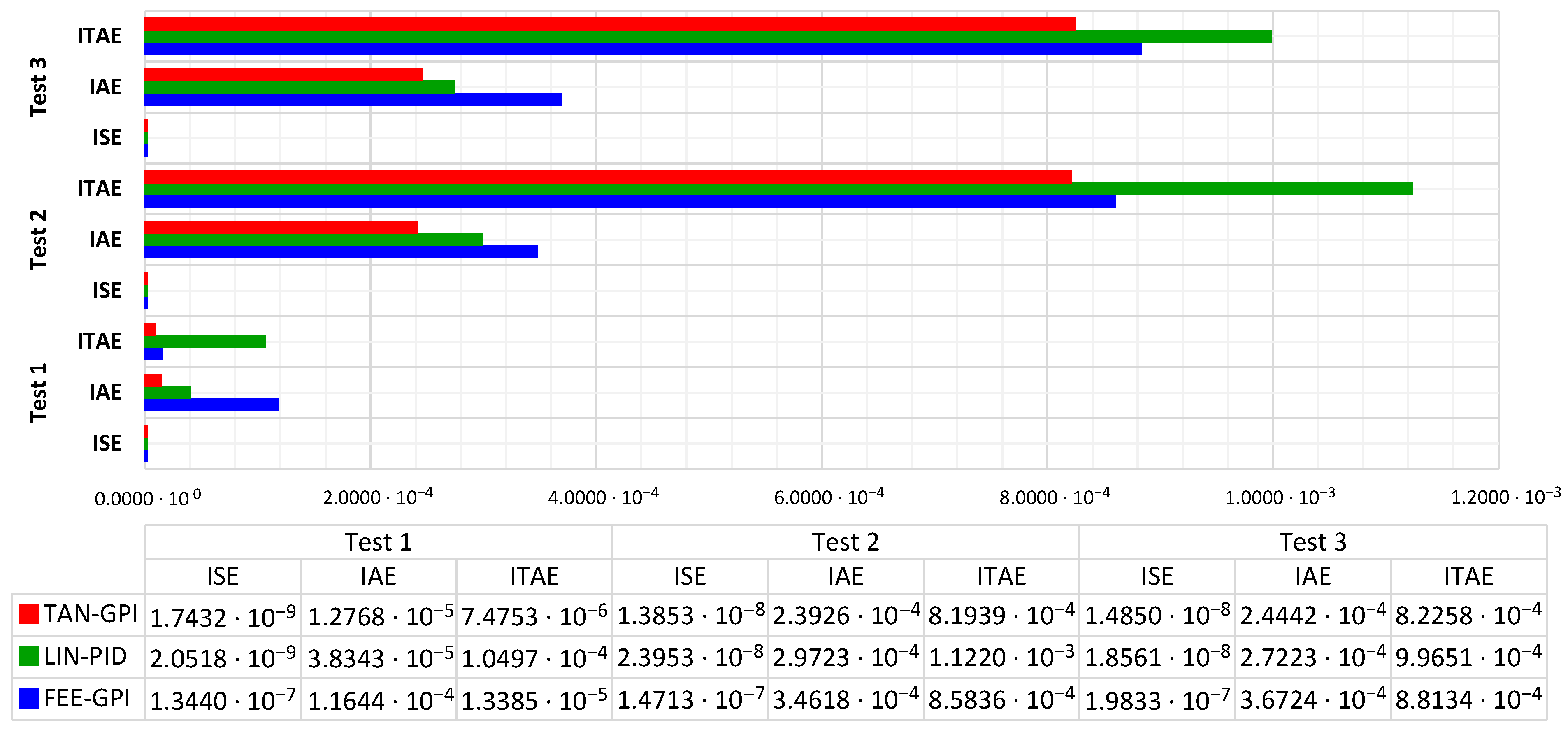
4.4. Comparison of the Controllers Based on Integral Criteria
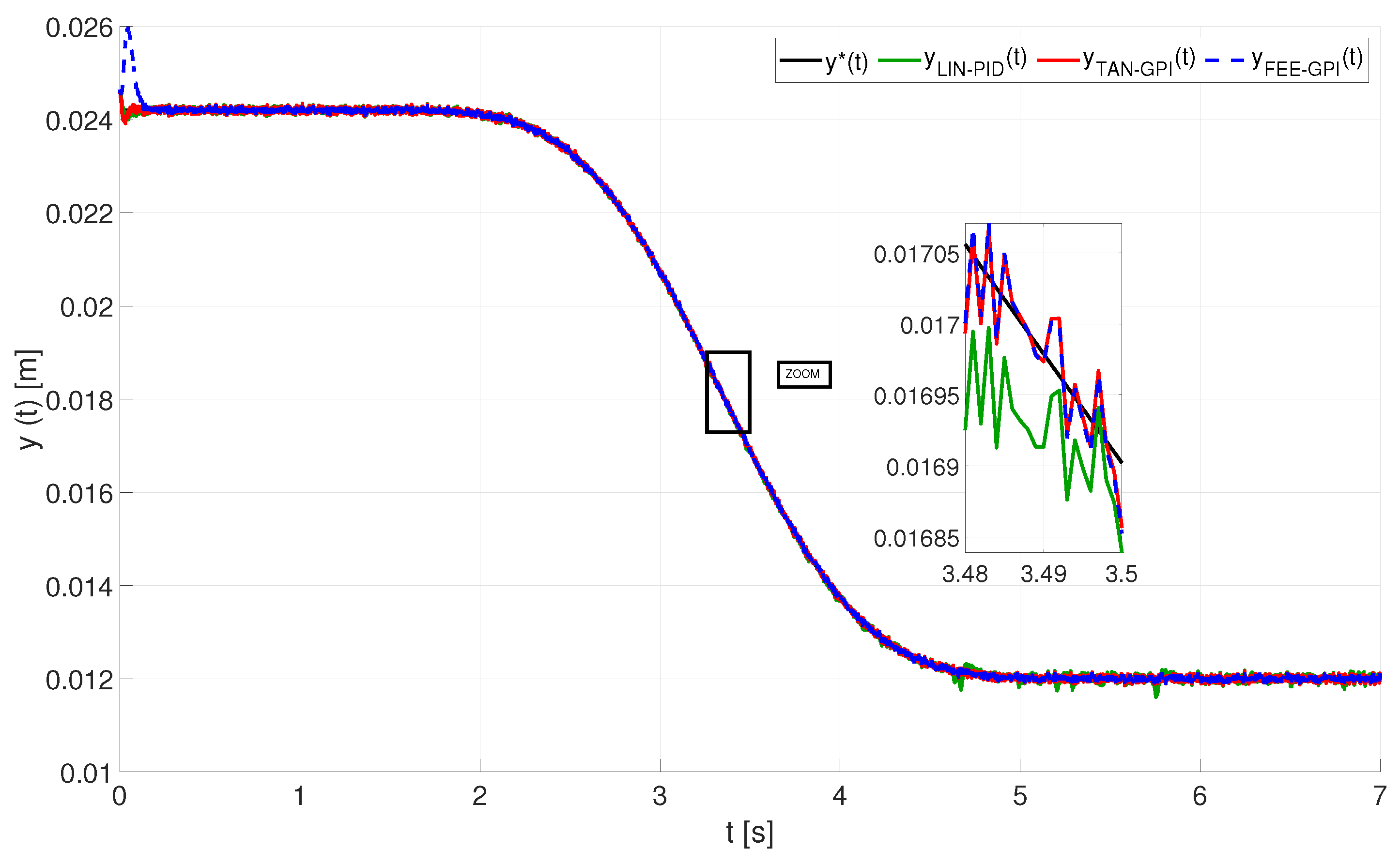
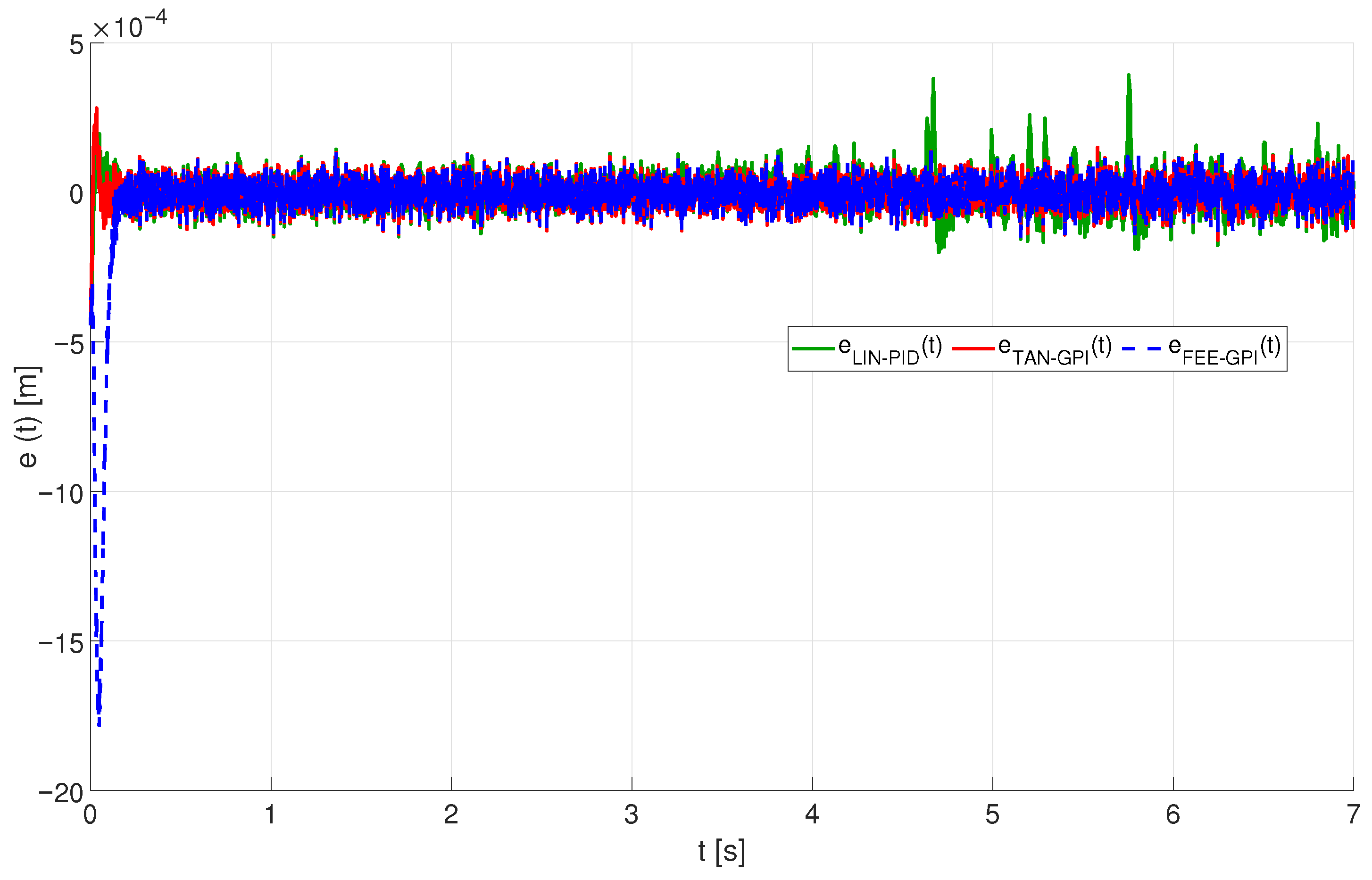
5. Experimental Results on the Magnetic Levitation Platform
5.1. Schematics of the Experimental Implementation of the Controller
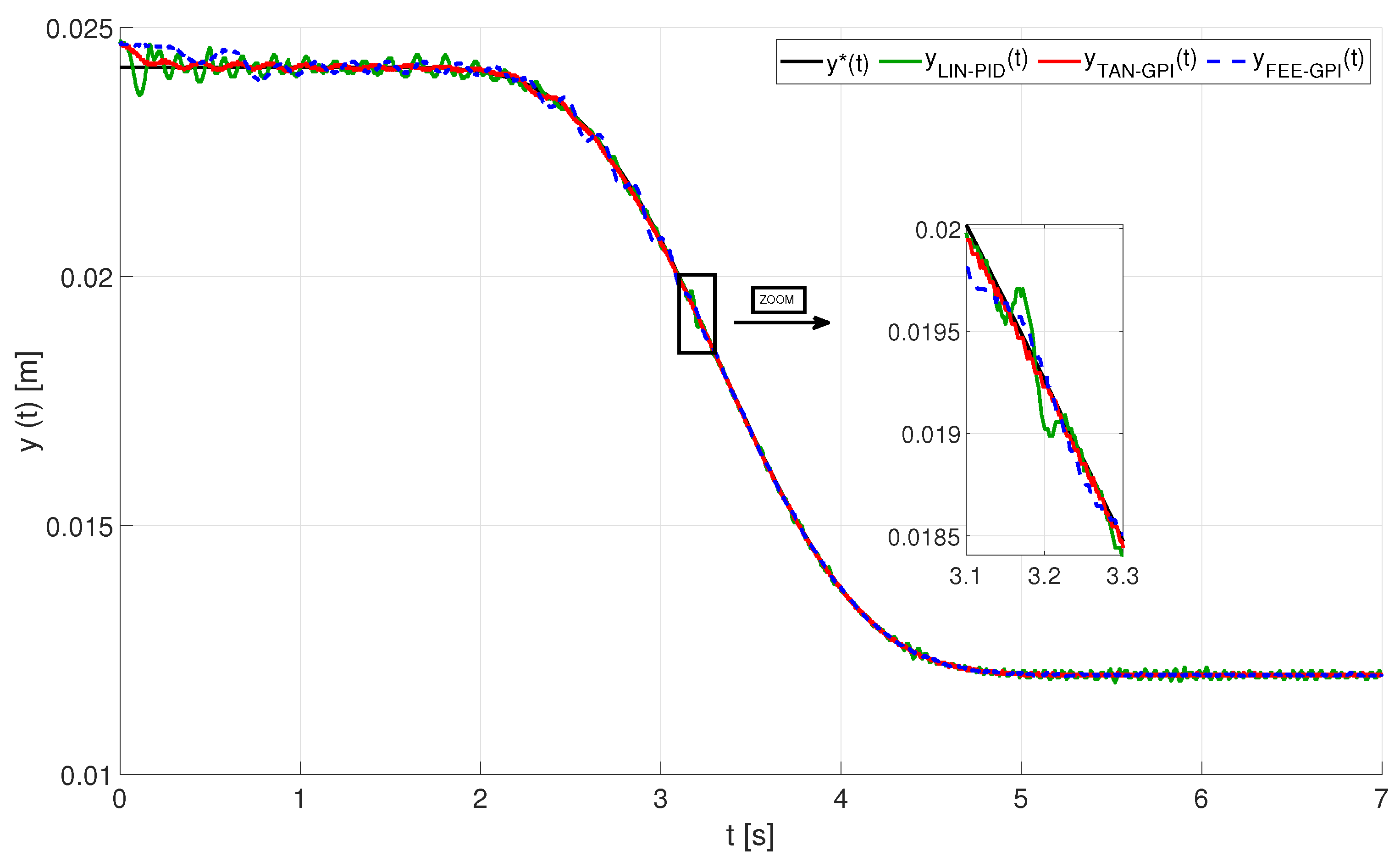
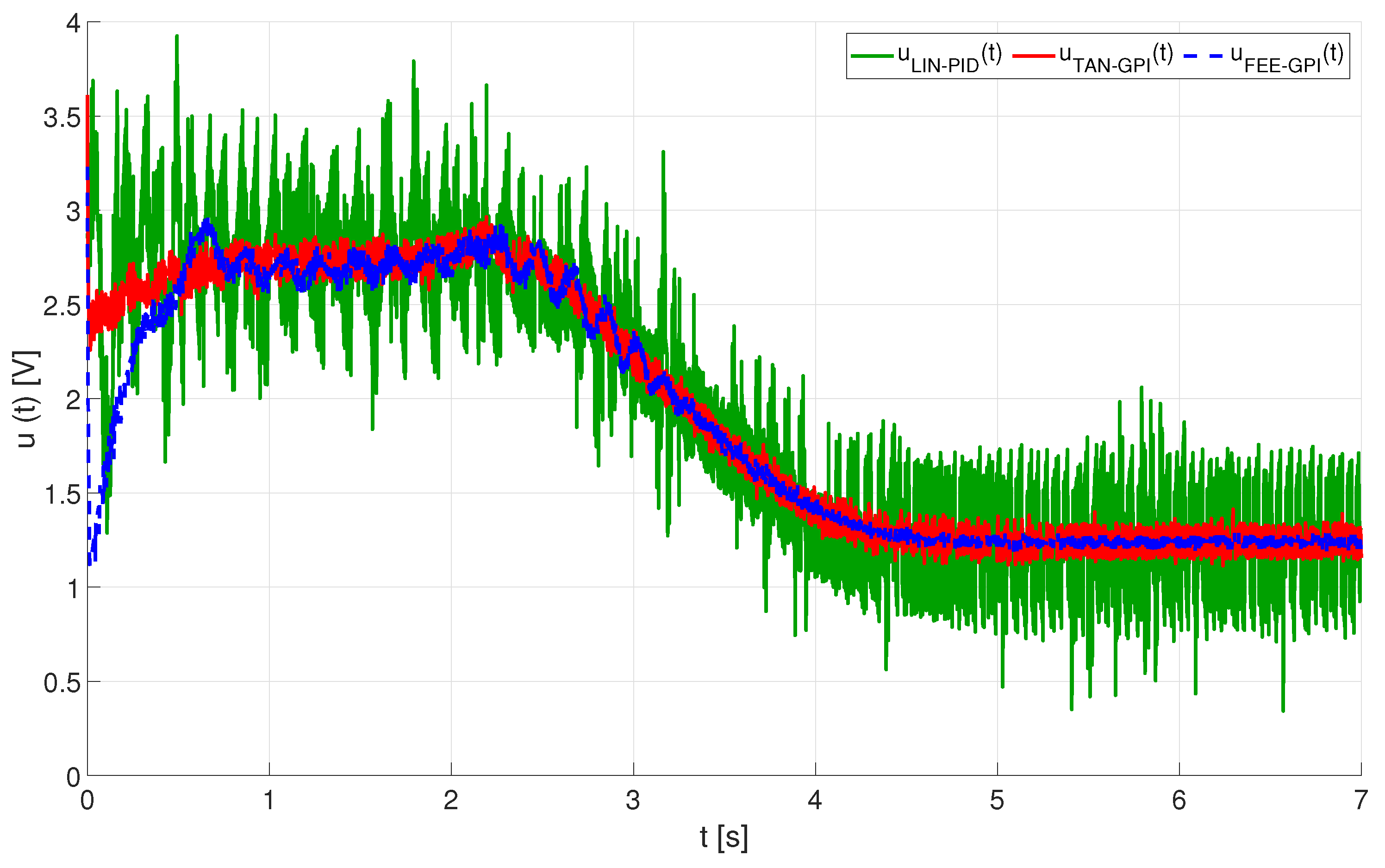
5.2. Results of the Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALS | Air Levitation System |
| FO | Fractional order |
| GPI | Generalised Proportional Integral |
| IAE | Integral Absolute Tracking Error |
| ISE | Integral Squared Tracking Error |
| ITAE | Integral Time Absolute Tracking Error |
| LQ | Linear Quadratic |
| LQR | Linear Quadratic Regulator |
| MISO | Multiple Input Single Output |
| MLS | Magnetic Levitation Systems |
| PI | Proportional Integral |
| PID | Proportional Integral Derivative |
| RTW | Real Time Workshop |
| RTWT | Real Time Windows Target |
| SISO | Single Input Single Output |
Appendix A. Closed-Loop Stability Analysis of the System against Errors in the Estimation of the β Parameter
References
- Lilienkamp, K.A. Low-cost magnetic levitation project kits for teaching feedback system design. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 2, pp. 1308–1313. [Google Scholar] [CrossRef]
- Ono, M.; Koga, S.; Ohtsuki, H. Japan’s superconducting Maglev train. IEEE Instrum. Meas. Mag. 2002, 5, 9–15. [Google Scholar] [CrossRef]
- Powell, J.; Maise, G.; Paniagua, J.; Rather, J. Maglev Launch and the Next Race to Space. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–20. [Google Scholar] [CrossRef]
- Khamesee, M.B.; Kato, N.; Nomura, Y.; Nakamura, T. Design and control of a microrobotic system using magnetic levitation. IEEE/ASME Trans. Mechatron. 2002, 7, 1–14. [Google Scholar] [CrossRef]
- Chacon, J.; Saenz, J.; Torre, L.D.l.; Diaz, J.M.; Esquembre, F. Design of a Low-Cost Air Levitation System for Teaching Control Engineering. Sensors 2017, 17, 2321. [Google Scholar] [CrossRef]
- Chacón, J.; Vargas, H.; Dormido, S.; Sánchez, J. Experimental Study of Nonlinear PID Controllers in an Air Levitation System. IFAC-PapersOnLine 2018, 51, 304–309. [Google Scholar] [CrossRef]
- Baranowski, J.; Piątek, P. Observer-based feedback for the magnetic levitation system. Trans. Inst. Meas. Control 2012, 34, 422–435. [Google Scholar] [CrossRef]
- Yang, Z.; Kunitoshi, K.; Kanae, S.; Wada, K. Adaptive Robust Output-Feedback Control of a Magnetic Levitation System by K-Filter Approach. IEEE Trans. Ind. Electron. 2008, 55, 390–399. [Google Scholar] [CrossRef]
- Hypiusová, M.; Rosinová, D.; Kozáková, A. Comparison of State Feedback Controllers for the Magnetic Levitation System. In Proceedings of the 2020 Cybernetics & Informatics (K&I), Velke Karlovice, Czech Republic, 29 January–1 February 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ni, F.; Zheng, Q.; Xu, J.; Lin, G. Nonlinear Control of a Magnetic Levitation System Based on Coordinate Transformations. IEEE Access 2019, 7, 164444–164452. [Google Scholar] [CrossRef]
- Chopade, A.S.; Khubalkar, S.W.; Junghare, A.S.; Aware, M.V.; Das, S. Design and implementation of digital fractional order PID controller using optimal pole-zero approximation method for magnetic levitation system. IEEE/CAA J. Autom. Sin. 2018, 5, 977–989. [Google Scholar] [CrossRef]
- Green, S.A.; Craig, K.C. Robust, Digital, Nonlinear Control of Magnetic-Levitation Systems. J. Dyn. Syst. Meas. Control 1998, 120, 488–495. [Google Scholar] [CrossRef]
- Yang, Z.; Tsubakihara, H.; Kanae, S.; Wada, K.; Su, C. A Novel Robust Nonlinear Motion Controller with Disturbance Observer. IEEE Trans. Control Syst. Technol. 2008, 16, 137–147. [Google Scholar] [CrossRef]
- Bidikli, B. An observer-based adaptive control design for the maglev system. Trans. Inst. Meas. Control 2020, 42, 2771–2786. [Google Scholar] [CrossRef]
- Zhang, Y.; Xian, B.; Ma, S. Continuous Robust Tracking Control for Magnetic Levitation System with Unidirectional Input Constraint. IEEE Trans. Ind. Electron. 2015, 62, 5971–5980. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Gonzalez, E.; Petlenkov, E.; Yeroglu, C. Model Reference Adaptive Control Scheme for Retuning Method-Based Fractional-Order PID Control with Disturbance Rejection Applied to Closed-Loop Control of a Magnetic Levitation System. J. Circuits Syst. Comput. 2018, 27, 1850176. [Google Scholar] [CrossRef]
- Alimohammadi, H.; Alagoz, B.B.; Tepljakov, A.; Vassiljeva, K.; Petlenkov, E. A NARX Model Reference Adaptive Control Scheme: Improved Disturbance Rejection Fractional-Order PID Control of an Experimental Magnetic Levitation System. Algorithms 2020, 13, 201. [Google Scholar] [CrossRef]
- Morales, R.; Sira-Ramírez, H.; Feliu, V. Adaptive control based on fast online algebraic identification and GPI control for magnetic levitation systems with time-varying input gain. Int. J. Control 2014, 87, 1604–1621. [Google Scholar] [CrossRef]
- Morales, R.; Sira-Ramírez, H. Trajectory tracking for the magnetic ball levitation system via exact feedforward linearisation and GPI control. Int. J. Control 2010, 83, 1155–1166. [Google Scholar] [CrossRef]
- Morales, R.; Feliu, V.; Sira-Ramirez, H. Nonlinear Control for Magnetic Levitation Systems Based on Fast Online Algebraic Identification of the Input Gain. IEEE Trans. Control Syst. Technol. 2011, 19, 757–771. [Google Scholar] [CrossRef]
- Levine, J. Analysis and Control of Nonlinear Systems. A Flatness-Based Approach; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Sira-Ramírez, H.; Agrawal, S. Differentially Flat Systems; Automation and Control Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of nonlinear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef]
- Rouchon, P.; Fliess, M.; Levine, J.; Martin, P. Flatness, motion planning and trailer systems. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; Volume 3, pp. 2700–2705. [Google Scholar] [CrossRef]
- Levine, J. Analysis and Control of Nonlinear Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Hurley, W.G.; Wolfle, W.H. Electromagnetic design of a magnetic suspension system. IEEE Trans. Educ. 1997, 40, 124–130. [Google Scholar] [CrossRef]
- Haykin, S. A unified treatment of recursive digital filtering. IEEE Trans. Autom. Control 1972, 17, 113–116. [Google Scholar] [CrossRef]
- Åström, K.; Hägglund, T. Advanced PID Control; ISA—The Instrumentation, Systems and Automation Society: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Riggs, J.B.; Karim, M.N. Chemical and Bio-Process Control; International Edition, 3/E; Pearson: New York, NY, USA, 2008. [Google Scholar]
- Horno, L.D.; Somolinos, J.A.; Segura, E.; Morales, R. A New Proposal for the Closed-Loop Orientation Control of a Windfloat Turbine System. J. Mar. Sci. Eng. 2021, 9, 26. [Google Scholar] [CrossRef]
- Schultz, W.C.; Rideout, V.C. Control system performance measures: Past, present, and future. IRE Trans. Autom. Control 1961, AC-6, 22–35. [Google Scholar] [CrossRef]
- Nagrath, I.J.; Gopal, M. Control Systems Engineering; New Age International Publishers: New Delhi, India, 2007. [Google Scholar]
- Panduro, R.; Segura, E.; Belmonte, L.M.; Fernández-Caballero, A.; Novais, P.; Benet, J.; Morales, R. Intelligent trajectory planner and generalised proportional integral control for two carts equipped with a red-green-blue depth sensor on a circular rail. Integr. Comput. Aided Eng. 2020, 27, 267–285. [Google Scholar] [CrossRef]
- Zurita-Bustamante, E.W.; Linares-Flores, J.; Guzman-Ramirez, E.; Sira-Ramirez, H. A Comparison Between the GPI and PID Controllers for the Stabilization of a DC–DC “Buck” Converter: A Field Programmable Gate Array Implementation. IEEE Trans. Ind. Electron. 2011, 58, 5251–5262. [Google Scholar] [CrossRef]
- Belmonte, L.M.; Morales, R.; Fernández-Caballero, A.; Somolinos, J.A. A Tandem Active Disturbance Rejection Control for a Laboratory Helicopter With Variable-Speed Rotors. IEEE Trans. Ind. Electron. 2016, 63, 6395–6406. [Google Scholar] [CrossRef]
- Morales, R.; Somolinos, J.; Sira-Ramírez, H. Control of a DC motor using algebraic derivative estimation with real time experiments. Measurement 2014, 47, 401–417. [Google Scholar] [CrossRef]
- Morales, R.; Segura, E.; Somolinos, J.; Núñez, L.; Sira-Ramírez, H. Online signal filtering based on the algebraic method and its experimental validation. Mech. Syst. Signal Process. 2016, 66–67, 374–387. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belmonte, L.M.; Segura, E.; Fernández-Caballero, A.; Somolinos, J.A.; Morales, R. Generalised Proportional Integral Control for Magnetic Levitation Systems Using a Tangent Linearisation Approach. Mathematics 2021, 9, 1424. https://doi.org/10.3390/math9121424
Belmonte LM, Segura E, Fernández-Caballero A, Somolinos JA, Morales R. Generalised Proportional Integral Control for Magnetic Levitation Systems Using a Tangent Linearisation Approach. Mathematics. 2021; 9(12):1424. https://doi.org/10.3390/math9121424
Chicago/Turabian StyleBelmonte, Lidia M., Eva Segura, Antonio Fernández-Caballero, José A. Somolinos, and Rafael Morales. 2021. "Generalised Proportional Integral Control for Magnetic Levitation Systems Using a Tangent Linearisation Approach" Mathematics 9, no. 12: 1424. https://doi.org/10.3390/math9121424
APA StyleBelmonte, L. M., Segura, E., Fernández-Caballero, A., Somolinos, J. A., & Morales, R. (2021). Generalised Proportional Integral Control for Magnetic Levitation Systems Using a Tangent Linearisation Approach. Mathematics, 9(12), 1424. https://doi.org/10.3390/math9121424








