Wavelet Numerical Solutions for a Class of Elliptic Equations with Homogeneous Boundary Conditions

Abstract

This paper focuses on a method to construct wavelet Riesz bases with homogeneous boundary condition and use them to a kind of second-order elliptic equation. First, we construct the splines on the interval $[0,1]$ and consider their approximation properties. Then we define the wavelet bases and illustrate the condition numbers of stiffness matrices are small and bounded. Finally, several numerical examples show that our approach performs efficiently.

1. Introduction

Let $\Omega$ be a Lebesgue measurable open subset of $\mathbb{R},L_p(\Omega )$ denotes the functions satisfying ${\parallel f\parallel }_{L_p(\Omega )}<\infty .$ The Fourier transform $\widehat{f}\left(\xi \right)$ for $f\left(x\right)\in L_1\left(\mathbb{R}\right)\bigcap L_2\left(\mathbb{R}\right)$ is defined by

$$\widehat{f}\left(\xi \right):={\int }_{\mathbb{R}}f\left(x\right)e^{-ix\xi }dx,\xi \in \mathbb{R}.$$

Let $\mu \ge 0$, $H^{\mu }\left(\mathbb{R}\right)$ denotes the Sobolev space such that ${|f|}_{H^{\mu }\left(\mathbb{R}\right)}:=(\frac{1}{2\pi }{\int }_{\mathbb{R}}|\widehat{f}\left(\xi \right){{|}^2{\xi }^{2\mu }d\xi )}^{\frac{1}{2}}$ < $\infty .$ The inner product given by

$${⟨f,g⟩}_{H^{\mu }\left(\mathbb{R}\right)}:=\frac{1}{2\pi }{\int }_{\mathbb{R}}\widehat{f}\left(\xi \right)\overline{\widehat{g}\left(\xi \right)}(1+{\xi }^{2\mu })d\xi ,f,g\in H^{\mu }\left(\mathbb{R}\right),$$

and the norm is given by ${\parallel f\parallel }_{H^{\mu }\left(\mathbb{R}\right)}:={({⟨f,g⟩}_{H^{\mu }(\mathbb{R})})}^{\frac{1}{2}}.$ We use $H_0^{\mu }(\Omega )$ to denote the closure of $C_c^{\infty }(\Omega )$ in $H^{\mu }\left(\mathbb{R}\right).$

In this paper let $\Omega =(0,1).$ We are interested in the following elliptic variable coefficient equation with the homogeneous boundary conditions:

$$\left\{\begin{array}{cc}-u^{″}\left(x\right)+q\left(x\right)u\left(x\right)=f\left(x\right),\hfill & x\in \Omega ,\hfill \\ u\left(0\right)=u\left(1\right)=0,\hfill \end{array}\right.$$

(1)

where $f\left(x\right)$ is a given function in $L_2(\Omega ),0\le q\left(x\right)\le c,c$ is a constant.

For $u,v\in H_0^1(\Omega )$, define a bilinear form $a:H_0^1(\Omega )\times H_0^1(\Omega )\to \mathbb{R}$,

$$a(u,v):={⟨u^{\prime },v^{\prime }⟩}_{L_2(\Omega )}+{⟨qu,v⟩}_{L_2(\Omega )}.$$

(2)

Hence, there exists a unique $u\in H_0^1(\Omega )$ such that

$$a(u,v)={⟨f,v⟩}_{L_2(\Omega )},\forall v\in H_0^1(\Omega ),$$

(3)

thanks to Lax-Milgram theorem.

To solve the variational problem $\left(3\right)$, we use finite-dimensional subspaces $V=\mathrm{span}\{v_1,v_2,\cdots ,v_m\}$ to approximate $H_0^1(\Omega ).$ Suppose $x_k\in \mathbb{C},k=1,2,\cdots ,m,$ such that $u\left(x\right):={\displaystyle \sum _{k=1}^m}{x}_k{v}_k\left(x\right)$ satisfies the following equation

$$a(u,v_j)={⟨f,v_j⟩}_{L_2(\Omega )},\forall v_j\in H_0^1(\Omega ),j=1,2,\cdots ,m,$$

(4)

or equivalently,

$$\sum _{k=1}^m{a}_{jk}{x}_k=b_j,j=1,2,\cdots ,m,$$

where $a_{jk}:=a(v_j,v_k),b_j=:⟨f,v_j⟩,j,k\in \{1,\cdots ,m\}.$

In 1992, Chui and Wang [1] studied semi-orthogonal wavelets generated from cardinal spline. Dahmen, Kunoth and Urban [2] gave biorthogonal spline wavelets in 1999. In 2006, Jia and Liu [3] constructed wavelet bases on the interval $[0,1]$ and applied them to the Sturm-Liouville Equation with the Dirichlet boundary condition. In 2011, Jia and Zhao [4] applied the wavelets bases on the unit square to the biharmonic equation and extended the method to general elliptic equation of fourth-order. However, to our knowledge, there is no numerical schemes based on wavelet bases to be derived.

This paper is organized as follows. In Section 2, we construct splines on the interval $[0,1]$ with homogeneous boundary condition and then investigate their approximation properties. The sufficient condition for norm equivalence is provided in Section 3. In Section 4, we describe the wavelet method and show that the condition number of the wavelet stiffness matrix is not only relatively small but also uniformly bounded. Finally, some numerical examples are given in Section 5 so as to demonstrate that our wavelet bases are very useful and efficient.

2. Splines and Approximation Property

In this section, we construct splines which satisfy the homogeneous boundary conditions on the interval $[0,1]$ and then investigate their some properties.

Let $j,d\in \mathbb{N}$ and $\mathcal{I}$ a countable index set. Suppose that ${\mathbf{t}}^{\mathbf{j}}:=\left(t_k^j\right)$ is the sequence such that $t_k^j<t_{k+1}^j$ for all $k\in \mathcal{I}$. The B-spline of order d is given by

$$B_{k,d}^j\left(x\right):=(t_{k+d}^j-t_k^j){[t_k^j,t_{k+1}^j,\dots ,t_{k+d}^j;{(t-x)}_{+}^{d-1}]}_t,x\in \mathbb{R},$$

where ${[t_k^j,t_{k+1}^j,\dots ,t_{k+d}^j;f\left(t\right)]}_t$ denotes the dth order divided difference at the points $t_k^j,t_{k+1}^j,\dots ,t_{k+d}^j$, and $x_{+}:=max\{x,0\}$, $x_{+}^m:={\left(x_{+}\right)}^m$.

From now on, suppose that $d=3$, $j⩾2$, ${\mathbf{t}}^{\mathbf{j}}:={\left(t_k^j\right)}_{k=1}^{2^j+3}$ is given by

$$t_k^j:=\left\{\begin{array}{c}k-1,k=1,\hfill \\ k-2,2⩽k⩽2^j+2,\hfill \\ k-3,k=2^j+3.\hfill \end{array}\right.$$

(5)

Many useful properties of B-spline can be established. For example, there exist complex numbers $c_k,(k\in \mathbb{Z})$ such that $p\left(x\right)={\displaystyle \sum _{k\in \mathbb{Z}}}{c}_k{B}_{k,3}^j\left(x\right),j\ge 3,k=2^j+3$. i.e., a polynomial p whose degree is at most 2 can be represented as a B-spline series.

Moreover, the above properties, we also have the following Lemma.

Lemma 1 

([5]). Let $j⩾2,I_j=\{1,2,\cdots ,2^j\}$, ${\mathbf{t}}^{\mathbf{j}}:={\left(t_k^j\right)}_{k=1}^{2^j+3}$ be given by (5), then one has

(i) 

$\mathrm{supp}{B}_{k,3}^j\left(x\right)=[t_k^j,t_{k+3}^j]$, $k\in I_j$;

(ii) 

$B_{k,3}^j\left(x\right)=B_{2^j-k+1,3}^j(2^j-x)$, $k\in I_j$, $x\in \mathbb{R}$;

(iii) 

$B_{k,3}^j\left(x\right)=B_{2,3}^j(x-k+2)$, $k\in I_j\backslash \{1,2^j\}$, $x\in \mathbb{R}$;

(iv) 

$B_{k,3}^j\left(x\right)=B_{k,3}^{j+1}\left(x\right)$, $k\in I_j\backslash \left\{2^j\right\}$, $x\in \mathbb{R}$.

From the properties $\left(ii\right),\left(iii\right),\left(iv\right)$ of Lemma 1, we can see that B-splines defined by (5) are divided into two kinds: $B_{k,3}^j\left(x\right),k=1,2^j,$ are symmetric boundary functions. The others are interior functions and can be obtained by shifting function $B_{2,3}^2\left(x\right)$. So we only need to discuss $B_{1,3}^2\left(x\right)$ and $B_{2,3}^2\left(x\right)$ especially, where

$$B_{1,3}^2\left(x\right):=2{[0,0,1,2;{(t-x)}_{+}^2]}_t=\left\{\begin{array}{cc}-\frac{3}{2}{x}^2+2x,\hfill & 0<x⩽1,\hfill \\ \frac{1}{2}{x}^2-2x+2,\hfill & 1<x⩽2,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

$$B_{2,3}^2\left(x\right):=3{[0,1,2,3;{(t-x)}_{+}^2]}_t=\left\{\begin{array}{cc}\frac{1}{2}{x}^2,\hfill & 0<x⩽1,\hfill \\ -x^2+3x-\frac{3}{2},\hfill & 1<x⩽2,\hfill \\ \frac{1}{2}{x}^2-3x+\frac{9}{2},\hfill & 2<x⩽3,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Lemma 2. 

If$j⩾2$, ${\mathbf{t}}^{\mathbf{j}}:={\left(t_k^j\right)}_{k=1}^{2^j+3}$is given by (5), then

(i) 

$B_{2,3}^2\left(x\right)=\frac{1}{4}{B}_{2,3}^2\left(2x\right)+\frac{3}{4}{B}_{2,3}^2(2x-1)+\frac{3}{4}{B}_{2,3}^2(2x-2)+\frac{1}{4}{B}_{2,3}^2(2x-3)$, $x\in \mathbb{R}$;

(ii) 

$B_{1,3}^2\left(x\right)=\frac{1}{2}{B}_{1,3}^2\left(2x\right)+\frac{3}{4}{B}_{2,3}^2\left(2x\right)+\frac{1}{4}{B}_{2,3}^2(2x-1)$, $x\in \mathbb{R}$;

(iii) 

$B_{2,3}^2\left(x\right)\in H^{\mu }\left(\mathbb{R}\right)$, $B_{1,3}^2\left(x\right)\in H^{\sigma }\left(\mathbb{R}\right),$ where $0<\mu <\frac{5}{2}$, $0<\sigma <\frac{3}{2}$.

Proof. 

It is easy to check $\left(i\right),\left(ii\right)$ are established.

$\left(iii\right)$ Let $\varphi \left(x\right):=B_{2,3}^2\left(x\right)$, one obtains

$$\widehat{\varphi }\left(\xi \right)={\left(\frac{sin\frac{\xi }{2}}{\frac{\xi }{2}}\right)}^3$$

by the Fourier transform of $\varphi \left(x\right)$.

Since

$$\begin{array}{c}{\int }_{\mathbb{R}}|\widehat{\varphi }{\left(\xi \right)|}^2{|{\xi }^2|}^{\mu }d\xi \hfill \\ ={\int }_{|\xi |⩽1}|\widehat{\varphi }{\left(\xi \right)|}^2|{\xi }^2{|}^{\mu }d\xi +{\int }_{|\xi |>1}|\widehat{\varphi }{\left(\xi \right)|}^2{|{\xi }^2|}^{\mu }d\xi \hfill \\ ⩽{\int }_{|\xi |⩽1}{|\widehat{\varphi }\left(\xi \right)|}^{2}d\xi +{\int }_{|\xi |>1}\frac{|sin\frac{\xi }{2}{|}^6}{{\xi }^{2(3-\mu )}}d\xi \hfill \\ ⩽{\int }_{|\xi |⩽1}{|\widehat{\varphi }\left(\xi \right)|}^{2}d\xi +{\int }_{|\xi |>1}\frac{1}{{\xi }^{2(3-\mu )}}d\xi .\hfill \end{array}$$

Hence, for $0<\mu <\frac{5}{2}$, one obtains

$${\int }_{\mathbb{R}}|\widehat{\varphi }{\left(\xi \right)|}^2{|{\xi }^2|}^{\mu }d\xi <\infty .$$

i.e., $\varphi \left(x\right)\in H^{\mu }\left(\mathbb{R}\right),0<\mu <\frac{5}{2}$. An analogous argument shows that $B_{1,3}^2\left(x\right)\in H^{\sigma }\left(\mathbb{R}\right)$, $0<\sigma <\frac{3}{2}$. □

Lemma 3. 

If${\varphi }_{j,k}\left(x\right):=2^{\frac{j}{2}}{B}_{k,3}^j\left(2^{j}x\right),k\in I_j,$then one has

(i) 

$\mathrm{supp}{\varphi }_{j,k}=[2^{-j}{t}_k^j,2^{-j}{t}_{k+3}^j]\subset \Omega$;

(ii) 

There exists a constant $C>0$ which is independent of j such that $\parallel {\varphi }_{j,k}{\parallel }_{L^2(\Omega )}⩽C;$

(iii) 

For $k\in I_j\backslash \{1,2^j\},{\varphi }_{j,k}\in H^{\mu }\left(\mathbb{R}\right)$ with $0<\mu <\frac{5}{2}$;

(iv) 

For $k\in \{1,2^j\},{\varphi }_{j,k}\in H^{\sigma }\left(\mathbb{R}\right)$ with $0<\sigma <\frac{3}{2}$;

(v) 

Let ${\Phi }_j:=\{{\varphi }_{j,k}\left(x\right):=2^{\frac{j}{2}}{B}_{k,3}^j\left(2^{j}x\right)\mid k\in I_j,x\in \mathbb{R}\},$ then

$${\Phi }_j=\frac{1}{\sqrt{2}}{M}_{j,0}^T{\Phi }_{j+1},$$

where

$$M_{j,0}^T={\left(\begin{array}{ccccccccccccc}\frac{1}{2}& \frac{3}{4}& \frac{1}{4}& 0& 0& 0& \cdots & 0& 0& 0& 0& 0& 0\\ 0& \frac{1}{4}& \frac{3}{4}& \frac{3}{4}& \frac{1}{4}& 0& \cdots & 0& 0& 0& 0& 0& 0\\ 0& 0& 0& \frac{1}{4}& \frac{3}{4}& \frac{3}{4}& \cdots & 0& 0& 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0& \cdots & \frac{3}{4}& \frac{3}{4}& \frac{1}{4}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \cdots & 0& \frac{1}{4}& \frac{3}{4}& \frac{3}{4}& \frac{1}{4}& 0\\ 0& 0& 0& 0& 0& 0& \cdots & 0& 0& 0& \frac{1}{4}& \frac{3}{4}& \frac{1}{2}\end{array}\right)}_{2^j\times 2^{j+1}};$$

(vi) 

${\Phi }_j$ is the Riesz sequence in the space $L_2(\Omega )$, and the Riesz bounds are independent of j.

Proof. 

The conclusions (i)–(v) can be obtainen easily.

$\left(vi\right)$ It is necessary to show that there exist $C_1>0$, $C_2>0$ which are independent of j such that

$$C_1\parallel c_j{\parallel }_{l_2\left(I_j\right)}⩽\parallel \sum _{k\in I_j}{c}_{j,k}{\varphi }_{j,k}{\parallel }_{L_2(\Omega )}⩽C_2{\parallel c_j\parallel }_{l_2\left(I_j\right)},c_j={\left(c_{j,k}\right)}_{k\in I_j}.$$

In fact,

$$\parallel \sum _{k\in I_j}{c}_{j,k}{\varphi }_{j,k}{\parallel }_{L_2(\Omega )}^2=c_j^T{G}_j{c}_j,$$

where $G_j=:{\left({⟨{\varphi }_{j,k},{\varphi }_{j,m}⟩}_{L^2(\Omega )}\right)}_{k,m\in I_j}$ is Gramian matrix. i.e.,

$$G_j={\left(\begin{array}{ccccccccccc}\frac{10}{3}& \frac{5}{24}& \frac{1}{120}& 0& 0& \cdots & 0& 0& 0& 0& 0\\ \frac{5}{24}& \frac{7}{10}& \frac{13}{60}& \frac{1}{120}& 0& \cdots & 0& 0& 0& 0& 0\\ \frac{1}{120}& \frac{13}{60}& \frac{7}{10}& \frac{13}{60}& \frac{1}{120}& \cdots & 0& 0& 0& 0& 0\\ 0& \frac{1}{120}& \frac{13}{60}& \frac{7}{10}& \frac{13}{60}& \cdots & 0& 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& \cdots & \frac{13}{60}& \frac{7}{10}& \frac{13}{60}& \frac{1}{120}& 0\\ 0& 0& 0& 0& 0& \cdots & \frac{1}{120}& \frac{13}{60}& \frac{7}{10}& \frac{13}{60}& \frac{1}{120}\\ 0& 0& 0& 0& 0& \cdots & 0& \frac{1}{120}& \frac{13}{60}& \frac{7}{10}& \frac{5}{24}\\ 0& 0& 0& 0& 0& \cdots & 0& 0& \frac{1}{120}& \frac{5}{24}& \frac{10}{3}\end{array}\right)}_{2^j\times 2^j}.$$

Thanks to the properties of the Rayleigh quotient [6], one has

$${\lambda }_{min}\left(G_j\right)\parallel c_j{\parallel }_{l_2\left(I_j\right)}^2⩽\parallel \sum _{k\in I_j}{c}_{j,k}{\varphi }_{j,k}{\parallel }_{L_2(\Omega )}^2⩽{\lambda }_{max}\left(G_j\right){\parallel c_j\parallel }_{l_2\left(I_j\right)}^2,$$

where ${\lambda }_{min}\left(G_j\right)$ and ${\lambda }_{max}\left(G_j\right)$ denote the minimal and maximal eigenvalue (in absolute value) of the matrix $G_j$ respectively.

To estimate the eigenvalues of $G_j$, one uses Gerschgorin’s theorem [7] to obtain that

$$\sigma \left(G_j\right)\subset B_{\frac{13}{60}}\left(\frac{10}{3}\right)\cup B_{\frac{9}{20}}\left(\frac{7}{10}\right),$$

where $B_r\left(x\right):=\{y\in \mathbb{R}\mid |x-y|⩽r\},\sigma \left(G_j\right)$ denotes the spectrum of the matrix $G_j.$ Therefore

$${\lambda }_{min}\left(G_j\right)⩾min\{\frac{10}{3}-\frac{13}{60},\frac{7}{10}-\frac{9}{20}\}=min\{\frac{187}{60},\frac{1}{4}\}=\frac{1}{4},$$

$${\lambda }_{max}\left(G_j\right)⩽max\{\frac{10}{3}+\frac{13}{60},\frac{7}{10}+\frac{9}{20}\}=max\{\frac{71}{20},\frac{23}{20}\}=\frac{71}{20}.$$

Hence, one obtains

$$\frac{1}{2}\parallel c_j{\parallel }_{l_2\left(I_j\right)}⩽\parallel \sum _{k\in I_j}{c}_{j,k}{\varphi }_{j,k}{\parallel }_{L_2(\Omega )}⩽\sqrt{\frac{71}{20}}{\parallel c_j\parallel }_{l_2\left(I_j\right)},$$

i.e., ${\Phi }_j$ is a Riesz sequence in $L_2(\Omega )$, and the Riesz bounds are independent of the level j. □

Theorem 1. 

Let$V_j:=\mathrm{span}{\Phi }_j,j⩾2$, then one obtains

(i) 

$V_j$ is a closed subspace of Sobolev space $H_0^{\mu }(\Omega )$, $0<\mu <\frac{3}{2}$;

(ii) 

$dim{V}_j=2^j$;

(iii) 

$V_j\subset V_{j+1}$;

(iv) 

${\mathcal{P}}_2(\Omega )\subset V_j$, where${\mathcal{P}}_2(\Omega )$denotes the space of all polynomials p of degree at most 2 on Ω.

For $j⩾2$, since $\{B_{k,3}^j\left(x\right),k\in I_j\}$ are local linear independence, one can find a continuous function ${\tilde{B}}_{m,3}^j\left(x\right),$ where $\mathrm{supp}{\tilde{B}}_{m,3}^j\left(x\right)\subset \mathrm{supp}{B}_{k,3}^j$ such that

$${⟨B_{k,3}^j,{\tilde{B}}_{m,3}^j⟩}_{L^2(\Omega )}={\delta }_{k,m}=\left\{\begin{array}{cc}1,\hfill & k=m,\hfill \\ 0,\hfill & k\ne m.\hfill \end{array}\right.$$

Obviously, there exists a positive constant M which is independent of j, such that$\parallel {\tilde{B}}_{m,3}^j{\parallel }_{L_2(\Omega )}⩽M$. Use the notation

$${\tilde{\varphi }}_{j,k}\left(x\right):=2^{\frac{j}{2}}{\tilde{B}}_{k,3}^j\left(2^{j}x\right),k\in I_j,x\in \mathbb{R},$$

then$\mathrm{supp}{\tilde{\varphi }}_{j,k}\subset \mathrm{supp}{\varphi }_{j,k}\subset \Omega$, ${⟨{\varphi }_{j,k},{\tilde{\varphi }}_{j,m}⟩}_{L^2(\Omega )}={\delta }_{k,m}.$

Define a family of projector$P_j:L_2(\Omega )\to V_j$,

$$P_{j}f\left(x\right):=\sum _{k\in I_j}{⟨f,{\tilde{\varphi }}_{j,k}⟩}_{L^2(\Omega )}{\varphi }_{j,k}\left(x\right),$$

(6)

then we have the following theorem.

Theorem 2. 

For any$f\in H^2(\Omega )\cap H_0^{\mu }(\Omega ),$one obtains

$$\parallel P_j{f-f\parallel }_{L^2(\Omega )}\lesssim 2^{-2j}{|f|}_{H^2(\Omega )},j⩾2,$$

where $0<\mu <\frac{3}{2}$. Here and throughout, the notation $A\lesssim B$ indicates that $A\le cB$ with a positive constant c which is independent of A and B. If $A\lesssim B$ and $B\lesssim A$, we call A and B are equivalent, denoted by $A\sim B$.

Proof. 

Let ${\square }_{j,k}:=\mathrm{supp}{\varphi }_{j,k}$, then $|{\square }_{j,k}|\sim 2^{-j}$. Since

$$\parallel P_j{f-f\parallel }_{L^2(\Omega )}^2\lesssim \sum _{k\in I_j}{\parallel P_{j}f-f\parallel }_{L^2\left({\square }_{j,k}\right)}^2,$$

using the triangle inequality, one obtains

$$\begin{array}{ccc}\hfill \parallel P_j{f-f\parallel }_{L^2\left({\square }_{j,k}\right)}& =& \parallel P_{j}f-P_j{p+p-f\parallel }_{L^2\left({\square }_{j,k}\right)}\hfill \\ & ⩽& {\parallel f-p\parallel }_{L^2\left({\square }_{j,k}\right)}+{\parallel P_{j}f-P_{j}p\parallel }_{L^2\left({\square }_{j,k}\right)}\hfill \\ & =& {\parallel f-p\parallel }_{L^2\left({\square }_{j,k}\right)}+{\parallel \sum _{m\in I_j}{⟨f-p,{\tilde{\varphi }}_{j,m}⟩}_{L^2(\Omega )}{\varphi }_{j,m}\parallel }_{L^2\left({\square }_{j,k}\right)}\hfill \\ & ⩽& {\parallel f-p\parallel }_{L^2\left({\square }_{j,k}\right)}+\sum _{\genfrac{}{}{0pt}{}{m\in I_j}{{}_{|{\square }_{j,k}\cap {\square }_{j,m}|}\ne \varnothing }}|{⟨f-p,{\tilde{\varphi }}_{j,m}⟩}_{L^2(\Omega )}|\parallel {\varphi }_{j,m}{\parallel }_{L^2\left({\square }_{j,k}\right)}.\hfill \end{array}$$

By the Cauchy-Schwartz inequality, $\parallel {\varphi }_{j,k}{\parallel }_{L^2(\Omega )}\lesssim 1$, $\parallel {\tilde{\varphi }}_{j,k}{\parallel }_{L^2(\Omega )}\lesssim 1$ and $\mathrm{supp}{\tilde{\varphi }}_{j,k}\subset \mathrm{supp}{\varphi }_{j,k}\subset \Omega$, one obtains that

$$\parallel P_j{f-f\parallel }_{L^2\left({\square }_{j,k}\right)}\lesssim {\parallel f-p\parallel }_{L^2\left({\square }_{j,k}\right)}$$

$$+\sum _{\genfrac{}{}{0pt}{}{m\in I_j}{{}_{|{\square }_{j,k}\cap {\square }_{j,m}|}\ne 0}}{\parallel f-p\parallel }_{L^2\left({\square }_{j,k}\right)}\parallel {\tilde{\varphi }}_{j,m}{\parallel }_{L^2(\Omega )}{\parallel {\varphi }_{j,k}\parallel }_{L^2(\Omega )}$$

$$\lesssim {\parallel f-p\parallel }_{L^2\left({\square }_{j,k}\right)}+\sum _{\genfrac{}{}{0pt}{}{m\in I_j}{{}_{|{\square }_{j,k}\cap {\square }_{j,m}|}\ne 0}}{\parallel f-p\parallel }_{L^2\left({\square }_{j,m}\right)}.$$

From the Whitney type estimate [8], one obtains

$$\underset{p\in {\mathcal{P}}_2}{inf}{\parallel f-p\parallel }_{L^2\left({\square }_{j,k}\right)}\lesssim h^2\parallel f^{\left(2\right)}{\parallel }_{L^2\left({\square }_{j,k}\right)}=2^{-2j}{|f|}_{H^2(\Omega )}.$$

Since only a fixed number of ${\square }_{j,k}$ overlap, one has

$$\begin{array}{ccc}\hfill \parallel P_j{f-f\parallel }_{L^2(\Omega )}^2& \lesssim & 2^{-4j}\sum _{k\in I_j}{|f|}_{H^2\left({\square }_{j,k}\right)}^2+2^{-4j}\sum _{k\in I_j}\sum _{\genfrac{}{}{0pt}{}{m\in I_j}{|{\square }_{j,k}\cap {\square }_{j,m}|\ne 0}}{|f|}_{H^2\left({\square }_{j,k}\right)}^2\hfill \\ & \lesssim & 2^{-4j}{|f|}_{H^2(\Omega )}^2.\hfill \end{array}$$

□

Now, we are in a position to construct the wavelet functions. Let

$$\begin{array}{ccc}\hfill \psi \left(x\right)& :=& B_{2,3}^2\left(2x\right)-B_{2,3}^2(2x-1)-B_{2,3}^2(2x-2)+B_{2,3}^2(2x-3),\hfill \\ \hfill {\psi }_b\left(x\right)& :=& B_{1,3}^2\left(2x\right)+B_{2,3}^2\left(2x\right)-B_{2,3}^2(2x-1).\hfill \end{array}$$

$$\begin{array}{c}\hfill {\psi }_{j,k}\left(x\right):=\left\{\begin{array}{cc}{2}^{\frac{j}{2}}{\psi }_b\left(2^{j}x\right),\hfill & k=1,\hfill \\ 2^{\frac{j}{2}}\psi (2^{j}x-k+2),\hfill & k=2,3,\dots ,2^j-1,\hfill \\ 2^{\frac{j}{2}}{\psi }_b\left(2^j(1-x)\right),\hfill & k=2^j.\hfill \end{array}\right.\end{array}$$

$${\Psi }_j:=\{{\psi }_{j,k},k=1,2,\dots ,2^j\}.$$

Then we have the following properties.

Theorem 3. 

For any$j⩾2$, one has

(i) 

$\psi \left(k\right)={\psi }_b\left(k\right)=0$, where $k\in \mathbb{Z}$;

(ii) 

$\mathrm{supp}\psi =[0,3]$, $\mathrm{supp}{\psi }_b=[0,2]$;

(iii) 

$$\begin{array}{c}\hfill \mathrm{supp}{\psi }_{j,k}\left(x\right)=\left\{\begin{array}{cc}[0,2^{-j+1}],\hfill & k=1,\hfill \\ \left[2^{-j}(k-2),2^{-j}(k+1)\right],\hfill & k=2,3,\dots ,2^j-1,\hfill \\ \left[2^{-j+1},1\right],\hfill & k=2^j.\hfill \end{array}\right.\end{array}$$

(iv) 

${\Psi }_j=\frac{1}{\sqrt{2}}{M}_{j,1}^T{\Phi }_{j+1}$, where

$$M_{j,0}^T={\left(\begin{array}{ccccccccccccc}1& 1& -1& 0& 0& 0& \cdots & 0& 0& 0& 0& 0& 0\\ 0& 1& -1& -1& 1& 0& \cdots & 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& -1& -1& \cdots & 0& 0& 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0& \cdots & -1& -1& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \cdots & 0& 1& -1& -1& 1& 0\\ 0& 0& 0& 0& 0& 0& \cdots & 0& 0& 0& -1& 1& 1\end{array}\right)}_{2^j\times 2^{j+1}}.$$

For all $j⩾2$, let $Q_j$ be the linear projection from $V_{j+1}$ onto $V_j$ given as follows: for $f_{j+1}\in V_{j+1}$, $f_j:=Q_j{f}_{j+1}$ is the unique element in $V_j$ determined by the interpolation condition [4]

$$f_j\left(\frac{k}{2^j}\right)=f_{j+1}\left(\frac{k}{2^j}\right),k=1,2,\dots ,2^{j-1},$$

then ${\psi }_{j,k}\in V_{j+1}$, and $Q_j{\psi }_{j,k}=0$. Define

$$W_j:=\mathrm{span}{\Psi }_j,$$

then $dim{W}_j=2^j$. Moreover, ${\Psi }_j$ is a Riesz basis of $W_j$ and its Riesz bounds are independent of j. Since $dim{V}_j+dim{W}_j=dim{V}_{j+1}$, one obtains

$$V_{j+1}=V_j\oplus W_j.$$

Therefore

$$V_{j+1}=V_2\oplus \underset{i=2}{\overset{j}{⨁}}{W}_i.$$

Suppose that

$$M_j:=(M_{j,0},M_{j,1}),$$

then from Lemma 3 $\left(v\right)$ and Theorem 3 $\left(iv\right)$, one obtains

$$\left(\begin{array}{c}{\Phi }_{j-1}\\ {\Psi }_{j-1}\end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{c}{M}_{j-1,0}^T\\ M_{j-1,1}^T\end{array}\right){\Phi }_j=\frac{1}{\sqrt{2}}{M}_{j-1}^T{\Phi }_j,(\forall j\ge 3).$$

Recursively, one has

$$\left(\begin{array}{c}{\Phi }_2\hfill \\ {\Psi }_2\hfill \\ {\Psi }_3\hfill \\ ⋮\hfill \\ {\Psi }_{j-1}\hfill \end{array}\right)=\left(\begin{array}{ccccc}\frac{1}{\sqrt{2}}{M}_2^T& & & & \\ & I_3& & & \\ & & I_4& & \\ & & & \ddots & \\ & & & & I_{j-1}\end{array}\right)\cdots \left(\begin{array}{cc}\frac{1}{\sqrt{2}}{M}_{j-2}^T& \\ & I_{j-1}\end{array}\right)\frac{1}{\sqrt{2}}{M}_{j-1}^T{\Phi }_j.$$

That is

$${\Psi }^j=T_j{\Phi }_j,$$

(7)

where

$$T_j:=\left(\begin{array}{ccccc}\frac{1}{\sqrt{2}}{M}_2^T& & & & \\ & I_3& & & \\ & & I_4& & \\ & & & \ddots & \\ & & & & I_{j-1}\end{array}\right)\cdots \left(\begin{array}{cc}\frac{1}{\sqrt{2}}{M}_{j-2}^T& \\ & I_{j-1}\end{array}\right)\frac{1}{\sqrt{2}}{M}_{j-1}^T,$$

(8)

$I_j$ is a $2^j\times 2^j$ unity matrix. Since the determinant of $M_j$ is equal to 0.5, one obtains ${\Psi }^{j+1}:={\Phi }_2\cup {\Psi }_2\cup {\Psi }_3\cup \cdots \cup {\Psi }_j$ is a basis of the space $V_{j+1}$.

3. Characterization Theorem

In this section, we use wavelet bases to characterize Sobolev space $H_0^{\mu }(\Omega )$, where $0<\mu <\frac{3}{2}$.

Let ${\nabla }_{y}f(·):=f(·)-f(·-y),{\nabla }_y^m:={\nabla }_y{\nabla }_y^{m-1},(m>1)$. For $x,y\in \mathbb{R},$ we use $[x,y]$ to denote the line segment $\{(1-t)x+ty:0\le t\le 1\},{\Omega }_y:=\{x\in \Omega :[x-y,x]\in \Omega \}.$ The modulus of continuity of f is given by

$$\omega {(f,h)}_p:=\underset{|y|⩽h}{sup}{\parallel {\nabla }_{y}f\parallel }_{L_p\left({\Omega }_y\right)},h>0.$$

The mth modulus of smoothness of f is given by

$${\omega }_m{(f,h)}_p:=\underset{|y|⩽h}{sup}{\parallel {\nabla }_y^{m}f\parallel }_{L_p\left({\Omega }_{my}\right)},h>0.$$

Let $\mu >0$, $1\le p,q\le \infty$, the Besov space $B_{p,q}^{\mu }(\Omega )$ is the collection of the functions $f\in L_p(\Omega )$ satisfying

$${|f|}_{B_{p,q}^{\mu }(\Omega )}:=\left\{\begin{array}{c}{\left({\displaystyle \sum _{k\in \mathbb{Z}}}{\left[2^{k\mu }{\omega }_m{(f,2^{-k})}_p\right]}^q\right)}^{\frac{1}{q}},1\le q<\infty ,\\ \underset{k\in \mathbb{Z}}{sup}\left\{2^{k\mu }{\omega }_m{(f,2^{-k})}_p\right\},q=\infty ,\end{array}\right.$$

where m is the least integer greater than $\mu$. The norm for $B_{p,q}^{\mu }(\Omega )$ is defined by

$${\parallel f\parallel }_{B_{p,q}^{\mu }(\Omega )}:={\parallel f\parallel }_{L_p(\Omega )}+{|f|}_{B_{p,q}^{\mu }(\Omega )}.$$

If $p=q=2$, the space $B_{2,2}^{\mu }\left(\mathbb{R}\right)$ is the same as the Sobolev space $H^{\mu }\left(\mathbb{R}\right)$, and the semi-norm ${|·|}_{B_{2,2}^{\mu }\left(\mathbb{R}\right)}$ and ${|·|}_{H^{\mu }\left(\mathbb{R}\right)}$ are equivalent [9].

In the following theorem, we give a characterization of the space $H_0^{\mu }(\Omega )$ via the B-spline wavelets constructed before.

Theorem 4. 

For any$f\in H_0^{\mu }(\Omega ),0<\mu <\frac{3}{2}$, there exists two constants $C_3>0,C_4>0$ such that

$$C_3{|f|}_{H_0^{\mu }(\Omega )}⩽\left(\right(2^{2\mu }\parallel P_2{f\parallel }_{L^2(\Omega )}{)}^2+\sum _{j=3}^{\infty }(2^{j\mu }\parallel (P_j-P_{j-1}){f\parallel }_{L^2(\Omega )}{)}^2{)}^{\frac{1}{2}}⩽C_4{|f|}_{H_0^{\mu }(\Omega )}.$$

(9)

Proof. 

According to paper [10], for any $f\in L_2(\Omega )$, one has

$$\parallel P_j{f-f\parallel }_{L^2(\Omega )}\lesssim {\omega }_3(f,2^{-j}).$$

Let $g_2:=P_{2}f,g_j:=P_{j}f-P_{j-1}f,j⩾3$, then one obtains $f={\displaystyle \sum _{j=3}^{\infty }}{g}_j$ is convergent in $L_2(\Omega )$.

(i)

First, we show that the left part in (9) is established. Since $g_j\in V_j$, one obtains

$$g_j=\sum _{k\in I_j}{b}_{j,k}{\varphi }_{j,k},j⩾2.$$

Please note that $\{2^{-j\mu }{\varphi }_{j,k}\mid j⩾2,k\in I_j\}$ is a Bessel sequence in space $H_0^{\mu }(\Omega )$ [11]. Therefore,

$${|f|}_{H_0^{\mu }(\Omega )}=|\sum _{j=2}^{\infty }\sum _{k\in I_j}{2}^{j\mu }{b}_{j,k}{2}^{-j\mu }{\varphi }_{j,k}{|}_{H_0^{\mu }(\Omega )}⩽C_1(\sum _{j=2}^{\infty }\sum _{k\in I_j}|2^{j\mu }{b}_{j,k}{{|}^2)}^{\frac{1}{2}}.$$

Since ${\Phi }_j$ is a Riesz bases of $V_j$ and the Riesz bounds are independent of j, one obtains

$$\sum _{k\in I_j}|b_{j,k}{|}^2⩽C_2^2{\parallel g_j\parallel }_{L^2(\Omega )}.$$

Therefore,

$${|f|}_{H_0^{\mu }(\Omega )}⩽C_1{C}_2(\sum _{j=2}^{\infty }(2^{j\mu }\parallel g_j{\parallel }_{L^2(\Omega )}{{)}^2)}^{\frac{1}{2}}.$$

(ii)

Next we show that the right part of inequality (9) is established. For any $f\in H_0^{\mu }(\Omega )$, according to Poincare inequality, one has

$$\parallel g_2{\parallel }_{L^2(\Omega )}=\parallel P_2{f\parallel }_{L^2(\Omega )}⩽\parallel P_2{\parallel \parallel f\parallel }_{L^2(\Omega )}⩽\tilde{C}{|f|}_{H_0^{\mu }(\Omega )}.$$

For $j⩾3$, one obtains

$$\begin{array}{cc}\parallel g_j{\parallel }_{L^2(\Omega )}\hfill & =\parallel P_{j}f-P_{j-1}{f\parallel }_{L^2(\Omega )}\hfill \\ & ⩽\parallel P_j{f-f\parallel }_{L^2(\Omega )}+{\parallel f-P_{j-1}f\parallel }_{L^2(\Omega )}\hfill \\ & ⩽{\omega }_3(f,2^{-j})+{\omega }_3(f,2^{-j}·2)\hfill \\ & \lesssim {\omega }_3(f,2^{-j}).\hfill \end{array}$$

From the definition of Besov space, one obtains

$$(\sum _{j=3}^{\infty }(2^{j\mu }\parallel g_j{\parallel }_{L^2(\Omega )}{)}^2{)}^{\frac{1}{2}}\lesssim {(\sum _{j=3}^{\infty }{(2^{j\mu }{\omega }_3(f,2^{-j}))}^2)}^{\frac{1}{2}}\lesssim {|f|}_{H_0^{\mu }(\Omega )}.$$

□

4. Wavelet Preconditioning

In this section, we show that our wavelet bases constructed in the previous section are very useful and efficient.

Let $u_j\in V_j$ such that

$$a(u_j,v_j)={⟨f,v_j⟩}_{L^2(\Omega )},\forall v_j\in V_j.$$

(10)

Recall that ${\Phi }_j$ is the base of $V_j$, then the above Equation (10) is equivalent to the systems

$$A_j{\overrightarrow{u}}_j={\overrightarrow{f}}_j,$$

(11)

where $A_j:={\left(a({\varphi }_{j,k},{\varphi }_{j,m})\right)}_{k,m\in I_j}$, ${\overrightarrow{f}}_j^T:={({⟨f,{\varphi }_{j,m}⟩}_{L^2(\Omega )})}_{m\in I_j},{\overrightarrow{u}}_j^T:={\left(u_{j,k}\right)}_{k\in I_j}.$

However, the following example shows that the condition number of the stiffness matrix $A_j$ is almost $\mathcal{O}\left(2^{2j}\right)(j\to \infty$). Hence, the system $\left(11\right)$ is very difficult to solve without preconditioning.

Example 1. 

In Equation (1), let the coefficient function $q\left(x\right)\equiv c,x\in \Omega .$ For $c\in \{0,0.1,1,10,100\}$, the condition numbers of the matrix $A_j$ are shown in Table 1. It is clearly seen that the condition numbers increase exponentially with respect to the level j.

Table 1. Condition numbers of the stiffness matrix $A_j$.

$\mathit{j}/\mathit{c}$	0	0.1	1	10	100
2	2.7836	2.7653	2.6168	1.9363	2.8893
3	10.0465	9.9519	9.1768	5.2604	1.8349
4	39.2159	38.8271	35.6489	19.6774	3.9295
5	155.7240	154.1682	141.4521	77.5918	14.3248
6	619.2913	613.1178	562.6423	308.6641	56.2159
7	2469.1144	2444.1941	2239.5977	1228.3905	223.5504
8	9857.4455	9756.4896	8935.0989	4896.3646	890.2448

In Table 2, the factors between two successive levels are indicated. The numbers show that the growth is by a factor of 4. Moreover, the increase rate is independent on the particular choice of c.

Table 2. Factors of condition numbers between level j and $j-1$.

$\mathit{j}/\mathit{c}$	0	0.1	1	10	100
2	—	—	—	—	—
3	3.6092	3.5988	3.5068	2.7167	0.6351
4	3.9034	3.9015	3.8847	3.7404	2.1416
5	3.9709	3.9706	3.9679	3.9432	3.6454
6	3.9769	3.9769	3.9776	3.9780	3.9244
7	3.9870	3.9865	3.9805	3.9797	3.9766
8	3.9923	3.9917	3.9896	3.9860	3.9823

To overcome the above difficulty, we use the wavelets preconditioning method. In fact, as we know, the collection of functions ${\Psi }^j:={\Phi }_2\cup {\Psi }_2\cup {\Psi }_3\cup \cdots \cup {\Psi }_{j-1}$ is also a basis of $V_j$, so we suppose that

$$u_j=\sum _{k\in I_2}{a}_{2,k}{\varphi }_{2,k}+\sum _{i=2}^{j-1}\sum _{k\in I_i}{b}_{i,k}{\psi }_{i,k}:={\overrightarrow{b}}_j^T{\Psi }^j,$$

(12)

where the vector ${\overrightarrow{b}}_j^T=\{a_{2,k},b_{i,m}|k\in I_2,i=2,\dots ,j-1,m\in I_i\}$ is the solution of the following equation

$$B_j{\overrightarrow{b}}_j={\overrightarrow{F}}_j,$$

(13)

where the matrix $B_j:={\left(a(\sigma ,\eta )\right)}_{\sigma ,\eta \in {\Psi }^j},{\overrightarrow{F}}_j^T:={({⟨f,\eta ⟩}_{L^2(\Omega )})}_{\eta \in {\Psi }^j}$.

In fact, we use the PCG (Preconditioned Conjugate Gradient) algorithm (please see, e.g., [12] pp. 94–95) to solve the system (13), that is

$$D_j^{-1}{B}_j{D}_j^{-1}{D}_j{\overrightarrow{b}}_j=D_j^{-1}{\overrightarrow{F}}_j,$$

where the preconditioner is a diagonal matrix

$$D_j:=diag(\underset{2^2}{\underbrace{2^2,\dots ,2^2}},\underset{2^2}{\underbrace{2^2,\dots ,2^2}},\underset{2^3}{\underbrace{2^3,\dots ,2^3}},\underset{2^4}{\underbrace{2^4,\dots ,2^4}},\dots ,\underset{2^{j-1}}{\underbrace{2^{j-1},\dots ,2^{j-1}}}).$$

(14)

Therefore, the system (13) is equivalent to the following equation

$${\mathbf{B}}_j{\overrightarrow{\mathbf{b}}}_j={\overrightarrow{\mathbf{F}}}_j,$$

(15)

where ${\mathbf{B}}_j:=D_j^{-1}{B}_j{D}_j^{-1},{\overrightarrow{\mathbf{b}}}_j:=D_j{\overrightarrow{b}}_j,{\overrightarrow{\mathbf{F}}}_j:=D_j^{-1}{\overrightarrow{F}}_j$.

To show the condition number of the matrix ${\mathbf{B}}_j$ is uniformly bounded, we give the following example.

Example 2. 

In Equation (1), let the coefficient function $q\left(x\right)\equiv c,x\in \Omega .$ For $c\in \{0,0.1,1,10,100\}$, the condition numbers of the matrix ${\mathbf{B}}_j$ are shown in Table 3. Comparing with the values in Table 1, it is clearly seen that the condition numbers of the matrix ${\mathbf{B}}_j$ are uniformly bounded with respect to the level j. Therefore, using ${\Psi }^j$ as a basis for $V_j$ yields an asymptotically preconditioned system (15).

Table 3. Condition numbers of the stiffness matrix ${\mathbf{B}}_j$.

$\mathit{j}/\mathit{c}$	0	0.1	1	10	100
3	537.2908	537.0562	535.2687	533.2748	651.7660
4	540.3562	539.5721	538.9766	536.2379	656.3201
5	545.8523	541.2897	540.3523	539.9642	663.8994
6	548.1359	546.0578	543.4826	542.8217	670.1432
7	550.9631	550.3573	548.2370	546.3572	673.3134
8	555.8472	553.9882	551.3587	550.3356	681.3874

However, Figure 1 shows that the matrix ${\mathbf{B}}_j$ is not sparse. The so-called finger structure is visible. Now we are facing the following situation:

Figure 1. The pattern of the stiffness matrix $A_j$ (left), $B_j$ (right) for $j=7$.

◊

the stiffness matrix $A_j$ with respect to the single-scale basis ${\Phi }_j$ is sparse but ill conditioned;

◊

the wavelet stiffness matrix ${\mathbf{B}}_j$ is asymptotically optimal preconditioned, but not sparse.

Till now, both methods cannot be used immediately. However,

$$B_j=a({\Psi }^j,{\Psi }^j)=a(T_j{\Phi }_j,T_j{\Phi }_j)=T_{j}a({\Phi }_j,{\Phi }_j)T_j^T=T_j{A}_j{T}_j^T,$$

$${\overrightarrow{F}}_j={⟨f,{\Psi }^j⟩}_{L^2(\Omega )}={⟨f,T_j{\Phi }_j⟩}_{L^2(\Omega )}=T_j{⟨f,{\Phi }_j⟩}_{L^2(\Omega )}=T_j{\overrightarrow{f}}_j.$$

where the matrix $T_j$ and $D_j$ given by (8) (14) respectively are both sparse. Therefore, we know that the matrix Hence ${\mathbf{B}}_j:=D_j^{-1}{T}_j{A}_j{T}_j^T{D}_j^{-1}$, ${\overrightarrow{\mathbf{F}}}_j:=D_j^{-1}{T}_j{\overrightarrow{f}}_j,$ can be expressed as the product of some sparse matrices. that is Equation (15) can be written as

$$D_j^{-1}{T}_j{A}_j{T}_j^T{D}_j^{-1}=D_j^{-1}{T}_j{\overrightarrow{f}}_j.$$

(16)

In fact, the above Equation (16) combines both positive effects.

5. Numerical Examples

In this Section, we focus on some numerical tests.

Supposed that u is the exact solution of Equation $\left(1\right)$, $u_j$ is the Galerkin approximation solution given by (12), then according to paper [6] and Theorem 2, one has

$$\parallel u-u_j{\parallel }_{L^2(\Omega )}\lesssim \underset{v_j\in V_j(\Omega )}{inf}\parallel u-v_j{\parallel }_{L^2(\Omega )}\lesssim 2^{-2j}{|u|}_{H^2(\Omega )}.$$

(17)

The following examples show that combining with the preconditional Galerkin method, our wavelet bases constructed before are very useful and efficient.

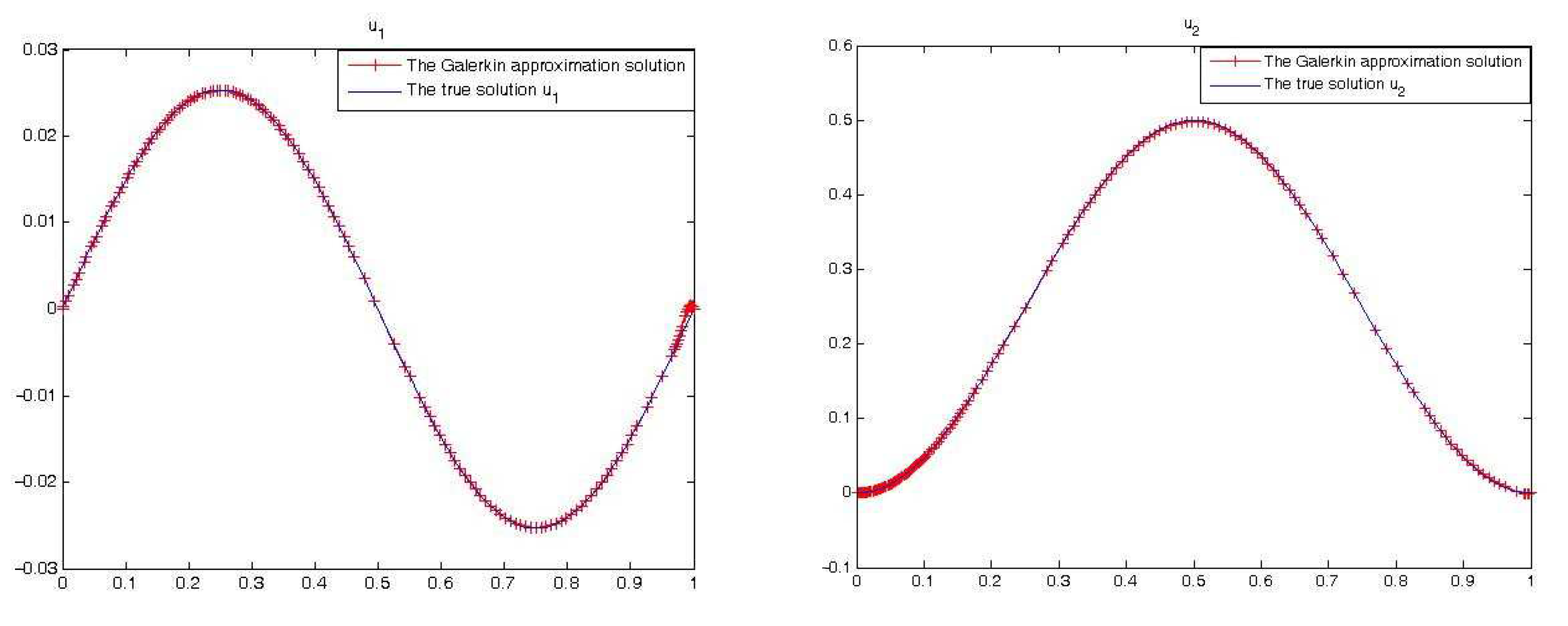
Example 3. 

In Equation (1), let $q\left(x\right)=0,f\left(x\right)=sin\left(2\pi x\right),x\in \Omega .$ Then the exact solution $u_1$ is given by

$$u_1\left(x\right)=\frac{1}{{\left(2\pi \right)}^2}sin\left(2\pi x\right),x\in \Omega .$$

Example 4. 

In Equation (1), let $q\left(x\right)=sin\left(2\pi x\right),f\left(x\right)=-{\pi }^{2}cos\left(2\pi x\right)+\frac{1}{4}sin\left(2\pi x\right)-\frac{1}{4}sin\left(2\pi x\right)cos\left(2\pi x\right),x\in \Omega .$ Then the exact solution $u_2$ is given by

$$u_2\left(x\right)=\frac{1-cos\left(2\pi x\right)}{4},x\in \Omega .$$

The exact solutions for the above two examples and their numerical solutions with $j=6$ are showed respectively in Figure 2. The error estimates in $L_2$ norm and convergence factor between successive level are given in Table 4 which demonstrates that the growth factor is almost by 4 which is the same as in (17).

Figure 2. The figure of the Galerkin approximation solution ($j=6$) and the exact solution $u_1$ (left), $u_2$ (right).

Table 4. Error estimates in $L_2$ norm and convergence factors.

	${\mathit{u}}_1$		${\mathit{u}}_2$
j	${\mathit{L}}_2-$Errors	Convergence Factors	${\mathit{L}}_2-$Errors	Convergence Factors
4	$4.4245\times {10}^{-4}$	—	$1.7798\times {10}^{-2}$	—
5	$1.1480\times {10}^{-4}$	3.854	$4.5754\times {10}^{-3}$	3.752
6	$2.8794\times {10}^{-5}$	3.987	$1.1752\times {10}^{-3}$	3.893
7	$7.2003\times {10}^{-6}$	3.999	$2.9709\times {10}^{-4}$	3.956
8	$1.8644\times {10}^{-6}$	3.862	$7.5905\times {10}^{-3}$	3.914