Oversampling Errors in Multimodal Medical Imaging Are Due to the Gibbs Effect
Abstract
1. Introduction
- one (or more) morphological, high-resolution image, usually obtained by Computed Tomography (CT) or by Magnetic resonance Imaging (MRI);
2. Preliminaries and Definitions
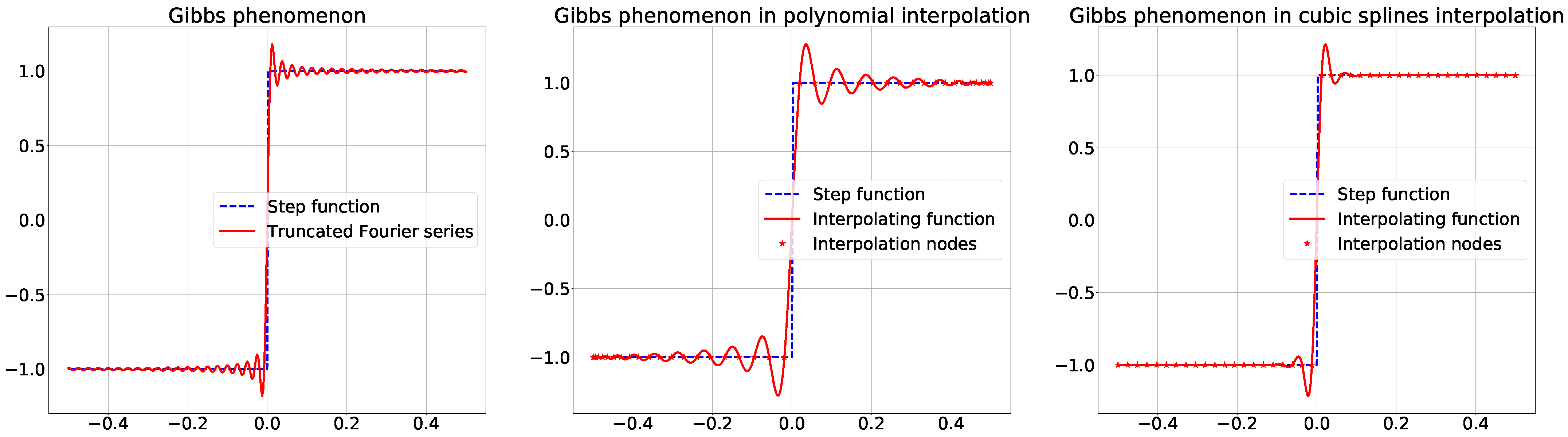
2.1. The Gibbs Effect
2.2. An Image and Its Sampling
2.3. Resampling an Image
2.4. Boolean Images and Morphological Operators
- the volume of M, as the cardinality of the corresponding index representation
- the restriction of F to M as the array of the values of F in the voxels where M is equal to one
- the shift by a vector
- the dilation by a structuring element
- the erosion by a structuring element
2.5. Segmentation of an Image
2.6. Statistical Moments of an Image Inside a Voi
3. Image Interpolation and Gibbs Effect
3.1. Basis Construction
- (I)
- Let , with the support radius, a function such that:
- (i)
- ;
- (ii)
- ;
- (iii)
- .
- (II)
- Let , with a set of equispaced points of the interval . Then we define for the univariate basiswith .This basis is cardinal for (i)–(ii), has compact support for (iii), radial as it depends on the absolute value of its argument, and is normalized for construction.
- (III)
- The trivariate interpolation basis corresponding to the set X iswhere is the separable kernel functionwith , , and .
3.2. Interpolation by Convolution
- compute ;
- then get ;
- at last .
3.3. Error Estimates for the Univariate Interpolation
- Case 1 (so ):with , ;
- Case 2 (so ):with , .
3.4. Error Estimates for the Trivariate Interpolation
4. Materials and Methods
4.1. Images
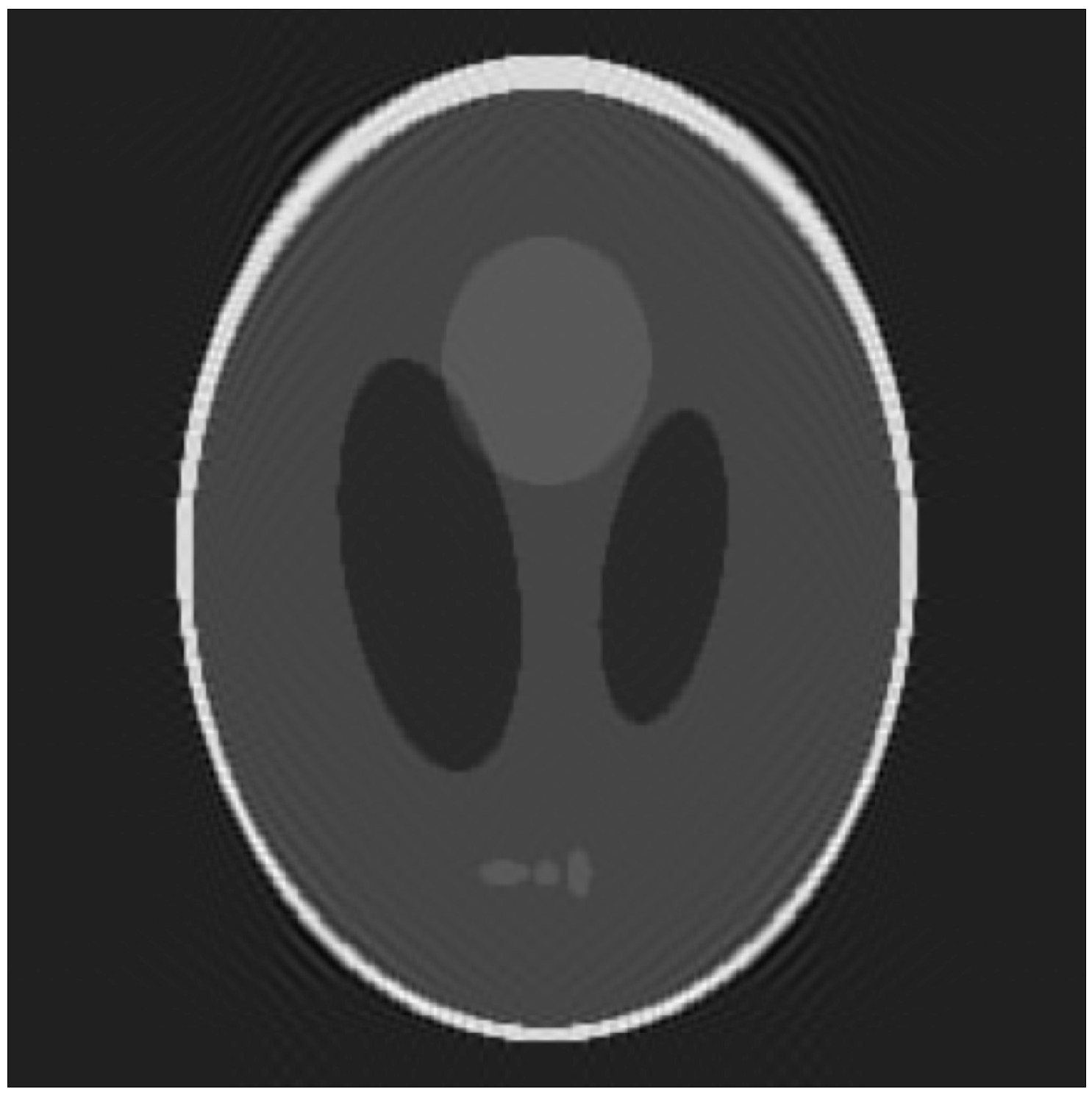
- The 3D Shepp–Logan (SL) phantom [26], a picewise-constant function made by the weighted sum of characteristic functions over different ellipsoids. The SL images were created in python with tomopy and nibabel [27] and saved in nifti format. The Segmention was made with a python script by grouping the voxels of the same intensity values. Size: ;
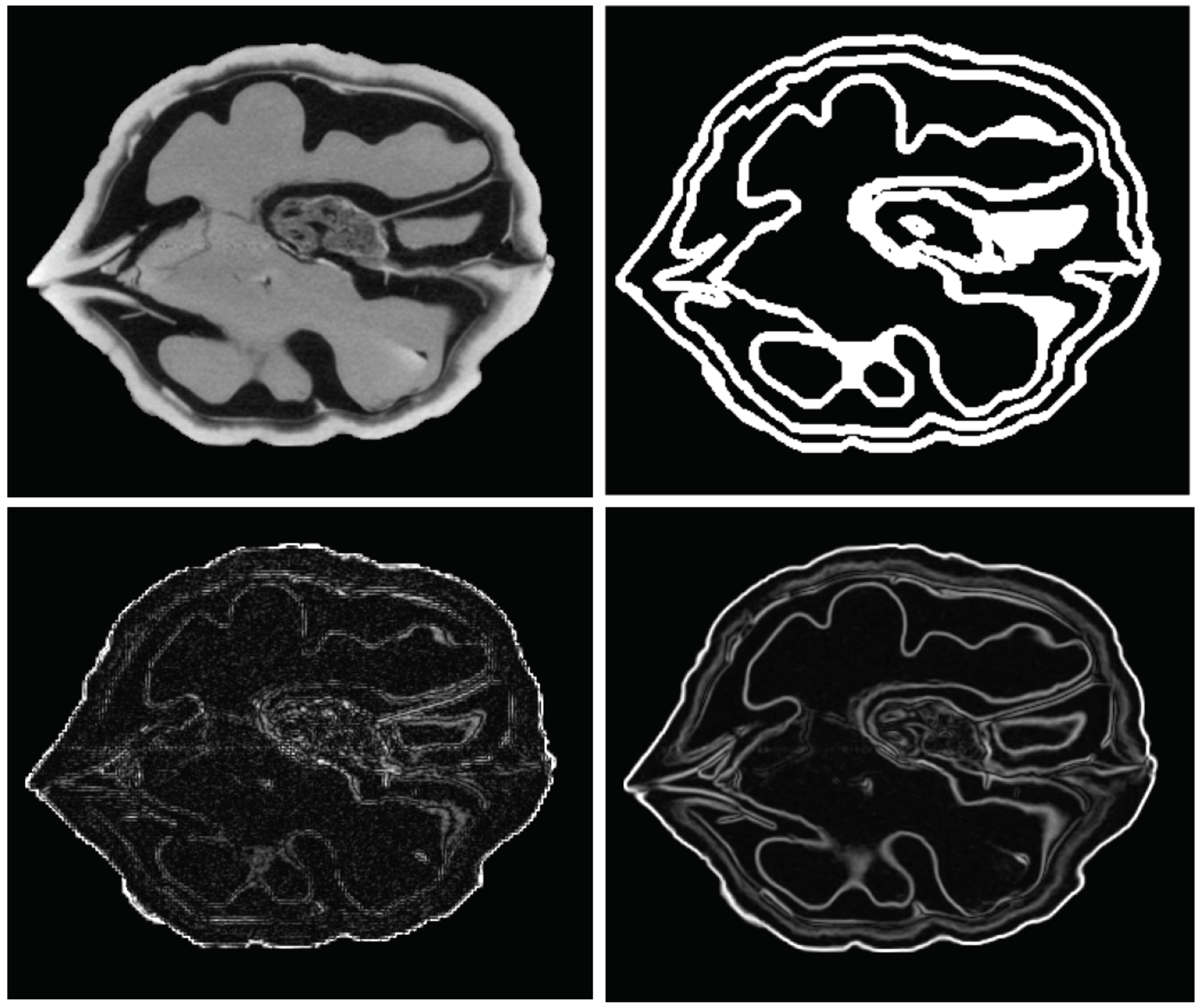
- A 3D isotropic MRI, T1-weighted of one of the authors’ heads. Skull-stripping and automatical segmentation was conducted with GIF [28]. Size: ;
- The CT of a walnut, downloaded from http://www.informatik.uni-leipzig.de/~wiebel/public_data/ (accessed on 9 June 2021) along with its segmentation image [29]. Size: .
4.2. Software Used
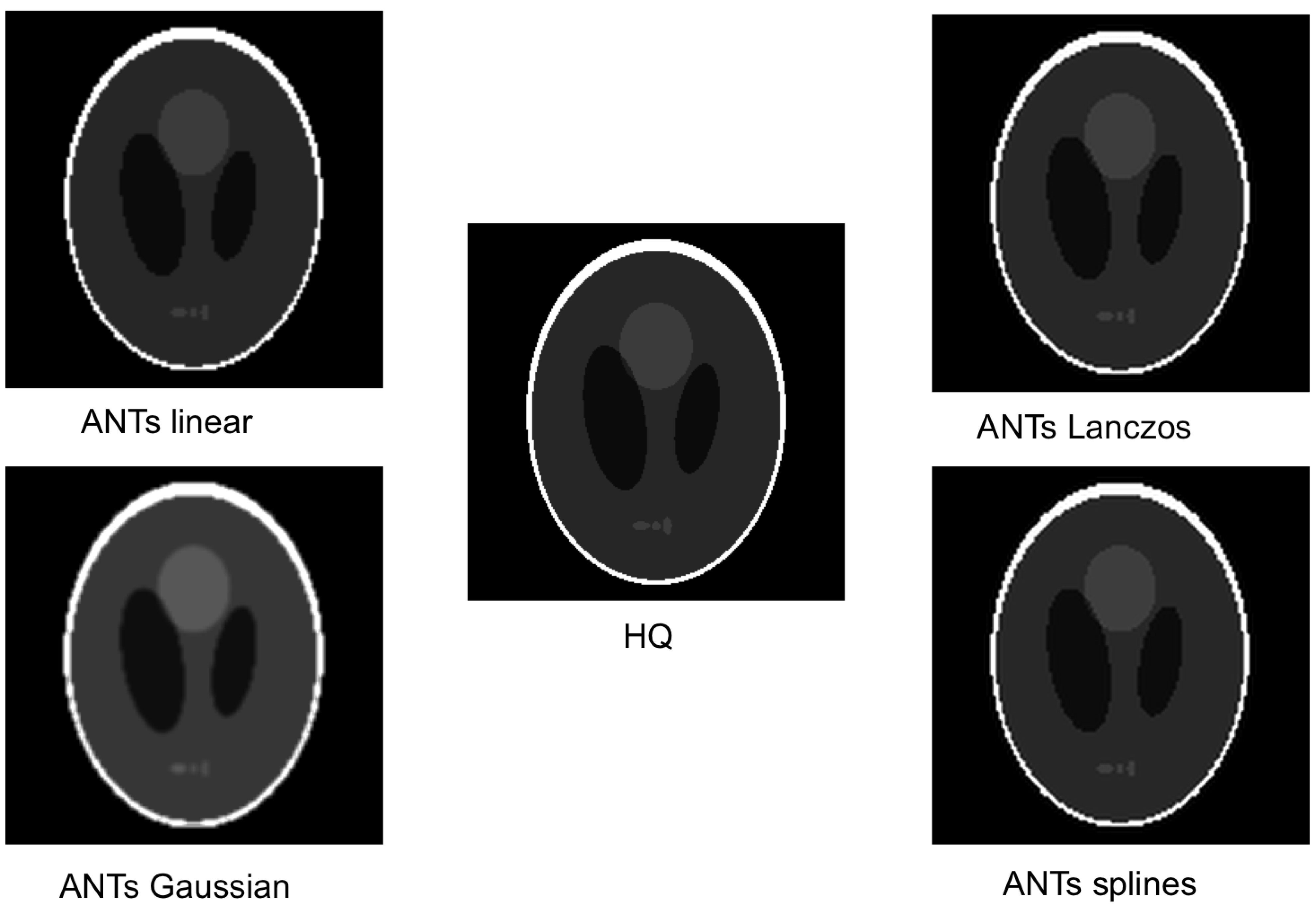
- antsApplyTransforms from Advanced Normalization Tools (ANTs) [31,32] v2.2.0, with interpolation options:
- (a)
- Nearest and Multilabel for undersampling segmentation;
- (b)
- Linear, Gaussian, LanczosWindowedSinc and Splines for oversampling functional image;
- (a)
- Nearest for undersampling;
- (b)
- Trilinear and Splines for oversampling;
- (a)
- Nearest for undersampling;
- (b)
- Trilinear and Splines for oversampling.
4.3. Evaluating the Error
- by using functional image F and undersampled segmentation
- by using oversampled functional image and segmentation M
4.4. Locating the Oversampling Error
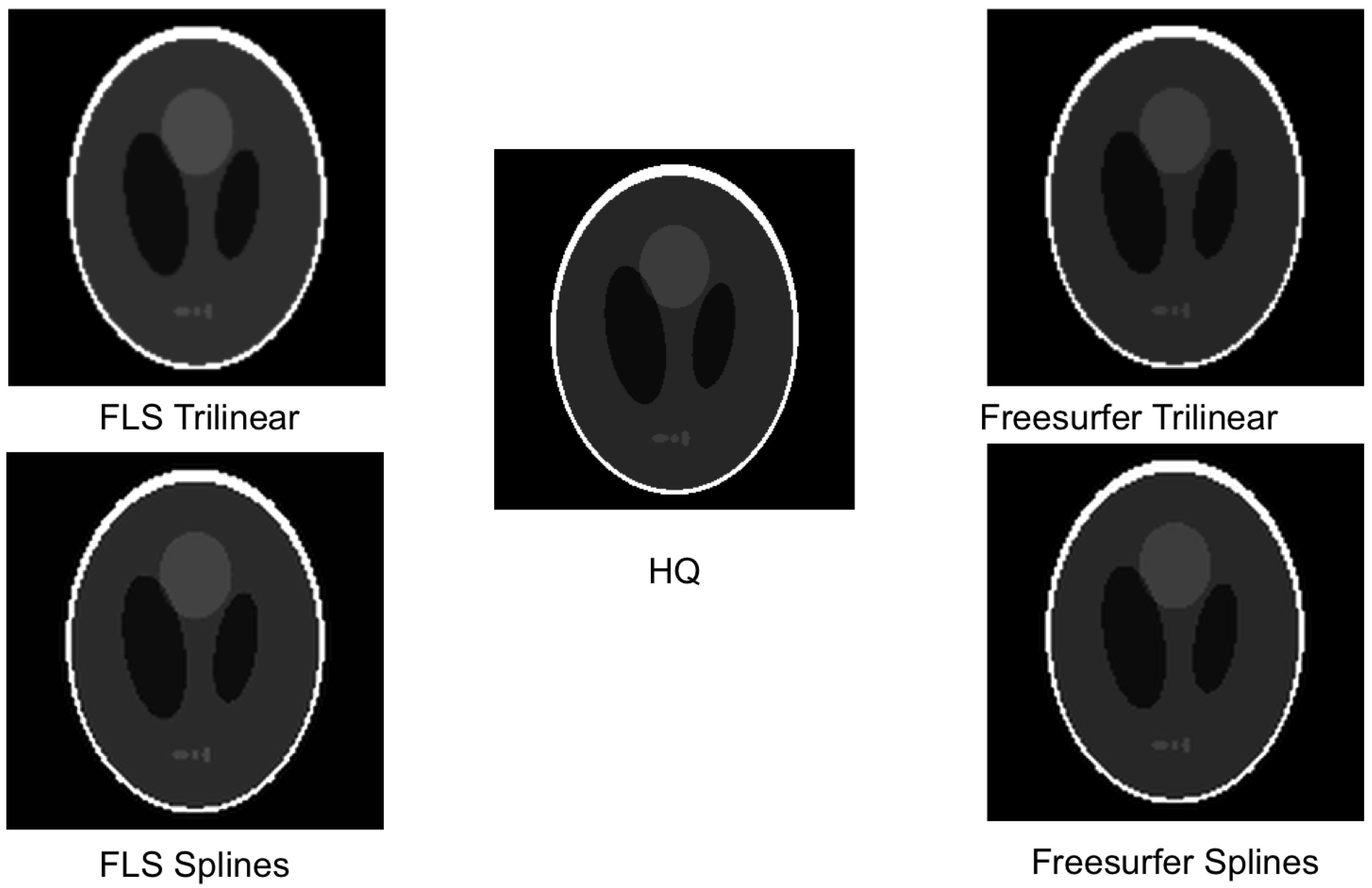
5. Experimental Results
6. Discussion
7. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ehman, E.C.; Johnson, G.B.; Villanueva-Meyer, J.E.; Cha, S.; Leynes, A.P.; Larson, P.E.Z.; Hope, T.A. PET/MRI: Where might it replace PET/CT? J. Magn. Reson. Imaging 2017, 46, 1247–1262. [Google Scholar] [CrossRef]
- Misri, R. Multimodality imaging, Molecular Imaging Techniques: New Frontiers. 2013, pp. 162–176. Available online: https://www.futuremedicine.com/doi/abs/10.4155/ebo.13.181 (accessed on 9 June 2021).
- Zhang, X.Y.; Yang, Z.L.; Lu, G.M.; Yang, G.F.; Zhang, L.J. PET/MR Imaging: New Frontier in Alzheimer’s Disease and Other Dementias. Front. Mol. Neurosci. 2017, 10, 343. [Google Scholar] [CrossRef]
- Cecchin, D.; Poggiali, D.; Riccardi, L.; Turco, P.; Bui, F.; De Marchi, S. Analytical and experimental FWHM of a gamma camera: Theoretical and practical issues. PeerJ 2015, 3, e722. [Google Scholar] [CrossRef]
- Millman, K.J.; Brett, M. Analysis of Functional Magnetic Resonance Imaging in Python. Comput. Sci. Eng. 2007, 9, 52–55. [Google Scholar] [CrossRef]
- De Marchi, S.; Erb, W.; Marchetti, F. Spectral filtering for the reduction of the gibbs phenomenon for polynomial approximation methods on lissajous curves with applications in MPI. Dolomites Res. Notes Approx. 2017, 10, 128–137. [Google Scholar] [CrossRef]
- Tustison, N.J.; Avants, B.B.; Cook, P.A.; Kim, J.; Whyte, J.; Gee, J.C.; Stone, J.R. Logical circularity in voxel-based analysis: Normalization strategy may induce statistical bias. Hum. Brain Mapp. 2012, 35, 745–759. [Google Scholar] [CrossRef]
- Dumitrescu, D.; Boiangiu, C.A. A Study of Image Upsampling and Downsampling Filters. Computers 2019, 8, 30. [Google Scholar] [CrossRef]
- Delgado, J.; Moure, J.C.; Vives-Gilabert, Y.; Delfino, M.; Espinosa, A.; Gómez-Ansón, B. Improving the Execution Performance of FreeSurfer. Neuroinformatics 2014, 12, 413–421. [Google Scholar] [CrossRef]
- Jerri, A. The Gibbs Phenomenon in Fourier Analysis, Splines, and Wavelet Approximations. Z. Angew. Math. Mech. 2005, 85, 224. [Google Scholar] [CrossRef]
- Lehmann, T.; Gonner, C.; Spitzer, K. Survey: Interpolation methods in medical image processing. IEEE Trans. Med. Imaging 1999, 18, 1049–1075. [Google Scholar] [CrossRef]
- Fischl, B.; Salat, D.H.; Busa, E.; Albert, M.; Dieterich, M.; Haselgrove, C.; van der Kouwe, A.; Killiany, R.; Kennedy, D.; Klaveness, S.; et al. Whole Brain Segmentation. Neuron 2002, 33, 341–355. [Google Scholar] [CrossRef]
- Cecchin, D.; Barthel, H.; Poggiali, D.; Cagnin, A.; Tiepolt, S.; Zucchetta, P.; Turco, P.; Gallo, P.; Frigo, A.C.; Sabri, O.; et al. A new integrated dual time-point amyloid PET/MRI data analysis method. Eur. J. Nucl. Med. Mol. Imaging 2017, 44, 2060–2072. [Google Scholar] [CrossRef]
- Fornberg, B.; Flyer, N. The Gibbs phenomenon for radial basis functions. In The Gibbs Phenomenon in Various Representations and Applications; Sampling Publishing: Potsdam, NY, USA, 2006. [Google Scholar]
- Chhoa, J.F. An Adaptive Approach to Gibbs’ Phenomenon. Master’s Thesis, The University of Southern Mississippi, Hattiesburg, MS, USA, 2020. [Google Scholar]
- Hamann, B. Modeling contours of trivariate data. ESAIM M2AN 1992, 26, 51–75. [Google Scholar] [CrossRef][Green Version]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image Analysis Using Mathematical Morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 4, 532–550. [Google Scholar] [CrossRef] [PubMed]
- Pham, D.L.; Xu, C.; Prince, J.L. Current Methods in Medical Image Segmentation. Annu. Rev. Biomed. Eng. 2000, 2, 315–337. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.K. Visual pattern recognition by moment invariants. IEEE Trans. Inform. Theory 1962, 8, 179–187. [Google Scholar] [CrossRef]
- Klęsk, P.; Kapruziak, M.; Olech, B. Statistical moments calculated via integral images in application to landmine detection from Ground Penetrating Radar 3D scans. Pattern Anal. Applic 2017, 21, 671–684. [Google Scholar] [CrossRef]
- Burger, W.; Burge, M.J. Principles of Digital Image Processing: Core Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 210–233. [Google Scholar]
- Moraes, T.; Amorim, P.; Da Silva, J.V.; Pedrini, H. Medical image interpolation based on 3D Lanczos filtering. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2019, 8, 294–300. [Google Scholar] [CrossRef]
- Getreuer, P. Linear Methods for Image Interpolation. Image Process. Line 2011, 1, 238–259. [Google Scholar] [CrossRef]
- Wendland, H. Fast Evaluation of Radial Basis Functions: Methods Based on Partition of Unity. In Approximation Theory X: Wavelets, Splines, and Applications; Vanderbilt University Press: Nashville, TN, USA, 2002; pp. 473–483. [Google Scholar]
- Jung, J.H. A note on the Gibbs phenomenon with multiquadric radial basis functions. Appl. Numer. Math. 2007, 57, 213–229. [Google Scholar] [CrossRef]
- Shepp, L.; Logan, B. The Fourier reconstruction of a head section. IEEE Trans. Nucl. Sci. 1974, 21, 21–43. [Google Scholar] [CrossRef]
- Brett, M.; Markiewicz, C.J.; Hanke, M.; Côté, M.A.; Cipollini, B.; McCarthy, P.; Jarecka, D.; Cheng, C.P.; Halchenko, Y.O.; Cottaar, M.; et al. nipy/nibabel: 3.2.1. Zenodo 2020. [Google Scholar] [CrossRef]
- Cardoso, M.J.; Modat, M.; Wolz, R.; Melbourne, A.; Cash, D.; Rueckert, D.; Ourselin, S. Geodesic Information Flows: Spatially-variant Graphs and Their Application to Segmentation and Fusion. IEEE Trans. Med. Imaging 2015, 34, 1976–1988. [Google Scholar] [CrossRef]
- Prassni, J.S.; Ropinski, T.; Hinrichs, K. Uncertainty-Aware Guided Volume Segmentation. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1358–1365. [Google Scholar] [CrossRef]
- Müller-Gärtner, H.W.; Links, J.M.; Prince, J.L.; Bryan, R.N.; McVeigh, E.; Leal, J.P.; Davatzikos, C.; Frost, J.J. Measurement of Radiotracer Concentration in Brain Gray Matter Using Positron Emission Tomography: Mri-based Correction for Partial Volume Effects. J. Cereb. Blood Flow Metab. 1992, 12, 571–583. [Google Scholar] [CrossRef]
- Avants, B.; Epstein, C.; Grossman, M.; Gee, J. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008, 12, 26–41. [Google Scholar] [CrossRef]
- Avants, B.B.; Tustison, N.J.; Song, G.; Cook, P.A.; Klein, A.; Gee, J.C. A reproducible evaluation of ANTs similarity metric performance in brain image registration. Neuroimage 2011, 54, 2033–2044. [Google Scholar] [CrossRef]
- Jenkinson, M.; Beckmann, C.F.; Behrens, T.E.; Woolrich, M.W.; Smith, S.M. Fsl. Neuroimage 2012, 62, 782–790. [Google Scholar] [CrossRef]
- Reuter, M.; Rosas, H.D.; Fischl, B. Highly accurate inverse consistent registration: A robust approach. Neuroimage 2010, 53, 1181–1196. [Google Scholar] [CrossRef]
- Smith, S.M.; Jenkinson, M.; Woolrich, M.W.; Beckmann, C.F.; Behrens, T.E.; Johansen-Berg, H.; Bannister, P.R.; De Luca, M.; Drobnjak, I.; Flitney, D.E.; et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004, 23. [Google Scholar] [CrossRef]
- Zou, K.H.; Warfield, S.K.; Bharatha, A.; Tempany, C.M.; Kaus, M.R.; Haker, S.J.; Wells, W.M.; Jolesz, F.A.; Kikinis, R. Statistical validation of image segmentation quality based on a spatial overlap index1. Acad. Radiol. 2004, 11, 178–189. [Google Scholar] [CrossRef]
- Mccormick, M.; Liu, X.; Jomier, J.; Marion, C.; Ibanez, L. ITK: Enabling reproducible research and open science. Front. Neuroinform. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]
- Kittler, J. On the accuracy of the Sobel edge detector. Image Vision Comput. 1983, 1, 37–42. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Marchetti, F. In Convergence rate in terms of the continuous SSIM (cSSIM) index in RBF interpolation. Dolomites Res. Notes Approx. 2021, 14. Available online: https://drna.padovauniversitypress.it/2021/1/31 (accessed on 9 June 2021).
- Cardoso, M.J.; Modat, M.; Vercauteren, T.; Ourselin, S. Scale factor point spread function matching: Beyond aliasing in image resampling. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2015; Volume 9350, pp. 675–683. [Google Scholar] [CrossRef]
- De Marchi, S.; Marchetti, F.; Perracchione, E.; Poggiali, D. Polynomial interpolation via mapped bases without resampling. J. Comput. Appl. Math. 2020, 364, 112347. [Google Scholar] [CrossRef]
- De Marchi, S.; Erb, W.; Francomano, E.; Marchetti, F.; Perracchione, E.; Poggiali, D. Fake Nodes approximation for Magnetic Particle Imaging. In Proceedings of the 2020 IEEE 20th Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 16–18 June 2020; pp. 434–438. [Google Scholar] [CrossRef]
- De Marchi, S.; Marchetti, F.; Perracchione, E.; Poggiali, D. Multivariate approximation at fake nodes. Appl. Math. Comput. 2021, 391, 125628. [Google Scholar] [CrossRef]
- Li, Y.; Iwamoto, Y.; Lin, L.; Xu, R.; Tong, R.; Chen, Y.W. VolumeNet: A Lightweight Parallel Network for Super-Resolution of MR and CT Volumetric Data. IEEE Trans. Image Process. 2021, 30, 4840–4854. [Google Scholar] [CrossRef] [PubMed]

| Name | Definition | a | ||
|---|---|---|---|---|
| (Truncated) Gaussian | 1 | 1 | ||
| Nearest Neighbor | 1 | 1 | 1 | |
| Linear | 1 | 1 | 1 | |
| Cubic | 2 | 0.75 | 1 | |
| Lanczos | 2 | 1 |
| Software | Sampling | Method | SL Phantom | Brain MRI | Walnut CT |
|---|---|---|---|---|---|
| ANTs | under | Nearest | 0.11715 | 0.00251 | 0.00029 |
| MultiLabel | 0.11714 | 0.00287 | 0.00098 | ||
| over | Linear | 0.16559 | 0.02427 | 0.01965 | |
| Gaussian | 0.24197 | 0.05616 | 0.04605 | ||
| Lanczos | 0.12989 | 0.01415 | 0.01425 | ||
| Splines | 0.12790 | 0.00791 | 0.00751 | ||
| FSL | under | Nearest | 0.10845 | 0.00327 | 0.00383 |
| over | Trilinear | 0.16528 | 0.02430 | 0.02025 | |
| Splines | 0.10403 | 0.00792 | 0.00759 | ||
| Freesurfer | under | Nearest | 0.11716 | 0.00252 | 0.00029 |
| over | Trilinear | 0.16559 | 0.02427 | 0.01965 | |
| Splines | 0.12644 | 0.00792 | 0.00751 |
| Software | Sampling | Method | SL Phantom | Brain MRI | Walnut CT |
|---|---|---|---|---|---|
| ANTs | under | Nearest | 0.12516 | 0.00425 | 0.00031 |
| MultiLabel | 0.12515 | 0.00441 | 0.00106 | ||
| over | Linear | 0.17679 | 0.03075 | 0.02246 | |
| Gaussian | 0.25852 | 0.06774 | 0.05099 | ||
| Lanczos | 0.13884 | 0.01929 | 0.01661 | ||
| Splines | 0.13646 | 0.01261 | 0.00940 | ||
| FSL | under | Nearest | 0.11173 | 0.00479 | 0.00526 |
| over | Trilinear | 0.17663 | 0.03077 | 0.02322 | |
| Splines | 0.11108 | 0.01265 | 0.00953 | ||
| Freesurfer | under | Nearest | 0.12516 | 0.00425 | 0.00031 |
| over | Trilinear | 0.17679 | 0.03075 | 0.02246 | |
| Splines | 0.13488 | 0.01262 | 0.00940 |
| Image | Software | Method | DSSIM | DSSIM() | % | ||
|---|---|---|---|---|---|---|---|
| SL | ANTs | Linear | 0.037153 | 0.031298 | 84.242829 | 100.000000 | 14.897966 |
| Gaussian | 0.047003 | 0.038652 | 82.233787 | ||||
| Lanczos | 0.042190 | 0.035423 | 83.961040 | ||||
| Splines | 0.041255 | 0.034414 | 83.418321 | ||||
| FSL | Trilinear | 0.029491 | 0.023908 | 81.068121 | |||
| Splines | 0.033593 | 0.027387 | 81.524186 | ||||
| Freesurfer | Trilinear | 0.037153 | 0.031298 | 84.242829 | |||
| Splines | 0.038853 | 0.031272 | 80.488007 | ||||
| Brain | ANTs | Linear | 0.062901 | 0.034254 | 54.457968 | 89.20926 | 18.886478 |
| Gaussian | 0.111262 | 0.051932 | 46.675099 | ||||
| Lanczos | 0.080985 | 0.033880 | 41.835420 | ||||
| Splines | 0.102826 | 0.033518 | 32.596547 | ||||
| FSL | Trilinear | 0.062913 | 0.034261 | 54.457173 | |||
| Splines | 0.102840 | 0.033526 | 32.599943 | ||||
| Freesurfer | Trilinear | 0.062901 | 0.034254 | 54.457961 | |||
| Splines | 0.102826 | 0.033518 | 32.596537 | ||||
| Walnut | ANTs | Linear | 0.044889 | 0.011284 | 25.137363 | 71.41374 | 14.234087 |
| Gaussian | 0.091228 | 0.028299 | 31.020122 | ||||
| Lanczos | 0.079741 | 0.021932 | 27.503712 | ||||
| Splines | 0.114494 | 0.021974 | 19.191816 | ||||
| FSL | Trilinear | 0.046841 | 0.012816 | 27.360825 | |||
| Splines | 0.114795 | 0.022474 | 19.577444 | ||||
| Freesurfer | Trilinear | 0.044889 | 0.011284 | 25.137374 | |||
| Splines | 0.114494 | 0.021973 | 19.191790 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poggiali, D.; Cecchin, D.; Campi, C.; De Marchi, S. Oversampling Errors in Multimodal Medical Imaging Are Due to the Gibbs Effect. Mathematics 2021, 9, 1348. https://doi.org/10.3390/math9121348
Poggiali D, Cecchin D, Campi C, De Marchi S. Oversampling Errors in Multimodal Medical Imaging Are Due to the Gibbs Effect. Mathematics. 2021; 9(12):1348. https://doi.org/10.3390/math9121348
Chicago/Turabian StylePoggiali, Davide, Diego Cecchin, Cristina Campi, and Stefano De Marchi. 2021. "Oversampling Errors in Multimodal Medical Imaging Are Due to the Gibbs Effect" Mathematics 9, no. 12: 1348. https://doi.org/10.3390/math9121348
APA StylePoggiali, D., Cecchin, D., Campi, C., & De Marchi, S. (2021). Oversampling Errors in Multimodal Medical Imaging Are Due to the Gibbs Effect. Mathematics, 9(12), 1348. https://doi.org/10.3390/math9121348








