Linear Independence of T-Spline Blending Functions of Degree One for Isogeometric Analysis
Abstract
1. Introduction
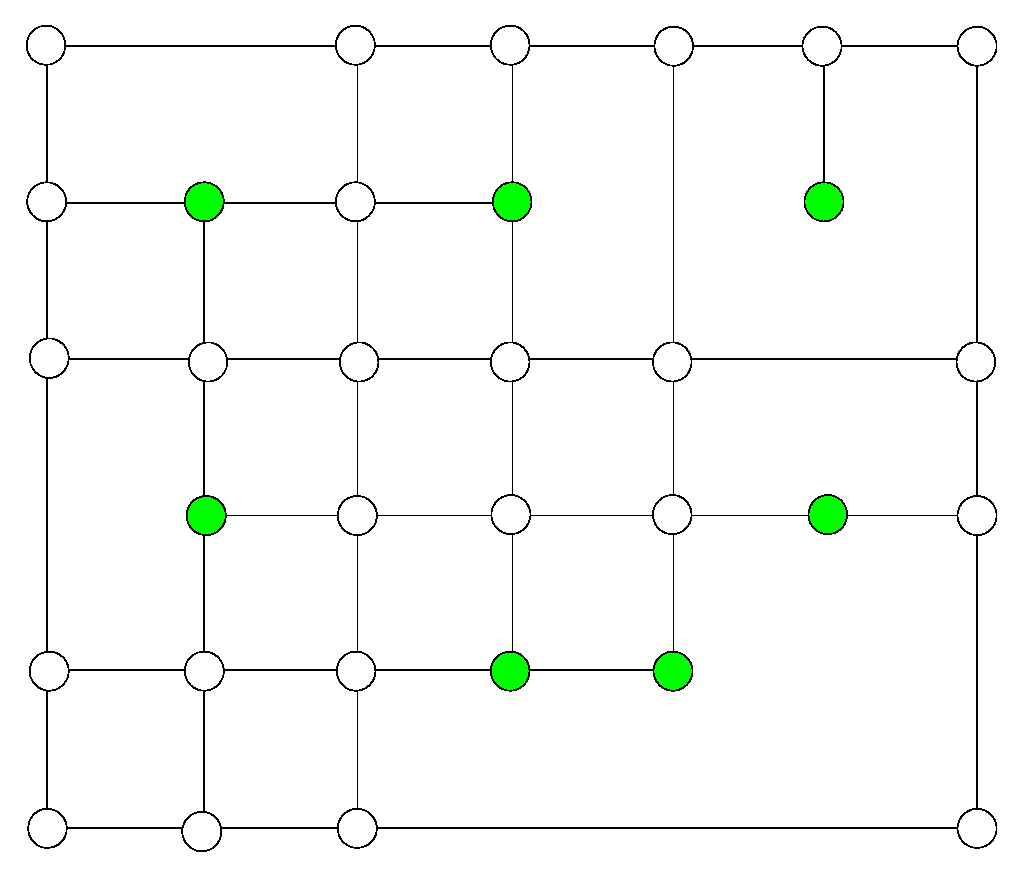
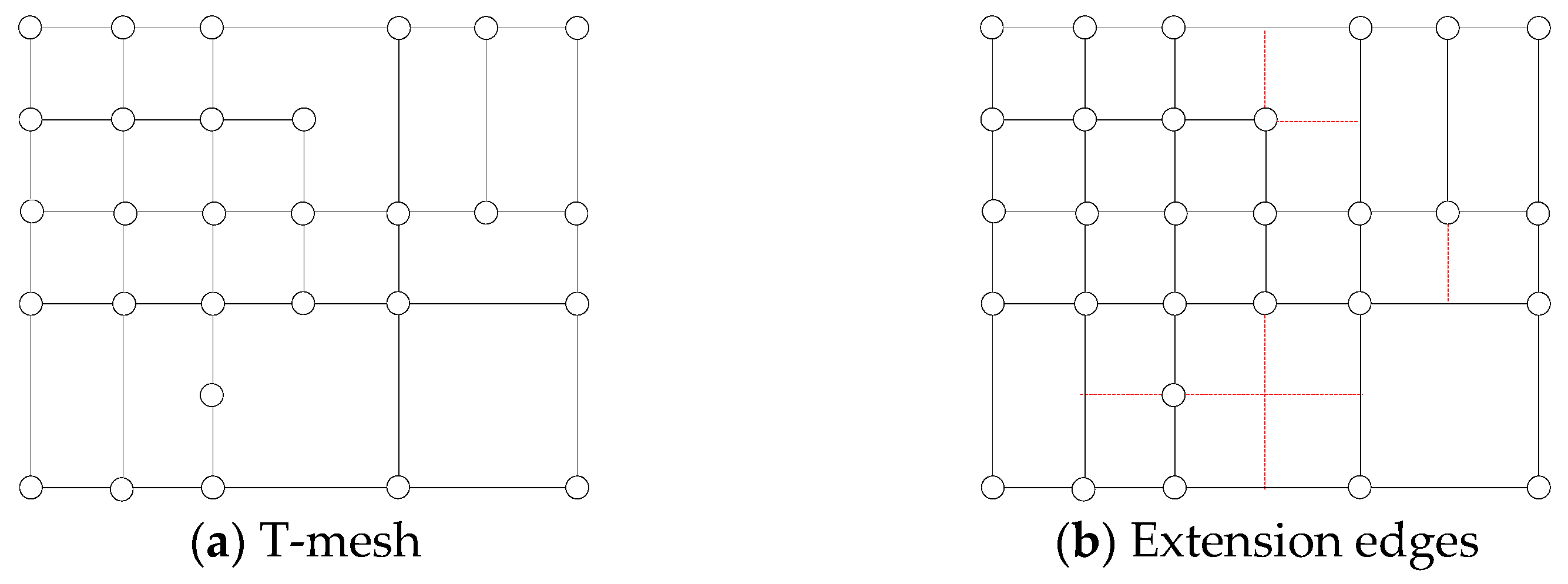
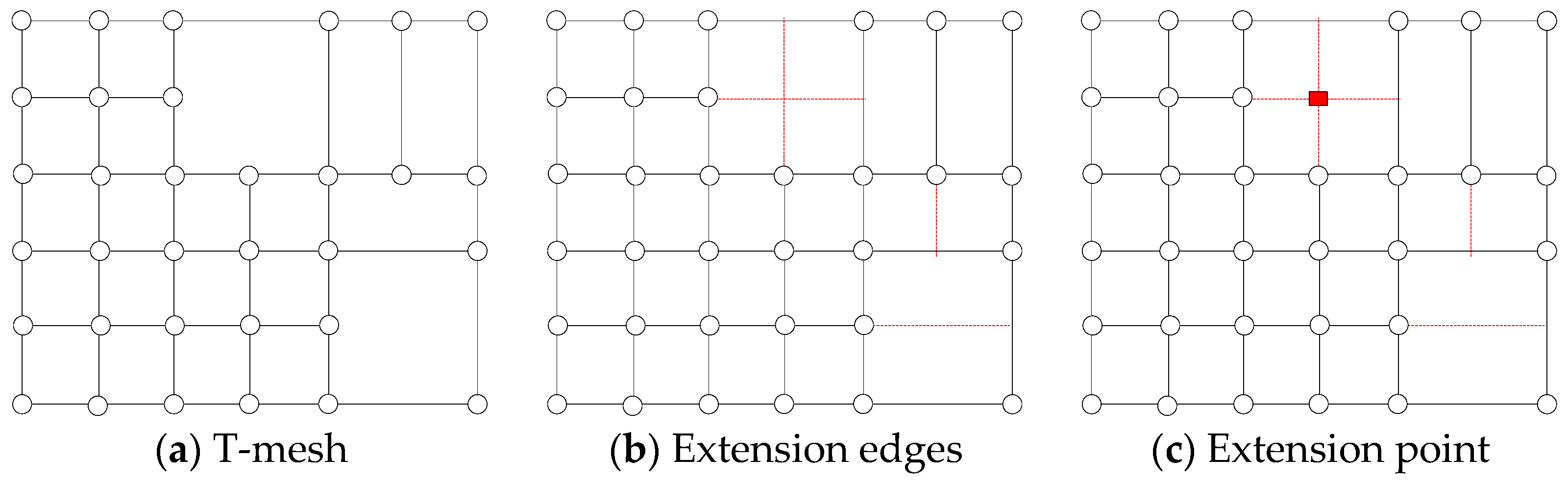
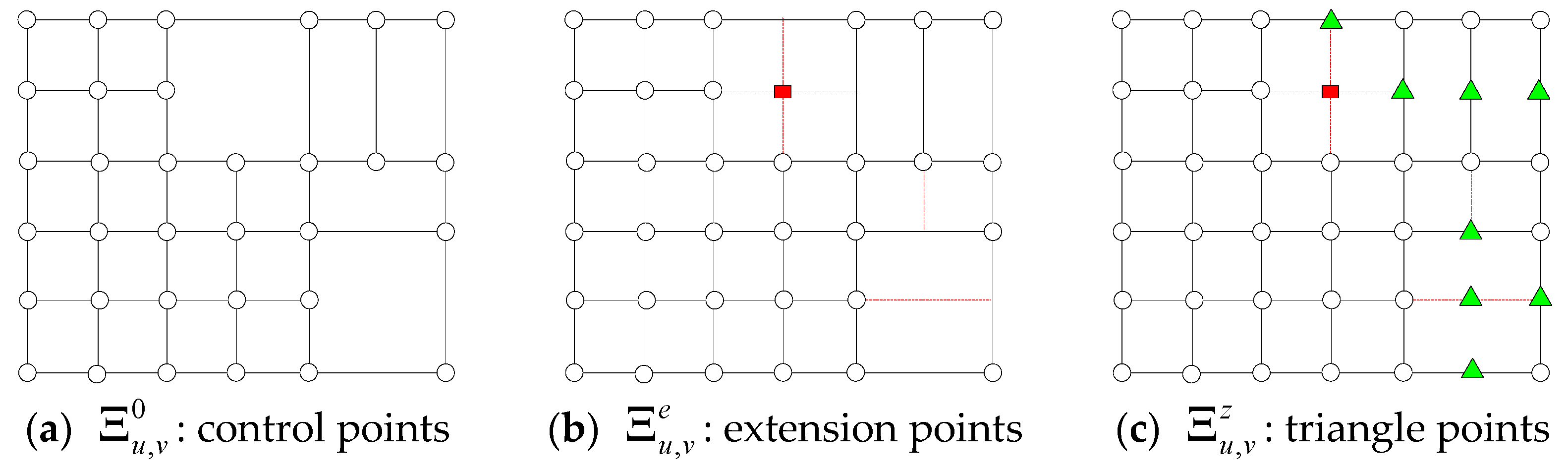
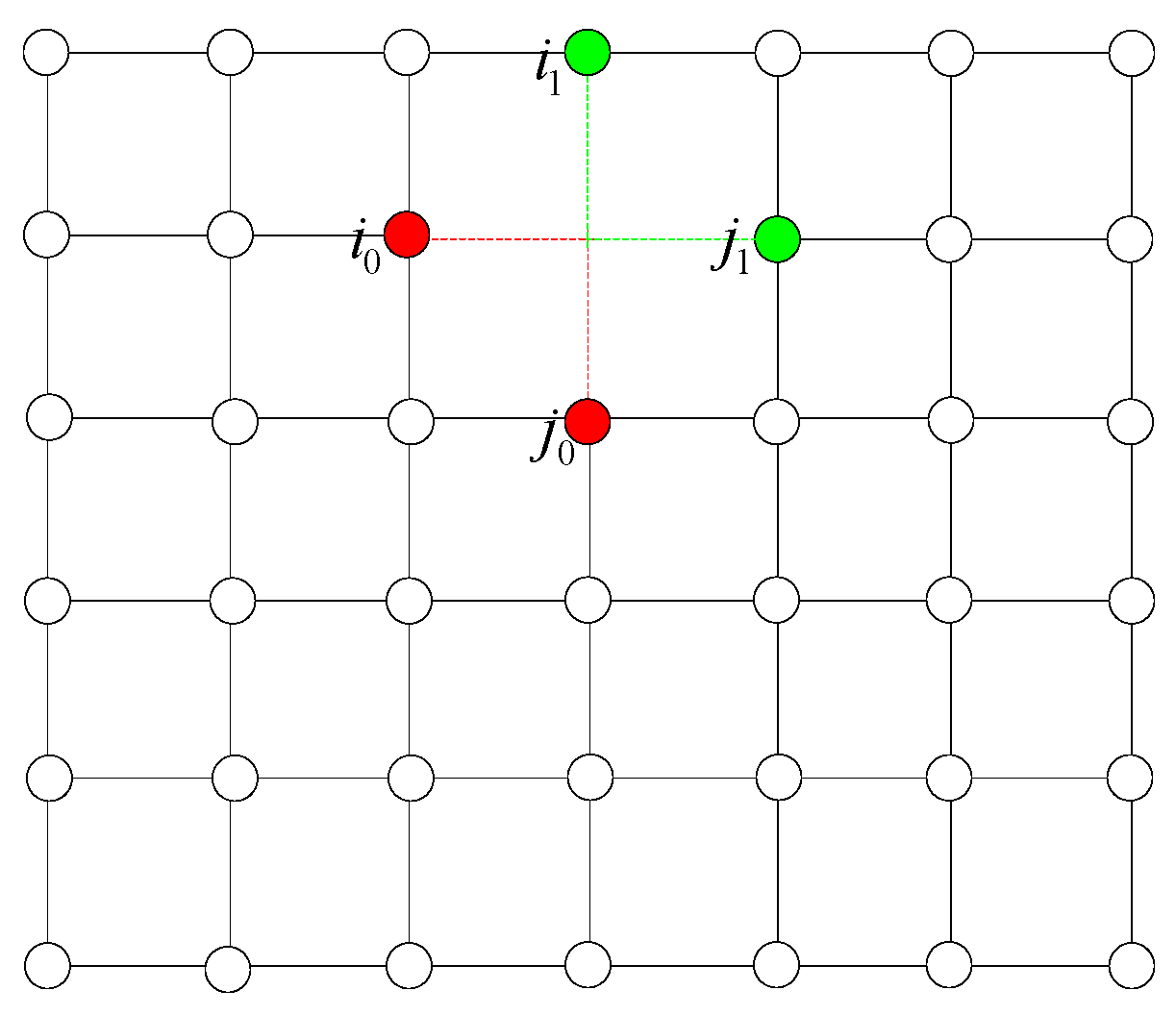
2. Linear Independence of Blending Functions of Degree One
2.1. B-Spline Functions of Degree One
2.2. Blending Functions of Degree One
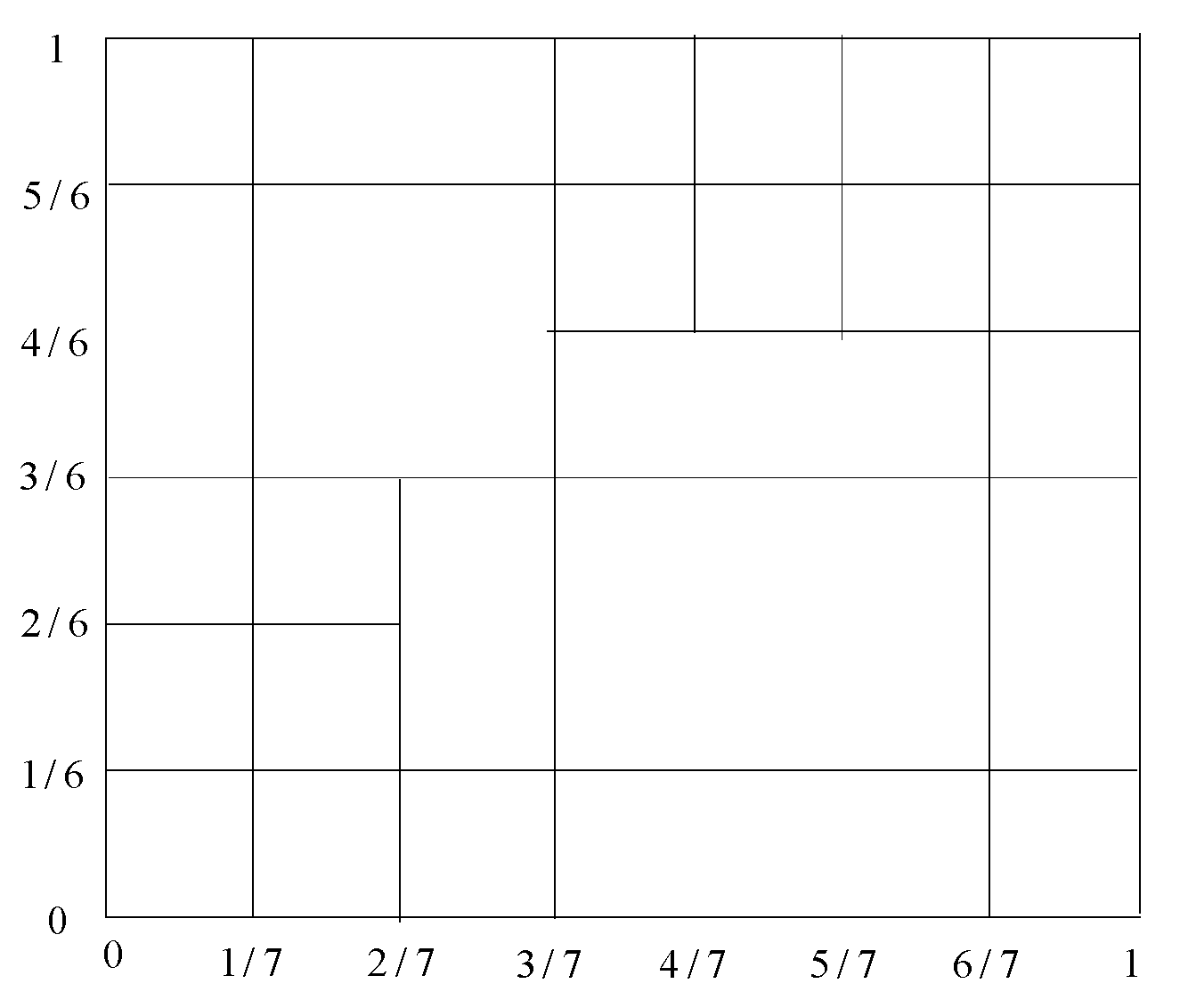
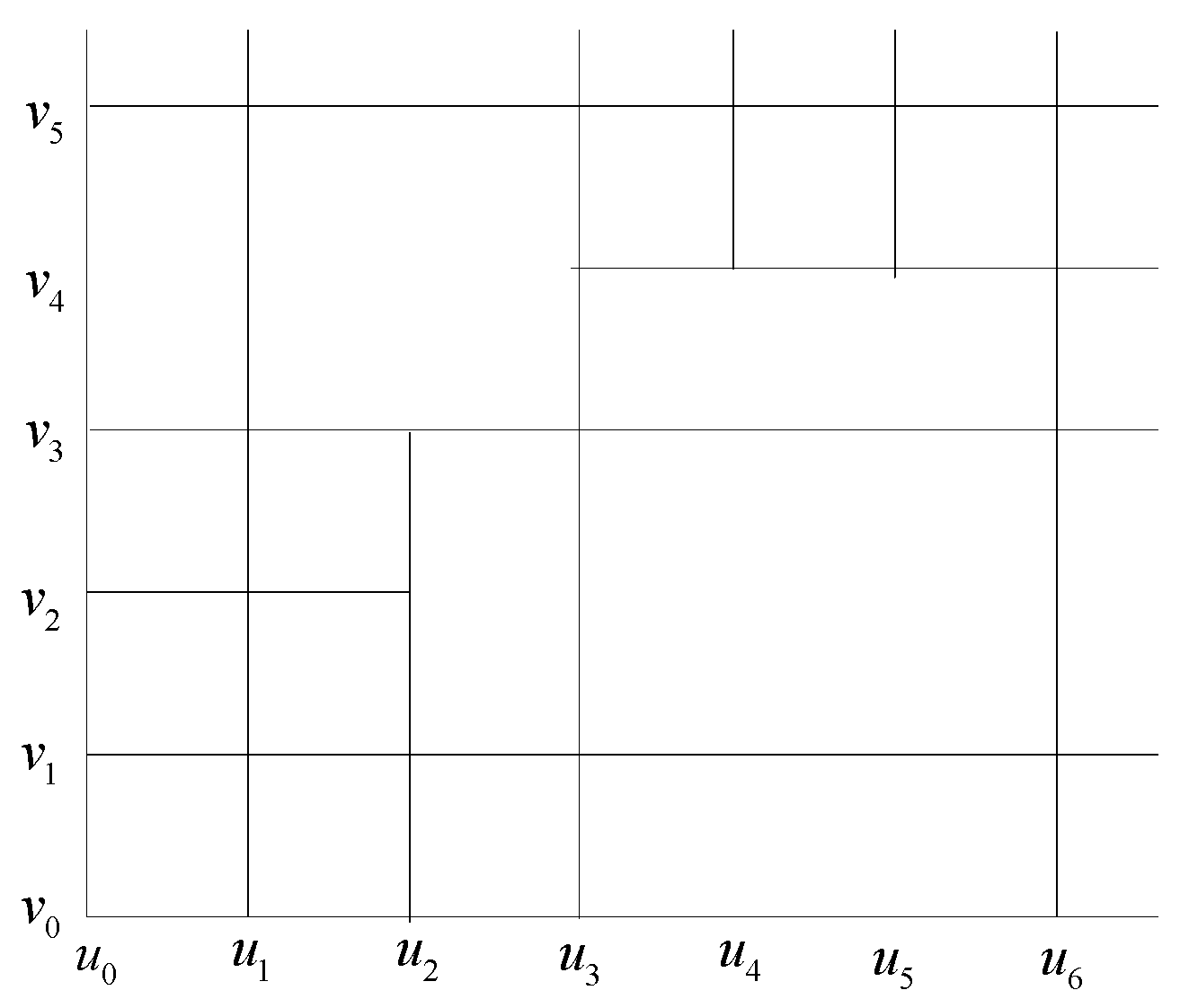
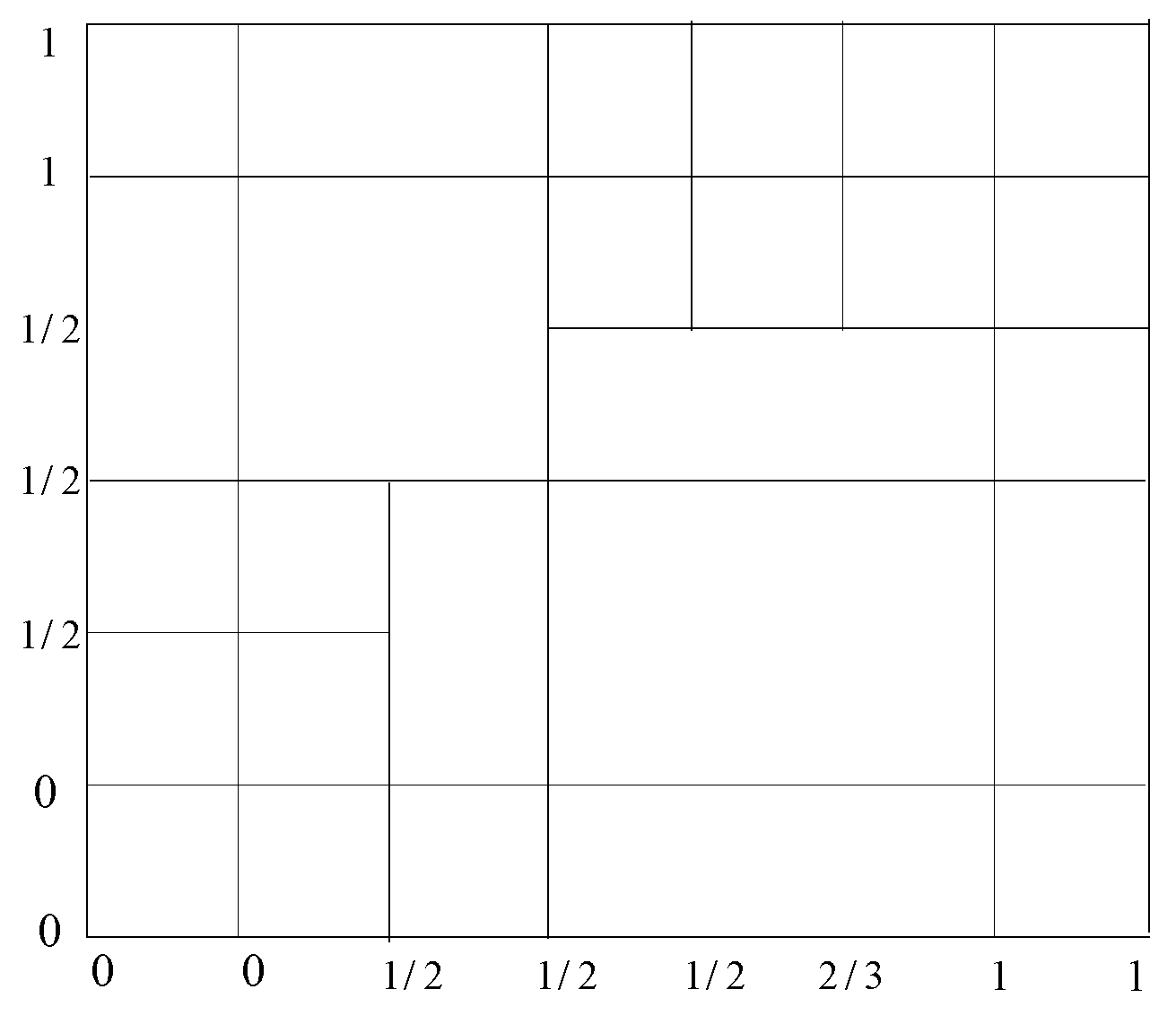
3. Examples of One Degree T-Splines
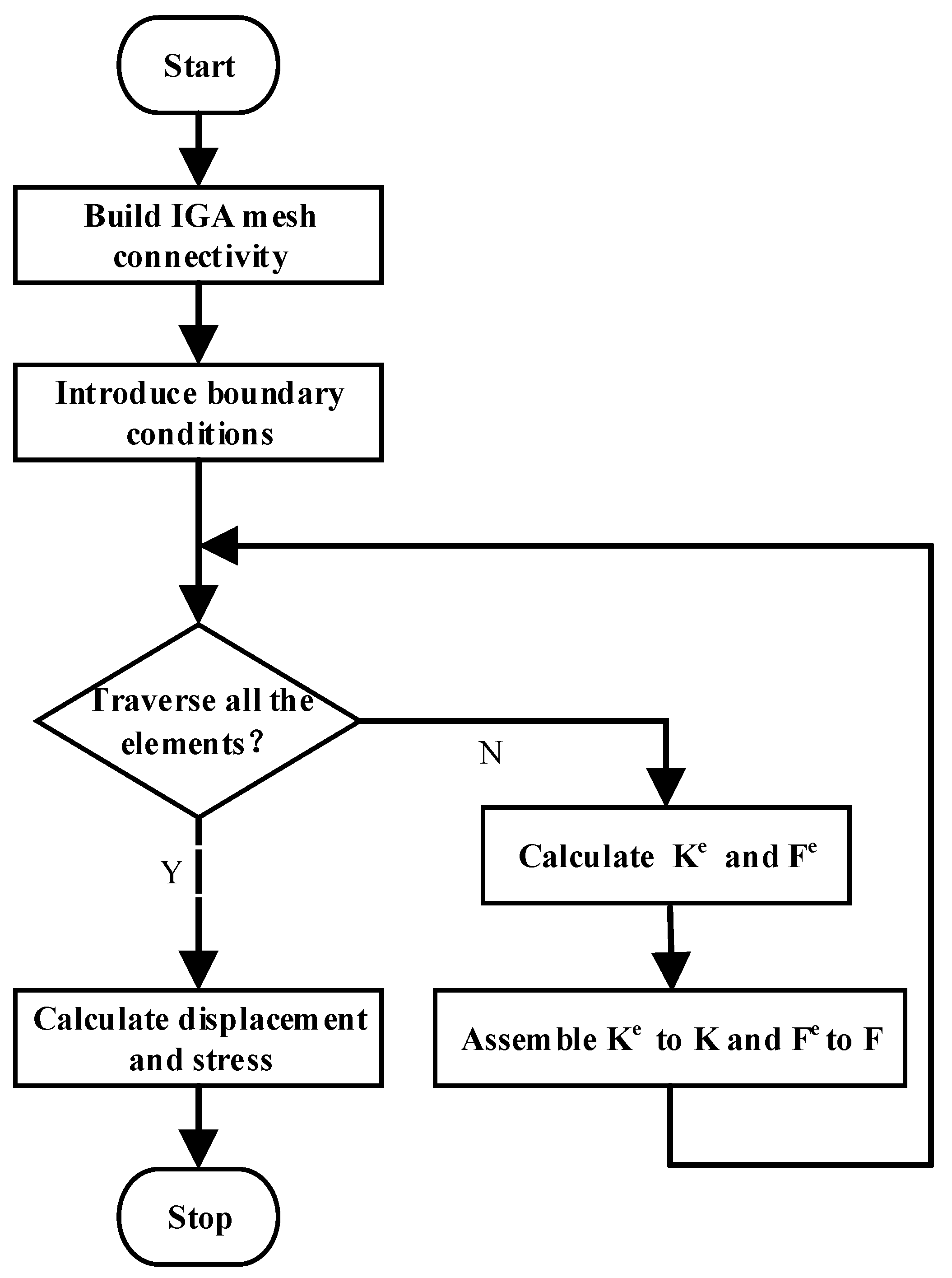
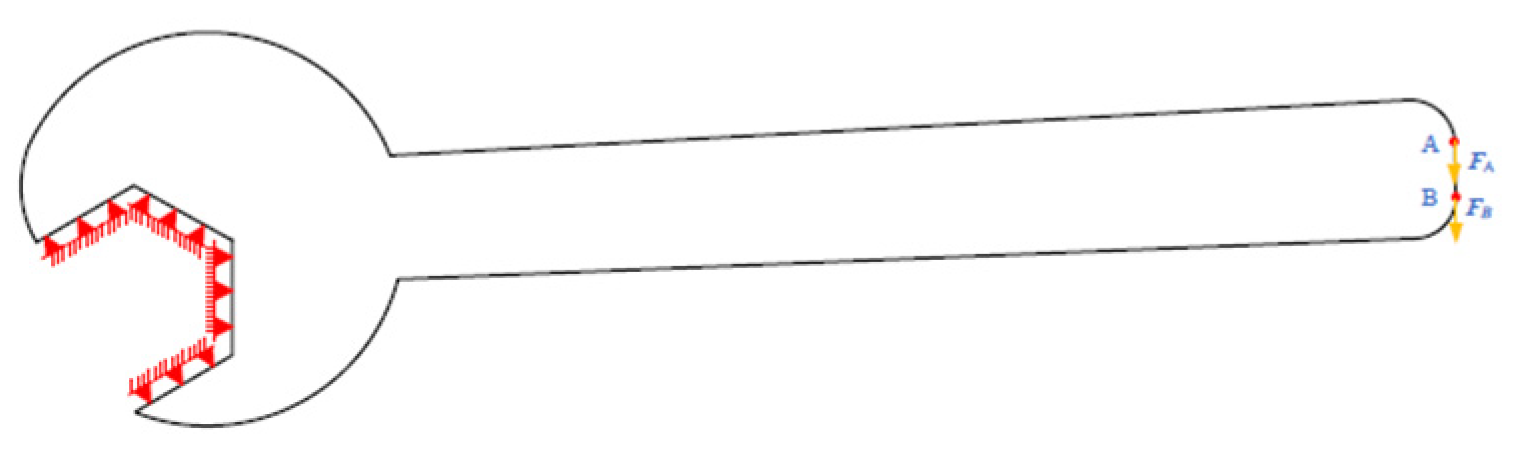
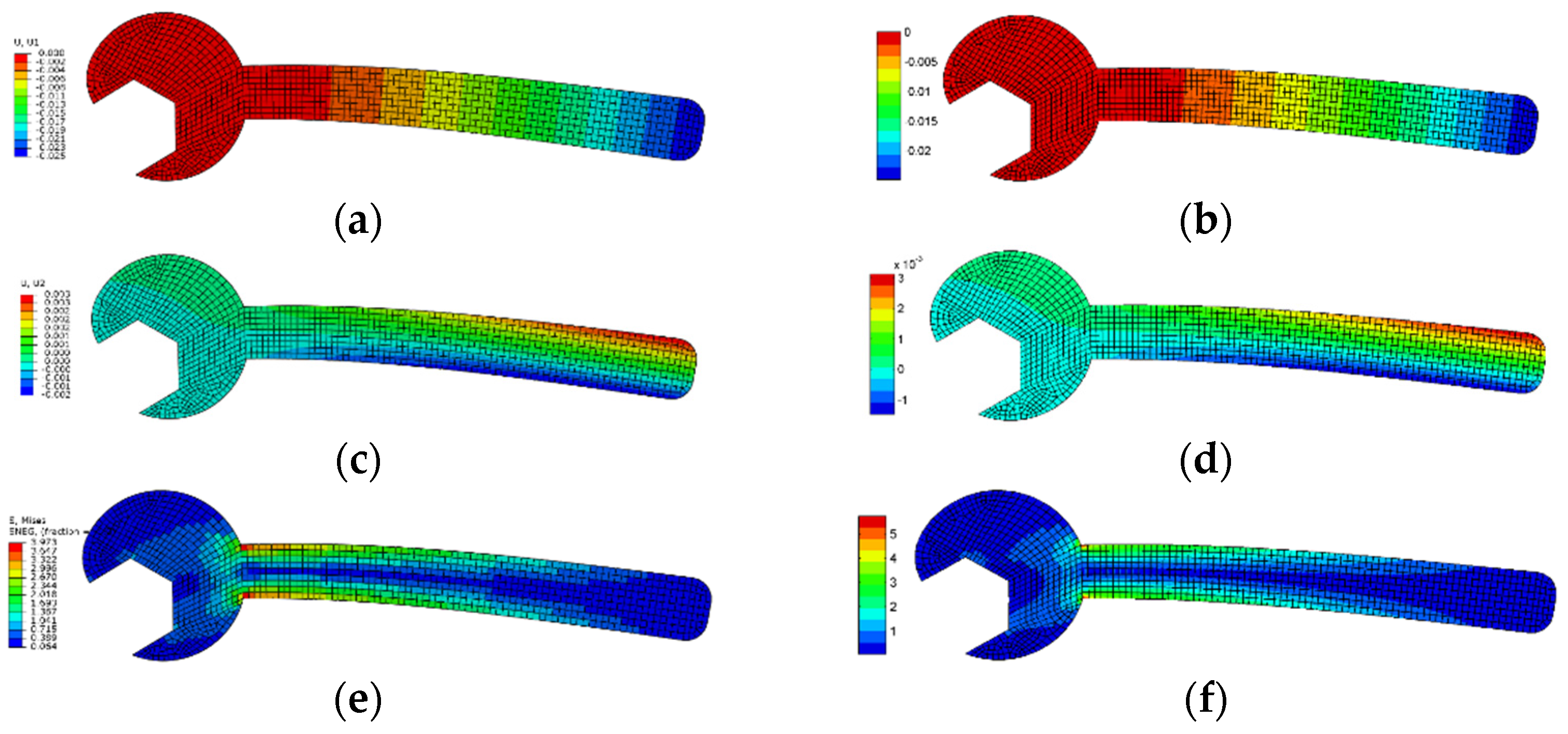
4. Isogeometric Analysis Example
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry, and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Cottrell, J.A.; Hughes, T.J.R.; Bazilev, Y. Isogeometric Analysis: Toward Integration of CAD and FEA; Wiley: Chichester, UK, 2009. [Google Scholar]
- Cottrell, J.A.; Hughes, T.J.R.; Reali, A. Studies of refinement and continuity in isogeometric structural analysis. Comput. Methods Appl. Mech. Eng. 2007, 196, 4160–4183. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Calo, V.; Cottrell, J.; Evans, J.; Hughes, T.J.R.; Lipton, S.; Scott, M.; Sederberg, T.W. Isogeometric analysis using T-splines. Comput. Methods Appl. Mech. Eng. 2010, 199, 229–263. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Zheng, J.; Bakenov, A.; Nasri, A. T-splines and T-NURCCs. ACM Trans. Graph. 2003, 22, 477–484. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Cardon, D.L.; Finnigan, G.T.; North, N.S.; Zheng, J.; Lyche, T. T-spline simplification and local refinement. ACM Trans. Graph. 2004, 23, 276–283. [Google Scholar] [CrossRef]
- Vázquez, R.; Buffa, A. Isogeometric analysis for electromagnetic problems. IEEE Trans. Magn. 2010, 46, 3305–3308. [Google Scholar] [CrossRef]
- Da Veiga, L.B.; Buffa, A.; Rivas, J.; Sangalli, G. Some estimates for h–p–k-refinement in Isogeometric Analysis. Numer. Math. 2010, 118, 271–305. [Google Scholar] [CrossRef]
- Buffa, A.; Cho, D.; Sangalli, G. Linear independence of the T-spline blending functions associated with some particular T-meshes. Comput. Methods Appl. Mech. Eng. 2010, 199, 1437–1445. [Google Scholar] [CrossRef]
- Wang, A.; Zhao, G. The Analysis of T-spline Blending Functions Linear Independence. Comput. Aided Des. Appl. 2011, 8, 735–745. [Google Scholar]
- Li, X.; Zheng, J.; Sederberg, T.W.; Hughes, T.J.R.; Scott, M.A. On linear independence of T-spline blending functions. Comput. Aided Geomet. Des. 2012, 29, 63–76. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J. AS++ T-splines: Linear independence and approximation. Comput. Methods Appl. Mech. Eng. 2018, 333, 462–474. [Google Scholar] [CrossRef]
- Phung-Van, P.; Thanh, C.L.; Nguyen-Xuan, H.; Abdel-Wahab, M. Nonlinear transient isogeometric analysis of FG-CNTRC nanoplates in thermal environments. Compos. Struct. 2018, 20, 882–892. [Google Scholar] [CrossRef]
- Hsu, M.-C.; Akkerman, I.; Bazilevs, Y. High-performance computing of wind turbine aerodynamics using isogeometric analysis. Comput. Fluid 2011, 49, 93–100. [Google Scholar] [CrossRef]
- Grossmann, D.; Jüttler, B.; Schlusnus, H.; Barner, J.; Vuong, A.V. Isogeometric simulation of turbine blades for aircraft engines. Comput. Aided Geom Des. 2012, 29, 519–531. [Google Scholar] [CrossRef]
- Phung-Van, P.; Thai, C.H.; Nguyen-Xuan, H.; Wahab, M.A. Porosity-dependent nonlinear transient responses of functionally graded nanoplates using isogeometric analysis. Compos. Part B Eng. 2019, 164, 215–225. [Google Scholar] [CrossRef]
- Phung-Van, P.; Lieu, Q.X.; Nguyen-Xuan, H.; Wahab, M.A. Size-dependent isogeometric analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Compos. Struct. 2017, 166, 120–135. [Google Scholar] [CrossRef]
- Thanh, C.L.; Tran, L.V.; Bui, T.Q.; Nguyen, H.X.; Abdel-Wahab, M. Isogeometric analysis for size-dependent nonlinear thermal stability of porous FG microplates. Compos. Struct. 2019, 221, 110838. [Google Scholar] [CrossRef]
- Hao, P.; Wang, Y.; Ma, R.; Liu, H.; Wang, B.; Li, G. A new reliability-based design optimization framework using isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2019, 345, 476–501. [Google Scholar] [CrossRef]
- Kwessi, E.; de Souza, G.; Djitte, N.; Ndiaye, M. The special atom space and Haar wavelets in higher dimensions. Demonstr. Math. 2020, 53, 131–151. [Google Scholar] [CrossRef]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Mineola, NY, USA, 2000. [Google Scholar]
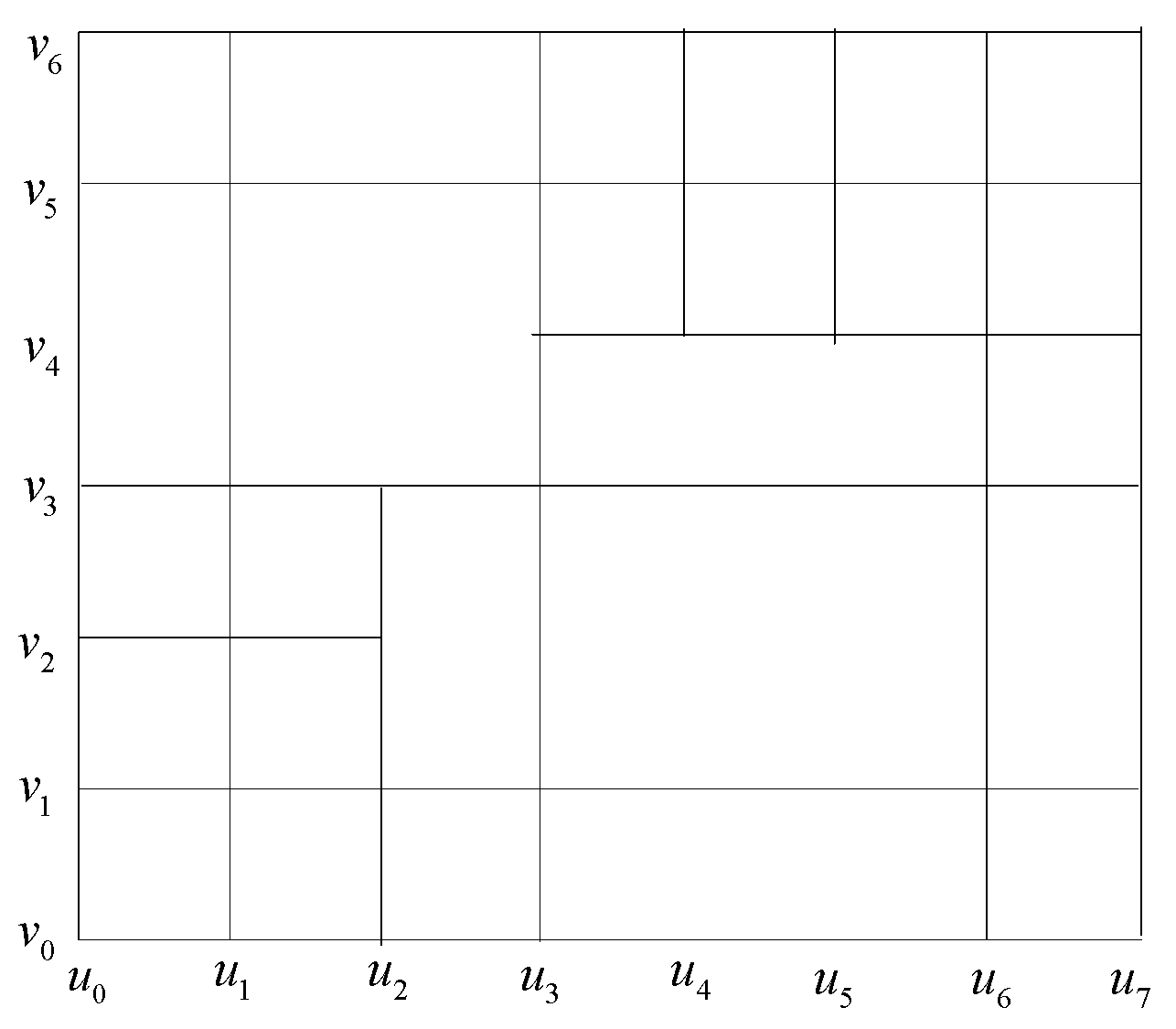

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Li, L.; Wang, W.; Du, X.; Xiao, F.; Cai, Z.; Zhao, G. Linear Independence of T-Spline Blending Functions of Degree One for Isogeometric Analysis. Mathematics 2021, 9, 1346. https://doi.org/10.3390/math9121346
Wang A, Li L, Wang W, Du X, Xiao F, Cai Z, Zhao G. Linear Independence of T-Spline Blending Functions of Degree One for Isogeometric Analysis. Mathematics. 2021; 9(12):1346. https://doi.org/10.3390/math9121346
Chicago/Turabian StyleWang, Aizeng, Ling Li, Wei Wang, Xiaoxiao Du, Feng Xiao, Zhanchuan Cai, and Gang Zhao. 2021. "Linear Independence of T-Spline Blending Functions of Degree One for Isogeometric Analysis" Mathematics 9, no. 12: 1346. https://doi.org/10.3390/math9121346
APA StyleWang, A., Li, L., Wang, W., Du, X., Xiao, F., Cai, Z., & Zhao, G. (2021). Linear Independence of T-Spline Blending Functions of Degree One for Isogeometric Analysis. Mathematics, 9(12), 1346. https://doi.org/10.3390/math9121346





