Optimal Investment in Preservation Technology for Variable Demand under Trade-Credit and Shortages

Abstract

In particular business transactions, the supplier usually provides an admissible delay in settlement to its vendor to encourage further sales. Additionally, the demand for the commodity is inversely proportional to the function of the sales price, which is non-linear and, in some situations, a holding cost rises over time. Moreover, many goods often deteriorate consistently and shall not be sold after their expiration dates. This study analyses a model for perishable products with a maximum life span with price-dependent demand and trade credit by assimilating these variations and under the supposition of time-varying holding cost. Furthermore, to diminish the rate of deterioration, investment for preservation technology is often taken into account beforehand. Based on real-life circumstances, shortages are admitted and backlogged partially, with an exponential rise in wait time before the new good emerges. The key ambition is to calculate the optimum investment under preservation, sales price, and cycle time using the classical optimization algorithm to maximize the vendor’s net profit. Additionally, to clarify the outcomes, the numerical illustrations are addressed, and the sensitivity analysis of significant parameters is eventually implemented.

1. Introduction

A majority of organizations are highly reliant on consumer demand. Additionally, no corporation will ever bother to worry about production without a demand. Furthermore, market demand is directly proportional to the sales price. As a result, the key that directly influences revenue is the sales price. In short, the demand rate is lowered by higher sale rates, whereas lower ones have the reverse effect. Thus, introducing a proper pricing strategy improves the convenience of businesses in handling inventory systems, and this model considers a non-linear function of a sales price. Further, it has been found that the holding cost for defective and useless goods is not always the same, and over time, the holding cost may increase or decrease. For example, expenditures related to rental charges may be decreased with time if hired for long-term use. Therefore, based on these real-world conditions, time-varying holding cost is assumed in this model.

In our everyday life, perishable items are very typical in the analysis of inventory management. These products are often divided into two categories: (1) things that are decomposed, degenerate, evaporative, or lapsed over time, such as meat, vegetables, drugs, fruits, cosmetics, volatile liquids, food packets; (2) items that loss part or total value over time due to new technology, such as cell phones, computer chips, fashion, and seasonal goods. The features of the maximum fixed lifespan are present in both categories. Researchers are, therefore, constantly studying the effect of perishable items, which impacts consumer buying decisions, to sustain innovations. Moreover, some items such as ice cream, cold beverages, vegetables, fruits, milk products, medicines need preservation to keep the thing fresh and preserve quality. Therefore, suppliers spend some money on preservation technologies to protect goods, and researchers have investigated the effects of preservation to keep products fresh so that customers can buy more things.

Trade credit policy has recently been commonly used in business transactions with any business, as it is helpful to both producers and suppliers. Trade credit is usually a form of commercial financing in which the buyer is authorized to buy products or services and pay the supplier later. Therefore, to maximize the demand for a commodity, this model is considered a permissible delay in the settlement where the supplier offers its vendor a mutually accepted trade credit period. Conversely, shortages are often considered in many realistic inventory control schemes, where the demand can be a backlog until the order is re-filled in the scheme, or it may be skipped depending on the customer’s preference brand and its products. The most important contribution of this research is summed up below:

Maximum fixed lifetime deteriorating items

• Time-varying holding cost
• Demand rate is the non-linear function of the sales price
• Preservation technology investment for preserve the deteriorating items
• One-layer trade credit policy
• Partially backlogged shortages accumulate at an exponential rate

2. Literature Review

Demand is a business principle that refers to a consumer’s desire to purchase goods and services and pay a particular interest or service price. Keeping all other variables constant, increasing the price of a good or service will decrease the amount requested, and vice versa. The researchers, therefore, considered the notion of demand and dynamic pricing below circumstances of perishability and partial backlogging. A lot-sizing model is developed in [1]. In [2], an inventory model with variable holding cost with stock-level-based demand is established. The price and inventory management strategies for declining goods with price-dependent demand were discussed in [3]. In [4], some distinct models under the variable holding cost and quadratic demand assumption are presented. In [5], a combined inventory model and pricing strategy for a maximum fixed lifetime declining rate with allowable shortages are discussed. An incomplete production model with price-sensitive demand under exponential partial backlogging shortages is proposed in [6], and in [7], a joint replenishment problem is presented with quantity discounts and minimum order constraints under stochastic demand. In [8], a multi-product manufacturing solution is proposed with a low failure rate and optimal energy consumption under variable demand. Recently, an economical production quantity (EPQ) model for the perishable items with price-stock-dependent demand was derived in [9], and in [10], the coordination supply chain management under flexible manufacturing is focused, a mixture of inventory and stochastic lead-time demand.

Customers are now paying more attention to the expiry dates of the goods and are not even prepared to purchase perishable items. Thus, perishable objects play a significant role in our everyday lives, and firstly a mathematical model with an exponential rate of perishable items is presented in [11]. In [12], an inventory is obtained by considering the three-parameter deterioration rate of the Weibull distribution. In [13], the supposition of time-varying holding cost with quadratic demand designed a mathematical prototype for perishable products with a constant rate. Then, in [14], the parabolic holding costs are measured and deliberated a model with sales price-dependence demand for deteriorating products with expiry dates. An inventory model is constituted in [15]; stock-based demand is considered for time-dependent perishable rate. For deteriorating goods with a non-instantaneous quality under price-sensitive demand and trade credit policy, in [16], an inventory model is developed. In [17], the Weibull distribution rate for deterioration products is considered with the sales price’s non-linear function and an exponentially partial shortage. In [18], the recycling of expiry dates is presented with deteriorating products under dissimilar supply chains. Recently in [19], an inventory model is discussed with the perishable goods having expiry dates under variable demand, and in [20], a fuzzy green model for non-instantaneous perishable items is demonstrated under carbon emission and trade credit policies.

Customers want to purchase products that look new and are of high quality in everyday life. However, certain goods, endlessly or overtime, lose quality. To preserve the product’s consistency, preservation methods such as pasteurization, vacuum sealing, freeze-drying, high-pressure food preservation, fermentation are used. Therefore, researchers have considered this fact. In [21], a study with the successful investment is designed in preservation technology under partial backlogging. However, in [22], a mathematical model under capital investment on preservation technology is developed under shortages. The investment is more critical for the preservation of technology. In [23], an inventory prototype with effective preservation technology investment under price-stock-based demand. Some optimal policies are examined in [24]: under-investment in preservation technology, quadratic demand, and trade credit policy. In [25], an integrated model is focused on demand and expenditure dependent on market price. In [26], an application of preservation technology is discussed in an integrated production system. In [27], an integrated production-inventory model is developed for controllable probabilistic deterioration in a two-echelon supply chain. The inventory model with a valuable investment for preservation technology under quadratic demand is established in [28]. In [29], optimum inventory management is industrialized with a backorder, controllable deterioration rate under carbon emissions, and in [30], the dynamic rate of investment is measured in the promotion throughout different ranges of an optimum price considering an investment in preservation technology.

Trade credit has recently developed into a highly advanced tool for taking every business ahead. A delayed payment policy draws more customers to purchase more and helps to promote goods. Trade credit is also a helpful tool that is useful for both suppliers and vendors in any business. By considering this fact in [31], an inventory model is constructed for a retailer, in which the supplier granted an admissible delay in payment to its vendor. In [32], the model has subsequently expanded with the discrepancy between unit cost and unit price. In [33], a model is constructed with the acceptable trade credit policy for a finite rate of replenishment, a combined pricing policy, and a management model with a non-instantaneous status under allowable payment delay and partial backlogging is developed in [34]. Then in [35], an integrated model is designed under allowable delay in payments with faulty units and variable lead time. A mathematical model for perishable goods with expiry dates with investment for preserving the items under a two-layer trade credit policy is developed in [36]. In [37], a model for perishable goods is designed with a non-instantaneous rate, where demand depends on the sale price under admitted shortages with trade credit policy. Recently, under the supposition of non-linear holding cost, a model is constructed in [38], and also an upstream trade credit policy is considered. In [39], applying the various price-discount policy is proposed under permissible delay in payments.

According to the literature analysis and

Table 1. Summary of the influence of the dissimilar authors.

Author(s)	Sales Price Dependent Demand	Time-Dependent Holding Cost	Time-Dependent Deterioration	Preservation Technology Investment	Shortages	Trade-Credit
Abad [1]	√				√
Zhang et al. [3]	√			√
Shah et al. [4]		√	√			√
Tiwari et al. [5]	√		√		√
Ghare and Schrader [11]	√	√	√			√
Kumar et al. [14]	√				√
Iqbal and Sarkar [18]	√			√	√
Dey et al. [25]	√				√	√
Ullah and Sarkar [27]			√	√		√
Chauhari et al. [28]	√				√	√
This paper	√	√	√	√	√	√

, there have been several articles and work on various combinations, but the novelty of this analysis is that all such combinations are considered that no one has discussed before. Additionally, the research gap for expiry dates perishable products with preservation technology investment under the assumption of time-varying holding cost is identified. Therefore, a model is built for products such as vegetables, meat, medicines, food packets, milk products, and other goods by considering the trade credit policy and shortages to shift towards an actual price-sensitive demand scenario. Moreover, this study optimizes the vendor’s pricing strategy for maximizing the net profit function with regard to the investment under preservation, sales price, and cycle time. A computational algorithm is generated for optimality, and numerical illustrations explain the hypothetical outcomes with various scenarios. Finally, the main parameters’ sensitivity analysis is performed on the optimal solution for the best case.

The remaining part of this article is presented in the following way: Section 3 characterizes the notation and assumptions applied throughout this study. Section 4 develops a mathematical model for different scenarios to maximize the vendor’s net profit function. Section 5 provides an algorithm to find the optimality for the net profit function. The numerical illustrations and sensitivity analysis for the significant parameters are discussed in Section 6. Finally, Section 7 moderate the conclusions of this study and its further prospects.

3. Notation and Assumptions

3.1. Notation

The following notation and assumptions are contained in this article to construct a mathematical model of the problem.

Parameters
$P$	purchasing cost; (in $/unit)
$H$	holding cost; (in $/unit/unit time)
$O$	ordering cost; (in $/order)
$\eta$	price elasticity constant; $\eta >1$
$\xi$	expiry dates of the product (in years)
μ	rate of preservation; $\mu >0$
$M$	upstream trade credit (in years)
$I_g$	vendor’s gained interest (percentage/year)
$I_l$	vendor’s lost interest (percentage/year)
$\varsigma$	backlogging parameter; $\varsigma >0$
$\beta$	amount of back-ordered demand (units)
$Q_o$	vendor’s order quantity (in units)
$c_{\beta }$	backlogging cost; (in $/unit time)
$c_l$	additional charge because of lost sales (in $/unit)
Decision variables
$T$	cycle time (in years)
$S$	selling price of an item (in $/unit)
$U$	investment for preservation technology (in $/unit)
Functions
$H\left(t\right)$	$=H\left(1+iH\cdot t\right)$; time-varying cost of holding, where the cost of holding increased by its $iH\%$ (in $/unit/year)
$t_1\left(T\right)$	$=\alpha T$; time is taken for inventory level to reach zero, where $\alpha >0$ (in years)
$I_1\left(t\right)$	level of inventory before the shortages; $0\le t\le t_1$(units)
$I_2\left(t\right)$	level of backordered; $t_1\le t\le T$ (units)
$L_S\left(t\right)$	amount of a sales loss at a time $t$ (units)
$T{P}_i\left(U,S,T\right)$	vendor’s net profit function per unit time per scenario; $i=1,2$ (in $)

3.2. Assumptions

• The inventory structure works with only a single product.
• The price-sensitive non-linear demand $R\left(S\right)=a{S}^{-\eta }$ is the sales price function $S$; where the scaling direction is denoted by $a$ and the price elasticity constant is denoted by $\eta$.
• The instant proportion of deterioration is specified by ${\theta }_d\left(t\right)=\frac{1}{1+\xi -T}$ where $\xi$ is the expiry dates of an item and also $0\le {\theta }_d\left(t\right)\le 1$. Moreover, as $\xi$ tends to infinity then ${\theta }_d\left(t\right)$ tends to zero which provides the idea that the product is non-declining.
• The amount for the condensed rate of deterioration is given by $f_n\left(U\right)=1-\frac{1}{1+\mu U}$ and also supposed to be continuously increasing. In other words, $f_n{}^{\prime }\left(U\right)>0$, $f_n{}^{″}\left(U\right)>0$ and without loss of generality, presume $f_n\left(0\right)=0$.
• A credit period of $M$ years is provided to its vendor by the supplier. The vendor will gain interest $I_g$ during the interval $\left[0,M\right]$ on sold items and, during the interval $\left[M,T\right]$, will lose interest $I_l$ in unsold stocks.
• The portion of backlogged shortages symbolized by $\varsigma \left(t\right)$, which is a declining function and also differentiable with regard to time $t$.
• For a negative inventory, an exponential partial backlogged sum is characterized as $e^{-\varsigma \left(T-t\right)}$; where $\varsigma >0$ indicates the parameter of backlogging with $\left(T-t\right)$, a wait time until the further refilling.
• The inventory scheduling limit is endless.
• The refilling amount is unlimited with no lead time.
• During cycle time, there is not an alternative or restoration for the deteriorating item.

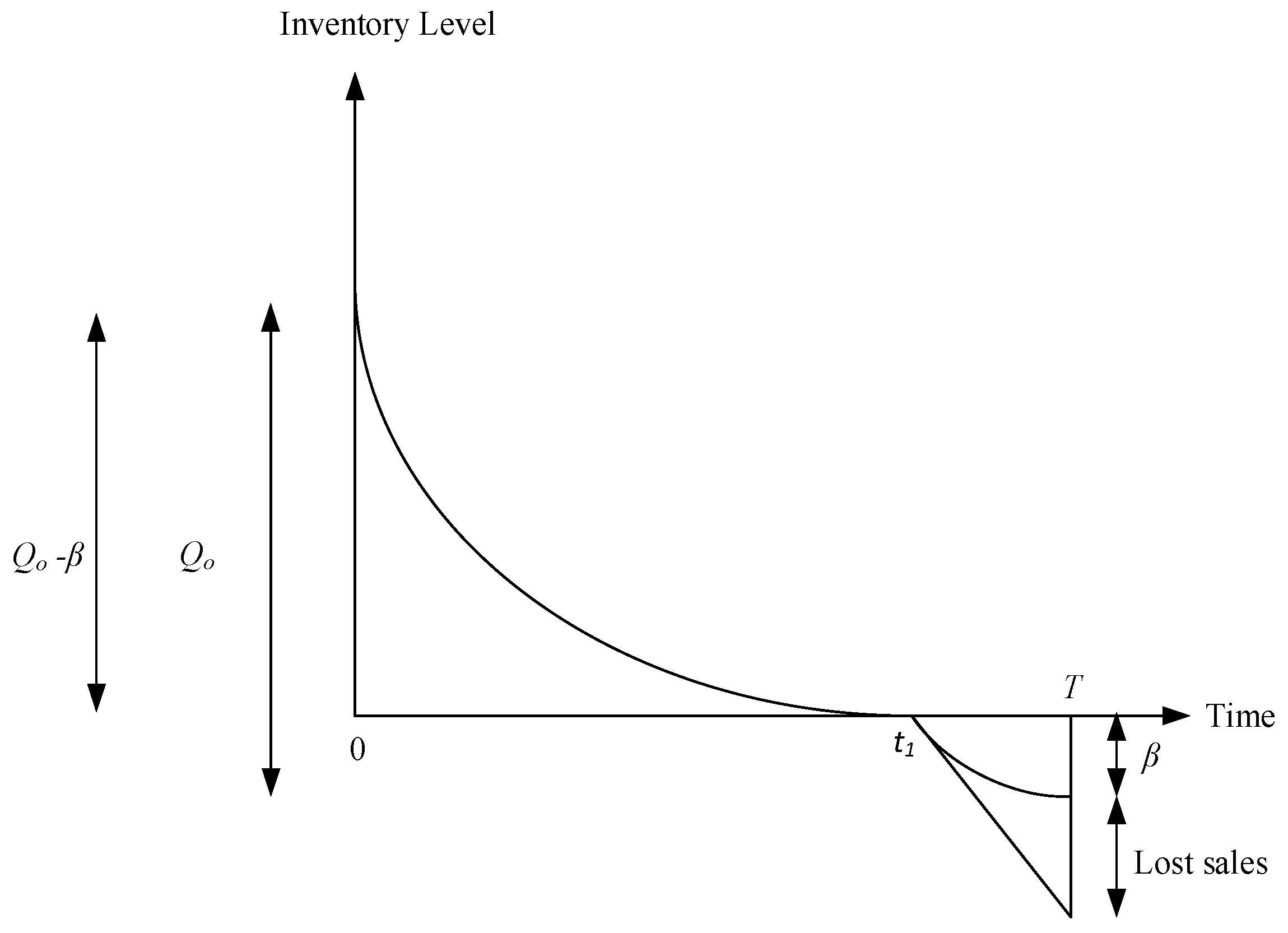
4. Mathematical Model

A mathematical model for maximum fixed lifespan deteriorating items and exponentially partially backlogged shortages under non-linear price-sensitive demand is derived from the notation as mentioned above and assumptions. Additionally, to condense the deterioration and maintain the items’ quality, investment in preservation technology is considered in this model. Moreover, Figure 1 shows the proposed problem and the graph of inventory level against time.

Now, the inventory level is reduced due to the assembled impact of deterioration and price-sensitive demand during the replacement period $\left[0,t_1\right]$, and on time $t_1$ it reaches out to zero. Consequently, the proportion of the variation in inventory level can be characterized by the expression:

$$\frac{d{I}_1}{dt}=-R\left(S\right)-{\theta }_d\left(t\right)\left(1-f_n\left(U\right)\right)I_1\left(t\right), t\in \left[0,t_1\right]$$

(1)

under the condition $I_1\left(t_1\right)=0$. Now, by using this condition, the inventory level $I_1\left(t\right)$ at any time $t$ can be determined as:

$$I_1\left(t\right)=\frac{a{S}^{-\eta }\left(\mu U+1\right)}{\mu U}\left(\left(1+\xi -t\right)-{\left(1+\xi -t_1\right)}^{\frac{\mu U}{\mu U+1}}{\left(1+\xi -t\right)}^{\frac{1}{\mu U+1}}\right).$$

(2)

Now, at the time $t=t_1$, the on-hand inventory amount disappears. After that, shortages arrive in the system and accumulate exponentially with the $\left(T-t\right)$ wait time before the system’s following stock appears.

Additionally, at the time, $t=T$ the maximum shortage level can be achieved, and that is indicated by $\beta$. As a result, the equation for the rate of change in inventory for a time $\left[t_1,T\right]$ can be specified as:

$$\frac{d{I}_2}{dt}=R\left(S\right)\left(e^{-\varsigma \left(T-t\right)}\right), t\in \left[t_1,T\right]$$

(3)

under the condition $I_2\left(t_1\right)=0$. Thus, by using this condition, the backlogging level can be determined as:

$$I_2\left(t\right)=\frac{a{S}^{-\eta }}{\varsigma }\left(e^{-\varsigma \left(T-t\right)}-e^{-\varsigma \left(T-t_1\right)}\right)$$

(4)

Additionally, by using the condition $I_2\left(T\right)=\beta$, one can easily identify the highest amount of back-ordered demand by:

$$\beta =\beta \left(T\right)=\frac{a{S}^{-\eta }}{\varsigma }\left(1-e^{-\varsigma \left(T-t_1\right)}\right)$$

(5)

Since, $I_1\left(0\right)=Q_o-\beta$, by using Equations (2) and (5), the economic order quantity $Q_o$ per replacement cycle time $T$ can be obtained as:

$$\begin{gathered} Q_o-\beta =\frac{a{S}^{-\eta }\left(\mu U+1\right)}{\mu U}\left(\left(1+\xi \right)-{\left(1+\xi -t_1\right)}^{\frac{\mu U}{\mu U+1}}{\left(1+\xi \right)}^{\frac{1}{\mu U+1}}\right) \\ \therefore Q_o=\frac{a{S}^{-\eta }}{\varsigma }\left(1-e^{-\varsigma \left(T-t_1\right)}\right)+\frac{a{S}^{-\eta }\left(\mu U+1\right)}{\mu U}\left(\left(1+\xi \right)-{\left(1+\xi -t_1\right)}^{\frac{\mu U}{\mu U+1}}{\left(1+\xi \right)}^{\frac{1}{\mu U+1}}\right) \end{gathered}$$

(6)

Next, during the interval $\left[t_1,T\right]$, the amount of loss in sales at a time $t$ can be established as:

$$\begin{gathered} L_S\left(t\right)={\displaystyle \underset{t_1}{\overset{t}{\int }}R\left(S\right)}\left(1-e^{-\varsigma \left(T-t\right)}\right)dt; t\in \left[t_1,T\right] \\ \therefore L_S\left(t\right)=\frac{a{S}^{-\eta }}{\varsigma }\left\{\varsigma \left(t-t_1\right)-\left(e^{-\varsigma \left(T-t\right)}-e^{-\varsigma \left(T-t_1\right)}\right)\right\}, t_1\le t\le T \end{gathered}$$

(7)

The supplier also provides the vendor with an allowable delay in payment. In various cases, the interest gained, the interest lost, and the net profit function is calculated as follows:

• Scenario-(i): $\left(0<M\le t_1\right)$

Here, in this scenario, the mutually agreed credit time $M$ takes place earlier than the time $t_1$. So, through the period starting from 0 up to $M$, the vendor gains the interest by the satisfied shortages of the preceding cycle. As a result, the interest gained by the vendor can be assessed as:

$${\mathrm{IG}}_1=S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S\right)}dt+S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}\beta \left(T\right)dt}$$

(8)

After payment of the account $M$, the vendor lost interest in the items, which are not sold through the time interval $\left[M,t_1\right]$. As a result, interest loss can be obtained by:

$${\mathrm{IL}}_1=P{I}_l{\displaystyle \underset{M}{\overset{t_1}{\int }}{I}_1\left(t\right)dt}.$$

(9)

• Scenario-(ii): $\left(t_1<M\le T\right)$

Here, in this scenario, the mutually agreed credit time $M$ takes place afterward the time $t_1$. Here, the vendor sold all the goods, purchased from the supplier on credit. As a result, the interest lost is zero (i.e., $I{C}_2=0$). Therefore, up to the credit period $M$, the vendor only gains interest for sold items and earns additional inventory interest through the time interval $t_1$. As a result, the interest acquired by the vendor can be assessed as:

$$I{G}_2=S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S\right)dt+S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}\beta \left(t\right)dt+S{I}_g}}R\left(S\right)\left(M-t_1\right)t_1.$$

(10)

Now, per the replenishment cycle time $T$, the vendor’s resulting revenue can be determined as:

$$SR=S{\displaystyle \underset{0}{\overset{t_1}{\int }}R\left(S\right)dt+S\beta \left(T\right)=Sa{S}^{-\eta }{t}_1+\frac{Sa{S}^{-\eta }}{\varsigma }\left(1-e^{-\varsigma \left(T-t_1\right)}\right)}$$

(11)

Next, per cycle time $T$, the vendor’s net cost apparatuses are assimilated as:

• Ordering cost; $\mathrm{OC}=O$
• Purchasing cost; $\mathrm{PC}=P{Q}_o$
• Average holding cost; $\mathrm{HC}={\displaystyle \underset{0}{\overset{t_1}{\int }}H\left(1+iH\cdot t\right)I_1\left(t\right)dt}$
• Preservation technology capital; $\mathrm{PTI}=UT$
• Backlogging cost: $\mathrm{BC}=c_{\beta }{\displaystyle \underset{t_1}{\overset{T}{\int }}{I}_2\left(t\right)dt}$
• Additional charge because of lost sales: $\mathrm{LC}=c_{l}R\left(S\right){\displaystyle \underset{t_1}{\overset{T}{\int }}\left(1-e^{-\varsigma \left(T-t\right)}\right)dt}$

Therefore, per unit time, the net profit for the vendor during the replacement time $T$ can be assessed by:

$$T{P}_i\left(U,S,T\right)=\frac{1}{T}\left(\mathrm{SR}-\mathrm{OC}-\mathrm{PC}-\mathrm{HC}-\mathrm{PTI}-\mathrm{BC}-\mathrm{LC}+{\mathrm{IG}}_{\mathrm{i}}-{\mathrm{IL}}_{\mathrm{i}}\right); \mathrm{i} =1,2.$$

i.e.,

$$T{P}_i\left(U,S,T\right)=\{\begin{array}{l}T{P}_1\left(U,S,T\right) ; \mathrm{if} 0<M\le t_1\\ T{P}_2\left(U,S,T\right) ; \mathrm{if} t_1<M\le T\end{array}$$

(12)

where,

$$T{P}_1\left(U,S,T\right)=\frac{1}{T}\left(\begin{array}{l}Sa{S}^{-\eta }{t}_1+\frac{Sa{S}^{-\eta }}{\varsigma }\left(1-e^{-\varsigma \left(T-t_1\right)}\right)-O-P{Q}_o-\\ {\displaystyle \underset{0}{\overset{t_1}{\int }}H\left(1+iH\cdot t\right)I_1\left(t\right)dt}-UT-c_{\beta }{\displaystyle \underset{t_1}{\overset{T}{\int }}{I}_2\left(t\right)dt}-c_{l}R\left(S\right){\displaystyle \underset{t_1}{\overset{T}{\int }}\left(1-e^{-\varsigma \left(T-t\right)}\right)dt}\\ +S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S\right)}dt+S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}\beta \left(T\right)dt}-P{I}_l{\displaystyle \underset{M}{\overset{t_1}{\int }}{I}_1\left(t\right)dt}\end{array}\right)$$

(13)

and

$$T{P}_2\left(U,S,T\right)=\frac{1}{T}\left(\begin{array}{l}Sa{S}^{-\eta }{t}_1+\frac{Sa{S}^{-\eta }}{\varsigma }\left(1-e^{-\varsigma \left(T-t_1\right)}\right)-O-P{Q}_o-\\ {\displaystyle \underset{0}{\overset{t_1}{\int }}H\left(1+iH\cdot t\right)I_1\left(t\right)dt}-UT-c_{\beta }{\displaystyle \underset{t_1}{\overset{T}{\int }}{I}_2\left(t\right)dt}-c_{l}R\left(S\right){\displaystyle \underset{t_1}{\overset{T}{\int }}\left(1-e^{-\varsigma \left(T-t\right)}\right)dt}\\ + S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S\right)dt+S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}\beta \left(t\right)dt+S{I}_g}}R\left(S\right)\left(M-t_1\right)t_1\end{array}\right)$$

(14)

5. Computational Algorithm

To solve the problem, the classical optimization method is used. The primary purpose is to maximize the net profit function $T{P}_i\left(U,S,T\right); i=1,2$. Here, the mathematical software Maple $XVIII$ is used to check the optimality of the decision parameters and the solution steps are as follows:

Step 1 Consign mathematic measures to each inventory parameter.

Step 2 compute and apply the below necessary condition of the partial derivative to net profit function by following:

$$\frac{\partial T{P}_i\left(U,S,T\right)}{\partial U}=0,\frac{\partial T{P}_i\left(U,S,T\right)}{\partial S}=0 and \frac{\partial T{P}_i\left(U,S,T\right)}{\partial T}=0 ; i=1,2$$

Step 3 Find all possible second-order partial derivates as follows:

$$\begin{array}{l}\frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial U^2},\frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial U\partial S},\frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial U\partial T},\\ \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial S\partial U},\frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial S^2},\frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial S\partial T},\\ \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial T\partial U},\frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial T\partial S},\frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial T^2}.\end{array}$$

Step 4 Generate the Hessian matrix as follows:

$$\begin{array}{l}{H}_i\left(S^{*},U^{*},T^{*}\right)=\\ \left[\begin{array}{ccc}\frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial U^2}& \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial U\partial S}& \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial U\partial T}\\ \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial S\partial U}& \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial S^2}& \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial S\partial T}\\ \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial T\partial U}& \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial T\partial S}& \frac{{\partial }^{2}T{P}_i\left(U^{*},S^{*},T^{*}\right)}{\partial T^2}\end{array}\right]\end{array}$$

Step 5 Find the Eigen-values of the Hessian matrix $H_i\left(U^{*},S^{*},T^{*}\right); i=1,2$.

Step 6 According to [40], if all the Eigen-values are positive, then the function does have a minimum value at $\left(U^{*},S^{*},T^{*}\right)$ and if all are negative, then the function does have a maximum value at $\left(U^{*},S^{*},T^{*}\right)$.

6. Numerical Illustrations and Sensitivity Analysis

6.1. Numerical Illustrations

To demonstrate the derived prototype, two numerical illustrations are to be reviewed, giving the best idea of an optimal solution for the vendor’s overall profit function.

Example 1.

(For Case: $0<M\le t_1$)

Considering the following criteria for an inventory system:

$a=10,000$ units/year, $\eta =1.4$, $O=\$40$ /order, $P=\$10$ /unit, $H=\$0.3$ /unit/year, $iH=12\%$, $\xi =2$ years, $\mu =4$, $\varsigma =0.5$, $c_{\beta }=0.5$, $c_l=0.6$, $M=0.3$ years, $I_g=0.1$ /$/year, $\alpha =0.8$, and $I_l=0.12$ /$/year.

Using the above solution procedure, the optimal measures of decision variables are $S^{*}=\$35.36$, $U^{*}=\$3.64$, $T^{*}=0.762$ years, and the total profit is $T{P}_1\left(S^{*},U^{*},T^{*}\right)=\$1667.03$.

Moreover, the initial optimum order quantity $Q_o{}^{*}=51.67$ units with backordering quantity ${\beta }^{*}=9.97$ units. Additionally, $t_1=\alpha T=0.610$ years and the eigenvalues are $\left\{-0.499, -0.758, -149.50\right\}$ which shows that $T{P}_1\left(U^{*},S^{*},T^{*}\right)$ is maximum.

Example 2.

(For Case: $t_1<M\le T$)

By above similar values, set as in Example 1, the optimal measures of decision variables are $S^{*}=\$35.05$, $U^{*}=\$3.21$, $T^{*}=0.608$ years, and the total profit is:

$$T{P}_2\left(S^{*},U^{*},T^{*}\right)=\$1660.37.$$

Moreover, the initial optimum order quantity $Q_o{}^{*}=41.67$ units with backordering quantity ${\beta }^{*}=8.11$ units. Additionally, $t_1=\alpha T=0.486$ years and the eigenvalues are $\left\{-0.567, -0.787, -357.19\right\}$ which shows that $T{P}_2\left(U^{*},S^{*},T^{*}\right)$ is maximum.

6.2. Sensitivity Analysis

In this portion, sensitivity analysis is implemented on Example 1 as the cumulative benefit for Case-(i) is maximal and reflects a shift in decision variables by adjusting inventory parameters up to $-20\%,-10\%,10\% \mathrm{and} 20\%$ along with the overall profit feature.

From

Table 2. Sensitivity analysis.

Parameters	Values	Cycle Time (T) (Years)	Sales Price (S) ($)	Preservation $\mathbf{Technology} \mathbf{Investment} \left(\mathit{U}\right)$ ($)	Order $\mathbf{Quantity} \left({\mathit{Q}}_{\mathit{o}}\right)$ (Units)	$\mathbf{Total} \mathbf{Profit} \left(\mathit{T}{\mathit{P}}_1\right)$ ($)
$a$	8000	0.870	35.58	3.48	46.80	1323.11
	9000	0.812	35.46	3.57	49.35	1494.86
	11,000	0.718	35.27	3.71	53.79	1839.51
	12,000	0.680	35.19	3.77	55.72	2012.27
$\eta$	1.12	0.438	92.74	2.53	27.44	5152.01
	1.26	0.617	48.58	3.40	46.24	2843.97
	1.54	0.909	29.05	3.65	50.65	1007.20
	1.68	1.072	25.41	3.54	46.68	618.50
$P$	8	0.709	28.26	3.67	65.82	1826.53
	9	0.737	31.81	3.65	57.96	1740.57
	11	0.785	38.91	3.63	46.53	1603.13
	12	0.805	42.47	3.62	42.26	1546.88
	32	0.659	35.17	3.36	45.06	1678.30
	36	0.712	35.26	3.51	48.49	1672.46
$O$	44	0.809	35.44	3.77	54.66	1661.94
	48	0.853	35.53	3.88	57.47	1657.13
	0.24	0.771	35.32	3.67	52.38	1668.06
	0.27	0.767	35.33	3.66	52.02	1667.55
$H$	0.33	0.757	35.37	3.63	51.33	1666.52
	0.36	0.753	35.39	3.62	50.99	1666.02
	0.096	0.762	35.35	3.64	51.70	1667.06
	0.108	0.762	35.35	3.64	51.69	1667.04
$iH$	0.132	0.762	35.35	3.64	51.66	1667.02
	0.144	0.762	35.36	3.64	51.64	1667.01
	1.6	0.758	35.37	3.95	51.44	1666.40
	1.8	0.760	35.36	3.78	51.56	1666.74
$\xi$	2.2	0.763	35.35	3.51	51.77	1667.30
	2.4	0.765	35.35	3.40	51.86	1667.54
	3.2	0.757	35.37	4.03	51.38	1666.18
	3.6	0.760	35.36	3.82	51.54	1666.64
$\mu$	4.4	0.764	35.35	3.49	51.79	1667.37
	4.8	0.765	35.35	3.35	51.90	1667.67
	0.4	0.786	35.40	3.71	53.32	1669.74
	0.45	0.774	35.38	3.67	52.47	1668.37
$\varsigma$	0.55	0.751	35.34	3.61	50.92	1665.72
	0.6	0.740	35.32	3.58	50.19	1664.43
	0.4	0.763	35.35	3.64	51.74	1667.13
	0.45	0.762	35.35	3.64	51.70	1667.08
$c_{\beta }$	0.55	0.761	35.36	3.64	51.64	1666.98
	0.6	0.761	35.36	3.64	51.61	1666.93
	0.48	0.762	35.35	3.64	51.71	1667.09
	0.54	0.762	35.35	3.64	51.69	1667.06
$c_l$	0.66	0.762	35.36	3.64	51.65	1667.00
	0.72	0.762	35.39	3.64	51.63	1666.97
	0.24	0.796	35.65	3.72	53.33	1657.06
	0.27	0.780	35.50	3.68	52.57	1661.93
$M$	0.33	0.742	35.21	3.60	50.64	1672.38
	0.36	0.720	35.06	3.54	49.44	1677.99
	0.08	0.789	35.49	3.71	53.25	1661.48
	0.09	0.776	35.42	3.68	52.47	1664.24
$I_g$	0.11	0.748	35.29	3.61	50.86	1669.86
	0.12	0.734	35.22	3.57	50.03	1672.71
	0.096	0.791	35.35	3.72	53.68	1668.12
	0.108	0.776	35.36	3.68	52.64	1667.56
$I_l$	0.132	0.749	35.38	3.60	50.78	1666.53
	0.144	0.737	35.38	3.57	49.96	1666.06

, the following insights are obtained:

• As the scaling demand rate $\left(a\right)$ rises, the investment $\left(U\right)$, quantity $\left(Q_o\right)$, and net profit rise whereas the sales price and cycle time decrease. Thus, the increase is beneficial as it helps increase the net profit of the vendor. The rise is advantageous to this model as it aims to increase the net benefit of the vendor.
• As the price elasticity constant $\left(\eta \right)$ increases, the cycle time also increases whereas the sales price and net profit decrease. Moreover, as the values $\left(\eta \right)$ increase the order quantity and investment $\left(U\right)$ increases linearly then decrease slowly. Thus, the rise has a detrimental effect as it lowers the net benefit function.
• As the purchase cost $\left(P\right)$ increases, the sales price and cycle time increase whereas the investment $\left(U\right)$, quantity $\left(Q_o\right)$, and net profit decrease. It is apparent that the rise in the sale price directly influences the demand rate and the decline in the overall profit feature. The rise is also not beneficial.
• As the $\left(O\right)$ increases, the quantity $\left(Q_o\right)$ and cycle time also increase while the $\left(H\right)$ increases, the quantity $\left(Q_o\right)$, and cycle time decrease. However, the rise in ordering and holding costs is not preferable as the net profit function decreases.
• As the rate of preservation $\left(\mu \right)$ and maximum fixed lifespan $\left(\xi \right)$ increases, the cycle time also increases slowly.
• The backlogging parameter $\left(\varsigma \right)$ increases, the order quantity, cycle time, preservation technology investment, sales price, and net profit decreases. Thus, the increase shows a negative effect as the overall profit function decreases.
• As the credit period $\left(M\right)$ rises, the quantity $\left(Q_o\right)$ and cycle time decrease whereas the net profit function increases. It suggests that if the credit time is longer, then the net profit is also higher.

7. Conclusions

This study examines the vendor’s replenishment policy for the time-varying perishable items in which the rate of demand is sensitive to a non-linear price function. The holding cost is also assumed to be a variable function that increases with time, making this research close to reality. Additionally, to reduce the rate of deterioration, the vendor also invests cash in preserving the items. Moreover, the supplier gives mutually agreed trade credit to its vendor. Furthermore, exponential partial backlogging shortages are allowed in which the rate of backlogging depends on the wait time before the emergence of the new product. Again, this model uses a classical optimization method to calculate the preservation technology investment, cycle time, and sales price. The principal goal of this study is to optimize the vendor’s net profit function. In this research, two numerical illustrations, drawn up based on discussed scenarios, are also examined. Finally, sensitivity analysis is performed on the best optimal solution to the key parameters and some managerial insights. This research shows that the net profit function increases with the increase in the scaling demand rate, while the increase in ordering cost and holding cost decreases the net profit function. Furthermore, it is observed from the sensitivity table that the rise in the credit period time does have an optimistic effect on the net profit. In contrast, the increase in the backlog parameter does harm the net profit. Therefore, the vendor should order more units before the level of inventory reaches zero. Additionally, supposing that the mutual credit time occurs before the shortages, in this case the vendor will get more profit because the ordering cost, holding cost, and backlogging parameter negatively affect the vendor’s net profit.

By considering advanced payments, the current research can be extended: two warehouses, inflation, two-stage trade credit financing, a multi-item integrated supply chain, and various methods of demand such as advertising-dependent, stock-dependent, quadratic demand, and probabilistic demand can be further generalized.