Numerical Solution of Two Dimensional Time-Space Fractional Fokker Planck Equation With Variable Coefficients
Abstract
1. Introduction
2. Numerically Implicit Finite Difference Scheme
- ,
- The functions and are positive definite monotone increasing functions in ω,
- The functions and are positive definite convex monotone decreasing functions in ω,
- and . i.e.,
- and . i.e.,
3. Stability of Implicit Finite Difference Scheme
4. Convergence of Implicit Finite Difference Scheme
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Aleroev, T.S.; Elsayed, A.M. Analytical and Approximate Solution for Solving the Vibration String Equation with a Fractional Derivative. Mathematics 2020, 8, 1154. [Google Scholar] [CrossRef]
- Elsayed, A.M.; Orlov, V.N. Numerical Scheme for Solving Time–Space Vibration String Equation of Fractional Derivative. Mathematics 2020, 8, 1069. [Google Scholar] [CrossRef]
- Günerhan, H.; Çelik, E. Analytical and approximate solutions of Fractional Partial Differential-Algebraic Equations. Appl. Math. Nonlinear Sci. 2020, 5, 109–120. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical simulation for fractional Benney–Lin equation arising in falling film problems using two novel techniques. Numer. Methods Partial. Differ. Equ. 2020, 37, 210–243. [Google Scholar] [CrossRef]
- Heinsalu, E.; Patriarca, M.; Goychuk, I.; Schmid, G.; Hänggi, P. Fractional Fokker-Planck dynamics: Numerical algorithm and simulations. Phys. Rev. E. 2006, 73, 046133. [Google Scholar] [CrossRef] [PubMed]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection–dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Kay, D.; Grau, V.; Rodriguez, B.; Burrage, K. Fractional Diffusion Models of Cardiac Electrical Propagation: Role of Structural Heterogeneity in Dispersion of Repolarization; Technical Report OCCAM 13/35; Oxford Centre for Collaborative Applied Mathematics: Oxford, UK, 2013. [Google Scholar]
- Aleroev, T.S.; Aleroeva, H.T.; Huang, J.; Tamm, M.V.; Tang, Y.; Zhao, Y. Boundary value problems of fractional Fokker–Planck equations. Comput. Math. Appl. 2017, 73, 959–969. [Google Scholar] [CrossRef]
- Arshad, S.; Baleanu, D.; Huang, J.; Al Qurashi, M.M.; Tang, Y.; Zhao, Y. Finite Difference Method for Time-Space Fractional Advection–Diffusion Equations with Riesz Derivative. Entropy 2018, 20, 321. [Google Scholar] [CrossRef] [PubMed]
- Shuqing, Y.; Mingrong, C. Finite difference scheme for the time-fractional Fokker–Planck equation with time- and space-dependent forcing. Int. J. Comput. Math. 2019, 96, 379–398. [Google Scholar]
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelasticallydamped structures. J. Guid. Control. Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. New solution and analytical techniques of the implicit numerical method for the anomalous subdiffusion equation. SIAM J. Numer. Anal. 2008, 46, 1079–1095. [Google Scholar] [CrossRef]
- Momani, S.; Arqub, O.A.; Freihat, A.; Al-Smadi, M. Analytical approximations for Fokker-Planck equations of fractional order in multistep schemes. Appl. Comput. Math. 2016, 15, 319–330. [Google Scholar]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burrage, K. Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F. Implicit difference approximation for the time fractional diffusion equation. J. Appl. Math. Comput. 2006, 22, 87–99. [Google Scholar] [CrossRef]
- Weiping, B.; Aiguo, X.; Yifa, T. Finite Difference Methods for Space Fractional Advection-Diffusion Equations with Variable Coefficients. In Communications in Computer and Information Science Part II, CCIS 327; Springer: Berlin/Heidelberg, Germany, 2012; pp. 95–104. [Google Scholar]
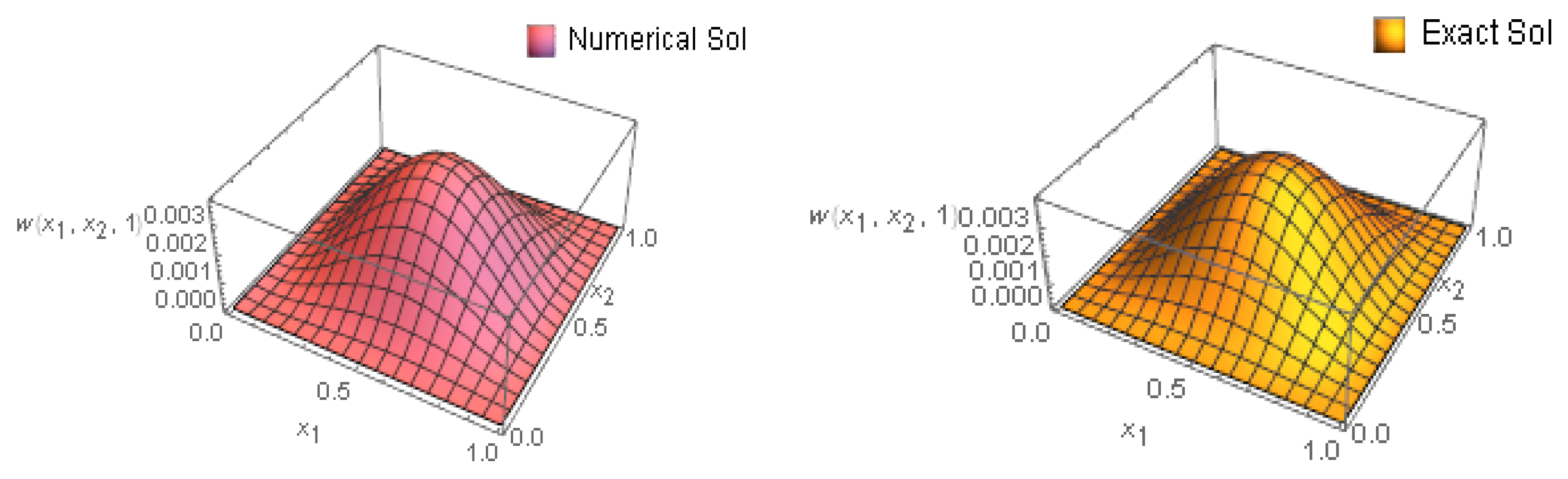
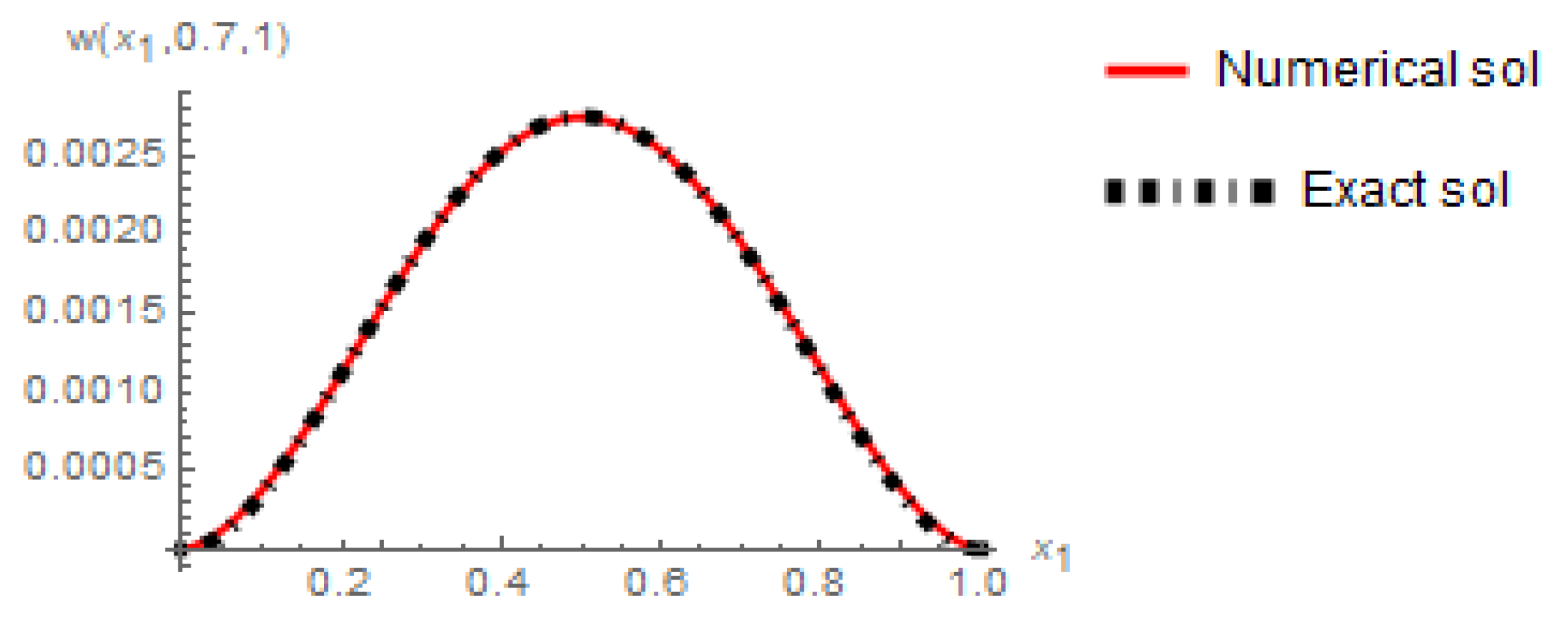
| 1/4 | ||||||||
| 1/8 | ||||||||
| 1/16 | ||||||||
| 1/32 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, E.I.; Orlov, V.N. Numerical Solution of Two Dimensional Time-Space Fractional Fokker Planck Equation With Variable Coefficients. Mathematics 2021, 9, 1260. https://doi.org/10.3390/math9111260
Mahmoud EI, Orlov VN. Numerical Solution of Two Dimensional Time-Space Fractional Fokker Planck Equation With Variable Coefficients. Mathematics. 2021; 9(11):1260. https://doi.org/10.3390/math9111260
Chicago/Turabian StyleMahmoud, Elsayed I., and Viktor N. Orlov. 2021. "Numerical Solution of Two Dimensional Time-Space Fractional Fokker Planck Equation With Variable Coefficients" Mathematics 9, no. 11: 1260. https://doi.org/10.3390/math9111260
APA StyleMahmoud, E. I., & Orlov, V. N. (2021). Numerical Solution of Two Dimensional Time-Space Fractional Fokker Planck Equation With Variable Coefficients. Mathematics, 9(11), 1260. https://doi.org/10.3390/math9111260







