Abstract
A simultaneous-approximation term is a non-reflecting boundary condition that is usually accompanied by summation-by-parts schemes for provable time stability. While a high-order convective flux based on reconstruction is often employed in a finite-volume method for compressible turbulent flow, finite-volume methods with the summation-by-parts property involve either equally weighted averaging or the second-order central flux for convective fluxes. In the present study, a cell-centered finite-volume method for compressible Naiver–Stokes equations was developed by combining a simultaneous-approximation term based on extrapolation and a low-dissipative discretization method without the summation-by-parts property. Direct numerical simulations and a large eddy simulation show that the resultant combination leads to comparable non-reflecting performance to that of the summation-by-parts scheme combined with the simultaneous-approximation term reported in the literature. Furthermore, a characteristic boundary condition was implemented for the present method, and its performance was compared with that of the simultaneous-approximation term for a direct numerical simulation and a large eddy simulation to show that the simultaneous-approximation term better maintained the average target pressure at the compressible flow outlet, which is useful for turbomachinery and aerodynamic applications, while the characteristic boundary condition better preserved the flow field near the outlet.
1. Introduction
Compressible turbulent flows are encountered in many engineering applications such as airplanes, high-speed vehicles, and turbomachinery. High-fidelity simulations of turbulence such as direct numerical simulations (DNS) or large eddy simulations (LES) require minimal numerical dissipation as upwind-biased schemes artificially dampen small-scale turbulent structures [1]. The adoption of low-dissipative schemes, however, leads to requiring non-reflecting boundary conditions at the subsonic compressible outlet, as the lack of numerical dissipation leads to the accumulation of incoming acoustic waves affecting the internal flow field unless exact outlet boundary conditions are imposed [2].
A simultaneous-approximation term (SAT) is a non-reflecting boundary condition that is often used with summation-by-parts (SBP) schemes, as the combination of an SBP scheme and an SAT (SBP–SAT approach) leads to provable time stability, meaning that the resultant numerical method is stable for long-time numerical integration [3,4,5,6].
The SBP–SAT approach was extensively studied for high-order finite-difference methods (FDMs) [5,6], but only a few studies regarding SBP–SAT approaches for finite-volume methods (FVMs) are available, while most research for FVMs concerns node-based FVMs. Nordström et al. [7] showed that the first derivative for unstructured node-centered FVM is on an SBP form given that equally weighted averaging is used for convective flux calculation, which led to the development of a node-based unstructured FVM solver by Shoeybi et al. [8]. Concerning a cell-centered FVM, a paper by Nordström and Björck [9] studied the SBP-SAT approach for a cell-centered FVM using scalar hyperbolic problems in one and two dimensions, but at the cost of introducing data nodes at the boundaries, and it was limited to the second-order central convective flux. An SBP–SAT approach for three-dimensional compressible Navier–Stokes equations in a cell-centered FVM was not reported in the literature.
While complex geometries encountered in practical engineering applications favor an FVM over an FDM due to geometrical flexibility and computational efficiency, DNS and LES often employ high-order convective fluxes based on the polynomial reconstruction of variables for FVMs [10,11,12], and the use of equally weighted averaging for convective flux calculation is not always possible due to the introduction of an upwind-biased flux for shock capturing [13]. Furthermore, while the SAT can be readily used in FDMs and node-based FVMs where unknowns are solved at the boundaries, SAT application for a cell-centered FVM is not straightforward as the cell-centered FVM does not have unknowns at the cell faces where the boundary conditions are imposed; this issue motivated Nordström and Björck [9] to introduce unknowns at the boundary.
In this paper, the SAT for compressible Navier–Stokes equations by Svärd et al. [4] is implemented by extrapolating cell-centered variables to cell faces instead of introducing additional unknowns at the boundaries. Rather than insisting on the SBP–SAT approach, which is not viable for high-order convective fluxes, a non-SBP cell-centered FVM by Khalighi et al. [10] was combined with the SAT based on extrapolation. While the resultant combination will be referred to as NSBP–SAT approach, it showed comparable non-reflecting performance to that of the SBP–SAT approach reported in the literature [8] for DNSs of a two-dimensional acoustic pulse and low Reynolds number flow around a two-dimensional circular cylinder, and an LES of flow over a circular cylinder at . Moreover, the non-reflecting performance of the SAT was compared with that of the characteristic boundary condition (CBC) for a DNS of convecting two-dimensional inviscid vortex and an LES of flow over a von Karman Institute (VKI) turbine cascade.
The present paper is organized as follows. Section 2 introduces governing equations for DNS and LES, and describes a subgrid-scale model employed for LES. Section 3 addresses details of numerical methods employed in the present study, and the implementation is verified and validated against numerical tests without non-reflecting boundary conditions. In Section 4, the SBP–SAT and the NSBP–SAT approaches are introduced and compared in numerical tests. A conducted comparative study of the SAT in the NSBP–SAT approach and the CBC for numerical tests is described in Section 5, followed by concluding remarks in Section 6.
2. Governing Equations and Turbulence Modeling
2.1. Unfiltered Navier–Stokes Equations
Navier–Stokes equations for compressible flows are written as follows [14]:
where t and are independent variables representing time and spatial coordinates. The summation convention over repeated indices is used. , , p, E, , and denote density, velocity vector, pressure, total energy per unit mass, shear-stress tensor, and heat flux, respectively. E, , and are given as follows:
where the heat-capacity ratio is given as . and are specific heat at constant pressure and constant volume, respectively. The rate of strain tensor is given as
Assuming the ideal gas model for air, the equation of state is given as
where the gas constant is .
Variation of with T is approximated by a power law , which is valid between 150 and 500 K. is given as , where is the Prandtl number.
Navier–Stokes equations are solved for DNS, which does not need a turbulence model given that flow structures are resolved by the Kolmogorov scale [15].
2.2. Spatially Filtered Navier–Stokes Equations
While DNS is prohibitively expensive for high Reynolds number flows encountered in practical applications, LES is an alternative high-fidelity simulation technique where large-scale turbulent eddies are directly solved, and small-scale eddies are modeled by a subgrid-scale (SGS) model.
A low-pass filter operation is defined as
where and are spatial coordinate vectors in the flow domain of . Filter kernel G satisfies the normalization condition and depends on the filter width defined as . A Favre filter is also defined as . For the definition of filter width, the definition of an element size in three-dimensional space [16] is as follows:
where denotes the filter width in the i direction.
Low-pass-filtered Navier–Stokes equations are given as follows [17]:
where is assumed following the work by Okong’o and Bellan [17]. , , , , , and are given as follows:
Last, it is assumed that , , and following the work by Okong’o and Bellan [17].
2.3. Subgrid-Scale Modeling
For LES, and are modeled by using eddy viscosity closures as follows:
where and are modeled using Yoshizawa parameterization [18] and the Vreman kernel [19], given as follows:
where , , and are defined as follows:
3. Numerical Methods, Verification, and Validation
The present numerical implementation uses Equations (1)–(3) for DNS, and Equations (11)–(13) for LES. As identical numerical methods were employed for both DNS and LES, descriptions of the numerical schemes are given for DNS.
Equations (1)–(3) are solved in cell-centered finite-volume form:
where is the vector of conserved variables averaged in the control volume. and are the face-normal Euler and viscous flux vectors, respectively, corresponding to the right-hand sides of Equations (1)–(3). is the volume of the control volume, is the summation over the cell faces per cell, and is the area of the cell face. The volume and the surface integrals are approximated with the second-order midpoint quadrature rule.
Following Khalighi et al. [10], biased polynomial reconstruction, which is maximal third-order accurate to the face centroid, is performed for primitive variables (, , and p) on both sides of each cell face. Using the face-reconstructed values on the left- and the right-hand sides of a cell face, and , a central flux is calculated in skew-symmetric form [8], while dissipative essentially non-oscillatory (ENO) flux [20] is calculated by using the HLLC Riemman solver [13]. For more details regarding face reconstruction for fluxes, refer to Khalighi et al. [10].
A blended flux is expressed as follows:
where is a blending parameter. Unlike the implicit LES where a global constant of [21] or [22,23] is used, Khalighi et al. [10] computed using the row norm of the symmetric part of the differencing operator for Euler fluxes D, as follows:
where was chosen from numerical tests [10]. The motivation to use Equation (29) was that a skew-symmetric operator () is stable and non-dissipative (energy-conserving) in the inviscid limit on a periodic domain [10]. The blending scheme by Khalighi et al. [10] is cost-effective, as is precomputed using grid information prior to the main calculation while the use of high-order spatial filter requires filtering at each time step in addition to the calculation of fluxes. A relative solution switch [10] is employed to activate dissipative ENO fluxes in regions with shocks by setting . A third-order low-storage Runge–Kutta scheme [24] is employed to advance the equations in time.
3.1. Two-Dimensional Propagating Inviscid Vortex
The accuracy of the present numerical scheme was verified by using an exact vortex solution to the Euler equations, which is given as follows [8]:
where and are the reference speed of sound and reference density, respectively.
A vortex of radius one and is initially located at and is diagonally convected to with the speed of . A box is discretized on , , , and cell uniform Cartesian grids. The exact solution is used for the initial condition, and periodic boundary conditions are imposed. The constant Courant–Friedrichs–Lewy (CFL) number of is set for all calculations, such that both spatial and temporal convergence rates are measured [8].
and norm error norms at are shown against the grid width in Figure 1. and norm errors both exhibit second-order convergence rates.
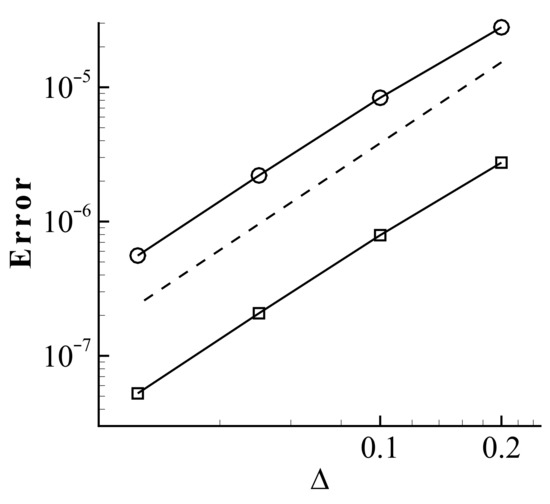
Figure 1.
Error convergence study for a 2D propagating vortex. □, error; ◯, error; 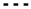 , second-order convergence.
, second-order convergence.
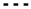 , second-order convergence.
, second-order convergence.
3.2. LES of Supersonic Turbulent Channel Flow
To assess the predictive capability of the present method for compressible near-wall turbulence, LES is performed for supersonic turbulent channel flow at and , where , , , and . is the speed of sound at the wall and denotes an average over time, and streamwise and spanwise directions. Periodic boundary conditions are imposed in the streamwise and the spanwise directions, while no-slip isothermal wall boundary conditions are imposed at and , where is the channel half width. The spatially uniform body force is imposed in the streamwise direction to drive channel flow, and is adjusted each time-step to conserve the global mass rate.
Two grids of and cells in the streamwise, wall-normal, and spanwise directions are used similarly to those of Lenormand et al. [25].
To close the SGS models given in Equations (20) and (21), a C of and of obtained from an a priori study of Moin et al. [26] are used. in Equation (22) is assumed to be negligible due to the DNS study of supersonic channel flow [27], where the contribution of the dilatation to the turbulent kinetic energy dissipation rate was found to be insignificant.
Profiles of the mean and the root mean square (RMS) of velocity and temperature obtained from the present LES are shown against DNS data by Coleman et al. [27] in Figure 2 and Figure 3, respectively. While the overprediction of the mean velocity in the core region and the peak of the RMS near the wall are well-known deficiencies of the eddy-viscosity SGS models [28], both the mean and the RMS of temperature showed favorable agreement with those of the DNS by Coleman et al. [27]. All the results show more accurate results on the fine grid () compared with those on the coarse grid ().
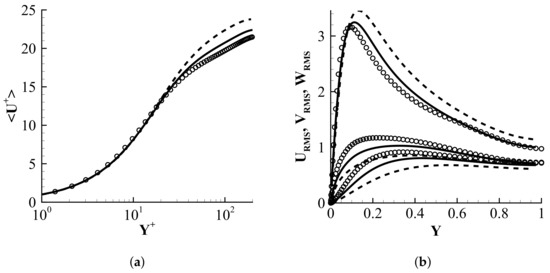
Figure 2.
(a) Mean velocity profiles in wall units and (b) RMS velocity profiles in wall coordinates. ◯, DNS of Coleman et al. [27];  , LES with cells;
, LES with cells;  , LES with cells.
, LES with cells.
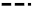 , LES with cells;
, LES with cells;  , LES with cells.
, LES with cells.
Figure 3.
(a) Mean temperature profiles in wall units and (b) RMS temperature profiles in wall coordinates. Notations are the same as those in Figure 2.
4. Simultaneous Approximation Term
4.1. SBP–SAT Approach
The SBP–SAT approach is first briefly introduced. A one-dimensional linear advection equation for a scalar variable with a positive unit advection speed is given by
on domain with an initial condition and a boundary condition . By multiplying to Equation (35) and applying integration by parts, one obtains
where . Equation (36) suggests that remains bounded for .
Next, consider a uniform grid with N nodes indexed from 1 to N for . For , can be approximated by using a second-order central difference method as where ,
P is a diagonal positive definite matrix that defines a norm such that . Q is a skew-symmetric matrix except at boundaries such that . Then, is called an SBP operator.
If a penalty term, which is called SAT and expressed as , is imposed at , discrete equations for Equation (35) become
where . By multiplying to Equation (38), one obtains
From Equation (40), given that , for . In other words, discretization is stable for long-time integration.
4.2. NSBP–SAT Approach for a Cell-Centered Finite-Volume Method
Usage of the SAT with non-SBP schemes (NSBP–SAT approach) was not reported in the literature, to the best of the authors’ knowledge, presumably because SAT is coupled with the SBP for provable time stability, and partially due to successful applications of the CBC to compressible Navier–Stokes equations.
While both FDMs and nodal FVMs have data nodes at boundaries where the SAT can be imposed, the cell-centered FVM does not have data nodes where variables are advanced in time. Regarding this issue, Nordström and Björck [9] introduced data nodes at boundaries to prove time stability for the cell-centered FVM.
In the present work, the SAT is imposed on the reconstructed variables at boundaries using extrapolation. It is subsequently shown for numerical tests that the NSBP–SAT approach leads to comparable non-reflecting performance at outlets to that of the SBP–SAT approach by Shoeybi et al. [8].
While cell-volume-averaged variables are stored at cell centers for the cell-centered FVM, variable distribution within a cell can be reconstructed using gradients. For example, for the scalar variables , , and shown in Figure 4, distributions of within cells can be reconstructed piecewise constantly (Figure 4a) or piecewise polynomially (Figure 4b). If an expression of the SAT at the boundary face b is given as , it is equivalent to assume a piecewise constant profile of for the cell B and impose an SAT at the boundary face b. For a more accurate representation of variables at the boundary, the piecewise polynomial reconstruction used for Equation (28) was employed. As variables outside boundaries are not available, linear extrapolations from the variables interior to the boundaries are used to calculate gradients required for the reconstruction. As a result, an SAT given as is used to drive the face-reconstructed variable at boundary b to boundary data given as .
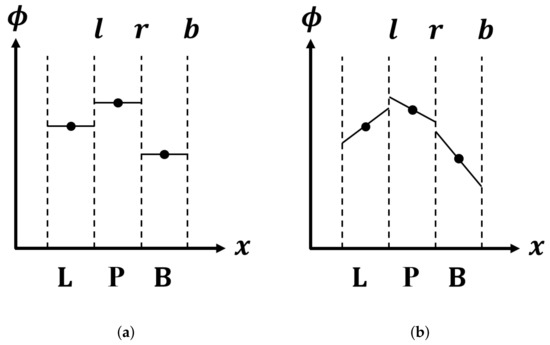
Figure 4.
(a) Piecewise constant profile and (b) piecewise linear profile for reconstructed distributions of a scalar variable within cells. L, P, and B denote cells. l and r denote internal faces between cells while b is a boundary face.
For a two-dimensional acoustic pulse, low Reynolds number flow around a two-dimensional circular cylinder and LES of flow over a circular cylinder at , it was demonstrated that the NSBP–SAT approach for a cell-centered FVM performs as well as the SBP–SAT reported in Shoeybi et al. [8], while both the present cell-centered FVM method and the node-based FVM method of Shoeybi et al. are formally second-order accurate [8,10].
4.3. Two-Dimensional Acoustic Pulse
To test the non-reflecting capability of the NSBP–SAT approach, a two-dimensional acoustic pulse [29] was simulated using the present cell-centered FVM. A -sized two-dimensional box was uniformly discretized using 64 cells in each direction. The initial field is given as follows:
where , and origin is located at the center of the box for Cartesian coordinates. The amplitude of a Gaussian isentropic pulse A was set to , and was used. While the SAT is applied to all boundaries, reference values are used for the boundary data required for the SAT (, , and ). The simulation was run until , when the acoustic wave entirely left the computational domain.
Figure 5 shows instantaneous contours of at and , while . At , the acoustic pulse exited the domain without a noticeable sign of reflection. At , the acoustic pulse exited the domain and the remaining perturbations were observed. While Shoeybi et al. [8] reported the maximal value of to be about of the initial amplitude of the acoustic pulse at , the NSBP–SAT approach resulted in of the initial amplitude of the acoustic pulse. Therefore, the non-reflecting performance of the NSBP–SAT approach was observed to be comparable to that of the SBP–SAT approach by Shoeybi et al. [8] for a two-dimensional acoustic pulse.
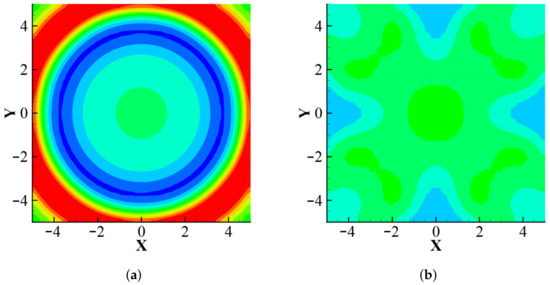
Figure 5.
Two-dimensional acoustic pulse (a) at for and (b) at for . 10 contour levels are shown.
4.4. Low Reynolds Number Flow around a Two-Dimensional Circular Cylinder
To further test the performance of the NSBP–SAT approach, unsteady compressible laminar flow around a two-dimensional circular cylinder was simulated. A Reynolds number of 100 was employed, where is freestream velocity and D is the diameter of the cylinder.
Two grids of and cells in the circumferential and the radial directions were employed for the coarse- and fine-grid cases, respectively, and the coarse grid is shown in Figure 6. The computational domain was a circle of radius , and the first grid spacing in the radial direction was [8]. The no-slip isothermal wall boundary condition was imposed around the cylinder, and the SAT with the freestream boundary data was imposed at the far field.
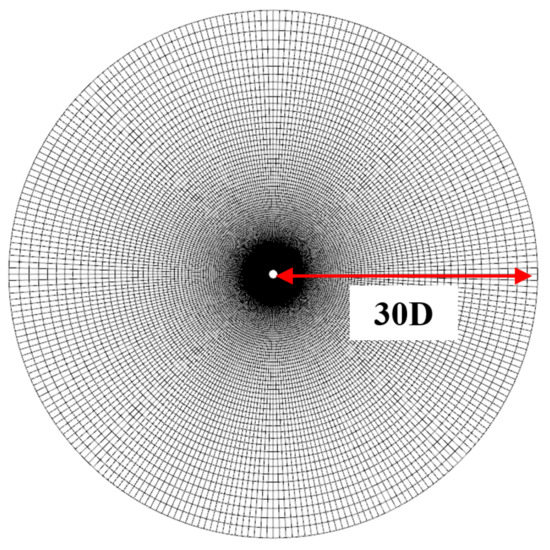
Figure 6.
Grid for flow around two-dimensional circular cylinder.
Figure 7 shows the contour of the instantaneous spanwise vorticity. Oscillatory shear layers are separated behind the cylinder forming Karman vortex streets.
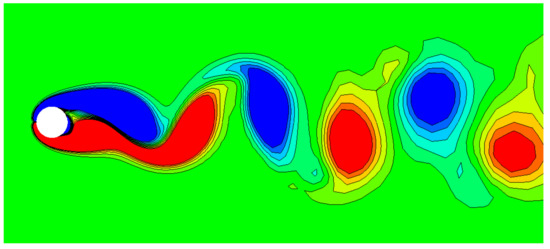
Figure 7.
Contour of instantaneous spanwise vorticity in the near wake of flow over a circular cylinder; 10 contour levels from to are shown.
Table 1 shows the time-averaged drag coefficient , maximal and minimal lift coefficients , and Strouhal number for the present simulations with the coarse and the fine grids; simulations by Svärd and Nordström [30], and Shoeybi et al. [8]; and experimental data obtained by Fey et al. [31]. Svärd and Nordström [30] employed the 5th-order accurate scheme with a fine grid of , and Shoeybi et al. [8] employed a 2nd-order accurate scheme with 260 grids in the circumferential direction. Both Shoeybi et al. [8] and Svärd and Nordström [30] employed the SBP–SAT approach. As results from the coarse grid were as accurate as those reported by Shoeybi et al. [8], and results from the fine grid converged to results by Svärd and Nordström [30], the NSBP–SAT approach performed as well as the SBP–SAT approaches did in terms of non-reflecting performance at the outlet.

Table 1.
Average drag coefficient , minimal and maximal values of lift coefficient , and Strouhal number for flow over a two-dimensional circular cylinder at .
4.5. LES of Flow over a Circular Cylinder at M = 0.4
To assess the non-reflecting performance of the NSBP–SAT approach for compressible turbulent flow, LES of flow over a circular cylinder at and was performed. A circle of radius with spanwise length of was used for the computational domain where the cylinder of a diameter of was located at the center of the radial and circumferential plane. A sponge layer [32] with thickness of was applied at the outer boundary to damp out vortices [33]. A grid of cells in the radial, circumferential, and spanwise directions, respectively, was used. Grid resolution was similar to that of Mani et al. [33] except for the finer grid resolution in the spanwise direction, considering that Mani et al. [33] used a 6th-order compact finite-difference code [34].
For SGS models, C of and of were used for Equations (20) and (21), while in Equation (22) was assumed to be zero due to the low Mach number [35].
Figure 8 shows the contour of the instantaneous spanwise vorticity to indicate the separating laminar shear layers. While coarse spanwise resolution is known to result in transition to turbulence in the separating shear layers closer to the cylinder [36], sufficient grid resolution in the spanwise direction for the present simulation could be confirmed from the elongated separating laminar shear layers.
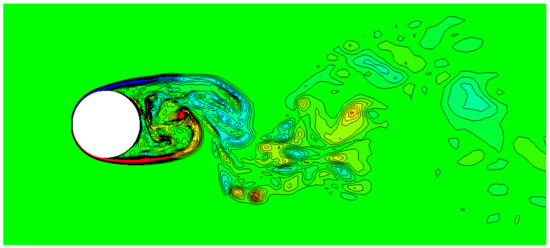
Figure 8.
Contour of instantaneous spanwise vorticity in the near wake of flow over a circular cylinder; 20 contour levels from to 6 are shown.
Table 2 shows a comparison of and calculated from the present LES with LES results by Mani et al. [33]. Although the present simulation used a similar number of grids, except for the finer spanwise resolution, to those of Mani et al. [33], and from the present simulation were quite close to those of Mani et al. [33] despite the lower order of accuracy for the present numerical method.

Table 2.
Average drag coefficient and Strouhal number for flow over a two-dimensional circular cylinder at .
Figure 9 shows density spectra in the wake for both LES results. While good agreement of low-frequency components, including the location of the peak, explains the accurate prediction of the Stouhal number in Table 2, slight overpredictions at high frequencies are attributed to the low order of accuracy of the present solver. Note that the present solver predicted high-frequency components that are qualitatively similar to those predicted by the high-order low-dissipative solver [33]. As Mittal and Moin [1] showed that even 5th-order accurate upwind-biased schemes lead to significant underprediction for high-wavenumber components of the energy spectra compared with the second-order central difference, effects of the SAT are found to be limited near the boundary; therefore, the present numerical method remained low-dissipative for the main flow feature of interest. For reference, temporal and spatial scales for small turbulent eddies in large eddy simulation are implicitly associated [37].
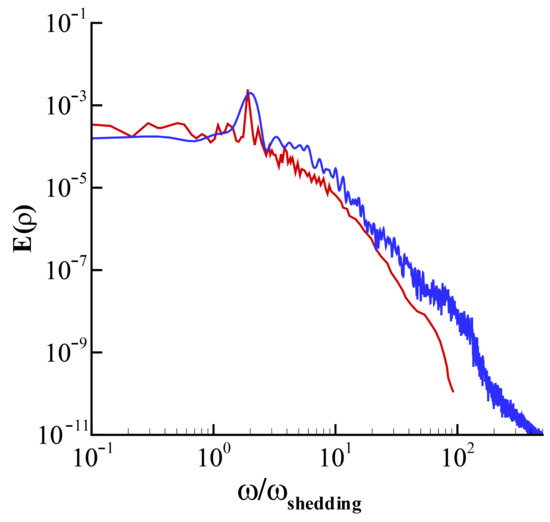
Figure 9.
Density spectra at wake centerline . denotes nondimensionalized density spectra using freestream velocity, freestream density, and D, while nondimensional frequencies are normalized by the Strouhal number.  , the present LES;
, the present LES;  , LES by Mani et al. [33].
, LES by Mani et al. [33].
 , the present LES;
, the present LES;  , LES by Mani et al. [33].
, LES by Mani et al. [33].
5. Comparative Study of the SAT and the CBC
5.1. Description of the Characteristic Boundary Condition
The characteristic boundary condition (CBC) is arguably the most well-known non-reflecting boundary condition for compressible Navier–Stokes equations. By applying one-dimensional characteristic analysis by Thompson [38] to the inviscid parts of the compressible Navier–Stokes equations, Poinsot and Lele [2] obtained
where are the amplitudes of characteristic waves that are defined as follows:
where are the characteristic velocities associated with that are defined as follows:
Because the characteristic velocity for Equation (49) is negative for subsonic flows, while upwind differencing requires data outside the computational domain, numerical calculations of spatial derivatives in Equation (49) involve downwind differencing, which is unstable [2]. To avoid this problem, Poinsot and Lele [2] modeled as follows:
where is a tunable parameter, c is the speed of sound, M is the reference Mach number, and is the target pressure at the outlet.
While the CBC by Poinsot and Lele [2] was limited to one-dimensional outward flows, Yoo et al. [39] proposed adding a transverse term to Equation (57) to account for the multidimensionality of outward flows (i.e., vortices):
where is another tunable parameter, and is defined as follows:
5.2. Characteristic Boundary Condition for a Cell-Centered FVM
Regarding the CBC for a cell-centered FVM, Gross and Fasel [40], and Motheau et al. [41] used spatial gradients modified by characteristic analysis to impose boundary conditions using ghost cells, which is referred to as a gradient-based CBC (GBCBC). For instance, an expression for a density gradient was given by Poinsot and Lele [2]:
where is modified using Equation (58). Using such modified gradients of variables required at outlets, one can calculate all variables required at ghost cells.
Alternatively, one can extrapolate variables to the boundary, and directly integrate Equations (44)–(48) at the boundary, which is referred to as the extrapolated original CBC (EOCBC) [42]. Kang and You [42] showed that the EOCBC performed better than the GBCBC for a convecting two-dimensional vortex and LES of a subsonic turbine cascade when the EOCBC and the GBCBC are implemented in a cell-centered FVM. Therefore, the EOCBC was implemented in the present study.
For the rest of the Section 5, the SAT refers to the SAT in the NSBP–SAT approach.
5.3. Convecting Two-Dimensional Inviscid Vortex
A convecting two-dimensional inviscid vortex is a well-known benchmark test for non-reflecting boundary conditions [2,39,40,41,43,44,45]. A single vortex is superimposed on a uniform flow aligned with the direction. The initial velocity field is given as follows [45]:
where is the strength of the vortex, and is the coordinate for the center of a computational domain. The computational domain is a square of dimension L of that is discretized by uniform cells. Initially, uniform pressure and temperature of 101,300 Pa and 300 K, respectively, were assumed. While the SAT was imposed at boundaries in the streamwise direction, periodic boundary conditions were imposed for the rest of the boundaries.
While a vortex case at a low Mach number (close to 0) presents a greater challenge than that of a case at a high Mach number (close to 1) for the non-reflecting outlet [43,44], a case with ( (m/s)) and [45] was chosen for the present test.
Figure 10 shows the exact solution, and obtained results using the CBC and the SAT from the top to the bottom row, respectively. For each case, streamwise velocity isocontours with normalized pressure field at ,, and are shown, where , , and is given as follows:
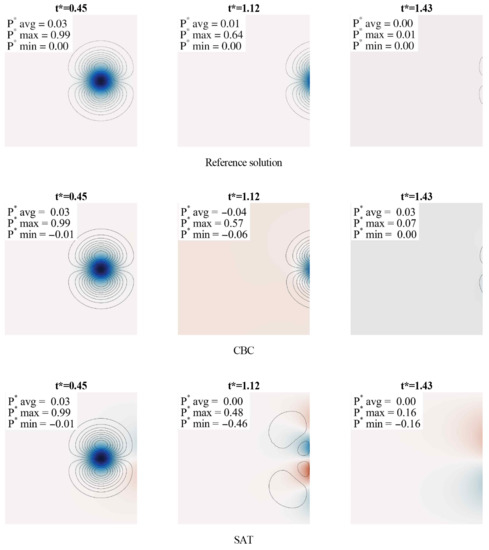
Figure 10.
Simulation results for two-dimensional vortex case using SAT and CBC compared with reference solutions. (top row) Reference solutions, (middle row) obtained results by using CBC, and (bottom row) obtained results by using SAT for three time instants.
Compared with the reference solution, the CBC allowed for the vortex to pass the outlet with small distortion, which was confirmed by the similar minimal and maximal pressure values at and , respectively, along with vortex structures shown by the streamwise velocity isocontours.
The SAT, on the other hand, seemed to destroy the vortex at the outlet, along with significant deviations of the streamwise velocity and the pressure fields from those of the reference solution. However, at and , spatially averaged pressure was maintained at , which is the target pressure imposed by the SAT. Results obtained using the CBC showed slightly larger deviations of from the reference value.
These observations can be understood from the difference between the CBC and the SAT. While the CBC utilizes linear characteristic analysis to model the local incoming characteristic wave, the SAT utilizes a linear characteristic analysis to impose a given boundary dataset, which is usually given to be either reference values or averaged values at the outlet [4]. In other words, while the CBC attempts to preserve flow structures at outlets by modeling the incoming wave, the SAT ignores such details and enforces variables at outlets to become closer to what is prescribed as boundary values.
The observation that the SAT slightly better keeps the spatially averaged pressure field close to the target pressure is encouraging as the accurate imposition of the mean pressure at the outlet is a particular interest for turbomachinery and aerodynamic applications. For example, while the performance of a compressor is often investigated through a thermodynamic-efficiency versus mass-flow rate graph for a multiple of operation conditions [46] obtained from a Reynolds-averaged Navier–Stokes technique [47], the mean mass-flow rate is determined by the mean pressure ratio at the inlet and the outlet [46]. Because LES is often performed at a specific operation condition due to computational cost [47], keeping the mean pressure at the outlet as close to a prescribed value as possible is desirable to simulate a certain operation condition. Time-averaged drag and lift coefficients are also often the primary interests for aerodynamic applications such as an airfoil [48] where the accurate imposition of the mean pressure is closely related to the accurate calculation of the drag and the lift.
The CBC, on the other hand, produces a more accurate flow field near the boundary along with more accurate pressure fluctuations from Figure 10. This is beneficial for flow simulations in which an accurate description of unsteady flow physics is more important than mean quantities such as the drag and the lift.
Another interesting aspect for the NSBP–SAT approach is that, unlike the SBP–SAT approach, which guarantees linear time stability, the NSBP–SAT approach does not allow for such provable stability, but it was found to be stable for the vortex test.
Last, the dissipative characteristic of the SAT observed in Figure 10 does not necessarily mean that it renders the present numerical method dissipative for the entire flow field if the outlet is sufficiently far from the flow feature of interest. For instance, the density spectrum shown in Figure 9 shows that the internal field was not noticeably affected by the SAT, as high-frequency components are qualitatively well-captured.
5.4. LES of Flow through the VKI Subsonic Turbine Cascade
To further test the NSBP–SAT approach, subsonic flow over a VKI turbine cascade at a Reynolds number of based on chord length was simulated by employing the SAT at the outlet. The LES result with the SAT was compared with the LES result obtained using the CBC and the experimental data by [49]. The VKI turbine cascade was also used by Granet et al. [45] to assess the non-reflecting capabilities of several variants of CBCs.
A blade with a chord length C of 140 mm was located from the inlet and the outlet by and , respectively. The three-dimensional domain was discretized by hexahedral cells in total, and the mesh is shown in Figure 11. The thickness of the domain in the spanwise direction was , for which 64 cells were used. While synthetic turbulence [50] is added to the uniform incoming flow at the Mach number of , uniform thermodynamic variables were assumed at the inlet. Either the CBC or the SAT was imposed at the outlet. Periodic conditions were applied to the rest of the boundaries. Statistics were collected for , where is bulk streamwise velocity. For further details regarding the geometry of the cascade, refer to Sieverding et al. [49].
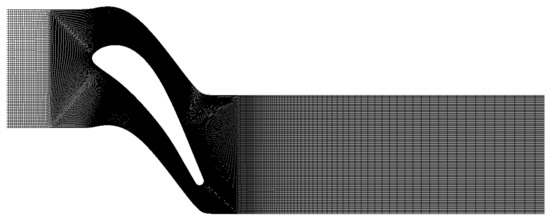
Figure 11.
Grid for simulating VKI turbine cascade.
The isentropic Mach number is defined as follows:
where is the total pressure given at the inlet and denotes pressure along the wall of the cascade.
For SGS models, C of and of were used for Equations (20) and (21), while in Equation (22) was assumed to be zero due to a low Mach number [35].
The isentropic Mach number distribution along the cascade, which is averaged in time, and the spanwise direction for simulations using the CBC and the SAT are shown in Figure 12. While both the SAT and the CBC produced reasonably accurate results, the SAT performed as well as the CBC did as a non-reflecting boundary condition. At the peak of the isentropic Mach number, the SAT result even showed slightly improved performance, which may have been due to the capability of the SAT to keep the time and spatially averaged pressure field closer to the target pressure, which was also observed in the two-dimensional inviscid vortex case.
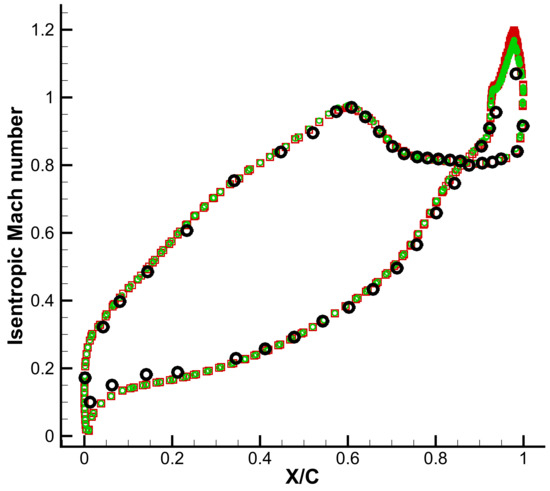
Figure 12.
Time and spanwise-averaged isentropic Mach number distribution along blade. Black circle, experimental data of Sieverding et al. [49]; red squares, obtained results using CBC; green circles, obtained results using SAT.
6. Concluding Remarks
A cell-centered finite-volume method for compressible turbulent flow was developed by combining a non-SBP low-dissipative discretization method and an SAT based on extrapolation, leading to an NSBP–SAT approach. Although the NSBP–SAT approach does not lead to provable time stability, it showed comparable non-reflecting performance to that of the SBP–SAT approach reported in the literature for a two-dimensional acoustic pulse, flow around a two-dimensional circular cylinder at a low Reynolds number, and LES of compressible flow over a circular cylinder at a Mach number of . The CBC was also implemented in the present finite-volume method and compared with the SAT in the NSBP–SAT approach against a convecting two-dimensional inviscid vortex and a subsonic turbine cascade in terms of non-reflecting performance. The SAT maintained the mean pressure field near the outlet slightly closer to the prescribed value than the CBC did, rendering the SAT slightly more beneficial for turbomachinery where accurate mean pressure imposition at the outlet is important for simulating a certain operation condition and airfoils where time-averaged drag and lift are the primary interests. The CBC, on the other hand, better preserved flow structures, leading to more accurate predictions of pressure fluctuations near the outlet. This is attractive for flow simulations where accurate descriptions of unsteady flow features are more important than accurate predictions of mean quantities are, such as the drag and the lift.
Author Contributions
Conceptualization, M.K. and D.Y.; Funding acquisition, D.Y.; Investigation, M.K.; Methodology, M.K.; Software, M.K.; Supervision, D.Y.; Validation, M.K.; Visualization, M.K.; Writing–original draft, M.K.; Writing–review–editing, D.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Korea Institute of Energy Technology Evaluation and Planning (KETEP), the Ministry of Trade, Industry and Energy (MOTIE) of the Republic of Korea (no. 20193020020160), and the National Research Foundation of Korea (NRF) under grant no. NRF-2019K1A3A1A74107685.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CBC | Characteristic boundary condition |
| DNS | Direct numerical simulation |
| ENO | Essentially non-oscillatory |
| EOCBC | Extrapolated original characteristic boundary condition |
| FDM | Finite-difference method |
| FVM | Finite-volume method |
| GBCBC | Gradient-based characteristic boundary condition |
| HLLC | Harten–Lax-van Leer–Contact |
| LES | Large eddy simulation |
| RMS | Root mean square |
| SAT | Simultaneous approximation term |
| SBP | Summation by parts |
| SGS | Subgrid scale |
| VKI | von Karman Institute for Fluid Dynamics |
References
- Mittal, R.; Moin, P. Suitability of upwind-biased finite difference schemes for large-eddy simulation of turbulent flows. AIAA J. 1997, 35, 1415–1417. [Google Scholar] [CrossRef]
- Poinsot, T.J.A.; Lele, S.K. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Carpenter, M.H.; Gottlieb, D.; Abarbanel, S. Time-stable boundary conditions for finite-difference schemes solving hyperbolic systems: Methodology and application to high-order compact schemes. J. Comput. Phys. 1994, 111, 220–236. [Google Scholar] [CrossRef]
- Svärd, M.; Carpenter, M.H.; Nordström, J. A stable high-order finite difference scheme for the compressible Navier–Stokes equations, far-field boundary conditions. J. Comput. Phys. 2007, 225, 1020–1038. [Google Scholar] [CrossRef]
- Svärd, M.; Nordström, J. Review of summation-by-parts schemes for initial–boundary-value problems. J. Comput. Phys. 2014, 268, 17–38. [Google Scholar] [CrossRef]
- Fernández, D.C.D.R.; Hicken, J.E.; Zingg, D.W. Review of summation-by-parts operators with simultaneous approximation terms for the numerical solution of partial differential equations. Comput. Fluids 2014, 95, 171–196. [Google Scholar] [CrossRef]
- Nordström, J.; Forsberg, K.; Adamsson, C.; Eliasson, P. Finite volume methods, unstructured meshes and strict stability for hyperbolic problems. Appl. Numer. Math. 2003, 45, 453–473. [Google Scholar] [CrossRef]
- Shoeybi, M.; Svärd, M.; Ham, F.E.; Moin, P. An adaptive implicit–explicit scheme for the DNS and LES of compressible flows on unstructured grids. J. Comput. Phys. 2010, 229, 5944–5965. [Google Scholar] [CrossRef]
- Nordström, J.; Björck, M. Finite volume approximations and strict stability for hyperbolic problems. Appl. Numer. Math. 2001, 38, 237–255. [Google Scholar] [CrossRef]
- Khalighi, Y.; Ham, F.; Nichols, J.; Lele, S.; Moin, P. Unstructured large eddy simulation for prediction of noise issued from turbulent jets in various configurations. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, OR, USA, 5 June–8 June 2011. AIAA 2011-2886. [Google Scholar]
- Peterson, D.M. Simulations of Injection, Mixing, and Combustion in Supersonic Flow Using a Hybrid RANS/LES Approach. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2011. [Google Scholar]
- Ma, P.C.; Lv, Y.; Ihme, M. An entropy-stable hybrid scheme for simulations of transcritical real-fluid flows. J. Comput. Phys. 2017, 340, 330–357. [Google Scholar] [CrossRef]
- Toro, E.F.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Garnier, E.; Adams, N.; Sagaut, P. Large Eddy Simulation for Compressible Flows; Springer Science & Business Media: Dordrecht, The Netherlands, 2009; pp. 6–8. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2012; pp. 344–357. [Google Scholar]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Okong’o, N.A.; Bellan, J. Consistent large-eddy simulation of a temporal mixing layer laden with evaporating drops. Part 1. Direct numerical simulation, formulation and a priori analysis. J. Fluid Mech. 2004, 499, 1–47. [Google Scholar] [CrossRef]
- Yoshizawa, A. Statistical theory for compressible turbulent shear flows, with the application to subgrid modeling. Phys. Fluids 1986, 29, 2152–2164. [Google Scholar] [CrossRef]
- Vreman, A.W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Tucker, P.G. Novel MILES computations for jet flows and noise. Int. J. Heat Fluid Flow 2004, 25, 625–635. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. Towards the prediction of noise from jet engines. Int. J. Heat Fluid Flow 2003, 24, 551–561. [Google Scholar] [CrossRef]
- Xia, H.; Tucker, P.G.; Eastwood, S. Large-eddy simulations of chevron jet flows with noise predictions. Int. J. Heat Fluid Flow 2009, 30, 1067–1079. [Google Scholar] [CrossRef]
- Le, H.; Moin, P. An improvement of fractional step methods for the incompressible Navier-Stokes equations. J. Comput. Phys. 1991, 92, 369–379. [Google Scholar] [CrossRef]
- Lenormand, E.; Sagaut, P.; Phuoc, L.T.; Comte, P. Subgrid-scale models for large-eddy simulations of compressible wall bounded flows. AIAA J. 2000, 38, 1340–1350. [Google Scholar] [CrossRef]
- Moin, P.; Squires, K.; Cabot, W.; Lee, S. A dynamic subgrid-scale model for compressible turbulence and scalar transport. Phys. Fluids 1991, 3, 2746–2757. [Google Scholar] [CrossRef]
- Coleman, G.N.; Kim, J.; Moser, R.D. A numerical study of turbulent supersonic isothermal-wall channel flow. J. Fluid Mech. 1995, 305, 159–184. [Google Scholar] [CrossRef]
- Silvis, M.H.; Remmerswaal, R.A.; Verstappen, R. Physical consistency of subgrid-scale models for large-eddy simulation of incompressible turbulent flows. Phys. Fluids 2017, 29, 015105. [Google Scholar] [CrossRef]
- Shoeybi, M. A Hybrid Implicit-Explicit Method for the LES of Compressible Flows on Unstructured Grids. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2010. [Google Scholar]
- Svärd, M.; Nordström, J. A stable high-order finite difference scheme for the compressible Navier–Stokes equations: No-slip wall boundary conditions. J. Comput. Phys. 2008, 227, 4805–4824. [Google Scholar] [CrossRef]
- Fey, U.; König, M.; Eckelmann, H. A new Strouhal–Reynolds-number relationship for the circular cylinder in the range 47 < Re < 2 × 105. Phys. Fluids 1998, 10, 1547–1549. [Google Scholar]
- Bodony, D.J. Analysis of sponge zones for computational fluid mechanics. J. Comput. Phys. 2006, 212, 681–702. [Google Scholar] [CrossRef]
- Mani, A.; Moin, P.; Wang, M. Computational study of optical distortions by separated shear layers and turbulent wakes. J. Fluid Mech. 2009, 625, 273–298. [Google Scholar] [CrossRef]
- Nagarajan, S.; Lele, S.K.; Ferziger, J.H. A robust high-order compact method for large eddy simulation. J. Comput. Phys. 2003, 191, 392–419. [Google Scholar] [CrossRef]
- Sayadi, T.; Moin, P. Large eddy simulation of controlled transition to turbulence. Phys. Fluids 2012, 24, 114103. [Google Scholar] [CrossRef]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at ReD = 3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: Berlin, Germany, 2006; p. 19. [Google Scholar]
- Thompson, K.W. Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 1987, 68, 1–24. [Google Scholar] [CrossRef]
- Yoo, C.S.; Wang, Y.; Trouvé, A.; Im, H.G. Characteristic boundary conditions for direct simulations of turbulent counterflow flames. Combust. Theory Model. 2005, 9, 617–646. [Google Scholar] [CrossRef]
- Gross, A.; Fasel, H.F. Characteristic ghost cell boundary condition. AIAA J. 2007, 45, 302–306. [Google Scholar] [CrossRef]
- Motheau, E.; Almgren, A.; Bell, J.B. Navier–Stokes characteristic boundary conditions using ghost cells. AIAA J. 2017, 55, 3399–3408. [Google Scholar] [CrossRef]
- Kang, M.; You, D. Study of a non-reflecting characteristic boundary condition for compressible flow simulation using a cell-centered finite-volume method. J. Comput. Fluid. Eng. 2020, 25, 123–134. [Google Scholar] [CrossRef]
- Prosser, R. Improved boundary conditions for the direct numerical simulation of turbulent subsonic flows. I. Inviscid flows. J. Comput. Phys. 2005, 207, 736–768. [Google Scholar] [CrossRef]
- Lodato, G.; Domingo, P.; Vervisch, L. Three-dimensional boundary conditions for direct and large-eddy simulation of compressible viscous flows. J. Comput. Phys. 2008, 227, 5105–5143. [Google Scholar] [CrossRef]
- Granet, V.; Vermorel, O.; Léonard, T.; Gicquel, L.; Poinsot, T. Comparison of nonreflecting outlet boundary conditions for compressible solvers on unstructured grids. AIAA J. 2010, 48, 2348–2364. [Google Scholar] [CrossRef]
- Dixon, S.L.; Hall, C. Fluid Mechanics and Thermodynamics of Turbomachinery; Butterworth-Heinemann: Oxford, UK, 2013; pp. 22, 27. [Google Scholar]
- Hah, C. Large eddy simulation of transonic flow field in NASA rotor 37. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Eppler, R. Airfoil Design and Data; Springer Science & Business Media: Berlin, Germany, 2012; pp. 81, 140. [Google Scholar]
- Sieverding, C.H.; Richard, H.; Desse, J.M. Turbine blade trailing edge flow characteristics at high subsonic outlet Mach number. J. Turbomach. 2003, 125, 298–309. [Google Scholar] [CrossRef]
- Magagnato, F.; Pritz, B.; Gabi, M. Generation of inflow conditions for large-eddy simulation of compressible flows. In Proceedings of the 8th International Symposium on Experimental and Computational Aerothermodynamics of Internal Flows, Lyon, France, 2 July–6 July 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).