Abstract
Rieck and Nedelman (1991) introduced the sinh-normal distribution. This model was built as a transformation of a N(0,1) distribution. In this paper, a generalization based on a flexible skew normal distribution is introduced. In this way, a more general model is obtained that can describe a range of asymmetric, unimodal and bimodal situations. The paper is divided into two parts. First, the properties of this new model, called flexible sinh-normal distribution, are obtained. In the second part, the flexible sinh-normal distribution is related to flexible Birnbaum–Saunders, introduced by Martínez-Flórez et al. (2019), to propose a log-linear model for lifetime data. Applications to real datasets are included to illustrate our findings.
1. Introduction
In this paper, a generalization of the sinh-normal distribution introduced by Rieck and Nedelman [1] is proposed. Recall that the sinh-normal model is defined as a transformation, , of a standard normal distribution
Rieck and Nedelman [1] showed that the probability density function (pdf) of Y is symmetric and can be unimodal or bimodal. The most relevant application of (1) is that the sinh-normal distribution can be used to propose a log-linear model for lifetime data distributed as a Birnbaum–Saunders (see [1] for details). This point is of crucial importance since the Birnbaum–Saunders distribution is used in a variety of situations, such as to model lifetime, economics and environmental data. In these applications, departures of the BS model are often found. In recent years, some improvements have been introduced to deal with this problem. In this sense, we highlight the flexible Birnbaum–Saunders model, proposed by Matínez-Flórez et al. [2], where two parameters, , , are added to the usual Birnbaum–Saunders model, in such a way that controls asymmetry (skewness) and is a shape parameter related to unimodality/bimodality of our proposal.
Throughout this paper, the next points are addressed.
First, details about the precedents, in which our proposal is based on, are given in Section 2.
Second, the flexible sinh-normal distribution is defined as result of applying (1) to Z distributed as a flexible skew-normal distribution, with and . Recall that the model was introduced by Gómez et al. [3], as a generalization of Azzalini skew-normal model [4], and it can deal with unimodal and bimodal situations. The properties of the flexible sinh-normal distribution are given in Section 3. These are explicit expressions for the pdf and cumulative distribution function (cdf), shape and modes of the distribution, location and scale changes, approximations, moments and quantiles, among others. All of them are based on the fact that the flexible sinh-normal is obtained as a given function of . The obtained properties are compared to those in the Rieck and Nedelman model. In addition, we discuss in which sense our proposal is more general than others previously introduced in literature. The relationship between the flexible sinh-normal distribution and the flexible Birnbaum–Saunders via the exponential (or neperian logarithm), which allows us to build a regression model for lifetime data, is also proven there. Section 4 is devoted to maximum likelihood estimation for the parameters in the flexible sinh-normal distribution.
Third, the flexible Log-linear Birnbaum–Saunders regression model is studied in Section 5. This can be used for non-negative lifetime variables following the flexible Birnbaum–Saunders model given in [2]. The model is built, particular cases of interest are cited, scores and maximum likelihood equations are given.
Applications to real datasets are included in Section 6. In Section 6.1, a positively skewed environmental dataset is considered. There, it is proven that the flexible sinh-normal model provides a better fit than other precedent skew models. In Section 6.2, a symmetric bimodal dataset is considered. Only a few models in the literature exhibit both properties. They are considered along with a mixture of normal distributions. It is shown that the flexible sinh-normal submodel with skewness parameter equal to zero provides a better fit than the other ones. Section 6.3 deals with failure time data in a fatigue test, where the values of stress are considered as known covariate. It is shown that the flexible log-linear Birnbaum–Saunders provides a superior fit to the log-Birnbaum–Saunders [1] and the log-skew-Birnbaum–Saunders model. A simulation study is presented in Section 7. A final discussion is given as Section 8.
2. Materials and Methods
For completeness, details about the most relevant precedents in which our proposal is based are introduced next.
- Flexible skew-normal distribution.
The flexible skew-normal (FSN) model was obtained and studied in detail by [5]. They proved that the FSN model can be bimodal for certain values of A random variable (rv) Z follows a FSN distribution, if its pdf is given by
where and are the pdf and cdf of the distribution, respectively, and
Particular cases of interest in the flexible skew-normal are the following:
- Sinh-normal or log-Birnbaum–Saunders distribution.
Rieck and Nedelman [1] developed the sinh-normal (SHN) distribution, which is given as the following transformation of a standard normal distribution
is a shape parameter, is a location parameter and is a scale parameter. (3) is denoted as .
Proposition 1.
(Properties of sinh-normal distribution). Let . Then,
- 1.
- Y is symmetric about the location parameter ξ.
- 2.
- The pdf of Y is unimodal for and bimodal for .
- 3.
- The mean and variance of Y are and , where is the variance when the scale parameter is equal to one (). There is no closed-expression for , but Rieck and Nedelman [1] provided asymptotic approximations for small and large values of γ.
- 4.
- Let . Then, converges in law to a distribution as .
The next lemma considers the particular case of a sinh-normal distribution in which the scale parameter is equal to 2, . This model is related to the Birnbaum–Saunders (BS) distribution. This result is the basis of the use of this distribution as a regression model, as shown in Section 5.
Lemma 1.
- 1.
- If, then
- 2.
- Reciprocally, if, thenfollows a sinh-normal distribution with shape parameter α, location parameterand scale parameter, that is.
Proof.
It can be seen in [1] (Theorem 1.1). □
Due to the result given in Lemma 1, the sinh-normal distribution is also named log-Birnbaum–Saunders distribution.
3. Results
- Flexible sinh-normal distribution.
This model is obtained by applying the transformation introduced in (3) to . The new model is called the flexible sinh-normal (FSHN) distribution. It is denoted as . By applying the change of variable formula, the pdf of Y, , is
where denotes the pdf of given in (2), and are
Explicitly, (4) can be written as
with .
The following are particular cases of interest in the model:
- -
- If , then the FSHN model reduces to the skew sinh-normal distribution studied by Leiva et al. [7].
- -
- If , then a symmetric model denoted by is obtained, which allows us to model symmetric bimodal data.
- -
- If , then the FSHN model reduces to the sinh-normal distribution introduced by Rieck and Nedelman [1].
Next, some results dealing with the inverse transformation to that introduced in (3) are given.
Proposition 2.
Let . Then,
Proof.
It is obtained by considering and applying the inverse transformation technique to
□
The following are particular cases of interest in Proposition 2:
- If , then follows the model studied by Castillo et al. [8].
- If , then .
- If , then .
Next, an explicit expression for the cumulative distribution function (cdf) of a FSHN distribution is given.
Theorem 1.
Let . Then, the cdf of Y is
where is defined in (5), denotes the cdf of a bivariate normal distribution, with mean vector and covariance matrix
Proof.
Since
Taking into account that is a monotonically increasing function of x, we have the following relationship between the cdf’s de Y and Z:
with .
By applying the expression for the cdf of given in [2] we have that, for , or, equivalently, for
and for , or, equivalently, for
where denotes the cdf of a bivariate normal distribution, with mean vector and covariance matrix given in (8). Thus, the proposed result holds. □
Next, some particular cases of interest for the cdf in the FSHN model are discussed.
Corollary 1.
Let.
- 1.
- If, then the cdf of Y reduces to
- 2.
- If, then the cdf of Y reduces tofor
Proof.
- If , then , where is given in (8). Recall that, in the bivariate normal distribution, uncorrelation implies independence, therefore
- If , then we have the cdf of the skew-sinh-normal distribution.
□
The result in Corollary 1 for corresponds to the model studied by Olmos et al. [9], whereas the result for is a particular case of models studied by Vilca-Labra and Leiva-Sanchez [10].
- Shape of .
Proposition 3.
Let The pdf given in (16) can be bimodal. The modes would be given as the solution of the following non-linear equations
- 1.
- solution of
- 2.
- solution ofwithand.
Proof.
Proposition 4.
Let with . Then, the pdf of Y is symmetrical with respect to ξ and can be bimodal for
Proof.
Symmetry follows from the fact that and are even functions. Bimodality for follows from Proposition 3. □
Proposition 5.
Let . Then, the pdf of Y is non-differentiable at .
Proof.
This result follows from the fact that, if , then and the non-differentiability of the absolute value function at zero. □
Some illustrative plots for the pdfs in the FSHN model are given in Figure 1, Figure 2 and Figure 3. In Figure 1 and Figure 2, we mainly focus on the study of the shape parameters, and , so in every figure a positive or negative value of is fixed, and a range of possible values is considered for (less and greater than two), since our aim is to compare with the sinh-normal distribution, which is strongly unimodal for and bimodal for [1]. In this way, the effect of and/or can be appreciated. Moreover, positive and negative values of are considered to assess the effect of the skewness parameter. In Figure 3, is fixed and therefore the symmetric submodel is plotted. Additional details are given next for every figure.
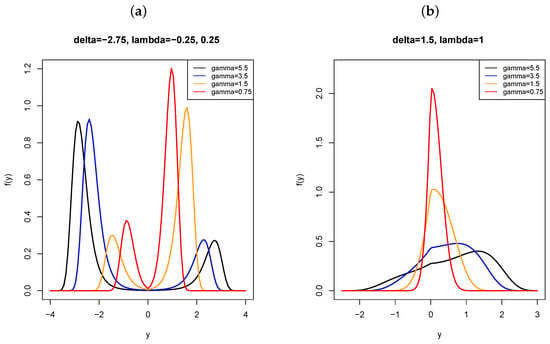
Figure 1.
FSHN pdfs: (a) (5.5, 0, 1, −2.75, −0.25) (black), (3.5, 0, 1, −2.75, −0.25) (blue), (1.5, 0, 1, −2.75, 0.25) (orange) and (0.75, 0, 1, −2.75, 0.25) (red); and (b) (5.5, 0, 1, 1.5, 1) (black), (3.5, 0, 1, 1.5, 1) (blue), (1.5, 0, 1, 1.5, 1) (orange) and (0.75, 0, 1, 1.5, 1) (red).
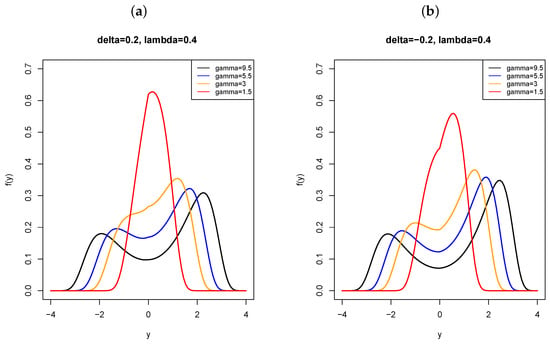
Figure 2.
FSHN pdfs: (a) (9.5, 0, 1, 0.2, 0.4) (black), (5.5, 0, 1, 0.2, 0.4) (blue), (3, 0, 1, 0.2, 0.4) (orange) and (1.5, 0, 1, 0.2, 0.4) (red); and In (b) (9.5, 0, 1, −0.2, 0.4) (black), (5.5, 0, 1, −0.2, 0.4) (blue), (3, 0, 1, −0.2, 0.4) (orange) and (1.5, 0, 1, −0.2, 0.4) (red).
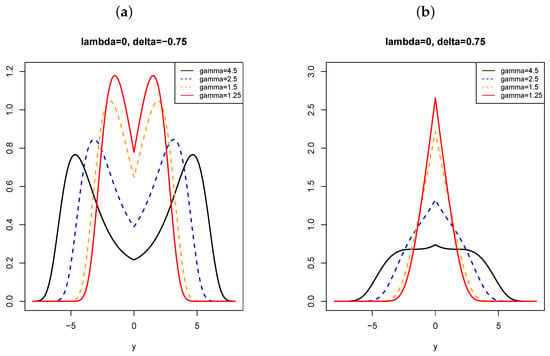
Figure 3.
FSHN pdfs: (a) (4.5, 0, 2.5, −0.75, 0) (black), (2.5, 0, 2.5, −0.75, 0) (blue), (1.5, 0, 2.5, −0.75, 0) (orange) and (1.25, 0, 2.5, −0.75, 0) (red); and (b) (4.5, 0, 2.5, 0.75, 0) (black), (2.5, 0, 2.5, 0.75, 0) (blue), (1.5, 0, 2.5, 0.75, 0) (orange) and (1.25, 0, 2.5, 0.75, 0) (red).
In Figure 1, without loss of generality for our purposes, the location and scale parameters are taken as and . We intend to highlight the effect of on the bimodality of FSHN model. In Figure 1a, small values are considered for the skewness parameter, and , and a clearly negative value of . All pdfs are bimodal. Note that the parameter and even for values of the pdf is bimodal. These plots suggest that a negative value of induces bimodality and the effect of is attenuated. It is also possible to appreciate the effect of the sign of skewness parameter in Figure 1a; note that black and blue plots correspond to negative , whereas orange and red ones correspond to positive . On the other hand, Figure 1b, a positive value of is considered (). We highlight that the distribution is unimodal even for values of .
In Figure 2, a small value of is fixed ( in Figure 2a and in Figure 2b); the plots suggest that, in this case, the bimodality depends on the value of . However, we must also be conscious that, in these plots , for large values of unimodal distributions are nearly always obtained for any values of and .
In Figure 3, the skewness parameter is fixed, therefore symmetric pdfs are always obtained. In Figure 3a, a negative value of is fixed and all plots are bimodal (even for values of the parameter in which the sinh-normal distribution is unimodal). In Figure 3b, is fixed and unimodal symmetric distributions are obtained.
Next, we show that the FSHN model is closed under location and scale changes.
Proposition 6.
Let. Then,
- 1.
- ,.
- 2.
- ,.
- 3.
- .
Proof.
- Let with . The result proposed follows from the fact that .
- Let . Then, .
- Let . Then, . Taking into account that is an even function,and, since is an odd function,and the result proposed is obtained.
□
Corollary 2.
Let . Then,
Next, the limit behavior of FSHN model when approaches to is studied.
Proposition 7.
Let . Then, converges in distribution to the flexible skew-normal distribution as .
Proof.
Let . By applying Proposition 6, . Therefore, its pdf is
Considering that , by L’Hôpital–Bernoulli rule,
Since and are continuous differentiable functions,
which is the pdf of a flexible skew-normal distribution. That is, the result proposed. □
Remark 1.
Given with γ close to zero, Proposition 7 allows us to approximate the distribution of Y, properly normalized, by a flexible skew-normal distribution. In addition, note that this result is analogous to the property of the sinh-normal distribution given in Proposition 1.
Next, it is shown that the quantile of Y can be obtained from the quantile of .
Theorem 2.
Let . Then, the pth quantile of Y, , with is given by
where denotes the pth quantile of
Proof.
It follows from (3) and the fact that the arcsinh function is monotonically increasing. □
- Submodel with .
For , can be obtained from the quantiles of the distribution.
Corollary 3.
If , then
As it can be seen in [1], recall that the log-Birnbaum–Saunders regression model is based on the relationship between the Birnbaum–Saunders and the sinh-normal distribution. In our proposal, a regression model is introduced next that is based on the relationship between the flexible Birnbaum–Saunders, studied in [2] and the FSHN distribution introduced in this paper. First, we recall the expression of the pdf for the flexible Birnbaum–Saunders.
- Flexible Birnbaum–Saunders.
Based on the flexible skew-normal model defined in (2), Martínez-Flórez et al. [2] proposed the flexible Birnbaum–Saunders (FBS) distribution, whose pdf is given by
with
, , , and and the pdf and cdf of a , respectively.
In (16), and are shape parameters. We highlight that is a parameter that controls asymmetry (or skewness) and is a shape parameter related to bimodality of FBS model. Specifically, it can be seen in [2] that (16) can be bimodal for some combinations of and parameters.
The following are particular cases of interest in (16):
- -
- If , then the model introduced by Olmos et al. [9] is obtained.
- -
- If , then the skew-Birnbaum–Saunders is obtained.
- -
- If , then the Birnbaum–Saunders is obtained.
Theorem 3.
Let . Then, .
Proof.
This result is obtained by applying the transformation technique for random variables and taking into account (16). □
In practice, it is usual to consider non-negative rv’s following a . Then, its neperian logarithm will follow a FSHN distribution, as established in next corollary.
Corollary 4.
Let . Then,
If T depends on a known set of covariates then it is of interest to build a generalized linear model related to T [11]. This issue is studied in Section 5.
Moments
Let . Recall that
Thus, the moments of Y can be expressed in terms of the moments of with respect to . To simplify the notation, let us introduce
In particular, we have that
4. Inference Based on Maximum Likelihood Estimation
Let . Let us denote the vector of unknown parameters by . Given a random sample of , let us consider the log-likelihood function for the parameter vector , which is given
where c denotes a constant independent of and
To maximize in , consider the score functions, denoted as , , , and , and given as the first derivatives of with respect to , , , and , respectively. Maximum likelihood estimates for the parameters are given as the solutions to , , , and , which are equivalent to the following equations
where denotes the function and
Iterative methods must be used to solve these equations [12]. Details about the previous maximum likelihood estimators (MLEs) are postponed to Section 5, where the MLEs for the parameters in the regression model based on the FSHN distribution are studied.
5. The Flexible Log-Birnbaum–Saunders Regression Model
In this section the flexible log-Birnbaum–Saunders regression model is introduced. Let be independent positive continuous random variables such as
Let us assume that the distribution of , proposed in (27), depends on a set of known explanatory variables, , satisfying for
- where and is a p-dimensional vector of unknown parameters.
- The shape and skewness parameters in (27) do not involve , that is, , and .
Let us consider . By applying Corollary 4, . Thus, can be written as a linear model
where the error term (Proposition 6 is applied) and are independent. As for the expectation, variance of and covariance of and (), taking into account (19), we have for
Taking
we can write
where the initial vector of unknown parameters has been partitioned into with .
By applying the ordinary least squares approach, an unbiased linear estimator of is
where and
The covariance matrix of is given by
The model previously introduced is named flexible log-Birnbaum–Saunders regression model and is denoted by .
- Particular cases of interest.
- If , then we have the log-Birnbaum–Saunders regression model proposed by Rieck and Nedelman [1], which is based on the sinh-normal distribution [1].
- If , then (28) reduces to the skewed log-Birnbaum–Saunders regression model studied by Lemonte [13], which is based on the skewed sinh-normal distribution introduced in Leiva et al. [7].
- If , then (28) reduces to the submodel flexible log-Birnbaum–Saunders, denoted by , which is based on the distribution introduced in this paper.
Likelihood Equations in the Regression Model
Let us consider the log-likelihood function for the parameter vector , which is given
where c denotes a constant independent of and
To maximize in , consider the score functions, given as the first derivatives of with respect to , (with ), and , respectively. They are denoted as , with , and ,
with .
where denotes the function and
Maximum likelihood estimators for the parameters are given as the solutions to , , , and , which requires numerical techniques.
6. Applications
6.1. Illustration 1
Dataset 1 consists of observations of daily ozone mean concentration in the atmosphere (in ppb ) in New York taken from May to September 1973 [14]. The average concentration of pollutants in the air is of interest in epidemiological studies due to its serious adverse effects on the human health. It is usually assumed that these data are independent, and therefore they do not require a cyclic trend analysis, see for instance the works of Gokhale and Khare [15], Nadarajah [16] and Leiva et al. [7], where this dataset is also studied.
Descriptive summaries. The sample mean, variance, skewness and kurtosis coefficients are: , , and . From these summaries and Figure 4, we can conclude that this dataset is positively (or right) skewed. Thus, sinh-normal, skew sinh-normal, Birnbaum–Saunders, extended Birnbaum–Saunders [7] and FSHN distributions can be considered as models for this dataset. Their performance is compared throughout the Akaike information criterion, and Bayesian information criterion, , where denotes the log-likelihood function evaluated at the MLEs of parameters and k is the number of parameters in the model. From the results in Table 1, the FSHN distribution provides the best fit to these data since its AIC and BIC are the smallest [17,18].
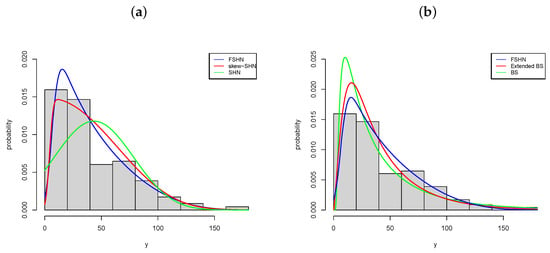
Figure 4.
Estimated pdfs: (a) FSHN (blue), skew-SHN (red) and SHN (green); and (b) FSHN (blue), extended BS (red) and BS (green).

Table 1.
Estimates of parameters and their standard errors in parentheses for sinh-Normal (SHN), skew-SHN, BS, extended BS and FSHN models.
On the other hand, since the sinh-normal, skew sinh-normal and FSHN are nested models, they can be compared by using the likelihood ratio test, [19].
First, let us consider the test
which is equivalent to testing the sinh-normal (SHN) versus a FSHN distribution. The associated likelihood ratio statistic is
which is asymptotically distributed as a chi-square variable with two degrees of freedom (df). After substituting the estimated values of the parameters, we obtain which is greater than the 5% chi-square critical value with 2 df, which is Therefore, the FSHN model is preferred to the SHN model for this dataset.
Second, we compare the FSHN model to the skew sinh-normal (skew-SHN) model. Let us now consider the following likelihood ratio statistic
which is asymptotically distributed as a chi-square variable with , .
After substituting the estimated values, we obtain which is greater than the 5% chi-square critical value with 1 df, which is Therefore, FSHN is preferred to skew-SHN model for this dataset.
Figure 4 presents the histogram and the fitted pdfs. Note that FSHN and extended BS provide a good fit to this dataset.
6.2. Illustration 2
Dataset 2 consists of observations of fetus weight (in grams) before birth obtained by ultrasound technique. Descriptive summaries are given in Table 2. The data are available at http://www.mat.uda.cl/hsalinas/cursos/2011/R/weight.rar (accessed on 17 May 2021). The variables b.weigt (fetal weight in grams) and a.weigt (birth weight in grams) can be found there. We study the b.weight variable.

Table 2.
Descriptive summaries for b.weight variable.
In Table 2, note that the mean and median are similar and the sample asymmetry coefficient is close to zero. Therefore, the distribution is fairly symmetrical. This fact can be seen in the histogram plotted in Figure 5, where we can also appreciate the bimodality of this dataset. Bimodality is due to the difference in weight, at the gestation stage, between males and females. Therefore, a symmetric bimodal model must be considered. In the literature, there are few models which exhibit both properties [20]. We propose the bimodal normal [21], the two-piece skew normal [22], the sinh-normal with and the submodel FSHN with . In addition, we consider a mixture of two normal distributions whose pdf is
with , and ,
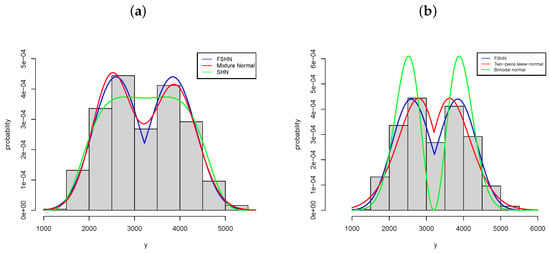
Figure 5.
b.weight histogram and fitted bimodal models: (a) FSHN (blue), mixture normal (red) and SHN (green); and (b) FSHN (blue), two-piece skew normal (red) and bimodal normal (green).
The estimated parameters in these models, along with their standard errors in parentheses, are given in Table 3. In this table, the following abbreviations are used: SHN (sinh-normal), TN (two-piece skew normal [22]), BN (bimodal normal [21]), MN (mixture of two normals given in (35)), (FSHN with ). From AIC and BIC in Table 3, we can conclude that the mixture of two normals and the model provide the best fit to this dataset. However, it is of interest to point out that the use of mixtures is a quite controversial issue in statistics, mainly due to non-identifiability problems (see, e.g., [23]).

Table 3.
Estimates of parameters, (standard errors) in models fitted in Dataset 2.
Since SHN and are nested models, we can test
which is equivalent to compare SHN versus . Taking into account that the Fisher information matrix is non-singular at , we can consider the likelihood ratio statistic
It is obtained that , which is greater than the . Thus, is rejected, leading to the conclusion that the proposed model fits better than the SHN considered in this case.
In Figure 5, the histogram of bebe weights is plotted along with the proposed bimodal models. There, the good fit provided by our proposal can be checked.
6.3. Illustration 3
Dataset 3 consists of 40 independent observations, which correspond to the failure time, T, for hardened steel specimens in a rolling contact fatigue test. The observations were taken at each of four values of contact stress, which is the covariate x in our proposal. This dataset can be seen in the work of Chan et al. [24]. Let and consider the regression model
We fit the log-Birnbaum–Saunders, the log-skew-Birnbaum–Saunders proposed by Lemonte et al. [13] and the log-flexible Birnbaum–Saunders introduced in this paper to this dataset. The estimated parameters along with the AIC and BIC are given in Table 4. According to AIC and BIC, log-flexible Birnbaum–Saunders provides a better fit than the other ones, so this model would be preferred.

Table 4.
MLEs in LBS, LSBS and LFBS models.
7. Simulation
Next, a simulation study is presented to illustrate the performance of our results. Two features are studied: (1) the global performance of MLEs of parameters if the sample size increases; and (2) the effect of varying every shape parameter, , and , on the performance of the rest of estimators under consideration. Both issues are studied in the use of the flexible sinh-normal distribution as a regression model.
7.1. Simulation I
The flexible sinh-normal distribution as a regression model with one covariate is considered, that is
where or, equivalently, independent for . The vector of unknown parameters is .
As sample sizes, we consider , simulations and values of the parameters . As x, covariate values of a distribution are considered. Values of the FSHN were generated from values of the FSN distribution, which were obtained by using the stochastic representation of FSN model given in [5]. The results are listed in Table 5, Table 6 and Table 7. As for measures of performance, the mean of estimates, their standard errors (sd) in parentheses, the relative bias and the square root of the mean squared error (MSE) are given.

Table 5.
Simulations for .

Table 6.
Simulations for , .

Table 7.
Simulations for and .
From the results in Table 5, Table 6 and Table 7, we can conclude that the MLEs are biased; in general, the standard error, relative bias and the squared root of MSE decrease if the sample size n increases. We highlight that, in this simulation, exhibits a good behavior, whereas the greater variability corresponds to .
Simulations were carried out by using the optim function of software R [25] by applying the Nelder–Mead method.
7.2. Simulation II
Next, a sensitivity study about the effect of varying the shape parameters (and the sample size) on the estimates of other parameters is presented.
Summaries varying the parameter are given in Table 8. Similarly, results varying the parameters and are given in Table 9 and Table 10, respectively.

Table 8.
Empirical sd, relative bias and for the model.

Table 9.
Empirical sd, relative bias and for the model.

Table 10.
Empirical sd, relative bias and for the model.
- Comments to Table 8 (varying ).
In this table, we consider , and sample sizes . For and , it can be seen that the relative biases are small. Moreover, we can appreciate that the relative bias, standard error and decrease when the sample size increases, especially for . and exhibit greater variability, but their relative bias, sd and also decrease when the sample size increases. As for , we can point out that this estimator is also well behaved when n increases. Its relative bias for small sample sizes, , is small and the is a moderate value.
- Comments to Table 9 (varying ).
In this table, we consider , and . We can see that, for and , the relative bias is small even for , and the relative bias, sd and decrease when n increases. Again, and exhibit greater variability than the other estimators, but the error measures under consideration are satisfactory. The relative bias, sd and of decrease when n increases, and their values are moderate even for small sample sizes.
- Comments to Table 10 (varying ).
In this case, we consider , and . Again, a similar behavior to the previously explained is obtained.
As final conclusion, we point out that these simulation studies cover a variety of situations as for the shapes of the FSHN distribution (unimodal and bimodal) and suggest that the estimators of the parameters are consistent when the sample size increases [26].
8. Discussion
The BS distribution is an asymmetric model used for survival time data and material lifetime subject to stress as it can be seen in [27]. Due to its practical and theoretical interest, a number of generalizations can be found in literature. We can cite the extensions provided in [28] to the family of elliptical distributions; in [10] based on the elliptical asymmetric distributions; and the extended Birnbaum–Saunders (EBS) distribution introduced in [7].
Other generalizations intend to solve specific deficiencies observed when this model is fitted to a dataset. In this sense, we can cite the epsilon-Birnbaum–Saunders model introduced in [8] to accommodate outliers; the extension based on the slash-elliptical family of distributions given in [3]; and the generalized modified slash Birnbaum–Saunders, which is based on the work in [29] and proposed in [30]. All these extensions are appropriate to fit data with greater or smaller asymmetry (or kurtosis) than that of the usual BS model, but they are not appropriate for fitting bimodal data. This issue is of great interest, as discussed by Olmos et al. [9], Bolfarine et al. [31], Martínez-Flórez et al. [2] and Elal-Olivero et al. [32]. The flexible BS distribution was proposed to model skewness and to fit data with and without bimodality. In this paper, this model is spread out to be used as a regression model in those situations in which regression models based on other generalizations of BS, such as those proposed in [7,13,33,34,35,36,37], do not provide a satisfactory fit.
Author Contributions
Conceptualization, G.M.-F., I.B.-C. and H.W.G.; formal analysis, G.M.-F., I.B.-C. and H.W.G.; investigation, G.M.-F., I.B.-C. and H.W.G.; methodology, G.M.-F., I.B.-C. and H.W.G.; Software, G.M.-F. and I.B.-C.; supervision, H.W.G.; validation, G.M.-F. and I.B.-C.; and visualization, H.W.G. All authors have read and agreed to the published version of the manuscript.
Funding
The research of G. Martínez-Flórez was supported by project: Distribuições de Probabilidade Mutivariadas Assimétricas e Flexíveis, Universidade Federal do Ceará, Fortaleza, Brazil. The research of H. W. Gómez was supported by Grant SEMILLERO UA-2021, Chile.
Data Availability Statement
Acknowledgments
G. Martínez-Flórez acknowledges the support given by Universidad de Córdoba, Montería, Colombia, and Universidade Federal do Ceará, Fortaleza, Brazil.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BS | Birnbaum–Saunders |
| cdf | cumulative distribution function |
| FBS | Flexible Birnbaum-Saunders |
| FSHN | Flexible sinh-normal |
| FSN | Flexible skew Normal |
| probability density function | |
| SHN | Sinh-normal |
References
- Rieck, J.R.; Nedelman, J.R. A log-linear model for the Birnbaum-Saunders distribution. Technometrics 1991, 33, 51–60. [Google Scholar]
- Martínez-Flórez, G.; Barranco-Chamorro, I.; Bolfarine, H.; Gómez, H.W. Flexible Birnbaum-Saunders Distribution. Symmetry 2019, 11, 1305. [Google Scholar] [CrossRef]
- Gómez, H.W.; Olivares-Pacheco, J.F.; Bolfarine, H. An extension of the generalized Birnbaum- Saunders distribution. Stat. Probab. Lett. 2009, 79, 331–338. [Google Scholar] [CrossRef]
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Gómez, H.W.; Elal-Olivero, D.; Salinas, H.S.; Bolfarine, H. Bimodal Extension Based on the Skew-normal Distribution with Application to Pollen Data. Environmetrics 2011, 22, 50–62. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. Censored bimodal symmetric-asymmetric families. Stat. Interface 2018, 11, 237–249. [Google Scholar] [CrossRef]
- Leiva, V.; Vilca-Labra, F.; Balakrishnan, N.; Sanhueza, A. A skewed sinh-normal distribution and its properties and application to air pollution. Commun. Stat. Theory Methods 2010, 39, 426–443. [Google Scholar] [CrossRef]
- Castillo, N.; Gomez, H.W.; Bolfarine, H. Epsilon Birnbaum-Saunders distribution family: Properties and inference. Stat. Pap. 2011, 52, 871–883. [Google Scholar] [CrossRef]
- Olmos, N.M.; Martínez-Flórez, G.; Bolfarine, H. Bimodal Birnbaum-Saunders Distribution with Application to Corrosion Data. Commun. Stat. Theory Methods 2017, 46, 6240–6257. [Google Scholar] [CrossRef]
- Vilca-Labra, F.; Leiva-Sanchez, V. A new fatigue life model based on the family of skew-elliptical distributions. Commun. Stat. Theory Methods 2006, 35, 229–244. [Google Scholar] [CrossRef]
- Calderín Ojeda, E.; Gómez Déniz, E.; Barranco Chamorro, I. Modelling Zero-Inflated Count Data With a Special Case of the Generalised Poisson Distribution. Astin Bull. 2019, 49, 689–707. [Google Scholar] [CrossRef]
- Rivera, P.A.; Barranco-Chamorro, I.; Gallardo, D.I.; Gómez, H.W. Scale mixture of Rayleigh distribution. Mathematics 2020, 8, 1842. [Google Scholar] [CrossRef]
- Lemonte, A. A log-Birnbaum-Saunders regression model with asymmetric errors. Improved statistical inference for the two-parameter Birnbaum-Saunders distribution. J. Stat. Comput. Stat. Simul. 2012, 82, 1775–1787. [Google Scholar] [CrossRef]
- Chambers, J.M.; Cleveland, W.S.; Kleiner, B.; Tukey, P.A. Graphical Methods for Data Analysis; Wadsworth: Belmont, CA, USA, 1983. [Google Scholar]
- Gokhale, S.; Khare, M. Statistical behavior of carbon monoxide from vehicular exhausts in urban environments. Environ. Model. Softw. 2007, 22, 526–535. [Google Scholar] [CrossRef]
- Nadarajah, S. A truncated inverted beta distribution with application to air pollution data. Stoch. Environ. Res. Risk Assess. 2008, 22, 285–289. [Google Scholar] [CrossRef]
- Akaike, H. A new look at statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Vuong, Q. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 1989, 57, 307–333. [Google Scholar] [CrossRef]
- Arnold, B.C.; Gómez, H.W.; Salinas, H.S. On multiple constraint skewed models. Statistics 2009, 43, 279–293. [Google Scholar] [CrossRef]
- Elal-Olivero, D. Alpha-skew-normal distribution. Proyecciones J. Math. 2010, 29, 224–240. [Google Scholar] [CrossRef]
- Kim, H.J. On a class of two-piece skew-normal distribution. Statistic 2005, 39, 537–553. [Google Scholar] [CrossRef]
- Marin, J.-M.; Mengersen, K.; Robert, C. Bayesian modelling and inference on mixtures of distributions. In Handbook of Statistics; Rao, C., Dey, D., Eds.; Springer: New York, NY, USA, 2005; Volume 25, pp. 1–56. [Google Scholar]
- Chan, P.S.; Ng, H.K.T.; Balakrishnan, N.; Zhou, Q. Point and interval estimation for extreme-value regression model under Type-II censoring. Comput. Stat. Data Anal. 2008, 52, 4040–4058. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Barranco Chamorro, I.; Jimenez Gamero, M.D. Asymptotic Results in Partially Non-Regular Log-Exponential Distributions. J. Stat. Comput. Simul. 2012, 82, 445–461. [Google Scholar] [CrossRef]
- Birnbaum, Z.W.; Saunders, S.C. A New Family of Life Distributions. J. Appl. Probab. 1969, 6, 319–327. [Google Scholar] [CrossRef]
- Díaz-García, J.A.; Leiva-Sánchez, V. A new family of life distributions based on the elliptically contoured distributions. J. Stat. Plann. Inference 2005, 128, 445–457. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gómez, H.W. Generalized modified slash distribution with applications. Commun. Stat. Theory Methods 2020, 49, 2025–2048. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gallardo, D.I.; Gómez, H.W. Generalized Modified Slash Birnbaum-Saunders Distribution. Symmetry 2018, 10, 724. [Google Scholar] [CrossRef]
- Bolfarine, H.; Martínez–Flórez, G.; Salinas, H.S. Bimodal symmetric-asymmetric families. Commun. Stat. Theory Methods 2018, 47, 259–276. [Google Scholar] [CrossRef]
- Elal-Olivero, D.; Olivares-Pacheco, J.F.; Venegas, O.; Bolfarine, H.; Gómez, H.W. On Properties of the Bimodal Skew-Normal Distribution and an Application. Mathematics 2020, 8, 703. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. An alpha-power extension for the Birnbaum-Saunders distribution. Statistics 2014, 48, 896–912. [Google Scholar] [CrossRef]
- Santana, L.; Vilca, F.; Leiva, V. Influence analysis in skew-Birnbaum-Saunders regression models and applications. J. Appl. Stat. 2011, 38, 1633–1649. [Google Scholar] [CrossRef]
- Barros, M.; Paula, G.A.; Leiva, V. A new class of survival regression models with heavy-tailed errors: Robustness and diagnostics. Lifetime Data Anal. 2008, 14, 316–332. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. The Log-Linear Birnbaum-Saunders Power Model. Methodol. Comput. Appl. Probab. 2017, 19, 913–933. [Google Scholar] [CrossRef]
- Ortega, E.M.; Bolfarine, H.; Paula, G.A. Influence diagnostics in generalized log-gamma regression models. Comput. Stat. Data Anal. 2003, 42, 165–186. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).