Abstract
The financial catastrophe resulting from the out-of-pocket payments necessary to access and use healthcare systems has been widely studied in the literature. The aim of this work is to predict the impact of the financial catastrophe a household will face as a result of out-of-pocket payments in long-term care in Spain. These predictions were made using machine learning techniques such as LASSO (Least Absolute Shrinkage and Selection Operator) penalized regression and elastic-net, as well as algorithms like k-nearest neighbors (KNN), MARS (Multivariate Adaptive Regression Splines), random forest, boosted trees and SVM (Support Vector Machine). The results reveal that all the classification methods performed well, with the complex models performing better than the simpler ones and showing no evidence of overfitting. Detecting and defining the profiles of individuals and families most likely to suffer from financial catastrophe is crucial in enabling the design of financial policies aimed at protecting vulnerable groups.
1. Introduction
Sustainable Development Goals (SDG) are the goals established by the United Nations to be achieved in the decade 2020–2030. Goal 3 includes the necessity to “ensure healthy lives and promote well-being for all at all ages”, while subgoal 3.8 explicitly states the following: “Achieve universal health coverage, including financial risk protection, access to quality essential health-care services and access to safe, effective, quality and affordable essential medicines and vaccines for all” [1]. One of the indicators used to measure the degree to which this goal has been achieved is indicator 3.8.2, defined as “the proportion of population with large household expenditure on health as a share of total household expenditure or income” [2].
It is well known that a person’s access to healthcare in most countries requires expenditures by their families through fees, co-payment or charges [3] called out-of-pocket (OOP) payments [4]. These OOP can put a great financial burden on families [5,6] and even make it impossible to receive healthcare services due to a lack of financial resources [7].
There are a large number of studies that have used 3.8.2 to analyze the magnitude and extent of a financial catastrophe [8,9] although with different nuances in their calculations [10]. A household is defined as catastrophic when the economic resources used to pay for healthcare exceed a specific percentage of the equivalent household income [11]. These thresholds are standards and can vary depending on the healthcare system, illness, country or moment in time. The thresholds the indicator 3.8.2 uses to make its evaluations are 10% and 25% [2]. The most frequently used thresholds in the literature are 10%, 20%, 30% and 40% [9,12].
A complementary intrinsic analysis of the financial catastrophe measure is the analysis of sociodemographic and health variables of households associated with this condition [8,9]. The econometric methodologies traditionally used to make this analysis are the binary probit and logit models [8], and to a lesser extent, the ordered and multinomial probit and logit models.
Therefore, the main objective of this study is to predict the rate of financial catastrophe in households in Spain as a result of OOP payments in long-term care (LTC) using different statistical techniques and automatic classification algorithms.
The rest of the paper is structured as follows. Section 2 reviews the literature on both the financial catastrophe and the methodologies used to estimate factors associated with financial catastrophes. Section 3 describes the main materials and methods used in the work (i.e., the characteristics of the database for Spain, the variables used and the algorithms applied). Section 4 contains an analysis of the main results obtained and, finally, after the discussion in Section 5, the main conclusions are highlighted in Section 6.
2. Review of the Literature
2.1. Financial Catastrophe Associated with Out-of-Pocket Healthcare Payments
Undoubtedly, the type of health system existing in each country conditions the relevance and impact of OOPs. The key aspects of health system design are the financing and regulation of the systems themselves (who pays to support health systems and the people working in health services?), together with the provision and organization of health services [13].
The combination of different options offers four models of health systems: the Beveridge model (based on taxation and with many public providers); the Bismarck model (funded by a social insurance system and with a mixture of public and private providers); the private insurance model; and the absence of a defined model (especially in Asian and African countries) [14].
The vast extant literature has demonstrated a greater vulnerability and risk of facing financial catastrophe as a result of healthcare expenses in low and middle-income countries [8], in areas of lower income per capita [9], in low-income families [8] or in households with unemployed members [15]. Sociodemographic profiles which increase the probability of financial catastrophe have also been identified, such as those families with elderly members [12,16], with members suffering from chronic diseases [17], with elderly members with chronic diseases [12,18], with disabled people [19,20] or with those with severe disabilities which make them dependent [21].
Given the vulnerability of less developed and developing countries, the literature has focused on these countries. This is because their healthcare systems are newly established and households are required to contribute an important amount to access this care, which results in the exclusion of many. Among examples of this are studies of Asian countries like Vietnam [9], Nepal [22], Thailand [23], Bangladesh [24] and systematic reviews of the Asian continent [25,26]. In Africa, different studies have been carried out in Nigeria [27], Zambia [28] or Kenya [29], as well as systematic reviews [30]. There have also been studies centered on South America and other Latin American countries [31,32].
Studies have also been carried out in Europe, but a review of these studies on this subject has shown them to be scarce and obsolete [33]. Some of the countries that have been studied in terms of OOP payments associated with healthcare systems are Portugal [34], Poland, Germany and Denmark [35], Italy [36], or in the area of access to private healthcare services, Greece [37]. However, despite the fact that the social protection models in European countries are extensive and provide generous coverage, there are some OOPs on healthcare expenditures that a significant percentage of households with financial restrictions have to pay.
In the little analyzed field of LTC, it has recently been demonstrated that the cost of LTC is always high with respect to household income, implying that LTC is often unaffordable in the absence of social protection [10], and not all countries have a consolidated LTC system.
2.2. Traditional Methodology vs. Innovative Methodology
Special attention has been paid to the different methods used to estimate financially catastrophic health spending. In this sense, the budget share method defined in the SDGs overestimates financial hardship among rich households and underestimates hardship among poor households [38], which makes it difficult to detect financially burdened households.
Apart from the study of this specific component, the traditional methodology used to develop sociodemographic and clinical profiles of financial catastrophe victims has been through OLS, binary, multinomial and ordered logit models, and binary, multinomial and ordered probit models. These models are able to capture the influences of different profiles on the basis of a functional ex-ante relationship among the potentially influential variables (usually sociodemographic or clinical) involved in a financial catastrophe. In fact, these models are called parametric since the dependent relationship among the variables is known, with the exception of the parameters that can be estimated from the data.
However, there is an emerging methodology that has been tentatively applied to the general field of healthcare economy or the specific area of financial catastrophe. This is the application of machine learning techniques and algorithms, with the main advantage or characteristic being that they do not impose functional relationships among variables a priori, thus permitting the modelling (and capturing) of more complex dependencies among the data. This mainly nonparametric modelling implies assuming additional efforts both in the availability of the data and the use of intensive computational techniques.
There is extensive literature that explores the application of this methodology in different fields of science. The contributions in the area of health sciences stand out [39] by providing a panoramic vision as well as a perspective of advances to come, while [40] carrying out a compilation of recent applications of machine learning related to medicine. Meanwhile, in the field of biocomputing and biotechnology [41], these contributions include a compilation on the potential different techniques could have when they are applied in fields such as proteomics, genomics and similar areas. The textbook used by [42] and [43] includes an updated state of the art view of this field as well as foreseeable future perspectives. In areas such as the economy and finance [44], this textbook provides an assessment of the early contributions of machine learning to economics and predictions about its future possibilities, while in [45] a textbook about the application of different techniques in the area of finance is included. However, as far as we know, the application of these techniques has been relatively limited in the literature on the economy of healthcare, and for this reason, this study aims to investigate the possible uses of these new methodologies to implement automatic systems of classification that can assist in the decision-making process. Correctly predicting the rate of catastrophe has relevant intrinsic value in establishing a decision-making system which could lead to detecting the profiles of catastrophes and taking action to remedy them.
To our knowledge, only one study has included machine learning algorithms to predict the financial hardship associated with OOP medical expenditures in Rwanda. Although 96% of the population in Rwanda is covered by health insurance from the community health service, and around 74% of the population has health insurance, there are relevant OOP medical expenditures which severely limit the access to and utilization of health services [46]. One of the possible solutions is to predict OOP medical expenditures with accuracy, and machine learning techniques and algorithms allow this to be done.
3. Materials and Methods
3.1. Database Characteristics
In Spain, the 2006 Act for the Promotion of Personal Autonomy and Care of Dependent Persons [47], commonly known as the Dependency Act (DA), is a national law designed to provide services to people who are permanently dependent on others to help them with the basic activities of daily living [48]. DA funding was theoretically established with about a third of the total cost of care paid for by the beneficiaries (depending on the economic resources of the household) and the remaining two-thirds by the Public Administration. The economic capacity of the household is made up of income received from employment, capital income and wealth [49].
The Spanish Disability and Dependency Survey (SDDS) conducted by the Spanish National Statistics Institute [50] was used to estimate, firstly, the OOP payments associated with LTC (detailed information can be found elsewhere [51]) and, consequently, to estimate the catastrophe rate resulting from these OOP payments using the measure of catastrophe defined by [9] (detailed information can be found elsewhere [21]). The next step was to classify the households into the above categories of catastrophe for the Spanish case. Specifically, five categories were defined in accordance with the thresholds established in the literature [9,52]: less than 10% if OOP payments for dependent care do not exceed 10% of equivalent household income; the 10–20% interval if OOP payments exceed 10% of equivalent household income and do not exceed 20%; the 20–30% interval if OOP payments exceed 20% of equivalent household income and do not exceed 30%; the 30–40% interval if OOP payments exceed 30% of equivalent household income and do not exceed 40%; more than 40% if OOP payments exceed 40% of equivalent household income.
3.2. Predictor Variables
The explanatory variables were selected from an extensive review of the literature, essentially comprising sociodemographic characteristics [8,12,18,21,25,52,53,54,55,56,57]. The sociodemographic characteristics are: gender (male, female); age; marital status (married, single, widowed, separated/divorced); educational level (very low: illiterate/primary school incomplete, low: primary or equivalent, medium: secondary school/vocational training, high: university degree or equivalent); activity status (receiving earnings-related pension, employed, unemployed, other situations [housewife, student, etc.]); household income (less than 500€, 500–1000€, 1000–1500€, 1500–2000€, more than 2000€); household members; level of dependence (level I [25–49 points], level II [50–74 points], level III [75–100 points]); regional Gross Domestic Product (GDP) per capita (low per capita GDP, medium per capita GDP, high per capita GDP); regions of Spain (Andalusia, Aragon, Asturias, Balearic Islands, Basque Country, Canary Islands, Cantabria, Castile-La Mancha, Castile-Leon, Catalonia, Extremadura, Galicia, Madrid, Murcia, Navarra, La Rioja, Valencia, Ceuta and Melilla); ideology of the government (left-wing, right-wing); number of informal care hours received and members with intellectual disabilities and mental illnesses.
3.3. Statistical Analysis
The group of techniques and algorithms that have been used to carry out this study include traditional classification techniques (multinomial logistics, LASSO penalized regression and elastic-net) as well as other algorithms associated with machine learning and artificial intelligence, such as k-nearest neighbors (KNN), MARS, random forest, boosted trees and SVM. As is well-known in the literature, see textbooks in [58,59,60,61], classic methods based on specific parameters (logistic regression) are adequate if the function specified a priori approximates reality; however, important biases could occur if this is not the case. On the other hand, these methods tend to be stable, and the estimations do not usually fluctuate much among different samples (except for the existence of important outliers or other anomalies in the data). The algorithms normally used in machine learning (KNN, random forest, SVM, etc.) are, in their majority, nonparametric or semi-parametric, and tend to have much less specification bias. Nevertheless, they are likely to show great changes among different samples. This type of trade-off is known in the literature as the bias–variance tradeoff. Therefore, these algorithms have the tendency towards overfitting; that is, the error rate obtained in the adjustment sample used to estimate the fitting sample is much lower than that obtained in the test sample. A general outline of the entire process is presented in Figure 1.

Figure 1.
General outline of the process.
3.3.1. Algorithms
The techniques and algorithms used in this work to predict the rates of catastrophe are the following ones [61]:
- Multinomial logistic regression. This parametric technique assumes that a logistic relation exists between the independent variables and the catastrophe rate and estimates the coefficients of said regression for each catastrophe rate category.
- Penalized multinomial logistic regression. This is a variation of the above multinomial logistic regression, which penalizes the elastic-net type coefficients [62]; that is, it is a combination of the penalization of absolute values and the squared estimated coefficients. The function to optimize is as follows:where is the log-likelihood of the i-th observation and the penalty terms are the L1 and L2 norms of beta coefficients, respectively. As particular cases of the elastic-net penalty, for α = 1 the LASSO regression [63] is obtained (which is the default in glmnet package), meanwhile α = 0 corresponds to ridge regression [64]. Any value 0 < α < 1 will provide a combination between LASSO and ridge regression. The parameter λ controls the overall preponderance of the penalty term in the optimization problem. Both parameters are determined using the training data.
- k-nearest neighbors and weighted KNN [65,66]. This fully nonparametric method determines the value of an observation based on the weight of the closest observations. In the tuning process, it is necessary to choose the type of distance used as well as the maximum number of neighbors considered and their kernel of weight. The kernel function sets the rule of weighting the neighboring observations by underweighting the most distant neighbors.
- MARS. This algorithm, named multivariate adaptive regression splines [67], creates piecewise linear functions as hinges to approximate nonlinear relations. It can also allow interactions among the functions of different variables. Among the tuning parameters are the degree of interaction and the pruning process.
- Random forest. This algorithm is based on the aggregation of classification trees through bootstrapping [68]. The singular characteristic of this algorithm is that, during the division process of each tree, only a subgroup is randomly chosen from all the available predictor variables to mitigate the effects of the multicollinearity present in large databases, in other words, the aggregated trees are decorrelated. The number of selected variables in each partition is determined using a tuning process.
- Support vector machines (SVM). This algorithm [58,69] performs a division of the space of the predictor variables where the boundaries can be nonlinear and a cost is assigned to the observations that are incorrectly classified. The tuning parameters are usually the global permitted cost, the type of kernel used to establish the boundaries and the sigma associated with the kernel.
- Boosted trees. The technique of boosting for trees [70,71,72] is based on constructing trees iteratively in such a way that the data for each tree are weighted differently from the residuals obtained from the previous trees. Among the tuning parameters, the maximum number of iterations, the maximum depth of each tree in each iteration and the learning rate of aggregation among trees are usually used.
Table 1 gives a summary of the classification techniques considered in the study as well as the relevant tuning parameters of each technique. All the techniques and algorithms were implemented in R language (version 4.0.5) [73] through the caret package (vers. 6.086) [61,74]. In fact, many algorithms were implemented in different packages [75,76,77,78,79,80,81] that are called by caret (information about which particular packages were used for each technique is given in Table 1). Furthermore, all the computations have been made using R 4.0.5 for Windows 10 in a workstation with 8 Cores and 16GB of RAM. The R code is available upon request.

Table 1.
Algorithms and statistical techniques used for classification of the catastrophic rate.
It is important to point out that the opinion of the authors about the suitability of the models has been eclectic from the beginning, and the usefulness of the models in this context should be considered solely on their predictive abilities in terms of catastrophe rates. Logically, all the techniques should be evaluated using the same a priori predictor variables (although some of the techniques can carry out predictive variable selection processes during their training phase) as well as the same group of observations.
3.3.2. Partition of Training and Test Data
Given that the techniques of complex classification are prone to overfitting, the database was first divided into two groups:
- The first group is called the training group and includes 80% of the data (5021 observations). This group was used to estimate the parameters of the models as well as to perform the tuning processes inherent in the majority of the techniques. It is important to point out that, although the training group was randomly selected, it should always be the same for all the techniques used.
- The second group is called the test group and includes the remaining 20% of the data (1253 observations). This group of data was not used in any moment to estimate or train the models and statistic algorithms. Therefore, the test group included new data which permitted the different techniques to be evaluated and compared.
Figure 2 shows the frequencies of the catastrophe rates in each category for the training group and the test group. As can be seen, the frequencies of each catastrophe category are, in percentages, quite similar in the training and test groups. This demonstrates that the results of the predictive evaluation in the test group are valid with respect to the entire database.

Figure 2.
Frequencies of the catastrophic rate in the training and test groups.
3.3.3. Metrics for Measuring Performance
Once the training process was carried out with the first group, the evaluation of the predictive performance of each technique took place on the test group. The option chosen to measure performance was the one which is the simplest and easiest to understand and the most consistent in evaluating the correct percentage of classifications obtained for each category. Furthermore, we evaluated general accuracy; that is, the correct percentage of classifications for the whole set of data tests of each algorithm. Finally, if no statistically significant differences existed among the predictive performance of the different models in the test group, the simplest models were chosen, following the parsimony principle.
3.3.4. Tuning Process
It is important to point out that all the tuning processes of each algorithm have been performed in the manner explained above; that is, using cross-validation, the training group was divided into five parts. Four of them were used to adjust the models for each combination of tuning parameters, and the remaining group evaluated the predictive quality. The process was repeated five times, changing the four groups used to adjust the models and the group evaluating the predictions each time. In this way, for each combination of tuning parameters, all the available data were used in the training but the overfitting effect common to complex techniques was mitigated. Finally, this process was repeated three times, changing the random cross-validation selection. The tuning parameters finally selected were those which maximized accuracy. In the specialized literature, this method is known as repeated cross-validation [61,82]. For the process to be homogeneous and reproducible with all the techniques and algorithms compared, the same random seeds were used to generate the entire process in a way such that all the algorithms used the same datasets.
4. Results
Descriptive information about the sociodemographic characteristics of the sample for different regions of Spain are included in Table 2. We can see that two out of every three dependent people are women (67.85%), and the mean age is 72.86 years (DE: 18.92). The most common marital status types are widowed (42.06%) and married (39.74%), the predominant educational level is basic (primary or equivalent and lower, 90.72%) and the number of equivalent members of the household is 1.92 (DE: 0.66). The majority receive a pension (84.08%). Level II and level III are recognized in 34.63% and 38.94% of the sample, respectively; two out of every three people have severe difficulties performing the basic activities of daily living (65.80%), while 27.66% have moderate difficulties.

Table 2.
Sociodemographic data of the sample, divided by values of catastrophe measures.
Almost a third of the population live in low, a third in middle and a third in high-income per capita GDP regions, while two out of three people live in communities governed by left-wing parties. The mean score of dependency obtained is 61.28 points (DE: 18.29), and two out of three people suffer from mental diseases (65.73%). A total of 18.98% of people receive professional care financed by their families, and the number of hours of informal care received is 36.33 (DE: 49.37). We can observe a similar behavioral pattern for all the variables in the different thresholds analyzed.
The most significant effect is in educational levels and levels of per capita income in the regions of residence. Levels of dependence also demonstrate disparate behavior. In the under 40% thresholds, level I is predominant (41.63% for the under 10% threshold, 40.51% for the under 20% threshold, 61.14% for the under 30% threshold and 50.67% for the under 40% threshold), while for the 40% threshold, the higher levels of dependence (levels II and III) have a greater weight in the overall sample (43.30% and 38.87%, respectively).
Figure 3 includes graphics reflecting the tuning process, which indicate the values of accuracy for each possible group of tuning parameters. As we can observe, the values of the parameters selected in the tuning process are those which maximize accuracy in each case. In addition, for most algorithms, the combination of parameters that maximize accuracy are selected for relatively complex models (high values of tuning parameters), indicating the possible existence of highly nonlinear and complex relations between the rate of catastrophe and the predictor variables.
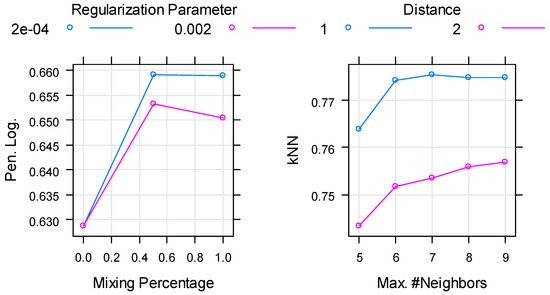

Figure 3.
Tuning process. The y-axis measures the accuracy (percentage of correct classifications) and the x-axis measures the tuning parameters of the corresponding algorithm.
Table 3 shows the classification tables with the correct percentages of classifications for each technique using the test data. While the columns represent the data on observed catastrophe rates in the test group, the rows show the predicted category for each algorithm on the same group of data. Each square represents the percentage with respect to the observed category in such a way that the columns always add up to 100.

Table 3.
Classification tables for each technique in the test group.
In general, we can see that all the classification methods perform well. The more complex classification models perform much better than the simpler models, and there is no evidence of overfitting in the types of models such as k-nearest neighbors (classification percentages: 82.09%, 86.99%, 80.08%, 73.10% and 58.91% for the categories <10%, 10–20%, 20–30%, 30–40%, >40% of catastrophe, respectively) and boosted trees (gbm) (90.67%, 85.97%, 77.64%, 69.66% and 62.38% for the five categories analyzed, respectively). The best classification techniques are SVM (classification percentages: 90.30%, 92.09%, 88.62%, 96.55% and 71.78%) and random forest (91.04%, 93.37%, 91.06%, 94.48% and 72.28%). In contrast, the parametric models show lower values for the classification percentages (for logistic regression: 72.39%, 83.42%, 56.10%, 46.21% and 48.51%; and penalized logistic regression: 71.27%, 83.42%, 56.10%, 46.21% and 49.01% for the five analyzed categories, respectively).
Table 4 summarizes the general accuracy (percentage of correct classifications) of each algorithm using the data test. This table again shows the better performance of the algorithms random forest and SVM over the rest of the techniques. Furthermore, in general, the semiparametric and non-parametric algorithms have much better performances than parametric models (logistic and penalized logistic models in our case).

Table 4.
General accuracy (% of correct classifications in test data).
Finally, Table 5 and Table 6 demonstrate the importance of the variables in the classification results for the models that perform the best (SVM and random forest). With SVM, the ranking and degree of dependence, monthly household income and per capita household income are the four variables that have the greatest weight in the classification of catastrophe risk in the different thresholds analyzed. Random forest includes being married as the most important predictive variable, followed by the dependence ranking and regional per capita income (highlighting Castile-La Mancha), and then the degree of dependence.

Table 5.
Importance of variables in SVM.

Table 6.
Importance of variables in Random forest.
5. Discussion
The first global studies showed that the percentage of catastrophic households due to healthcare OOP payments varied from 0.01% in the Czech Republic to 10.45% in Vietnam (in a study of 59 countries), demonstrating that those countries with advanced social security structures or healthcare systems financed by taxes protected their population financially [8]. In a review of 89 countries representing 89% of the world’s population, a catastrophe rate of 1.47% was obtained, showing that 18 countries have a rate of catastrophe that exceeds 4% [52]. A recent systematic review carried out in 133 countries revealed that in 2010, the global rate of catastrophic spending in PDB on healthcare for the 10% threshold was 11.7%, revealing that 808 million people had catastrophic healthcare expenses [83].
A specific analysis of less developed countries and continents showed that in Asia, where a study was carried out in eleven low to middle-income countries (which represent 79% of the Asian population and 48% of the world’s population), the incidence of poverty increased by 14% when the analysis considered OOP healthcare payments [25]. A review of Sub-Saharan African countries found large variations depending on the country under study, reflecting an average rate of 17% for the 40% threshold, which especially worsened when the person suffered from HIV/ART and malaria, causing the catastrophe rate to reach 100% of households [30]. When twelve Latin American and Caribbean countries were analyzed, in the 30% threshold, the average catastrophe rate was 8.23%; this was with important heterogeneity since this rate was quite high in countries such as Nicaragua (19.9%), Guatemala (16.3%) and Ecuador (15.8%) [31].
To the best of our knowledge, the literature has presented the profile or profiles of the types of families most at risk of financial catastrophe caused by OOP payments in different areas of expenditure. These profiles include, for example, being male [34,84], being married [85], having a lower level of education [14], being unemployed [15], having a lower household income [38], suffering from diseases such as cancer [5], diabetes or cardiovascular diseases [18] or chronic diseases [17], being elderly [21,52], being elderly and suffering from chronic diseases [12,18], and being disabled [19,20] or dependent [21]. Specifically singled out risk factors are belonging to a poor household and suffering from a chronic disease [86], living in the city [12,34], living in regions with medium and high levels of GDP per capita [18,52] and living in low and middle-income countries [8].
Among the recommendations based on the explicative method, a study found that direct OOP payments for healthcare expenditures increased poverty. The researchers denounced the need for more effective policies, focusing on the Asian population who live on less than a dollar a day, including 2.7% of the 78 million people studied [87]. In this sense, it was recommended that that governments consider additional measures to increase financial protection for poor households faced with payments for medical treatment, concretely, in their study, for the treatment of cancer [88]. Another study found that in Africa, social protection assistance based on subsidies for medicines, free medical care or the extension of social security have not sufficiently protected households financially due to nonmedical costs that are nevertheless intrinsically related, such as transport and food [30]. A proposal to reduce financial catastrophe could be implemented progressively in the healthcare financing system by substituting OOP payments for funds from indirect financial sources [7].
In this work, through a design intended to obtain a correct and precise classification of families at greater risk of catastrophe, we used methods of machine learning which, as far as we know, have not been used in this field of study before. In order to do so, we selected the groups of parameters, which maximized the accuracy of each of the techniques studied. Therefore, if the result of the training group was representative and there was no overfitting, the classification obtained with the test group should be optimal. It is important to point out that if the parameters chosen in the tuning process were those which maximize accuracy in each case, other options presented in the literature have also been considered as, for example, selecting the group of parameters with the lowest value so that its accuracy was within the typical deviation of optimum accuracy [58,59,60,61].
To our knowledge, only one study has used machine learning techniques to detect financial catastrophe derived from OOP medical expenditures in Rwanda [46]. This study considers these algorithms: random forest, decision tree models, gradient boosting and regression tree models. Most of these algorithms are based on tree models and, therefore, represent only a part of the set of algorithms available in machine learning (although all of them are very useful tools for making predictions). In the present study, the algorithms included were the following: multinomial logistic regression and penalized multinomial logistic regression (with elastic-net penalties), k-nearest neighbors, MARS, random forest, support vector machines (SVM) and boosted trees. In fact, our choice of algorithms was made with the intention of covering the greatest prediction possibilities to make the comparison more extensive. Furthermore, although in our case random forest achieved very good results, the SVM algorithm (not based on trees) achieved similar results. To sum up, in our opinion, the papers focused on different algorithms and the previous study [47] restrict the comparison mainly to algorithms based on trees, while our paper is more extensive in the set of prediction tools used, by adding algorithms based on different backgrounds.
To continue with the results of this study, we found that those models with greater complexity performed better than the simpler models, with no evidence of overfitting. This demonstrates that the most frequently used parametric models (logistic regression) can have specification bias and that the instability associated with nonparametric models (bias–variance trade-off) can be reduced to a great extent by performing model aggregation through simulation. In fact, in this work, an improvement in predictive terms can be discerned, which compensates for having to implement more computationally complex systems. In addition, once the machine learning algorithms have been trained (random forest, SVM, etc.), since they work automatically, they can be used to obtain predictions in real time at a cost, which is similar to the other techniques. Logically, this predictive gain by the more complex machine learning techniques is a result of applying these algorithms (with high computational cost) to a heterogeneous and sufficiently extensive database to allow the most complex relations among the data to be learned.
Among the most complex models, the ones which are fundamentally nonparametric performed the best (specifically, random forest and SVM). There is evidence that there are nonlinearities in the data, and that they probably cannot be captured using functional relations. In fact, as is well-known in the literature [60], if nonlinearities do not exist in the data, multinomial logistic regression should show results similar to SVM, while in this case, the performance of the latter was clearly superior. This could be explained by the nonlinear partition of the space generated by the predictor variables that the algorithm SVM makes when it uses a nonlinear kernel (as in this case). This partition is not able to replicate itself through parametric models and, for this reason, this type of model has greater difficulties in adequately classifying the categories of catastrophe with less frequent observations (especially those over 20%). The success obtained by random forest could be explained by the fact that the value of mtry selected was quite high, for which quite a few predictors were used in each partition. This induced, in each individual tree, a tendency of overfitting and instability in the results obtained but, in performing bootstrapping among the different trees inherent in this technique, the instability (or variance) of the algorithm was reduced, maintaining its capacity to distinguish the areas with the best classification ability inside the space generated by the predictors. The complex model which obtained the worst results was boosting. This could be because since this technique performed the tuning process considering the residuals of each stage, instead of performing random bootstrapping (like random forest), it could be more affected by overfitting than the other techniques.
A problem, which was detected in the analysis, has to do with the category “Upper 40%”, which systematically had the worst predictive performance and, more seriously, a large part of the classification errors go to the farthest categories. This category is the one that most worries the literature since the families included in this category are in situations of absolute financial vulnerability [21]. The problems with this category could be due to the great heterogeneity that exists among the observations of this category [15], which implies that any method would have problems in categorizing it adequately. However, it is true that there was an improvement in classification with the more complex techniques (random forest and SVM) in this category as well, so it could be expected that if there were more observations in the dataset which allowed their greater heterogeneity to be captured, the difference in the predictive performance of this category with respect to the other categories would be reduced (at least for the models with the best predictive ability).
This work has the following limitations. The first one is in reference to the estimation carried out on the specific database of a population at a concrete moment in time. It is necessary to extend it with more recent databases from other countries in order to analyze whether the present empirical case of success using these techniques is maintained in other international micro databases. The second limitation has to do with the lack of consideration in this study of some machine learning algorithms, like neural networks and deep learning. They have not been used due to the good results obtained with SVM and random forest (since they are highly complex models, we have considered the area to be covered in this case). Nevertheless, it could be relevant to include them in a future comparison, especially if larger databases are available and there is greater heterogeneity.
6. Conclusions
In summary, to the best of our knowledge, this is the first study in the financial catastrophe literature that has developed a classification of financial catastrophe risk caused by OOP payments; in this concrete example, payments associated with LTC expenses.
While no methodology allows for an instantaneous classification of an applicant’s profile, the methodology presented here permits the risk of financial catastrophe to be classified, which can direct the recommendations made throughout the literature in a more specific way and with better results. All the classification methods performed well, with the complex models performing better than the simpler ones and showing no evidence of overfitting.
In the specific casuistry of LTC in Spain, the subject of study in this work, 68.07% of families have to use more than 40% of their income for OOP payments, with an average monthly addition over that amount of 341.66€ for the greatest degree of dependence (level III) [51]. Specifically, the sociodemographic factors that increase the probability of becoming a victim of financial catastrophe are: being elderly, being single, widowed or separated, having lower levels of household income and education, having greater levels of dependence [21], being unemployed, living in a region with lower per capita income and living in a region governed by right-wing parties [15]. The four essential classifying variables of catastrophe obtained in this study are the ranking and degree of dependence, being married (which was the most relevant category in the studies mentioned above) and regional per capita income.
It is claimed that “there is no universal formula that can be used to help poor countries design ways to increase reliance on prepayment and reduce out-of-pocket payments” [52]. For this desire to find an alternative perspective of classificatory analysis, the use of these types of methodologies is proposed for a problem that worries health authorities globally, as subgoal SDG 3.8 [1] exemplifies. Proposing this methodology as a third indicator of the degree to which this subgoal has been achieved together with the existing instruments 3.8.1 and 3.8.2 [89], is the main objective of this study.
The comparison between the two approaches used, parametric versus semiparametric and non-parametric algorithms, demonstrates an almost perfect correlation between the statistically significant variables in the first approach and the greater predictive weight in the second. The reason for this is that, although it is very complicated to evaluate functional dependency between the catastrophe rate and the group of independent predictor variables with many of the techniques used in machine learning, it is possible to measure the importance of each predictor variable in average predictive performance [59,61]. Nevertheless, it is necessary to keep in mind that these types of techniques (in some cases black-box) are designed with a predictive approach, not an explicative one, so that their ability to measure influences among variables is less than parametric techniques such as logistic regression.
With the complexities among the dependencies of the data, MARS predicted better than multinomial logistic regression, although their performance was worse than random forest and SVM. This is because, although these are more complex than linear or logistic techniques (for example, MARS induces non-linearity, allowing the existence of thresholds in the linear relationships, and includes products of predictor functions to capture the interactions among them), they are less adaptable than more complex fully non-parametric models. Since in this particular case there appear to be very complex dependencies, the intermediate models (MARS) did not obtain the best results.
This leads us to conclude that the penalized methods barely improve the predictions of the nonpenalized methods. As has been previously mentioned, the existence of strong nonlinearities in the dependencies of the variables means that none of these techniques is able to capture them if the parametric specification is not suitable. Penalizing the coefficients or performing variable selection will not improve the approximation.
Future lines of research applying the group of methodologies presented here in large databases related to financial catastrophe caused by healthcare payments are necessary to corroborate our results. This would permit the establishment or design of procedures for legislators and authorities who implement social and healthcare policies to detect those individuals or families at greater risk of financial catastrophe, and attempt to protect them financially with exemptions or alternative OOP payment designs. In addition, given the results obtained in this research, it would be very interesting to compare the best algorithms (random forest and SVM) with the performance of other nonparametric algorithms, such as neural networks, to attempt to discover if the complexity of the relationships can be fully captured using different alternatives. Another important future line of research is the consideration of n-dimensional groups (combining two, three, or more one-dimensional groups) as explanatory variables, in order to set up a multi-perspective analysis of data which offers a complete design of the financial catastrophe profiles.
Author Contributions
Each of the authors indicated in this manuscript have equally contributed to the conceptualization, methodology, software, validation and formal analysis, as well as to the investigation and provision of resources and data management. Finally, the writing task has also been tackled by all the authors, by providing new perspectives and improving it. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Cátedra Mutua Madrileña-USPCEU, grant number 060516-USPMM-01/17, AEI-Ministry of Science and Innovation (PID2019-107800GB-I00 and PID2019-104901RB-I00) and the Spanish State Programme of R+D+I (ECO2017-83771-C3-1-R).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.ine.es/dyngs/INEbase/es/operacion.htm?c=Estadistica_C&cid=1254736176782&menu=resultados&idp=1254735573175#!tabs-1254736195313, accessed on 15 May 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, B.X.; Kjaerulf, F.; Turner, S.; Cohen, L.; Donnelly, P.D.; Muggah, R.; Davis, R.; Realini, A.; Kieselbach, B.; MacGregor, L.S. Transforming our world: Implementing the 2030 agenda through sustainable development goal indicators. J. Public Health Policy 2016, 37, 13–31. [Google Scholar] [CrossRef]
- United Nations. The Sustainable Development Goal Indicators Website. Metadata Repository 2020. Available online: https://unstats.un.org/sdgs/metadata/files/Metadata-03-08-02.pdf (accessed on 18 May 2020).
- World Health Organization. World Health Statistics 2016: Monitoring Health for the SDGs Sustainable Development Goals; World Health Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Ke, X.; Saksena, P.; Holly, A. The Determinants of Health Expenditure: A Country-Level Panel Data Analysis; World Health Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Altice, C.K.; Banegas, M.P.; Tucker-Seeley, R.D.; Yabroff, K.R. Financial hardships experienced by cancer survivors: A systematic review. J. Natl. Cancer Inst. 2017, 109, 2. [Google Scholar] [CrossRef] [PubMed]
- Yabroff, K.R.; Zhao, J.; Han, X.; Zheng, Z. Prevalence and correlates of medical financial hardship in the USA. J. Gen. Intern. Med. 2019, 34, 1494–1502. [Google Scholar] [CrossRef]
- Kolasa, K.; Kowalczyk, M. Does cost sharing do more harm or more good? A systematic literature review. BMC Public Health 2016, 16, 992. [Google Scholar] [CrossRef]
- Xu, K.; Evans, D.B.; Kawabata, K.; Zeramdini, R.; Klavus, J.; Murray, C.J. Household catastrophic health expenditure: A multicountry analysis. Lancet 2003, 362, 111–117. [Google Scholar] [CrossRef]
- Wagstaff, A.; van Doorslaer, E. Catastrophe and impoverishment in paying for health care: With applications to Vietnam 1993-1998. Health Econ. 2003, 12, 921–934. [Google Scholar] [CrossRef] [PubMed]
- Muir, T. Measuring social protection for long-term care. OECD Health Work. Pap. 2017, 93. [Google Scholar] [CrossRef]
- Wyszewianski, L. Families with catastrophic health care expenditures. Health Serv. Res. 1986, 21, 617. [Google Scholar] [PubMed]
- Wang, Z.; Li, X.; Chen, M. Catastrophic health expenditures and its inequality in elderly households with chronic disease patients in China. Int. J. Equity Health 2015, 14, 8. [Google Scholar] [CrossRef]
- World Health Organization. The World Health Report 2000: Health Systems: Improving Performance; World Health Organization: Geneva, Switzerland, 2000. [Google Scholar]
- Lameire, N.; Joffe, P.; Wiedemann, M. Healthcare systems—An international review: An overview. Nephrol. Dial. Transpl. 1999, 14, 3–9. [Google Scholar] [CrossRef]
- Del Pozo-Rubio, R.; Jiménez-Rubio, D. Catastrophic risk associated with out-of-pocket payments for long term care in Spain. Health Policy 2019, 123, 582–589. [Google Scholar] [CrossRef]
- Scheil-Adlung, X.; Bonan, J. Gaps in social protection for health care and long-term care in Europe: Are the elderly faced with financial ruin? Int. Soc. Secur. Rev. 2013, 66, 25–48. [Google Scholar] [CrossRef]
- Choi, J.W.; Choi, J.W.; Kim, J.H.; Yoo, K.B.; Park, E.C. Association between chronic disease and catastrophic health expenditure in Korea. BMC Health Serv. Res. 2015, 15, 26. [Google Scholar] [CrossRef] [PubMed]
- Arsenijevic, J.; Pavlova, M.; Rechel, B.; Groot, W. Catastrophic Health Care Expenditure among Older People with Chronic Diseases in 15 European Countries. PLoS ONE 2016, 11, e0157765. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-E.; Shin, H.-I.; Do, Y.K.; Yang, E.J. Catastrophic Health Expenditures for Households with Disabled Members: Evidence from the Korean Health Panel. J. Korean Med. Sci. 2016, 31, 336–344. [Google Scholar] [CrossRef] [PubMed]
- Mitra, S.; Findley, P.A.; Sambamoorthi, U. Health Care Expenditures of Living with a Disability: Total Expenditures, Out-of-Pocket Expenses, and Burden, 1996 to 2004. Arch. Phys. Med. Rehabil. 2009, 90, 1532–1540. [Google Scholar] [CrossRef] [PubMed]
- Del Pozo-Rubio, R.; Mínguez-Salido, R.; Pardo-García, I.; Escribano-Sotos, F. Catastrophic long-term care expenditure: Associated socio-demographic and economic factors. Eur. J. Health Econ. 2019, 20, 691–701. [Google Scholar] [CrossRef]
- Saito, E.; Gilmour, S.; Rahman, M.M.; Gautam, G.S.; Shrestha, P.K.; Shibuya, K. Catastrophic household expenditure on health in Nepal: A cross-sectional survey. Bull. World Health Organ. 2014, 92, 760–767. [Google Scholar] [CrossRef]
- Limwattananon, S.; Tangcharoensathien, V.; Prakongsai, P. Catastrophic and poverty impacts of health payments: Results from national household surveys in Thailand. Bull. World Health Organ. 2007, 85, 600–606. [Google Scholar] [CrossRef]
- Fahim, S.M.; Bhuayan, T.A.; Hassan, M.Z.; Abid Zafr, A.H.; Begum, F.; Rahman, M.M.; Alam, S. Financing health care in B angladesh: Policy responses and challenges towards achieving universal health coverage. Int. J Health Plan. Manag. 2019, 34, e11–e20. [Google Scholar] [CrossRef]
- van Doorslaer, E.; O’Donnell, O.; Rannan-Eliya, R.P.; Somanathan, A.; Adhikari, S.R.; Garg, C.C.; Harbianto, D.; Herrin, A.N.; Huq, M.N.; Ibragimova, S.; et al. Effect of payments for health care on poverty estimates in 11 countries in Asia: An analysis of household survey data. Lancet 2006, 368, 1357–1364. [Google Scholar] [CrossRef]
- Wang, H.; Torres, L.V.; Travis, P. Financial protection analysis in eight countries in the WHO South-East Asia Region. Bull. World Health Organ. 2018, 96, 610. [Google Scholar] [CrossRef]
- Aregbeshola, B.S.; Khan, S.M. Out-of-pocket payments, catastrophic health expenditure and poverty among households in Nigeria 2010. Int. J. Health Policy Manag. 2018, 7, 798. [Google Scholar] [CrossRef] [PubMed]
- Masiye, F.; Kaonga, O.; Kirigia, J.M. Does User Fee Removal Policy Provide Financial Protection from Catastrophic Health Care Payments? Evidence from Zambia. PLoS ONE 2016, 11, e0146508. [Google Scholar] [CrossRef]
- Barasa, E.W.; Maina, T.; Ravishankar, N. Assessing the impoverishing effects, and factors associated with the incidence of catastrophic health care payments in Kenya. Int. J. Equity Health 2017, 16, 31. [Google Scholar] [CrossRef]
- Njagi, P.; Arsenijevic, J.; Groot, W. Understanding variations in catastrophic health expenditure, its underlying determinants and impoverishment in sub-Saharan African countries: A scoping review. Syst. Rev. 2018, 7, 136. [Google Scholar] [CrossRef] [PubMed]
- Knaul, F.M.; Wong, R.; Arreola-Ornelas, H.; Méndez, O.; Bitran, R.; Campino, A.C.; Flórez Nieto, C.E.; Giedion, U.; Maceira, D.; Rathe, M. Household catastrophic health expenditures: A comparative analysis of twelve Latin American and Caribbean Countries. Salud. Publica Mex. 2011, 53 (Suppl. 2), 85–95. [Google Scholar]
- Amaya-Lara, J.L. Catastrophic expenditure due to out-of-pocket health payments and its determinants in Colombian households. Int. J. Equity Health 2016, 15, 182. [Google Scholar] [CrossRef] [PubMed]
- Yerramilli, P.; Fernández, Ó.; Thomson, S. Financial protection in Europe: A systematic review of the literature and mapping of data availability. Health Policy 2018, 122, 493–508. [Google Scholar] [CrossRef] [PubMed]
- Kronenberg, C.; Barros, P.P. Catastrophic healthcare expenditure—Drivers and protection: The Portuguese case. Health Policy 2014, 115, 44–51. [Google Scholar] [CrossRef]
- Zawada, A.; Kolasa, K.; Kronborg, C.; Rabczenko, D.; Rybnik, T.; Lauridsen, J.T.; Ceglowska, U.; Hermanowski, T. A Comparison of the Burden of Out-of-Pocket Health Payments in Denmark, Germany and Poland. Glob. Policy 2017, 8, 123–130. [Google Scholar] [CrossRef]
- Maruotti, A. Fairness of the national health service in Italy: A bivariate correlated random effects model. J. Appl. Stat. 2009, 36, 709–722. [Google Scholar] [CrossRef]
- Grigorakis, N.; Floros, C.; Tsangari, H.; Tsoukatos, E. Out of pocket payments and social health insurance for private hospital care: Evidence from Greece. Health Policy 2016, 120, 948–959. [Google Scholar] [CrossRef]
- Cylus, J.; Thomson, S.; Evetovits, T. Catastrophic health spending in Europe: Equity and policy implications of different calculation methods. Bull. World Health Organ. 2018, 96, 599. [Google Scholar] [CrossRef]
- Rajkomar, A.; Dean, J.; Kohane, I. Machine learning in medicine. N. Engl. J. Med. 2019, 380, 1347–1358. [Google Scholar] [CrossRef]
- Cleophas, T.J.; Zwinderman, A.H. Machine Learning in Medicine—A Complete Overview; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Larrañaga, P.; Calvo, B.; Santana, R.; Bielza, C.; Galdiano, J.; Inza, I.; Lozano, J.A.; Armananzas, R.; Santafé, G.; Pérez, A. Machine learning in bioinformatics. Brief. Bioinform. 2006, 7, 86–112. [Google Scholar] [CrossRef] [PubMed]
- Dinov, I.D. Data Science and Predictive Analytics: Biomedical and Health Applications Using R; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Oliveira, A.L. Biotechnology, big data and artificial intelligence. Biotechnol. J. 2019, 14, 1800613. [Google Scholar] [CrossRef]
- Athey, S. The impact of machine learning on economics. In The Economics of Artificial Intelligence: An agenda; National Bureau of Economic Research, Ed.; University of Chicago Press: Chicago, IL, USA, 2018; pp. 507–547. [Google Scholar]
- López De Prado, M. Advances in Financial Machine Learning; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Muremyi, R.; François, N.; Ignace, K.; Joseph, N.; Haughton, D. Comparison of Machine Learning Algorithms for Predicting the Out of Pocket Medical Expenditures in Rwanda. J. Health Sci. Med. Res 2019, 1, 32–41. [Google Scholar]
- Official Bulletin State of Spain. Act 39/2006 of 14th December on Promotion of Personal Autonomy and Assistance for Persons in a Situation of Dependency; Official Bulletin State of Spain: Madrid, Spain, 2006. [Google Scholar]
- De La Maisonneuve, C.; Martins, J.O. Public Spending on Health and Long-term Care. OECD Econ. Policy Pap. 2013, 6. [Google Scholar] [CrossRef]
- Official Bulletin State of Spain. Resolución de 13 de Julio de 2012, de la Secretaría de Estado de Servicios Sociales e Igualdad, por la que se Publica el Acuerdo del Consejo Territorial del Sistema para la Autonomía y Atención a la Dependencia para la Mejora del Sistema para la Autonomía y Atención a la Dependencia; Official Bulletin State of Spain: Madrid, Spain, 2012. [Google Scholar]
- Spanish National Statistics Institute. Spanish Disability and Dependency Survey 2008; Spanish National Statistics Institute: Madrid, Spain, 2008.
- Del Pozo-Rubio, R.; Pardo-García, I.; Escribano-Sotos, F. Financial Catastrophism Inherent with Out-of-Pocket Payments in Long Term Care for Households: A Latent Impoverishment. Int. J. Environ. Res. Public Health 2020, 17, 295. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Evans, D.B.; Carrin, G.; Aguilar-Rivera, A.M.; Musgrove, P.; Evans, T. Protecting households from catastrophic health spending. Health Aff. 2007, 26, 972–983. [Google Scholar] [CrossRef]
- Brinda, E.M.; Andres, A.R.; Enemark, U. Correlates of out-of-pocket and catastrophic health expenditures in Tanzania: Results from a national household survey. BMC Int. Health Hum. Rights 2014, 14, 5. [Google Scholar]
- López-López, S.; del Pozo-Rubio, R.; Ortega-Ortega, M.; Escribano-Sotos, F. Catastrophic Household Expenditure Associated with Out-of-Pocket Healthcare Payments in Spain. Int. J. Environ. Res. Public Health 2021, 18, 932. [Google Scholar] [CrossRef] [PubMed]
- Carrington, A.M.; Fieguth, P.W.; Qazi, H.; Holzinger, A.; Chen, H.H.; Mayr, F.; Douglas, G.M. A new concordant partial AUC and partial c statistic for imbalanced data in the evaluation of machine learning algorithms. BMC Med. Inform. Decis. Mak. 2020, 20, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Couronné, R.; Probst, P.; Boulesteix, A.-L. Random forest versus logistic regression: A large-scale benchmark experiment. BMC Bioinform. 2018, 19. [Google Scholar] [CrossRef]
- Cinaroglu, S. Modelling Unbalanced Catastrophic Health Expenditure Data by Using Machine Learning Methods. Intell. Syst. Account. Financ. Manag. 2020, 1–14. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Efron, B.; Hastie, T. Computer Age Statistical Inference; Cambridge University Press: Cambridge, UK, 2016; Volume 5. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Johnson, K.; Kuhn, M. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Cost, S.; Salzberg, S. A weighted nearest neighbor algorithm for learning with symbolic features. Machine Learning 1993, 10, 57–78. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 532. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training 2020, R Package Version 6.0-86. Available online: https://CRAN.R-project.org/package=caret (accessed on 1 January 2021).
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Springer: New York, NY, USA, 2002. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. Available online: https://www.jstatsoft.org/v33/i01/ (accessed on 1 January 2021). [CrossRef]
- Schliep, K.; Hechenbichler, K. kknn: Weighted k-Nearest Neighbors, R Package Version 1.3.1. 2016. Available online: https://CRAN.R-project.org/package=kknn (accessed on 1 January 2021).
- Milborrow, S.; Hastie, T.; Tibshirani, R. Earth: Multivariate Adaptive Regression Splines, R Package Version 5.3. 2020. Available online: https://CRAN.R-project.org/package=earth (accessed on 1 January 2021).
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R. News 2002, 2, 18–22. Available online: https://CRAN.R-project.org/doc/Rnews (accessed on 1 January 2021).
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. kernlab—An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11, 1–20. Available online: http://www.jstatsoft.org/v11/i09 (accessed on 1 January 2021). [CrossRef]
- Greenwell, B.; Boehmke, B.; Cunningham, J. GBM Developers. GMB: Generalized Boosted Regression Models. R Package Version 2.1.8. 2020. Available online: https://CRAN.R-project.org/package=gbm (accessed on 1 January 2021).
- Kuhn, M.; Johnson, K. Feature Engineering and Selection: A Practical Approach for Predictive Models; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Wagstaff, A.; Flores, G.; Hsu, J.; Smitz, M.-F.; Chepynoga, K.; Buisman, L.R.; van Wilgenburg, K.; Eozenou, P. Progress on catastrophic health spending in 133 countries: A retrospective observational study. Lancet Glob. Health 2018, 6, e169–e179. [Google Scholar] [CrossRef]
- Brinda, E.M.; Kowal, P.; Attermann, J.; Enemark, U. Health service use, out-of-pocket payments and catastrophic health expenditure among older people in India: The WHO Study on global AGEing and adult health (SAGE). J. Epidemiol. Community Health 2015, 69, 489–494. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.W.; Shin, J.Y.; Cho, K.H.; Nam, J.Y.; Kim, J.Y.; Lee, S.G. Medical security and catastrophic health expenditures among households containing persons with disabilities in Korea: A longitudinal population-based study. Int. J. Equity Health 2016, 15, 119. [Google Scholar] [CrossRef]
- Zhao, Y.; Oldenburg, B.; Mahal, A.; Lin, Y.; Tang, S.; Liu, X. Trends and socio-economic disparities in catastrophic health expenditure and health impoverishment in China: 2010 to 2016. Trop. Med. Int. Health 2020, 25, 236–247. [Google Scholar] [CrossRef] [PubMed]
- van Doorslaer, E.; O’Donnell, O.; Rannan-Eliya, R.P.; Somanathan, A.; Adhikari, S.R.; Garg, C.C.; Harbianto, D.; Herrin, A.N.; Huq, M.N.; Ibragimova, S.; et al. Catastrophic payments for health care in Asia. Health Econ. 2007, 16, 1159–1184. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kwon, S. Impact of the policy of expanding benefit coverage for cancer patients on catastrophic health expenditure across different income groups in South Korea. Soc. Sci. Med. 2015, 138, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Transforming our world: The 2030 agenda for sustainable development. In General Assembley 70 Session; UN: New York, NY, USA, 2015.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).