Abstract
In this paper, under the framework of Extended Chebyshev space, four new generalized quasi cubic trigonometric Bernstein basis functions with two shape functions and are constructed in a generalized quasi cubic trigonometric space span, which includes lots of previous work as special cases. Sufficient conditions concerning the two shape functions to guarantee the new construction of Bernstein basis functions are given, and three specific examples of the shape functions and the related applications are shown. The corresponding generalized quasi cubic trigonometric Bézier curves and the corner cutting algorithm are also given. Based on the new constructed generalized quasi cubic trigonometric Bernstein basis functions, a kind of new generalized quasi cubic trigonometric B-spline basis functions with two local shape functions and is also constructed in detail. Some important properties of the new generalized quasi cubic trigonometric B-spline basis functions are proven, including partition of unity, nonnegativity, linear independence, total positivity and continuity. The shape of the parametric curves generated by the new proposed B-spline basis functions can be adjusted flexibly.
1. Introduction
The construction of basis functions with good properties, including partion of unity, nonnegativity and total positivity, is a basic subject within computer aided geometric design (GAGD) and Computer Graphics (CG). Basis functions with desirable properties have an important role in curves and surfaces construction.
In order to control the shape of the curves flexibly, various spline curves possessing shape parameters have been proposed. In [1], a kind of continuous rational cubic spline curves with tension shape parameters was developed. In [2], a kind of continuous Beta-spline curves with local bias and tension parameters was proposed. In [3], in the polynomial space , a kind of variable degree spline curves was constructed. In [4], a kind of changeable degree spline curves was constructed. In [5], new cubic rational B-spline curves with two shape parameters were constructed. In the space span, a class of –Bernstein basis functions and the related B-spline form with two local shape parameters was proposed in [6]. In [7], a kind of –Bernstein basis functions with two exponential functions was developed in the space span.
Blossom theory plays a significant role in the construction of B-splines, which is first stated in [8]. In [9], Mazure and Laurent proposed a general notion of blossom which can be extended to Chebyshev splines. In [10], the necessary and sufficient conditions for the existence of blossoms for splines with connection matrices and with sections in different four-dimensional quasi-Chebyshev spaces were explored. In [11], Mazure showed how the existence of blossoms in some spaces automatically leads to optimal bases. The approximation power and the conditions of existence of a normalized B-basis were further studied in [12]. In [13], the dimension elevation process from Quasi Extended Chebyshev spaces was analyzed and a new insight into some special cases was given. In [14], a new space of variable degree polynomial was proposed, where a Bernstein basis was shown and some generalized tension properties were given.
Some trigonometric basis functions with shape parameters have been proposed for curve design. In 2004, in the space span, Han presented a kind of cubic trigonometric Bernstein basis function possessing a shape parameter in [15]. In 2008, Wu and their coauthors proposed quadratic trigonometric Bernstein basis functions with shape parameters in the space span in [16]. Later, in the space span , a kind of cubic trigonometric Bernstein basis functions possessing two shape parameters was presented in [17], which includes the cubic trigonometric Bernstein basis functions in [15] as a special case. In 2015, in the space span, Zhu and Han constructed a kind of trigonometric Bernstein basis functions with two exponential shape parameters in [18]. In 2018, a class of rational trigonometric Bernstein basis functions were proposed in the space span in [19]. In 2019, Zhu and Liu proposed a family of trigonometric Bernstein basis functions with four shape parameters in the space span in [20], which includes the trigonometric Bernstein basis functions given in [15,16,17,18] as special cases. In [21], five new trigonometric blending functions possessing two shape parameters of exponential form were proposed. Recently, Majeed [22] and their coauthors proposed a kind of trigonometric B-spline curves holding the shape-adjustable quality that the classical B-spline curves does not hold.
The purpose of this paper is to propose a new kind of generalized quasi cubic trigonometric Bernstein basis functions with two shape functions and constructed in the space , which form a normalized optimal totally positive basis and include the functions in [15,16,17,18,19,20] as special cases. In [23,24,25], the concept of normalized B-basis related to the normalized optimal totally positive basis is mentioned, which corresponds to the optimal shape preserving properties. This kind of new generalized quasi cubic trigonometric Bernstein basis functions has good generality and wide applications, as different shape functions and lead to different kinds of spaces mentioned in [15,16,17,18,19,20]. In order to construct more new basis functions conveniently, we propose some simplified constructive conditions. Based on those simplified constructive conditions, we construct three specific examples of the shape functions and , and give the corresponding applications of those three examples. What is more, after verification, the space mentioned in [19] is a special case that satisfies the simplified constructive conditions. Moreover, the corresponding quasi cubic trigonometric B-spline basis functions with two local shape functions and are also constructed, and the shape functions and satisfy some additional conditions.
The rest of this paper is organized as follows. In Section 2, the meterial and methods are introduced. In Section 3, the construction and properties of the generalized quasi trigonometric Bernstein basis and the corresponding quasi trigonometric Bézeir curves are given, including the simplified constructive conditions that the two shape functions satisfy. Three specific examples are given. Section 4 gives the definitions and properties of the generalized quasi cubic trigonometric B-spline basis functions and corresponding curves, including the additional conditions that the two shape functions satisfy. In Section 5, our conclusions are given.
2. Materials and Methods
2.1. Bernstein Basis Functions and Bézeir Curves
Definition 1.
Given control points or (i = 0, 1, …, n), the Bézier curve can be defined as
where the Bernstein basis functions , are defined as follows
Some important properties of the Bernstein basis functions , are listed as follows.
(A) Nonnegativity. For any , , .
(B) End-point properties. , .
(C) Partition of unity.
(D) Symmetry.
(E) Recurrence.
(F) Total positivity. For any sequence of points , the collocation matrix is totally positive, which means that all its minors are nonnegative.
From the properties of Bernstein basis functions above, the following properties of Bézier curves can be obtained.
(A) Affine invariance. Since the Bernstein basis functions have the property of partition of unity, the corresponding Bézier curve has the property of affine invariance.
(B) End-point property. The starting point and end point of Bézier curve coincide with and .
(C) Convex hull property. Since the Bernstein basis functions have nonnegativity and partition of unity, the Bézier curve must lie inside the control polygon spanned by the control points.
(D) Symmetry. A new Bézier curve is constructed from the control vertex , which has the same shape as the original Bézier curve and the opposite direction.
(E) Variation diminishing property. Since the Bernstein basis functions form a group of optimal normalized totally positive bases, the corresponding Bézier curve possesses variation diminishing property, that is no plane intersects a Bézier curve more often than it intersects the corresponding control polygon.
2.2. Extended Chebyshev Space and Blossom Theory
In this subsection, we shall give a brief presentation of Chebyshev spaces and blossom theory, which will be used further in the following construction.
Definition 2.
Given a real interval I, we call a k-dimensional space U as an Extended Chebyshev space (EC space) on I if any nonzero element of U has at most k − 1 zeros (counted with multiplicities) in I. It is said to be a complete extended Chebyshev space (ECC space) on I if there exists a nested sequence
where is an i-dimensional EC space on I, for i = 1, 2, …, k.
Remark 1.
On a closed bounded interval I = [a, b], an EC space is an ECC space.
The related proofs are given in [26].
Remark 2.
A given k-dimensional subspace U is an ECC space on I iff there exists k positive functions such that , where D stands for the ordinary differentiation and are called weight functions associated with U. For , the differential operators are defined by
Blossom is a useful tool for curves and surfaces construction, and it is especially powerful when used to analyze splines. More details are shown in [8]. Using means of intersections of convenient osculating flats, it is possible to define a notion of blossom.
Definition 3.
A geometrically regular function of order k, , is said to be a piecewise smooth Chebyshev function of order k on I, if for all distinct points and all positive integers whose sum is equal to k, the affine flat consists of a single point. The function so defined is called the blossom of Φ. It is a symmetric function and it satisfies
Let ε be the associated space of Φ. For any affine map h: aff, the blossom of the ε-function will be defined by
The detailed proofs and properties are given in [27].
3. Generalized Quasi Cubic Trigonometric Bernstein Basis Functions
3.1. Construction and Properties
In this subsection, for , we shall work with the generalized quasi cubic trigonometric function space , which possesses good generality. In the cases of [15,16,17,18,19,20], the expressions of the shape functions are
respectively. The corresponding properties and applications have been stated in detail in [15,16,17,18,19,20].
In order to construct more new basis functions conveniently, here we give some simplified constructive conditions that satisfy
The expression of the associated mother-function is
Firstly, we are about to show that the following space
is a 3-dimensional EC-space on . Then by Theorem 2.1 of [28], we can see the existence of blossom in , which implies that the new space is suited for curves design.
Theorem 1.
Proof of Theorem 1.
For any , , we consider a linear equation
For , from Equation (3), we can immediately obtain . Similarly, for , from Equation (3), we can obtain . Furthermore, finally, we can draw the conclusion that . Thus, the space is a 3-dimensional space on .
Next, we are about to prove that the space is a 3-dimensional ECC-space in . For any , let
and
The computation of derivatives gives that
Thus, the expression of the Wronskian of and gives that
For , three weight functions are defined as follows
where are three arbitrary positive real numbers. It is obvious that these weight functions are bounded, positive and on . Consider the following ECC-space defined by the weight functions
it is easy to check that these functions () are in fact some linear combinations of , which implies that the space is an ECC-space on . As are arbitrary subintervals of , we can draw the conclusion that the space is an ECC-space in .
Next, we are about to prove that the space is also an EC-space on . We only need to prove that any nonzero element of the space has at most two zeroes (counting multiplicities as far as possible up to 2) on . For , consider the nonzero function
Since the space is an ECC-space in , has at most 2 zeroes in . If we assume that the function vanishes at 0, then we can obtain that . In this case, if , then has a singular zero at 0 and a singular zero at 1. If , it is obvious that 0 is a double zero of . If , vanishes only one time at 0 and it does not vanish anywhere else on . If , vanishes only one time at 0 and it does not vanish at . For , the computation of the second derivative of F(t) gives that
When , then , in (0,), it is obvious that and . By applying the condition in Equation (1), we have
so . When and , . Thus, is a monotonic function in (0,). By Rolle’s theorem, we can conclude that has at most one zero in (0,). Similarly, by analyzing the case that vanishes at , we can also obtain the conclusion that has at most two zeroes on . Summarizing, the space is an EC-space on . □
Since the space is an EC-space on , by Theorem 4.1 of [28], we can obtain that the space has a kind of normalized Bernstein basis on . In the following theorem, we shall give the expression of Chebyshev–Bézier points of the mother-function defined in Equation (2) and the associated generalized quasi cubic trigonometric Bernstein basis of the space .
Theorem 2.
Moreover, the associated four generalized quasi cubic trigonometric Bernstein basis functions of the space are given by
Proof of Theorem 2.
From the definition of the mother-function given in Equation (2), we have
Thus, by simply computing, we have
For any , from together with , we can easily deduce the expressions of the generalized quasi cubic trigonometric Bernstein basis , . □
Remark 3.
By analyzing the expressions of the generalized quasi cubic trigonometric Bernstein basis functions given in Equation (5), it is easy to conclude that these basis functions possess the properties of linear independence, nonnegativity and partition of unity. What is more, for , the end-point properties are given as follows
Moreover, vanishes two times at and vanishes two times at 0 (counting multiplicities as far as possible up to 2). Therefore, by Definition 2.10 of [28], we can see that the system is precisely the normalized Bernstein basis of the space span , which indicates that the generalized quasi cubic trigonometric Bernstein basis is totally positive and possesses optimal shape preserving properties. In [23,24,25], the concept of normalized B-basis conincides with the normalized Bernstein basis, which corresponds to the optimal shape preserving properties.
These shape preserving properties mainly include monotonicity preserving and variation diminishing, with more details stated in [23,24,25,29,30]. On the one hand, monotonicity preserving indicates that the curve has the same monotonicity as the monotone control points, and the length of the generated parametric curves is bounded above by the length of their control polygon. If the control polygon is planar and convex, then the curve is also planar and convex. On the other hand, the basis functions have variation diminishing property, so the curve never crosses a hyperplane more often than its control polygon does.
There are many shape functions that satisfy Equation (1). Here we analyze three specific examples and show some plots of these examples. In order to state conveniently, in the following discussion, we will also denote the four generalized quasi cubic trigonometric Bernstein basis functions as , or , and .
Example 1.
We consider the simple example without parameters. The expressions of the shape functions are
Next, we analyze that these two shape functions of Equation (6) satisfy Equation (1) mentioned above. By substituting the endpoint value 0 and and calculating the corresponding derivation, we have
Then, we will prove . By simple analysis, we have
which implies that We shall further prove . For this, we only need to prove that
Suppose
So reaches the maximum value when and reaches the minimum value when t=, since
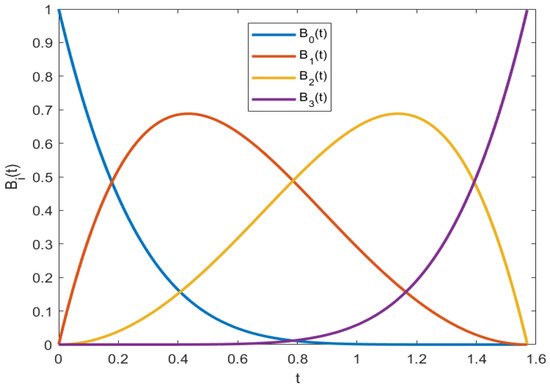
so we have . So satisfies Equation (1). The analysis of is the same. The figure of the corresponding generalized quasi cubic trigonometric Bernstein basis functions defined in Equation (5) are shown below in Figure 1.

Figure 1.
The plot of the generalized quasi cubic trigonometric Bernstein basis functions with and given in Equation (6).
Example 2.
We consider the shape functions with denominator parameters. The expression of the shape functions are
where . Next, we analyze that these two shape functions satisfy Equation (1) mentioned above. When , it has been stated in [6] in detail. Then we prove the case of . The other cases are the same. It is obvious that
Then, we further prove that
By simple calculations, we only need to prove
Suppose
The expression of the partial derivative is
The axis of symmetry of is , so monotonically decreases on . After calculation, we find that
we know that has only one zero on , and the function increases monotonically first and then decreases monotonically. The minimum value of the function is
By simple analysis, the axis of symmetry of is , and the axis of symmetry of is , so
So we have proved that . Then we will further prove .
We only need to prove
Suppose
Then, we have
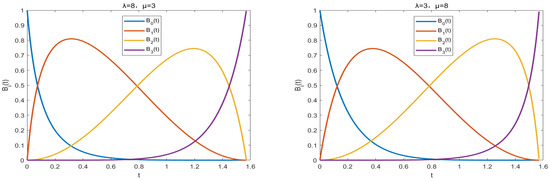
By analyzing the structure of the function , we have on . So satisfies Equation (1). The analysis of is the same. The figure of the corresponding generalized quasi cubic trigonometric Bernstein basis functions defined in Equation (5) are shown below in Figure 2.

Figure 2.
Some plots of the generalized quasi cubic trigonometric Bernstein basis functions with and given in Equation (7) and p = q = 1.
Example 3.
We consider the shape functions with exponential parameters. The expression of the shape functions are
where . Next, we are about to prove that these two shape functions of Equation (8) also satisfy Equation (1). We take as an example, and other cases are the same. It’s obvious that
Then we will further prove By simple calculations, combining with the range of parameters, we have
So satisfies Equation (1).
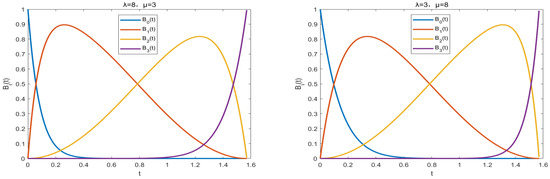
The analysis of is the same. The figure of the corresponding generalized quasi cubic trigonometric Bernstein basis functions with exponential parameters defined in Equation (5) are shown in Figure 3.

Figure 3.
Some plots of the generalized quasi cubic trigonometric Bernstein basis functions with and given in Equation (8) and p = q = 2.
3.2. New Generalized Quasi Cubic Trigonometric Bézier Curve
Definition 4.
Given control points in or , satisfying Equation (1), then
is called a generalized quasi cubic trigonometric Bézier curve with two shape functions and .
In [30], Bernstein–Bezier methods are emphasized. As the new generalized quasi cubic trigonometric Bernstein basis given in Equation (5) possesses the properties of partition of unity, nonnegativity and total positivity, we can conclude that the corresponding generalized quasi cubic trigonometric Bézier curve given in Equation (9) possesses the properties of affine invariance, convex hull and variation diminishing, which are crucial properties in the field of curve design and surface construction. With exact computation, the end-point properties of the generalized quasi cubic trigonometric Bézier curve are as follows
The above end-point properties imply that for any and satisfying Equation (1), the generalized quasi cubic trigonometric Bézier curve has end-point interpolation property and , are the tangent lines of the curve at the points and , respectively. From these equations, we can conclude that the generalized quasi cubic trigonometric Bézier curve has some properties analogous to the similar properties of the cubic Bézier curve.
Corner cutting algorithm is an efficient and stable method of computing the generalized quasi cubic trigonometric Bézier curve and it is formed by convex combinations. In order to develop such an algorithm, we rewrite the generalized quasi cubic trigonometric Bézier curve in Equation (9) in the following matrix form
From these, we can easily obtain a corner cutting algorithm for computing the generalized quasi cubic trigonometric Bernstein–Bézier curve, and more details for the Bernstein–Bézeier curve is stated in detail in [29]. While dealing with the approximation of control polygon, shape preserving approximations are considered in [31]. Analogous to these approximation methods mentioned in [31], Figure 4 gives the structure of the corner cutting algorithm and the corresponding applications of three specific examples, respectively. Moreover, for , we rewrite Equation (9) as the following form
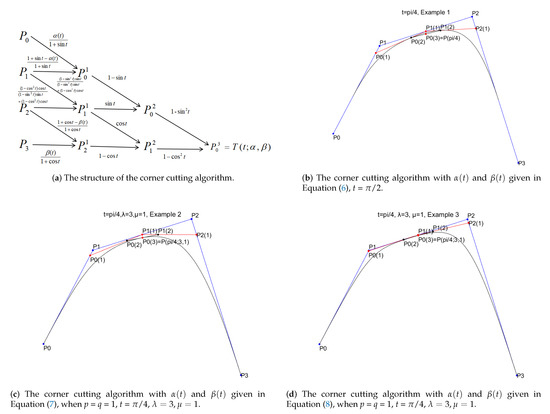
Figure 4.
Corner cutting algorithm for computing the quasi trigonometric Bézier curve.
From Equation (10), we can check that the shape functions and only affect the curve on the control edge and , respectively. Moreover, for any fixed , decreases with the increase of , which implies that the curve moves in the same direction of the edge as increases. Inversely, when decreases, the curve moves in the opposite direction to the edge . The effect of the shape function on the edge is similar. When the shape functions satisfy , with the increase or the decrease of , the curve moves in the same direction or the opposite direction to the edge , respectively. Furthermore, when and increase at the same time, the curve tends to the edge . Thus, we can see that the shape functions and can be seen as local tension parameters.
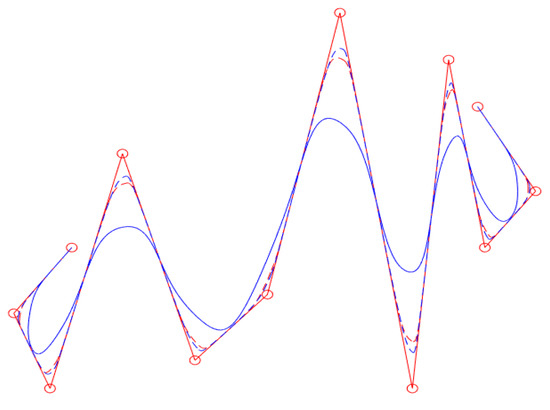
Figure 5 shows the effect of the shape parameters on the generalized quasi cubic trigonometric Bézier curves. Figure 6 shows the comparison among the new proposed generalized quasi cubic trigonometric Bézier curves (blue dashed lines, black solid lines and black dashed lines), the classical cubic rational Bézier curves (red dashed lines) and –Bézier curves (red solid lines) defined by the –Bernstein basis functions given in [7], constructed in the space span. Clearly, for the same weights, the classical cubic rational Bézier curve is the farmost away from the control polygon among the three curves, and the proposed generalized quasi trigonometric Bézier curves are closer to the control polygon than the –Bézier curves given in [7] under the same control points.
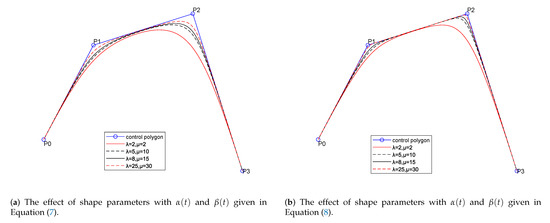
Figure 5.
The effect of shape parameters on the generalized quasi cubic trigonometric Bézier curves, when .
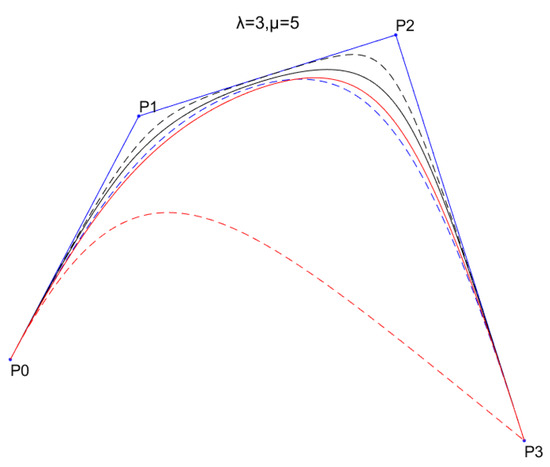
Figure 6.
Comparisons among generalized quasi cubic trigonometric Bézier curves (blue dashed lines with and given in Equation (6), black solid lines with and given in Equation (7) and black dashed lines with and given in Equation (8)), –Bézier curves (red solid lines) defined by the –Bernstein basis functions in [7] and classical cubic rational Bézier curves (red dashed lines), where .
4. New Generalized Quasi Cubic Trigonometric B-Spline Basis with Two Shape Functions
In this section, similar with the construction of cubic B-spline basis starting from cubic Bernstein basis, we will propose a new kind of generalized quasi cubic trigonometric B-spline basis starting from the generalized quasi cubic trigonometric Bernstein basis given in Equation (5).
4.1. New Generalized Quasi Cubic Trigonometric B-Spline Basis Functions
Given knots , we denote as a knot vector. Let , and For any functions () satisfying Equation (1) and some additional conditions
we want to construct the associated generalized quasi cubic trigonometric B-spline basis functions as follows
where are the generalized quasi cubic trigonometric Bernstein basis functions given in Equation (5). continuity at each of knots and the property of partition of unity on the interval are considered. From these conditions, we will calculate the expression of the coefficients . Function having continuity at each of knots needs to satisfy that the function, the first derivative and the second derivative are continuous at this node, respectively. Obviously, has continuity at . Then when has continuity at , we have
Further simplification
When has continuity at , we have
Further simplification
When has continuity at , we have
Further simplification
The above calculation results are summarized as follows
where
To form a partition of unity on the interval , these generalized quasi cubic trigonometric B-spline basis functions need to satisfy the equation as follows
For ,
For any , from , we can deduce the following equations about the relation among the coefficients ()
Use for other coefficients and bring them into the equations, we get
To solve the system of equations, we get
Combine the above calculations, when these generalized quasi cubic trigonometric B-spline basis functions have continuity at each of knots and form a partition of unity on the interval , we will get the expression of the coefficients as follows
Definition 5.
Remark 4.
By changing the range of some parameters, Equation (7) and Equation (8) also satisfy the additional Equation (11).
For equidistant knots, the and the knot vector U are called a uniform generalized quasi cubic trigonometric B-spline basis function and a uniform vector. For non-equidistant knots, and U are called that of non-uniform ones, respectively. Figure 7 gives some plots of generalized quasi cubic trigonometric B-spline basis functions with different shape parameters with and given in Equations (13) and (14).
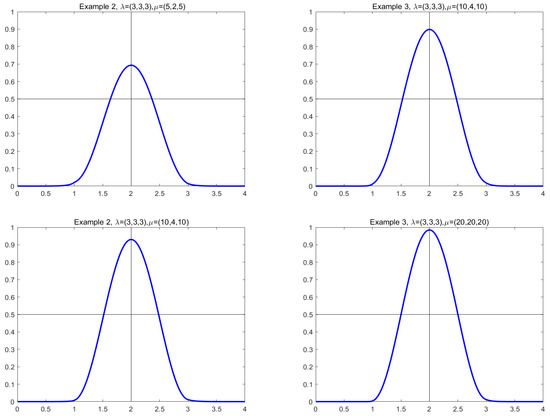
Remark 5.
Remark 6.
The coefficients of the B-spline stated in Equation (12) are positive, so the generalized quasi cubic trigonometric B-spline is also positive. Moreover, with the nonnegativity of the generalized quasi cubic trigonometric Bernstein basis functions, the corresponding corner cutting algorithm is stable, then the convex combination is formed, so the overall stability is guaranteed. Instability may only occur when caculating the trigonometric functions.
With straightforward caculation, the following lemma is given, which is effecient when working with the partition of unity and the continuity of the generalized quasi cubic trigonometric B-spline basis functions.
Lemma 1.
For all possible , the following equations hold
4.2. Properties of the New Generalized Quasi Cubic Trigonometric B-Spline Basis Functions
In this subsection, we are about to show that the new generalized quasi cubic trigonometric B-spline basis given in Equation (12) possesses some significant properties for curves and surfaces construction, such as partition of unity (Theorem 3), nonnegativity (Theorem 4), linear independence (Theorem 5), total positivity (Theorem 6) and continuity (Theorem 7).
Theorem 3.
For , we have .
Proof of Theorem 3.
For it is easy to check that for Since
by using Lemma 1, we have
This indicates that the new proposed generalized quasi cubic trigonometric B-spline basis has the property of partition of unity. □
Proof of Theorem 4.
Theorem 5.
Proof of Theorem 5.
For , , let
For functions satisfying Equations (1) and (11), direct computation gives that
where . Thus, we can conclude the following linear systems of equations about , ,
Notice that , in order to compute the determinant of the coefficient matrix given by the above linear systems of equations, we add the first and the third column to the second column, respectively. For the specific expression of the determinant, we have
Therefore, we can conclude that for . □
Theorem 6.
Proof of Theorem 6.
Since the system () is the normalized B-basis of the space . By Theorem 4.2 of [25], it is sufficient to conclude that is a nonsingular stochastic and totally positive matrix. For any functions satisfying Equations (1) and (11), for all possible , , it is easy to check that , , . In addition, from Lemma 1, we can conclude that is stochastic. We want to prove that is a totally positive matrix, we need to check the nonnegativity of all its minors. With direct computation, we have
From these, we can deduce that is nonsingular and the nonnegativity of all its remaining minors is proved, which implies the theorem. □
Theorem 7.
4.3. New Generalized Quasi Cubic Trigonometric B-Spline Curves
Definition 6.
Obviously, for , , the curve can be represented by the following curve segment
From Theorems 3 and 4, we know that the generalized quasi cubic trigonometric B-spline basis has the properties of partition of unity and nonnegativity, so the corresponding new generalized quasi cubic trigonometric B-spline curve has affine invariance. Furthermore, for , lies in the convex hull of the points , , , . Similarly, from Theorem 6, as the generalized quasi cubic trigonometric B-spline basis has the property of total positivity, the new generalized quasi cubic trigonometric B-spline curve has variation diminishing property, which implies that is suited for the shape control. As a direct result of Theorem 7, we have the following theorem.
Theorem 8.
With a non-uniform knot vector, at each of the knots, the new generalized quasi cubic trigonometric B-spline curve has continuity. Moreover, if is a simple knot, then for , we have
Example 4.

Figure 8 shows the open spline curves with and given in Equation (13) with different shape parameters, which implies the shape of a rabbit. The first one is constructed by setting all . The second one is constructed by changing one from 2.4 to 6 based on the first one. The third one is constructed by changing other two from 2.4 to 4 based on the second one.

Figure 8.
Close curves with uniform knot vector of the shape functions with and given in Equation (13).
Example 5.
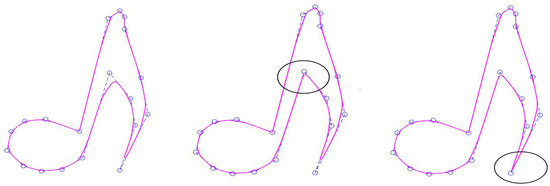
Similarly, Equation (14) also satisfies the additional conditions. Figure 9 shows the open spline curves with and given in Equation (14) with different shape parameters, which describes the shape of a note. The first one is constructed by setting all . The second one is constructed by changing one from 2.5 to 6 based on the first one. The third one is constructed by changing another one from 2.5 to 6 based on the second one.

Figure 9.
Close curves with uniform knot vector of the shape functions with and given in Equation (14).
Figure 10 shows the comparison among the new proposed generalized quasi cubic trigonometric B-spline curves (blue dashed lines with and given in Equation (13) and red dashed lines with and given in Equation (14)) and the trigonometric B-spline basis functions defined in [18] (blue solid lines). It is easy to conclude that for the same weights, the proposed generalized quasi trigonometric B-spline curves are closer to the control polygon than trigonometric B-spline basis functions defined in [18] under the same control points and the same parameters. What is more, the shape of the new proposed curves are more smooth.
5. Conclusions
We have proposed a new class of generalized quasi cubic trigonometric Bernstein basis with two shape functions, which has totally positive property and optimal shape preserving property. These two shape functions satisfy some conditions with wide range of use, and three specific examples are given. The corresponding generalized quasi cubic trigonometric Bézeir curve and the corresponding corner cutting algorithm are shown. Based on the basis, with additional conditions, a new class of generalized quasi cubic trigonometric B-spline basis functions is developed, which has partition of unity, nonnegativity, linear independence, total positivity and continuity. The corresponding generalized quasi cubic trigonometric B-spline curve and its applications are given. There are also some worthwhile work to study further, such as exploring more practical applications of those generalized basis with two shape functions. These will be our future work.
Author Contributions
Conceptualization, Y.F. and Y.Z.; methodology, Y.F. and Y.Z.; Software, Y.F. and Y.Z.; validation, Y.F.; formal analysis, Y.F. and Y.Z.; investigation, Y.F. and Y.Z.; resources, Y.F.; data curation, Y.F.; writing—original draft preparation, Y.F. and Y.Z.; writing—review and editing, Y.F. and Y.Z.; visualization, Y.F.; supervision, Y.Z.; project administration, Y.Z.; funding acquisition, Y.Z. Both authors have read and agreed to the published version of the manuscript.
Funding
The research is supported by the National Natural Science Foundation of China (No. 61802129), the Natural Science Foundation Guangdong Province, China (No. 2018A030310381), the National Training Program of Innovation and Entrepreneurship for Undergraduates (No. 202010561123), and the Hundred steps climbing plan of South China University of Technology (No. j2tw2021020012).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the associate editor and the referees for their insightful comments and invaluable suggestions.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EC | Extended Chebychev |
| ECC | Extended Complete Chebychev |
References
- Nielson, G.M. A locally controllable spline with tension for interactive curve design. Comput. Aided Geom. Des. 1984, 1, 199–205. [Google Scholar] [CrossRef]
- Brian, A.B. Local control of bias and tension in Beta-splines. ACM Trans. Graph. 1983, 2, 109–134. [Google Scholar] [CrossRef]
- Costantini, P. Curve and surface construction using variable degree polynomial splines. Comput. Aided Geom. Des. 2000, 17, 419–446. [Google Scholar] [CrossRef]
- Shen, W.Q.; Wang, G.Z.; Yin, P. Explicit representations of changeable degree spline basis functions. J. Comput. Appl. Math. 2013, 238, 39–50. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L. New cubic rational basis with tension shape parameters. Appl. Math. J. Chin. Univ. Ser. B 2015, 30, 273–298. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L.; Liu, S.J. Curve construction based on four αβ-Bernstein-like basis functions. J. Comput. Appl. Math. 2015, 273, 160–181. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L. Curves and surfaces construction based on new basis with exponential functions. Acta Appl. Math. 2014, 129, 183–203. [Google Scholar] [CrossRef]
- Ramshaw, L. Blossoming: A Connect-the-Dots Approach to Splines; Digital Systems Research: Palo Alto, CA, USA, 1987. [Google Scholar]
- Mazure, M.L.; Laurent, P.J. Piecewise smooth spaces in duality: Application to blossoming. J. Approx. Theory 1999, 98, 316–353. [Google Scholar] [CrossRef]
- Mazure, M.L. Quasi-Chebychev splines with connexion matrices: Application to variable degree polynomial splines. Comput. Aided Geom. Des. 2001, 18, 287–298. [Google Scholar] [CrossRef]
- Mazure, M.L. Blossoms and optimal bases. Adv. Comput. Math. 2004, 20, 177–203. [Google Scholar] [CrossRef]
- Costantini, P.; Lyche, T.; Manni, C. On a class of weak Tchebysheff systems. Numer. Math. 2005, 101, 333–354. [Google Scholar] [CrossRef]
- Mazure, M.L. On dimension elevation in Quasi Extended Chebyshev spaces. Numer. Math. 2008, 109, 459–475. [Google Scholar] [CrossRef]
- Costantini, P.; Pelosi, F.; Sampoli, M.L. New spline spaces with generalized tension properties. BIT Numer. Math. 2008, 48, 665–688. [Google Scholar] [CrossRef]
- Han, X.L. Cubic trigonometric polynomial curves with a shape parameter. Comput. Aided Geom. Des. 2004, 21, 535–548. [Google Scholar] [CrossRef]
- Wu, X.Q.; Han, X.L.; Luo, S. Quadratic trigonometric polynomial Bézier curves with a shape parameter. J. Eng. Graph. 2008, 1, 82–87. [Google Scholar] [CrossRef]
- Han, X.A.; Ma, Y.C.; Huang, X.L. The cubic trigonometric Bézier curve with two shape parameters. Appl. Math. Lett. 2008, 22, 226–231. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L. New trigonometric basis possessing exponential shape parameters. J. Comput. Math. 2015, 33, 642–684. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, G.C.; Nhon, N.T. New trigonometric basis possessing denominator shape parameters. Math. Probl. Eng. 2018, 9569834. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Liu, Z. A class of trigonometric Bernstein-type basis functions with four shape parameters. Math. Probl. Eng. 2019. [Google Scholar] [CrossRef]
- Han, X.L.; Zhu, Y.P. Curve construction based on five trigonometric blending functions. BIT Numer. Math. 2012, 52, 953–979. [Google Scholar] [CrossRef]
- Majeed, A.; Abbas, M.; Qayyum, F.; Miura, K.T.; Misro, M.Y.; Nazir, T. Geometric modeling using new cubic trigonometric B-spline functions with shape parameter. Mathematics 2020, 8, 2102. [Google Scholar] [CrossRef]
- Peña, J.M. Shape Preserving Representations in Computer-Aided Geometric Design; Nova Science Publishers: Hauppauge, NY, USA, 1999. [Google Scholar]
- Peña, J.M. Shape preserving representations for trigonometric polynomial curves. Comput. Aided Geom. Des. 1997, 14, 5–11. [Google Scholar] [CrossRef]
- Carnicer, J.M.; Peña, J.M. Total positive bases for shape preserving curve design and optimality of B-splines. Comput. Aided Geom. Des. 1994, 11, 635–656. [Google Scholar] [CrossRef]
- Pottmann, H. The geometry of Tchebycheffian splines. Comput. Aided Geom. Des. 1993, 10, 181–210. [Google Scholar] [CrossRef]
- Mazure, M.L. Blossoming: A Geometrical Approach. Constr. Approx. 1999, 15, 33–68. [Google Scholar] [CrossRef]
- Mazure, M.L. Which spaces for design? Numer. Math. 2008, 110, 357–392. [Google Scholar] [CrossRef]
- Farin, G. Curves and Surfaces for Computer Aided Geometric Design; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Gori, L.; Pitolli, F. Totally positive refinable functions with general dilation M. Appl. Numer. Math. 2017, 112, 17–26. [Google Scholar] [CrossRef]
- Goodman, T.N. Total Positivity and the Shape of Curves. In Total Positivity and Its Applications; Gasca, M., Micchelli, C.A., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; pp. 157–186. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).