Queuing-Inventory Models with MAP Demands and Random Replenishment Opportunities
Abstract
1. Introduction
2. General Description
- The subscript refers to the model under consideration.
- The symbol stands for the transpose notation.
- , whose dimension should be clear in the context. Where more clarity is needed, the dimension will be mentioned, e.g., is a column vector of 1s of dimension m.
- , where 1 is in the ith position.
- I denotes an identity matrix, whose dimension is dictated by the context.
- denotes a diagonal matrix with diagonal (possibly block) entries given by through . In the context where this notation is used, it will be clear whether the entities are scalars or vectors or matrices.
3. Opportunistic Model 1
- to be the number of customers in the system (including one in service),
- to be the level of the inventory,
- to be the phase of the service (if the server is idle, this will not be defined),
- to be the phase of the arrival process,
- , probabilities of demands greater than i, are computed as
- P, a square matrix of dimension is defined asA quick look at P indicates that the customers’ demands are taken into consideration at the time of their arrivals. The first column of P justifies that the structure due to the customers’ demands are met partially. It is easy to verify that

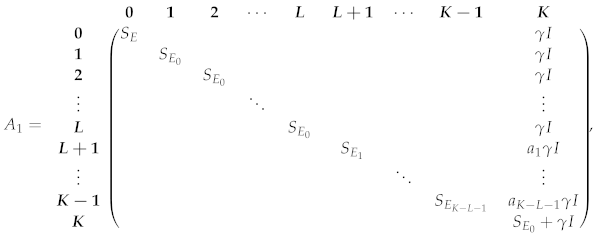
3.1. Computation of R
3.2. Selected System Measures in Steady-State
- 1.
- Server idle probability: .
- 2.
- Probability of idle server with positive inventory:
- 3.
- Percent of server idle time with positive inventory:
- 4.
- Mean number of customers in the system: .
- 5.
- Variance of the number of customers in the system:
- 6.
- Probability of customer loss (at arrivals):
- 7.
- Mean inventory level:
- 8.
- Variance of the inventory level:
- 9.
- Mean cycle time of replenishment:
- 10.
- Mean replenishment quantity:
- 11.
- Probability of procuring an order when a replenishment opportunity arises:
4. Opportunistic Model 2
- to be the number of customers in the system,
- to be the level of the inventory,
- to be the phase of the service (if the server is idle, this will not be defined),
- to be the phase of the arrival process,
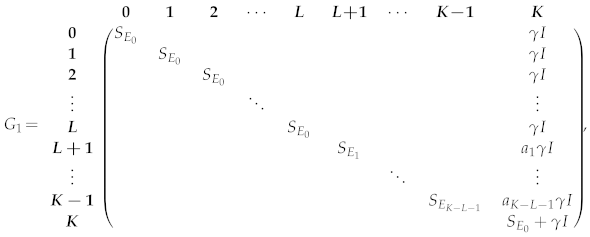
4.1. Computation of and
4.2. Selected System Measures in Steady-State
- 1.
- Server idle probability:
- 2.
- Probability of idle server with positive inventory:
- 3.
- Percent of server idle time with positive inventory:
- 4.
- Mean number of customers in the system: .
- 5.
- Variance of the number of customers in the system:
- 6.
- Probability of customer loss at arrivals:
- 7.
- Mean inventory level:
- 8.
- Variance of the inventory level:
- 9.
- Mean cycle time of replenishment:
- 10.
- Mean replenishment quantity:
- 11.
- Probability of procuring an order when a replenishment opportunity arises:
5. Illustrative Numerical Examples
- ERA
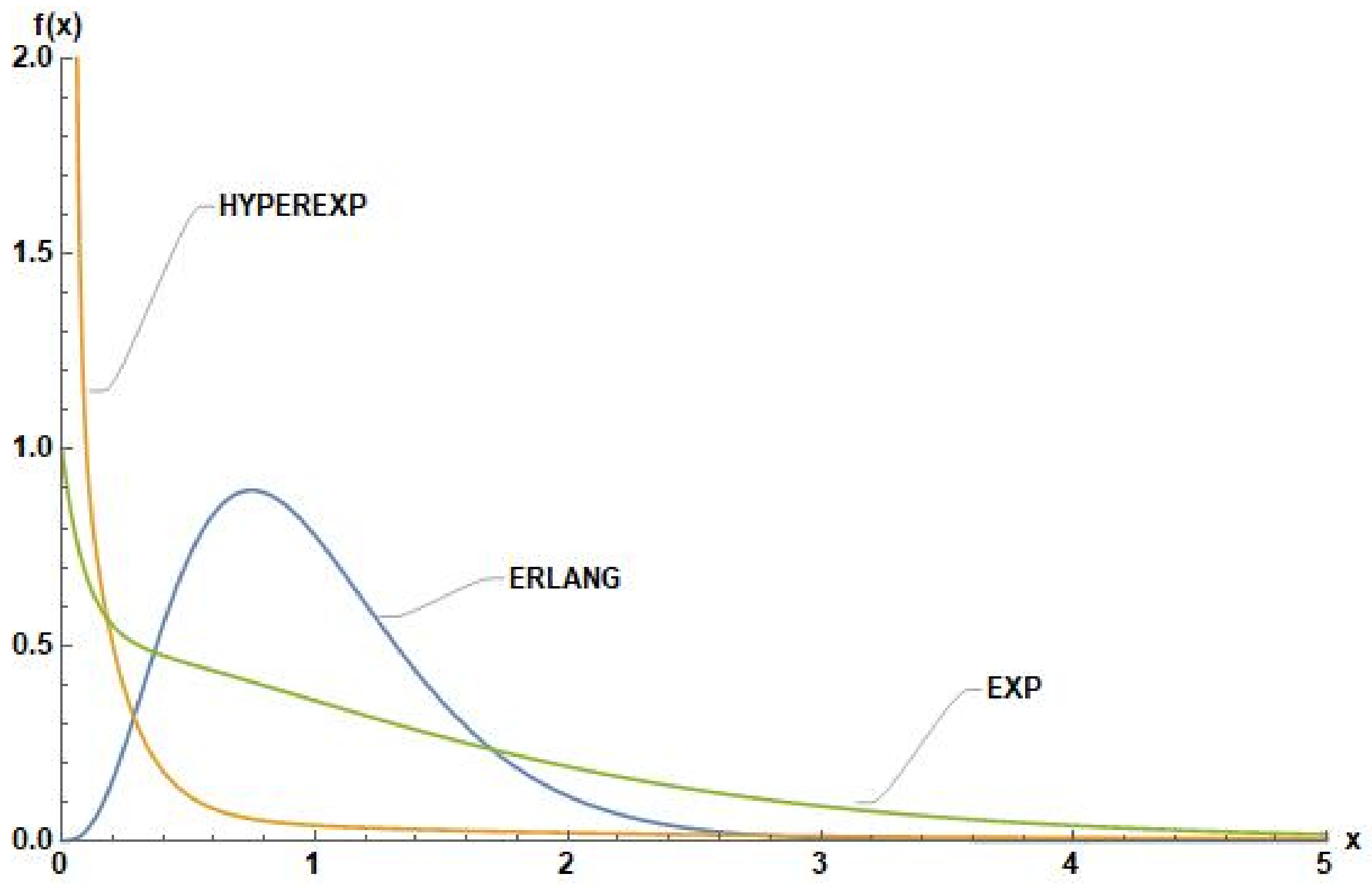
- Erlang distributed inter-arrival times with density , , and (standard deviation ).
- HEA
- Hyperexponential inter-arrival times with density , , , and (standard deviation ).
- PCA
- Markov arrival process with positive correlation (standard deviation ), where
- ERS
- Erlang distributed service times having density with .
- EXS
- Exponentially distributed service times of rate .
- HES
- Hyperexponentially distributed service times with density , , and .
- In ISS, inventory is consumed and replenished as needed and is characterized by the parameters , and the distribution of the time between two opportunities for replenishment. The arrival process to CSS impacts ISS through the demand for items. ], ], ], ], ] represent the measures of performance for ISS for Model 1 [Model 2].
- In CSS, customers arrive, receive service (plus items from inventory), and depart and are characterized by the arrival and service processes. Some arrivals are lost due to lack of inventory at the time of arrival. In Model 2, customers may also be lost at a service completion epoch due to lack of inventory at that moment. Customer loss is impacted by the availability of inventory in ISS. , , , , represent measures of performance for CSS for Model 1 [Model 2].
5.1. Impact of Service Rate and Service Time Distribution
5.2. Effect of Arrival Process
5.3. Impact of
5.4. Impact of K and L
5.5. Cost Analysis
5.6. Comparing Model 1 and Model 2
5.7. Comparing System with System
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Friend, J.K.; Kaminsky, F.C. Stock Control with Random Opportunities for Replenishment. J. Oper. Res. Soc. 1960, 11, 130–136. [Google Scholar] [CrossRef]
- Hurter, A.P.; Kaminsky, F.C. Inventory Control with a Randomly Available Discount Purchase Price. Oper. Res. Q. 1968, 19, 433–444. [Google Scholar] [CrossRef]
- Silver, E.A.; Robb, D.J.; Rahnama, M.R. Random Opportunities for Reduced Cost Replenishments. IIE Trans. 1993, 25, 111–120. [Google Scholar] [CrossRef]
- Gurnani, H. Optimal ordering policies in inventory systems with random demand and random deal offerings. Eur. J. Oper. Res. 1996, 95, 299–312. [Google Scholar] [CrossRef]
- Moinzadeh, K. Replenishment and Stocking Policies for Inventory Systems with Random Deal Offerings. Manag. Sci. 1997, 43, 334–342. [Google Scholar] [CrossRef]
- Feng, Y.; Sun, J. Computing the optimal replenishment policy for inventory systems with random discount opportunities. Oper. Res. 2001, 49, 790–795. [Google Scholar] [CrossRef]
- Goh, M.; Sharafali, M. Price-dependent inventory models with discount offers at random times. Prod. Oper. Manag. 2002, 11, 139–156. [Google Scholar] [CrossRef]
- Chaouch, B.A. Inventory control and periodic price discounting campaigns. Nav. Res. Logist. 2007, 54, 94–108. [Google Scholar] [CrossRef]
- Tajbakhsh, M.M.; Lee, C.-G.; Zolfaghari, S. An inventory model with random discount offerings. Omega 2011, 39, 710–718. [Google Scholar] [CrossRef]
- Karimi-Nasab, M.; Konstantaras, I. An inventory control model with stochastic review interval and special sale offer. Eur. J. Oper. Res. 2013, 227, 81–87. [Google Scholar] [CrossRef]
- Den Boer, A.; Perry, O.; Zwart, B. Dynamic pricing policies for an inventory model with random windows of opportunities. Nav. Res. Logist. 2018, 65, 660–675. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Shajin, D.; Narayanan, V. Inventory with positive service time: A survey. In Advanced Trends in Queueing Theory; Mathematics and Statistics Series; ISTE & Wiley: London, UK, 2019. [Google Scholar]
- Choi, K.H.; Yoon, B.K.; Moon, S.A. Queueing Inventory Systems with Phase-type Service Distributions: A Literature Review. Ind. Eng. Manag. Syst. 2019, 18, 330–339. [Google Scholar] [CrossRef]
- Melikova, A. Z.; Shahmaliyeva, M. O. Markov Models of Inventory Management Systems with a Positive Service Time. J. Comput. Syst. Sci. Int. 2018, 57, 766–783. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Maity, A.; Gupta, U.C. Modeling and Analysis of Bulk Service Queues with an Inventory under (s,S) Policy. Ann. Operat. Res. 2017, 258, 263–283. [Google Scholar] [CrossRef]
- Chakravarthy, S.R. Queueing-inventory models with batch demands and positive service times. Math. Game Theory Appl. 2019, 11, 95–120. [Google Scholar]
- Chakravarthy, S.R.; Rumyantsev, A. Analytical and simulation studies of queueing-inventory models with MAP demands in batches and positive phase type services. Simul. Model. Pract. Theory 2020, 103, 102092. [Google Scholar] [CrossRef]
- Alfa, A.S. Queueing Theory for Telecommunications; Springer Science+Business Media, LLC: Berlin, Germany, 2010. [Google Scholar]
- Artalejo, J.R.; Gomez-Correl, A.; He, Q.M. Markovian arrivals in stochastic modelling: A survey and some new results. SORT 2010, 34, 101–144. [Google Scholar]
- Chakravarthy, S.R. The batch Markovian arrival process: A review and future work. In Advances in Probability Theory and Stochastic Processes; Krishnamoorthy, A., Ed.; Notable Publications Inc.: Trenton, NJ, USA, 2001; pp. 21–39. [Google Scholar]
- Chakravarthy, S.R. Markovian Arrival Processes. In Wiley Encyclopedia of Operations Research and Management Science; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Chakravarthy, S.R. Matrix-Analytic Queueing Models. In An Introduction to Queueing Theory, 2nd ed.; Narayan Bhat, U., Ed.; Birkhauser; Springer Science + Business Media: New York, NY, USA, 2015; Chapter 8. [Google Scholar]
- He, Q.-M. Fundamentals of Matrix-Analytic Methods; Springer: New York, NY, USA, 2014. [Google Scholar]
- Lucantoni, D.M.; Meier-Hellstern, K.S.; Neuts, M.F. A single-server queue with server vacations and a class of nonrenewal arrival processes. Adv. Appl. Probl. 1990, 22, 676–705. [Google Scholar] [CrossRef]
- Lucantoni, D.M. New results on the single server queue with a batch Markovian arrival process. Stoch. Model. 1991, 7, 1–46. [Google Scholar] [CrossRef]
- Neuts, M.F. A versatile Markovian point process. J. Appl. Prob. 1979, 16, 764–779. [Google Scholar] [CrossRef]
- Neuts, M.F. Structured Stochastic Matrices of M/G/1 Type and Their Applications; Marcel Dekker, Inc.: New York, NY, USA, 1989. [Google Scholar]
- Neuts, M.F. Models based on the Markovian arrival process. IEICE Trans. Commun. 1992, E75B, 1255–1265. [Google Scholar]
- Neuts, M.F. Algorithmic Probability: A Collection of Problems; Chapman and Hall: New York, NY, USA, 1995. [Google Scholar]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; The Johns Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]
- Neuts, M.F. Probability distributions of phase type. In Liber Amicorum Prof. Emeritus H. Florin; Department of Mathematics, University of Louvain: Ottignies-Louvain-la-Neuve, Belgium, 1975; pp. 173–206. [Google Scholar]
- Marcus, M.; Minc, H. A Survey of Matrix Theory and Matrix Inequalities; Courier Corporation: Chelmsford, MA, USA, 1992. [Google Scholar]
- Steeb, W.-H.; Hardy, Y. Matrix Calculus and Kronecker Product: A Practical Approach to Linear and Multilinear Algebra, 2nd ed.; World Scientific Publishing Company: Singapore, 2011. [Google Scholar]
- Latouche, G.; Ramaswami, V. Introduction to Matrix Analytic Methods in Stochastic Modeling; ASA-SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]

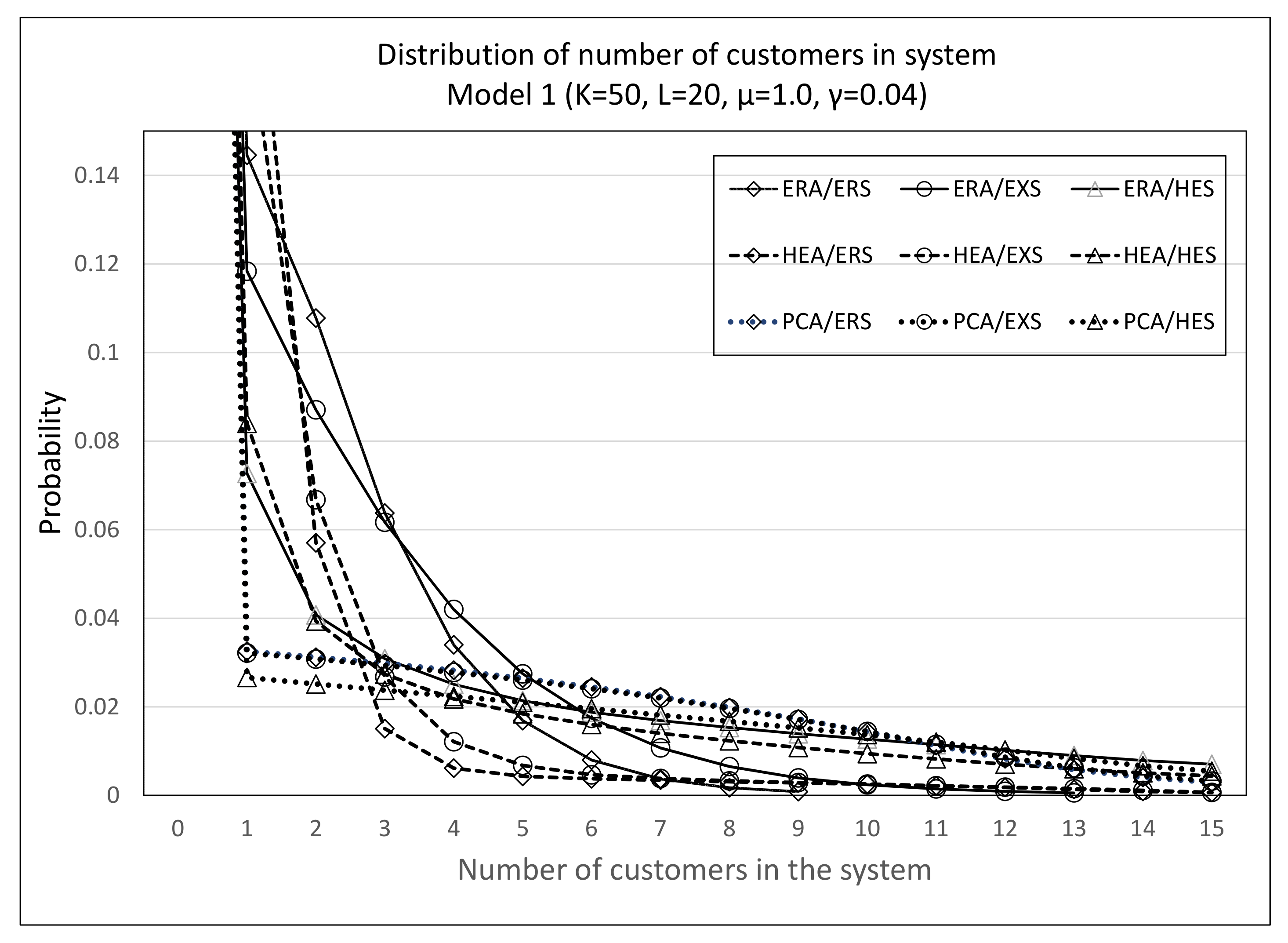
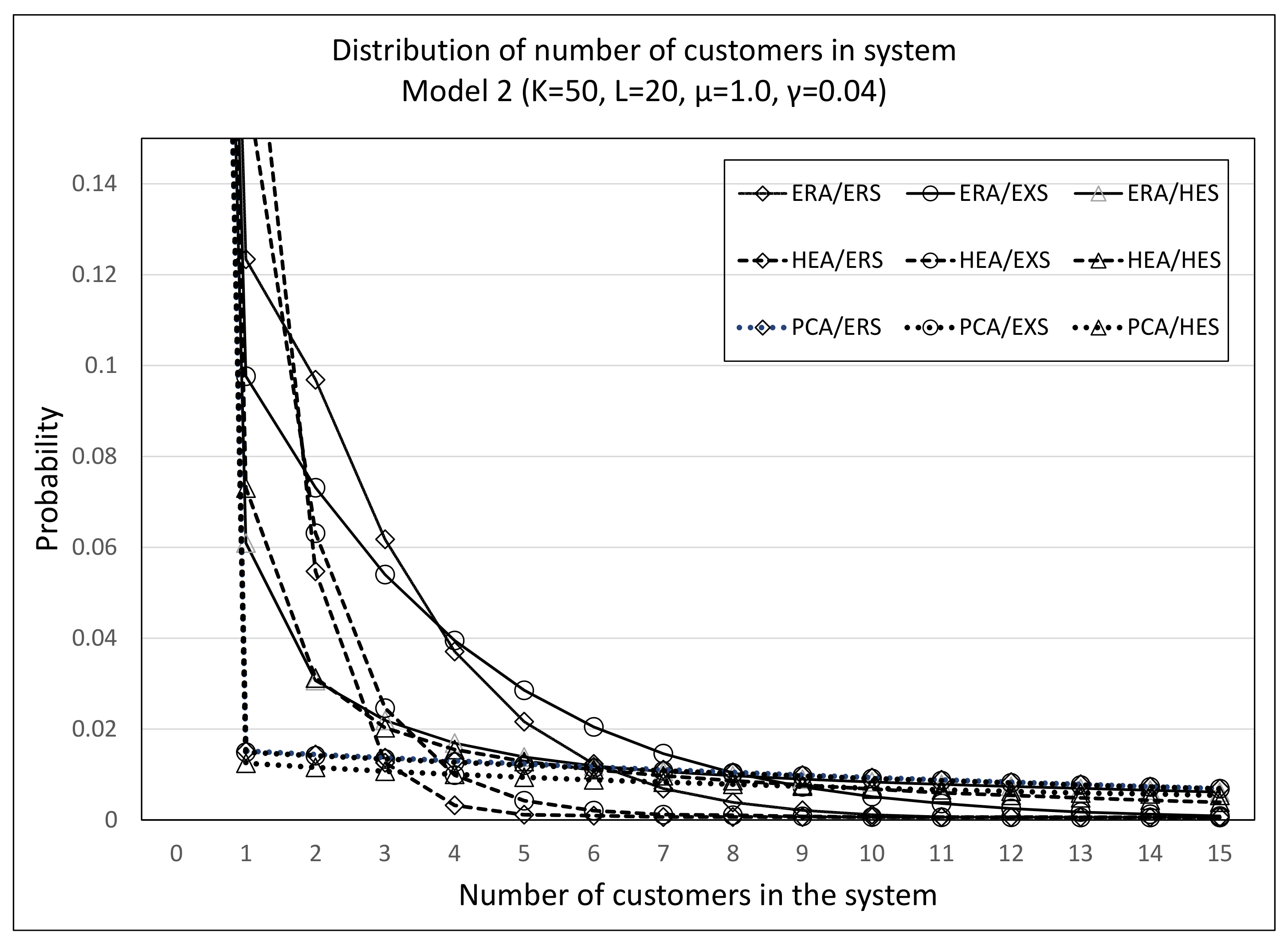
| Model 1 | Model 2 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Arr. | Ser. | ||||||||||||||
| ERA | ERS | 0.05 | 50 | 20 | 0.800 | 1.243 | 0.594 | 0.146 | 0.553 | 0.851 | 1.387 | 0.605 | 0.140 | 0.520 | 0.046 |
| ERA | ERS | 0.05 | 50 | 30 | 0.841 | 1.284 | 0.581 | 0.151 | 0.539 | 0.896 | 1.433 | 0.591 | 0.145 | 0.505 | 0.045 |
| ERA | ERS | 0.05 | 60 | 20 | 0.929 | 1.362 | 0.552 | 0.162 | 0.507 | 0.978 | 1.500 | 0.564 | 0.156 | 0.476 | 0.044 |
| ERA | ERS | 0.05 | 60 | 30 | 0.982 | 1.412 | 0.536 | 0.169 | 0.490 | 1.033 | 1.554 | 0.548 | 0.161 | 0.460 | 0.043 |
| ERA | ERS | 0.1 | 50 | 20 | 1.307 | 1.536 | 0.394 | 0.295 | 0.333 | 1.356 | 1.683 | 0.414 | 0.275 | 0.300 | 0.056 |
| ERA | ERS | 0.1 | 50 | 30 | 1.412 | 1.618 | 0.368 | 0.314 | 0.305 | 1.465 | 1.770 | 0.388 | 0.292 | 0.275 | 0.052 |
| ERA | ERS | 0.1 | 60 | 20 | 1.467 | 1.657 | 0.355 | 0.325 | 0.290 | 1.504 | 1.789 | 0.377 | 0.302 | 0.263 | 0.051 |
| ERA | ERS | 0.1 | 60 | 30 | 1.590 | 1.754 | 0.328 | 0.348 | 0.261 | 1.632 | 1.889 | 0.349 | 0.323 | 0.236 | 0.048 |
| ERA | HES | 0.05 | 50 | 20 | 3.598 | 7.554 | 0.594 | 0.301 | 0.554 | 4.493 | 10.916 | 0.646 | 0.282 | 0.461 | 0.149 |
| ERA | HES | 0.05 | 50 | 30 | 3.899 | 8.040 | 0.581 | 0.310 | 0.539 | 4.827 | 11.457 | 0.633 | 0.291 | 0.447 | 0.150 |
| ERA | HES | 0.05 | 60 | 20 | 4.553 | 9.000 | 0.551 | 0.335 | 0.506 | 5.160 | 11.827 | 0.613 | 0.311 | 0.420 | 0.154 |
| ERA | HES | 0.05 | 60 | 30 | 4.976 | 9.648 | 0.536 | 0.346 | 0.490 | 5.580 | 12.476 | 0.598 | 0.321 | 0.404 | 0.154 |
| ERA | HES | 0.1 | 50 | 20 | 8.942 | 14.632 | 0.394 | 0.522 | 0.333 | 6.785 | 13.328 | 0.504 | 0.474 | 0.263 | 0.192 |
| ERA | HES | 0.1 | 50 | 30 | 10.233 | 16.246 | 0.368 | 0.549 | 0.305 | 7.428 | 14.150 | 0.483 | 0.494 | 0.242 | 0.189 |
| ERA | HES | 0.1 | 60 | 20 | 10.935 | 17.085 | 0.355 | 0.565 | 0.290 | 7.590 | 14.288 | 0.474 | 0.509 | 0.231 | 0.191 |
| ERA | HES | 0.1 | 60 | 30 | 12.650 | 19.147 | 0.328 | 0.596 | 0.261 | 8.368 | 15.260 | 0.452 | 0.532 | 0.210 | 0.187 |
| HEA | ERS | 0.05 | 50 | 20 | 1.854 | 3.755 | 0.702 | 0.591 | 0.672 | 4.103 | 9.868 | 0.729 | 0.527 | 0.368 | 0.334 |
| HEA | ERS | 0.05 | 50 | 30 | 1.940 | 3.866 | 0.695 | 0.597 | 0.664 | 4.411 | 10.366 | 0.717 | 0.534 | 0.355 | 0.334 |
| HEA | ERS | 0.05 | 60 | 20 | 2.433 | 4.633 | 0.664 | 0.618 | 0.630 | 4.898 | 11.088 | 0.699 | 0.544 | 0.337 | 0.332 |
| HEA | ERS | 0.05 | 60 | 30 | 2.560 | 4.790 | 0.655 | 0.627 | 0.620 | 5.305 | 11.715 | 0.685 | 0.552 | 0.323 | 0.330 |
| HEA | ERS | 0.1 | 50 | 20 | 3.140 | 5.378 | 0.589 | 0.811 | 0.548 | 6.310 | 12.724 | 0.630 | 0.707 | 0.202 | 0.391 |
| HEA | ERS | 0.1 | 50 | 30 | 3.363 | 5.637 | 0.576 | 0.821 | 0.533 | 7.104 | 13.825 | 0.606 | 0.718 | 0.186 | 0.381 |
| HEA | ERS | 0.1 | 60 | 20 | 4.135 | 6.737 | 0.546 | 0.836 | 0.500 | 7.416 | 14.206 | 0.597 | 0.723 | 0.179 | 0.378 |
| HEA | ERS | 0.1 | 60 | 30 | 4.469 | 7.121 | 0.530 | 0.848 | 0.483 | 8.441 | 15.577 | 0.570 | 0.736 | 0.162 | 0.365 |
| HEA | HES | 0.05 | 50 | 20 | 2.724 | 6.166 | 0.702 | 0.584 | 0.672 | 6.331 | 17.011 | 0.738 | 0.530 | 0.396 | 0.315 |
| HEA | HES | 0.05 | 50 | 30 | 2.863 | 6.385 | 0.695 | 0.590 | 0.664 | 6.756 | 17.756 | 0.728 | 0.536 | 0.385 | 0.316 |
| HEA | HES | 0.05 | 60 | 20 | 3.608 | 7.659 | 0.664 | 0.611 | 0.630 | 7.351 | 18.528 | 0.709 | 0.549 | 0.361 | 0.319 |
| HEA | HES | 0.05 | 60 | 30 | 3.818 | 7.975 | 0.655 | 0.619 | 0.620 | 7.897 | 19.437 | 0.697 | 0.556 | 0.348 | 0.318 |
| HEA | HES | 0.1 | 50 | 20 | 5.208 | 10.094 | 0.589 | 0.781 | 0.548 | 8.912 | 20.301 | 0.654 | 0.702 | 0.240 | 0.379 |
| HEA | HES | 0.1 | 50 | 30 | 5.610 | 10.656 | 0.576 | 0.790 | 0.533 | 9.735 | 21.506 | 0.636 | 0.710 | 0.226 | 0.374 |
| HEA | HES | 0.1 | 60 | 20 | 6.863 | 12.535 | 0.546 | 0.806 | 0.501 | 10.192 | 21.985 | 0.623 | 0.719 | 0.212 | 0.374 |
| HEA | HES | 0.1 | 60 | 30 | 7.468 | 13.348 | 0.530 | 0.817 | 0.483 | 11.226 | 23.441 | 0.604 | 0.729 | 0.196 | 0.368 |
| PCA | ERS | 0.05 | 50 | 20 | 0.762 | 2.337 | 0.673 | 0.473 | 0.640 | 2.372 | 12.737 | 0.682 | 0.462 | 0.419 | 0.230 |
| PCA | ERS | 0.05 | 50 | 30 | 0.798 | 2.407 | 0.660 | 0.498 | 0.626 | 2.641 | 13.843 | 0.669 | 0.486 | 0.396 | 0.239 |
| PCA | ERS | 0.05 | 60 | 20 | 0.978 | 3.094 | 0.645 | 0.517 | 0.610 | 3.020 | 15.335 | 0.658 | 0.503 | 0.375 | 0.248 |
| PCA | ERS | 0.05 | 60 | 30 | 1.028 | 3.195 | 0.632 | 0.546 | 0.595 | 3.408 | 16.816 | 0.643 | 0.531 | 0.349 | 0.257 |
| PCA | ERS | 0.1 | 50 | 20 | 1.553 | 4.613 | 0.553 | 0.727 | 0.508 | 4.362 | 19.515 | 0.574 | 0.701 | 0.218 | 0.311 |
| PCA | ERS | 0.1 | 50 | 30 | 1.654 | 4.825 | 0.537 | 0.768 | 0.490 | 5.186 | 22.225 | 0.555 | 0.740 | 0.188 | 0.320 |
| PCA | ERS | 0.1 | 60 | 20 | 2.092 | 6.237 | 0.529 | 0.765 | 0.481 | 5.427 | 23.006 | 0.555 | 0.736 | 0.187 | 0.321 |
| PCA | ERS | 0.1 | 60 | 30 | 2.238 | 6.543 | 0.513 | 0.806 | 0.464 | 6.573 | 26.474 | 0.536 | 0.774 | 0.158 | 0.328 |
| PCA | HES | 0.05 | 50 | 20 | 2.132 | 5.285 | 0.673 | 0.525 | 0.640 | 5.142 | 22.448 | 0.701 | 0.496 | 0.432 | 0.239 |
| PCA | HES | 0.05 | 50 | 30 | 2.290 | 5.552 | 0.660 | 0.549 | 0.626 | 5.574 | 23.685 | 0.688 | 0.516 | 0.413 | 0.244 |
| PCA | HES | 0.05 | 60 | 20 | 2.616 | 6.316 | 0.645 | 0.568 | 0.610 | 6.030 | 24.915 | 0.678 | 0.534 | 0.390 | 0.256 |
| PCA | HES | 0.05 | 60 | 30 | 2.811 | 6.634 | 0.632 | 0.594 | 0.595 | 6.589 | 26.449 | 0.664 | 0.556 | 0.369 | 0.261 |
| PCA | HES | 0.1 | 50 | 20 | 4.248 | 9.239 | 0.553 | 0.762 | 0.508 | 7.712 | 28.419 | 0.607 | 0.712 | 0.254 | 0.314 |
| PCA | HES | 0.1 | 50 | 30 | 4.606 | 9.777 | 0.537 | 0.797 | 0.490 | 8.545 | 30.479 | 0.590 | 0.742 | 0.230 | 0.319 |
| PCA | HES | 0.1 | 60 | 20 | 5.195 | 11.193 | 0.529 | 0.796 | 0.481 | 8.870 | 31.287 | 0.588 | 0.742 | 0.222 | 0.325 |
| PCA | HES | 0.1 | 60 | 30 | 5.625 | 11.838 | 0.513 | 0.830 | 0.464 | 9.930 | 33.825 | 0.571 | 0.772 | 0.199 | 0.329 |
| Model 1 | Model 2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Arr. | |||||||||||||
| ERA | 0.05 | 50 | 20 | 11.692 | 16.321 | 47.055 | 0.735 | 27.228 | 12.398 | 16.642 | 46.897 | 0.718 | 27.861 |
| ERA | 0.05 | 50 | 30 | 12.410 | 16.727 | 44.536 | 0.804 | 24.878 | 13.155 | 17.034 | 44.260 | 0.789 | 25.342 |
| ERA | 0.05 | 60 | 20 | 15.421 | 19.918 | 56.746 | 0.677 | 29.537 | 16.253 | 20.247 | 56.578 | 0.660 | 30.296 |
| ERA | 0.05 | 60 | 30 | 16.403 | 20.333 | 54.240 | 0.735 | 27.215 | 17.223 | 20.632 | 54.003 | 0.720 | 27.791 |
| ERA | 0.10 | 50 | 20 | 18.142 | 17.416 | 44.610 | 0.583 | 17.158 | 18.849 | 17.486 | 44.379 | 0.566 | 17.678 |
| ERA | 0.10 | 50 | 30 | 19.864 | 17.752 | 40.356 | 0.673 | 14.855 | 20.583 | 17.778 | 40.015 | 0.658 | 15.206 |
| ERA | 0.10 | 60 | 20 | 22.995 | 20.644 | 54.013 | 0.515 | 19.433 | 23.727 | 20.715 | 53.788 | 0.500 | 20.003 |
| ERA | 0.10 | 60 | 30 | 25.101 | 20.820 | 49.822 | 0.583 | 17.155 | 25.839 | 20.818 | 49.509 | 0.569 | 17.592 |
| HEA | 0.05 | 50 | 20 | 22.059 | 22.423 | 47.842 | 0.529 | 37.781 | 23.096 | 21.213 | 46.314 | 0.499 | 40.081 |
| HEA | 0.05 | 50 | 30 | 22.786 | 22.726 | 46.149 | 0.563 | 35.502 | 23.943 | 21.331 | 43.373 | 0.557 | 35.894 |
| HEA | 0.05 | 60 | 20 | 26.855 | 26.413 | 57.532 | 0.499 | 40.049 | 28.058 | 24.908 | 55.905 | 0.462 | 43.287 |
| HEA | 0.05 | 60 | 30 | 27.820 | 26.714 | 55.848 | 0.529 | 37.782 | 29.090 | 24.932 | 53.056 | 0.511 | 39.182 |
| HEA | 0.10 | 50 | 20 | 28.909 | 21.539 | 46.540 | 0.376 | 26.572 | 28.910 | 19.603 | 43.757 | 0.363 | 27.541 |
| HEA | 0.10 | 50 | 30 | 30.178 | 21.720 | 44.134 | 0.410 | 24.368 | 30.311 | 19.383 | 39.322 | 0.431 | 23.199 |
| HEA | 0.10 | 60 | 20 | 34.649 | 25.150 | 55.954 | 0.348 | 28.752 | 34.484 | 22.873 | 52.992 | 0.328 | 30.487 |
| HEA | 0.10 | 60 | 30 | 36.260 | 25.219 | 53.575 | 0.376 | 26.573 | 36.080 | 22.419 | 48.708 | 0.382 | 26.208 |
| PCA | 0.05 | 50 | 20 | 16.747 | 17.684 | 45.521 | 0.615 | 32.508 | 17.322 | 17.644 | 45.190 | 0.603 | 33.193 |
| PCA | 0.05 | 50 | 30 | 18.184 | 18.117 | 41.838 | 0.697 | 28.701 | 18.788 | 18.022 | 41.335 | 0.688 | 29.058 |
| PCA | 0.05 | 60 | 20 | 21.269 | 21.103 | 55.111 | 0.553 | 36.149 | 21.979 | 21.000 | 54.703 | 0.539 | 37.141 |
| PCA | 0.05 | 60 | 30 | 23.030 | 21.436 | 51.562 | 0.615 | 32.510 | 23.778 | 21.255 | 50.943 | 0.604 | 33.102 |
| PCA | 0.10 | 50 | 20 | 23.346 | 17.188 | 42.458 | 0.454 | 22.055 | 23.965 | 16.855 | 41.808 | 0.440 | 22.751 |
| PCA | 0.10 | 50 | 30 | 25.980 | 17.206 | 36.985 | 0.541 | 18.480 | 26.618 | 16.736 | 36.101 | 0.534 | 18.762 |
| PCA | 0.10 | 60 | 20 | 28.547 | 20.167 | 51.733 | 0.394 | 25.408 | 29.262 | 19.730 | 50.926 | 0.379 | 26.462 |
| PCA | 0.10 | 60 | 30 | 31.492 | 19.905 | 46.540 | 0.454 | 22.055 | 32.211 | 19.311 | 45.446 | 0.444 | 22.564 |
| Model 1 ( = 1.1, = 0.1, K = 50) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Arr. | Ser. | |||||||||||
| ERA | ERS | 20 | 1.307 | 1.536 | 18.142 | 17.416 | 44.610 | 17.158 | 0.394 | 0.295 | 0.333 | 0.000 |
| ERA | ERS | 30 | 1.412 | 1.618 | 19.864 | 17.752 | 40.356 | 14.855 | 0.368 | 0.314 | 0.305 | 0.000 |
| ERA | EXS | 20 | 1.844 | 2.391 | 18.143 | 17.415 | 44.609 | 17.158 | 0.394 | 0.345 | 0.333 | 0.000 |
| ERA | EXS | 30 | 2.023 | 2.566 | 19.867 | 17.751 | 40.353 | 14.855 | 0.368 | 0.366 | 0.305 | 0.000 |
| ERA | HES | 20 | 8.942 | 14.632 | 18.141 | 17.415 | 44.608 | 17.165 | 0.394 | 0.522 | 0.333 | 0.000 |
| ERA | HES | 30 | 10.233 | 16.246 | 19.865 | 17.750 | 40.348 | 14.861 | 0.368 | 0.549 | 0.305 | 0.000 |
| HEA | ERS | 20 | 3.140 | 5.378 | 28.909 | 21.539 | 46.540 | 26.572 | 0.589 | 0.811 | 0.548 | 0.000 |
| HEA | ERS | 30 | 3.363 | 5.637 | 30.178 | 21.720 | 44.134 | 24.368 | 0.576 | 0.821 | 0.533 | 0.000 |
| HEA | EXS | 20 | 3.244 | 5.605 | 28.909 | 21.539 | 46.540 | 26.570 | 0.589 | 0.809 | 0.548 | 0.000 |
| HEA | EXS | 30 | 3.476 | 5.878 | 30.178 | 21.720 | 44.134 | 24.366 | 0.576 | 0.819 | 0.533 | 0.000 |
| HEA | HES | 20 | 5.208 | 10.094 | 28.909 | 21.539 | 46.540 | 26.573 | 0.589 | 0.781 | 0.548 | 0.000 |
| HEA | HES | 30 | 5.610 | 10.656 | 30.177 | 21.720 | 44.134 | 24.367 | 0.576 | 0.790 | 0.533 | 0.000 |
| PCA | ERS | 20 | 1.553 | 4.613 | 23.346 | 17.188 | 42.458 | 22.055 | 0.553 | 0.727 | 0.508 | 0.000 |
| PCA | ERS | 30 | 1.654 | 4.825 | 25.980 | 17.206 | 36.985 | 18.480 | 0.537 | 0.768 | 0.490 | 0.000 |
| PCA | EXS | 20 | 1.681 | 4.771 | 23.345 | 17.190 | 42.460 | 22.050 | 0.553 | 0.732 | 0.508 | 0.000 |
| PCA | EXS | 30 | 1.793 | 4.991 | 25.982 | 17.205 | 36.983 | 18.479 | 0.537 | 0.772 | 0.490 | 0.000 |
| PCA | HES | 20 | 4.248 | 9.239 | 23.345 | 17.189 | 42.458 | 22.055 | 0.553 | 0.762 | 0.508 | 0.000 |
| PCA | HES | 30 | 4.606 | 9.777 | 25.978 | 17.207 | 36.987 | 18.480 | 0.537 | 0.797 | 0.490 | 0.000 |
| ERA | ERS | 20 | 1.356 | 1.683 | 18.849 | 17.486 | 44.379 | 17.678 | 0.414 | 0.275 | 0.356 | 0.156 |
| ERA | ERS | 30 | 1.465 | 1.770 | 20.583 | 17.778 | 40.015 | 15.206 | 0.388 | 0.292 | 0.327 | 0.160 |
| ERA | EXS | 20 | 1.916 | 2.678 | 19.334 | 17.625 | 44.312 | 18.046 | 0.428 | 0.314 | 0.371 | 0.210 |
| ERA | EXS | 30 | 2.101 | 2.860 | 21.112 | 17.925 | 39.932 | 15.509 | 0.402 | 0.332 | 0.342 | 0.217 |
| ERA | HES | 20 | 6.785 | 13.328 | 22.408 | 18.541 | 44.228 | 20.777 | 0.504 | 0.474 | 0.454 | 0.422 |
| ERA | HES | 30 | 7.428 | 14.150 | 24.551 | 19.020 | 40.071 | 18.015 | 0.483 | 0.494 | 0.431 | 0.439 |
| HEA | ERS | 20 | 6.310 | 12.724 | 28.910 | 19.603 | 43.757 | 27.541 | 0.630 | 0.707 | 0.593 | 0.659 |
| HEA | ERS | 30 | 7.104 | 13.825 | 30.311 | 19.383 | 39.322 | 23.199 | 0.606 | 0.718 | 0.567 | 0.673 |
| HEA | EXS | 20 | 6.480 | 13.190 | 29.025 | 19.635 | 43.826 | 27.733 | 0.632 | 0.706 | 0.595 | 0.654 |
| HEA | EXS | 30 | 7.280 | 14.306 | 30.446 | 19.437 | 39.457 | 23.427 | 0.609 | 0.717 | 0.570 | 0.668 |
| HEA | HES | 20 | 8.912 | 20.301 | 30.279 | 19.907 | 44.550 | 30.039 | 0.654 | 0.702 | 0.619 | 0.612 |
| HEA | HES | 30 | 9.735 | 21.506 | 31.912 | 19.896 | 40.902 | 26.200 | 0.636 | 0.710 | 0.600 | 0.624 |
| PCA | ERS | 20 | 4.362 | 19.515 | 23.965 | 16.855 | 41.808 | 22.751 | 0.574 | 0.701 | 0.529 | 0.587 |
| PCA | ERS | 30 | 5.186 | 22.225 | 26.618 | 16.736 | 36.101 | 18.762 | 0.555 | 0.740 | 0.509 | 0.630 |
| PCA | EXS | 20 | 4.568 | 20.087 | 24.067 | 16.891 | 41.823 | 22.856 | 0.576 | 0.702 | 0.533 | 0.584 |
| PCA | EXS | 30 | 5.392 | 22.750 | 26.719 | 16.774 | 36.134 | 18.851 | 0.557 | 0.740 | 0.512 | 0.625 |
| PCA | HES | 20 | 7.712 | 28.419 | 25.607 | 17.460 | 42.148 | 24.912 | 0.607 | 0.712 | 0.568 | 0.552 |
| PCA | HES | 30 | 8.545 | 30.479 | 28.307 | 17.489 | 36.858 | 20.822 | 0.590 | 0.742 | 0.549 | 0.581 |
| Service Dist. | ERS | EXS | HES | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Arr. | 40 | 50 | 60 | 40 | 50 | 60 | 40 | 50 | 60 | |
| Model 1 | ||||||||||
| ERA | 10 | 13.085 | 12.946 | 13.125 | 13.084 | 12.942 | 13.123 | 13.080 | 12.941 | 13.123 |
| ERA | 20 | 13.982 | 13.695 | 13.799 | 13.981 | 13.695 | 13.797 | 13.979 | 13.691 | 13.796 |
| ERA | 30 | 15.304 | 14.751 | 14.718 | 15.303 | 14.750 | 14.717 | 15.301 | 14.745 | 14.708 |
| HEA | 10 | 15.453 | 15.999 | 16.667 | 15.453 | 16.000 | 16.669 | 15.453 | 16.000 | 16.668 |
| HEA | 20 | 15.925 | 16.470 | 17.145 | 15.926 | 16.471 | 17.146 | 15.926 | 16.470 | 17.146 |
| HEA | 30 | 16.444 | 16.982 | 17.662 | 16.445 | 16.983 | 17.663 | 16.444 | 16.983 | 17.663 |
| PCA | 10 | 14.161 | 14.445 | 14.976 | 14.164 | 14.446 | 14.981 | 14.162 | 14.444 | 14.979 |
| PCA | 20 | 15.355 | 15.448 | 15.886 | 15.356 | 15.451 | 15.888 | 15.355 | 15.449 | 15.885 |
| PCA | 30 | 17.125 | 16.807 | 17.046 | 17.127 | 16.810 | 17.050 | 17.125 | 16.808 | 17.047 |
| Model 2 | ||||||||||
| ERA | 10 | 13.258 | 13.184 | 13.412 | 13.363 | 13.333 | 13.598 | 13.913 | 14.120 | 14.596 |
| ERA | 20 | 14.169 | 13.928 | 14.077 | 14.281 | 14.084 | 14.260 | 14.871 | 14.957 | 15.364 |
| ERA | 30 | 15.541 | 14.993 | 14.979 | 15.656 | 15.144 | 15.161 | 16.158 | 16.000 | 16.289 |
| HEA | 10 | 15.622 | 16.262 | 17.034 | 15.635 | 16.283 | 17.062 | 15.778 | 16.507 | 17.358 |
| HEA | 20 | 16.280 | 16.786 | 17.465 | 16.292 | 16.812 | 17.502 | 16.423 | 17.089 | 17.901 |
| HEA | 30 | 17.263 | 17.557 | 18.106 | 17.258 | 17.577 | 18.143 | 17.229 | 17.795 | 18.550 |
| PCA | 10 | 14.306 | 14.664 | 15.277 | 14.333 | 14.703 | 15.323 | 14.618 | 15.096 | 15.803 |
| PCA | 20 | 15.533 | 15.681 | 16.174 | 15.556 | 15.720 | 16.228 | 15.787 | 16.093 | 16.710 |
| PCA | 30 | 17.360 | 17.072 | 17.347 | 17.375 | 17.107 | 17.401 | 17.428 | 17.373 | 17.817 |
| System ( = 0.1, = 1.1, K = 60, L = 20) | System ( = 0.1, = 1.1, S = 60, s = 20) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | |||||||||||||||
| Arr. | Ser. | ||||||||||||||
| ERA | ERS | 0.355 | 0.290 | 1.467 | 1.657 | 22.995 | 20.644 | 19.433 | 0.423 | 0.365 | 1.209 | 1.475 | 15.660 | 16.179 | 16.221 |
| ERA | EXS | 0.355 | 0.290 | 2.116 | 2.644 | 22.999 | 20.642 | 19.439 | 0.423 | 0.365 | 1.686 | 2.267 | 15.663 | 16.178 | 16.222 |
| ERA | HES | 0.355 | 0.290 | 10.935 | 17.085 | 22.986 | 20.646 | 19.437 | 0.423 | 0.365 | 7.784 | 13.214 | 15.657 | 16.179 | 16.223 |
| HEA | ERS | 0.546 | 0.500 | 4.135 | 6.737 | 34.649 | 25.150 | 28.752 | 0.629 | 0.592 | 2.438 | 4.414 | 24.481 | 19.098 | 25.437 |
| HEA | EXS | 0.546 | 0.501 | 4.272 | 7.014 | 34.650 | 25.149 | 28.749 | 0.629 | 0.592 | 2.520 | 4.601 | 24.481 | 19.098 | 25.436 |
| HEA | HES | 0.546 | 0.501 | 6.863 | 12.535 | 34.649 | 25.150 | 28.751 | 0.629 | 0.592 | 4.018 | 8.259 | 24.481 | 19.098 | 25.437 |
| PCA | ERS | 0.529 | 0.481 | 2.092 | 6.237 | 28.547 | 20.167 | 25.408 | 0.568 | 0.525 | 1.220 | 3.468 | 21.748 | 16.972 | 21.571 |
| PCA | EXS | 0.529 | 0.482 | 2.239 | 6.409 | 28.550 | 20.163 | 25.411 | 0.568 | 0.525 | 1.338 | 3.620 | 21.749 | 16.970 | 21.571 |
| PCA | HES | 0.529 | 0.481 | 5.195 | 11.193 | 28.547 | 20.163 | 25.415 | 0.568 | 0.525 | 3.677 | 7.968 | 21.747 | 16.972 | 21.572 |
| Model 2 | |||||||||||||||
| Arr. | Ser. | ||||||||||||||
| ERA | ERS | 0.377 | 0.315 | 1.504 | 1.789 | 23.727 | 20.715 | 20.003 | 0.441 | 0.385 | 1.271 | 1.637 | 16.357 | 16.730 | 16.748 |
| ERA | EXS | 0.391 | 0.330 | 2.151 | 2.883 | 24.273 | 20.838 | 20.445 | 0.453 | 0.398 | 1.796 | 2.600 | 16.843 | 16.946 | 17.113 |
| ERA | HES | 0.474 | 0.421 | 7.590 | 14.288 | 27.673 | 21.708 | 23.619 | 0.524 | 0.476 | 6.418 | 12.959 | 19.846 | 18.270 | 19.642 |
| HEA | ERS | 0.597 | 0.556 | 7.416 | 14.206 | 34.484 | 22.873 | 30.487 | 0.651 | 0.616 | 5.766 | 12.099 | 25.218 | 18.109 | 26.769 |
| HEA | EXS | 0.599 | 0.559 | 7.594 | 14.674 | 34.623 | 22.909 | 30.690 | 0.653 | 0.618 | 5.931 | 12.567 | 25.307 | 18.153 | 26.928 |
| HEA | HES | 0.623 | 0.586 | 10.192 | 21.985 | 36.118 | 23.210 | 33.174 | 0.675 | 0.643 | 8.199 | 19.488 | 26.326 | 18.629 | 28.909 |
| PCA | ERS | 0.555 | 0.508 | 5.427 | 23.006 | 29.262 | 19.730 | 26.462 | 0.583 | 0.540 | 4.024 | 18.494 | 22.363 | 17.226 | 22.283 |
| PCA | EXS | 0.557 | 0.512 | 5.641 | 23.527 | 29.380 | 19.768 | 26.565 | 0.585 | 0.543 | 4.220 | 19.058 | 22.436 | 17.207 | 22.384 |
| PCA | HES | 0.588 | 0.547 | 8.870 | 31.287 | 31.069 | 20.387 | 28.799 | 0.617 | 0.578 | 7.246 | 27.332 | 23.755 | 17.800 | 24.279 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakravarthy, S.R.; Rao, B.M. Queuing-Inventory Models with MAP Demands and Random Replenishment Opportunities. Mathematics 2021, 9, 1092. https://doi.org/10.3390/math9101092
Chakravarthy SR, Rao BM. Queuing-Inventory Models with MAP Demands and Random Replenishment Opportunities. Mathematics. 2021; 9(10):1092. https://doi.org/10.3390/math9101092
Chicago/Turabian StyleChakravarthy, Srinivas R., and B. Madhu Rao. 2021. "Queuing-Inventory Models with MAP Demands and Random Replenishment Opportunities" Mathematics 9, no. 10: 1092. https://doi.org/10.3390/math9101092
APA StyleChakravarthy, S. R., & Rao, B. M. (2021). Queuing-Inventory Models with MAP Demands and Random Replenishment Opportunities. Mathematics, 9(10), 1092. https://doi.org/10.3390/math9101092







