Exchange Market Liquidity Prediction with the K-Nearest Neighbor Approach: Crypto vs. Fiat Currencies
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Data and Hypothesis
3.2. ARMA and GARCH Models
3.3. Nearest Neighbor Method
- (1)
- The time series considered, , is transformed into a series of -dimensional vectors:where , with being the number of lags and being the delay parameter. In the KNN forecasting algorithm, and are pre-determined parameters.
- (2)
- To simplify, we shall only consider the case of , then the resulting time series of vectors is denoted by , with , which represents a vector of consecutive observations that can be characterized as a point in -dimensional space:These -dimensional vectors are often called -histories, whereas the -dimensional space is referred to as the phase space of time series.
- (3)
- The distance between the last vector, also called focal, and each vector in the time series with is computed. The distance used in this study is the sum over all dimensions of the absolute difference between the values of the cases ( and with ) also called the Manhattan distance or city block metric.
- (4)
- The vector closest to is selected and denoted by . The parameter is also pre-determined using a criteria selection, generally the with the lowest sum of squares residuals (SSRs).
- (5)
- Given the neighboring vectors ; their subsequent values, , are averaged to obtain the forecast, .
4. Results
4.1. Descriptive Statistics
4.2. ARMA Models
4.3. GARCH Models
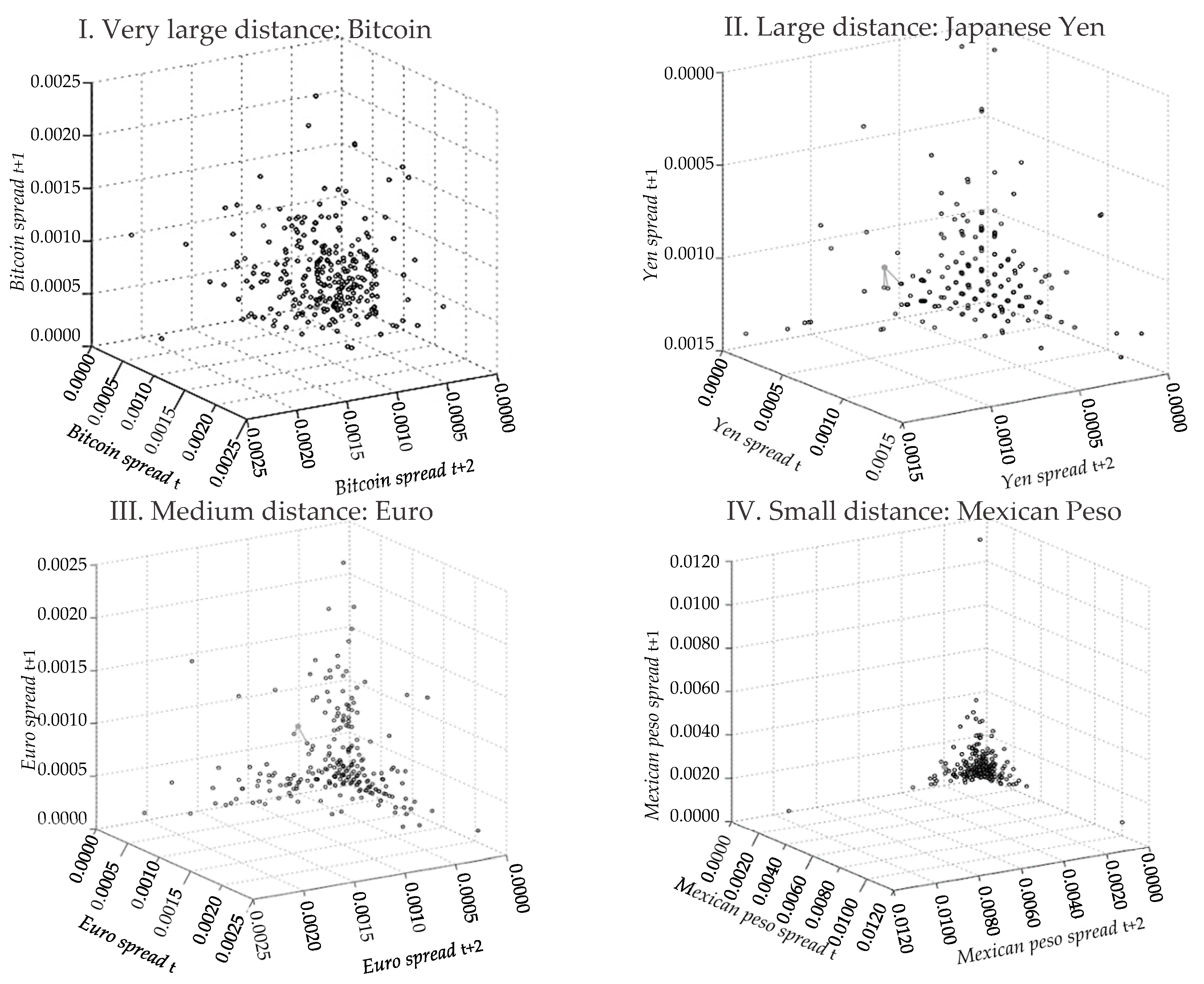
4.4. KNN Approach
- Very large distance: Bitcoin ( = 2), Ethereum ( = 3), and Ripple ( = 3)
- Large distance: Australian dollar ( = 2), Danish krone ( = 3), Japanese yen ( = 3), Norwegian krone ( = 2), and Taiwanese dollar ( = 2)
- Medium distance: British pound ( = 1), Canadian dollar ( = 2), euro ( = 2), Swedish krona ( = 3), and Swiss franc ( = 2)
- Small distance: Brazilian real ( = 2), Mexican peso ( = 1), New Zealand dollar ( = 1), Singaporean dollar ( = 1), South African rand ( = 2), and South Korean won ( = 1)
4.5. Comparative Analysis
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Balcilar, M.; Bouri, E.; Gupta, R.; Roubaud, D. Can volume predict Bitcoin returns and volatility? A quantiles-based approach. Econ. Model 2017, 64, 74–81. [Google Scholar] [CrossRef]
- Yermack, D. Is Bitcoin a Real Currency? An Economic Appraisal. In Handbook of Digital Currency: Bitcoin, Innovation, Financial Instruments, and Big Data; Chuen, D.L.K., Ed.; Academic Press: London, UK, 2015; pp. 31–43. [Google Scholar] [CrossRef]
- Bouoiyour, J.; Selmi, R.; Tiwari, A.K.; Olayeni, O.R. What drives Bitcoin price. Econ. Bull. 2016, 36, 843–850. [Google Scholar]
- Gandal, N.; Halaburda, H. Can we predict the winner in a market with network effects? Competition in cryptocurrency market. Games. SSRN Electron. J. 2016, 7, 16. [Google Scholar] [CrossRef]
- Dwyer, G.P. The economics of Bitcoin and similar private digital currencies. J. Financ. Stab. 2015, 17, 81–91. [Google Scholar] [CrossRef]
- Hayes, A.S. Cryptocurrency value formation: An empirical study leading to a cost of production model for valuing bitcoin. Telemat. Inform. 2017, 34, 1308–1321. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf/ (accessed on 27 December 2016).
- Bas, D.S. Hayek and the cryptocurrency revolution. Iber. J. Hist. Econ. Thought 2020, 7, 15–28. [Google Scholar] [CrossRef]
- Encrybit Revealed Real-Time Cryptocurrency Exchange Problems—Survey Insights. Available online: https://medium.com/@enbofficial/encrybit-revealed-real-time-cyptocurrency-exchange-problems-survey-report-announced-650bba659a6d/ (accessed on 18 May 2020).
- Crook, M. Bringing liquidity to the new crypto economy. J. Digit. Bank. 2019, 3, 279–287. [Google Scholar]
- Jiang, S.; Li, X.; Wang, S. Exploring evolution trends in cryptocurrency study: From underlying technology to economic applications. Financ. Res. Lett. 2020, status (in press; corrected proof). [Google Scholar] [CrossRef]
- Dyhrberg, A.H.; Foley, S.; Svec, J. How investible is Bitcoin? Analyzing the liquidity and transaction costs of Bitcoin markets. Econ. Lett. 2018, 171, 140–143. [Google Scholar] [CrossRef]
- Wei, W.C. Liquidity and market efficiency in cryptocurrencies. Econ. Lett. 2018, 168, 21–24. [Google Scholar] [CrossRef]
- Sójka, B.B.; Hinc, T.; Kliber, A. Volatility and Liquidity in Cryptocurrency Markets—The Causality Approach. In Contemporary Trends and Challenges in Finance; Jajuga, K., Junge, H.L., Orlowski, L., Staehr, K., Eds.; Springer: Cham, Switzerland, 2020; pp. 1–43. [Google Scholar] [CrossRef]
- Brauneis, A.; Mestel, R.; Theissen, E. What Drives the Liquidity of Cryptocurrencies? A Long-Term Analysis. Financ. Res. Lett. 2020, status (in press; corrected proof). [Google Scholar] [CrossRef]
- Scharnowski, S. Understanding bitcoin liquidity. Financ. Res. Lett. 2020, status (in press; corrected proof). [Google Scholar] [CrossRef]
- Brauneis, A.; Mestel, R.; Riordan, R.; Theissen, E. How to measure the liquidity of cryptocurrencies? SSRN Electron. J. 2020, 3503507. [Google Scholar] [CrossRef]
- Hong, K. Bitcoin as an alternative investment vehicle. J. Inf. Technol. Manag. 2017, 18, 265–275. [Google Scholar] [CrossRef]
- Khuntia, S.; Pattanayak, J.K. Adaptive long memory in volatility of intra-day bitcoin returns and the impact of trading volume. Financ. Res. Lett. 2020, 32, 101077. [Google Scholar] [CrossRef]
- Phillip, A.; Chan, J.; Peiris, S. On long memory effects in the volatility measure of cryptocurrencies. Financ. Res. Lett. 2019, 28, 95–100. [Google Scholar] [CrossRef]
- Ruppert, D. GARCH Models. In Statistics and Data Analysis for Financial Engineering; Springer: New York, NY, USA, 2011. [Google Scholar]
- Nelson, D.B. Conditional heteroskedasticity in asset returns: A new approach. Econom. J. Econom. Soc. 1991, 59, 347–370. [Google Scholar] [CrossRef]
- Venter, P.J.; Maré, E. GARCH Generated Volatility Indices of Bitcoin and CRIX. J. Risk Financ. Manag. 2020, 13, 121. [Google Scholar] [CrossRef]
- Lovreta, L.; Pascual, J.L. Structural breaks in the interaction between bank and sovereign default risk. Ser. J. Span. Econ. Assoc. 2020, 11, 531–559. [Google Scholar] [CrossRef]
- Kyriazis, Ν.A.; Daskalou, K.; Arampatzis, M.; Prassa, P.; Papaioannou, E. Estimating the volatility of cryptocurrencies during bearish markets by employing GARCH models. Heliyon 2019, 5, e02239. [Google Scholar] [CrossRef]
- Walther, T.; Klein, T.; Bouri, E. Exogenous drivers of Bitcoin and Cryptocurrency volatility–A mixed data sampling approach to forecasting. J. Int. Financ. Mark. Inst. Money 2019, 63, 101133. [Google Scholar] [CrossRef]
- Acereda, B.; Leon, A.; Mora, J. Estimating the expected shortfall of cryptocurrencies: An evaluation based on backtesting. Financ. Res. Lett. 2020, 33, 101181. [Google Scholar] [CrossRef]
- Fakhfekh, M.; Jeribi, A. Volatility dynamics of crypto-currencies’ returns: Evidence from asymmetric and long memory GARCH models. Res. Int. Bus. Financ. 2020, 51, 101075. [Google Scholar] [CrossRef]
- Cerqueti, R.; Giacalone, M.; Mattera, R. Skewed non-Gaussian GARCH models for cryptocurrencies volatility modelling. Inf. Sci. 2020, 527, 1–26. [Google Scholar] [CrossRef]
- Köchling, G.; Schmidtke, P.; Posch, P.N. Volatility forecasting accuracy for Bitcoin. Econ. Lett. 2020, 191, 108836. [Google Scholar] [CrossRef]
- Stenfors, A. Bid-ask spread determination in the FX swap market: Competition, collusion or a convention? J. Int. Financ. Mark. Inst. Money 2018, 54, 78–97. [Google Scholar] [CrossRef]
- Kim, T. On the transaction cost of Bitcoin. Financ. Res. Lett. 2017, 23, 300–305. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S.; Salvi, A. Long-range memory, distributional variation and randomness of bitcoin volatility. Chaos Solitons Fractals 2018, 107, 43–48. [Google Scholar] [CrossRef]
- Khaldi, R.; El Afia, A.; Chiheb, R. Forecasting of BTC volatility: Comparative study between parametric and nonparametric models. Prog. Artif. Intell. 2019, 8, 511–523. [Google Scholar] [CrossRef]
- Saadah, S.; Whafa, A.A. Monitoring Financial Stability Based on Prediction of Cryptocurrencies Price Using Intelligent Algorithm. In Proceedings of the 2020 International Conference on Data Science and Its Applications (ICoDSA), Bandung, Indonesia, 5–6 August 2020; pp. 1–10. [Google Scholar]
- Devroye, L.; Gyorfi, L.; Krzyzak, A.; Lugosi, G. On the strong universal consistency of nearest neighbor regression function estimates. Ann. Stat. 1994, 22, 1371–1385. [Google Scholar] [CrossRef]
- Katsiampa, P. Volatility estimation for Bitcoin: A comparison of GARCH models. Econ. Lett. 2017, 158, 3–6. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control, Time Series Analysis: Forecasting and Control; Holden-Day Inc.: San Francisco, CA, USA, 1976. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Koehler, A.B.; Murphree, E.S. A comparison of the Akaike and Schwarz criteria for selecting model order. Appl. Stat. 1988, 37, 187–195. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econ. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Mitchell, H.; McKenzie, M.D. GARCH model selection criteria. Quant. Financ. 2003, 3, 262–284. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L. Discriminatory Analysis, Nonparametric Discriminators: Consistency Properties; Technical Report 4; School of Aviation Medicine, Randolph Field: Texas, CA, USA, 1951. [Google Scholar]
- Cover, T.M.; Hart, P.E. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Rubio, O.B.; Sosvilla-Rivero, S.; Rodríguez, F.F. Non-Linear Forecasting Methods: Some Applications to the Analysis of Financial Series; FEDEA Working Paper 2002-01; Fundación de Estudios de Economía Aplicada: Madrid, Spain, 2002. [Google Scholar] [CrossRef]
- Fernández-Rodríguez, F.; Sosvilla-Rivero, S.; Andrada-Félix, J. Exchange-rate forecasts with simultaneous nearest-neighbour methods: Evidence from the EMS. Int. J. Forecast. 1999, 15, 383–392. [Google Scholar] [CrossRef]
- Finkenstädt, B.; Kuhbier, P. Forecasting nonlinear economic time series: A simple test to accompany the nearest neighbor approach. Empir. Econ. 1995, 20, 243–263. [Google Scholar] [CrossRef]
- Arroyo, J.; Maté, C. Forecasting histogram time series with k-nearest neighbours methods. Int. J. Forecast. 2009, 25, 192–207. [Google Scholar] [CrossRef]
- Brock, W.A.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A test for independence based on the correlation dimension. Econ. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Ong, B.; Lee, T.M.; Li, G.; Chuen, D.L.K. Evaluating the Potential of Alternative Cryptocurrencies. In Handbook of Digital Currency: Bitcoin, Innovation, Financial Instruments, and Big Data; Chuen, D.L.K., Ed.; Academic Press: London, UK, 2015; pp. 81–135. [Google Scholar] [CrossRef]
- Jahani, E.; Krafft, P.M.; Suhara, Y.; Moro, E.; Pentland, A.S. Scamcoins, s*** posters, and the search for the next bitcoinTM: Collective sensemaking in cryptocurrency discussions. Proc. ACM Hum. Comput. Interact. 2018, 2, 1–28. [Google Scholar] [CrossRef]
- Park, S.; Park, H.W. Diffusion of cryptocurrencies: Web traffic and social network attributes as indicators of cryptocurrency performance. Qual. Quant. 2020, 54, 297–314. [Google Scholar] [CrossRef]
| Currency | Mean a | SD a | Skewness a | Kurtosis a | ||||
|---|---|---|---|---|---|---|---|---|
| % | Rank b | % | Rank b | Value | Rank b | Value | Rank b | |
| Brazilian real | −0.049% | 15 | 0.973% | 05 | 0.697 | 02 | 3.242 | 01 |
| Ripple c | −0.342% | 18 | 6.355% | 01 | 0.737 | 01 | 2.170 | 02 |
| Ethereum c | −0.737% | 19 | 6.066% | 02 | 0.308 | 04 | 2.063 | 03 |
| Bitcoin c | −0.315% | 17 | 4.181% | 03 | −0.345 | 18 | 1.597 | 04 |
| Mexican peso | −0.004% | 02 | 0.785% | 06 | −0.398 | 19 | 1.478 | 05 |
| New Zealand dollar | −0.026% | 08 | 0.537% | 09 | 0.081 | 08 | 1.120 | 06 |
| Danish krone | −0.031% | 11 | 0.437% | 13 | −0.260 | 16 | 0.803 | 07 |
| British pound | −0.028% | 09 | 0.498% | 12 | 0.028 | 09 | 0.780 | 08 |
| Euro | −0.030% | 10 | 0.436% | 14 | −0.249 | 15 | 0.643 | 09 |
| Swedish krona | −0.051% | 16 | 0.585% | 07 | 0.223 | 05 | 0.602 | 10 |
| Japanese yen | −0.004% | 01 | 0.391% | 16 | 0.025 | 10 | 0.514 | 11 |
| Australian dollar | −0.036% | 13 | 0.553% | 08 | 0.003 | 11 | 0.435 | 12 |
| South Korean won | −0.009% | 04 | 0.501% | 11 | 0.092 | 07 | 0.389 | 13 |
| Taiwanese dollar | −0.018% | 05 | 0.270% | 18 | 0.187 | 06 | 0.384 | 14 |
| Swiss franc | −0.026% | 07 | 0.378% | 17 | −0.112 | 13 | 0.294 | 15 |
| Norwegian krone | −0.033% | 12 | 0.523% | 10 | −0.137 | 14 | 0.143 | 16 |
| Singaporean dollar | −0.008% | 03 | 0.265% | 19 | −0.020 | 12 | 0.099 | 17 |
| Canadian dollar | −0.020% | 06 | 0.426% | 15 | 0.341 | 03 | 0.067 | 18 |
| South African rand | −0.043% | 14 | 1.029% | 04 | −0.283 | 17 | −0.045 | 19 |
| Currency | Mean | SD | Skewness | Kurtosis | ||||
|---|---|---|---|---|---|---|---|---|
| % | Rank a | % | Rank a | Value | Rank a | Value | Rank a | |
| Mexican peso | 0.097% | 10 | 0.090% | 10 | 6.895 | 03 | 74.027 | 01 |
| Singaporean dollar | 0.049% | 12 | 0.125% | 05 | 7.413 | 02 | 67.219 | 02 |
| South Korean won | 0.208% | 02 | 0.333% | 01 | 7.653 | 01 | 60.429 | 03 |
| South African rand | 0.299% | 01 | 0.232% | 02 | 3.635 | 04 | 17.463 | 04 |
| Brazilian real | 0.047% | 14 | 0.056% | 12 | 3.060 | 05 | 14.781 | 05 |
| New Zealand dollar | 0.192% | 03 | 0.177% | 03 | 2.836 | 06 | 13.686 | 06 |
| Swedish krona | 0.110% | 08 | 0.081% | 11 | 2.550 | 07 | 9.588 | 07 |
| Japanese yen | 0.024% | 19 | 0.023% | 19 | 2.356 | 10 | 7.302 | 08 |
| Canadian dollar | 0.045% | 15 | 0.045% | 15 | 2.548 | 08 | 7.232 | 09 |
| Swiss franc | 0.055% | 11 | 0.053% | 13 | 2.430 | 09 | 6.807 | 10 |
| British pound | 0.105% | 09 | 0.107% | 08 | 2.284 | 11 | 6.206 | 11 |
| Euro | 0.038% | 17 | 0.037% | 18 | 1.990 | 12 | 4.188 | 12 |
| Ethereum b | 0.134% | 06 | 0.108% | 07 | 1.870 | 13 | 4.099 | 13 |
| Norwegian krone | 0.169% | 05 | 0.120% | 06 | 1.732 | 14 | 3.860 | 14 |
| Australian dollar | 0.114% | 07 | 0.095% | 09 | 1.548 | 15 | 2.264 | 15 |
| Bitcoin b | 0.049% | 13 | 0.040% | 17 | 1.302 | 16 | 2.167 | 16 |
| Danish krone | 0.042% | 16 | 0.048% | 14 | 1.125 | 18 | 1.363 | 17 |
| Ripple b | 0.181% | 04 | 0.133% | 04 | 1.135 | 17 | 0.912 | 18 |
| Taiwanese dollar | 0.037% | 18 | 0.042% | 16 | 0.877 | 19 | −0.246 | 19 |
| Currency | ADF a | ARMA(p,q) b | Dim2 c | Dim3 c | Dim4 c | Dim5 c |
|---|---|---|---|---|---|---|
| Canadian dollar f | −4.949 | 7,2 | 0.009 d | 0.009 d | 0.008 d | 0.006 d |
| British pound f | −2.940 | 5,8 | 0.003 d | 0.002 d | −0.002 d | −0.006 d |
| Ethereum | −3.725 | 5,7 | 0.014 | 0.020 | 0.026 | 0.030 |
| Australian dollar | −4.024 | 5,7 | 0.011 e | 0.019 | 0.023 | 0.020 e |
| Euro f | −4.023 | 5,5 | 0.007 d | 0.003 d | 0.004 d | −0.001 d |
| Japanese yen | −3.993 | 5,5 | 0.014 | 0.017 d | 0.019 d | 0.015 d |
| Danish krone | −4.881 | 5,5 | 0.012 | 0.018 | 0.026 | 0.027 |
| Mexican peso | −4.424 | 5,5 | 0.002 d | 0.014 d | 0.025 | 0.027 |
| South African rand f | −4.908 | 5,4 | 0.002 d | −0.001 d | −0.010 d | −0.016 d |
| Swedish krona | −5.232 | 5,4 | 0.034 | 0.044 | 0.039 | 0.036 |
| Norwegian krone | −4.298 | 5,4 | 0.018 | 0.032 | 0.036 | 0.036 |
| Swiss franc f | −4.260 | 5,0 | 0.014 e | 0.018 d | 0.017 d | 0.014 d |
| New Zealand dollar f | −4.910 | 4,5 | 0.009 d | 0.011 d | 0.008 d | 0.005 d |
| Bitcoin | −12.554 | 3,2 | 0.008 e | 0.018 | 0.022 | 0.025 |
| Taiwanese dollar f | −13.999 | 2,2 | 0.008 d | 0.009 d | 0.009 d | 0.010 d |
| Brazilian real | −8.028 | 1,2 | 0.007 d | 0.014 d | 0.021 e | 0.034 |
| Ripple | −2.913 | 1,1 | 0.016 | 0.033 | 0.039 | 0.042 |
| Singaporean dollar f | −16.508 | 1,0 | −0.015 d | −0.017 d | −0.017 d | −0.020 d |
| South Korean won | −16.017 | 0,1 | −0.014 d | −0.030 e | −0.041 | −0.034 e |
| Currency | ARCH a | GARCH b | Dim2 d | Dim3 d | Dim4 d | Dim5 d | ||
|---|---|---|---|---|---|---|---|---|
| Coeff. | Rank c | Coeff. | Rank c | |||||
| New Zealand dollar | −0.022 | 18 | 1.014 | 01 | −0.010 e | −0.023 f | −0.030 f | −0.033 |
| South Korean won g | 0.041 | 10 | 1.013 | 02 | 0.000 e | 0.000 e | −0.001 e | −0.001 e |
| British pound g | 0.031 | 13 | 0.939 | 03 | −0.002 e | −0.012 e | −0.026 f | −0.032 f |
| Swiss franc g | 0.037 | 11 | 0.936 | 04 | 0.000 e | −0.006 e | −0.013 e | −0.016 e |
| Canadian dollar | 0.023 | 14 | 0.907 | 05 | −0.006 e | −0.028 f | −0.049 | −0.056 |
| Euro | 0.016 | 15 | 0.886 | 06 | −0.005 e | −0.021 e | −0.032 f | −0.033 |
| Danish krone g | 0.016 | 16 | 0.862 | 07 | 0.008 e | 0.006 e | 0.003 e | 0.001 e |
| Japanese yen g | 0.050 | 09 | 0.839 | 08 | 0.002 e | 0.004 e | 0.002 e | 0.001 e |
| Bitcoin g | 0.111 | 07 | 0.835 | 09 | 0.000 e | −0.003 e | −0.003 e | −0.003 e |
| Taiwanese dollar g | 0.084 | 08 | 0.834 | 10 | 0.002 e | 0.009 e | 0.008 e | 0.005 e |
| Mexican peso g | 0.205 | 04 | 0.717 | 11 | −0.012 e | −0.022 f | −0.029 f | −0.032 f |
| Norwegian krone g | 0.036 | 12 | 0.712 | 12 | −0.003 e | −0.010 e | −0.010 e | 0.001 e |
| Ripple g | 0.262 | 03 | 0.663 | 13 | 0.002 e | 0.005 e | 0.000 e | 0.003 e |
| Brazilian real g | 0.491 | 01 | 0.644 | 14 | 0.004 e | 0.001 e | −0.004 e | 0.000 e |
| Ethereum g | 0.274 | 02 | 0.605 | 15 | 0.003 e | 0.003 e | 0.002 e | 0.001 e |
| Singaporean dollar g | −0.009 | 17 | 0.558 | 16 | −0.021 f | −0.027 e | −0.029 e | −0.032 e |
| Australian dollar g | −0.034 | 19 | 0.490 | 17 | −0.010 e | −0.017 e | −0.022 e | −0.022 e |
| South African rand g | 0.120 | 06 | −0.208 | 18 | 0.000 e | 0.004 e | −0.002 e | −0.010 e |
| Swedish krona g | 0.124 | 05 | −0.859 | 19 | 0.001 e | −0.002 e | −0.004 e | −0.002 e |
| Currency | Neighbor(s) a | Distance(s) b | Observed/Predicted c |
|---|---|---|---|
| 13 November 2018, 7 November 18, 21 November 2018 | 0.000002, 0.000003, 0.000005 | 0.000001/0.000001 | |
| Ethereum | 7 August 2018, 16 November 2018, 12 June 2018 | 0.000232, 0.000274, 0.000326 | 0.000727/0.000744 |
| Japanese yen | 26 December 2018, 14 February 2018, 27 September 2018 | 0.000112, 0.000141, 0.000194 | 0.000110/0.000111 |
| Ripple | 5 June 2018, 2 July 2018, 5 April 2018 | 0.000353, 0.000432, 0.000843 | 0.000000/0.000253 |
| Swedish krona | 25 April 2018, 26 September 2018, 24 October 2018 | 0.000174, 0.000254, 0.000259 | 0.000460/0.000470 |
| Australian dollar | 24 October 2018, 1 August 2018 | 0.000146, 0.000255 | 0.000281/0.000415 |
| Bitcoin | 16 April 2018, 11 September 2018 | 0.000094, 0.000084 | 0.000407/0.000404 |
| Brazilian real | 10 January 2019, 30 January 2019 | 0.000391, 0.00111 | 0.002959/0.002774 |
| Canadian dollar | 4 May 2018, 27 Abril 2018 | 0.000166, 0.00017 | 0.000529/0.000449 |
| Euro | 22 August 2018, 12 November 2018 | 0.000205, 0.000264 | 0.000176/0.000132 |
| Norwegian krone | 12 December 2018, 16 January 2019 | 0.000013, 0.00003 | 0.000854/0.000855 |
| South African rand | 9 May 2018, 17 October 2018 | 0.001357, 0.002655 | 0.002545/0.002034 |
| Swiss franc | 26 December 2018, 20 November 2018 | 0.000239, 0.000308 | 0.000301/0.000299 |
| Taiwanese dollar | 20 February 2018, 10 May 2018 | 0.00024, 0.000244 | 0.000555/0.000558 |
| British pound | 11 December 2018 | 0.000303 | 0.000696/0.000641 |
| Mexican peso | 14 November 2018 | 0.000295 | 0.000764/0.001021 |
| New Zealand dollar | 9 January 2019 | 0.00034 | 0.000885/0.000884 |
| Singaporean dollar | 21 February 2018 | 0.000786 | 0.000136/0.000265 |
| South Korean won | 21 January 2019 | 0.001488 | 0.000224/0.001702 |
| Currency | ARMA a | GARCH b | KNN c | |||
|---|---|---|---|---|---|---|
| SSR d | Rank e | SSR d | Rank e | SSR d | Rank e | |
| South African rand | 0.0010380 | 02 | 0.0037240 | 02 | 0.0000134 | 01 |
| New Zealand dollar | 0.0004680 | 03 | 0.0026110 | 03 | 0.0000078 | 02 |
| Mexican peso | 0.0001520 | 07 | 0.0004550 | 14 | 0.0000068 | 03 |
| Ethereum | 0.0000846 | 10 | 0.0007740 | 06 | 0.0000019 | 04 |
| Swedish krona | 0.0000825 | 11 | 0.0004860 | 12 | 0.0000017 | 05 |
| Ripple | 0.0002380 | 05 | 0.0022430 | 04 | 0.0000016 | 06 |
| Norwegian krone | 0.0001480 | 08 | 0.0020730 | 05 | 0.0000015 | 07 |
| Singaporean dollar | 0.0003930 | 04 | 0.0004710 | 13 | 0.0000014 | 08 |
| Australian dollar | 0.0000995 | 09 | 0.0005720 | 10 | 0.0000010 | 09 |
| British pound | 0.0001540 | 06 | 0.0005830 | 09 | 0.0000008 | 10 |
| South Korean won | 0.0028720 | 01 | 0.0039790 | 01 | 0.0000008 | 11 |
| Brazilian real | 0.0000651 | 12 | 0.0007250 | 07 | 0.0000004 | 12 |
| Swiss franc | 0.0000524 | 13 | 0.0001520 | 15 | 0.0000004 | 13 |
| Bitcoin | 0.0000283 | 16 | 0.0001020 | 17 | 0.0000002 | 14 |
| Danish krone | 0.0000307 | 15 | 0.0001060 | 16 | 0.0000002 | 15 |
| Taiwanese dollar | 0.0000373 | 14 | 0.0000810 | 18 | 0.0000002 | 16 |
| Canadian dollar | 0.0000275 | 17 | 0.0006370 | 08 | 0.0000001 | 17 |
| Euro | 0.0000136 | 18 | 0.0005300 | 11 | 0.0000001 | 18 |
| Japanese yen | 0.0000085 | 19 | 0.0000280 | 19 | 0.0000001 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortez, K.; Rodríguez-García, M.d.P.; Mongrut, S. Exchange Market Liquidity Prediction with the K-Nearest Neighbor Approach: Crypto vs. Fiat Currencies. Mathematics 2021, 9, 56. https://doi.org/10.3390/math9010056
Cortez K, Rodríguez-García MdP, Mongrut S. Exchange Market Liquidity Prediction with the K-Nearest Neighbor Approach: Crypto vs. Fiat Currencies. Mathematics. 2021; 9(1):56. https://doi.org/10.3390/math9010056
Chicago/Turabian StyleCortez, Klender, Martha del Pilar Rodríguez-García, and Samuel Mongrut. 2021. "Exchange Market Liquidity Prediction with the K-Nearest Neighbor Approach: Crypto vs. Fiat Currencies" Mathematics 9, no. 1: 56. https://doi.org/10.3390/math9010056
APA StyleCortez, K., Rodríguez-García, M. d. P., & Mongrut, S. (2021). Exchange Market Liquidity Prediction with the K-Nearest Neighbor Approach: Crypto vs. Fiat Currencies. Mathematics, 9(1), 56. https://doi.org/10.3390/math9010056







