Abstract
Greenhouse peppers are one of the most important crops globally. However, as in any production activity, especially agricultural, they are subject to important risk factors such as price fluctuations, pests, or the use of bad quality water. This article aims to evaluate the viability of these types of crops by using discounted cash flows. Risk evaluation has been carried out through the analysis of pepper plantations for 2016 and 2017. The traditional application of this tool has significant limitations, such as the discount rate to be used or the estimation of future cash flows. However, by using discount functions that decrease over time in combination with decoupled net present value, these limitations are expected to improve. The use of decoupled net present value has permitted an increase in the accuracy and quantification of risks, isolating the main risks such as price drops (EUR 3720 ha−1 year−1) and structural risks (EUR 1622 € ha−1 year−1). The use of decreasing discount functions has permitted a more realistic investment estimation. Finally, the sensitivity analysis shows that decoupled net present value (DNPV) is little affected by changes in interest rates in contrast to traditional net present value (NPV).
1. Introduction
Pepper crops are highly important globally and they occupy the third largest cultivated area of greenhouse crops, after tomatoes and cucumbers, but they are second in terms of economic importance. Sweet peppers are one of the most valuable crops in the Mediterranean area and they are usually cultivated in greenhouses, which permit higher yield and exceptional fruit quality in comparison with open field (conventional cultivation) conditions [1].
Spain is considered the fifth largest pepper-producer in the world (1,275,457 t in 2018, [2], and the second exporter behind Mexico with 775,771 t [2]. Due to overlapping production calendars, Turkey is Spain’s main competitor [3]. Currently, pepper production and marketing are conditioned by economic, environmental, and quality aspects. With respect to their production characteristics, peppers are a species where technical improvements have a decisive impact on yields and quality. These aspects are crucial to the competitiveness of this agricultural activity.
Some of the fundamental competitive factors in Spanish horticulture are production and commercial infrastructure. Resource consumption should be efficient, production and crop calendars should be diversified, and technology in particular should be adopted in greenhouses to enhance the use of renewable energies and improve mechanization and automatization. This will help to reduce production costs and increase yields, and will entail a shrewd business decision process which aims to increase possible benefits and reduce risks.
In order to improve yields, different technologies are used to improve production in greenhouse pepper crops, such as: the use of carbon dioxide [4], semi-forced cultivation [5,6], shade meshes [5,7,8], thermal screens [9,10]; hydroponic cultivation [11,12] or heating [13].
Although pesticides can also be used to achieve better production, their use is becoming increasingly limited because they cause environmental pollution as well as harm to human health and fauna [14], as seen in bees. Additionally, the fact that pests are becoming more and more resistant to the use of pesticides, causes a risk to crops. The fundamental risks to pepper crops from pests and diseases are biotic problems such as nematodes [15,16,17], aphids [18,19], virus [20,21] and whitefly [22]. There are also abiotic problems caused by the shortage and salinity of water [23,24,25,26,27,28,29,30,31,32,33,34,35] due to climatic changes, among others.
Last but not least important is the risk arising from adverse movements in the selling prices of peppers. Growers establish their crops with the expectation of reaching prices that are similar to those from previous campaigns. However, these prices can experience significant fluctuations that endanger the profitability of current as well as future production campaigns [36,37], which can even lead to growers abandoning the crop. In this study, the analysis of costs is also of particular importance [37,38].
If all these risks are not adequately overcome, it could lead to an important reduction in present and future profits, and for this reason, an adequate analysis of their viability is recommended. Although risk can be construed as the chances of injury, damage, or loss, it is not easy to provide an accurate definition. Cienfuegos [39] and Terje and Ortwin [40] consider that risk should have certain characteristics, such as being equal to expected loss [41], being a combination of probability of an event and its consequences [42], or being an uncertain consequence of an event or an activity with respect to something that people value [43]. Crisis management is the activity which consists of identifying risks, managing threats, and managing crisis situations [44]. The use of net present value (NPV) stands out among the traditional methods for evaluating investment projects [45]. However, the use of a single discount rate to value the whole investment project has serious drawbacks, often leading to erroneous decisions. This method is based on the weighted average cost of capital (WACC), requiring the same return on investments as the cost of financing via equity or debt funds.
The introduction of risk in investment projects is usually done by increasing the discount rate. However, this procedure generates different problems, such as penalizing long-term projects or those that present high values in net cash flows over time [46,47,48]. This problem can be resolved by using hyperbolic discount functions [49,50,51] or gamma functions [52]. Other more criticized methodologies such as the use of real options or decision analysis try to improve these aspects; however, despite the difficulty in implementing and understanding them, in practice they have been used basically to increase NPV results [45,53,54].
To solve these problems, we use the methodology introduced by Espinoza [55,56]. It is a methodology that first identifies the risks, then through probabilistic analysis combined with the valuation of options, it introduces the values of these risks as a cost of the project. In line with Espinoza and Rojo [57], in decoupled net present value (DNPV), the investor is compensated by all the risks assumed which have not been diversified. Its applications can be followed in Espinoza et al. [58] for the valuation of long-term infrastructure investments, and also in Espinoza and Rojo [57] in the mining sector.
The sensitivity analysis is mainly useful for situations such as the one under analysis here, where the correct choice of the discount rate and its variability directly affect the decision to invest [59,60,61]. Some authors have used applied sensitivity and the decision tree approach [62]; however, Monte Carlo simulation techniques have been used for risk analysis to a greater extent [63,64,65,66]. For a better understanding of the variability of the discount rate, the value at risk is particularly suitable. It was originally used in the finance sector, but it has also been used in studies on agricultural valuation, as found in Manfredo and Leuthold [67] and Brotons et al. [68]
Therefore, according to the bibliographic review carried out, it can be affirmed that the cultivation of peppers is subject to numerous risks, most of which have not been economically quantified. As is the case for the majority of cash crops, the economic valuation of pepper crops is carried out by increasing the discount rate, which can lead to erroneous decision-making, in the sense that there is a preference for crops with higher short-term yields. For this reason, the implementation of many projects could be badly affected simply by applying the discount rate incorrectly.
For all the above reasons, in this article, we aim to carry out a correct valuation of the cultivation of greenhouse peppers. This activity requires a very high initial investment; the construction of the greenhouse followed by subsequent investments to replace different elements during its useful life. In order to make a correct valuation, NPV will be used in combination with a correct analysis of the inherent risks of the operation using DNPV. In particular, an analysis will be made of the temporal and permanent fall in prices throughout the useful life of the installation. Other risks will also be analyzed, such as losses due to pests because of not being treated in time, or due to a poor response to phytosanitary treatments. In addition, risk due to a worsening in the quality of irrigation is introduced. All of the above will enable us to determine a present investment value that is very close to the real value. Finally, combining the Monte Carlo methodology with value at risk (VaR) will permit a sensitivity analysis of the results obtained.
2. Materials and Methods
Cash flow is a function , where R is the set of real numbers and c is the cash amount received at moment t or before.
In a discrete environment, the perception of amounts can be represented in as . In the same way, the linear combination of cash flows can be defined as a function of such that .
Let be a step function at time s
In the discrete case, cash flow can be written as the linear combination .
The operator present value converts a cash flow into its present value and indicates that when the latter value in zero it is no difference from a cash flow of amount in t. Thus,
Given that the function is the present value, for each s there is a real number such that:
where the present values can be broken down as the product of future cash flows by the discounting function. Below, some points are taken into consideration regarding both factors.
- (a)
- Discounting function . Traditionally, exponential functions are used; however, their use means penalizing projects whose profits occur in the final period of their useful life. Some authors such as Chichilnisky [69] or Weitzman [52] use hyperbolic functions. In particular, Almansa and Martínez [46] use decreasing discounting functions for the valuation of future environmental impacts. By using a discount function as follows:where in order to have interest rates decreasing over time, we assume that is a random variable whose probability function is a gamma function:
Whose expected value is:
Given that it is a gamma distribution function, the mean and the variance can be obtained as y . In this way expression (7) can be rewritten as:
Finally, the marginal or instantaneous effective discount rate can be obtained as the quotient between the derivative of the discount function and the discount function itself.
- (b)
- Cash flows. They are obtained as the difference between income and foreseen payments. In most cases, future net cash flows () can be considered as uncertain. In any case, they can be defined as the difference between cash inflows and cash outflows , which are also considered uncertain
In an environment of uncertainty there are two estimation methods:
- (a)
- Certainty equivalent. In this case, the uncertain value is multiplied by a factor which fluctuates between 0 and 1 and represents the reduction in value required by the investor to transform a risk investment into a risk-free investment.
- (b)
- Decoupled net present value. In general, the problem with risk investments is due to the fact that the real value of future cash flows tends to be worse than the foreseen value. For this reason, future income and expense flow is reduced with the value of the corresponding synthetic insurance, which protects the investor from future risks of loss in value of future cash flows. In this sense, the value of the synthetic insurance of inflows is , and that of outflows is .
In this way, by combining the decreasing discount function and decoupled net present value, it is possible to obtain a project’s value in several years’ time without future income losing excessive weight, while taking into account the real risk of future cash flows.
2.1. Risks to Be Evaluated
(a) Temporary price fall. The risk of a temporary price fall has been calculated by considering that if the price does not fall below the profitability threshold, this decline can be considered circumstantial, and it is therefore foreseeable that in the following years, prices will recover. It is the risk that prices will not reach the expected values during the campaign. In this case, the price is considered to be distributed normally, with mean µ and standard deviation σ. The expectation of all values that are lower than the expected price in a normal distribution is obtained according to:
To carry out this study, the analysis was based on market prices provided by the Ministry of Agriculture, Food and Environment [3] corresponding to the years 2004 to 2018. Next, weekly production was obtained and the mean prices from the Ministry were valued. In the valuation of the costs, fixed costs (those incurred initially through the installation and setting-up of infrastructure) have been separated from variable costs (those arising year to year through crop production), and the profitability threshold or minimum price necessary to cover variable costs has been determined.
To obtain this risk, the probability of the price being between the weekly mean and the profitability threshold has been obtained weekly. Following this, the expectation of all the values between the mean price and the fixed minimum price has been obtained. Loss will be the difference between the mean price and this expectation. The product of loss through the probability of the prices being in this band and through weekly mean production permits obtaining the weekly risk in euros. The sum of all the weekly risks divided by the value of mean production indicates the risk value in percentage.
(b) Risk due to permanent fall in prices. The risk of a permanent fall in prices has been obtained in a similar way, but the possibility of the price falling below the profitability threshold has also been valued.
(c) Risk due to existence of nematodes and aphids. Risks due to the most common and harmful pests in peppers, such as nematodes and aphids, have been obtained based on the bibliography consulted [14,15,16,17,18,19], comparing the production of plants affected and unaffected by this circumstance. Risk has been obtained as the product of the probability of these episodes occurring through loss in affected plants.
(d) Risk due to existence of bad quality irrigation water. For the risk of having to use water with a greater concentration of salt, which is harmful to plants, three scenarios were considered according to the bibliography consulted [32,33]. In these scenarios, production was compared to control production, and they were assigned probabilities of occurrence of episodes when waters have worse conditions.
(e) Risk due to an increase in costs. Surveys of growers have been carried out, observing what increases in costs could occur and the occurrence probability, obtaining the risk of loss as a product of both.
To obtain geometric DNPV, a prior NPV has been obtained without considering the risks previously calculated. This NPV has been obtained for each of the 24 years that the investment lasts and serves as a basis for obtaining the risk of a permanent fall in prices. Once this is obtained, all the risks obtained as an additional cost have been considered and the NPV of the project as well as yearly net yield have been obtained.
Interest rate has been considered as that of 10-year government bonds, which was 1.62% when this study was carried out [70].
2.2. Sensitivity Analysis
For this analysis, the Monte Carlo simulation was used, assuming variability in the discount rates used and in their standard deviations in order to obtain DNPV and NPV. To do so, these variables are considered normal. To analyze them, Excel spreadsheets with 20,000 iterations combined with the value at risk (VaR) have been used.
Let NPV be a random variable with cumulative distribution function and let VaR be a fixed value of NPV such that,
The VaR is defined as the inverse of the cumulative distribution function
Then, VaR is the lowest value of a variable for a determined level of confidence α, that is to say, the value for which α% of the possible values of this variable is lower than this value and (1 − α)% is greater.
Level of confidence for , is the level of confidence so that can be obtained as the probability of NPV being lower or equal to zero.
3. Results
Mid-May (week 16) is the start of the harvest of peppers cultivated in the Murcia region under thermal greenhouse covering. This means that two or three weeks in advance of the period they would be harvested without thermal covering. The mean price for this week was 1.04 €/kg with a standard error of 0.10 €/kg. This volatility is transmitted along food supply chains thereby exposing all chain actors to risk and uncertainty [71]. The price trend is clearly decreasing until it drops to prices around 0.45 €/kg, where it stabilizes until almost the end of the campaign (Figure 1).
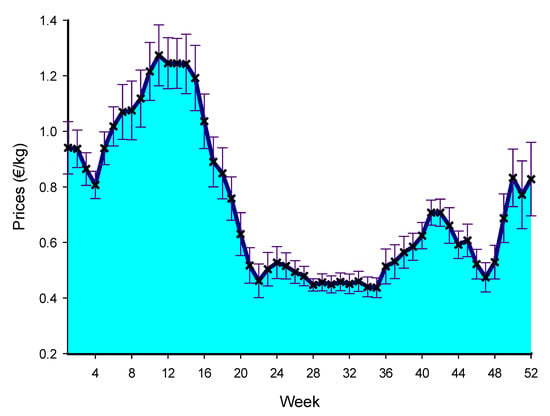
Figure 1.
Evolution of mean weekly prices and standard error.
Like any other economic activity, pepper growing is carried out under the expectation that prices permit reaching at least break-even point. In this case, and given the evolution of the prices in the last few years, the grower tries to bring the harvest forward in order to benefit from higher prices. Therefore, the fall in prices in this initial stage of the campaign is an important risk, as it is during the rest of the campaign, when, even as prices continue to be low, the cumulative volume of production is much higher.
3.1. Risk of Temporary Fall in Prices
During many campaigns, prices may not reach values considered as normal. This risk could be caused by circumstantial issues, such as occasional imbalances between supply and demand, which mean that profit perspectives are not met for a specific year although the causes do not continue over time. This fall tends to be such that in spite of not obtaining the expected profit, the crop continues to be profitable for the grower.
For this reason, it will firstly be necessary to determine the profitability threshold; that is to say, the price at which the grower recovers at least the variable costs, because they would not be willing to produce if prices do not reach this value. To calculate this value, it will be necessary to first consider the variable costs, which are shown in Table 1. Based on this table, it is evident that the value of production should cover at the very least the costs of 45,606 €/ha, for it to be in the grower’s interest to carry on with the activity. At any lower price, it is not in the grower’s interest to produce.

Table 1.
Production per m2 for the years 2016 and 2017 in kg ha−1.
Table 1 shows annual production under a micro tunnel greenhouse. Mean production reaches 120,707 kg/ha, and a price of 0.378 €/kg would cover costs. This means that the grower has to sell their product at higher prices to be able to cover at least the variable costs and part of the fixed costs or costs of setting it up. Conversely, the grower can be expected to abandon production.
Due to weekly fluctuations, the weekly price is considered a normal variable, with the corresponding mean and standard deviation for each week. Weekly analysis is normally used for this kind of horticultural crop [72]. Figure 2 shows the weekly probability that the price will be higher than the corresponding price at threshold profitability, that it will be lower than this threshold, or that it will be between threshold profitability, and the mean price of the week in question.
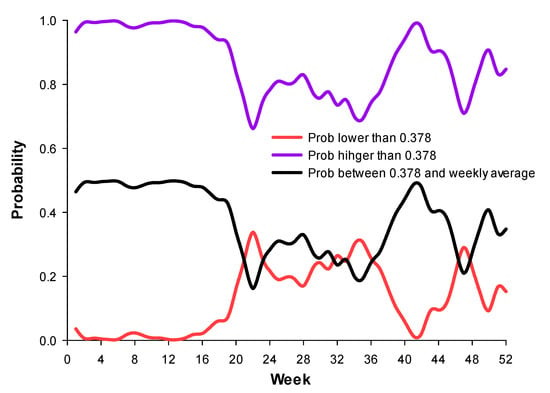
Figure 2.
Probability that the price of peppers will be higher or lower than 0.378 € kg−1.
Figure 3 shows the situation for week 24, which has been taken as an example. The mean price for this week is 0.53 € kg−1. There is a risk of a temporary fall in prices down to threshold profitability (0.378 € kg−1). In accordance with (13), the center of gravity has been obtained from part of the curve between 0.378 and 0.53 € kg−1, obtaining a value of 0.458 € kg−1. In this way, we can summarize all the prices in this range into a single price, 0.458 €/kg. For this price, the loss is 0.07 € kg−1. In addition, the probability of the price being between 0.378 and 0.53 € kg−1 is 0.31. Consequently, the product of loss through its probability permits obtaining risk as a percentage, which multiplied by mean production of the given week (12.473 € kg−1) involves a risk of EUR 122.36 (Table 2) for the given week. This methodology has also been used for the analysis of investments in the energy sector, where Espinoza and Rojo [73] study the variation of solar radiation.
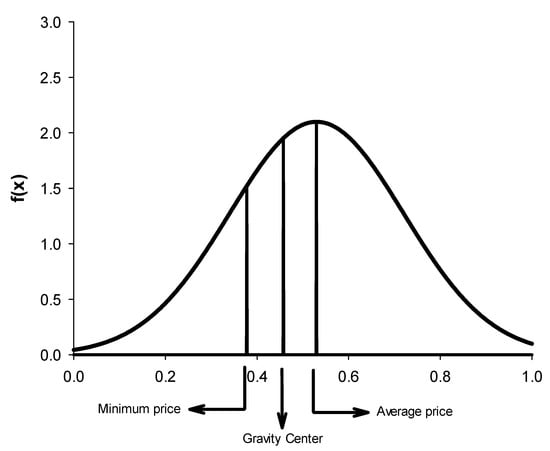
Figure 3.
Density function of the prices for week 24 in € kg−1.

Table 2.
Obtaining weekly risk due to a temporary fall in prices based on the mean and standard deviation.
This process is repeated weekly. As to be expected, the probability of the price being between 0.378 € kg−1 and the weekly mean decreases as the mean prices decrease. This happens until week 21 (third week of May), when it remains more or less stable until week 35 (end of August), when this probability begins to increase. The result obtained is EUR 3720.27. That is to say, the annual risk that the grower assumes due to a temporary price fall is EUR 3720.27, which was 3.08 % of the production value. It should be remembered that most of the risk is due to precocity in the first weeks of harvest (the first three weeks present a risk of EUR 2542.34).
3.2. Probability of Permanent Drop in the Price of Peppers
The previous section gives an analysis of the risk of a fall in prices from the mean value to profitability threshold; that is to say, to the value that covers only the variable production costs (0.378). However, if the price drops below this figure, the grower will abandon production, in which case the loss is considered definitive.
The procedure used is similar to the one in the first section and the results obtained are given in Table 3. For each week, the mean price and its standard deviations are indicated, as well as the probability of the price falling below 0.378. The central value of prices lower than 0.378 has been obtained in order to determine loss (0.378—Expected value). The product of loss through occurrence probability multiplied by the mean production of the given week allows us to obtain the risk of expected loss in euros. The value obtained is EUR 1622.90 annually, which means 1.34%. It should be remembered that this value will be applied to the NPV for the remaining years until the end of the installation’s useful life. To do this, it will be necessary to obtain a previous NPV according to the expected net yields until the end of the greenhouse’s useful life.

Table 3.
Obtaining weekly risk of pepper production as product of weekly production per estimated loss and its probability.
3.3. Risk due to Nematodes and Aphids
Table 4 shows the mean production of healthy plants (treated) and those affected by nematodes and aphids. Loss for not having treated the plants or because treatment was unsuccessful has been calculated, resulting in 34% for nematodes and 28% for aphids. Occurrence probability has been indicated for both based on past experiences. It should be noted that production values are not the same, because the treatment against aphids was applied on a more productive cultivar. For production per hectare and loss risk profile, production has been homogenized at 88,000 kg ha−1. The product of loss per probability gives a risk occurrence of 3.41% for nematodes and 0.28% for aphids.

Table 4.
Risk due to nematodes and aphids.
Based on the consulted bibliography [14,15,16,17,18,19], production has been obtained for plants if they were not treated with phytosanitary products for controlling these pests. Table 4 indicates the difference in yield between plants treated and untreated for nematodes and aphids; loss being 34% and 28%. It has been estimated that even if treatment is given, there is a 10% risk of becoming infected by these “pests”, thus real loss could be estimated between 3.41 and 1.41%.
Figure 4 summarizes the previous information. Production with each type of pest is indicated with their occurrence probability, and the loss risk profile obtained as base production (88,000 kg ha−1) minus production for each case. For nematode risk, the loss risk profile is 30,000 kg ha−1, being the difference between 88,000 kg ha−1 and production obtained without treatment (58,000 kg ha−1). Espinoza and Rojo [73] make a similar analysis to evaluate the tariff risk profile in renewable energies.
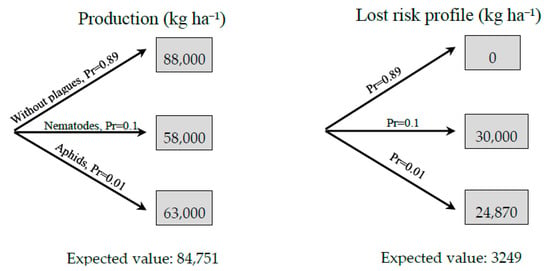
Figure 4.
Decision tree of loss due to nematodes and aphids.
3.4. Risk Due to Bad Quality Irrigation Waters
Salinity is one of the main stressors limiting plant development and crop productivity. The competition for good-quality water is forcing farmers to use brackish waters for irrigation [74].
Loss due to salinity has been obtained from the consulted biography [32]. Three levels of salinity in water have been determined, with each one permitting a different production and consequently a loss, which becomes greater according to the increase in salinity of the water. There are different studies that establish three levels of salinity; for example, Cámara-Zapata et al. [75] carried out a study on the profitability of tomatoes. Given that the quality of the water is not an option for the grower, an occurrence probability for each of the scenarios is considered in accordance with the information gathered from the growers, and a loss of EUR 0.90, 1.80 and 1, respectively, is obtained, which is a total of 3.7% and is 5.87% with respect to control production (Table 5 and Figure 5). Other similar applications can be found in Espinoza and Rojo [73].

Table 5.
Risk due to salinity.
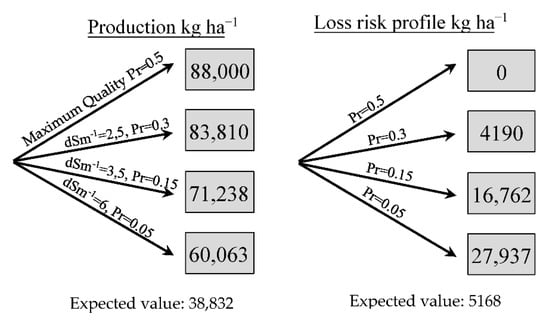
Figure 5.
Decision tree of loss due to salinity in kg ha−1.
3.5. Risk due to Increase in Costs
Table 6 shows the estimated increase in costs due to renovations, such as whitewashing and plastic drip irrigation system. These are the elements that have to be replaced in a greenhouse. The table indicates initial price, expected increase in euros, and their occurrence probability. The last two columns transform the previous increases into certain values, multiplying the increase by their occurrence probability. As can be observed, the increases in costs considered for these three concepts are quite low (EUR 2.75 and 69) respectively, but despite this, they have been considered. For the rest of the costs, we have considered an evolution similar to the consumer price index as well as for future income.

Table 6.
Summary of risk of increase in costs.
3.6. Obtaining Present Value
The annual income is shown in Table 7, with the indication of weekly production, weekly mean price, and total amount for each of the two years. Annual costs are summarized in Table 8. It is an activity with a high prevalence of variable costs [6], where labor has a very important weight in the final cost of the product. Besides, additional whitewashing when there are heavy rains (on average, approximately every three years) should be considered in the variable costs [10]. Pluriannual projected costs are shown in Table 9, where useful life is also indicated. The cost of the greenhouse, the main investment, is the one the that determines the duration of the project, while the drip irrigation installation has to be changed every 10 years and the covering of the greenhouse has to be changed every three years. This structure is similar to other studies, such as in [76].

Table 7.
Summary of annual income.

Table 8.
Summary of annual costs.

Table 9.
Pluriannual costs.
3.7. Obtaining the DNPV
Table 10 summarizes the main risks. As can be observed, the total sum of risks is 15,086.87 € ha−1 for year 1. Traditional calculation involves determining some annual yields of EUR 25,814, but with this methodology we are able to identify the crop risks, focusing predominantly on problems related to pests and variations in prices. Therefore, the risk-free net yield is reduced to EUR 10,727.01 in the first year and to EUR 14,936.76 in the last year.

Table 10.
Summary of risks considered.
It should be noted that the percentage of lost income caused by a temporary reduction means a reduction in the same proportion of income for the period, but the percentages for permanent loss means a reduction in NPV for the period, having a greater effect if this reduction occurs in the first years than if it happens in the last years.
NPV has been obtained from estimated annual income and expenses, as well as the correct discounting of pluriannual costs (installation and assembly, plastics, installation of drip irrigation, which are shown in Table 11). In accordance with DNPV, risks are considered as a lower income or higher expense according to cases.

Table 11.
Total costs of installation and assembly.
As a result, a DPNV of EUR 84,658 is obtained, using a risk-free interest of 1.62%. By using a risk premium of 6.35% as mean value of the indicator values, as performed by different authors such as Siegel [77], Dimson et al. [78] or Fernández et al. [79] among others, an NPV of EUR 125,265 is obtained. For its part, using a decreasing gamma discount function of mean 1.62% and standard deviation 0.97, a DNPV of 88,324 is obtained, similar to the traditional discount function. By applying the decreasing gamma discount function, a present net value of EUR 178,394 is obtained, which is much higher than the traditional NPV.
These calculations illustrate how the use of NPV generates a lot more uncertainty; in this case, the risks to crops or to installations with useful lives that extend over time are introduced into the model thereby increasing the discount rate. The use of discount functions such as gamma discount do not reduce uncertainty, although they generate higher current values. Besides, because the discount rate used is very low, the use of decreasing discount functions hardly changes the result. By contrast, the use of DNPV makes a correct analysis of all the risks and is more recommendable than the method used by other authors such as de Oliveira [80], 2015, who suggests the use of a methodology based on multi-indices.
Figure 6 shows the sensitivity analysis of the results obtained in the discount rate. To achieve this, the Monte Carlo method is used, which can be easily implemented in typical Excel spreadsheets [7] and [8], considering a risk-free rate of interest of 1.62% (used for DNPV), and a premium that is distributed normally with mean 7.97% and standard deviation 4.78%. The discount rate used in DNPV with a decreasing discount function is distributed N (1.62%, 0.97%) and its standard deviation is distributed N (0.97%, 0.58%). Finally, the discount rate for NPV is distributed N (7.97%, 4.78%), and its standard deviation is distributed N (4.78%, 2.87%). The results are shown in Figure 6. As can be observed, the probability of obtaining a higher result with the decreasing discount function for DPNV is 0.49, which indicates that it hardly changes the result obtained. The traditional method (NPV), on the other hand, gives a probability of 0.32, which is a lower result, and is reduced to 0.25 using decreasing discount functions. A similar methodology was applied by Smith et al. [81] (2014), who used descending cumulative probability curves for 10-year disease loss and control costs for five different control strategies used in the sensitivity analysis
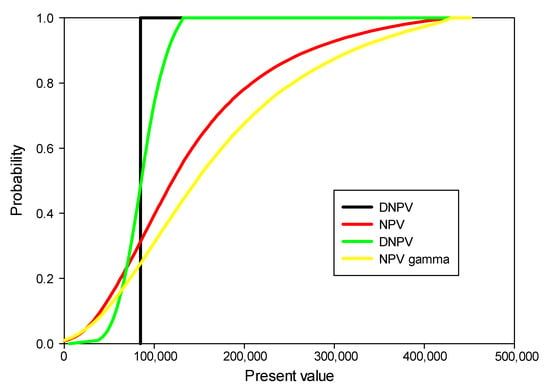
Figure 6.
Probability of obtaining the indicated net present value (NPV) or a lower NPV (V = NPV, D = decoupled net present value (DNPV), g = use of gamma discount function).
Finally, in Figure 7, the results obtained are compared and the probabilities that some of the methodologies outweigh others are obtained, which is coherent with other studies, such as Almansa et Martínez-Paz [46]. In principle, it cannot be affirmed that some methodologies lead to higher results than the rest, but it is significant that:
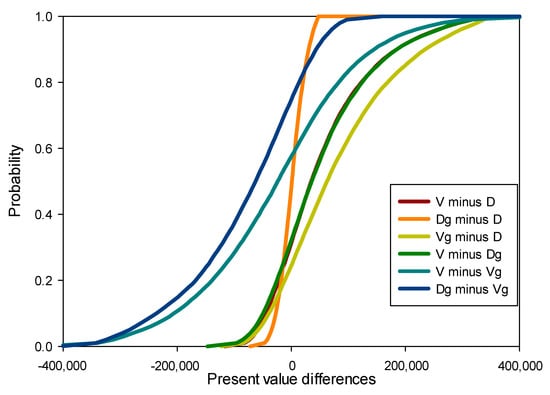
Figure 7.
Comparisons per pairs of updated values obtained (V = NPV, D = DNPV, g = gamma discount function).
- DNPV is not affected by the use of decreasing discount functions;
- NPV with decreasing rate is higher than traditional NPV in 58% of occasions;
- In the comparison between NPV and DNPV, the latter is higher in 68% of the cases and in 75% when decreasing discount functions are used.
4. Conclusions
The methodology used has enabled the isolation and valuation of real risks in the cultivation of greenhouse peppers. Firstly, the risks have been identified in relation to the prices of products that experience falls, which can stop the grower from achieving the expected profitability. These are calculated as a risk of a temporary fall in prices and a risk of a permanent fall in prices. If the fall in prices is not very sharp, the grower’s profits will be reduced, but it will not change the decision to grow peppers in future campaigns. However, if there is a sharp price fall, the grower will perceive it as a change in trends, and it is possible that they will replant the crop in the following years. The risk for the former has been valued at 3720 € ha−1 year−1 and the latter at 1622 € ha−1 for the first year, a risk which decreases as the greenhouse’s end of useful life approaches. Other risks considered are the loss caused by pests, valued at −3248.70 € ha−1 per year and risks from loss in water quality (−5168.25 € ha−1 per year). Finally, although the amount is small, risks from the increase in costs of pluriannual projection elements that need to be replaced have also been considered.
With respect to the comparison between methodologies, it should be noted that the use of DNPV is much more accurate because it enables quantification of the risks while NPV is limited to increasing the discounting rate. The use of decreasing discount functions helps to partly mitigate the strong impact from the increase in interests on the discounted cash flows over time. This use of these decreasing functions only slightly affects the results obtained in DNPV, while it is more pronounced in traditional NPV, because it uses higher interest rates and therefore penalizes future cash flows more.
Finally, a sensitivity analysis was made, regarding the variation in the interest rates, reaching the conclusion that this does not affect DNPV, and that the use of decreasing functions increases the result in traditional NPV, although the value depends on the interest rates used. It is therefore not possible to reach any conclusion a priori about which methodology generates the best results in the valuation of an agriculture holding.
Author Contributions
Conceptualization, J.L.-M., A.G., F.M.d.A. and J.M.B.; methodology, J.L.-M. and J.M.B.; software, J.M.B.; validation, J.L.-M., F.M.d.A. and J.M.B.; formal analysis, J.M.B.; investigation, J.L.-M. and J.M.B.; resources, J.L.-M., A.G., F.M.d.A. and writing—original draft preparation, J.L.-M. and J.M.B.; writing—review and editing, J.L.-M. and J.M.B.; supervision J.L.-M., F.M.d.A. and J.M.B.; project administration, J.L.-M. and J.M.B.; funding acquisition J.M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Convocatoria de ayudas a la investigación de la Universidad Miguel Hernández de Elche 2020. DF1007VF.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest and the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Serret, M.D.; Yousfi, S.; Vicente, R.; Piñero, M.C.; Otálora-Alcón, G.; del Amor, F.M.; Araus, J.L. Interactive effects of CO2 concentration and water regime on stable isotope signatures, nitrogen assimilation and growth in sweet pepper. Front. Plant Sci. 2018, 8, 2180. [Google Scholar] [CrossRef] [PubMed]
- FAOSTAT. Available online: http://www.fao.org/faostat/es/#home (accessed on 15 July 2020).
- Magrama. Available online: http://www.magrama.gob.es/es/estadistica/temas/estadisticas-alimentacion/observatorio-precios (accessed on 2 September 2020).
- Fan, X.; Cao, X.; Zhou, H.; Hao, H.; Dong, W.; He, C.; Xu, M.; Wu, H.; Wang, L.; Chang, Z.; et al. Carbon dioxide fertilization effect on plant growth under soil water stress associates with changes in stomatal traits, leaf photosynthesis, and foliar nitrogen of bell pepper (Capsicum annuum L.). Environ. Exp. Bot. 2020, 179, 104203. [Google Scholar] [CrossRef]
- Díaz-Pérez, J. Bell Pepper (Capsicum annum L.) Grown on Plastic Film Mulches: Effects on Crop Microenvironment, Physiological Attributes, and Fruit Yield. HortScience 2014, 45, 1196–1204. [Google Scholar] [CrossRef]
- López-Marin, J.; Gálvez, A.; Porras, I.; Brotons-Martinez, J.M. Use of a PSNM to Increase Precocity and Its Benefits in Greenhouse-Grown Sweet Pepper. J. Agric. Sci. Technol. 2017, 19, 1005–1018. [Google Scholar]
- Ben-Yakir, D.; Antignus, Y.; Offir, Y.; Shahak, Y. Colored shading nets impede insect invasion and decrease the incidences of insect-transmitted viral diseases in vegetable crops. Entomol. Exp. Appl. 2012, 144, 249–257. [Google Scholar] [CrossRef]
- López-Marin, J.; Rodriguez, M.; Del Amor, F.; Gálvez, A.; Brotons-Martinez, J. Cost-Benefit Analysis of Tomato Crops under Different Greenhouse Covers. J. Agric. Sci. Technol. 2019, 21, 235–248. [Google Scholar]
- Möller, M.; Assouline, S. Effects of a shading screen on microclimate and crop water requirements. Irrig. Sci. 2007, 25, 171–181. [Google Scholar] [CrossRef]
- López-Marín, J.; Egea-Gilabert, C.; González, A.; Pérez-Alfocea, F.; Fernández, J.A. Grafting is an efficient alternative to shading screens to alleviate thermal stress in greenhouse-grown sweet pepper. Sci. Hortic. Amsterdam. 2013, 149, 39–46. [Google Scholar] [CrossRef]
- Savvas, D.; Gruda, N. Application of soilless culture technologies in the modern greenhouse industry—A review. Eur. J. Hortic. Sci. 2018, 83, 280–293. [Google Scholar] [CrossRef]
- Singh, H.; Dunn, B.L.; Payton, M.; Brandenberger, L. Selection of Fertilizer and Cultivar of Sweet Pepper and Eggplant for Hydroponic Production. Agronomy 2019, 9, 433. [Google Scholar] [CrossRef]
- Buchholz, M.; Jochum, P.; Zaragoza, G. Basic Water, Heat and Food Supply from a Closed Greenhouse—The Watergy Project. Acta Hortic. 2005, 691, 509–516. [Google Scholar] [CrossRef]
- Núñez-Zofío, M.; Larregla, S.; Garbisu, C.; Lacasa, A. Application of sugar beet vinasse followed by solarization reduces the incidence of Meloidogyne incognita in pepper crops while improving soil quality. Phytoparasitica 2013, 41, 181–191. [Google Scholar] [CrossRef]
- Ros, M.; Garcia, C.; Hernandez, T.; Lacasa, A.; Fernández, P.; Fernández, J.A. Effects of biosolarization as methyl bromide alternative for Meloidogyne incognita control on quality of soil under pepper. Biol. Fertil. Soils 2008, 45, 37. [Google Scholar] [CrossRef]
- Sogut, M.A.; Elekcioglu, I.H. Methyl bromide alternatives for controlling Meloidogyne incognita in pepper cultivars in the Eastern Mediterranean Region of Turkey. Turk. J. Agric. For. 2007, 31, 31–40. [Google Scholar]
- Tzortzakakis, E.A.; Petsas, S.E. Investigation of alternatives to methyl bromide for management of Meloidogyne javanica on greenhouse grown tomato. Pest. Manag. Sci. 2003, 59, 1311–1320. [Google Scholar] [CrossRef] [PubMed]
- Frantz, J.A.; Gardner, J.; Hoffmann, M.P.; Jahn, M.M. Greenhouse screening of Capsicum accessions for resistance to green peach aphids (Myzus persciae). Hortscience 2004, 39, 1332–1335. [Google Scholar] [CrossRef]
- Herman, M.A.B.; Nault, B.A.; Smart, C.D. Effects of plant growth-promoting rhizobacteria on bell pepper production and green peach aphid infestations in New York. Crop Prot. 2008, 27, 996–1002. [Google Scholar] [CrossRef]
- Anurag, S. The occurrence and disease incidence of Tospovirus infecting pepper (Capsicum annuum L.) in Southern Thailand. Philipp. Agric. Sci. 2012, 95, 411–415. [Google Scholar]
- Fortes, I.M.; Moriones, E.; Navas-Castillo, J. Tomato chlorosis virus in pepper: Prevalence in commercial crops in southeastern Spain and symptomatology under experimental conditions. Plant Pathol. 2012, 61, 994–1001. [Google Scholar] [CrossRef]
- Avila-Valdez, J.; Wolfenbarger, D.A. Yellow Traps and Insecticides for Control of a Strain of Sweet Potato Whitefly and Associated Virus Incidence on Pepper. J. Entomol. Sci. 1995, 30, 342–348. [Google Scholar] [CrossRef]
- Aktas, H.; Abak, K.; Cakmak, I. Genotypic variation in the response of pepper to salinity. Sci. Hortic. 2006, 110, 260–266. [Google Scholar] [CrossRef]
- Anjum, S.A.; Farooq, M.; Xie, X.Y.; Liu, X.J.; Ijaz, M.F. Antioxidant defense system and proline accumulation enables hot pepper to perform better under drought. Sci. Hortic. 2012, 140, 66–73. [Google Scholar] [CrossRef]
- Arrowsmith, S.; Egan, T.P.; Meekins, J.F.; Powers, D.; Metcalfe, M. Effects of salt stress on capsaicin content, growth, and fluorescence in a Jalapeno cultivar of Capsicum annuum (Solanaceae). Bios 2012, 83, 1–7. [Google Scholar] [CrossRef]
- Azuma, R.; Ito, N.; Nakayama, N.; Suwa, R.; Nguyen, N.T.; Larrinaga-Mayoral, J.A.; Esaka, M.; Fujiyama, H.; Saneoka, H. Fruits are more sensitive to salinity than leaves and stems in pepper plants (Capsicum annuum L.). Sci. Hortic. 2010, 125, 171–178. [Google Scholar] [CrossRef]
- Dagdelen, N.; Yilmaz, E.; Sezgin, F.; Gürbüz, T. Effects of water stress at differentgrowth stages on processing pepper (Capsicum annuum) yield, water use andquality characteristics. Pak. J. Biol. Sci. 2004, 7, 2167–2172. [Google Scholar]
- De Pascale, S.; Ruggiero, C.; Barbieri, G. Physiological responses of pepper to salinity and drought. J. Am. Soc. Hortic. Sci. 2003, 128, 48–54. [Google Scholar] [CrossRef]
- Delfine, S.; Tognetti, R.; Loreto, F.; Alvino, A. Physiological and growth responses to water stress in field-grown bell pepper (Capsicum annuum L.). J. Hortic. Sci. Biotechnol. 2002, 77, 697–704. [Google Scholar] [CrossRef]
- Fernández, M.D.; Gallardo, M.; Bonachela, S.; Orgaz, F.; Thompson, R.B.; Fereres, E. Water use and production of a greenhouse pepper crop under optimum and limited water supply. J. Hortic. Sci. Biotechnol. 2005, 80, 87–96. [Google Scholar] [CrossRef]
- Rameshwaran, P.; Tepe, A.; Yazar, A.; Ragab, R. The Effect of Saline Irrigation Water on the Yield of Pepper: Experimental and Modelling Study. Irrig. Drain 2015, 64, 41–49. [Google Scholar] [CrossRef]
- Savvas, D.; Stamati, E.; Tsirogiannis, I.L.; Mantzos, N.; Barouchas, P.E.; Katsoulas, N.; Kittas, C. Interactions between salinity and irrigation frequency in greenhouse pepper grown in closed-cycle hydroponic systems. Agric. Water Manag. 2007, 91, 102–111. [Google Scholar] [CrossRef]
- Wagner, H.M. Global sensitivity analysis. Oper. Res. 1995, 43, 948–969. [Google Scholar] [CrossRef]
- Penella, C.; González Nebauer, S.; López-Galarza, S.V.; San Bautista-Primo, A.; Rodríguez-Burruezo, A.; Calatayud, A. Evaluation of some pepper genotypes as rootstocks in water stress conditions. Hortic. Sci. 2014, 41, 192–200. [Google Scholar] [CrossRef]
- Fuentes, S.; Trejo-Alonso, J.; Quevedo, A.; Fuentes, C.; Chávez, C. Modeling Soil Water Redistribution under Gravity Irrigation with the Richards Equation. Mathematics 2020, 8, 1581. [Google Scholar] [CrossRef]
- Fearon, J.; Asare, J.; Okran, E.O. Contemporary Price Trends and their Economic Significance in the Ashanti Region of Ghana. Biol. Agric. Healthc. 2014, 4, 38–47. [Google Scholar]
- Lopez-Marin, J.; Brotons-Martinez, J.M.; Galvez, A.; Porras, I. Pepper grafting (Capsicum annuum): Benefits and profitability. ITEA 2016, 112, 127–146. [Google Scholar]
- Imran, M.; Habib, M.; Hussain, A.; Ahmed, N.; Al-Ahmari, A.M. Inventory Routing Problem in Supply Chain of Perishable Products under Cost Uncertainty. Mathematics 2020, 8, 382. [Google Scholar] [CrossRef]
- Cienfuegos, I. Risk Management theory: The integrated perspective and its application in the public sector. Estado Gob. Gestión Pública 2013, 21, 89–126. [Google Scholar] [CrossRef]
- Terje, A.; Ortwin, R. On risk defined as an event where the outcome is uncertain. J. Risk Res. 2009, 12, 1–11. [Google Scholar]
- ISO. Risk Management Vocabulary. ISO/IEC Guide; ISO: Geneva, Switzerland, 2002. [Google Scholar]
- IRGC. White Paper on Risk Governance. Towards an Integrative Approach; IRGC: Geneva, Switzerland, 2005. [Google Scholar]
- Willis, H.H. Guiding resource allocations based on terrorism risk. Risk Anal. 2007, 27, 597–606. [Google Scholar] [CrossRef]
- Skomra, W. Risk management as part of crisis management tasks. Found. Manag. 2017, 9. [Google Scholar] [CrossRef]
- Brotons, J.M. Supuestos de Valoración de Inversiones: Métodos Clásicos y Opciones Reales; Universidad Miguel Hernández: Elche, Spain, 2017. [Google Scholar]
- Almansa, C.; Martínez-Paz, J.M. What weight should be assigned to future environmental impacts? A probabilistic cost benefit analysis using recent advances on discounting. Sci. Total Environ. 2011, 409, 1305–1314. [Google Scholar] [CrossRef] [PubMed]
- Halliwell, L.J. A critique of risk-adjusted discounting. In Proceedings of the 32nd International Actuarial Studies in Non-Life Insurance Colloquium, Washington, DC, USA, 8–11 July 2001. [Google Scholar]
- Groom, B.; Hepburn, C.; Koundouri, P.; Pearce, D. Declining Discount Rates: The Long and the Short of it. Environ. Resour. Econ. 2005, 32, 445–493. [Google Scholar] [CrossRef]
- Almansa, C.; Calatrava, J. Reconciling sustainability in cost benefit analysis: A methological proposal. Ecol. Econ. 2007, 60, 712–725. [Google Scholar]
- Loewenstein, G.; Prelec, D. Anomalies in intertemporal choice: Evidence and interpretation. Q. J. Econ. 1992, 107, 573–597. [Google Scholar] [CrossRef]
- Henderson, N.; Bateman, I. Empirical and public choice evidence for hyperbolic social discount rates and the implications for intergenerational discounting. Environ. Resour. Econ. 1995, 5, 413–423. [Google Scholar] [CrossRef]
- Weitzman, M. Gamma discounting. Am. Econ. Rev. 2001, 91, 261–271. [Google Scholar] [CrossRef]
- Borison, A. Real option analysis: Where are the Emperor’s clothes? J. Appl. Corp. Financ. 2005, 17, 17–31. [Google Scholar] [CrossRef]
- Brotons, J.M. Matemáticas Financieras. La Gestión del Riesgo de Interés; Universidad Miguel Hernández: Elche, Spain, 2014. [Google Scholar]
- Espinoza, R.D.; Morris, J.W.F. Decouple NPV: A simple method to improve valuation of infrastructure investments. Constr. Manag. Econ. 2013, 31, 471–496. [Google Scholar] [CrossRef]
- Espinoza, R.D. Separating project risk from the time value of money: A step toward integration of risk management and valuation of infrastructure investments. INT J. Proj. Manag. 2014, 32, 1056–1072. [Google Scholar] [CrossRef]
- Espinoza, R.D.; Rojo, J. Towards sustainable mining (Part I): Valuing investment opportunities in the mining sector. Resour. Policy 2017, 52, 7–18. [Google Scholar] [CrossRef]
- Espinoza, D.; Rojo, J.; Cifuentes, A.; Morris, J. DNPV: A valuation methodology for infrastructure and Capital investments consistent with prospect theory. Constr. Manag. Econ. 2020, 38, 259–274. [Google Scholar] [CrossRef]
- Chiwaula, L.S.; Kawiya, C.; Kambewa, P.S. Evaluating Economic Viability of Large Fish Solar Tent Dryers. Agric. Res. 2020, 9, 270–276. [Google Scholar] [CrossRef]
- Costa, L.D.; Gianquinto, G. Water stress and water table depth influence yield, water use efficiency, and nitrogen recovery in bell pepper: Lysimeter studies. Aust. J. Agric. Res. 2002, 53, 201–210. [Google Scholar] [CrossRef]
- Cruz-Rambaud, S.; Sánchez-Pérez, A.M. Discounted and Expected Utility from the Probability and Time Trade-Off Model. Mathematics 2020, 8, 601. [Google Scholar] [CrossRef]
- Lanaa, N.; Sanjinb, I.; Todorc, M. Economic efficiency of breeding Tsigai sheep in the Central and South—East Europe (naslov ne postoji na srpskom). Ekon. Poljopr. 2020, 67, 175–188. [Google Scholar]
- Russell, A.D.; Ranasinghe, M. Analytical approach for economic risk quantification of large engineering projects. Constr. Manag. Econ. 1992, 10, 277–301. [Google Scholar] [CrossRef]
- Ye, S.; Tiong, R.L. NPV-at-risk method in infrastructure project investment evaluation. J. Constr. Eng. Manag. 2000, 126, 227–233. [Google Scholar] [CrossRef]
- Chiara, N.; Garvin, M.J. Variance models for project financial risk analysis with applications to greenfield BOT highway projects. Constr. Manag. Econ. 2008, 26, 925–939. [Google Scholar] [CrossRef]
- Liou, F.M.; Huang, C.P. Automated approach to negotiations of BOT contracts with the consideration of project risk. J. Constr. Eng. Manag. 2008, 134, 18–24. [Google Scholar] [CrossRef]
- Manfredo, M.R.; Leuthold, R.M. Value-at-Risk Analysis: A Review and the Potential for Agricultural Applications. Rev. Agric. Econ. 1999, 21, 99–111. [Google Scholar] [CrossRef]
- Brotons-Martínez, J.M.; Martin-Gorriz, B.; Torregrosa, A.; Porras, I. Economic evaluation of mechanical harvesting of lemons. Outlook Agric. 2018, 47, 44–50. [Google Scholar] [CrossRef]
- Chichilnisky, G. An axiomatic approach to sustainable development. Soc. Choice Welf. 1996, 13, 219–248. [Google Scholar] [CrossRef]
- Stock Exchanges and Markets. Available online: https://www.bmerf.es/esp/aspx/comun/posiciones.aspx?Mercado=SDP&menu=47 (accessed on 20 July 2020).
- Assefa, T.T.; Meuwissen, M.P.M.; Lansink, A.G.J.M.O. Price Volatility Transmission in Food Supply Chains: A Literature Review. Agribusiness 2016, 31, 3–13. [Google Scholar] [CrossRef]
- Heuvelink, E. Growth, development and yield of a tomato crop—Periodic destructive measurements in a greenhouse. Sci. Hortic. 1995, 61, 77–99. [Google Scholar] [CrossRef]
- Espinoza, R.D.; Rojo, J. Using DNPV for valuing investments in the energy sector: A solar project case study. Renew. Energy 2015, 75, 44–49. [Google Scholar] [CrossRef]
- Piñero, M.C.; Pérez-Jiménez, M.; López-Marín, J.; del Amor, F.M. Fruit quality of sweet pepper as affected by foliar Ca applications to mitigate the supply of saline water under a climate change scenario. J. Sci. Food Agric. 2018, 98, 1071–1078. [Google Scholar] [CrossRef] [PubMed]
- Cámara-Zapata, J.M.; Brotons-Martínez, J.M.; Simón-Grao, S.; Martinez-Nicolás, J.J.; García-Sánchez, F. Cost-benefit analysis of tomato in soilless culture systems with saline water under greenhouse conditions. J. Sci. Food Agric. 2019, 99, 5842–5851. [Google Scholar] [CrossRef]
- López-Marín, J.; Gálvez, A.; Otalora, G.; Del Amor, F.M. Photoselective shade nets for pepper cultivation in Southeastern Spain. Acta Hortic. 2019, 1252, 183–190. [Google Scholar] [CrossRef]
- Siegel, J.J. Perspectives on the Equity Risk Premium. Financ. Anal. J. 2005, 61, 61–71. [Google Scholar] [CrossRef]
- Dimson, E.; Marsh, P.; Staunton, M. The Worldwide Equity Premium: A Smaller Puzzle. In Handbook of Investments: Equity Risk Premium; Mehra, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 467–514. [Google Scholar]
- Fernández, P.; Aguirreamalloa, J.; Corres, L. Prima de Riesgo del Mercado Utilizada para España; Documento de investigación DI-921; IESE Business School—Universidad de Navarra: Barcelona, Spain, 2011. [Google Scholar]
- de Oliveira, A.B.; Lachowski, D.C.; Leal, D.R.; Catapan, A.; Martins, P.F.; Benner, L.C.; Cardoso, A. Cultivation of pomodoro tomatoes in a greenhouse: An analysis of financial viability through multi-indices methodology. Cust Agronegocio 2015, 11, 126–154. [Google Scholar]
- Smith, R.L.; Sanderson, M.W.; Jones, R.; N’Guessan, Y.; Renter, D.; Larson, R.; White, B.J. Economic risk analysis model for bovine viral diarrhea virusbiosecurity in cow-calf herds. Prev. Vet. Med. 2014, 113, 492–503. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).