On BC-Subtrees in Multi-Fan and Multi-Wheel Graphs

Abstract

The BC-subtree (a subtree in which any two leaves are at even distance apart) number index is the total number of non-empty BC-subtrees of a graph, and is defined as a counting-based topological index that incorporates the leaf distance constraint. In this paper, we provide recursive formulas for computing the BC-subtree generating functions of multi-fan and multi-wheel graphs. As an application, we obtain the BC-subtree numbers of multi-fan graphs, r multi-fan graphs, multi-wheel (wheel) graphs, and discuss the change of the BC-subtree numbers between different multi-fan or multi-wheel graphs. We also consider the behavior of the BC-subtree number in these structures through the study of extremal problems and BC-subtree density. Our study offers a new perspective on understanding new structural properties of cyclic graphs.

1. Introduction

A topological index is a numerical graph invariant that can quantitatively characterize the properties of the corresponding structure. Topological indices in general have applications in numerous areas such as network design, compounds synthesis, pharmacology, and biology. Consequently a large number (approximately four hundred) of topological indices have been introduced during previous decades.

Among various topological indices, distance-based [1,2,3,4], degree-based [5,6,7,8], counting-based [9,10,11,12,13] have received much attention [14,15,16,17], and many indices have been employed as tools for characterization of molecular topology [18,19,20,21].

Compared to the subtree number index [22,23,24,25,26], the BC-subtree number index is a counting-based topological index that incorporates leaf distance constraint. First of all, a BC-tree is a tree in which any two leaves are at even distance apart. This important structure was introduced by F. Harary et al. [27,28]. The BC-subtree number index or simply the BC-subtree index was first introduced in [13], as the number of all non-empty BC-subtrees (subtrees that are also BC-trees) of a graph.

Much work has been done on the BC-trees and BC-subtree number index. Some examples include generic chemical structures storage problem [29,30], fault-tolerant computing and parallel scheduling [31,32], recognizing and identifying special substructures [33,34,35], the flow network simplification [36], Markovian queueing systems decomposition [37], matching problem [38,39], extremal and density problems [13,40], and enumerating algorithm design [13,41].

We are particularly interested in the enumeration of BC-subtrees. Using a generating functional approach proposed by Yan and Yeh in [12] (for general subtrees), Yang et al. [13] presented algorithms of enumerating BC-subtrees of trees. Later Yang et al. [41] solved the BC-subtree enumeration problem on uni-cyclic and edge-disjoint bicyclic graphs and further generalized this study to spiro and polyphenyl hexagonal chains [40].

Previous studies show that the multi-fan and multi-wheel graphs (Definitions 1 and 2) have many interesting properties and applications in circuit layout and interconnection network design. The $W_{n+1}$ is also useful in designing efficient wireless ad hoc networks [42]. The wheel-transposition graphs (graphs generated by wheel graphs) could be used in parallel and distributed system [43]. Both the multi-fan graphs and the wheel graphs $W_{n+1}(n\ne 6)$ are among the graphs that can be determined by its Laplacian spectra [44,45]. Moreover, the Hilbert series of fan graphs, multi-fan graphs and multi-wheel graphs were derived in [46]. Subtrees of Fan Graphs, Wheel Graphs, and “Partitions” of Wheel Graphs under Dynamic Evolution was studied in [47]. In this paper we will consider the BC-subtree number index for these two structures.

We first introduce related preliminary information in Section 2. The BC-subtree generating functions of multi-fan graphs and multi-wheel graphs are provided in Section 3 and Section 4. Some special cases are also discussed as immediate consequences. In Section 5 we make use of our findings to consdier the behavior of the BC-subtree number in the above mentioned structures. Extremal problems are studied. We summarize our work in Section 6.

2. Preliminaries

Before introducing our main results there are quite some preparations to do. Let $G=\left(V\right(G),E(G);f,g)$ be a weighted graph with vertex set $V\left(G\right)$, edge set $E\left(G\right)$, vertex-weight function $f=(f_o\left(u\right),f_e\left(u\right))$ ($f_o\left(u\right)$ and $f_e\left(u\right)$ are the odd, even weight of $u\in V\left(G\right)$, respectively) and edge-weight function $g=g\left(e\right)$ for $e\in E\left(G\right)$. First we list the necessary notations and terminologies.

2.1. Basic Notations

• $d_G(u,v)$: the distance between $u\in V\left(G\right)$ and $v\in V\left(G\right)$.
• $G\backslash Y$: the graph after removing Y from G.
• $L\left(T\right)$: the leaf set of T.
• $f_o\left(u\right)$, $f_e\left(u\right)$: the odd, even weight of $u\in V\left(G\right)$, respectively.
• $S(G;X)$: the subtree set of G containing X, where X can be a vertex set or an edge set (or both), or a subtree of G.
• $S(G;v,\mathrm{odd})$: the subtree set of G containing v such that all leaves (excluding v) have odd distance from v; the subtrees in $S(G;v,\mathrm{odd})$ are called the $v_{odd}$-subtrees of G.
• $S(G;v,\mathrm{even})$: the subtree set of G containing v such that all leaves (excluding v) have even distance from v; Note that the single vertex tree v itself is included in this set and we call subtrees in $S(G;v,\mathrm{even})$ the $v_{even}$-subtrees of G.
• ${\omega }_v^o\left(T_1\right)$, ${\omega }_v^e\left(T_1\right)$: the ${\omega }_v^o$, ${\omega }_v^e$ weight of subtree $T_1\in S(G;v)$, respectively.
• $S_{BC}\left(G\right)$: the BC-subtree set of G.
• $S_{BC}(G;X)$: the set of BC-subtrees of G containing X, where X can be a vertex set or an edge set (or both), or a subtree of G.
• ${\omega }_{bc}\left(T_2\right)$: the BC-weight of $T_2\in S_{BC}\left(G\right)$.
• $F_{BC}(·)$: the sum of BC-weight of BC-subtrees in $S_{BC}(·)$.
• ${\eta }_{BC}(.)$: the number of BC-subtrees in set $S_{BC}(.)$.

Given $T_1\in S(G;v)$ and v a fixed vertex of $V\left(G\right)$, let

$$S_o\left(T_1\right)=\left\{u\right|u\in V\left(T_1\right)\wedge d_{T_1}(v,u)\equiv 1\left(\mathrm{mod}2\right)\}$$

and

$$S_e\left(T_1\right)=\left\{u\right|u\in V\left(T_1\right)\wedge d_{T_1}(v,u)\equiv 0\left(\mathrm{mod}2\right)\}.$$

Then:

• the ${\omega }_v^o$ weight of $T_1$, denoted by ${\omega }_v^o\left(T_1\right)$, is:

  -

  If $T_1$ is a weighted single vertex v, then ${\omega }_v^o\left(T_1\right)=f_o\left(v\right)$;

  -

  otherwise,

  $${\omega }_v^o\left(T_1\right)=(1+f_o\left(v\right))\prod _{u\in S_o\left(T_1\right)}{f}_e\left(u\right)\prod _{\begin{array}{c}u\in S_e\left(T_1\right)\backslash v\\ u\notin L\left(T_1\right)\end{array}}(1+f_o\left(u\right))\prod _{\begin{array}{c}u\in S_e\left(T_1\right)\backslash v\\ u\in L\left(T_1\right)\end{array}}{f}_o\left(u\right)\prod _{e\in E\left(T_1\right)}g\left(e\right).$$

• the ${\omega }_v^e$ weight of $T_1$, denoted by ${\omega }_v^e\left(T_1\right)$, is defined as:

  -

  If $T_1$ is a weighted single vertex v, then ${\omega }_v^e\left(T_1\right)=f_e\left(v\right)$;

  -

  otherwise, ${\omega }_v^e\left(T_1\right)={\displaystyle \prod _{u\in S_e\left(T_1\right)}}{f}_e\left(u\right){\displaystyle \prod _{\begin{array}{c}u\in S_o\left(T_1\right)\\ u\notin L\left(T_1\right)\end{array}}}(1+f_o\left(u\right)){\displaystyle \prod _{\begin{array}{c}u\in S_o\left(T_1\right)\\ u\in L\left(T_1\right)\end{array}}}{f}_o\left(u\right){\displaystyle \prod _{e\in E\left(T_1\right)}}g\left(e\right)$.

The odd, even generating function of $S(G;v)$ are respectively defined as

$$F(G;f,g;v,\mathrm{odd})=\sum _{T_1\in S(G;v)}{\omega }_v^o\left(T_1\right)=\sum _{T_1\in S(G;v,\mathrm{odd})}{\omega }_v^o\left(T_1\right),$$

and

$$F(G;f,g;v,\mathrm{even})=\sum _{T_1\in S(G;v)}{\omega }_v^e\left(T_1\right)=\sum _{T_1\in S(G;v,\mathrm{even})}{\omega }_v^e\left(T_1\right).$$

Similarly, for a given BC-subtree $T_2$ of a weighted graph G, we define

$$B{S}_e\left(T_2\right)=\left\{u\right|u\in V\left(T_2\right)\wedge d_{T_2}(u,v_l)\equiv 0\left(\mathrm{mod}2\right)\}$$

and

$$B{S}_o\left(T_2\right)=\left\{u\right|u\in V\left(T_2\right)\wedge d_{T_2}(u,v_l)\equiv 1\left(\mathrm{mod}2\right)\}$$

where $v_l\in L\left(T_2\right)$.

The BC-weight of $T_2\in S_{BC}\left(G\right)$ is

$${\omega }_{bc}\left(T_2\right)=\prod _{u\in B{S}_e\left(T_2\right)}{f}_e\left(u\right)\prod _{e\in E\left(T_2\right)}g\left(e\right)$$

and the BC-subtree generating function of G is

$$F_{BC}(G;f,g)=\sum _{T\in S_{BC}\left(G\right)}{\omega }_{bc}\left(T\right).$$

Similarly,

$$F_{BC}(G;f,g;X)=\sum _{T\in S_{BC}(G;X)}{\omega }_{bc}\left(T\right).$$

Let $\eta (G;v,\mathrm{odd})$ (resp. $\eta (G;v,\mathrm{even})$) denote the number of $v_{odd}$-subtrees (resp. $v_{even}$-subtrees) in $S(G;v,\mathrm{odd})$ (resp. $S(G;v,\mathrm{even})$). Then

$$\eta (G;v,\mathrm{odd})=F(G;(0,1),1;v,\mathrm{odd}),$$

$$\eta (G;v,\mathrm{even})=F(G;(0,1),1;v,\mathrm{even})$$

and

$${\eta }_{BC}\left(G\right)=F_{BC}(G;(0,1),1),{\eta }_{BC}(G;X)=F_{BC}(G;(0,1),1;X)$$

2.2. Facts

With the above notations we introduce some previously established results that will be used in our arguments.

Let $T=\left(V\right(T),E(T);f,g)$ be a weighted tree of order $n>1$ with vertex weight function $f\left(u\right)=(f_o\left(u\right),f_e\left(u\right))$ for $u\in V\left(T\right)$ and edge weight function $g=g\left(e\right)$ for $e\in E\left(T\right)$, assume $\tilde{w}\ne v_i$ be a pendant vertex and $\tilde{e}=(\tilde{w},\tilde{u})$ the pendant edge of T, let $T^{\prime }=(V\left(T^{\prime }\right),E\left(T^{\prime }\right);f^{\prime },g^{\prime })$ of order $n-1$ be the weighted tree constructed from T through “contracting” $\tilde{w}$ as follows: $V\left(T^{\prime }\right)=V\left(T\right)\backslash \tilde{w}$, $E\left(T^{\prime }\right)=E\left(T\right)\backslash \tilde{e}$, and

$$\begin{array}{cc}\hfill f_o^{\prime }\left(v_s\right)& =\left\{\begin{array}{cc}{f}_o\left(\tilde{u}\right)(1+g\left(\tilde{e}\right)f_e\left(\tilde{w}\right))+g\left(\tilde{e}\right)f_e\left(\tilde{w}\right)\hfill & \mathrm{if}{v}_s=\tilde{u},\hfill \\ f_o\left(v_s\right)\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill f_e^{\prime }\left(v_s\right)& =\left\{\begin{array}{cc}{f}_e\left(\tilde{u}\right)(1+g\left(\tilde{e}\right)f_o\left(\tilde{w}\right))\hfill & \mathrm{if}{v}_s=\tilde{u},\hfill \\ f_e\left(v_s\right)\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(2)

for any $v_s\in V\left(T^{\prime }\right)$, and $g^{\prime }\left(e\right)=g\left(e\right)$ for any $e\in E\left(T^{\prime }\right)$.

Lemma 1

([13]). Following the above notations, we have $F(T;f,g;v_i,\mathit{odd})=F(T^{\prime };f^{\prime },g^{\prime };v_i,\mathit{odd})$ and $F(T;f,g;v_i,\mathit{even})=F(T^{\prime };f^{\prime },g^{\prime };v_i,\mathit{even})$.

Lemma 2

([13]). Let $P_n$ be a path on n vertices with vertex weight function $f\left(v\right)=(0,y)$ for all $v\in V\left(P_n\right)$ and edge weight function $g\left(e\right)=z$ for all $e\in E\left(P_n\right)$. Then,

$$\begin{array}{c}\hfill F_{BC}(P_n;f,g)=\sum _{i=1}^{\lceil \frac{n}{2}\rceil -1}(n-2i)y^2{z}^2{\left(y{z}^2\right)}^{i-1}\end{array}$$

Lemma 3

([13]). Let $K_{1,n}$ be a star on $n+1$ vertices with vertex weight function $f\left(v\right)=(0,y)$ for all $v\in V\left(K_{1,n}\right)$ and edge weight function $g\left(e\right)=z$ for all $e\in E\left(K_{1,n}\right)$. Then,

$$\begin{array}{c}\hfill F_{BC}(K_{1,n};f,g)=\sum _{i=2}^n\left(\genfrac{}{}{0pt}{}{n}{i}\right)y^i{z}^i\end{array}$$

A unicyclic graph is a connected graph whose number of edges is equal to the number of vertices.

Lemma 4

([41]). Let $U_n=(V\left(U_n\right),E\left(U_n\right);f,g)$ be a weighted unicyclic graph of order n with no pendant vertices, whose vertex weight function $f\left(v\right)=(0,y)$ for all $v\in V\left(U_n\right)$ and edge weight function $g\left(e\right)=z$ for all $e\in E\left(U_n\right)$. Then,

$$\begin{array}{c}\hfill F_{BC}(U_n;f,g)=\sum _{i=1}^{\lceil \frac{n}{2}\rceil -1}n{y}^2{z}^2{\left(y{z}^2\right)}^{i-1}\end{array}$$

2.3. Observations

We now move on to establish some new observations to facilitate our discussion of the main results later.

Let $T=\left(V\right(T),E(T);f,g)$ be a weighted tree on $n(\ge 2)$ vertices, with the vertex weight function $f\left(u\right)=(f_o\left(u\right),f_e\left(u\right))$ for $u\in V\left(T\right)$ and the edge weight function $g=g\left(e\right)$ for $e\in E\left(T\right)$. Let $T_v$ be a subtree of T and define $T_v^{*}=(V\left(T_v^{*}\right),E\left(T_v^{*}\right);f^{*},g^{*})$ the weighted subtree constructed from T through contracting leaves of T recursively with $V\left(T_v^{*}\right)=V\left(T_v\right)$, and $E\left(T_v^{*}\right)=E\left(T_v\right)$ as follows:

• Choose a pendant vertex $\tilde{w}(\in L\left(T\right)\wedge \notin V\left(T_v\right))$ and let $\tilde{e}=(\tilde{w},\tilde{u})$ denote the pendant edge;
• Update the odd, even weight of $\tilde{u}$, and edge weight with rule as described in Lemma 1;
• Remove the vertex $\tilde{w}$, edge $\tilde{e}$ and set $T:T\backslash \{\tilde{w},\tilde{e}\}$;
• Repeat the contracting process until the remaining tree is the weighed tree $T_v^{*}=(V\left(T_v^{*}\right)$, $E\left(T_v^{*}\right);f^{*},g^{*})$ with $V\left(T_v^{*}\right)=V\left(T_v\right)$, and $E\left(T_v^{*}\right)=E\left(T_v\right)$.

From Lemma 1 we have the following two observations as immediate consequences. We skip the repetitive details.

Theorem 1.

Given $T_v$ a subtree of $T=\left(V\right(T),E(T);f,g)$ containing vertex v, and let $T_v^{*}=(V\left(T_v^{*}\right),E\left(T_v^{*}\right);f^{*},g^{*})$ be the weighted subtree defined above, then, the odd and even generating functions of $S(T;T_v)$, denoted by $F(T;f,g;T_v,odd)$ and $F(T;f,g;T_v,even)$, respectively, are

$$\begin{array}{c}\hfill F(T;f,g;T_v,\mathit{odd})=\left(\prod _{u\in V_o\left(T_v^{*}\right)}{f}_e^{*}\left(u\right)\prod _{\begin{array}{c}u\in V_e\left(T_v^{*}\right)\backslash v\\ u\notin L\left(T_v^{*}\right)\end{array}}(1+f_o^{*}\left(u\right))\prod _{\begin{array}{c}u\in V_e\left(T_v^{*}\right)\backslash v\\ u\in L\left(T_v^{*}\right)\end{array}}{f}_o^{*}\left(u\right)\right)(1+f_o^{*}\left(v\right))\prod _{e\in E\left(T_v^{*}\right)}{g}^{*}\left(e\right),\end{array}$$

(3)

$$\begin{array}{c}\hfill F(T;f,g;T_v,\mathit{even})=\prod _{e\in E\left(T_v^{*}\right)}{g}^{*}\left(e\right)\left(\prod _{u\in V_e\left(T_v^{*}\right)}{f}_e^{*}\left(u\right)\prod _{\begin{array}{c}u\in V_o\left(T_v^{*}\right)\\ u\notin L\left(T_v^{*}\right)\end{array}}(1+f_o^{*}\left(u\right))\prod _{\begin{array}{c}u\in V_o\left(T_v^{*}\right)\\ u\in L\left(T_v^{*}\right)\end{array}}{f}_o^{*}\left(u\right)\right),\end{array}$$

(4)

where $V_o\left(T_v^{*}\right)=\left\{u\right|u\in V\left(T_v^{*}\right)\wedge d_{T_v^{*}}(u,v)\equiv 1\left(\mathit{mod}2\right)\}$, and $V_e\left(T_v^{*}\right)=\left\{u\right|u\in V\left(T_v^{*}\right)\wedge d_{T_v^{*}}(u,v)\equiv 0\left(\mathit{mod}2\right)\}$.

Theorem 2.

Given $T_v$ a subtree of $T=\left(V\right(T),E(T);f,g)$, and let $T_v^{*}=(V\left(T_v^{*}\right),E\left(T_v^{*}\right);f^{*},g^{*})$ be the weighted subtree obtained from T defined above, then, the BC-subtree generating function of T containing the subtree $T_v$ is

$$\begin{array}{cc}\hfill F_{BC}(T;f,g;T_v)=& (f_o^{*}\left(v_l\right)\prod _{u\in V_o\left(T_v^{*}\right)}{f}_e^{*}\left(u\right)\prod _{\begin{array}{c}u\in V_e\left(T_v^{*}\right)\\ u\notin L\left(T_v^{*}\right)\end{array}}(1+f_o^{*}\left(u\right))\prod _{\begin{array}{c}u\in V_e\left(T_v^{*}\right)\\ u\in L\left(T_v^{*}\right)\end{array}}{f}_o^{*}\left(u\right)\hfill \\ \hfill & +f_e^{*}\left(v_l\right)\prod _{u\in V_e\left(T_v^{*}\right)}{f}_e^{*}\left(u\right)\prod _{\begin{array}{c}u\in V_o\left(T_v^{*}\right)\\ u\notin L\left(T_v^{*}\right)\end{array}}(1+f_o^{*}\left(u\right))\prod _{\begin{array}{c}u\in V_o\left(T_v^{*}\right)\\ u\in L\left(T_v^{*}\right)\end{array}}{f}_o^{*}\left(u\right))\prod _{e\in E\left(T_v^{*}\right)}{g}^{*}\left(e\right),\hfill \end{array}$$

(5)

where $v_l\in L\left(T_v^{*}\right)$ is a leaf, $V_o\left(T_v^{*}\right)=\left\{u\right|u\in V\left(T_v^{*}\right)\wedge d_{T_v^{*}}(u,v_l)\equiv 1\left(\mathit{mod}2\right)\}$, and $V_e\left(T_v^{*}\right)=\left\{u\right|u\in V\left(T_v^{*}\right)\wedge d_{T_v^{*}}(u,v_l)\equiv 0\left(\mathit{mod}2\right)\}$.

We now establish the following for general graphs.

Theorem 3.

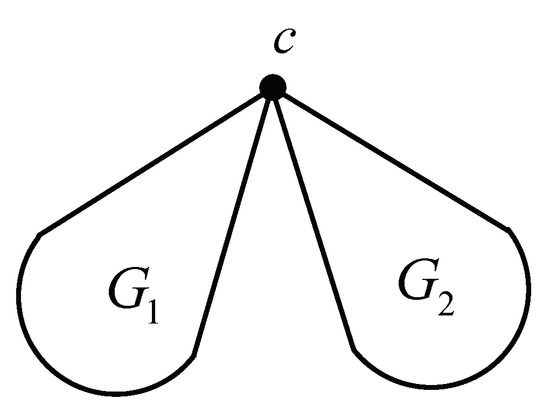
Let graph $G=\left(V\right(G),E(G);f,g)$ be obtained from $G_1$ and $G_2$ by identifying the unique common vertex c (see Figure 1), with the vertex weight function $f\left(v\right)=(f_o\left(v\right),f_e\left(v\right))$ for $v\in V\left(G\right)$ and the edge weight function $g\left(e\right)=z$ for $e\in E\left(G\right)$. Then

$$\begin{array}{cc}\hfill F_{BC}(G;f,g;c)=& F_{BC}(G_1;f,g;c)+\frac{1}{(1+f_o\left(c\right))}\prod _{i=1}^{2}F(G_i;f,g;c,\mathit{odd})\hfill \\ \hfill & +\frac{1}{f_e\left(c\right)}\prod _{i=1}^2(F(G_i;f,g;c,\mathit{even})-f_e\left(c\right))+F_{BC}(G_2;f,g;c).\hfill \end{array}$$

(6)

Figure 1. Weighted graph G.

If the vertex weight function $f\left(v\right)=(0,y)$ for $v\in V\left(G\right)$, then we have

$$\begin{array}{cc}\hfill F_{BC}(G;f,g;c)=& F_{BC}(G_1;f,g;c)+\prod _{i=1}^{2}F(G_i;f,g;c,\mathit{odd})\hfill \\ \hfill & +\frac{1}{y}\prod _{i=1}^2(F(G_i;f,g;c,\mathit{even})-y)+F_{BC}(G_2;f,g;c).\hfill \end{array}$$

(7)

Proof. 

We will prove the claimed expression by considering different cases of the BC-subtrees of G containing c:

$$S_{BC}(G;c)={\mathcal{T}}_1\cup {\mathcal{T}}_2\cup {\mathcal{T}}_3$$

where

(i)

${\mathcal{T}}_1$ is the set of BC-subtrees in $S_{BC}(G;c)$ such that all edges of each BC-subtree are only in $G_1$;

(ii)

${\mathcal{T}}_2$ is the set of BC-subtrees in $S_{BC}(G;c)$ such that all edges of each BC-subtree are only in $G_2$;

(iii)

${\mathcal{T}}_3$ is the set of BC-subtrees in $S_{BC}(G;c)$ such that edges of each BC-subtree are in both $G_1$ and $G_2$.

It is easy to see that the BC-subtree generating function of ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ are

$$F_{BC}(G_1;f,g;c)$$

and

$$F_{BC}(G_2;f,g;c).$$

Next, note that

$${\mathcal{T}}_3={\mathcal{T}}_3^1\cup {\mathcal{T}}_3^2$$

where

(a)

${\mathcal{T}}_3^1=\{T_1\cup T_2|T_1\in S(G_1;c,\mathrm{odd}),T_2\in S(G_2;c,\mathrm{odd})\}$, where $T_1\cup T_2$ are the trees obtained from $T_1$ and $T_2$ by identifying the vertex c;

(b)

${\mathcal{T}}_3^2=\{T_3\cup T_4|T_3\in S(G_1;c,\mathrm{even})\backslash c,T_4\in S(G_2;c,\mathrm{even})\backslash c\}$, where $T_3\cup T_4$ are the trees obtained from $T_3$ and $T_4$ by identifying their vertex c.

From these cases we can obtain the BC-subtree generating function of BC-subtree in ${\mathcal{T}}_3$ as

$$\frac{1}{(1+f_o\left(c\right))}\prod _{i=1}^{2}F(G_i;f,g;c,\mathrm{odd})+\frac{1}{f_e\left(c\right)}\prod _{i=1}^2(F(G_i;f,g;c,\mathrm{even})-f_e\left(c\right))$$

The theorem thus follows. □

Through similar analysis we can also obtain the odd and even generating functions of $S(G;c)$. We skip the technical details.

Theorem 4.

Let graph $G=\left(V\right(G),E(G);f,g)$ be obtained from $G_1$ and $G_2$ with the unique common vertex c (see Figure 1), with the vertex weight function $f\left(v\right)=(f_o\left(v\right),f_e\left(v\right))$ for $v\in V\left(G\right)$ and the edge weight function $g\left(e\right)=z$ for $e\in E\left(G\right)$. Then

$$\begin{array}{cc}\hfill F(G;f,g;c,odd)=& F(G_1;f,g;c,odd)+F(G_2;f,g;c,\mathit{odd})\hfill \\ \hfill & +\frac{1}{(1+f_o\left(c\right))}\prod _{i=1}^{2}F(G_i;f,g;c,\mathit{odd})\hfill \end{array}$$

(8)

and

$$\begin{array}{c}\hfill F(G;f,g;c,even)=\frac{1}{f_e\left(c\right)}\prod _{i=1}^{2}F(G_i;f,g;c,\mathit{even}).\end{array}$$

(9)

If the vertex weight function $f\left(v\right)=(0,y)$ for $v\in V\left(G\right)$, then we have

$$\begin{array}{cc}\hfill F(G;f,g;c,odd)=& F(G_1;f,g;c,odd)+F(G_2;f,g;c,\mathit{odd})\hfill \\ \hfill & +\prod _{i=1}^{2}F(G_i;f,g;c,\mathit{odd})\hfill \end{array}$$

(10)

and

$$\begin{array}{c}\hfill F(G;f,g;c,even)=\frac{1}{y}\prod _{i=1}^{2}F(G_i;f,g;c,\mathit{even}).\end{array}$$

(11)

2.4. Further Definitions

We now introduce the graph structures under consideration in this paper.

Recall that $K_{1,n}$ is a star on $n+1$ vertices, $P_n$ is a path on n vertices, and $C_n$ is a cycle on n vertices. A fan graph, denoted by $F_{n+1}$, is a graph formed by adding an additional vertex adjacent to every vertex of $P_n$. A wheel graph $W_{n+1}$ is a graph formed from a cycle $C_n$ by adding a vertex adjacent to every vertex of $C_n$.

Assume $G_1$ and $G_2$ are two disjoint graphs, a graph $G=G_1+G_2$ is called the disjoint union of $G_1$ and $G_2$, if $V\left(G\right)=V\left(G_1\right)\cup V\left(G_2\right)$ and $E\left(G\right)=E\left(G_1\right)\cup E\left(G_2\right)$. Moreover, let the product $G_1\times G_2$ denote the graph obtained from $G_1+G_2$ by adding edges $(a,b)$ with $a\in V\left(G_1\right)$ and $b\in V\left(G_2\right)$. In the specifal case when $G_2$ is a single vertex c, we write $G_1\times G_2$ as $G_1\times c$.

Definition 1.

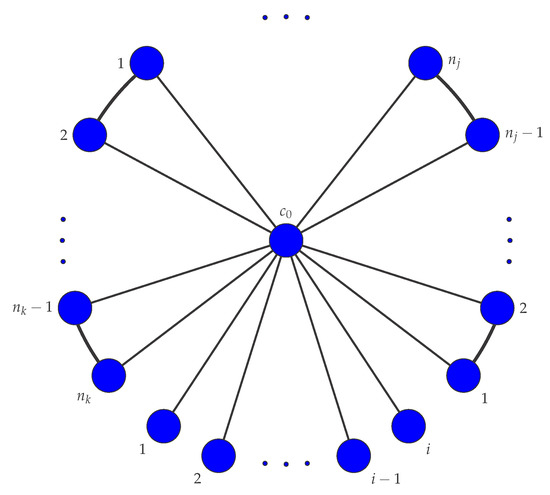
Let $P_{l_i}$ $(l_i\ge 1$, and $l_i\ne l_j,\mathit{if}1\le i\ne j\le k)$ ($i=1,2,\cdots ,k$) be k distinct paths on $l_i$ vertices, and each $P_{l_i}$ has $n_i$ copies with ${\displaystyle \sum _{i=1}^k}{n}_i{l}_i=n$, then, the graph

$$(n_1{P}_{l_1}+n_2{P}_{l_2}+\cdots +n_k{P}_{l_k})\times c_0$$

is called a multi-fan graph, where $n_1{P}_{l_1}+n_2{P}_{l_2}+\cdots +n_k{P}_{l_k}$ is the disjoint union of ${\displaystyle \sum _{i=1}^k}{n}_i$ paths $(n_i\mathit{is}\mathit{the}\mathit{number}\mathit{of}\mathit{paths}\mathit{of}\mathit{length}{l}_i-1)$ and $c_0$ is the center vertex (see Figure 2).

Figure 2. The multi-fan graph $(i{P}_1+P_{n_j+1}+\cdots +P_{n_k})\times c_0$.

Clearly, in the case of $k=1$ and $n_1=1$, the multi-fan graph is just the fan graph $F_{n+1}$. For convenience we call the subgraph $P_{l_i}\times c_0$ ($i=1,2,\cdots ,k$) of multi-fan graph $(n_1{P}_{l_1}+n_2{P}_{l_2}+\cdots +n_k{P}_{l_k})\times c_0$ the sub-fan graph $F_{l_i+1}$. It is easy to see that the fan graph $F_1$ is the single vertex $c_0$ for the case $l_i=0$, and $F_2$ is an edge for the case $l_i=1$.

Definition 2.

Let $C_{l_i}$ $(l_i\ge 3,$ and $l_i\ne l_j,\mathit{if}1\le i\ne j\le k)$ ($i=1,2,\cdots ,k$) be k distinct cycles on $l_i$ vertices. Suppose each $C_{l_i}$ has $n_i$ copies with ${\displaystyle \sum _{i=1}^k}{n}_i{l}_i=n$. Then, the graph

$$(n_1{C}_{l_1}+n_2{C}_{l_2}+\cdots +n_k{C}_{l_k})\times c_0$$

is called a multi-wheel graph, where $n_1{C}_{l_1}+n_2{C}_{l_2}+\cdots +n_k{C}_{l_k}$ is the disjoint union of ${\displaystyle \sum _{i=1}^k}{n}_i$ cycles $\left(n_i\mathit{is}\mathit{the}\mathit{number}\mathit{of}\mathit{cycles}\mathit{of}\mathit{length}{l}_i\right)$ and $c_0$ is the center vertex.

Clearly, in the case of $k=1$ and $n_1=1$, the multi-wheel graph is just the wheel graph $W_{n+1}$. Similarly, we call the subgraph $C_{l_i}\times c_0$ ($i=1,2,\cdots ,k$) of multi-wheel graph $(n_1{C}_{l_1}+n_2{C}_{l_2}+\cdots +n_k{C}_{l_k})\times c_0$ the sub-wheel graph $W_{l_i+1}$.

Definition 3.

Let $G=(n_1{P}_{l_1}+n_2{P}_{l_2}+\cdots +n_k{P}_{l_k})\times c_0$ be the multi-fan graph with ${\displaystyle \sum _{i=1}^k}{n}_i{l}_i=n$. Then we also call G the $r(1\le r\le n,r\mathit{is}\mathit{an}\mathit{integer})$ multi-fan graph, and is denoted by $F_{n+1}^r$.

If $\left(n\mathit{mod}r\right)\ne 0$, then let $k=2$, $l_1=r,n_1=\lfloor \frac{n}{r}\rfloor$, $l_2=1,n_2=\left(n\mathit{mod}r\right)$, and we call $F_{n+1}^r$ the r quasi-regular multi-fan graph.

Otherwise, let $k=1$, $l_1=r,n_1=\lfloor \frac{n}{r}\rfloor$, and we call $F_{n+1}^r$ the r regular multi-fan graph.

3. BC-Subtree Generating Functions of Multi-Fan Graphs

We now move on to study the BC-subtree generating functions. First we consider the multi-fan graphs in this section.

Theorem 5.

Let $G=(n_1{P}_{l_1}+n_2{P}_{l_2}+\cdots +n_k{P}_{l_k})\times c_0$ be a multi-fan graph with center vertex $c_0$, the vertex weight function $f\left(v\right)=(0,y)$ for $v\in V\left(G\right)$ and the edge weight function $g\left(e\right)=z$ for $e\in E\left(G\right)$. For convenience we denote $F(F_{l_i+1};f,g;c_0,\mathit{odd})$ by $F_{F_{l_i+1}}^{\mathit{odd}}\left(c_0\right)$ and $F(F_{l_i+1};f,g;c_0,\mathit{even})$ by $F_{F_{l_i+1}}^{\mathit{even}}\left(c_0\right)$. Then

$$\begin{array}{cc}\hfill F_{BC}(G;f,g)=& \sum _{i=1}^{k-1}\left({(1+F_{F_{l_i+1}}^{\mathit{odd}}\left(c_0\right))}^{n_i}-1\right)\sum _{t=1}^{k-i}\left[\sum _{i+1\le r_1<r_2<\cdots <r_t\le k}\prod _{s=1}^t\left({(1+F_{F_{l_{r_s}+1}}^{\mathit{odd}}\left(c_0\right))}^{n_{r_s}}-1\right)\right]\hfill \\ \hfill & +\sum _{i=1}^{k-1}\left(y^{1-n_i}{(F_{F_{l_i+1}}^{\mathit{even}}\left(c_0\right))}^{n_i}-y\right)\left[y^{i-k}\prod _{s=i+1}^k{y}^{1-n_s}{(F_{F_{l_s+1}}^{\mathit{even}}\left(c_0\right))}^{n_s}-1\right]\hfill \\ \hfill & +\sum _{i=1}^k((F_{F_{l_i+1}}^{\mathit{even}}\left(c_0\right)-y)\sum _{j=1}^{n_i-1}\left[y^{-j}{(F_{F_{l_i+1}}^{\mathit{even}}\left(c_0\right))}^j-1\right]\hfill \\ \hfill & +F_{F_{l_i+1}}^{\mathit{odd}}\left(c_0\right)\sum _{j=1}^{n_i-1}[{(1+F_{F_{l_i+1}}^{\mathit{odd}}(c_0))}^j-1]+n_i{F}_{BC}(F_{l_i+1};f,g;c_0))\hfill \\ \hfill & +\sum _{i=1}^k\sum _{j=1}^{\lceil \frac{l_i}{2}\rceil -1}{n}_i(l_i-2j)y^{j+1}{z}^{2j};\hfill \end{array}$$

(12)

and

$$\begin{array}{cc}\hfill F_{BC}(F_{l_i+1};f,g;c_0)=& F_{BC}(F_{l_i};f,g;c_0)+\sum _{s=0}^{\lfloor \frac{l_i-1}{2}\rfloor }{y}^{s+1}{z}^{2s+1}{F}_{F_{l_i-2s}}^{\mathit{odd}}\left(c_0\right)\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}{F}_{F_{l_i-2p-2q+2}}^{\mathit{odd}}\left(c_0\right)\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2p+2q-1}{y}^{q+p}{F}_{F_{l_i-2p-2q+2}}^{\mathit{even}}\left(c_0\right)\hfill \\ \hfill & +2\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p{F}_{F_{l_i-2p+1}}^{\mathit{even}}\left(c_0\right)\hfill \end{array}$$

(13)

with

$$\begin{array}{cc}\hfill F_{F_{l_i+1}}^{\mathit{odd}}\left(c_0\right)=& yz+(yz+1)F_{F_{l_i}}^{\mathit{odd}}\left(c_0\right)+\sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}{y}^{k+1}{z}^{2k+1}(1+F_{F_{l_i-2k}}^{\mathit{odd}}\left(c_0\right))\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}(1+F_{F_{l_i-2p-2q+2}}^{\mathit{odd}}\left(c_0\right)),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill F_{F_{l_i+1}}^{\mathit{even}}\left(c_0\right)=& \sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p\left(F_{F_{l_i-2p+1}}^{\mathit{even}}\left(c_0\right)+\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2q-1}{y}^q{F}_{F_{l_i-2p-2q+2}}^{\mathit{even}}\left(c_0\right)\right)\hfill \\ \hfill & +\sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }{y}^k{z}^{2k}{F}_{F_{l_i-2k+1}}^{\mathit{even}}\left(c_0\right)+F_{F_{l_i}}^{\mathit{even}}\left(c_0\right),\hfill \end{array}$$

(15)

and $F_{BC}(F_2;f,g;c_0)=0$, $F_{F_1}^{\mathit{odd}}\left(c_0\right)=0$, $F_{F_1}^{\mathit{even}}\left(c_0\right)=y$.

Proof. 

First we consider two cases for the BC-subtrees of multi-fan graph $G=(n_1{P}_{l_1}+n_2{P}_{l_2}+\cdots +n_k{P}_{l_k})\times c_0$:

(i)

ones not containing the center $c_0$;

(ii)

ones containing the center $c_0$.

With Lemma 2, we have the BC-subtree generating function of case (i) as

$$\sum _{i=1}^k(n_i\sum _{j=1}^{\lceil \frac{l_i}{2}\rceil -1}(l_i-2j)y^2{z}^2{\left(y{z}^2\right)}^{j-1}).$$

(16)

With slightly more complicated structure analysis, Theorems 3 and 4, we have the BC-subtree generating function of case (ii) as

$$\begin{array}{cc}\hfill & \sum _{i=1}^{k-1}F(\left(n_i{P}_{l_i}\right)\times c_0;f,g;c_0,\mathrm{odd})\sum _{t=1}^{k-i}\left[\sum _{i+1\le r_1<r_2<\cdots <r_t\le k}\prod _{s=1}^{t}F(\left(n_{r_s}{P}_{l_{r_s}}\right)\times c_0;f,g;c_0,\mathrm{odd})\right]\hfill \\ \hfill & +\sum _{i=1}^{k-1}\left(F(\left(n_i{P}_{l_i}\right)\times c_0;f,g;c_0,\mathrm{even})-y\right)\left[y^{i-k}\prod _{s=i+1}^{k}F(\left(n_s{P}_{l_s}\right)\times c_0;f,g;c_0,\mathrm{even})-1\right]\hfill \\ \hfill & +\sum _{i=1}^k{F}_{BC}(\left(n_i{P}_{l_i}\right)\times c_0;f,g;c_0).\hfill \end{array}$$

(17)

Similarly, the odd and even generating functions, the BC-subtree generating functions of multi-fan graph $\left(n_i{P}_{l_i}\right)\times c_0$ ($i=1,2,\cdots ,k$) containing $c_0$ are, respectively,

$$\begin{array}{c}\hfill F(\left(n_i{P}_{l_i}\right)\times c_0;f,g;c_0,\mathrm{odd})={(1+F(F_{l_i+1};f,g;c_0,\mathrm{odd}))}^{n_i}-1,\end{array}$$

(18)

$$\begin{array}{c}\hfill F(\left(n_i{P}_{l_i}\right)\times c_0;f,g;c_0,\mathrm{even})=y^{1-n_i}F{(F_{l_i+1};f,g;c_0,\mathrm{even})}^{n_i},\end{array}$$

(19)

$$\begin{array}{cc}\hfill F_{BC}(\left(n_i{P}_{l_i}\right)\times c_0;f,g;c_0)& =F(F_{l_i+1};f,g;c_0,\mathrm{odd})\sum _{j=1}^{n_i-1}[{(1+F(F_{l_i+1};f,g;c_0,\mathrm{odd}))}^j-1]\hfill \\ \hfill & +(F(F_{l_i+1};f,g;c_0,\mathrm{even})-y)\sum _{j=1}^{n_i-1}[y^{-j}F{(F_{l_i+1};f,g;c_0,\mathrm{even})}^j-1]\hfill \\ \hfill & +n_i{F}_{BC}(F_{l_i+1};f,g;c_0).\hfill \end{array}$$

(20)

We now label the non-center vertices of the sub-fan graph $F_{l_i+1}=P_{l_i}\times c_0$ ($i=1,2,\cdots ,k$) as $c_1,c_2,\cdots ,c_{l_i}$ in counterclockwise order. In what follows, we further focus on computing the odd and even generating functions, and the BC-subtree generating functions of $F_{l_i+1}$ ($i=1,2,\cdots ,k$) containing $c_0$.

Let $e_i=(c_0,c_{l_i})$, then we have

$$S(F_{l_i+1};c_0)={\mathcal{S}}_1\cup {\mathcal{S}}_2\cup {\mathcal{S}}_3\cup {\mathcal{S}}_4$$

and

$$S_{BC}(F_{l_i+1};c_0)={\mathcal{S}}_1^{*}\cup {\mathcal{S}}_2^{*}\cup {\mathcal{S}}_3^{*}\cup {\mathcal{S}}_4^{*}$$

where

• ${\mathcal{S}}_1$ (resp. ${\mathcal{S}}_1^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0$, but not $(c_0,c_{l_i})$ or $(c_{l_i-1},c_{l_i})$;
• ${\mathcal{S}}_2$ (resp. ${\mathcal{S}}_2^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0$, $(c_0,c_{l_i})$, but not $(c_{l_i-1},c_{l_i})$;
• ${\mathcal{S}}_3$ (resp. ${\mathcal{S}}_3^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0$, $(c_{l_i-1},c_{l_i})$, but not $(c_0,c_{l_i})$;
• ${\mathcal{S}}_4$ (resp. ${\mathcal{S}}_4^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0$, $(c_0,c_{l_i})$ and $(c_{l_i-1},c_{l_i})$.

We now study each case:

(a)

${\mathcal{S}}_1=S(F_{l_i};c_0)$;

(b)

${\mathcal{S}}_2=\{T_1+e_i|T_1\in {\mathcal{S}}_1\}$, where $T_1+e_i$ is the tree obtained from $T_1$, by attaching an edge $e_i$ at vertex $c_0$;

(c)

The set ${\mathcal{S}}_3$ can be written as

$$\begin{array}{c}\hfill {\mathcal{S}}_3=\{T+(c_0,c_{l_i-k})+\bigcup _{h=2-k}^r(c_{l_i-k-h+1},c_{l_i-k-h+2})|T\in S(F_{l_i-k-r+1};c_0)\},\end{array}$$

where $k=1,2,\cdots ,l_i-1,r=1,2,\cdots ,l_i-k$;

(d)

Evidently, each $T_4\in {\mathcal{S}}_4$ must not contain the edge $(c_0,c_{l_i-1})$. We further consider these subtrees by cases of containing edges $(c_0,c_{l_i}){\displaystyle \bigcup _{r=1}^k}(c_{l_i-r},c_{l_i-r+1})$ but not $(c_{l_i-k-1},c_{l_i-k})$, for $k=1,2,\cdots ,l_i-1$, which can be rewritten as:

$$\begin{array}{c}\hfill {\mathcal{S}}_4=\{T+(c_0,c_{l_i})+\bigcup _{h=1}^k(c_{l_i-h},c_{l_i-h+1})|T\in S(F_{l_i-k};c_0)\}\end{array}$$

where $k=1,2,\cdots ,l_i-1$. Note that $S(F_1;c_0)$ is the single vertex $c_0$.

By the definitions of ${\omega }_v^o$ weight, ${\omega }_v^e$ weight, odd, even generating function of subtrees containing a fixed vertex, (a)–(d), and Theorem 1, we have the followings.

$$\sum _{T_1\in {\mathcal{S}}_1}{\omega }_v^o\left(T_1\right)=F(F_{l_i};f,g;c_0,\mathrm{odd}),$$

(21)

$$\sum _{T_1\in {\mathcal{S}}_1}{\omega }_v^e\left(T_1\right)=F(F_{l_i};f,g;c_0,\mathrm{even}),$$

(22)

$$\begin{array}{cc}\hfill \sum _{T_2\in {\mathcal{S}}_2}{\omega }_v^o\left(T_2\right)=& (1+\sum _{T_1\in {\mathcal{S}}_1}{\omega }_v^o\left(T_1\right))f_e\left(c_{l_i}\right)g\left(e_i\right)\hfill \\ \hfill =& yz\left(1+F(F_{l_i};f,g;c_0,\mathrm{odd})\right),\hfill \end{array}$$

(23)

$$\begin{array}{c}\hfill \sum _{T_2\in {\mathcal{S}}_2}{\omega }_v^e\left(T_2\right)=F(F_{l_i};f,g;c_0,\mathrm{even})f_o\left(c_{l_i}\right)g\left(e_i\right)=0,\end{array}$$

(24)

$$\begin{array}{cc}\hfill \sum _{T_3\in {\mathcal{S}}_3}{\omega }_v^o\left(T_3\right)=& \sum _{k=1}^{l_i-1}[f_e\left(c_{l_i-k}\right)f_o{\left(c_{l_i}\right)}^{\frac{1-{(-1)}^k}{2}}\prod _{s=1}^{\lceil \frac{k-1}{2}\rceil }((1+f_o\left(c_{l_i-k+2s-1}\right))f_e\left(c_{l_i-k+2s}\right))\hfill \\ \hfill & \prod _{s=0}^{k-1}g\left((c_{l_i-k+s},c_{l_i-k+s+1})\right)\left]\right[\sum _{r=1}^{l_i-k}(\prod _{s=1}^{r-1}g\left((c_{l_i-k-s},c_{l_i-k-s+1})\right)\hfill \\ \hfill & \prod _{s=1}^{\lfloor \frac{r-1}{2}\rfloor }\left((1+f_o\left(c_{l_i-k-2s+1}\right))f_e\left(c_{l_i-k-2s}\right)\right)f_o{\left(c_{l_i-k-r+1}\right)}^{\frac{1+{(-1)}^r}{2}})\hfill \\ \hfill & g\left((c_0,c_{l_i-k})\right)\left(1+F(F_{l_i-k-r+1};f,g;c_0,\mathrm{odd})\right)]\hfill \\ \hfill =& \sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}\left(1+F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\right)\right),\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill \sum _{T_3\in {\mathcal{S}}_3}{\omega }_v^e\left(T_3\right)=& \sum _{k=1}^{l_i-1}g\left((c_0,c_{l_i-k})\right)\left[f_o{\left(c_{l_i}\right)}^{\frac{1+{(-1)}^k}{2}}\prod _{s=0}^{\lfloor \frac{k-1}{2}\rfloor }\right((1+f_o\left(c_{l_i-k+2s}\right))f_e\left(c_{l_i-k+2s+1}\right))\hfill \\ \hfill & \prod _{s=0}^{k-1}g\left((c_{l_i-k+s},c_{l_i-k+s+1})\right)\left]\right[F(F_{l_i-k};f,g;c_0,\mathrm{even})+\hfill \\ \hfill & f_e\left(c_{l_i-k-1}\right)\sum _{r=2}^{l_i-k}F(F_{l_i-k-r+1};f,g;c_0,\mathrm{even})f_o{\left(c_{l_i-k-r+1}\right)}^{\frac{1-{(-1)}^r}{2}}\hfill \\ \hfill & \left(\prod _{s=1}^{r-1}g\left((c_{l_i-k-s},c_{l_i-k-s+1})\right)\prod _{s=1}^{\lfloor \frac{r-2}{2}\rfloor }(1+f_o\left(c_{l_i-k-2s}\right))f_e\left(c_{l_i-k-2s-1}\right)\right)]\hfill \\ \hfill =& \sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p\left(F(F_{l_i-2p+1};f,g;c_0,\mathrm{even})+\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2q-1}{y}^{q}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even})\right),\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill \sum _{T_4\in {\mathcal{S}}_4}{\omega }_v^o\left(T_4\right)=& f_e\left(c_{l_i}\right)g\left(e_i\right)\sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }[f_o\left(c_{l_i-2k+1}\right)\prod _{r=1}^{k-1}\left((1+f_o\left(c_{l_i-2r+1}\right))f_e\left(c_{l_i-2r}\right)\right)\hfill \\ \hfill & \prod _{t=1}^{2k-1}g\left((c_{l_i-t},c_{l_i-t+1})\right)]\left(1+F(F_{l_i-2k+1};f,g;c_0,\mathrm{odd})\right)\hfill \\ \hfill & +\sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}\left[\prod _{r=1}^k\left((1+f_o\left(c_{l_i-2r+1}\right))f_e\left(c_{l_i-2r}\right)\right)\prod _{t=1}^{2k}g\left((c_{l_i-t},c_{l_i-t+1})\right)\right]\hfill \\ \hfill & f_e\left(c_{l_i}\right)g\left(e_i\right)\left(1+F(F_{l_i-2k};f,g;c_0,\mathrm{odd})\right)\hfill \\ \hfill =& \sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}{y}^{k+1}{z}^{2k+1}\left(1+F(F_{l_i-2k};f,g;c_0,\mathrm{odd})\right),\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \sum _{T_4\in {\mathcal{S}}_4}{\omega }_v^e\left(T_4\right)=& g\left(e_i\right)\sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}[f_o\left(c_{l_i-2k}\right)\prod _{r=1}^k\left((1+f_o\left(c_{l_i-2r+2}\right))f_e\left(c_{l_i-2r+1}\right)\right)\hfill \\ \hfill & \prod _{t=1}^{2k}g\left((c_{l_i-t},c_{l_i-t+1})\right)]F(F_{l_i-2k};f,g;c_0,\mathrm{even})\hfill \\ \hfill & +g\left(e_i\right)\sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }\left[\prod _{r=1}^k\left((1+f_o\left(c_{l_i-2r+2}\right))f_e\left(c_{l_i-2r+1}\right)\right)\prod _{t=1}^{2k-1}g\left((c_{l_i-t},c_{l_i-t+1})\right)\right]\hfill \\ \hfill & F(F_{l_i-2k+1};f,g;c_0,\mathrm{even})\hfill \\ \hfill =& \sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }{y}^k{z}^{2k}F(F_{l_i-2k+1};f,g;c_0,\mathrm{even}),\hfill \end{array}$$

(28)

with $F(F_1;f,g;c_0,\mathrm{odd})=0$, $F(F_1;f,g;c_0,\mathrm{even})=y$.

Hence, by Equations (21)–(28) we have

$$\begin{array}{cc}\hfill F(F_{l_i+1};f,g;c_0,\mathrm{odd})=& \sum _{T_1\in {\mathcal{S}}_1}{\omega }_v^o\left(T_1\right)+\sum _{T_2\in {\mathcal{S}}_2}{\omega }_v^o\left(T_2\right)+\sum _{T_3\in {\mathcal{S}}_3}{\omega }_v^o\left(T_3\right)+\sum _{T_4\in {\mathcal{S}}_4}{\omega }_v^o\left(T_4\right)\hfill \\ \hfill =& \sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}\left(1+F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\right)\right)\hfill \\ \hfill & +\sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}{y}^{k+1}{z}^{2k+1}\left(1+F(F_{l_i-2k};f,g;c_0,\mathrm{odd})\right)\hfill \\ \hfill & +(yz+1)F(F_{l_i};f,g;c_0,\mathrm{odd})+yz,\hfill \end{array}$$

(29)

and

$$\begin{array}{cc}\hfill F(F_{l_i+1};f,g;c_0,\mathrm{even})=& \sum _{T_1\in {\mathcal{S}}_1}{\omega }_v^e\left(T_1\right)+\sum _{T_2\in {\mathcal{S}}_2}{\omega }_v^e\left(T_2\right)+\sum _{T_3\in {\mathcal{S}}_3}{\omega }_v^e\left(T_3\right)+\sum _{T_4\in {\mathcal{S}}_4}{\omega }_v^e\left(T_4\right)\hfill \\ \hfill =& \sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p(F(F_{l_i-2p+1};f,g;c_0,\mathrm{even})+\hfill \\ \hfill & \sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2q-1}{y}^{q}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even}))\hfill \\ \hfill & +\sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }{y}^k{z}^{2k}F(F_{l_i-2k+1};f,g;c_0,\mathrm{even})\hfill \\ \hfill & +F(F_{l_i};f,g;c_0,\mathrm{even})\hfill \end{array}$$

(30)

with $F(F_1;f,g;c_0,\mathrm{odd})=0$, $F(F_1;f,g;c_0,\mathrm{even})=y$.

Similarly for the BC-subtrees, through case analysis of BC-subtree generating function, BC-weight ${\omega }_{bc}\left(T\right)$ of $T\in S_{BC}\left(G\right)$, and by Theorem 2, we have

$$\sum _{T_1^{*}\in {\mathcal{S}}_1^{*}}{\omega }_{bc}\left(T_1^{*}\right)=F_{BC}(F_{l_i};f,g;c_0),$$

(31)

$$\sum _{T_2^{*}\in {\mathcal{S}}_2^{*}}{\omega }_{bc}\left(T_2^{*}\right)=yzF(F_{l_i};f,g;c_0,\mathrm{odd}),$$

(32)

$$\begin{array}{cc}\hfill \sum _{T_3^{*}\in {\mathcal{S}}_3^{*}}{\omega }_{bc}\left(T_3^{*}\right)=& \sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2p+2q-1}{y}^{q+p}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even})\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^{p}F(F_{l_i-2p+1};f,g;c_0,\mathrm{even}),\hfill \end{array}$$

(33)

and

$$\begin{array}{cc}\hfill \sum _{T_4^{*}\in {\mathcal{S}}_4^{*}}{\omega }_{bc}\left(T_4^{*}\right)=& \sum _{s=1}^{\lfloor \frac{l_i-1}{2}\rfloor }{y}^{s+1}{z}^{2s+1}F(F_{l_i-2s};f,g;c_0,\mathrm{odd})\hfill \\ \hfill & +\sum _{s=1}^{\lceil \frac{l_i-1}{2}\rceil }{y}^s{z}^{2s}F(F_{l_i-2s+1};f,g;c_0,\mathrm{even}),\hfill \end{array}$$

(34)

Combining the Equations (31)–(34), we have

$$\begin{array}{cc}\hfill F_{BC}(F_{l_i+1};f,g;c_0)=& \sum _{T_1^{*}\in {\mathcal{S}}_1^{*}}{\omega }_v^e\left(T_1^{*}\right)+\sum _{T_2^{*}\in {\mathcal{S}}_2^{*}}{\omega }_v^e\left(T_2^{*}\right)+\sum _{T_3^{*}\in {\mathcal{S}}_3^{*}}{\omega }_v^e\left(T_3^{*}\right)+\sum _{T_4^{*}\in {\mathcal{S}}_4^{*}}{\omega }_v^e\left(T_4^{*}\right)\hfill \\ \hfill =& F_{BC}(F_{l_i};f,g;c_0)+\sum _{s=0}^{\lfloor \frac{l_i-1}{2}\rfloor }{y}^{s+1}{z}^{2s+1}F(F_{l_i-2s};f,g;c_0,\mathrm{odd})\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2p+2q-1}{y}^{q+p}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even})\hfill \\ \hfill & +2\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^{p}F(F_{l_i-2p+1};f,g;c_0,\mathrm{even})\hfill \end{array}$$

(35)

with $F_{BC}(F_2;f,g;c_0)=0$, $F(F_{l_i+1};f,g;c_0,\mathrm{odd})$, $F(F_{l_i+1};f,g;c_0,\mathrm{even})$ given in Equations (29) and (30), respectively, and $F(F_1;f,g;c_0,\mathrm{odd})=0$, $F(F_1;f,g;c_0,\mathrm{even})=y$.

Combining Equations (16)–(20), (29), (30), and (35), we have the BC-subtree generating function of multi-fan graph $G=(n_1{P}_{l_1}+n_2{P}_{l_2}+\cdots +n_k{P}_{l_k})\times c_0$ as claimed in (12). □

Next we consider the BC-subtree generating function of some special cases of multi-fan graphs. First of all the BC-subtree generating function of the r multi-fan graph $F_{n+1}^r$ ($1\le r\le n,r\mathrm{is}\mathrm{an}\mathrm{integer}$) follows from Theorem 5.

Theorem 6.

Let $F_{n+1}^r$ ($1\le r\le n$ is a positive integer) be the r multi-fan graph defined in Definition 3 with vertex weight function $f\left(v\right)=(0,y)$ for $v\in V\left(F_{n+1}^r\right)$ and the edge weight function $g\left(e\right)=z$ for $e\in E\left(F_{n+1}^r\right)$, then

$$\begin{array}{cc}\hfill F_{BC}(F_{n+1}^r;f,g)=& \lfloor \frac{n}{r}\rfloor \left(F_{BC}(F_{r+1};f,g;c_0)-F_{F_{r+1}}^{\mathit{odd}}\left(c_0\right)-F_{F_{r+1}}^{\mathit{even}}\left(c_0\right)+\sum _{j=1}^{\lceil \frac{r}{2}\rceil -1}(r-2j)y^{j+1}{z}^{2j}\right)\hfill \\ \hfill & +{(1+yz)}^{n-r\lfloor \frac{n}{r}\rfloor }{(1+F_{F_{r+1}}^{\mathit{odd}}\left(c_0\right))}^{\lfloor \frac{n}{r}\rfloor }+y^{1-\lfloor \frac{n}{r}\rfloor }{(F_{F_{r+1}}^{\mathit{even}}\left(c_0\right))}^{\lfloor \frac{n}{r}\rfloor }\hfill \\ \hfill & -(n-r\lfloor \frac{n}{r}\rfloor )yz+(\lfloor \frac{n}{r}\rfloor -1)y-1\hfill \end{array}$$

(36)

with

$$\begin{array}{cc}\hfill F_{BC}(F_{r+1};f,g;c_0)=& F_{BC}(F_r;f,g;c_0)+\sum _{s=0}^{\lfloor \frac{r-1}{2}\rfloor }{y}^{s+1}{z}^{2s+1}{F}_{F_{r-2s}}^{\mathit{odd}}\left(c_0\right)\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{r-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{r-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}{F}_{F_{r-2p-2q+2}}^{\mathit{odd}}\left(c_0\right)\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{r}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{r+1}{2}\rfloor -p}{z}^{2p+2q-1}{y}^{q+p}{F}_{F_{r-2p-2q+2}}^{\mathit{even}}\left(c_0\right)\hfill \\ \hfill & +2\sum _{p=1}^{\lfloor \frac{r}{2}\rfloor }{z}^{2p}{y}^p{F}_{F_{r-2p+1}}^{\mathit{even}}\left(c_0\right),\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill F_{F_{r+1}}^{\mathit{odd}}\left(c_0\right)=& yz+(yz+1)F_{F_r}^{\mathit{odd}}\left(c_0\right)+\sum _{k=1}^{\lceil \frac{r}{2}\rceil -1}{y}^{k+1}{z}^{2k+1}(1+F_{F_{r-2k}}^{\mathit{odd}}\left(c_0\right))\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{r-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{r-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}(1+F_{r-2p-2q+2}^{\mathit{odd}}\left(c_0\right)),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill F_{F_{r+1}}^{\mathit{even}}\left(c_0\right)=& \sum _{p=1}^{\lfloor \frac{r}{2}\rfloor }{z}^{2p}{y}^p\left(F_{F_{r-2p+1}}^{\mathit{even}}\left(c_0\right)+\sum _{q=1}^{\lfloor \frac{r+1}{2}\rfloor -p}{z}^{2q-1}{y}^q{F}_{F_{r-2p-2q+2}}^{\mathit{even}}\left(c_0\right)\right)\hfill \\ \hfill & +\sum _{k=1}^{\lfloor \frac{r}{2}\rfloor }{y}^k{z}^{2k}{F}_{F_{r-2k+1}}^{\mathit{even}}\left(c_0\right)+F_{F_r}^{\mathit{even}}\left(c_0\right),\hfill \end{array}$$

(39)

and $F_{BC}(F_2;f,g;c_0)=0$, $F_{F_1}^{\mathit{odd}}\left(c_0\right)=0$, $F_{F_1}^{\mathit{even}}\left(c_0\right)=y$.

Letting $y=z=1$ in the above statements we immediately have the following two consequences.

Corollary 1.

Let $G=(n_1{P}_{l_1}+n_2{P}_{l_2}+\cdots +n_k{P}_{l_k})\times c_0$ be a multi-fan graph, then the BC-subtree number of G is

$$\begin{array}{cc}\hfill {\eta }_{BC}\left(G\right)=& \sum _{i=1}^{k-1}\left({(1+a_{(l_i+1)})}^{n_i}-1\right)\sum _{t=1}^{k-i}\left[\sum _{i+1\le r_1<r_2<\cdots <r_t\le k}\prod _{s=1}^t\left({(1+a_{(l_{r_s}+1)})}^{n_{r_s}}-1\right)\right]\hfill \\ \hfill & +\sum _{i=1}^{k-1}\left(b_{(l_i+1)}^{n_i}-1\right)\left(\prod _{s=i+1}^k{b}_{(l_s+1)}^{n_s}-1\right)+\sum _{i=1}^k((b_{(l_i+1)}-1)\sum _{j=1}^{n_i-1}[b_{(l_i+1)}^j-1]\hfill \\ \hfill & +a_{(l_i+1)}\sum _{j=1}^{n_i-1}[{(1+a_{(l_i+1)})}^j-1]+n_i{\eta }_{BC}(F_{l_i+1};c_0))\hfill \\ \hfill & +\sum _{i=1}^k\sum _{j=1}^{\lceil \frac{l_i}{2}\rceil -1}{n}_i(l_i-2j)\hfill \end{array}$$

(40)

with

$$\begin{array}{cc}\hfill {\eta }_{BC}(F_{l_i+1};c_0)=& {\eta }_{BC}(F_{l_i};c_0)+\sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{a}_{(l_i-2p-2q+2)}+\sum _{s=0}^{\lfloor \frac{l_i-1}{2}\rfloor }{a}_{(l_i-2s)}\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{b}_{(l_i-2p-2q+2)}+2\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{b}_{(l_i-2p+1)},\hfill \end{array}$$

(41)

$$\begin{array}{c}\hfill a_{(l_i+1)}=1+2a_{l_i}+\sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}\left(1+a_{(l_i-2k)}\right)+\sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }\left(1+a_{(l_i-2p-2q+2)}\right),\end{array}$$

(42)

and

$$\begin{array}{c}\hfill b_{(l_i+1)}=\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }(b_{(l_i-2p+1)}+\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{b}_{(l_i-2p-2q+2)})+\sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }{b}_{(l_i-2k+1)}+b_{l_i},\end{array}$$

(43)

and ${\eta }_{BC}(F_2;c_0)=0,a_1=0,b_1=1$.

Corollary 2.

The BC-subtree number of the r multi-fan graph $F_{n+1}^r$ (see Definition 3), the fan graph $F_{r+1}$ ($r\ge 1$), and the fan graph $F_{r+1}$ ($r\ge 1$) containing $c_0$ are, respectively, the following:

$$\begin{array}{cc}\hfill {\eta }_{BC}\left(F_{n+1}^r\right)=& \lfloor \frac{n}{r}\rfloor ({\eta }_{BC}(F_{r+1};c_0)-a_{r+1}-b_{r+1})+2^{n-r\lfloor \frac{n}{r}\rfloor }{\left(1+a_{r+1}\right)}^{\lfloor \frac{n}{r}\rfloor }\hfill \\ \hfill & +b_{r+1}^{\lfloor \frac{n}{r}\rfloor }+\lfloor \frac{n}{r}\rfloor \left((r-\lceil \frac{r}{2}\rceil )(\lceil \frac{r}{2}\rceil -1)+r+1\right)-n-2,\hfill \end{array}$$

(44)

$${\eta }_{BC}\left(F_{r+1}\right)={\eta }_{BC}(F_{r+1};c_0)+(r-\lceil \frac{r}{2}\rceil )(\lceil \frac{r}{2}\rceil -1),$$

(45)

$$\begin{array}{cc}\hfill {\eta }_{BC}(F_{r+1};c_0)=& {\eta }_{BC}(F_r;c_0)+\sum _{p=1}^{\lfloor \frac{r-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{r-2p}{2}\rceil }{a}_{(r-2p-2q+2)}+\sum _{s=0}^{\lfloor \frac{r-1}{2}\rfloor }{a}_{(r-2s)}\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{r}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{r+1}{2}\rfloor -p}{b}_{(r-2p-2q+2)}+2\sum _{p=1}^{\lfloor \frac{r}{2}\rfloor }{b}_{(r-2p+1)},\hfill \end{array}$$

(46)

with

$$\begin{array}{c}\hfill a_{r+1}=1+2a_r+\sum _{k=1}^{\lceil \frac{r}{2}\rceil -1}\left(1+a_{(r-2k)}\right)+\sum _{p=1}^{\lfloor \frac{r-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{r-2p}{2}\rceil }\left(1+a_{(r-2p-2q+2)}\right),\end{array}$$

(47)

$$\begin{array}{c}\hfill b_{r+1}=\sum _{p=1}^{\lfloor \frac{r}{2}\rfloor }(b_{(r-2p+1)}+\sum _{q=1}^{\lfloor \frac{r+1}{2}\rfloor -p}{b}_{(r-2p-2q+2)})+\sum _{k=1}^{\lfloor \frac{r}{2}\rfloor }{b}_{(r-2k+1)}+b_r,\end{array}$$

(48)

${\eta }_{BC}(F_2;c_0)=0,a_1=0,b_1=1$.

Remark 1.

From Corollary 2 we have ${\eta }_{BC}\left(F_{n+1}^1\right)=2^n-n-1$ for the case of 1 multi-fan graph (i.e., the star $K_{1,n}$), agreeing with Lemma 3.

4. BC-Subtree Generating Functions of Multi-Wheel Graphs

We now study the BC-subtree generating functions of the multi-wheel graphs (Definition 2).

Theorem 7.

Let $G=(n_1{C}_{l_1}+n_2{C}_{l_2}+\cdots +n_k{C}_{l_k})\times c_0$ be a multi-wheel graph with center vertex $c_0$, the vertex weight function $f\left(v\right)=(0,y)$ for $v\in V\left(G\right)$ and the edge weight function $g\left(e\right)=z$ for $e\in E\left(G\right)$. Let $F(W_{l_i+1};f,g;c_0,\mathit{odd})$ be denoted by $F_{W_{l_i+1}}^{\mathit{odd}}\left(c_0\right)$, $F(W_{l_i+1};f,g;c_0,\mathit{even})$ by $F_{W_{l_i+1}}^{\mathit{even}}\left(c_0\right)$, $F(F_{l_i+1};f,g;c_0,\mathit{odd})$ by $F_{F_{l_i+1}}^{\mathit{odd}}\left(c_0\right)$ and $F(F_{l_i+1};f,g;c_0,\mathit{even})$ by $F_{F_{l_i+1}}^{\mathit{even}}\left(c_0\right)$. Then

$$\begin{array}{cc}\hfill F_{BC}(G;f,g)=& \sum _{i=1}^{k-1}\left({(1+F_{W_{l_i+1}}^{\mathit{odd}}\left(c_0\right))}^{n_i}-1\right)\sum _{t=1}^{k-i}\left[\sum _{i+1\le r_1<r_2<\cdots <r_t\le k}\prod _{s=1}^t\left({(1+F_{W_{l_{r_s}+1}}^{\mathit{odd}}\left(c_0\right))}^{n_{r_s}}-1\right)\right]\hfill \\ \hfill & +\sum _{i=1}^{k-1}\left(y^{1-n_i}{(F_{W_{l_i+1}}^{\mathit{even}}\left(c_0\right))}^{n_i}-y\right)\left[y^{i-k}\prod _{s=i+1}^k{y}^{1-n_s}{(F_{W_{l_s+1}}^{\mathit{even}}\left(c_0\right))}^{n_s}-1\right]\hfill \\ \hfill & +\sum _{i=1}^k((F_{W_{l_i+1}}^{\mathit{even}}\left(c_0\right)-y)\sum _{j=1}^{n_i-1}[y^{-j}{(F_{W_{l_i+1}}^{\mathit{even}}\left(c_0\right))}^j-1]\hfill \\ \hfill & +F_{W_{l_i+1}}^{\mathit{odd}}\left(c_0\right)\sum _{j=1}^{n_i-1}[{(1+F_{W_{l_i+1}}^{\mathit{odd}}\left(c_0\right))}^j-1]+n_i{F}_{BC}(W_{l_i+1};f,g;c_0))\hfill \\ \hfill & +\sum _{i=1}^k\sum _{j=1}^{\lceil \frac{l_i}{2}\rceil -1}{n}_i{l}_i{y}^{j+1}{z}^{2j}\hfill \end{array}$$

(49)

with

$$\begin{array}{cc}\hfill F_{W_{l_i+1}}^{\mathit{odd}}\left(c_0\right)=& 2\sum _{k=0}^{l_i-2}\sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}(1+F_{F_{l_i-2p-2q+2}}^{\mathit{odd}}\left(c_0\right))\right)\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}(1+F_{F_{l_i-2p-2q+2}}^{\mathit{odd}}\left(c_0\right))\right)\hfill \\ \hfill & +\sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}{y}^{k+1}{z}^{2k+1}(1+F_{F_{l_i-2k}}^{\mathit{odd}}\left(c_0\right))+(yz+1)F_{F_{l_i}}^{\mathit{odd}}\left(c_0\right)+yz,\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill F_{W_{l_i+1}}^{\mathit{even}}\left(c_0\right)=& 2\sum _{k=0}^{l_i-2}\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p\left(F_{F_{l_i-2p+1}}^{\mathit{even}}\left(c_0\right)+\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2q-1}{y}^q{F}_{F_{l_i-2p-2q+2}}^{\mathit{even}}\left(c_0\right)\right)\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p\left(F_{F_{l_i-2p+1}}^{\mathit{even}}\left(c_0\right)+\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2q-1}{y}^q{F}_{F_{l_i-2p-2q+2}}^{\mathit{even}}\left(c_0\right)\right)\hfill \\ \hfill & +\sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }{y}^k{z}^{2k}{F}_{F_{l_i-2k+1}}^{\mathit{even}}\left(c_0\right)+F_{F_{l_i}}^{\mathit{even}}\left(c_0\right)\hfill \end{array}$$

(51)

and

$$\begin{array}{cc}\hfill F_{BC}(W_{l_i+1};f,g;c_0)=& 2\sum _{k=0}^{l_i-2}[\sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}{F}_{F_{l_i-2p-2q+2}}^{\mathit{odd}}\left(c_0\right)\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2p+2q-1}{y}^{q+p}{F}_{F_{l_i-2p-2q+2}}^{\mathit{even}}\left(c_0\right)\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p{F}_{F_{l_i-2p+1}}^{\mathit{even}}\left(c_0\right)]+F_{BC}(F_{l_i+1};f,g;c_0)\hfill \end{array}$$

(52)

with $F_{BC}(F_{l_i+1};f,g;c_0)$, $F_{F_{l_i+1}}^{\mathit{odd}}\left(c_0\right)$, $F_{F_{l_i+1}}^{\mathit{even}}\left(c_0\right)$ as in Equations (13)–(15), respectively, and $F_{BC}(F_2;f,g;c_0)=0$, $F_{F_1}^{\mathit{odd}}\left(c_0\right)=0$, $F_{F_1}^{\mathit{even}}\left(c_0\right)=y$.

Proof. 

Firstly, consider the BC-subtrees of multi-wheel graph $G=(n_1{C}_{l_1}+n_2{C}_{l_2}+\cdots +n_k{C}_{l_k})\times c_0$ in two cases:

(i)

ones not containing the center $c_0$;

(ii)

ones containing the center $c_0$.

From Lemma 4, we have the BC-subtree generating function for case (i) as

$$\sum _{i=1}^k(n_i\sum _{j=1}^{\lceil \frac{l_i}{2}\rceil -1}{l}_i{y}^2{z}^2{\left(y{z}^2\right)}^{j-1}).$$

(53)

Similar to the previous section, we have the BC-subtree generating function of case (ii) as

$$\begin{array}{cc}\hfill & \sum _{i=1}^{k-1}F(\left(n_i{C}_{l_i}\right)\times c_0;f,g;c_0,\mathrm{odd})\sum _{t=1}^{k-i}\left[\sum _{i+1\le r_1<r_2<\cdots <r_t\le k}\prod _{s=1}^{t}F(\left(n_{r_s}{C}_{l_{r_s}}\right)\times c_0;f,g;c_0,\mathrm{odd})\right]\hfill \\ \hfill & +\sum _{i=1}^{k-1}\left(F(\left(n_i{C}_{l_i}\right)\times c_0;f,g;c_0,\mathrm{even})-y\right)\left[y^{i-k}\prod _{s=i+1}^{k}F(\left(n_s{C}_{l_s}\right)\times c_0;f,g;c_0,\mathrm{even})-1\right]\hfill \\ \hfill & +\sum _{i=1}^k{F}_{BC}(\left(n_i{C}_{l_i}\right)\times c_0;f,g;c_0)\hfill \end{array}$$

(54)

where

$$\begin{array}{c}\hfill F(\left(n_i{C}_{l_i}\right)\times c_0;f,g;c_0,\mathrm{odd})={(1+F(W_{l_i+1};f,g;c_0,\mathrm{odd}))}^{n_i}-1,\end{array}$$

(55)

$$\begin{array}{c}\hfill F(\left(n_i{C}_{l_i}\right)\times c_0;f,g;c_0,\mathrm{even})=y^{1-n_i}F{(W_{l_i+1};f,g;c_0,\mathrm{even})}^{n_i},\end{array}$$

(56)

$$\begin{array}{cc}\hfill F_{BC}(\left(n_i{C}_{l_i}\right)\times c_0;f,g;c_0)& =F(W_{l_i+1};f,g;c_0,\mathrm{odd})\sum _{j=1}^{n_i-1}[{(1+F(W_{l_i+1};f,g;c_0,\mathrm{odd}))}^j-1]\hfill \\ \hfill & +(F(W_{l_i+1};f,g;c_0,\mathrm{even})-y)\sum _{j=1}^{n_i-1}[y^{-j}F{(W_{l_i+1};f,g;c_0,\mathrm{even})}^j-1]\hfill \\ \hfill & +n_i{F}_{BC}(W_{l_i+1};f,g;c_0).\hfill \end{array}$$

(57)

Now label the $l_i$ non-center vertices of wheel graph $W_{l_i+1}=C_{l_i}\times c_0$ ($i=1,2,\cdots ,k$) with $c_1,c_2,\cdots ,c_{l_i}$. For convenience we let $e_t=(c_0,c_t)$ ($t=1,2,\cdots ,l_i$), $e_{l_i}^{*}=(c_1,c_{l_i})$ and $e_{l_i-r}^{*}=(c_{l_i-r},c_{l_i-r+1})$ ($r=1,2,\cdots ,l_i-1$). We partition the set of $S(W_{l_i+1};c_0)$ and $S_{BC}(W_{l_i+1};c_0)$ into five cases:

$$S(W_{l_i+1};c_0)={\overline{\mathcal{S}}}_1\cup {\overline{\mathcal{S}}}_2\cup {\overline{\mathcal{S}}}_3\cup {\overline{\mathcal{S}}}_4\cup {\overline{\mathcal{S}}}_5$$

$$S_{BC}(W_{l_i+1};c_0)={\overline{\mathcal{S}}}_1^{*}\cup {\overline{\mathcal{S}}}_2^{*}\cup {\overline{\mathcal{S}}}_3^{*}\cup {\overline{\mathcal{S}}}_4^{*}\cup {\overline{\mathcal{S}}}_5^{*}$$

where

• ${\overline{\mathcal{S}}}_1$ (resp. ${\overline{\mathcal{S}}}_1^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0$, but not $(c_1,c_{l_i})$;
• ${\overline{\mathcal{S}}}_2$ (resp. ${\overline{\mathcal{S}}}_2^{*}$) is the set of subtrees (resp. BC-subtrees) that contains $c_0$ and $(c_1,c_{l_i})$, but neither $(c_0,c_{l_i})$ nor $(c_{l_i-1},c_{l_i})$;
• ${\overline{\mathcal{S}}}_3$ (resp. ${\overline{\mathcal{S}}}_3^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0$, $(c_0,c_{l_i})$ and $(c_1,c_{l_i})$, but not $(c_{l_i-1},c_{l_i})$;
• ${\overline{\mathcal{S}}}_4$ (resp. ${\overline{\mathcal{S}}}_4^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0$, $(c_0,c_{l_i})$, $(c_{l_i-1},c_{l_i})$ and $(c_1,c_{l_i})$;
• ${\overline{\mathcal{S}}}_5$ (resp. ${\overline{\mathcal{S}}}_5^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0$, $(c_{l_i-1},c_{l_i})$ and $(c_1,c_{l_i})$, but not $(c_0,c_{l_i})$.

Studying each cases, we have:

(a) ${\overline{\mathcal{S}}}_1=S(F_{l_i+1};c_0)$;

(b) ${\overline{\mathcal{S}}}_2=S(W_{l_i+1}\backslash (e_{l_i-1}^{*}\cup e_{l_i});e_{l_i}^{*})$. Note that $W_{l_i+1}\backslash e_{l_i-1}^{*}\cong F_{l_i+1}$, thus we have ${\overline{\mathcal{S}}}_2\cong {\mathcal{S}}_3$, where ${\mathcal{S}}_3=S(F_{l_i+1};c_0)$;

(c) ${\overline{\mathcal{S}}}_3=S(W_{l_i+1}\backslash e_{l_i-1}^{*};e_{l_i}\cup e_{l_i}^{*})$. Similarly, ${\overline{\mathcal{S}}}_3\cong {\mathcal{S}}_4$, where ${\mathcal{S}}_4=S(F_{l_i+1};c_0)$;

(d) We can further divide the subtree set ${\overline{\mathcal{S}}}_4$ into cases of subtrees containing edge set $\{e_{l_i},{\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*}\}$, but not $\{e_{l_i-k-1}^{*},{\displaystyle \bigcup _{r=1}^k}{e}_{l_i-r}\}$ (recursively for $k=1,2,\cdots ,l_i-2$). That is,

$${\overline{\mathcal{S}}}_4=\{T|T\in S(W_{l_i+1}\backslash (e_{l_i-k-1}^{*}\bigcup _{r=1}^k{e}_{l_i-r});e_{l_i}\bigcup _{r=0}^k{e}_{l_i-r}^{*})\};$$

where $k=1,2,\cdots ,l_i-2$;

(e) ${\overline{\mathcal{S}}}_5$ is the subtree set of $S(W_{l_i+1}\backslash e_{l_i};c_0\cup {\displaystyle \bigcup _{r=0}^1}{e}_{l_i-r}^{*})$. Denote by ${\tilde{W}}_{l_i+1}^{l_i-k}(k=0,1,\cdots ,l_i-2)$ the graph after removing edge set ${\displaystyle \bigcup _{r=1}^k}{e}_{l_i-r+1}$ from $W_{l_i+1}$. Thus ${\tilde{W}}_{l_i+1}^{l_i-k}=W_{l_i+1}\backslash {\displaystyle \bigcup _{r=1}^k}{e}_{l_i-r+1}$ and evidently ${\tilde{W}}_{l_i+1}^{l_i}=W_{l_i+1}$,

Similar to the previous case, we partition the set of $S({\tilde{W}}_{l_i+1}^{l_i-k};c_0\cup {\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*})$ and $S_{BC}({\tilde{W}}_{l_i+1}^{l_i-k};c_0\cup {\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*})$ into four cases:

$$S({\tilde{W}}_{l_i+1}^{l_i-k};c_0\cup \bigcup _{r=0}^k{e}_{l_i-r}^{*})={\overline{\mathcal{S}}}_{l_i-k,1}\cup {\overline{\mathcal{S}}}_{l_i-k,2}\cup {\overline{\mathcal{S}}}_{l_i-k,3}\cup {\overline{\mathcal{S}}}_{l_i-k,4}$$

$$S_{BC}({\tilde{W}}_{l_i+1}^{l_i-k};c_0\cup \bigcup _{r=0}^k{e}_{l_i-r}^{*})={\overline{\mathcal{S}}}_{l_i-k,1}^{*}\cup {\overline{\mathcal{S}}}_{l_i-k,2}^{*}\cup {\overline{\mathcal{S}}}_{l_i-k,3}^{*}\cup {\overline{\mathcal{S}}}_{l_i-k,4}^{*}$$

where

• ${\overline{\mathcal{S}}}_{l_i-k,1}$ (resp. ${\overline{\mathcal{S}}}_{l_i-k,1}^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0\cup {\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*}$, but not $e_{l_i-k}$ or $e_{l_i-k-1}^{*}$;
• ${\overline{\mathcal{S}}}_{l_i-k,2}$ (resp. ${\overline{\mathcal{S}}}_{l_i-k,2}^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0\cup {\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*}$ and $e_{l_i-k}$, but not $e_{l_i-k-1}^{*}$;
• ${\overline{\mathcal{S}}}_{l_i-k,3}$ (resp. ${\overline{\mathcal{S}}}_{l_i-k,3}^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0\cup {\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*}$, $e_{l_i-k}$ and $e_{l_i-k-1}^{*}$;
• ${\overline{\mathcal{S}}}_{l_i-k,4}$ (resp. ${\overline{\mathcal{S}}}_{l_i-k,4}^{*}$) is the set of subtrees (resp. BC-subtrees) that contain $c_0\cup {\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*}$ and $e_{l_i-k-1}^{*}$, but not $e_{l_i-k}$.

Again, we have that ${\tilde{W}}_{l_i+1}^{l_i-k}\backslash (e_{l_i-k}\cup e_{l_i-k-1}^{*})$ $(k=0,1,\cdots ,l_i-2)$ is the graph obtained from $W_{l_i+1}$ after removing edge set $\{e_{l_i-k-1}^{*},{\displaystyle \bigcup _{r=1}^{k+1}}{e}_{l_i-r+1}\}$. Clearly, ${\tilde{W}}_{l_i+1}^{l_i-k}\backslash (e_{l_i-k}\cup e_{l_i-k-1}^{*})\cong F_{l_i+1}\backslash {\displaystyle \bigcup _{r=0}^k}(c_0,c_{l_i-r})$.

We also have

$$\begin{array}{cc}\hfill \sum _{T_2\in {\overline{\mathcal{S}}}_{l_i-k,2}}{\omega }_v^o\left(T_2\right)+\sum _{T_3\in {\overline{\mathcal{S}}}_{l_i-k,3}}{\omega }_v^o\left(T_3\right)=& \sum _{T_1\in {\overline{\mathcal{S}}}_{l_i-k,1}}{\omega }_v^o\left(T_1\right),\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill \sum _{T_2\in {\overline{\mathcal{S}}}_{l_i-k,2}}{\omega }_v^e\left(T_2\right)+\sum _{T_3\in {\overline{\mathcal{S}}}_{l_i-k,3}}{\omega }_v^e\left(T_3\right)=& \sum _{T_1\in {\overline{\mathcal{S}}}_{l_i-k,1}}{\omega }_v^e\left(T_1\right),\hfill \end{array}$$

(59)

and

$$\begin{array}{c}\hfill \sum _{T\in S({\tilde{W}}_{l_i+1}^{l_i-k};c_0\cup {\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*})}{\omega }_v^o\left(T\right)=2\sum _{T_1\in {\overline{\mathcal{S}}}_{l_i-k,1}}{\omega }_v^o\left(T_1\right)+\sum _{T\in S({\tilde{W}}_{l_i+1}^{l_i-(k+1)};c_0\cup {\displaystyle \bigcup _{r=0}^{k+1}}{e}_{l_i-r}^{*})}{\omega }_v^o\left(T\right),\end{array}$$

(60)

$$\begin{array}{c}\hfill \sum _{T\in S({\tilde{W}}_{l_i+1}^{l_i-k};c_0\cup {\displaystyle \bigcup _{r=0}^k}{e}_{l_i-r}^{*})}{\omega }_v^e\left(T\right)=2\sum _{T_1\in {\overline{\mathcal{S}}}_{l_i-k,1}}{\omega }_v^e\left(T_1\right)+\sum _{T\in S({\tilde{W}}_{l_i+1}^{l_i-(k+1)};c_0\cup {\displaystyle \bigcup _{r=0}^{k+1}}{e}_{l_i-r}^{*})}{\omega }_v^e\left(T\right),\end{array}$$

(61)

From the cases (a)–(e), Theorem 1, and by the definitions of ${\omega }_v^o$ weight, ${\omega }_v^e$ weight, odd, even generating function of subtrees containing a fixed vertex, we have

$$\sum _{T_1\in {\overline{\mathcal{S}}}_1}{\omega }_v^o\left(T_1\right)=F(F_{l_i+1};f,g;c_0,\mathrm{odd}),$$

(62)

$$\sum _{T_1\in {\overline{\mathcal{S}}}_1}{\omega }_v^e\left(T_1\right)=F(F_{l_i+1};f,g;c_0,\mathrm{even}),$$

(63)

$$\begin{array}{c}\hfill \sum _{T_3\in {\overline{\mathcal{S}}}_3}{\omega }_v^o\left(T_3\right)+\sum _{T_4\in {\overline{\mathcal{S}}}_4}{\omega }_v^o\left(T_4\right)=\sum _{T_2\in {\overline{\mathcal{S}}}_2}{\omega }_v^o\left(T_2\right)=\sum _{T\in {\overline{\mathcal{S}}}_{l_i,1}}{\omega }_v^o\left(T\right),\end{array}$$

(64)

$$\begin{array}{cc}\hfill \sum _{T\in {\overline{\mathcal{S}}}_{l_i-k,1}}{\omega }_v^o\left(T\right)=& \sum _{j=k+1}^{l_i-1}[f_e\left(c_{l_i-j}\right)f_o{\left(c_{l_i}\right)}^{\frac{1-{(-1)}^j}{2}}\prod _{s=1}^{\lceil \frac{j-1}{2}\rceil }\left((1+f_o\left(c_{l_i-j+2s-1}\right))f_e\left(c_{l_i-j+2s}\right)\right)\hfill \\ \hfill & \prod _{s=0}^{j-1}g\left((c_{l_i-j+s},c_{l_i-j+s+1})\right)\left]\right[\sum _{r=1}^{l_i-j}(\prod _{s=1}^{r-1}g\left((c_{l_i-j-s},c_{l_i-j-s+1})\right)\hfill \\ \hfill & \prod _{s=1}^{\lfloor \frac{r-1}{2}\rfloor }\left((1+f_o\left(c_{l_i-j-2s+1}\right))f_e\left(c_{l_i-j-2s}\right)\right)f_o{\left(c_{l_i-j-r+1}\right)}^{\frac{1+{(-1)}^r}{2}})\hfill \\ \hfill & g\left((c_0,c_{l_i-j})\right)\left(1+F(F_{l_i-j-r+1};f,g;c_0,\mathrm{odd})\right)]\hfill \\ \hfill =& \sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}\left(1+F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\right)\right),\hfill \end{array}$$

(65)

where $k=0,1,\cdots ,l_i-2$;

$$\begin{array}{c}\hfill \sum _{T_3\in {\overline{\mathcal{S}}}_3}{\omega }_v^e\left(T_3\right)+\sum _{T_4\in {\overline{\mathcal{S}}}_4}{\omega }_v^e\left(T_4\right)=\sum _{T_2\in {\overline{\mathcal{S}}}_2}{\omega }_v^e\left(T_2\right)=\sum _{T\in {\overline{\mathcal{S}}}_{l_i,1}}{\omega }_v^e\left(T\right),\end{array}$$

(66)

$$\begin{array}{cc}\hfill \sum _{T\in {\overline{\mathcal{S}}}_{l_i-k,1}}{\omega }_v^e\left(T\right)=& \sum _{j=k+1}^{l_i-1}g\left((c_0,c_{l_i-j})\right)[f_o{\left(c_{l_i}\right)}^{\frac{1+{(-1)}^j}{2}}\prod _{s=0}^{\lfloor \frac{j-1}{2}\rfloor }\left((1+f_o\left(c_{l_i-j+2s}\right))f_e\left(c_{l_i-j+2s+1}\right)\right)\hfill \\ \hfill & \prod _{s=0}^{j-1}g\left((c_{l_i-j+s},c_{l_i-j+s+1})\right)\left]\right[F(F_{l_i-j};f,g;c_0,\mathrm{even})+\hfill \\ \hfill & f_e\left(c_{l_i-j-1}\right)\sum _{r=2}^{l_i-j}F(F_{l_i-j-r+1};f,g;c_0,\mathrm{even})f_o{\left(c_{l_i-j-r+1}\right)}^{\frac{1-{(-1)}^r}{2}}\hfill \\ \hfill & \left(\prod _{s=1}^{r-1}g\left((c_{l_i-j-s},c_{l_i-j-s+1})\right)\prod _{s=1}^{\lfloor \frac{r-2}{2}\rfloor }(1+f_o\left(c_{l_i-j-2s}\right))f_e\left(c_{l_i-j-2s-1}\right)\right)]\hfill \\ \hfill =& \sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p(F(F_{l_i-2p+1};f,g;c_0,\mathrm{even})\hfill \\ \hfill & +\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2q-1}{y}^{q}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even})),\hfill \end{array}$$

(67)

where $k=0,1,\cdots ,l_i-2$.

Thus, by Equations (29), (30) and (62)–(67) we have

$$\begin{array}{cc}\hfill F(W_{l_i+1};f,g;c_0,\mathrm{odd})=& \sum _{T_1\in {\overline{\mathcal{S}}}_1}{\omega }_v^o\left(T_1\right)+\sum _{T_2\in {\overline{\mathcal{S}}}_2}{\omega }_v^o\left(T_2\right)+\sum _{T_3\in {\overline{\mathcal{S}}}_3}{\omega }_v^o\left(T_3\right)+\sum _{T_4\in {\overline{\mathcal{S}}}_4}{\omega }_v^o\left(T_4\right)\hfill \\ \hfill =& 2\sum _{k=0}^{l_i-2}\sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}\left(1+F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\right)\right)\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}\left(1+F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\right)\right)\hfill \\ \hfill & +\sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}{y}^{k+1}{z}^{2k+1}\left(1+F(F_{l_i-2k};f,g;c_0,\mathrm{odd})\right)\hfill \\ \hfill & +(yz+1)F(F_{l_i};f,g;c_0,\mathrm{odd})+yz,\hfill \end{array}$$

(68)

and

$$\begin{array}{cc}\hfill F(W_{l_i+1};f,g;c_0,\mathrm{even})=& \sum _{T_1\in {\overline{\mathcal{S}}}_1}{\omega }_v^e\left(T_1\right)+\sum _{T_2\in {\overline{\mathcal{S}}}_2}{\omega }_v^e\left(T_2\right)+\sum _{T_3\in {\overline{\mathcal{S}}}_3}{\omega }_v^e\left(T_3\right)+\sum _{T_4\in {\overline{\mathcal{S}}}_4}{\omega }_v^e\left(T_4\right)\hfill \\ \hfill =& 2\sum _{k=0}^{l_i-2}\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p(F(F_{l_i-2p+1};f,g;c_0,\mathrm{even})+\hfill \\ \hfill & \sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2q-1}{y}^{q}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even}))\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p(F(F_{l_i-2p+1};f,g;c_0,\mathrm{even})+\hfill \\ \hfill & \sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2q-1}{y}^{q}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even}))\hfill \\ \hfill & +\sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }{y}^k{z}^{2k}F(F_{l_i-2k+1};f,g;c_0,\mathrm{even})\hfill \\ \hfill & +F(F_{l_i};f,g;c_0,\mathrm{even})\hfill \end{array}$$

(69)

with $F(F_{l_i+1};f,g;c_0,\mathrm{odd})$, $F(F_{l_i+1};f,g;c_0,\mathrm{even})$ as in Equations (29) and (30), respectively, and $F(F_1;f,g;c_0,\mathrm{odd})=0$, $F(F_1;f,g;c_0,\mathrm{even})=y$.

Through similar reasoning, we have

$$\sum _{T_1^{*}\in {\overline{\mathcal{S}}}_1^{*}}{\omega }_{bc}\left(T_1^{*}\right)=F_{BC}(F_{l_i+1};f,g;c_0),$$

(70)

$$\sum _{T_3^{*}\in {\overline{\mathcal{S}}}_3^{*}}{\omega }_{bc}\left(T_3^{*}\right)+\sum _{T_4^{*}\in {\overline{\mathcal{S}}}_4^{*}}{\omega }_{bc}\left(T_4^{*}\right)=\sum _{T_2^{*}\in {\overline{\mathcal{S}}}_2^{*}}{\omega }_{bc}\left(T_2^{*}\right)=\sum _{T^{*}\in {\overline{\mathcal{S}}}_{l_i,1}^{*}}{\omega }_{bc}\left(T^{*}\right),$$

(71)

$$\begin{array}{cc}\hfill \sum _{T^{*}\in {\overline{\mathcal{S}}}_{l_i-k,1}^{*}}{\omega }_{bc}\left(T^{*}\right)=& \sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2p+2q-1}{y}^{q+p}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even})\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^{p}F(F_{l_i-2p+1};f,g;c_0,\mathrm{even}),\hfill \end{array}$$

(72)

where $k=0,1,\cdots ,l_i-2$.

Combining Equations (35), (70)–(72), we have

$$\begin{array}{cc}\hfill F_{BC}(W_{l_i+1};f,g;c_0)=& \sum _{j=1}^5\sum _{T_j^{*}\in {\overline{\mathcal{S}}}_j^{*}}{\omega }_v^e(T_j^{*})\hfill \\ \hfill =& 2\sum _{k=0}^{l_i-2}[\sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{odd})\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{z}^{2p+2q-1}{y}^{q+p}F(F_{l_i-2p-2q+2};f,g;c_0,\mathrm{even})\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^{p}F(F_{l_i-2p+1};f,g;c_0,\mathrm{even})]\hfill \\ \hfill & +F_{BC}(F_{l_i+1};f,g;c_0)\hfill \end{array}$$

(73)

with $F_{BC}(F_{l_i+1};f,g;c_0)$, $F(F_{l_i+1};f,g;c_0,\mathrm{odd})$, $F(F_{l_i+1};f,g;c_0,\mathrm{even})$ as in Equations (29), (30), (35), respectively, and $F_{BC}(F_2;f,g;c_0)=0$, $F(F_1;f,g;c_0,\mathrm{odd})=0$, $F(F_1;f,g;c_0,\mathrm{even})=y$.

Our conclusion now follows from Equations (53)–(57), (68), (69), and (73). □

The BC-subtree generating function of the wheel graph $W_{n+1}(n\ge 3)$ (where n is a positive integer) follows from Theorem 7 and Lemma 4.

Theorem 8.

Let $W_{n+1}(n\ge 3)$ be a wheel graph on $n+1$ vertices with vertex weight function $f\left(v\right)=(0,y)$ for $v\in V\left(W_{n+1}\right)$ and the edge weight function $g\left(e\right)=z$ for $e\in E\left(W_{n+1}\right)$, then

$$\begin{array}{cc}\hfill F_{BC}(W_{n+1};f,g)=& 2\sum _{k=0}^{n-2}[\sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{n-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{n-2p}{2}\rceil }{z}^{2p+2q-1}{y}^{q+p}{F}_{F_{n-2p-2q+2}}^{\mathit{odd}}\left(c_0\right)\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{n}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{n+1}{2}\rfloor -p}{z}^{2p+2q-1}{y}^{q+p}{F}_{F_{n-2p-2q+2}}^{\mathit{even}}\left(c_0\right)\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }{z}^{2p}{y}^p{F}_{F_{n-2p+1}}^{\mathit{even}}\left(c_0\right)]+F_{BC}(F_{n+1};f,g;c_0)\hfill \\ \hfill & +\sum _{i=1}^{\lceil \frac{n}{2}\rceil -1}n{y}^{i+1}{z}^{2i}\hfill \end{array}$$

(74)

with $F_{BC}(F_{n+1};f,g;c_0)$, $F_{F_{n+1}}^{\mathit{odd}}\left(c_0\right)$, $F_{F_{n+1}}^{\mathit{even}}\left(c_0\right)$ given in Equations (13)–(15), respectively, and $F_{BC}(F_2;f,g;c_0)=0$, $F_{F_1}^{\mathit{odd}}\left(c_0\right)=0$, $F_{F_1}^{\mathit{even}}\left(c_0\right)=y$.

Letting $y=z=1$ in Theorems 7 and 8, respectively, we immediately have the following.

Corollary 3.

Let $G=(n_1{C}_{l_1}+n_2{C}_{l_2}+\cdots +n_k{C}_{l_k})\times c_0$ be the multi-wheel graph. Then the BC-subtree number of G is

$$\begin{array}{cc}\hfill {\eta }_{BC}\left(G\right)=& \sum _{i=1}^{k-1}({(1+{\overline{a}}_{(l_i+1)})}^{n_i}-1)\sum _{t=1}^{k-i}\left[\sum _{i+1\le r_1<r_2<\cdots <r_t\le k}\prod _{s=1}^t({(1+{\overline{a}}_{(l_{r_s}+1)})}^{n_{r_s}}-1)\right]\hfill \\ \hfill & +\sum _{i=1}^{k-1}\left({\overline{b}}_{(l_i+1)}^{n_i}-1\right)\left(\prod _{s=i+1}^k{\overline{b}}_{(l_s+1)}^{n_s}-1\right)+\sum _{i=1}^k(({\overline{b}}_{(l_i+1)}-1)\sum _{j=1}^{n_i-1}[{\overline{b}}_{(l_i+1)}^j-1]\hfill \\ \hfill & +{\overline{a}}_{(l_i+1)}\sum _{j=1}^{n_i-1}[{(1+{\overline{a}}_{(l_i+1)})}^j-1]+n_i{\eta }_{BC}(W_{l_i+1};c_0))\hfill \\ \hfill & +\sum _{i=1}^k\sum _{j=1}^{\lceil \frac{l_i}{2}\rceil -1}{n}_i{l}_i,\hfill \end{array}$$

(75)

with

$$\begin{array}{cc}\hfill {\eta }_{BC}(W_{l_i+1};c_0)=& {\eta }_{BC}(F_{l_i+1};c_0)+2\sum _{k=0}^{l_i-2}[\sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{l_i-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }{a}_{(l_i-2p-2q+2)}\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{b}_{(l_i-2p-2q+2)}+\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }{b}_{(l_i-2p+1)}],\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill {\overline{a}}_{(l_i+1)}=& 2\sum _{k=0}^{l_i-2}\sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }\left(1+a_{(l_i-2p-2q+2)}\right)\right)+\sum _{p=1}^{\lfloor \frac{l_i-1}{2}\rfloor }\left(\sum _{q=1}^{\lceil \frac{l_i-2p}{2}\rceil }\left(1+a_{(l_i-2p-2q+2)}\right)\right)\hfill \\ \hfill & +\sum _{k=1}^{\lceil \frac{l_i}{2}\rceil -1}\left(1+a_{(l_i-2k)}\right)+2a_{l_i}+1,\hfill \end{array}$$

(77)

and

$$\begin{array}{cc}\hfill {\overline{b}}_{(l_i+1)}=& 2\sum _{k=0}^{l_i-2}\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{l_i}{2}\rfloor }\left(b_{(l_i-2p+1)}+\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{b}_{(l_i-2p-2q+2)}\right)\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{l_i}{2}\rfloor }\left(b_{(l_i-2p+1)}+\sum _{q=1}^{\lfloor \frac{l_i+1}{2}\rfloor -p}{b}_{(l_i-2p-2q+2)}\right)+\sum _{k=1}^{\lfloor \frac{l_i}{2}\rfloor }{b}_{(l_i-2k+1)}+b_{l_i},\hfill \end{array}$$

(78)

with ${\eta }_{BC}(F_{l_i+1};c_0)$ as in Equation (41), ${\eta }_{BC}(F_2;c_0)=0$, $a_{(l_i+1)}$, $b_{(l_i+1)}$ as in Equations (42) and (43), respectively, and $a_1=0,b_1=1$.

Corollary 4.

The BC-subtree number of $W_{n+1}$ $(n\ge 3)$ is

$$\begin{array}{cc}\hfill {\eta }_{BC}\left(W_{n+1}\right)=& {\eta }_{BC}(F_{n+1};c_0)+2\sum _{k=0}^{n-2}[\sum _{p=\lceil \frac{k+1}{2}\rceil }^{\lfloor \frac{n-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{n-2p}{2}\rceil }{a}_{(n-2p-2q+2)}\hfill \\ \hfill & +\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{n}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{n+1}{2}\rfloor -p}{b}_{(n-2p-2q+2)}+\sum _{p=\lfloor \frac{k+3}{2}\rfloor }^{\lfloor \frac{n}{2}\rfloor }{b}_{(n-2p+1)}]\hfill \\ \hfill & +n(\lceil \frac{n}{2}\rceil -1),\hfill \end{array}$$

(79)

where

$$\begin{array}{cc}\hfill {\eta }_{BC}(F_{n+1};c_0)=& {\eta }_{BC}(F_n;c_0)+\sum _{p=1}^{\lfloor \frac{n-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{n-2p}{2}\rceil }{a}_{(n-2p-2q+2)}+\sum _{s=0}^{\lfloor \frac{n-1}{2}\rfloor }{a}_{(n-2s)}\hfill \\ \hfill & +\sum _{p=1}^{\lfloor \frac{n}{2}\rfloor }\sum _{q=1}^{\lfloor \frac{n+1}{2}\rfloor -p}{b}_{(n-2p-2q+2)}+2\sum _{p=1}^{\lfloor \frac{n}{2}\rfloor }{b}_{(n-2p+1)},\hfill \end{array}$$

(80)

and

$$\begin{array}{c}\hfill a_{n+1}=1+2a_n+\sum _{k=1}^{\lceil \frac{n}{2}\rceil -1}\left(1+a_{(n-2k)}\right)+\sum _{p=1}^{\lfloor \frac{n-1}{2}\rfloor }\sum _{q=1}^{\lceil \frac{n-2p}{2}\rceil }\left(1+a_{(n-2p-2q+2)}\right),\end{array}$$

(81)

$$\begin{array}{c}\hfill b_{n+1}=\sum _{p=1}^{\lfloor \frac{n}{2}\rfloor }(b_{(n-2p+1)}+\sum _{q=1}^{\lfloor \frac{n+1}{2}\rfloor -p}{b}_{(n-2p-2q+2)})+\sum _{k=1}^{\lfloor \frac{n}{2}\rfloor }{b}_{(n-2k+1)}+b_n,\end{array}$$

(82)

with ${\eta }_{BC}(F_2;c_0)=0,a_1=0,b_1=1$.

Directly from Corollary 4 we may generate the BC-subtree number of $W_{n+1}(n=3,4,\cdots ,50)$ (see Table 1).

Table 1. The BC-subtree number of wheel graph $W_{n+1}$ ($n=3,4,\cdots ,50$).

$\mathit{n}$	${\mathbf{\eta }}_{\mathit{BC}}\left({\mathit{W}}_{\mathit{n}}\right)$	$\mathit{n}$	${\mathbf{\eta }}_{\mathit{BC}}\left({\mathit{W}}_{\mathit{n}}\right)$	$\mathit{n}$	${\mathbf{\eta }}_{\mathit{BC}}\left({\mathit{W}}_{\mathit{n}}\right)$
3	16	19	32,983,507	35	44,956,112,462,965
4	51	20	79,507,829	36	109,018,361,948,171
5	131	21	191,713,586	37	264,446,533,681,852
6	340	22	462,509,681	38	641,651,556,370,739
7	841	23	1,116,289,936	39	1,557,326,469,215,175
8	2067	24	2,695,367,516	40	3,780,724,965,944,533
9	5026	25	6,510,870,551	41	9,180,821,777,073,118
10	12,147	26	15,733,892,896	42	22,299,504,128,100,416
11	29,305	27	38,036,865,379	43	54,176,661,898,045,614
12	70,508	28	91,989,932,352	44	131,652,455,330,130,629
13	169,664	29	222,555,514,089	45	319,993,939,502,205,010
14	407,988	30	538,634,836,904	46	777,941,764,394,823,593
15	981,517	31	1,304,079,385,141	47	1,891,653,259,171,010,731
16	2,361,611	32	3,158,367,596,891	48	4,600,677,046,844,511,460
17	5,684,920	33	7,651,840,948,554	49	11,191,401,704,559,183,703
18	13,690,201	34	18,544,255,820,839	50	27,228,679,901,334,157,132

5. The Behavior of the BC-Subtrees

With the theoretical foundation that was established in the previous sections, we will study the behavior of the BC-subtree number in the multi-fan and multi-wheel graphs. We first mention an extremal result as a simple consequence. We also briefly discuss the change of the BC-subtree numbers between different multi-fan or multi-wheel graphs. Lastly we consider the BC-subtree density in these structures.

5.1. BC-Subtree Number of $F_{n+1}^r$

The extremely problems with respect to a topological index concerns finding the extremal structures, among a given class of graphs, that maximize or minimize the index. These graphs always possess the best or worst of some desired properties [48,49,50]. We first point out the following simple fact.

Proposition 1.

The $F_{n+1}^1$ has $2^n-n-1$ BC-subtrees, fewer than any other $F_{n+1}^r(r\ne 1)$; the $F_{n+1}^n$ has more BC-subtrees than any other $F_{n+1}^r(r\ne n)$.

It is often interesting to know, when studying extremal problems, which graph structures have the second or third largest or smallest values of a certain index. To shed some light on this we ran some simulation, whose result is shown in Figure 3, with Cartesian and semi-log (Log-Y) coordinate, respectively.

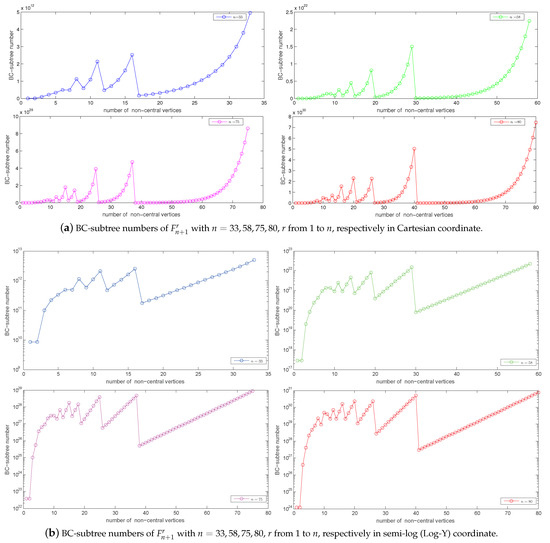
Figure 3. BC-subtree numbers of $F_{n+1}^r$ with $n=33,58,75,80$, r from 1 to n, respectively.

From Figure 3a, it appears that among all $F_{n+1}^r(2\le r\le n-1)$, $F_{n+1}^{n-1}$ seems to have the second largest BC-subtree number, and the $F_{n+1}^{n-2}$ seems to be the third largest BC-subtree number for odd (or sufficient large) n.

It is also interesting to observe the change of the BC-subtree number as r changes, with the “local minimum” spread out for smaller values of r.

From Corollary 4 we can obtain data of similar nature for $W_{n+1}$ $(n\ge 3)$. Figure 4 confirms the simple fact that the BC-subtree numbers of $W_{n+1}$ increase very fast. The asymptotic expression of the BC-subtree number of $W_{n+1}$ seems to be ${\eta }_{BC}\left(W_{n+1}\right)\approx exp(0.0909+0.893n)$. This is something that can be further verified through analytic combinatorics approaches.

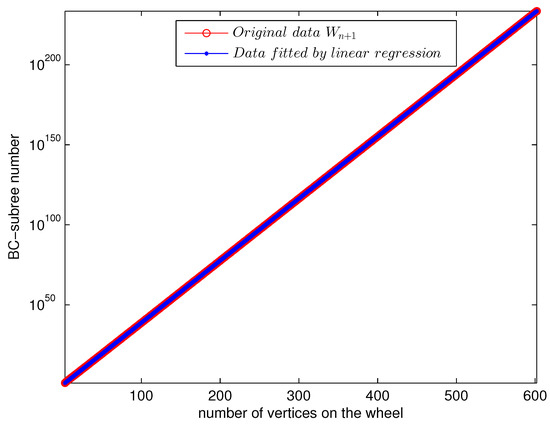
Figure 4. Original BC-subtree number and the corresponding data fitted by linear regression of $W_{n+1}(n=3,4,\cdots ,602)$.

5.2. BC-Subtree Density

The generating function approach provides us with much more information than just the BC-subtree number. In particular, we will examine the BC-subtree density here, for r multi-fan graph $F_{n+1}^r$ ($1\le r\le n,r\mathrm{is}\mathrm{an}\mathrm{integer}$) and $W_{n+1}$, respectively. For some of the work on this topic one may see [40].

Definition 4

([40]). Assume G is a graph with n vertices and k BC-subtrees of orders $n_1,n_2,\cdots ,n_k$, then ${\mu }_{BC}\left(G\right)=\frac{1}{k}{\displaystyle \sum _{i=1}^k}{n}_i$ denotes the average order of BC-subtrees of G, and the BC-subtree density of G is defined as $D_{BC}\left(G\right)=\frac{{\mu }_{BC}\left(G\right)}{n}$.

First it is easy to see that

$$n\left(F_{n+1}^r\right)=n\left(W_{n+1}\right)=n+1$$

(83)

Letting $y=1$ in Theorem 6 and Theorem 8, we could obtain the so called edge generating function of BC-subtrees of $F_{n+1}^r$ and $W_{n+1}$, respectively, i.e., $F_{BC}(F_{n+1}^r;(0,1),z)$ and $F_{BC}(W_{n+1};(0,1),z)$).

By the definition of BC-subtree density and Equation (83), the BC-subtree density of $G^{*}$ ($G^{*}=F_{n+1}^r$ or $W_{n+1}$) is simply

$$D_{BC}\left(G^{*}\right)=\frac{\frac{\partial (F_{BC}(G;(0,1),z)\times z)}{\partial z}{|}_{z=1}}{F_{BC}(G^{*};(0,1),1)\times n\left(G^{*}\right)}.$$

(84)

We may now provide the BC-subtree densities of $F_{n+1}^r(1\le r\le n)$ in Figure 5, with related data in Table 2.

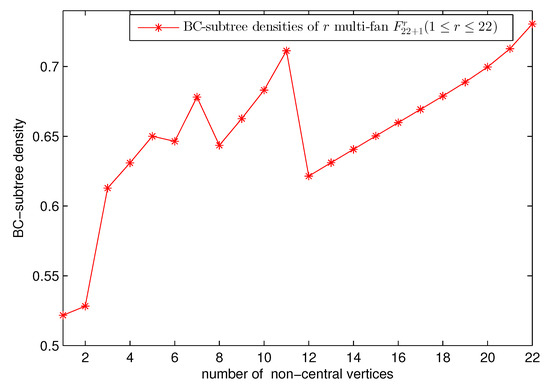
Figure 5. BC-subtree densities of r multi-fan $F_{22+1}^r$ $(1\le r\le 22)$.

Table 2. Data related to BC-subtrees of $F_{n+1}^r$, with $n=22$ and $r=1,2,\cdots ,22$.

$\mathit{r}$	${\mathit{P}}_{\mathit{z}}\left({\mathit{F}}_{\mathit{n}+\mathbf{1}}^{\mathit{r}}\right)$	${\mathbf{\eta }}_{\mathit{BC}}\left({\mathit{F}}_{\mathit{n}+\mathbf{1}}^{\mathit{r}}\right)$	${\mathit{D}}_{\mathit{BC}}\left({\mathit{F}}_{\mathit{n}+\mathbf{1}}^{\mathit{r}}\right)$
1	50,331,603	4,194,281	0.5217415249997297
2	53,106,905	4,371,427	0.5282018593848684
3	285,872,367	20,279,905	0.6128841997941354
4	473,222,721	32,609,837	0.6309415442046974
5	744,621,994	49,805,736	0.6500229070874051
6	717,819,208	48,287,696	0.6463247031419493
7	1,460,830,943	93,663,206	0.6781146144633033
8	703,383,187	47,521,825	0.6435333174946917
9	1,091,991,586	71,647,232	0.662661958015046
10	1,742,448,206	110,913,152	0.6830444927953532
11	3,063,687,819	187,270,907	0.7112894381260796
12	448,577,818	31,383,926	0.6214449840120178
13	556,641,580	38,350,250	0.6310730132420768
14	690,781,206	46,878,694	0.6406741083329001
15	857,549,247	57,340,131	0.6502383098769903
16	1,065,571,361	70,221,005	0.6597625540775962
17	1,326,780,941	86,192,884	0.6692678698344194
18	1,659,024,388	106,256,288	0.678844485235874
19	2,091,899,843	132,053,383	0.6887530256377947
20	2,680,301,328	166,568,142	0.6996226226010619
21	3,536,505,225	215,724,226	0.7127669413407951
22	4,906,885,913	292,065,325	0.73046283663632

$P_z\left(F_{n+1}^r\right)$ stands for $\frac{\partial (F_{BC}(F_{n+1}^r;(0,1),z)\times z)}{\partial z}{|}_{z=1}$.

Similarly, with Theorem 8 we obtain the generating function $F_{BC}(W_{n+1};(0,1),z)$. Together with Equation (84) we can obtain the BC-subtree densities of $W_{n+1}$ (see Figure 6 and Table 3).

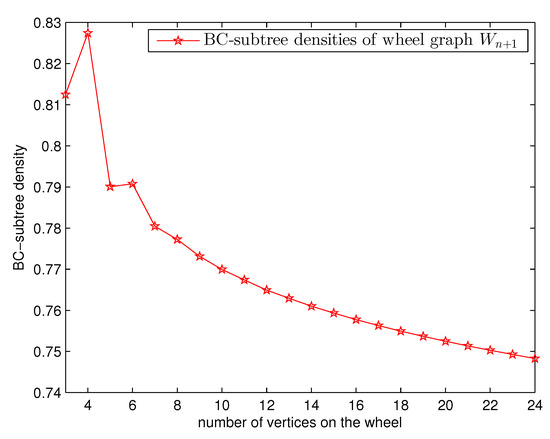
Figure 6. BC-subtree densities of wheel graph $W_{n+1}$ $(3\le n\le 24)$.

Table 3. Data related to BC-subtrees of wheel graph $W_{n+1}$ $(n=3,4\cdots ,24)$.

$\mathit{k}$	${\mathit{P}}_{\mathit{z}}\left({\mathit{W}}_{\mathit{k}+\mathbf{1}}\right)$	${\mathit{D}}_{\mathit{BC}}\left({\mathit{W}}_{\mathit{k}+\mathbf{1}}\right)$	$\mathit{k}$	${\mathit{P}}_{\mathit{z}}\left({\mathit{W}}_{\mathit{k}+\mathbf{1}}\right)$	${\mathit{D}}_{\mathit{BC}}\left({\mathit{W}}_{\mathit{k}+\mathbf{1}}\right)$
3	52	0.8125	14	4,657,240	0.7610093107313614
4	211	0.8274509803921568	15	11,924,887	0.7593403247218337
5	621	0.7900763358778626	16	30,421,819	0.7577533999908885
6	1882	0.7907563025210084	17	77,392,093	0.7563098024637501
7	5251	0.7804696789536266	18	196,372,903	0.7549499052182229
8	14,459	0.7772402300704188	19	497,180,696	0.7536807653594871
9	38,857	0.7731197771587743	20	1,256,299,889	0.7524833703900728
10	102,877	0.7699394538120149	21	3,168,978,905	0.7513525707135758
11	269,864	0.7674003298640732	22	7,981,278,895	0.7502807835703772
12	701,132	0.7649235656837631	23	20,073,455,736	0.749262321576641
13	1,812,214	0.7629423869698766	24	50,423,103,620	0.7482928145521214

$P_z\left(W_{k+1}\right)$ stands for $\frac{\partial (F_{BC}(W_{k+1};(0,1),z)\times z)}{\partial z}{|}_{z=1}$.

From Table 2 and Figure 5, we see that $F_{22+1}^1$, $F_{22+1}^2$ and $F_{22+1}^3$ ranks the first to the third with the smallest BC-subtree density, respectively. From Table 3 and Figure 6, we see that the BC-subtree density of $W_{n+1}(3\le n\le 24)$ maximized at $n=4$, and decreases gradually when $n\ge 6$.

6. Concluding Remarks

Motivated from the past studies of BC-trees, BC-subtrees, as well as the applications of structural properties of network graphs [51], we provide recursive formulae for computing the BC-subtree generating functions of multi-fan and multi-wheel graphs, and also derive the BC-subtree numbers of multi-fan graphs, r multi-fan graphs, multi-wheel (wheel) graphs. Moreover, the behavior of the BC-subtree numbers between different multi-fan or multi-wheel graphs, and extremal problems and BC-subtree density are also briefly discussed. These findings are likely useful in further understanding the properties and behaviors of these graphs. For future work it would be interesting to consider other well known topological indices on the multi-fan and multi-wheel graphs and compare their behaviors with that of the BC-subtree number.