Extended Fuzzy Analytic Hierarchy Process (E-FAHP): A General Approach
Abstract
1. Introduction
- From a theoretical point of view, all the valid results for E-FAHP using (m,n)-trapezoidal numbers are also valid for triangular numbers and it serves to derive priorities from a set of fuzzy judgments.
- From a practical point of view, it seems helpful for practitioners to be aware that, regardless of the form adopted by fuzzy judgments (linear or nonlinear) they are formulating a particular case of the E-FAHP. In this way, an improved understanding of the linkages between both approaches is provided.
2. Materials and Methods
2.1. Background and Literature Review
2.2. Mikhailov’s Model: Fuzzy Preference Programming (FPP)
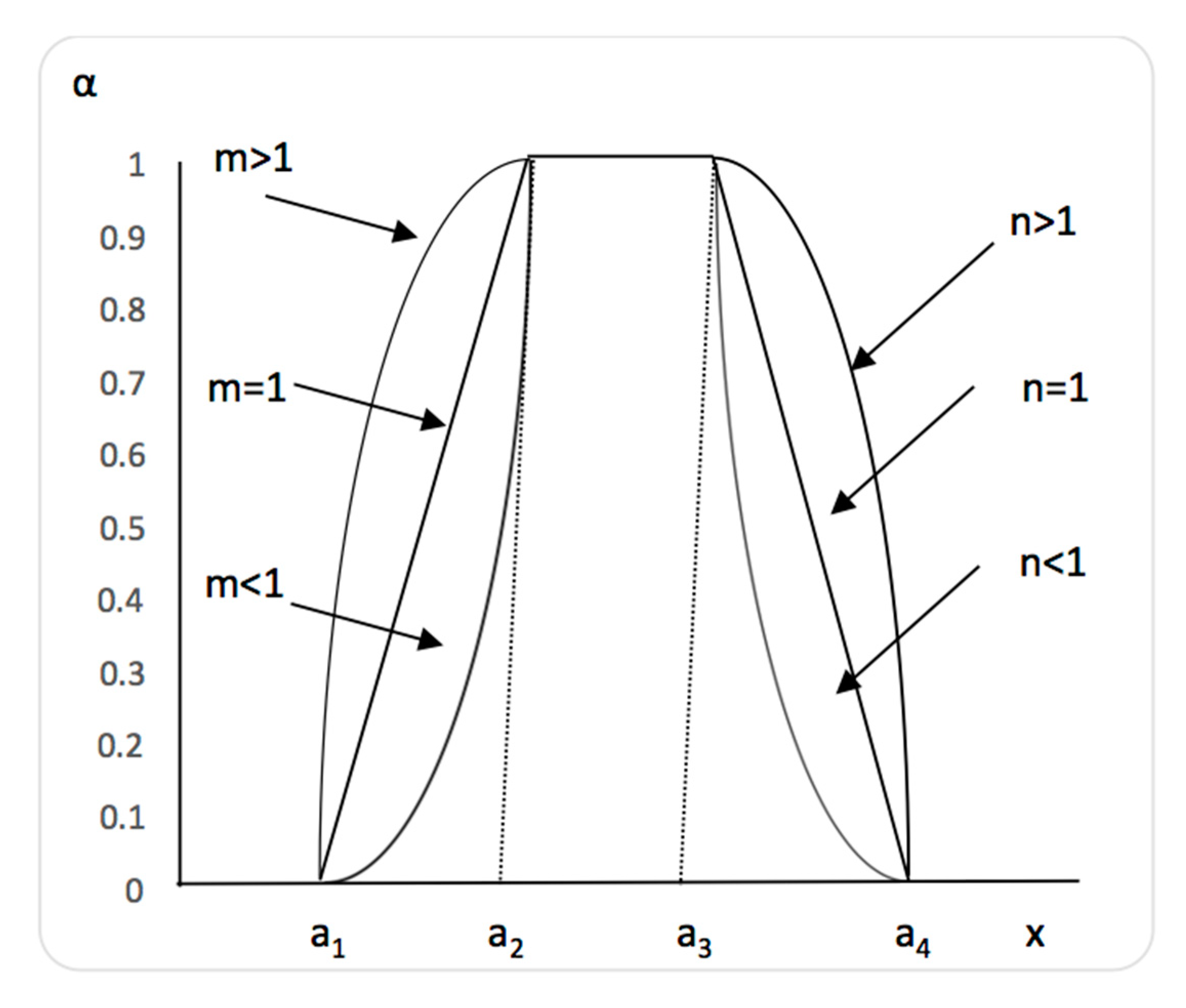
2.3. Extended FAHP (E-FAHP) with (m,n)-Trapezoidal Numbers
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill Inc.: New York, NY, USA, 1980; ISBN 0070543712. [Google Scholar]
- Chai, J.; Liu, J.N.K.; Ngai, E.W.T. Application of decision-making techniques in supplier selection: A systematic review of literature. Expert Syst. Appl. 2013, 40, 3872–3885. [Google Scholar] [CrossRef]
- Tavana, M.; Zareinejad, M.; Di Caprio, D.; Kaviani, M.A. An integrated intuitionistic fuzzy AHP and SWOT method for outsourcing reverse logistics. Appl. Soft Comput. J. 2016, 40, 544–557. [Google Scholar] [CrossRef]
- Medasani, S.; Kim, J.; Krishnapuram, R. An overview of membership function generation techniques for pattern recognition. Int. J. Approx. Reason. 1998, 19, 391–417. [Google Scholar] [CrossRef]
- Medaglia, A.L.; Fang, S.C.; Nuttle, H.L.W.; Wilson, J.R. An efficient and flexible mechanism for constructing membership functions. Eur. J. Oper. Res. 2002, 139, 84–95. [Google Scholar] [CrossRef]
- Mikhailov, L. Deriving priorities from fuzzy pairwise comparison judgements. Fuzzy Sets Syst. 2003, 134, 365–385. [Google Scholar] [CrossRef]
- Appadoo, S.S. Possibilistic Fuzzy Net Present Value Model and Application. Math. Probl. Eng. 2014, 2014, 865968. [Google Scholar] [CrossRef]
- Mikhailov, L.; Tsvetinov, P. Evaluation of services using a fuzzy analytic hierarchy process. Appl. Soft Comput. J. 2004, 5, 23–33. [Google Scholar] [CrossRef]
- Deng, H.D.H. Multicriteria analysis with fuzzy pairwise comparison. In Proceedings of the FUZZ-IEEE’99. 1999 IEEE International Fuzzy Systems Conference Proceedings (Cat. No.99CH36315), Seoul, Korea, 22–25 August 1999; Volume 2, pp. 726–731. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Chang, D.-Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Enea, M.; Piazza, T. Project selection by constrained fuzzy AHP. Fuzzy Optim. Decis. Mak. 2004, 3, 39–62. [Google Scholar] [CrossRef]
- Krejčí, J.; Pavlačka, O.; Talašová, J. A fuzzy extension of Analytic Hierarchy Process based on the constrained fuzzy arithmetic. Fuzzy Optim. Decis. Mak. 2017, 16, 89–110. [Google Scholar] [CrossRef]
- Cakir, O.; Canbolat, M.S. A web-based decision support system for multi-criteria inventory classification using fuzzy AHP methodology. Expert Syst. Appl. 2008, 35, 1367–1378. [Google Scholar] [CrossRef]
- Isaai, M.T.; Kanani, A.; Tootoonchi, M.; Afzali, H.R. Intelligent timetable evaluation using fuzzy AHP. Expert Syst. Appl. 2011, 38, 3718–3723. [Google Scholar] [CrossRef]
- Buyukozkan, G.; Guleryuz, S. A new integrated intuitionistic fuzzy group decision making approach for product development partner selection. Comput. Ind. Eng. 2016, 102, 383–395. [Google Scholar] [CrossRef]
- Zheng, G.; Zhu, N.; Tian, Z.; Chen, Y.; Sun, B. Application of a trapezoidal fuzzy AHP method for work safety evaluation and early warning rating of hot and humid environments. Saf. Sci. 2012, 50, 228–239. [Google Scholar] [CrossRef]
- Calabrese, A.; Costa, R.; Menichini, T. Using Fuzzy AHP to manage Intellectual Capital assets: An application to the ICT service industry. Expert Syst. Appl. 2013, 40, 3747–3755. [Google Scholar] [CrossRef]
- Ishizaka, A.; Nguyen, N.H. Calibrated fuzzy AHP for current bank account selection. Expert Syst. Appl. 2013, 40, 3775–3783. [Google Scholar] [CrossRef]
- Alavi, I. Fuzzy ahp method for plant species selection in mine reclamation plans: Case study sungun copper mine. Iran. J. Fuzzy Syst. 2014, 11, 23–38. [Google Scholar]
- Somsuk, N.; Laosirihongthong, T. A fuzzy AHP to prioritize enabling factors for strategic management of university business incubators: Resource-based view. Technol. Forecast. Soc. Chang. 2014, 85, 198–210. [Google Scholar] [CrossRef]
- Chan, H.K.; Wang, X.; Raffoni, A. An integrated approach for green design: Life-cycle, fuzzy AHP and environmental management accounting. Br. Account. Rev. 2014, 46, 344–360. [Google Scholar] [CrossRef]
- Tan, R.R.; Aviso, K.B.; Huelgas, A.P.; Promentilla, M.A.B. Fuzzy AHP approach to selection problems in process engineering involving quantitative and qualitative aspects. Process Saf. Environ. Prot. 2014, 92, 467–475. [Google Scholar] [CrossRef]
- Rezaei, J.; Fahim, P.B.M.; Tavasszy, L. Supplier selection in the airline retail industry using a funnel methodology: Conjunctive screening method and fuzzy AHP. Expert Syst. Appl. 2014, 41, 8165–8179. [Google Scholar] [CrossRef]
- Song, Z.; Zhu, H.; Jia, G.; He, C. Comprehensive evaluation on self-ignition risks of coal stockpiles using fuzzy AHP approaches. J. Loss Prev. Process Ind. 2014, 32, 78–94. [Google Scholar] [CrossRef]
- Dong, M.; Li, S.; Zhang, H. Approaches to group decision making with incomplete information based on power geometric operators and triangular fuzzy AHP. Expert Syst. Appl. 2015, 42, 7846–7857. [Google Scholar] [CrossRef]
- Erdogan, M.; Kaya, I. An integrated multi-criteria decision-making methodology based on type-2 fuzzy sets for selection among energy alternatives in turkey. Iran. J. Fuzzy Syst. 2015, 12, 1–25. [Google Scholar] [CrossRef]
- Mangla, S.K.; Kumar, P.; Barua, M.K. Risk analysis in green supply chain using fuzzy AHP approach: A case study. Resour. Conserv. Recycl. 2015, 104, 375–390. [Google Scholar] [CrossRef]
- Mosadeghi, R.; Warnken, J.; Tomlinson, R.; Mirfenderesk, H. Comparison of Fuzzy-AHP and AHP in a spatial multi-criteria decision making model for urban land-use planning. Comput. Environ. Urban Syst. 2015, 49, 54–65. [Google Scholar] [CrossRef]
- Lupo, T. A fuzzy framework to evaluate service quality in the healthcare industry: An empirical case of public hospital service evaluation in Sicily. Appl. Soft Comput. 2016, 40, 468–478. [Google Scholar] [CrossRef]
- Tuljak-suban, D.; Bajec, P. The Influence of Defuzzification Methods to Decision Support Systems Based on Fuzzy AHP with Scattered Comparison Matrix: Application to 3PLP Selection as a Case Study. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2018, 26, 475–491. [Google Scholar] [CrossRef]
- Akbar, M.A.; Shameem, M.; Mahmood, S.; Alsanad, A.; Gumaei, A. Prioritization Based Taxonomy of Cloud-based Outsource Software Development Challenges: Fuzzy AHP Analysis. Appl. Soft Comput. J. 2020, 95, 106557. [Google Scholar] [CrossRef]
- Jung, H. A fuzzy AHP-GP approach for integrated production-planning considering manufacturing partners. Expert Syst. Appl. 2011, 38, 5833–5840. [Google Scholar] [CrossRef]
- Shaw, K.; Shankar, R.; Yadav, S.S.; Thakur, L.S. Supplier selection using fuzzy AHP and fuzzy multi-objective linear programming for developing low carbon supply chain. Expert Syst. Appl. 2012, 39, 8182–8192. [Google Scholar] [CrossRef]
- Abdullah, L.; Zulkifli, N. Integration of fuzzy AHP and interval type-2 fuzzy DEMATEL: An application to human resource management. Expert Syst. Appl. 2015, 42, 4397–4409. [Google Scholar] [CrossRef]
- Vatansever, K.; Uluköy, M. Kurumsal Kaynak Planlaması Sistemlerinin Bulanık Ahp Ve Bulanık Moora Yöntemleriyle Seçimi: Üretim Sektöründe Bir Uygulama. Celal Bayar Üniversitesi Sos. Bilim. Derg. 2013, 11, 274–293. [Google Scholar]
- Akkaya, G.; Turanoǧlu, B.; Öztaş, S. An integrated fuzzy AHP and fuzzy MOORA approach to the problem of industrial engineering sector choosing. Expert Syst. Appl. 2015, 42, 9565–9573. [Google Scholar] [CrossRef]
- Kutlu, A.C.; Ekmekçioǧlu, M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP. Expert Syst. Appl. 2012, 39, 61–67. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Çifçi, G. A combined fuzzy AHP and fuzzy TOPSIS based strategic analysis of electronic service quality in healthcare industry. Expert Syst. Appl. 2012, 39, 2341–2354. [Google Scholar] [CrossRef]
- Taylan, O.; Bafail, A.O.; Abdulaal, R.M.S.; Kabli, M.R. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. J. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Patil, S.K.; Kant, R. A fuzzy AHP-TOPSIS framework for ranking the solutions of Knowledge Management adoption in Supply Chain to overcome its barriers. Expert Syst. Appl. 2014, 41, 679–693. [Google Scholar] [CrossRef]
- Sun, L.; Ma, J.; Zhang, Y.; Dong, H.; Hussain, F.K. Cloud-FuSeR: Fuzzy ontology and MCDM based cloud service selection. Future Gener. Comput. Syst. 2016, 57, 42–55. [Google Scholar] [CrossRef]
- Ar, I.M.; Erol, I.; Peker, I.; Ozdemir, A.I.; Medeni, T.D.; Medeni, I.T. Evaluating the feasibility of blockchain in logistics operations: A decision framework. Expert Syst. Appl. 2020, 158, 113543. [Google Scholar] [CrossRef]
- Yalcin, N.; Bayrakdaroglu, A.; Kahraman, C. Application of fuzzy multi-criteria decision making methods for financial performance evaluation of Turkish manufacturing industries. Expert Syst. Appl. 2012, 39, 350–364. [Google Scholar] [CrossRef]
- Chang, S.-C.; Tsai, P.-H.; Chang, S.-C. A hybrid fuzzy model for selecting and evaluating the e-book business model: A case study on Taiwan e-book firms. Appl. Soft Comput. 2015, 34, 194–204. [Google Scholar] [CrossRef]
- Li, N.; Zhao, H. Performance evaluation of eco-industrial thermal power plants by using fuzzy GRA-VIKOR and combination weighting techniques. J. Clean. Prod. 2016, 135, 169–183. [Google Scholar] [CrossRef]
- Mandic, K.; Delibasic, B.; Knezevic, S.; Benkovic, S. Analysis of the financial parameters of Serbian banks through the application of the fuzzy AHP and TOPSIS methods. Econ. Model. 2014, 43, 30–37. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Chen, Y. Supplier selection using axiomatic fuzzy set and TOPSIS methodology in supply chain management. Fuzzy Optim. Decis. Mak. 2012, 11, 147–176. [Google Scholar] [CrossRef]
- Kaya, Ö.; Alemdar, K.D.; Çodur, M.Y. A novel two stage approach for electric taxis charging station site selection. Sustain. Cities Soc. 2020, 62, 102396. [Google Scholar] [CrossRef]
- Chen, J.-F.; Hsieh, H.-N.; Do, Q.H. Evaluating teaching performance based on fuzzy AHP and comprehensive evaluation approach. Appl. Soft Comput. 2015, 28, 100–108. [Google Scholar] [CrossRef]
- Javanbarg, M.B.; Scawthorn, C.; Kiyono, J.; Shahbodaghkhan, B. Fuzzy AHP-based multicriteria decision making systems using particle swarm optimization. Expert Syst. Appl. 2012, 39, 960–966. [Google Scholar] [CrossRef]
- Che, Z.H.; Wang, H.S.; Chuang, C.L. A fuzzy AHP and DEA approach for making bank loan decisions for small and medium enterprises in Taiwan. Expert Syst. Appl. 2010, 37, 7189–7199. [Google Scholar] [CrossRef]
- Krejčí, J. Additively reciprocal fuzzy pairwise comparison matrices and multiplicative fuzzy priorities. Soft Comput. 2017, 21, 3177–3192. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, H. Intuitionistic fuzzy analytic hierarchy process. IEEE Trans. Fuzzy Syst. 2014, 22, 749–761. [Google Scholar] [CrossRef]
- Mikhailov, L. A fuzzy programming method for deriving priorities in the analytic hierarchy process. J. Oper. Res. Soc. 2000, 51, 341–349. [Google Scholar] [CrossRef]
- Appadoo, S.S. Pricing Financial Derivatives with Fuzzy Algebraic Models: A Theoretical and Computational Approach. Ph.D. Thesis, University of Manitoba, Winnipreg, MB, Canada, 2006. [Google Scholar]
| Papers | Area | Method | Fuzzy Number |
|---|---|---|---|
| [15] | Inventory classification system | FAHP | TN |
| [16] | Transportation | TN | |
| [17] | Service quality in health | TN | |
| [18] | Job security | TrN | |
| [19] | Intellectual capital management | TN | |
| [20] | Current bank account selection | TN | |
| [21] | Mining Project | TN | |
| [22] | Evaluation of the university business incubators | TN | |
| [23] | Designing environment friendly products | TN | |
| [24] | Process engineering | TN | |
| [25] | Supplier choice in airline retail industry | TN | |
| [26] | Evaluation on self-ignition risks of coal stockpiles | TN | |
| [27] | Investment project selection | TN/TrN | |
| [28] | Selection among energy alternative | TYPE-2 | |
| [29] | Risk evaluation | TN | |
| [30] | Urban land-use planning | TN | |
| [31] | Service quality in health | TN | |
| [32] | Application to 3PSP selection | TN | |
| [33] | Prioritization based taxonomy of Cloud-based Outsource Software Development Challenges | TN | |
| [34] | Integrated manufacture planning | FAHP/GP | TN |
| [35] | Supply chain | FAHP/FLP | TN |
| [36] | Human resources management | FAHP/FD | TrN |
| [37] | Choice of ERP software system | FAHP/FMOORA | TN |
| [38] | Industrial engineering sector choosing | TN | |
| [39] | Failure modes and effect analysis | FAHP/FTOPSIS | TN |
| [40] | Healthcare industry | TN | |
| [41] | Construction project | TN | |
| [42] | Knowledge management | TN | |
| [43] | Cloud service selection | TN | |
| [44] | Evaluating the feasibility of blockchain in logistics operations | FAHP/FVIKOR | Intuitionistic |
| [45] | Financial performance of industrial sector | FAHP/TOPSIS/VIKOR | TN |
| [46] | E-book business model | FAHP/TOPSIS/VIKOR/GRA | TN |
| [47] | Performance evaluation of eco-industrial thermal power plants | FAHP//VIKOR/GRA | TN |
| [48] | Financial performance of Banks | FAHP/TOPSIS | TN |
| [49] | Supply chain management | TrN | |
| [50] | Electric taxi charging station site selection | TN | |
| [3] | Outsourcing reverse Logistic | FAHP/SWOT | TIN |
| [51] | Evaluating teaching performance | FAHP/FCEM | TN |
| [52] | Nonlinear optimization | FAHP/PSO | TN |
| [53] | Bank loan decision for enterprises | FAHP/DEA | TN |
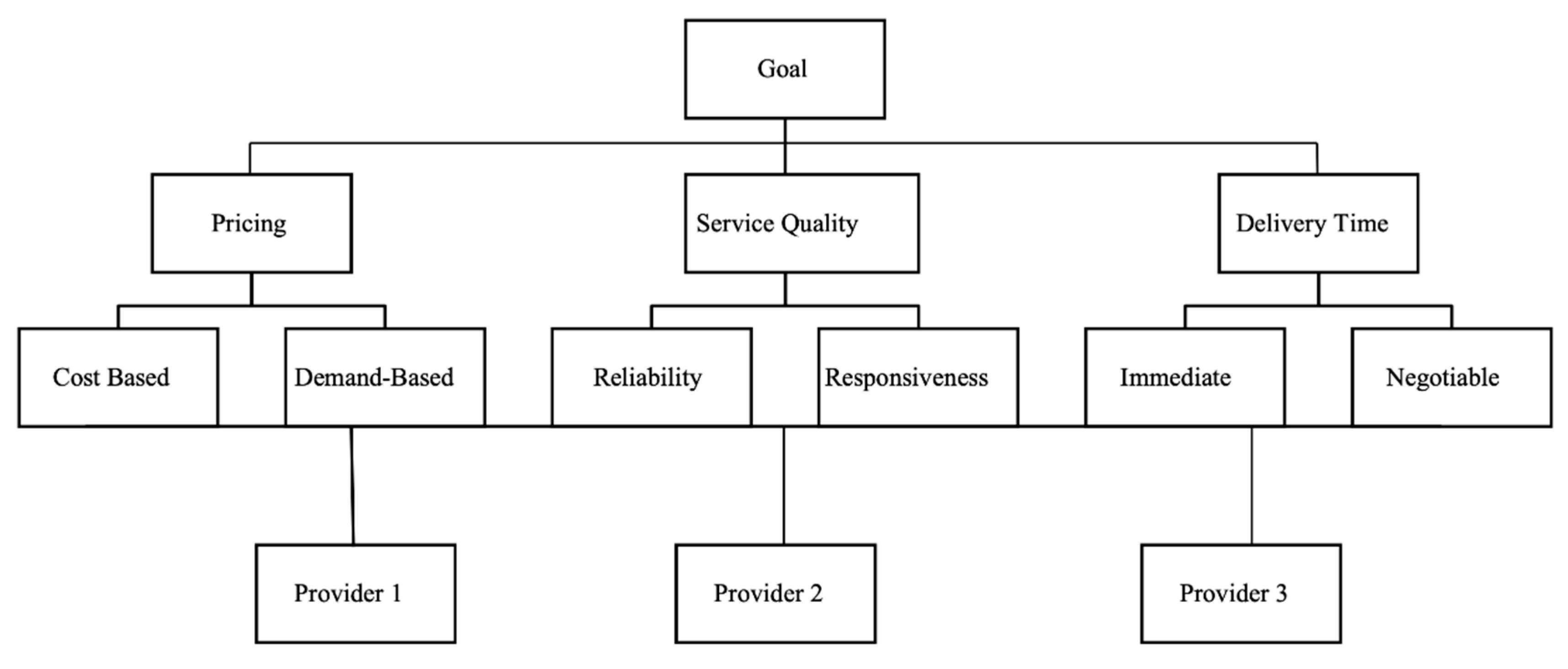
| Goal | Pricing | Service Quality | Delivery Time |
|---|---|---|---|
| Pricing | (2, 3, 4) | (1, 2, 3) | |
| Service Quality | 1 | ||
| Delivery Time | 1 |
| Goal | Pricing | Service Quality | Delivery Time |
|---|---|---|---|
| Pricing | 1 | (2, 3, 3, 4)(1,1) | (1, 2, 2, 3)(1,1) |
| Service Quality | 1 | ||
| Delivery Time | 1 |
| Goal | Pricing | Service Quality | Delivery Time |
|---|---|---|---|
| Pricing | 1 | (1, 2, 3, 4)(1,1) | |
| Service Quality | 1 | ||
| Delivery Time | 1 |
| Goal | Pricing | Service Quality | Delivery Time |
|---|---|---|---|
| Pricing | 1 | (1, 2, 3, 4)(6,5) | |
| Service Quality | 1 | ||
| Delivery Time | 1 |
| FAHP | E-FAHP | |||
|---|---|---|---|---|
| Mikhailov and Tsvetinov | ||||
| 0.538 | 0.538 | 0.500 | 0.471 | |
| 0.170 | 0.170 | 0.167 | 0.163 | |
| 0.292 | 0.292 | 0.333 | 0.366 | |
| 0.838 | 0.838 | 1 | 0.493 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reig-Mullor, J.; Pla-Santamaria, D.; Garcia-Bernabeu, A. Extended Fuzzy Analytic Hierarchy Process (E-FAHP): A General Approach. Mathematics 2020, 8, 2014. https://doi.org/10.3390/math8112014
Reig-Mullor J, Pla-Santamaria D, Garcia-Bernabeu A. Extended Fuzzy Analytic Hierarchy Process (E-FAHP): A General Approach. Mathematics. 2020; 8(11):2014. https://doi.org/10.3390/math8112014
Chicago/Turabian StyleReig-Mullor, Javier, David Pla-Santamaria, and Ana Garcia-Bernabeu. 2020. "Extended Fuzzy Analytic Hierarchy Process (E-FAHP): A General Approach" Mathematics 8, no. 11: 2014. https://doi.org/10.3390/math8112014
APA StyleReig-Mullor, J., Pla-Santamaria, D., & Garcia-Bernabeu, A. (2020). Extended Fuzzy Analytic Hierarchy Process (E-FAHP): A General Approach. Mathematics, 8(11), 2014. https://doi.org/10.3390/math8112014






