Abstract
Numerous studies have addressed the relationship between performance in mathematics problem-solving and reading comprehension in students of all educational levels. This work presents a new proposal to measure the complexity of arithmetic word problems through the student reading comprehension of the problem statement and the use of learning analytics. The procedure to quantify this reading comprehension comprises two phases: (a) the division of the statement into propositions and (b) the computation of the time dedicated to read each proposition through a technological environment that records the interactions of the students while solving the problem. We validated our approach by selecting a collection of problems containing mathematical concepts related to fractions and their different meanings, such as fractional numbers over a natural number, basic mathematical operations with a natural whole or fractional whole and the fraction as an operator. The main results indicate that a student’s reading time is an excellent proxy to determine the complexity of both propositions and the complete statement. Finally, we used this time to build a logistic regression model that predicts the success of students in solving arithmetic word problems.
1. Introduction
Previous work has studied the relationship between performance in mathematics problem-solving and reading comprehension in students of all educational levels [1,2,3]. Authors such as Pólya [4] and Puig and Cerdán [5] have shown that reading and understanding the statement are key phases of the problem-solving process. The National Council of Teachers of Mathematics (NCTM) [6] determined that, in solving a mathematical problem, many of the necessary skills present in all areas of the educational curriculum are required, such as reading, reflection and understanding. The latest PISA report [7] indeed highlights that a solid reading competence is fundamental for academic achievement in all subjects of the educational system (including mathematics), while being a prerequisite for successful participation in most adult life [8,9,10].
Our research is framed within the context of arithmetic word problems (from now on AWPs or AWP in singular) and focuses on how to measure the complexity of the statements involved. To this end, we computed the reading comprehension of students through a technological environment and use learning analytics to predict student performance in solving this sort of problems.
1.1. Complexity of Arithmetic Word Problems
AWPs are texts or statements describing real-life situations in which unknown quantities need to be determined from other amounts that are known [5,11,12]. AWPs are some of the first problem-solving activities in the elementary school mathematics curriculum, and as such, they deserve special care and attention.
The complexity of AWPs has been conceptualized through research on the resolution of verbal problems and on the difficulties they present for schoolchildren. Daroczy et al. [13] showed that these difficulties can be caused by either one or a combination of linguistic and numerical complexity. Linguistic complexity refers to the linguistic and morphological aspects of the statement (e.g., how words are combined to form the text). Numerical complexity, in turn, refers to the numerical factors of the statement (e.g., both the quantities and the relationships between them).
According to Castro et al. [14], the complexity of AWPs can be measured following four main approaches:
- The linguistic approach, based on the student’s reading ability [15] and the readability of external texts different from the AWP statement [16].
- The structural variables approach, based on the so-called task variables (e.g., syntactic variables or context variables) as defined by Kilpatrick [17] or Goldin and McClintock [18].
- The open sentences approach, based on the situation of the question within the statement [19].
- The semantic approach, based on the semantic structure of the statement, considered as a whole [5] or divided into segments [19], so that an association can be built between keywords and operators in a partial problem-solving process.
To the author’s knowledge, none of the previous approaches has yet measured the complexity of AWPs through the students’ reading comprehension of the statement itself. This aspect makes our research a novel and original contribution to the state of the art of mathematical problem-solving.
1.2. Measuring the Complexity of AWP Statements through a Technological Environment
To measure the complexity of an AWP, we split its statement into propositions, as follows from the partial semantic approach defined above. Our unit of analysis is thus a proposition, which contains a verb and a quantity associated with the related action. Figure 1 shows an example of an AWP statement [20] divided into three propositions.

Figure 1.
Example of an arithmetic word problem (AWP) statement ([20]) divided into propositions.
Propositions can be classified into levels to facilitate comparability and to determine their complexity. Hunt [21] names these constructions T-units or minimal terminable units of language. T-units each consist of a main clause plus the subordinate clauses it may include, and they can be organized on a number of levels: declarative sentences represent level 0; level 1 adds a subordination to sentences of level 0; level 2 adds a subordination to those of level 1 and so on. The higher the level, the more complex the sentence will be. This way, Proposition 1 in Figure 1 belongs to level 0, and Propositions 2 and 3 are of level 1, since they are respectively subordinate by the terms “of them” and “now”.
We measure the complexity of each proposition by obtaining the time per word that students spent while reading the corresponding segment of the AWP statement. The time per word is computed through a technological learning environment able to control which information is displayed at any time and to register the interaction of students with the content. This novel approach is more powerful than to control reading from printed texts.
The use of intelligent tutors or technological learning environments (e.g., Moodle, Edmodo or Bakpax) has increased in recent years across all educational stages [22]. However, these environments have not yet been used to measure reading comprehension and the complexity of AWPs. These tools can usually be accessed through mobile devices and smart screens and allow one to register student–computer, student–teacher or student–content interactions [23,24,25,26], thereby giving rise to the so-called learning analytics research field. This field deals with applying data analytics to education and it is defined as the area of investigation in charge of measuring, compiling and analyzing data sets obtained through the use of computer-assisted learning platforms that track and record student digital interactions [27,28].
Technological environments and learning analytics are a cutting-edge approach to detect patterns on student strategies when solving a learning task. They are also helpful in understanding study habits, the use of teaching materials or the time dedicated to the proposed activities [29], sometimes supplemented by information on attendance, participation or motivation [30].
This work focuses on the analysis of the student–computer and student–content interactions obtained through the Read and Learn (R&L) technological environment [24,31]. R&L is a research tool to carry out experiments that analyze the strategies of students when they first have to read a text or problem statement and then answer a series of questions in a digital context.
1.3. Predicting Student Performance When Solving AWPs
Mathematical models have been extensively used to try to predict the probability of correctly solving a learning task. These models are commonly used to build a personalized route that guides students through an adapted teaching–learning process [32].
Logistic and Bayesian knowledge tracing models stand out among the statistical prediction models used for this purpose. The former have been used to predict the probability of success from the students’ previous skills and the difficulty of the task [33]. The latter use hidden Markov models to estimate latent parameters and predict student success [32].
Following previous work on the matter [26,34], this work presents a binary logistic regression model to predict student performance from the complexity of an AWP measured by the reading comprehension of its statement.
The remainder of the paper is organized as follows. Section 2 describes the materials and methods used to measure the complexity of AWPs, the features of the R&L technological environment, a validation experiment for a sample population and the tested hypotheses. Section 3 presents the experimental results that determined the feasibility of our approach for assessing the complexity of mathematical problems through reading comprehension. Section 4 shows how to build a logistic model to predict student performance from the complexity computed for an AWP. Finally, discussion and conclusions are drawn in Section 5 in the context of the state-of-the-art literature.
2. Material and Methods
2.1. Procedure for Measuring the Complexity of AWPs
The complexity of an AWP can be derived from the complexity of all the propositions that form its statement. To estimate the complexity of a proposition, we compute the reading time per word for a group of students using the R&L technological environment. The reading time of proposition j in task i ( in Equation (1)) thus comprises the time spent by each student () in the group (of size n) and the number of words in the proposition (k).
The total complexity of an AWP can in turn be measured by averaging the previous reading times per student for all propositions (Equation (2)), where m represents the number of propositions in the statement.
2.2. Instrument
R&L is a technological environment in which to design research experiments on reading comprehension in text and image-related learning tasks. It is a web tool that can be accessed through mobile devices, computers and smart screens using any browser on any operating system.
Experiments in R&L can include enriched texts with a list of questions and answers. A number of configuration settings are available, such as the possibility of accessing the statement at any time or only under certain conditions, the effect of alternatively hiding and showing parts of texts by clicking on them (Figure 2), the use of open-ended or multiple-choice questions, the number of attempts allowed to complete the task or the definition of feedback to be given after answering the questions.
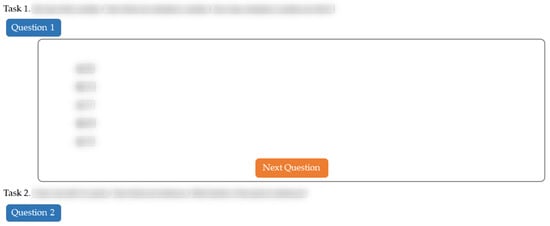
Figure 2.
An example of an experimental setting in R&L wherein the texts of both questions and answer options are totally hidden.
R&L records all user interactions with the statements, questions and response options along with timestamps, which allows tracking the access history to the learning content with a level of precision of milliseconds. Any user action is registered, such as displaying a hidden proposition, moving the focus from the statement to the questions and vice versa. This way, we can determine aspects such as: what part of the statement the student is focused on, which point in time a certain proposition is read, how long a student remains in the same proposition, how many times a proposition is consulted and in which order students access the statement, the questions and the answer options.
R&L is able to digest these learning data flows and compute the variables of interest from the previously recorded data (e.g., the time reading a proposition or answering a question). Data can then be exported in CSV so it can be further used in any preferred data analysis software (e.g., R or SPSS). For more details on R&L the interested reader can check out the literature [24] and keep up with our website about data analytics and technological tools in education https://go.uv.es/grimo/datte.
2.3. Experimental Design
To test our proposal we have conducted a descriptive quantitative study involving a group of 70 students, 26 girls and 44 boys, aged between 15 and 16 years old.
At the time of the study, the students belonged to two public secondary schools in Spain selected by a convenience non-probability sampling. One school is located in an upper-middle socioeconomic area of a town of twelve thousand inhabitants. The other one is located in a multicultural suburb with medium-low socioeconomic status in a city of eight hundred thousand inhabitants.
Informed consent was obtained from schools, teachers and students before the start of the experiment. Anonymity of the data was guaranteed by just collecting the year of birth, gender, course and a dummy school code for each student. Any combination of data with a frequency of less than 5 observations was considered subject to statistical secrecy and it was removed to prevent de-anonymization.
The experiment was run individually using the school’s computer room. Students were introduced to the R&L technological environment before starting the session. Following fair and ethical practices, participants were made aware that they were involved in a research study. They were clearly informed about the aims of the study and that their performance would not be considered in their grades.
Participants were asked to solve a couple of AWPs presented as two tasks with their corresponding statement and five answer options. The statements were designed taking in to account the mathematical and the grammatical complexity. We built two isomorphic tasks [35] dealing with mathematical introductory concepts related fractional numbers over a natural number, basic mathematical operations with a fractional whole and the fraction as an operator. In addition, we classify the propositions of the statements into levels as defined by Hunt [21], which allows the measured reading comprehension to be compared.
Tasks were written in Spanish since all participants were native Spanish speakers. For the sake of readability, we also show the translation of the statement into English as follows:
- Task 1: We have thirty candies. Two-thirds of them are strawberry flavored. How many strawberry candies do we have? (From the original: Tenemos treinta caramelos. Si dos tercios son de fresa, ¿cuántos caramelos son de fresa?) The possible answers are 5, 10, 17, 20 and 45.
- Task 2: I have one-half of a pizza. Two-thirds of it is margherita. What fraction of the pizza is margherita? (From the original: Tengo media pizza. Si dos tercios son de margarita, ¿qué porción de pizza es de margarita?) The possible answers are , , , and .
Both tasks have an equal mathematical structure, expressed in terms of the relationships between the variables and quantities involved. This means that they are solved by applying the same rules, procedures, and algorithms. The question is placed at the end of the statement following the pattern where a and b are known quantities. Note that the semantic relationship between the variables and the unknown quantity, the lack of data in the question and the absence of irrelevant data is equivalent in both statements. The tasks can be classified as two AWPs of multiplicative comparison according to Puig and Cerdán [5]. This sort of problems use a scalar function (I) to link two extensive quantities (E) of the same type of magnitude (, the Schwartz relation [36]). For example, the scalar function in task 1 is “two-thirds of,” while the two extensive quantities are “thirty candies” and the unknown quantity of “strawberry candies”.
The proposed AWPs use the fraction (i.e., two-thirds) as an operator [37] that transforms an initial quantity (i.e., thirty candies or one-half of a pizza) into a final quantity (e.g., strawberry candies or a fraction of the pizza). This transformation is associated with the scalar function and the multiplication operator, as shown in Figure 3. The tasks are consistent [38] since they can be solved by directly translating the key terms in the statement (e.g., are or is) into the operation to be performed, in this case a multiplication.
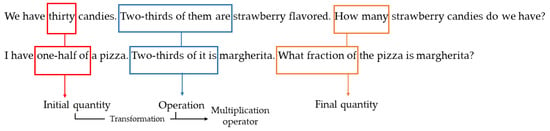
Figure 3.
Use of the fraction as an operator in the proposed AWPs.
We can determined the grammatical complexity of the tasks by dividing the statement into propositions and analyzing their syntax. Each statement is composed of three propositions, as shown in Table 1. The first two relate to the informative part of the statement and the third one is the question. We configured the tasks in R&L so that just one proposition could be displayed at a time while the rest of them remained hidden (see the different colored segments in Figure 4).

Table 1.
Propositions of tasks 1 and 2.

Figure 4.
Informative and question parts of the statements.
The length of the informative parts is the same in both statements (i.e., 3 + 6 words for P11 + P12 and P21 + P22 as from the original text in Spanish). The number of words in the question part differs (i.e., 5 to 7 words for P13 and P23 as shown in Table 2) due to the introduction of rational numbers that change the Spanish quantifier “cuántos” by “qué porción de,” although it keeps the same length in English.

Table 2.
Syntax of the propositions from the original text in Spanish.
The grammatical complexity of each proposition is also represented by the number of nous, verbs, numerals, prepositions and conjunctions in Table 2. The type of sentences can be categorized into levels as defined by Hunt [21]. Propositions P11 and P21 are declarative sentences of level 0. The rest of propositions are level 1 since they include a subordination to the previous sentences by the terms “of them” (P12), “of it” (P22), “candies” (P13) and “of the pizza” (P23) respectively.
2.4. Research Hypotheses
We pose the following hypotheses in line with previous work on the mathematical concepts dealt with by our study:
- H1: The change from natural to fractional numbers increases the complexity of AWPs. According to Perera Dzul [39], difficulties begin when students face the study of fractions, without having prior knowledge and enough situations in daily life that present problems related to rational numbers. Gairín and Muñoz [40], in a study on textbooks for the teaching of rational numbers in secondary education in Spain, affirm that rational numbers are overshadowed by the study of procedural aspects, making it difficult to transfer this concept to daily life problems.
- H2: The use of the fraction as an operator makes statements harder to understand. Authors like Hart [41] have already shown how challenging a syntagm of the type “two-thirds of them are” can be. Sanz, Figueras and Gómez [42] have also observed that students from 15 to 16 years old find it difficult to tackle this expression when presented literally in simple operative exercises.
- H3: Operating on a rational whole is more difficult than operating on a natural whole. Problems arise when the concept of the whole is reformulated. If the whole is not a natural but a fractional number, solving an AWP becomes a more difficult task [43].
Hypotheses 1 and 3 were tested by comparing the average reading times of propositions of the same level. Regarding H1, an increase in complexity from P11 to P21 was due to the mere presence of fractional instead of natural numbers. By comparing the complexity of P12 and P22 we checked the effect of reformulating the whole (H3) from a natural number (i.e., thirty candies) to a fractional one (i.e., one-half of a pizza).
To test H2, we compared the average reading times of level 1 subordinate propositions with that of proposition P21. Propositions P12 and P22 include the syntagms “of them are” and “of them it is” that refer to the use of the fraction as an operator (from now on, we refer only to syntagms “of them are” in order to improve readability). We take proposition P21 as the reference level 0 declarative sentence since it also uses a rational number (i.e., one-half of a pizza), but it does so as a fractional quantity.
3. Analysis and Results
Reading times were rather dispersed in our group of students, as shown by the high standard deviations in Table 3 (values are expressed in seconds per word or s/word). The Kolmogorov–Smirnov test confirmed that the times recorded did not follow a normal distribution (p-value ) for the propositions () or the complete statement (). Therefore, we use the median as a good representative of each set of times. We did not use the mean in our analysis, since it is affected by outliers in the obtained asymmetric distributions. For example, see how most of the students read faster than the average reading time (empty circle) in the box-plots shown in Figure 5.

Table 3.
Reading times (s/word) for each proposition () and task ().
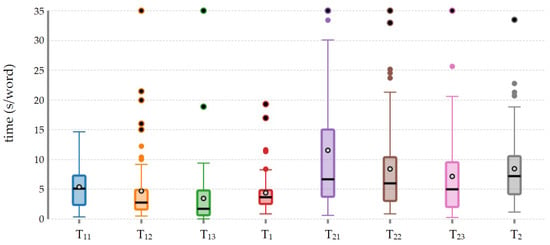
Figure 5.
Distribution of reading times for each proposition () and task ().
We checked for differences in the reading times due to the socioeconomic context and the gender of students. Differences between school were not statistically significant following the non-parametric Wilcoxon signed-rank test for paired samples (p-values ). Reading times were also not statistically different between boys and girls (p-values ). We can then use the data obtained for the whole group to study the complexity of the statements.
By comparing the reading times in Table 3 we can test our hypotheses as follows:
- H1: The change from natural to fractional numbers increases the complexity of AWPs. The median reading time of propositions P11 and P21 increases from 5.12 s/word to 6.68 s/word (see also the difference reported in Figure 5). This rise in complexity is due to the change from a natural to a fractional initial quantity. The difference in medians is statistically significant according to the Wilcoxon signed-rank test (p-value ). The results thus confirm this hypothesis.
- H2: The use of the fraction as an operator makes statements harder to understand. The median reading time of propositions that use the fraction as an operator (i.e., 2.78 s/word for P12 and 6.01 s/word for P22) is shorter than that of the proposition using the fraction as a quantity (i.e., 6.68 s/word for P21). The difference in medians is not statistically significant for task 2 according to the Wilcoxon signed-rank test (p-value ). The difference is significant for task 1 (p-value ) mainly due to the ease of operating on a natural whole, as we analyze below in H3. Thus, the syntagm “of them are” does not introduce further complexity to the statements in the AWPs studied.
- H3: Operating on a rational whole is more difficult than operating on a natural whole. The median reading time of proposition P22 (i.e., 6.01 s/word) is longer than that of proposition P12 (i.e., 2.78 s/word). Differences are statistically significant according to the Wilcoxon signed-rank test (p-value ), as is also shown in Figure 5. Those results confirm the hypothesis that it was more complex to operate on a rational whole (e.g., one-half of a pizza) than to operate on a natural whole (e.g., thirty candies).
Student performance was rather good when solving the two proposed tasks. The success rate was 94.3% for task 1 and 62.9% for task 2. The median reading time of all propositions in task 2 was longer than that of task 1 (7.21 s/word and 3.67 s/word respectively) and the distribution was more sparse (e.g., compare and in Figure 5). The previous results confirm that solving task 2 was more complicated than solving task 1.
4. Predicting Student Success from the Proposed Complexity Measure
We use a binary logistic regression model to predict the student success when solving an AWP. The model estimates the probability of succeeding (or failing) in completing a task from the complexity of its statement, measured as the reading time per word. The data obtained in our study were used to train a model for each task, as described by Equation (3), where is the time taken by students to read each proposition (j) of the problem (i).
We discarded outliers from our data and kept the results of 58 students to build the model for task 1 and of 57 students for task 2. We trained the models with a random sample of 50 students and validated them with the remaining eight students (task 1) and seven students (task 2). Table 4 shows the relation between the reading time per proposition and the success of students from direct observation of the data. Faster reading times led to better performance in task 1 (indirect relation), whereas slower students were the best performers in task 2 (direct relation). These results are in line with the complexity of the statements analyzed above.

Table 4.
Relation between the reading time per proposition and student success.
The model built for task 1 is shown in Equation (4). It explains between 0.142 (Cox and Snell value) and 0.424 (Nagelkerke value) of the dependent variable. It gives an accuracy of 98.3% when calibrating on the train set and it correctly predicts the success of the eight students in the validation set. The sign of the coefficients obtained for each proposition () reproduces the indirect relation previously found between the reading time and the probability of successfully solving task 1 (see Table 4).
We analyzed the odds ratio (OR) to understand the magnitude of the effect, that is, how much the probability of success changes as a result of increasing by one second the reading time of a proposition, the rest being constant. An OR greater than one indicates an increase in the probability while an OR less than one implies a decrease. Taking more time to read proposition P12 (i.e., higher values of ) lowers the probability of success since . Increasing the reading time for propositions P11 and P13 does not affect the student’s success that much since OR remains near to one ( and respectively).
The model built for task 2 (see Equation (5)) is more limited since it explains between 0.056 (Cox and Snell value) and 0.175 (Nagelkerke value) of the dependent variable. It gives an accuracy of 65.4% when calibrating on the train set and it correctly predicts the success of four students in the validation set. All coefficients are positive and confirm the direct relation found in Table 4. They are also close to zero, which makes OR rather close to one. For example, increasing the reading time of proposition P22 slightly raises the probability of success (); the time taken to read propositions P21 and P23 does not have any significant effect on student success ( and respectively).
Far from being contradictory, the models represent the different complexities of the two statements. The overall reading time for task 1 was half the overall time for task 2 (e.g., see and in Table 3). Students having reading comprehension problems in task 1 thus showed higher probabilities of failure. On the contrary, task 2 appeared as a more complex AWP whose successful resolution could benefit from investing more time in reading its propositions.
5. Discussion and Conclusions
We have presented a novel proposal to measure the complexity of an AWP through the student reading comprehension of its statement. The approach allowed us to predict the students’ success from their reading times when solving the task. The students’ reading time has demonstrated to be a good proxy to determine the complexity of AWPs and it can become an essential tool for the design of problem statements. By analyzing the statement propositions, one can adjust the level of complexity of the task to focus on certain student profiles.
The paper also introduces the use of the R&L technological environment to compute the complexity of a problem statement, without the need to use traditional paper-and-pencil questionnaires. In addition to that, R&L enables the collection of extensive data on student interactions and opens the way for more data-driven research on the topic.
The results obtained confirm that our procedure for measuring the complexity of AWPs is consistent with previous findings [14]. The two tasks under study can be classified as multiplicative comparison problems according to the semantic approach [5], whose difficulty lies in the introduction of fractional versus natural numbers [39,40,41].
We identified the complexity of the syntagms “of are” or “of them it is” (or its equivalent “son de” in Spanish), which is related to the multiplication operator and to the concept of “fraction of” or “part of” [37]. These ideas begin to be developed in the school curriculum from the fourth year of primary education. The complexity of this concept, though, increases when it is applied to a fraction. These results may be linked to the design of tasks for current textbooks, where the concept of natural number is introduced through graphic support and considering the whole as a discrete quantity. However, when this concept is introduced over a fraction in the sixth year of primary education, the visual representation is usually removed and the whole becomes a continuum. That results in the mathematical concept being taught through a rote rule, which associates this expression with the multiplication of fractions and leads to possible errors in later courses, as shown by researchers at the Rational Number Project (http://www.cehd.umn.edu/ci/rationalnumberproject/) and the National Assessment of Educational Progress (https://nces.ed.gov/nationsreportcard/). Our work confirmed this issue with a sample group of students of the last year from compulsory secondary education.
The complexity of the statement propositions has been used to build binary logistic regression models that predict the probability of success in solving AWPs. The models confirmed that the propositions that most affect probability are those that involved a more difficult mathematical concept. In our study, these propositions are the ones that deal with the fraction as an operator over both a natural and a rational number.
It is worth noting that our approach also proposes the segmentation of the statement into propositions, whose complexity can be measured and compared following the classification into levels by Hunt [21]. In our study, first level propositions are declarative alphanumeric sentences where the numerical values are either natural numbers or fractions. Second level propositions introduce a subordinate clause through the syntagms “of them are” or “of it is”. This fact goes far beyond evaluating the complexity by the success rate [44] and allows comparing the complexity of mathematical concepts within and across AWPs.
This work opens up a line of research on using technological environments and data analytics to determine the complexities of AWPs by measuring the level of understanding of each the statements and dealing with the mathematical concepts that make them more difficult to solve. Next steps include the design of a longitudinal study by students’ age that analyzes the evolution of the concepts and the possible blockages that occur. Future work will also help to define an index that allows creating AWPs statements with prefixed complexities by weighting the propositions in the statement according to their level following the classification by Hunt [21].
These sorts of metrics and tools can be implemented by intelligent tutors designed to teach maths through problem-solving. They can help to track personalized teaching–learning paths for each student while using reading comprehension as one of the key drivers for predicting students’ skills [26]. Despite the benefits provided by technological environments, the development of digital teaching competence continues to be a challenge for the education system [45,46]. However, the introduction of emerging tools and data analytics is progressively providing teachers and researchers with new experimental scenarios to study, for example, the possible impact of the use of feedback oriented to success when students interact with a given statement [31]. As Alonso et al. pointed out [22], the development of good teaching practices that integrate technology in the classroom can help teachers to start applying digital learning tools effectively and to improve their digital competence.
Author Contributions
Conceptualization, M.T.S. and E.L.-I.; data curation, M.T.S., E.L.-I., D.G.-C. and F.G.; writing—original draft preparation, M.T.S. and E.L.-I.; writing—review and editing, M.T.S., E.L.-I., D.G.-C. and F.G.; supervision, M.T.S., E.L.-I. and F.G.; project administration, F.G.; funding acquisition, F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Spanish Ministry of Science, Innovation and Universities (MCIU), the Spanish State Research Agency (AEI) and the European Regional Development Fund (ERDF) under project RTI2018-095820-B-I00 and the projects UV-SFPIE-PID19-1098335, UV-SFPIE-PID19-1095187.
Acknowledgments
The authors would like to thank the support of the Capgemini-University of Valencia Chair for Innovation in Software Development.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boonen, A.J.; van Wesel, F.; Jolles, J.; van der Schoot, M. The role of visual representation type, spatial ability, and reading comprehension in word problem solving: An item-level analysis in elementary school children. Int. J. Educ. Res. 2014, 68, 15–26. [Google Scholar] [CrossRef]
- Pape, S.J. Middle school children’s problem-solving behavior: A cognitive analysis from a reading comprehension perspective. J. Res. Math. Educ. 2004, 35, 187–219. [Google Scholar] [CrossRef]
- Vilenius-Tuohimaa, P.M.; Aunola, K.; Nurmi, J.E. The association between mathematical word problems and reading comprehension. Educ. Psychol. 2008, 28, 409–426. [Google Scholar] [CrossRef]
- Pólya, G. How to Solve It; Princeton University: Princeton, NJ, USA, 1945. [Google Scholar]
- Puig Espinosa, L.; Cerdán Pérez, F. Problemas Aritméticos Escolares [School Arithmetic Problems]; Síntesis: Madrid, Spain, 1988. [Google Scholar]
- NCTM. Principios y Estándares Para la Educación Matemática [Principles and Standards for School Mathematics Education]; SAEM THALES: Sevilla, Spain, 2003. [Google Scholar]
- OECD. PISA 2018 Assessment and Analytical Framework. 2019. Available online: https://doi.org/10.1787/b25efab8-en (accessed on 1 April 2020).
- Cunningham, A.E.; Stanovich, K.E. Early reading acquisition and its relation to reading experience and ability 10 years later. Dev. Psychol. 1997, 33, 934. [Google Scholar] [CrossRef] [PubMed]
- OECD. OECD Skills Outlook 2013: First Results from the Survey of Adult Skills. 2013. Available online: http://dx.doi.org/10.1787/9789264204256-en (accessed on 1 April 2020).
- Smith, M.C.; Mikulecky, L.; Kibby, M.W.; Dreher, M.J.; Dole, J.A. What Will Be the Demands of Literacy in the Workplace in the Next Millennium? Read. Res. Q. 2000, 35, 378–383. [Google Scholar] [CrossRef]
- Riley, M.S.; Greeno, J.G. Developmental analysis of understanding language about quantities and of solving problems. Cogn. Instr. 1988, 5, 49–101. [Google Scholar] [CrossRef]
- Verschaffel, L.; Greer, B.; De Corte, E. Making Sense of Word Problems; Swets & Zeitlinger: Lisse, The Netherlands, 2000. [Google Scholar]
- Daroczy, G.; Wolska, M.; Meurers, W.D.; Nuerk, H.C. Word problems: A review of linguistic and numerical factors contributing to their difficulty. Front. Psychol. 2015, 6, 348. [Google Scholar] [CrossRef]
- Castro Martínez, E.; Rico Romero, L.; Gil Cuadra, F. Enfoques de investigación en problemas verbales aritméticos aditivos [Research approaches in additive arithmetic word problems]. Ense Nanza Cienc. Rev. Investig. Exp. Didácticas 1992, 10, 243–253. [Google Scholar]
- Aiken, L.R., Jr. Verbal factors and mathematics learning: A review of research. J. Res. Math. Educ. 1971, 2, 304–313. [Google Scholar] [CrossRef]
- Moyer, J.C.; Sowder, L.; Threadgill-Sowder, J.; Moyer, M.B. Story problem formats: Drawn versus verbal versus telegraphic. J. Res. Math. Educ. 1984, 15, 342–351. [Google Scholar] [CrossRef]
- Kilpatrick, J. Variables and methodologies in research on problem solving. In Mathematical Problem Solving: Papers from a Research Workshop; Eric Clearinghouse for Science, Mathematics, and Environmental Education: Columbus, OH, USA, 1978; pp. 7–20. [Google Scholar]
- Goldin, G.A.; McClintock, C.E. Task Variables in Mathematical Problem Solving; ERIC Clearinghouse for Science, Mathematics, and Environmental Education: Columbus, OH, USA, 1979.
- Castro, E.; Rico, L.; Batanero, C.; Castro, E. Dificultad en problemas de estructura multiplicativa de comparacioó [Difficulty in multiplicative comparison word problems]. In Proceedings of the Fifteenth PME Conference, Assisi, Italy, 29 June–4 July 1991; Volume 1, pp. 192–198. [Google Scholar]
- Vergnaud, G. A classification of cognitive tasks and operations of thought involved in addition and subtraction problems. In Addition and Subtraction; Carpenter, T., Moser, J., Eds.; Romberg: London, UK, 1982; pp. 39–59. [Google Scholar]
- Hunt, K.W. Syntactic maturity in schoolchildren and adults. Monogr. Soc. Res. Child. Dev. 1970, 35. [Google Scholar] [CrossRef]
- Alonso-García, S.; Aznar-Díaz, I.; Cáceres-Reche, M.P.; Trujillo-Torres, J.M.; Romero-Rodríguez, J.M. Systematic Review of Good Teaching Practices with ICT in Spanish Higher Education. Trends and Challenges for Sustainability. Sustainability 2019, 11, 7150. [Google Scholar] [CrossRef]
- Conole, G.; Gašević, D.; Long, P.; Siemens, G. Message from the LAK 2011 general & program chairs. In International Learning Analytics & Knowledge Conference 2011; Association for Computing Machinery (ACM): New York, NY, USA, 2011. [Google Scholar]
- López-Iñesta, E.; Costa, D.G.; Grimaldo, F.; Vidal-Abarca Gámez, E. Read&Learn: Una herramienta de investigación para el aprendizaje asistido por ordenador [Read&Learn: A research tool for computer-assisted learning]. Magister Rev. Misc. Investig. 2018, 30, 21–28. Available online: https://doi.org/10.17811/msg.30.1.2018.21-28 (accessed on 1 May 2020).
- Romero, C.; Ventura, S.; García, E. Data mining in course management systems: Moodle case study and tutorial. Comput. Educ. 2008, 51, 368–384. [Google Scholar] [CrossRef]
- Sanz, M.T.; González-Calero, J.A.; Arnau, D.; Arevalillo-Herráez, M. Uso de la comprensión lectora para la construcción de un modelo predictivo del éxito de estudiantes de 4° de Primaria cuando resuelven problemas verbales en un sistema inteligente [Using reading comprehension to build a predictive model for the fourth-grade grade students’ achievement when solving word problems in an intelligent tutoring system]. Rev. Educ. 2019, 384, 41–69. [Google Scholar]
- Gašević, D.; Dawson, S.; Siemens, G. Let’s not forget: Learning analytics are about learning. TechTrends 2015, 59, 64–71. [Google Scholar] [CrossRef]
- Siemens, G.; Long, P. Penetrating the fog: Analytics in learning and education. EDUCAUSE Rev. 2011, 46, 30. [Google Scholar]
- Hernández-Lara, A.B.; Perera-Lluna, A.; Serradell-López, E. Applying learning analytics to students’ interaction in business simulation games. The usefulness of learning analytics to know what students really learn. Comput. Hum. Behav. 2019, 92, 600–612. [Google Scholar] [CrossRef]
- Wong, J.; Baars, M.; de Koning, B.B.; van der Zee, T.; Davis, D.; Khalil, M.; Houben, G.J.; Paas, F. Educational theories and learning analytics: From data to knowledge. In Utilizing Learning Analytics to Support Study Success; Springer: Berlin/Heidelberg, Germany, 2019; pp. 3–25. [Google Scholar]
- López-Iñesta, E.; Garcia-Costa, D.; Grimaldo, F.; Sanz, M.T.; Vila-Francés, J.; Forte, A.; Botella, C.; Rueda, S. Efecto de la Retroalimentación Orientada al Acierto: Un Caso de Estudio de Analítica del Aprendizaje [The Effect of Task-Oriented Feedback: A Learning Analytics Case Study]; Actas de las Jornadas sobre Enseñanza Universitaria de la Informática (JENUI), 2020; Volume 5, pp. 337–340. Available online: http://www.aenui.net/ojs/index.php?journal=actas_jenui&page=article&op=view&path%5B%5D=551 (accessed on 1 June 2020).
- MacLellan, C.J.; Liu, R.; Koedinger, K.R. Accounting for Slipping and Other False Negatives in Logistic Models of Student Learning. In Proceedings of the International Conference on Educational Data Mining (EDM), Madrid, Spain, 26–29 June 2015. [Google Scholar]
- Rasch, G. Studies in Mathematical Psychology: I. Probabilistic Models for some Intelligence and Attainment Tests; Danmarks pædagogiske Institut: Copenhagen, Denmark, 1960. [Google Scholar]
- Pitarque, A.; Roy, J.F.; Ruiz, J.C. Redes neurales vs modelos estadísticos: Simulaciones sobre tareas de predicción y clasificación [Neural network and statistical models: Simulations on prediction and classification tasks]. Psicológica 1998, 19, 387–400. [Google Scholar]
- Reed, S.K. A structure-mapping model for word problems. J. Exp. Psychol. Learn. Mem. Cogn. 1987, 13, 124. [Google Scholar] [CrossRef]
- Schwartz, J.L. The Role of Semantic Understanding in Solving Multiplication & Division Word Problems. Final Report; Division for Study & Research in Education, Massachusetts Institute of Technology: Cambridge, MA, USA, 1981. [Google Scholar]
- Kieren, T.E. (Ed.) The rational number construct: Its elements and mechanisms. In Recent Research on Number Learning; ERIC Clearinghouse for Science, Mathematics, and Environmental Education: Columbus, OH, USA, 1980; pp. 125–149. [Google Scholar]
- Hegarty, M.; Mayer, R.E.; Monk, C.A. Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers. J. Educ. Psychol. 1995, 87, 18. [Google Scholar] [CrossRef]
- Perera Dzul, P.B.; Valdemoros Álvarez, M.E. Enseñanza experimental de las fracciones en cuarto grado [Fraction experimental teaching in fourth grade]. Educ-Mat 2009, 21, 29–61. [Google Scholar]
- Gairín, J.; Múñoz, J.M. El Número Racional Positivo en la Práctica Educativa: Estudio de una Propuesta Editorial [The Rational Number in Educational Practice: The Examination of a Publisher Proposal]. IX Simposio SEIEM. 2005. Available online: https://www.seiem.es/docs/comunicaciones/GruposIX/pna/gairinmunoz.pdf (accessed on 1 June 2020).
- Hart, K.M. Ratio: Children’s Strategies and Errors: A Report of the Strategies and Errors in Secondary Mathematics Project; Nfer Nelson: Berkshire, UK, 1984. [Google Scholar]
- Sanz, M.T.; Figueras, O.; Gómez, B. Las fracciones, habilidades de alumnos de 15 a 16 años [Fractions, student’s skills from 15 to 16 years old]. Rev. Educ. Univ. Granada 2018, 25, 257–279. [Google Scholar]
- Sanz, M.T.; Valenzuela, C.; Figueras, O. “De lo que queda”, hacia un sistema tutorial inteligente [“What remains”, towards an intelligent tutorial system]. In Investigación en Educación Matemática XXIII; Sociedad Española de Investigación en Educación Matemática, SEIEM: Valladolid, Spain, 2019; p. 654. [Google Scholar]
- Ivars, P.; Fernández, C. Aprendiendo a mirar profesionalmente el pensamiento matemático de los estudiantes en el contexto de las prácticas de enseñanza. El papel de las narrativas [Learning to notice students’ mathematical thinking in the context of the teaching practices. The role of the narrative]. Ensayos. Rev. Fac. Educ. Albacete 2015, 30, 45–54. [Google Scholar]
- Garzón, E.; Sola, T.; Ortega, J.L.; A, M.J.; Gómez, G.E. Teacher Training in Lifelong Learning—The Importance of Digital Competence in the Encouragement of Teaching Innovation. Sustainability 2020, 12, 2852. [Google Scholar] [CrossRef]
- Rodríguez-García, A.M.; Aznar, I.; Cáceres, P.; Gomez, G. Digital competence in higher education: Analysis of the impact of scientific production indexed in Scopus database. Rev. Espacios 2019, 40, 14. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).