1. Introduction
Stability of delay systems has been examined intensively by the academics from the control community [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13], because several physical systems, like networked control systems, biological systems and chemical systems, are generally associated with time delays, [
14,
15,
16,
17,
18,
19]. Indeed, time delay can vary over time. For example, in real time communication and control systems, the signals are transmitted through the networks and subject to variable time delays because of the network traffic changes/uncertainties. In addition to that, when the parameters of the system are varied, the so-called phenomenal, Neimark–Sacker bifurcation, appears [
20]. Thus, stability analysis and control of such dynamical systems with variable parameters and time varying delays is essential. To attain stability conditions, two main strategies can be followed due to the time varying nature of the delay. Independent of delay (i.o.d) results are applicable when the size of the delay is arbitrary or if there is no information about the delay. This deficiency leads to conservative criteria, particularly if the delay is relatively small. When information about the size of delay can be included, less conservative delay-dependent (d.d) conditions can be provided [
21].
In the literature, many stability conditions for time delay systems are obtained by transforming the problem into a resolution of linear matrix inequalities (LMIs) [
22]. However, the size of these LMIs increases with order/complexity of the system and this is obviously a disadvantage of such a technique. That is why there is a need to develop methods that lead to verifying a few number of stability conditions, regardless of order/complexity of the system; that is what we try to do in this study, to determine easy to test stability conditions for nonlinear discrete time systems with time varying delay.
New delay dependent stability conditions are obtained by transforming the studied system under an arrow form state space representation [
9,
10,
11], using the Koteleyanski lemma [
23] and by applying Lyapunov functional technique and M-matrix properties. The main obtained result is simple, and in fact it consists of verifying a scalar condition, without the need of solving any LMIs. It allows a great freedom by a judicious choice of some scalar parameters. The obtained results can be applied to large class of systems. As an example of these systems, we may mention the famous Lure Postnikov system, see [
9] and the references therein. Moreover, we show how to use our method to design a state feedback controller that stabilizes a discrete time Lure system with time varying delay and sector bounded nonlinearity [
24,
25,
26,
27,
28,
29,
30,
31]. Note that this system is one of the most important classes of nonlinear control systems and remains one of the main problems in control theory which is intensively examined due to its various practical applications [
32,
33,
34,
35,
36,
37,
38].
This paper is organized as follows: the utilized notations, the definition of M-matrices as well as some preliminary results are described in
Section 2. The main results of this paper are represented in
Section 3. Subsequently, the utility of these results if applied to the well known Lure systems is shown in
Section 4. Finally, in
Section 5 and
Section 6, we provide some illustrative examples and a brief conclusion, respectively.
2. Preliminaries
We present, in this part, some preliminary results including some definitions and lemmas used in the proof of the main results. Let us first fix the notation used throughout this paper. The set of a real number is denoted by R, designates the set of non-negative integers, and denotes an dimensional linear vector space over the reals with the norm . The notations refer to the Euclidean vector norm or the induced matrix norm, as appropriate. Let denote the identity matrix and denote the transpose of matrix M. Matrices, if their dimensions are not explicitly stated, are assumed to have compatible dimensions.
To characterize an M matrix, several equivalent conditions are given in the below definitions:
Definition 1. , is an M-matrix if one of the following conditions is satisfied:
- 1.
; and the successive minors of M are positive.
- 2.
is called (−M)-matrix when is an M-matrix.
- 3.
If ; , and for any real vector , the algebraic equation: , has a solution .
The below two lemmas play an important role in the proof of the main results.
Lemma 1 (Kotelyanski lemma [23]).The real parts of the eigenvalues of a matrix M are inside the open disk of radius μ if and only if all those of the matrix , are positive. Remark 1. It is obvious, for , that if the matrix checks the Kotelyanski conditions, matrix is considered as an M-matrix.
Consider the following arrow form matrix , which will be used in the next sectionwhere , ; , . Lemma 2. Any matrix having the form presented in (1) is (−M)-matrix when the following conditions are satisfied: - 1.
- 2.
Proof. In case the matrix
is (-M)-matrix,
is an M-matrix. Based on Kotelyanski lemma and Remark 1, successive principal minors of
with positive signs yields to
,
. It comes the first condition of lemma. For
,
it comes,
which completes the proof. □
3. Main Results
The class of nonlinear delay systems studied in this manuscript are governed by the following difference equation:
where
y is the system output, and
denotes a time varying delay. In practice, the time delay may be unknown and can vary over time in a certain interval. It is thus assumed that
has an upper limit
so that
,
.
,
:
, are the nonlinear functions of the time
k,
and
,
,
…,
where
, and
is a connected domain of
. For ease of exposition, let
be the supremum of
calculated over
, where
can be any of
and
and their algebraic combination.
Define the state variables:
which leads to
System (
3) is reformulated as follows
Let
. The system (
3) can be re-written as
where
Apply the state transformation,
where
with
,
.
The system (
3) becomes
where
for any
and
We treat in the rest of this part the two cases of constant delay and variable delay.
3.1. Constant Delay Case
Before stating the main result, let us define the following matrix:
where
Theorem 1. The time delay system (3) with constant delay, , is asymptotically stable if there exist distinct real numbers, , , such that the following inequality holds true, Proof. Choosing a radially unbounded, positive definite Lyapunov function candidate such that
where
with
Because
, so that
. We obtain the difference
under the solution of (
8) as follows:
We notice that
therefore
and
Knowing that
and
the substitution of (
22) in (20) gives
it comes from (
18), (
22) and (20),
As nonlinear elements of
, in the last column, are isolated, we obtain constant eigenvector
relative to the eigenvalue
, where
is such that
[
9]. Then
if
is the opposite of an M−matrix.
In fact, by Definition 3, ∀
, the equation,
, has a solution. Let
this solution, it comes
. Then from (
23), we obtain:
Moreover,
,
, are arbitrary, we choose
with
,
. It is noted, from Lemmas 1 and 2, that when
is an
M-matrix. Thus, the proof is finished. □
3.2. Time Varying Delay Case
We take into account, in this sub-section, system
with time varying delay which satisfies the below condition:
where
,
and
.
, are the initial conditions. In this case, some modifications are carried on the matrix
to obtain the matrix
relative to
for stability condition.
where
with
Theorem 2. The time varying delayed system (3) is delay dependent asymptotically stable, if there exist distinct real numbers, , , such that the following inequality holds true Proof. Since
,
, are arbitrary, we choose
with
,
, so that
is an arrow form matrix
-matrix. Thus, it follows from Lemmas 1 and 2 that if
Let
be a constant vector so that
remains true for
. Therefore, we choose the radially unbounded, positive definite Lyapunov function candidate given below
where
with
Because
, so that
. The difference
under the solution of (
8) is given by
The overvaluation of
necessitates overvaluing of
. The difference below is first computed:
because
and since
, we have
and
It then follows from (
39)
which yields
Knowing that
this allows us to obtain
which yields
since
and the proof is completed. □
Remark 2. Note first that the advantage of Theorems 1 and 2 is its simple and scalar conditions, where no Linear Matrix Inequality is present to be solved the usually adopted method for solving such problems, see [27,28] and the references therein. It accommodates the parameter uncertainties. It allows great freedoms of a judicious choice of , .
Theorems 1 and 2 enable stability analysis for the discrete time systems with time delay, where the nonlinear elements of , , could be time-varying, including both the system’s coefficient functions, and ; and artificially introduced parameters, , .
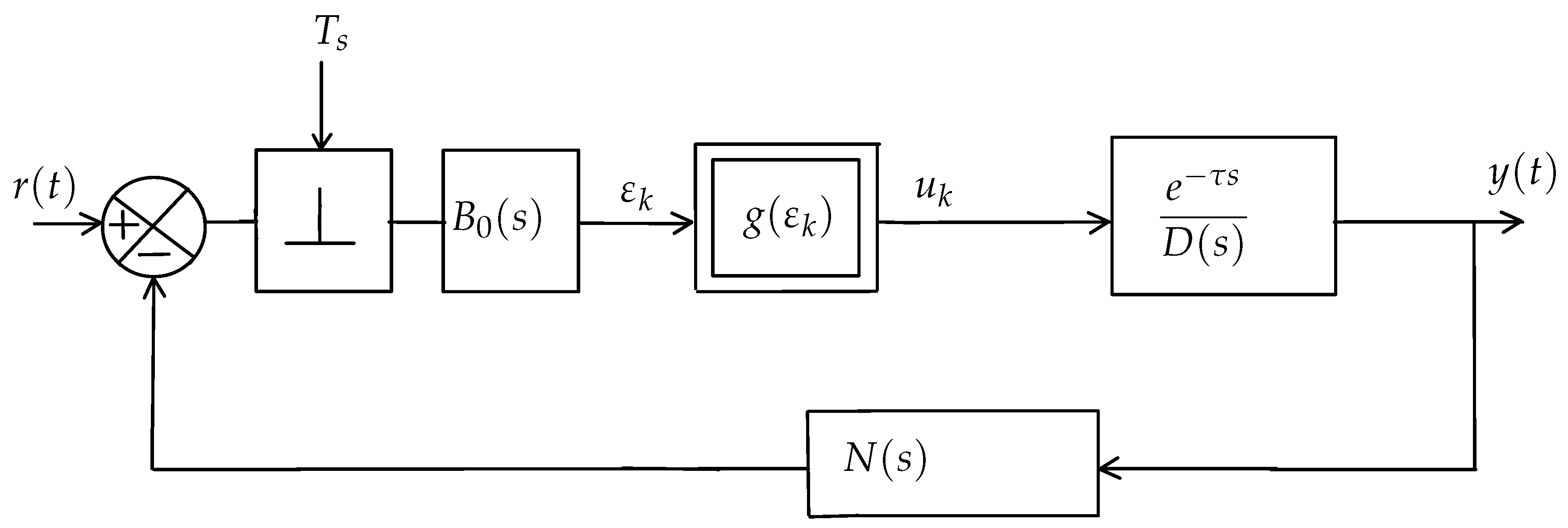
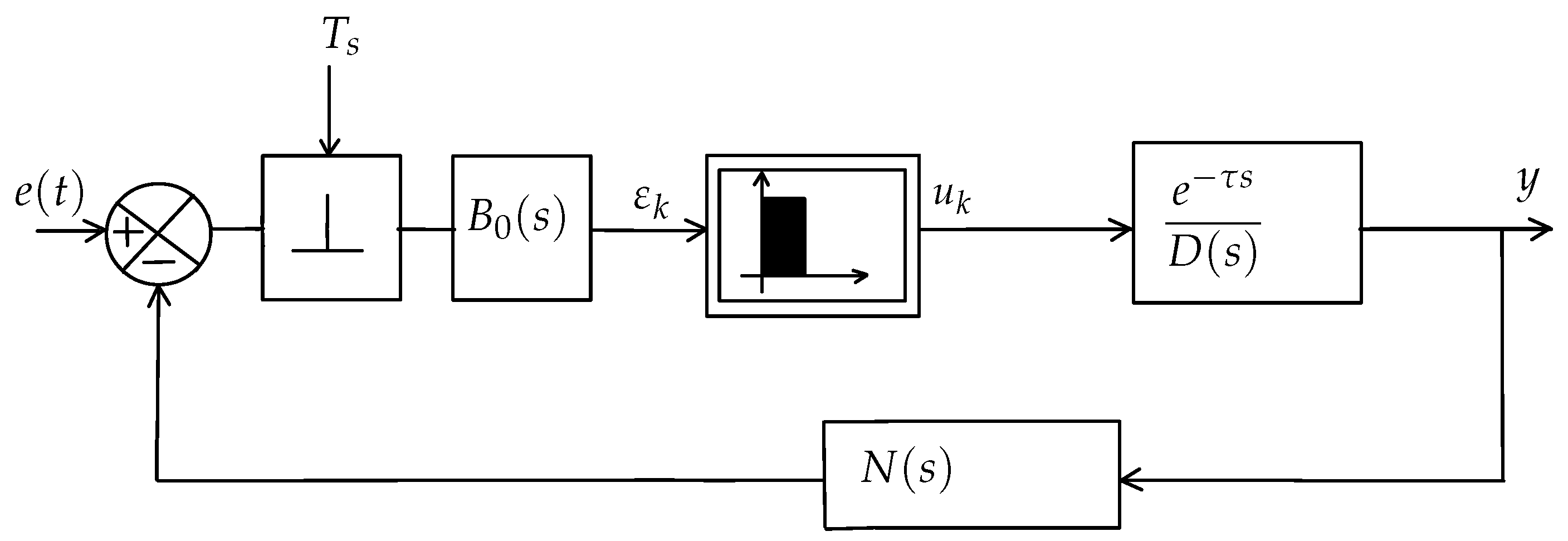
4. Application to Delayed Lure Systems
Consider the Lure type discrete time system presented in
Figure 1. The model consists of a static nonlinearity in cascade with a dynamic linear time delay system.
The structure of this system where only the variable
is nonlinearly modulated, allows us to investigate the Lure type discrete-time system by the following nonlinear regression equation:
Setting the following variable:
with the following notation:
Applying Theorem 1 leads to sufficient condition of the same form (
12), but depending on
. The obtained results are often difficult to implement, furthermore its interpretations with respect to the linear and nonlinear characteristics of the studied processes are generally limited. These considerations are due to the fact that the matrix description, from which the study is conducted, comes with a base change. The choice of a prior representation of Frobenius type allows to set similar to the previous stability conditions in which the coefficients depend only
. By introducing the following variable changes,
and by choosing the state vector
the corresponding expression in terms of state space representation (
41) becomes:
where:
and
This system is particular case of (
3) where
, and
where
,
, where
is a function satisfying the sector bound condition,
is the Z transform and
z the complex variable of this transformation,
is a zero order holder,
the sampling time and
the time delay.
4.1. Sufficient Stability Conditions: Autonomous Case
Let us first consider the autonomous case (
). The obtained system is a special case of (
3) where
,
∀
,
and
. The following change of coordinates is employed:
where
The transformation results in the following system
where
and
A sufficient stability condition for this system is given in the following theorem.
Theorem 3. The Lure type discrete-time system presented in Figure 1 is (i.o.d) asymptotically stable, if there exist distinct real numbers, , , such that the following inequality holds true Remark 3. L. Hou et al. in [37] established ultimate boundedness results for PWM feedback systems which can be considered a particular case of Theorem 1 when is considered as function. They show that the solutions are ultimately bounded only when system is Hurwitz stable. Our result stated in Theorem 3 is obviously more general because it remains true when the system contains one unstable root and with delay. If has all its roots such that , and , then condition of Theorem 3 simplifies considerably. The following corollary gives this simplified condition. Corollary 1. The Lure type discrete-time system presented in Figure 1 is (i.o.d) asymptotically stable, if there exist distinct real numbers, , , such that the following inequality holds true , and Proof. It is sufficient to take in the condition of Theorem 3, in this case . Another important condition can be obtained when admits distinct roots with module inside the unit circle and the nth root can be outside the unit circle. This condition is given by the following corollary. □
Corollary 2. The Lure type discrete-time system presented in Figure 1 is (i.o.d) asymptotically stable, if there exist distinct real numbers, , , such that the following inequality holds true Proof. It is sufficient to take equal to the roots of that are inside the unit circle. In this case terms in condition of Theorem 3 becomes and . □
Remark 4. The last condition can also be simplified. In fact, if the roots of verify , and , we obtain a new simple condition given by the following corollary.
Corollary 3. If the conditions of Corollary 3 and Remark 4 are satisfied the system is stable if the following condition is satisfied: Proof. Assuming that , and are satisfied then one can remark that , and knowing that then the result of corollary is obtained. □
4.2. Feedback Stabilization
In this case, take
with
, then the obtained system has the same form as (
3), with
The stabilizing values of K can be obtained by making the following changes: , and . Then a sufficient stability condition for this system is given in the following theorem.
Theorem 4. The Lure type discrete time system presented in Figure 1 is stabilizable via feedback control gain K, if there exist distinct real numbers, , , such that the vector gain satisfies the following inequality Remark 5. The above result of Theorem 4 gives an explicit way how to calculate the stabilizing values of the feedback gain vector K.
5. Examples
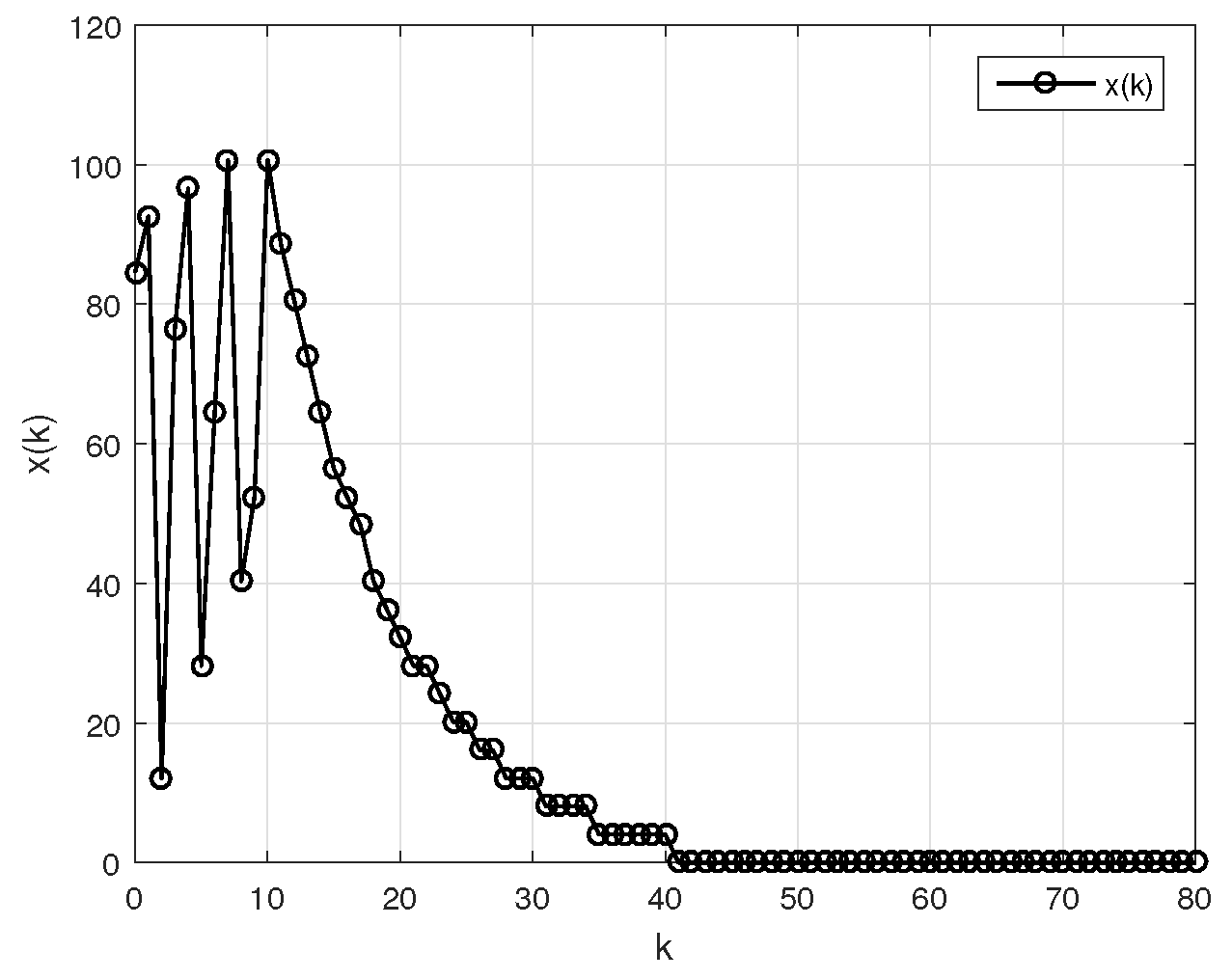
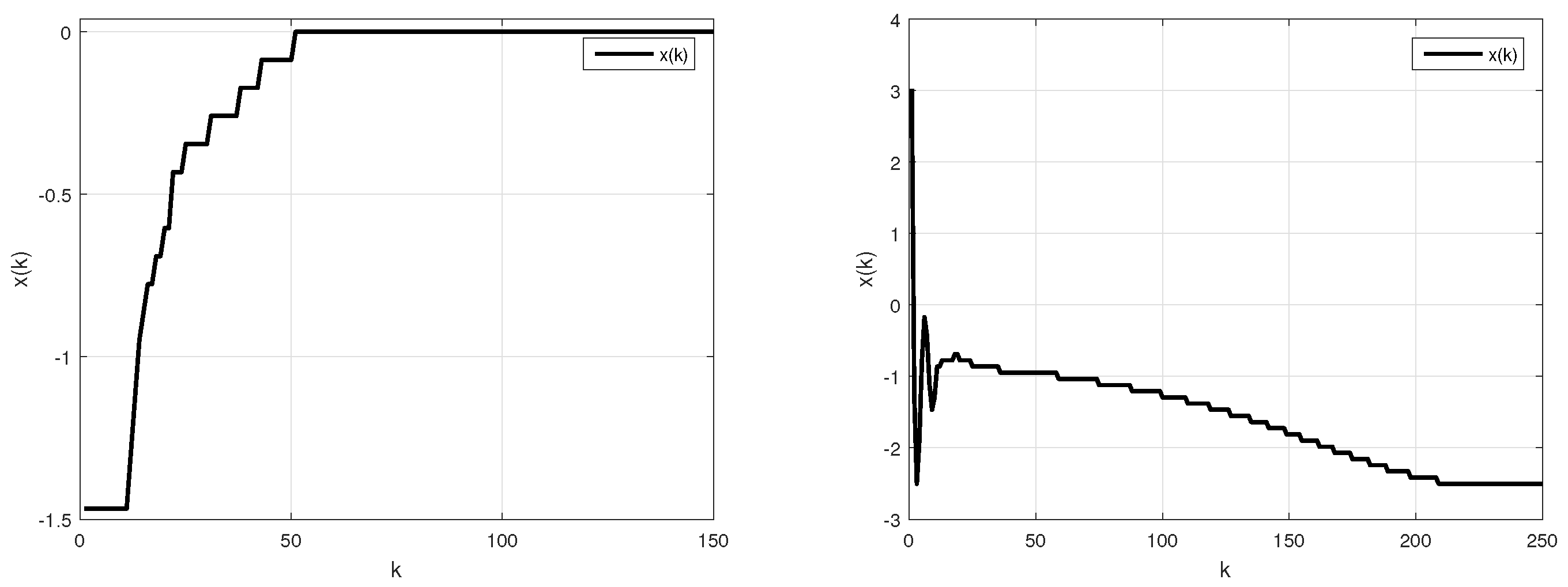
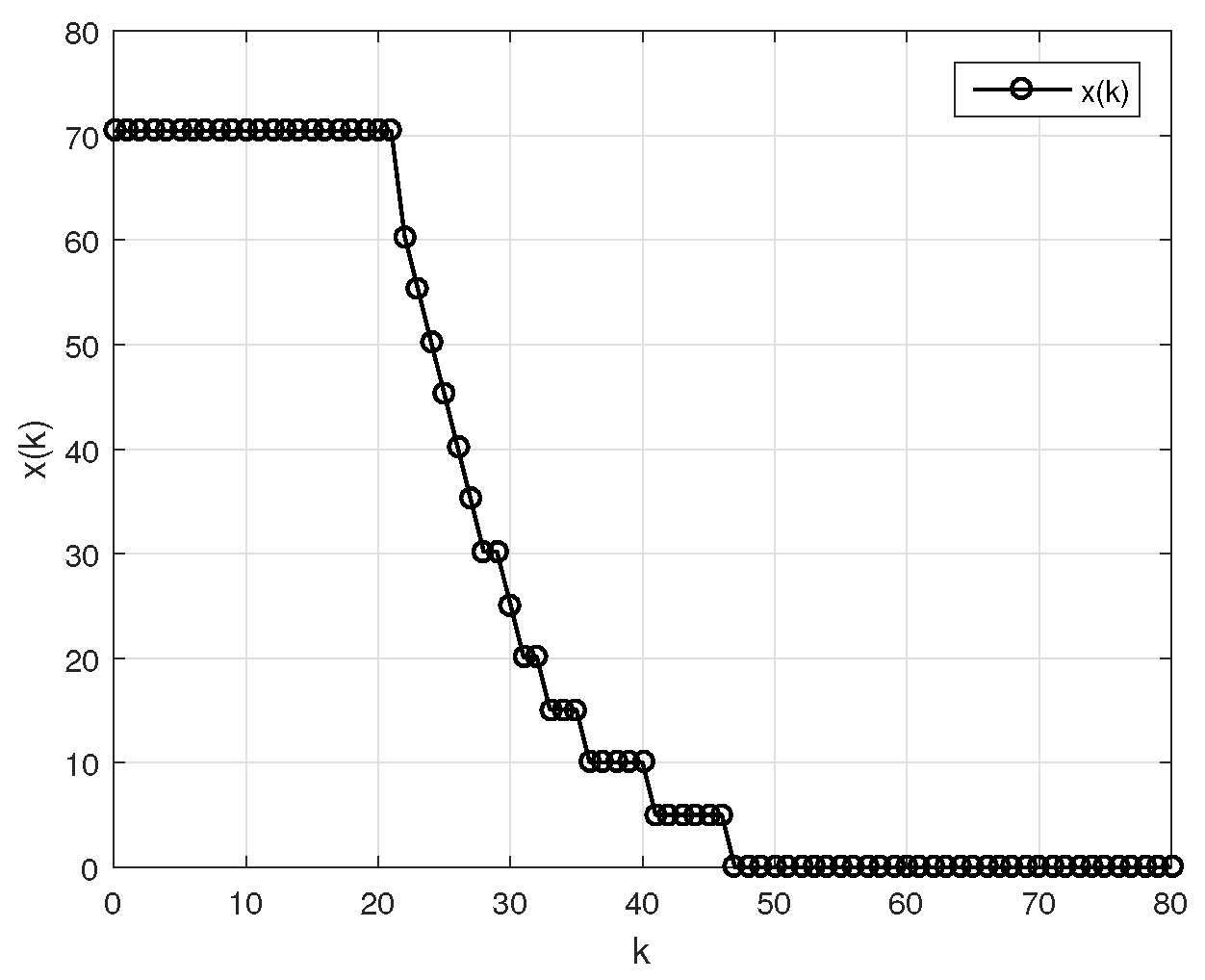
Example 1. In order to compare the different obtained results, we consider the linearized Clark equation with variable delay (the usual situation in its applications to population dynamics), that is,where . Using Theorem 2, and choosing yields and and the stability condition is;orif the delay is constant the last condition becomes: For and from (57) we have . Taking for example , the dynamic evolution of for an initial condition is given in Figure 2 for k = 70 and in Figure 3 and Figure 4 respectively for k=150 and k=250 Example 2. Consider the example in [29]where , and , are constants and satisfies the following conditionwith and are nonnegative constants. In this example we havewhere In our case, has real roots , . We can consider . Hence, choosing and , we get , , . Using Theorem 1, the stability condition for this system is given by: Knowing that , the above yieldswhich can be re-written as the following form Example 3. Consider the example in [27] with added complexity: the interconnection between the nonlinear part and the linear part has a time delay h. In this case, the state space of the system is evaluated as Now, the use of Theorem 3 leads to the following sector bound conditionwhich is equivalent to One can conclude that the origin of the considered example is globally asymptotically stable for any nonlinearity φ belonging to the sector which is larger than given in [27]. Example 4. Consider the study of a DC motor controlled by pulse width modulation from a tachometer given by Figure 5. The control pulses are rectangular, with a constant amplitude equal to and the sign of the error signal is defined at the sampling instants. Let be the sampling time, be the duration of the impulse in unsaturated regime and , be the time constants of the DC motor. The output of the modulator is a sequence of pulses of height and the width of the control pulses is related to the error function at the sampling instants by a relationship of the form:or simply under the following relation:where From which, we can havewhere and . The choice of yields . By Theorem 3, the stability condition in this particular case is given bywhere . A simple calculation leads to the following equalities: and .
Now, let , it comes Because and taking into account of (62) we obtain , which gives The above-mentioned results are shown in Figure 6. 6. Conclusions
This study addresses stability checking of nonlinear discrete time systems with time varying delay. By using aggregation techniques and the M-matrix approach, new explicit and easy to check, stability conditions are determined. An advantage of the proposed approach is that it avoids transforming the problem into a Linear Matrix Inequalities (LMI). The proposed approach is then applied to discrete time Lure systems with time varying delay and sector bounded nonlinearity.
Author Contributions
Both authors have contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of a Tunisian-South African cooperation scientific research project. We thank the Ministry of Higher Education and Scientific Research of Tunisia that has supported this research. Qing-Guo WANG acknowledges the financial support of the National Research Foundation of South Africa (Grant Numbers: 113340, 120106), which partially funded his research on this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, M.F.; Gao, Z.S. Entire solutions of certain type of nonlinear differential equations and differential-difference equations. J. Comput. Anal. Appl. 2018, 24, 137–147. [Google Scholar]
- Pekar, L.; Gao, Q. Spectrum analysis of LTI continuous-time systems with constant delays: A literature overview of some recent results. IEEE Access 2018, 6, 35457–35491. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Xi, Q.; Duan, P. Review of stability and stabilization for impulsive delayed systems. Math. Biosci. Eng. 2018, 15, 1495–1515. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Song, S. Effect of delayed impulses on input-to-state stability of nonlinear systems. Automatica 2017, 76, 378–382. [Google Scholar] [CrossRef]
- Kurulay, G.; Ozbay, H. Design of first order controllers for a flexible robot arm with time delay. Appl. Comput. 2017, 16, 48–58. [Google Scholar]
- Li, X.; Song, S. Stabilization of delay systems: Delay-dependent impulsive control. IEEE Trans. Automat. Control 2017, 62, 406–411. [Google Scholar] [CrossRef]
- Kang, W.; Zhong, S.; Shi, K.; Cheng, J. Finite-time stability for discrete-time systems with time varying delay and nonlinear perturbations. ISA Trans. 2016, 60, 67–73. [Google Scholar] [CrossRef]
- Liu, P.L. Delayed decomposition appraoch to the robust absolute stability of a Lure control system with time varying delay. Appl. Math. Model. 2016, 40, 2333–2345. [Google Scholar] [CrossRef]
- Elmadssia, S.; Saadaoui, K.; Benrejeb, M. New stability conditions for nonlinear time varying delay systems. Int. J. Syst. Sci. 2016, 47, 2009–2021. [Google Scholar] [CrossRef]
- Elmadssia, S.; Saadaoui, K.; Benrejeb, M. New delay-dependent stability conditions for linear systems with delay. Syst. Sci. Control Eng. Open Access J. 2013, 1, 2–11. [Google Scholar] [CrossRef]
- Elmadssia, S. New Stability Approaches of Time Delay Systems: Stability and Stabilization: Francophone; Academic Press: Berlin, Germany, 2012. [Google Scholar]
- Malek-Zavarei, M.; Jamshidi, M. Time-Delay Systems: Analysis, Optimization and Applications; North-Holland: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Bellman, R.; Cooke, K.L. Differential—Difference Equations; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Magdi, S.M.; Mutaz, M.H.; Uthman, A.B. Modeling and control of Cyber-Physical Systems subject to cyber attacks: A survey of recent advances and challenges. Neurocomputing 2019, 338, 101–115. [Google Scholar]
- Magdi, S.M.; Yuanqing, X. Networked Control Systems: Cloud Control and Secure Control; Elsevier: Oxford, UK, 2019. [Google Scholar]
- Wang, Q.; Lam, J.; Xu, S.; Gao, H. Delay-dependent and delay-independent energy-to-peak model approximation for systems with time varying delay. Int. J. Syst. Sci. 2005, 36, 445–460. [Google Scholar] [CrossRef]
- Park, J.H.; Tang, Z.; Feng, J. Pinning Cluster Synchronization of Delay-Coupled Lur’e Dynamical Networks in A Convex Domain. Nonlinear Dyn. 2017, 89, 623–638. [Google Scholar] [CrossRef]
- Alquran, M.; Al-Khaled, K.; Chattopadhyay, J. Analytical solutions of fractional population diffusion model: Residual power series. Nonlinear Stud. 2015, 22, 31–39. [Google Scholar]
- Györi, I.; Ladas, G. Oscillation Theory of Delay Differential Equations with Applications; Clarendon Press: New York, NY, USA, 1991. [Google Scholar]
- He, Z.; Lai, X.; Hou, A. Stability and Neimark-Sacker bifurcation of numerical discretization of delay differential equations. Chaos Solitons Fractals 2009, 41, 2010–2017. [Google Scholar] [CrossRef]
- Richard, J.P. Time-delay systems: An overview of some recent advances and open problems. Automatica 2003, 39, 1667–1694. [Google Scholar] [CrossRef]
- Fridman, E. Discrete-Time Delay Systems: Introduction to Time-Delay Systems, Systems & Control: Foundations & Applications; Birkhauser: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Kotelyanski, D.M. Some properties of matrices with positive elements. Mat. Sb. 1952, 31, 497–506. [Google Scholar]
- Čermák, J.; Jánský, J. Stability switches in linear delay difference equations. Appl. Math. Comput. 2014, 243, 755–766. [Google Scholar]
- González, A. Robust stabilization of linear discrete-time systems with time varying input delay. Automatica 2013, 49, 2919–2922. [Google Scholar] [CrossRef]
- Diblík, J.; Ružičková, M.; Šutá, Z. Asymptotic convergence of the solutions of a discrete equation with several delays. Appl. Math. Comput. 2012, 218, 5391–5401. [Google Scholar]
- Carlos, A.C.G.; Marc, J.; Jamal, D. Stability analysis of discrete-time Lur’e systems. Automatica 2012, 48, 2277–2283. [Google Scholar]
- Kwang, K.; Kevin, K.; Richard, D.B. Stability Analysis of Discrete-time Lur’e Systems with Slope-restricted Odd Monotonic Nonlinearities. arXiv 2015, arXiv:1509.01302. [Google Scholar]
- Rigoberto, M. Aizerman’s problem for nonlinear discrete-time control systems. J. Differ. Equ. Appl. 2011, 17, 299–308. [Google Scholar]
- He, Y.; Wu, M.; She, J.-H.; Liu, G.-P. Robust stability for delay Lure control systems with multiple nonlinearities. J. Comput. Appl. Math. 2005, 176, 371–380. [Google Scholar] [CrossRef]
- Gil, M.I. On Aizerman-Myshkis problem for systems with delay. Automatica 2000, 36, 1669–1673. [Google Scholar] [CrossRef]
- Liu, B. Stability of solutions for stochastic impulsive systems via comparison approach. IEEE Trans. Autom. Control 2008, 53, 2128–2133. [Google Scholar] [CrossRef]
- Barrado, A.; Olias, E.; Lazaro, A.; Pleite, J.; Vazquez, R. PWM-PD multiple output DC/DC converters: Operation and control-loop modeling. IEEE Trans. Power Electron. 2004, 19, 140–149. [Google Scholar] [CrossRef]
- He, Y.; Wu, M. Absolute stability for multiple delay general Lure control systems with multiple nonlinearities. J. Comput. Appl. Math. 2003, 159, 241–248. [Google Scholar] [CrossRef]
- Han, Q.L. Absolute stability of time-delaysy stems with sector-bounded nonlinearity. Automatica 2005, 41, 2171–2176. [Google Scholar] [CrossRef]
- Datta, K. Stability of pulse-width-modulated feedback systems. Int. J. Control 1972, 16, 977–983. [Google Scholar] [CrossRef]
- Hou, L.; Michel, A.N. Stability analysis of pulse-width-modulated feedback systems. Automatica 2001, 37, 1335–1349. [Google Scholar] [CrossRef]
- Balestrino, A.; Eisinberg, A.; Sciavicco, L. A generalized approach to the stability analysis of PWM feedback control systems. J. Frankl. Inst. 1974, 298, 45–58. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).