Nonlinear Position Control Using Differential Flatness Concept with Load Torque Observer for Electro Hydraulic Actuators with Sinusoidal Load Torque
Abstract
1. Introduction
- The proposed method improves the position tracking performance under the sinusoidal load torque in EHAs.
- The proposed position controller is designed with the consideration of the EHS dynamics.
- The proposed load torque observer is designed to estimate the load torque without considering its maximum frequency.
2. Modeling
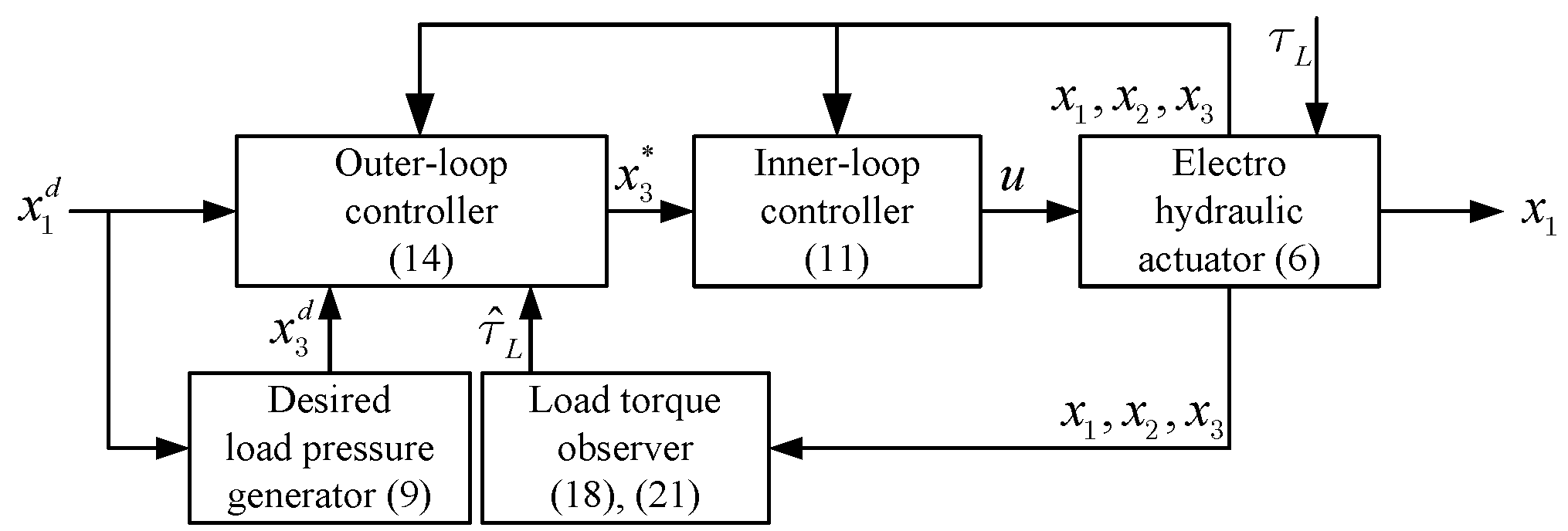
3. Controller Design
3.1. Position Controller
3.2. Load Torque Observer
3.3. Stability Analysis of the Closed-Loop System
4. Simulations
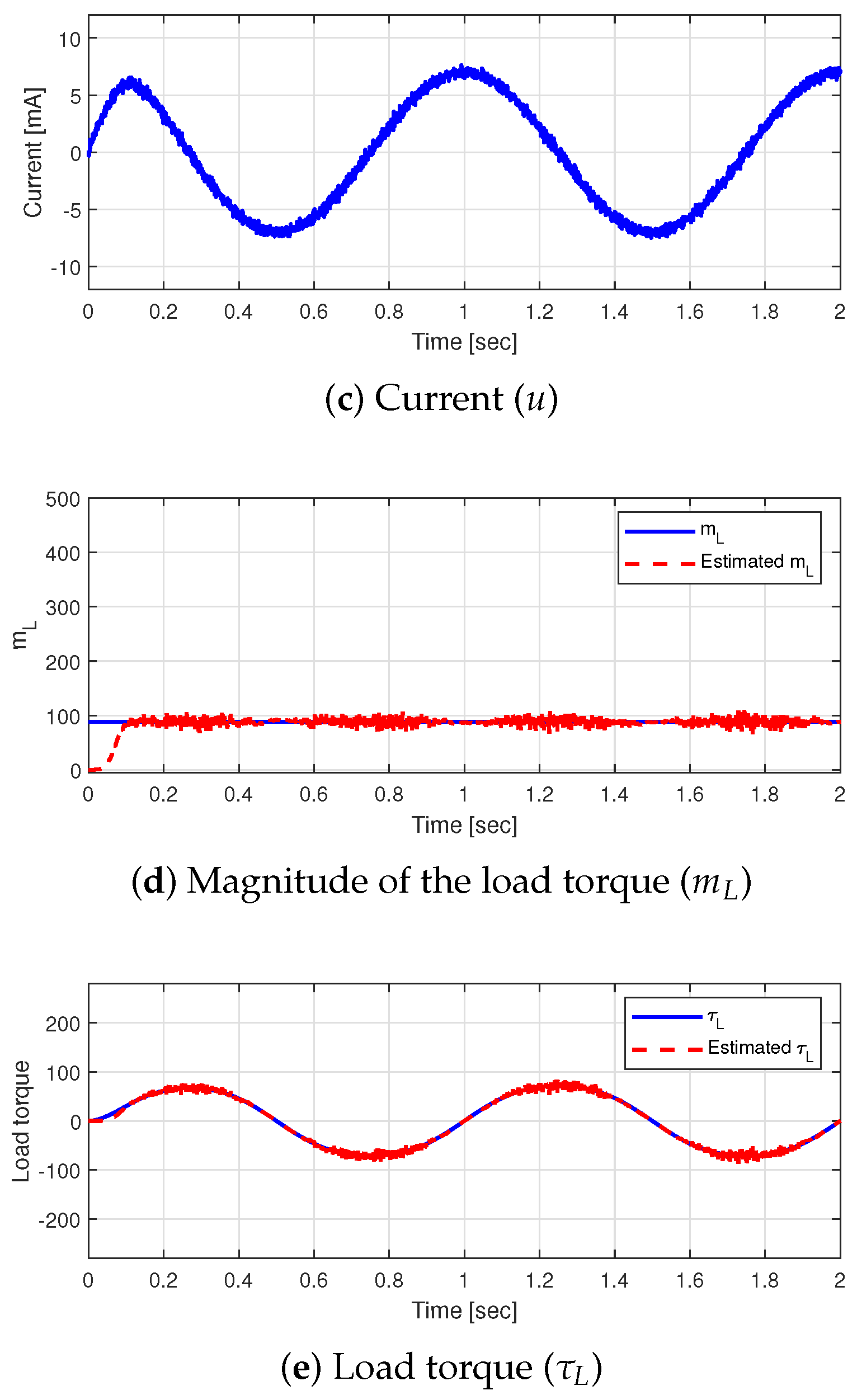
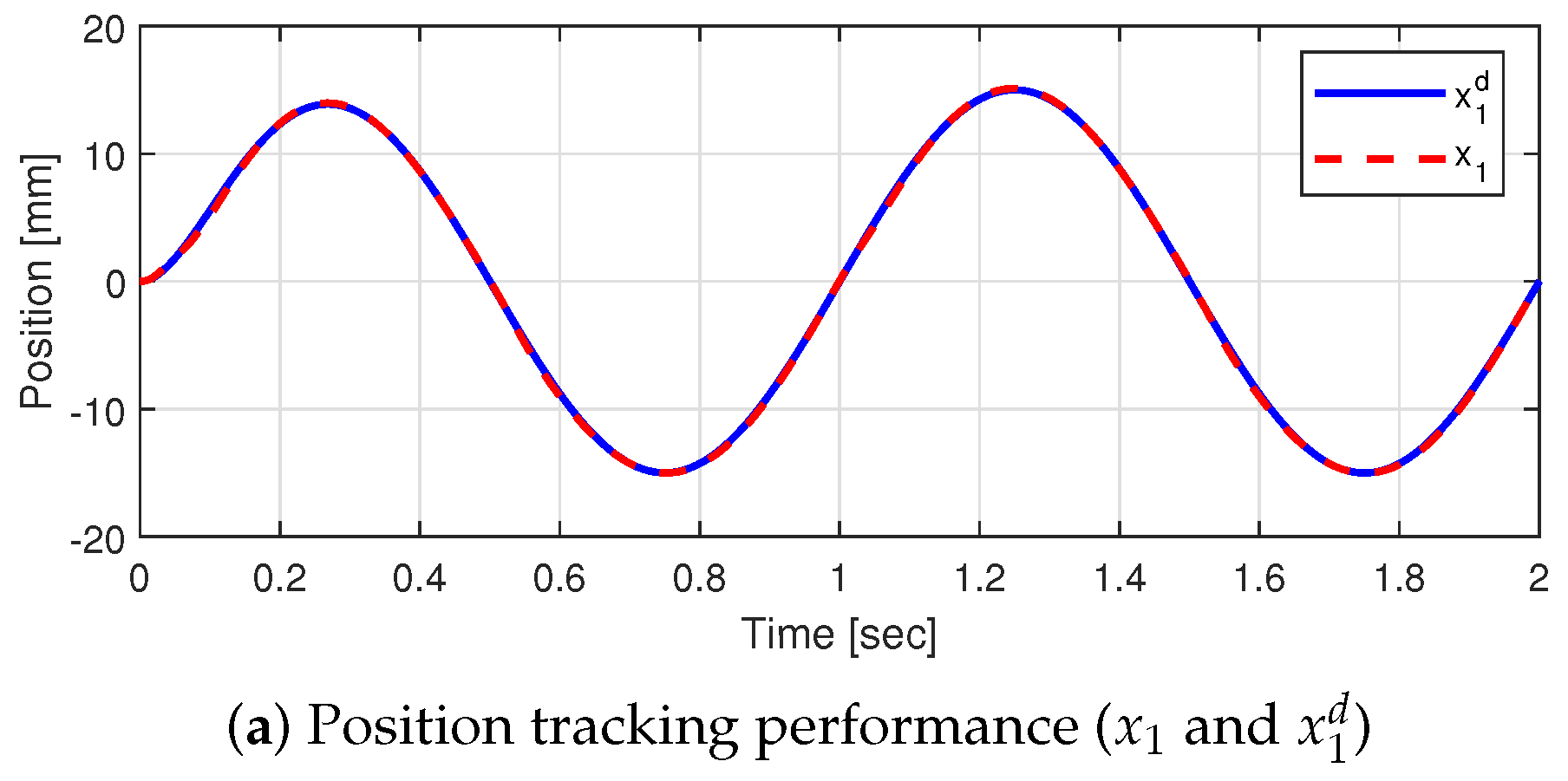
4.1. Case 1
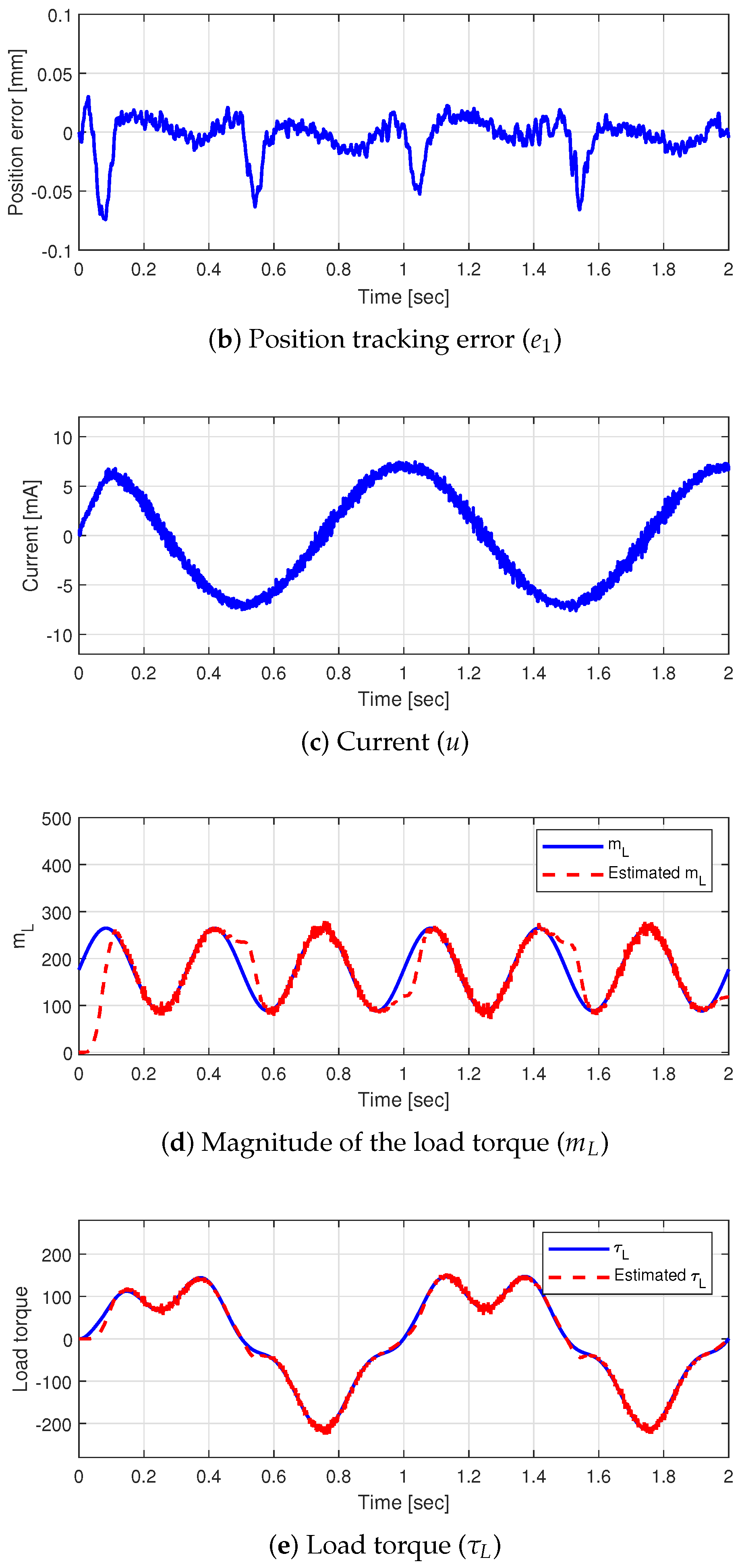
4.2. Case 2
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Merrit, H.E. Hydraulic Control System; Wiley and Sons: New York, NY, USA, 1967. [Google Scholar]
- Chen, T.; Wu, Y. An optimal variable structure control with integral compensation for electrohydraulic position servo control systems. IEEE Trans. Ind. Elec. 1992, 39, 460–463. [Google Scholar] [CrossRef]
- Jerouane, M.; Lamnabhi-Lagarrigue, F. A new sliding mode controller for a hydraulic actuators. In Proceedings of the Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 908–913. [Google Scholar]
- Bonchis, A.; Corke, P.I.; Rye, D.C.; Ha, Q.P. Variable structure methods in hydraulic servo systems control. Automatica 2001, 37, 589–595. [Google Scholar] [CrossRef]
- Li, Y.; He, L. Counterbalancing speed control for hydrostatic drive heavy vehicle under longdown-slope. IEEE/ASME Trans. Mechatron. 2015, 20, 1533–1542. [Google Scholar] [CrossRef]
- Hahn, H.; Piepenbrink, A.; Leimbach, K.-D. Input/output linearization control of an electro servo-hydraulic actuator. In Proceedings of the IEEE 1994 Conference on Control Applications, Glasgow, UK, 24–26 August 1994; pp. 995–1000. [Google Scholar]
- Vossoughi, G.; Donath, M. Dynamic feedback linearization for electrohydraulically actuated control systems. J. Dyn. Syst. Meas. Control 1995, 117, 468–477. [Google Scholar] [CrossRef]
- Eryilmaz, B.; Wilson, B.H. Improved Tracking Control of Hydraulic Systems. J. Dyn. Syst. Meas. Control 2001, 123, 457–462. [Google Scholar] [CrossRef]
- Ayalew, B.; Kulakowski, B.T. Cascade tuning for nonlinear position control of an electro-hydraulic actuator. In Proceedings of the IEEE 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 4627–4632. [Google Scholar]
- Alleyne, A.; Liu, R. Systematic control of a class of nonlinear systems with application to electrohydraulic cylinder pressure control. IEEE Trans. Control Syst. Technol. 2000, 8, 623–634. [Google Scholar] [CrossRef]
- Yao, B.; Bu, F.; Reedy, J.; Chiu, G.T.-C. Adaptive robust motion control of single-rod hydraulic actuators: Theory and experiments. IEEE/ASME Trans. Mechatron. 2000, 5, 79–91. [Google Scholar]
- Kaddissi, C.; Kenné, J.; Saad, M. Identification and real-time control of an electrohydraulic servo system based on nonlinear backstepping. IEEE/ASME Trans. Mechatron. 2007, 12, 12–22. [Google Scholar] [CrossRef]
- Zeng, H.; Sepehri, N. Tracking control of hydraulic actuators using a LuGre friction model compensation. ASME J. Dyn. Syst. Meas. Control 2008, 120, 014502. [Google Scholar] [CrossRef]
- Guan, C.; Pan, S. Nonlinear adaptive robust control of single-rod electro-hydraulic actuator with unknown nonlinear parameters. IEEE Trans. Control Syst. Technol. 2008, 16, 434–445. [Google Scholar] [CrossRef]
- Kim, W.; Won, D.; Shin, D.; Chung, C.C. Output feedback nonlinear control for electro-hydraulic systems. Mechatronics 2012, 22, 766–777. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Tomizuka, M. High gain observer based integral sliding mode control for position tracking of electro-hydraulic systems. IEEE/ASME Trans. Mechatron. 2017, 22, 2695–2704. [Google Scholar] [CrossRef]
- Wrat, G.; Ranjan, P.; Bhola, M.; Mishra, S.K.; Das, J. Position control and performance analysis of hydraulic system using two pump-controlling strategies. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 233, 1093–1105. [Google Scholar] [CrossRef]
- Imani, M.; Ghoreishi, S.F.; Braga-Neto, U.M. Bayesian control of large MDPs with unknown dynamics in data-poor environments. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 8146–8156. [Google Scholar]
- Banerjee, S.; Samynathan, B.; Abraham, J.; Chatterjee, A. Real-time error detection in nonlinear control systems using machine learning assisted state-space encoding. IEEE Trans. Depend. Secur. Comput. 2019. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Shin, D.; Chung, C.C. High gain disturbance observer based backstepping control with output tracking error constraint for electro-hydraulic systems. IEEE Trans. Control Syst. Technol. 2015, 23, 787–795. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, M.Y.; Celler, B.G.; Su, S.W. Backstepping control of electro-hydraulic system based on extended-state-observer with plant dynamics largely unknown. IEEE Trans. Ind. Electron. 2016, 63, 6909–6920. [Google Scholar] [CrossRef]
- Wang, C.; Quan, L.; Zhang, S.; Meng, H.; Lan, Y. Reduced-order model based active disturbance rejection control of hydraulic servo system with singular value perturbation theory. ISA Trans. 2017, 67, 455–465. [Google Scholar] [CrossRef] [PubMed]
- Won, D.; Kim, W.; Tomizuka, M. Nonlinear control with high gain extended state observer for position tracking of electro-hydraulic systems. IEEE/ASME Trans. Mechatron. 2020. [Google Scholar] [CrossRef]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suh, S.; Kim, W. Nonlinear Position Control Using Differential Flatness Concept with Load Torque Observer for Electro Hydraulic Actuators with Sinusoidal Load Torque. Mathematics 2020, 8, 1484. https://doi.org/10.3390/math8091484
Suh S, Kim W. Nonlinear Position Control Using Differential Flatness Concept with Load Torque Observer for Electro Hydraulic Actuators with Sinusoidal Load Torque. Mathematics. 2020; 8(9):1484. https://doi.org/10.3390/math8091484
Chicago/Turabian StyleSuh, Sangmin, and Wonhee Kim. 2020. "Nonlinear Position Control Using Differential Flatness Concept with Load Torque Observer for Electro Hydraulic Actuators with Sinusoidal Load Torque" Mathematics 8, no. 9: 1484. https://doi.org/10.3390/math8091484
APA StyleSuh, S., & Kim, W. (2020). Nonlinear Position Control Using Differential Flatness Concept with Load Torque Observer for Electro Hydraulic Actuators with Sinusoidal Load Torque. Mathematics, 8(9), 1484. https://doi.org/10.3390/math8091484





