Mathematical Model of Decomposition of Methane Hydrate during the Injection of Liquid Carbon Dioxide into a Reservoir Saturated with Methane and Its Hydrate

Abstract

The article describes a mathematical model of pumping of heated liquid carbon dioxide into a reservoir of finite extent, the pores of which in the initial state contain methane and methane gas hydrate. This model takes into account the existence in the reservoir of three characteristic regions. We call the first region “near”, the second “intermediate”, and the third “far”. According to the problem statement, the first region contains liquid CO₂ and hydrate, the second region is saturated with methane and water, the third contains methane and hydrate. The main features of mathematical models that provide a consistent description of the considered processes are investigated. It was found that at sufficiently high injection pressures and low pressures at the right reservoir boundary, the boundary of carbon dioxide hydrate formation can come up with the boundary of methane gas hydrate decomposition. It is also shown that at sufficiently low values of pressure of injection of carbon dioxide and pressure at the right boundary of the reservoir, the pressure at the boundary of hydrate formation of carbon dioxide drops below the boiling pressure of carbon dioxide. In this case, for a consistent description of the considered processes, it is necessary to correct the mathematical model in order to take into account the boiling of carbon dioxide. Maps of possible solutions have been built, which show in what ranges of parameters one or another mathematical model is consistent.

1. Introduction

The researchers’ attention is focused on the study of the properties and characteristics of hydrate production in connection with virtually untouched deposits [1,2,3]. Currently, the main methods of gas production from gas hydrate deposits are the following: pressure reduction at the production well bottom, reservoir heating or injection of inhibitors [3,4,5]. Often the use of these methods of extraction is not economically feasible and may also have an adverse environmental impact [3,4,5,6]. In this regard, a new method of natural gas production was proposed, consisting in the injection of carbon dioxide into natural deposits of gas hydrates [7,8,9,10,11,12,13]. Also, the problem of CO₂ utilization can be solved by using this method.

According to experimental data, the transition of CH₄ hydrate to CO₂ hydrate during carbon dioxide injection can occur in two different modes [14,15,16,17]. A characteristic feature of the first mode is the absence of free water release. In the second mode, there is an intermediate zone of methane hydrate dissociation to water and gas, and the subsequent formation of CO₂ hydrate from water and carbon dioxide. In this case, the released heat can accelerate the decomposition of methane gas hydrate. Experiments were carried out to study the formation of CO₂ hydrates in [18,19,20,21,22]. It should be noted that experimental works, which study these processes, were carried out in examples of small size. Due to the small size of the samples, the processes of formation and decomposition of gas hydrate are limited by kinetic mechanisms. The possibility of replacement of CH₄ by CO₂ in gas hydrate upon the injection of carbon dioxide is due to the negative value of the Gibbs free energy of this reaction (i.e., the negative value of the change in the Gibbs free energy) [23]. The thermodynamic conditions of the CH₄–CO₂ replacement reaction are maintained even without the additional influence of external factors. For cases when natural reservoirs of real length are considered, the limitation of formation of gas hydrate CO₂ and decomposition of CH₄ gas hydrate are determined not by the kinetics of the phase transition processes, but by heat and mass transfer in the reservoir, as well as the release and absorption of heat during phase transitions. These do not allow comparing the results of mathematical modeling of the formation and decomposition of gas hydrates in extended natural reservoirs with the experimental data available to date. Therefore, in our opinion, it is necessary to examine mathematical models describing the studied processes.

There are works devoted to mathematical modeling of the development of gas hydrate deposits by injection of CO₂. In [24,25,26,27], approximate analytical solutions are given for replacing CH₄ hydrate with CO₂ when CO₂ is injected into a reservoir. In these works, self-similar solutions for a semi-infinite reservoir are constructed. These self-similar solutions can adequately describe only the initial process. The solution is consistent only until the pressure perturbation reaches the reservoir right boundary. In the future, over time, the effect on the course of the process will completely depend on the conditions on the right boundary. In [28], the case of mathematical modeling of CO₂ injection in a gaseous state into a natural reservoir containing methane and its gas hydrate was considered. A similar problem was considered in [29], but instead of CO₂ in the gaseous state, carbon dioxide in the liquid state was supplied. However, in [29], only the case when the recovery of methane from the hydrate occurs in the replacement mode and is not accompanied by dissociation of methane gas hydrate is studied in detail. In the present work, unlike in [29], the injection mode of liquid CO₂ reservoir into a gas hydrate of finite length, accompanied by dissociation of CH₄ gas hydrate and the subsequent formation of CO₂ hydrate, is studied in detail.

In [29], only the case when a direct transition of methane hydrate to carbon dioxide hydrate occurs in a reservoir is studied in detail. In contrast to [29], the presented work considers another physical process. Namely, the case is considered when methane gas hydrate decomposes first to gas and water (at the far boundary of phase transitions), and then carbon dioxide gas hydrate is formed from the released water and injected carbon dioxide. Since in [29] and in the presented work two different physical processes are considered, the mathematical description of these processes is also different. For example, in [29], one moving boundary of phase transitions is considered, dividing the reservoir into two zones. Two different systems of differential equations correspond to the mathematical description of the processes of heat and mass transfer in these two zones. At the boundary separating these two zones, a system of differential equations is written, which follows from the conditions for the balances of mass and heat. In contrast to [29], the presented work considers two moving boundaries of phase transitions, dividing the reservoir into three zones. Three different systems of differential equations correspond to the mathematical description of the processes of heat and mass transfer in these three zones. On the two boundaries of the phase transitions separating these three zones, two different systems of differential equations are written, arising from the conditions for the balances of mass and heat.

The main purpose of the presented work is to study the main features of mathematical models that provide a consistent description of the considered processes. This is due to the lack of a clear understanding of even the qualitative features of the behavior of the system when injecting carbon dioxide into an extended gas hydrate reservoir. Due to the formation and decomposition of gas hydrates, boiling of carbon dioxide, as well as thermal and hydrodynamic effects on the reservoir, the pressure and temperature of the system can change significantly. Therefore, it is unknown in advance what phase transformations will occur, nor their nature. In such cases, a detailed numerical study of the considered processes is possible only after the consistent mathematical models will be constructed for describing the processes and identifying the limits of applicability of these models. Due to these reasons, for the construction of such mathematical models, it is required to involve certain assumptions, and the constructed mathematical models have certain and previously unknown limits of applicability. When going beyond the limits of applicability of a mathematical model, the numerical solution may contradict the original problem formulation.

Thus, due to the above reasons, a detailed numerical study of the considered processes is possible only after solving two main problems. The first problem is to identify the main features of mathematical models that provide a consistent description. The second problem is the construction of maps of possible solutions, which show in what ranges of parameters different mathematical models are consistent. The presented work is devoted to the solution of these two problems.

The results obtained can be used to create software for geological and hydrodynamic modeling of the development of gas hydrate deposits by the injection of carbon dioxide, when planning and carrying out a complex of geological and technological measures at gas hydrate deposits, to select the most effective strategy for gas recovery.

2. Mathematical Model

The mathematical formulation of most problems on non-isothermal multiphase flows in a porous medium accompanied by phase transitions is currently presented in the form of an initial-boundary value problem for a system of nonlinear partial differential equations. However, the problems formulated at the moment are rather complicated, the existence and uniqueness theorems have not been proved for them, and the use of numerical methods is currently constrained by the lack of a clear understanding of the qualitative features of the thermodynamic behavior of systems. In this regard, first of all, researches are needed to determine the possible structures of the problems mathematical solution.

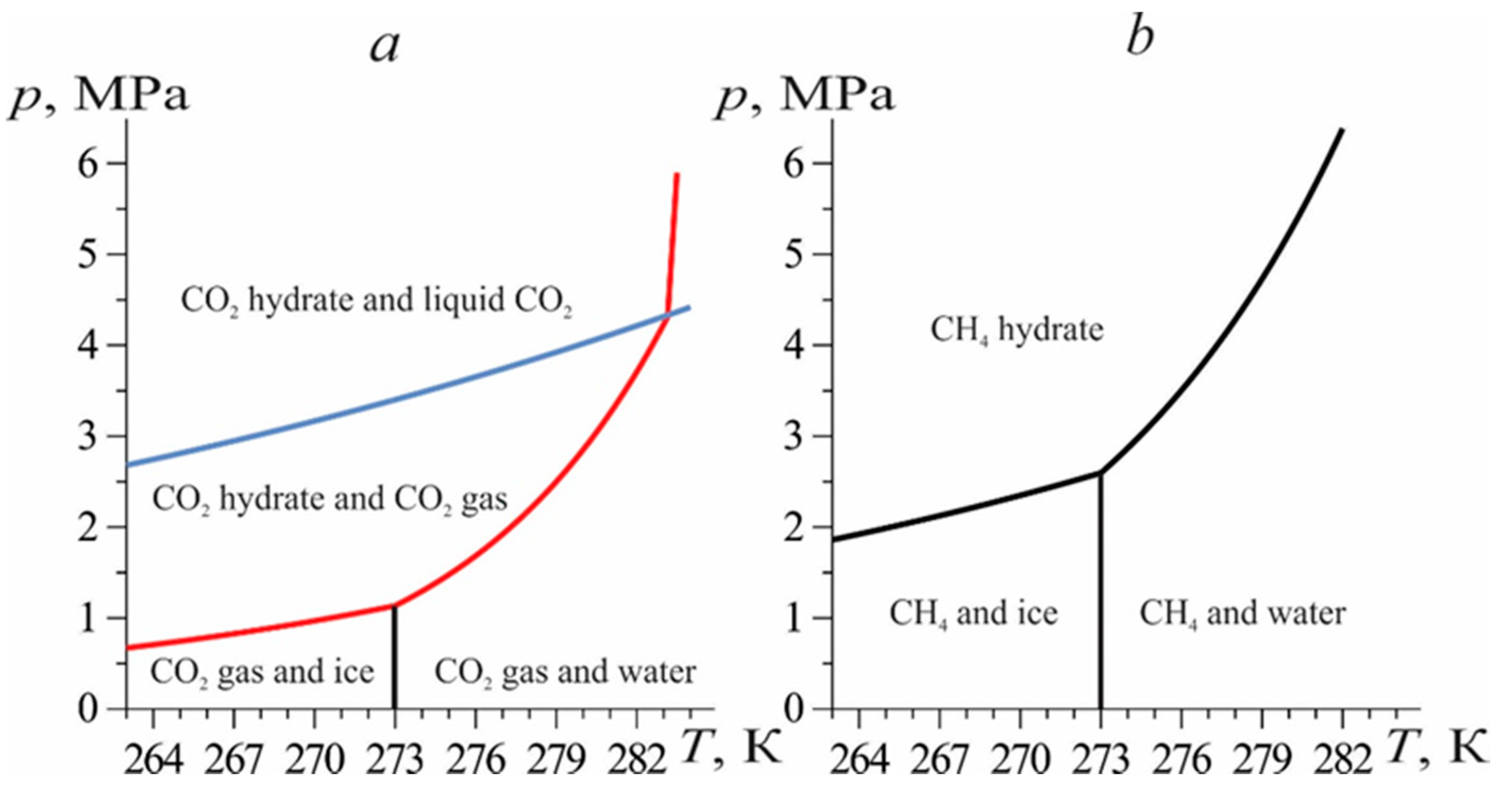
Consider the following problem statement. Consider a natural reservoir with a porous structure and length L. The pores of the reservoir are saturated with methane and methane hydrate. The temperature and pressure of the formation correspond to the conditions for the stable existence of a hydrate. In accordance with the problem statement, the injection of liquid CO₂ through the left border (x = 0) of the reservoir is considered. The temperature T_e and injection pressure p_e are selected in the phase diagram Figure 1 in such a way that they correspond to the conditions for the existence of CO₂ in the liquid state and the conditions for the existence of CO₂ hydrate [30].

The statement of the problem, which is solved in this work, corresponds to the case of continuous injection of carbon dioxide into the formation. This is due to the fact that on the left boundary of the reservoir (through which liquid carbon dioxide is pumped), at time values of $t\ge 0$, a constant pressure is maintained that exceeds the pressure on the right boundary:

p_e > p₀ (for t ≥ 0).

Injection of CO₂ starts the decomposition of methane hydrate. The next stage is associated with the formation of CO₂ hydrate, and its formation requires released water and carbon dioxide. In [31], it was shown that in natural porous layers, filtration (convective) transfer significantly dominates over diffusion transfer. In addition, currents in natural reservoirs are laminar, and the viscosity of carbon dioxide exceeds the viscosity of methane. In this regard, in this paper we will assume the stability of the front of displacement of methane by carbon dioxide.

The specific features of the processes of formation and decomposition of gas hydrates are indeed in many cases strongly dependent on these processes’ kinetics. However, one of the main goals of this work is to study the possibility of boiling liquid carbon dioxide during its injection into a reservoir, accompanied by the formation and decomposition of gas hydrate. The possibility of boiling carbon dioxide during its filtration in a gas hydrate reservoir depends primarily on the hydrodynamic and temperature fields in the reservoir. At low values of permeability considered in the work and high values of the drops of pressure and temperature, the hydrodynamic and temperature fields depend on filtration mass transfer in the reservoir, as well as convective and conductive heat transfer. Therefore, in this case, to study the possibility of boiling liquid carbon dioxide, the kinetics of the processes of formation and decomposition of gas hydrates in comparison with heat and mass transfer in the reservoir can be neglected.

In addition, in this work, we will consider the case when the reservoir has a sufficiently large extent (L ≥ 100 m), as well as low permeability (k < 10⁻¹³ m²). In this case the process of filling the reservoir with injected carbon dioxide will proceed rather slowly, and since there was no carbon dioxide in the initial state, the process of conversion of CH₄ hydrate to CO₂ hydrate will also occur very slowly (i.e., limited by the rate of filtration). Therefore, for the considered process (when the reservoir length L > 100 m), times of the order of several tens of days are of practical interest. At such long times, which significantly exceed the characteristic time of the process kinetics (which, according to experimental data, is on the order of several hours), the kinetic mechanisms no longer limit the process of the transition of CH₄ hydrate to CO₂ hydrate. Therefore, considering sufficiently large time values (on the order of several days or ten days), the kinetics of the processes of formation and decomposition of gas hydrates can be neglected. In this regard, the constructed model is valid only for large time scales, relatively long reservoir length (L ≥ 100 m) and low permeability (k < 10⁻¹³ m²).

Thus, it can be assumed that, under the above conditions, three characteristic regions are formed in the reservoir. According to the problem statement, the near (first) region of the pore is saturated with liquid CO₂ and its hydrate. In the intermediate (second) region, only methane and water are present in the reservoir. In the far (third) region, in addition to methane, its hydrate is present in the pores Figure 2. Methane hydrate decomposition is present only between the 2 and 3 boundaries, respectively, on the moving frontal surface. In this case, the formation of CO₂ hydrate occurs only at the border between 1 and 2 regions.

To describe the processes that occur when carbon dioxide is injected into a porous layer, we make the following assumption. Also, assume that the initial hydrate saturation value is small (no more than 0.2). Then the filtration of water released during the decomposition of the gas hydrate can be neglected. The system of basic equations in the straight-parallel case has the form [32,33,34,35,36]:

$$\begin{gathered} \frac{\partial }{\partial t}\left({\rho }_j\phi S_j\right)+\frac{\partial }{\partial x}\left({\rho }_j\phi S_j{\upsilon }_j\right)=0, (j=c, m) \\ \rho C\frac{\partial T}{\partial t}+{\rho }_j{C}_j\phi S_j{\upsilon }_j\frac{\partial T}{\partial x}-\frac{\partial }{\partial x}\left(\lambda \frac{\partial T}{\partial x}\right)=0, \\ \phi S_j{\upsilon }_j=-\frac{k_j}{{\mu }_j}\frac{\partial p}{\partial x}, \\ {\rho }_c={\rho }_{0c}\exp \left(\beta (p-p_0)\right), {\rho }_m=p/R_{m}T, k_j=k_0{S}_j^3 \end{gathered}$$

(1)

Here φ is the porosity; T is the temperature; p is pressure; ρ_j, S_j, υ_j, k_j, C_j and μ_j are density, saturation, speed, phase permeability, specific heat capacity and dynamic viscosity of carbon dioxide (j = c) and methane (j = m) respectively; R_m is the gas constant of methane; β is the compressibility factor of CO₂; k₀ is the absolute permeability; ρC and λ are the specific volumetric heat capacity and system thermal conductivity coefficient.

The last relation in the system (1) means that to describe the dependence of the relative (phase) permeability of carbon dioxide k_c on its saturation S_c, the following relation is used [25,37]:

$$k_c=k_0{S}_c^3$$

where S_c is the carbon dioxide saturation. The saturation of carbon dioxide in the first region is equal to:

$$S_c=1-S_{hc}$$

where S_hc is the saturation for carbon dioxide gas hydrate.

Thus, to describe the dependence of the relative (phase) permeability of carbon dioxide k_c on the hydrate saturation of S_hc, the following relation is used:

$$k_c=k_0{(1-S_{hc})}^3$$

Analogically, to describe the dependence of the relative (phase) permeability of methane k_m on its saturation S_m, the following relation is used:

$$k_m=k_0{S}_m^3$$

where S_m is the methane saturation.

The saturation value of methane S_m(3) in the third region is equal to:

$$S_{m(3)}=1-\nu$$

where ν is the saturation for methane gas hydrate in the third region.

Therefore, to describe the dependence of the relative (phase) permeability of methane k_m in the third region on the saturation of methane gas hydrate ν, the following relation is used:

$$k_{m(3)}=k_0{(1-\nu )}^3$$

The equations of mass balance of CO₂ and CH₄ on the border between the first and second areas are:

$$\phi S_c{\rho }_c\left({\upsilon }_c-{\dot{x}}_{(n)}\right)=\phi S_{hc}{\rho }_{hc}{G}_c{\dot{x}}_{(n)}, \phi S_m{\rho }_m\left({\upsilon }_m-{\dot{x}}_{(n)}\right)=0$$

where G_c, ρ_hc, S_hc are the mass concentrations in hydrate of carbon dioxide, density and saturation of carbon dioxide gas hydrate; ${\dot{x}}_{(n)}$ is the speed of movement of the near boundary of phase transitions. Hereinafter, to describe the thermophysical characteristics at the boundary between 1 and 2 regions, the index n is used.

The ratio of mass and heat balance at the boundary between 1 and 2 areas has the form:

$$\begin{gathered} -\frac{k_c}{{\mu }_c}\frac{\partial p_{(1)}}{\partial x}=\phi \left(\frac{{\rho }_{hc}}{{\rho }_c}{S}_{hc}{G}_c+S_c\right){\dot{x}}_{(n)}, -\frac{k_{m(2)}}{{\mu }_m}\frac{\partial p_{(2)}}{\partial x}=\phi S_{m(2)}{\dot{x}}_{(n)} \\ \phi S_{hc}{\rho }_{hc}(1-G_c){\dot{x}}_{(n)}=\phi S_l{\rho }_l{\dot{x}}_{(n)} \\ \lambda \frac{\partial T_{(1)}}{\partial x}-\lambda \frac{\partial T_{(2)}}{\partial x}=\phi S_{hc}{\rho }_{hc}{L}_{hc}{\dot{x}}_{(n)} \end{gathered}$$

(2)

Here, L_hc is the heat of the carbon dioxide gas hydrate formation, T_(i) and p_(i) are the temperature and the pressure; index i = 1 and i = 2 belong to the first and second area; S_l and ρ_l are the pore saturation and density of water. The pressure and temperature at the boundary between 1 and 2 areas are assumed to be continuous.

The ratio of mass and heat balance at the boundary between 2 and 3 areas has the form:

$$\begin{gathered} \frac{k_{m(2)}}{{\mu }_m}\frac{\partial p_{(2)}}{\partial x}-\frac{k_{m(3)}}{{\mu }_m}\frac{\partial p_{(3)}}{\partial x}=\phi \left(\frac{{\rho }_{hm}}{{\rho }_{m(d)}}\nu G_m+S_{m(3)}-S_{m(2)}\right){\dot{x}}_{(d)} \\ \phi S_l{\rho }_l{\dot{x}}_{(d)}=\phi \nu {\rho }_{hm}(1-G_m){\dot{x}}_{(d)} \\ \lambda \frac{\partial T_{(3)}}{\partial x}-\lambda \frac{\partial T_{(2)}}{\partial x}=\phi \nu {\rho }_{hm}{L}_{hm}{\dot{x}}_{(d)} \end{gathered}$$

(3)

Here S_m(i), T_(i) and p_(i) are pore saturation, temperature and pressure of methane, index i = 3 belong to the third area; G_m, ${\rho }_{hm}$, ν, L_hm are the mass concentrations in hydrate of methane, density, saturation and heat of the methane gas hydrate formation; ${\dot{x}}_{(d)}$ is the speed of movement of the far border of phase transitions. The pressure and temperature on this surface are related by the phase equilibrium condition for methane and its hydrate [30]:

$$\ln p=A-B/T,$$

(4)

where A = 29.112, B = 7694.30.

The initial conditions, as well as the conditions at the reservoir boundaries, are presented as:

$$\{\begin{array}{l}t=0: p=p_0, T=T_0 \left(0\le x\le L\right),\\ x=0: p=p_e, T=T_e \left(t>0\right),\\ x=L: p=p_0, \frac{\partial T}{\partial x}=0 \left(t>0\right).\end{array}$$

(5)

The equations of piezoconductivity and thermal conductivity, obtained from the system of Equation (1), have the form:

$$\frac{\partial p_{(1)}}{\partial t}=\frac{k_c}{\phi S_c{\mu }_c\beta \exp {\left(\beta (p_{(1)}-p_0)\right)}^{}}\frac{\partial }{\partial x}\left(\exp \left(\beta (p_{(1)}-p_0)\right) \frac{\partial p_{(1)}}{\partial x}\right)$$

(6)

$$\frac{1}{T_{(i)}}\frac{\partial p_{(i)}}{\partial t}={\chi }_{(i)}^p\frac{\partial }{\partial x}\left(\frac{p_{(i)}}{T_{(i)}}\frac{\partial p_{(i)}}{\partial x}\right), (i = 2, 3)$$

(7)

$$\frac{\partial T_{(i)}}{\partial t}=\frac{\partial }{\partial x}\left({\chi }^{(T)}\frac{\partial T_{(i)}}{\partial x}\right)+{\chi }^{(T)}{X}_{(i)}\frac{\partial p_{(i)}}{\partial x}\frac{\partial T_{(i)}}{\partial x}, (i = 1, 2, 3)$$

(8)

where ${\chi }_{(2)}^{(p)}=\frac{k_{m(2)}}{\phi S_{m(2)}{\mu }_m}$, ${\chi }_{(3)}^{(p)}=\frac{k_{m(3)}}{\phi {\mu }_m(1-\nu )}$, $X_{(1)}=\frac{C_c{k}_c{\rho }_{c0}}{\lambda {\mu }_c}\exp \left(\beta (p_{(1)}-p_0)\right)$, $X_{(2)}=\frac{C_m{k}_{m(2)}}{\lambda R_m{\mu }_m}\frac{p_{(2)}}{T_{(2)}}$, $X_{(3)}=\frac{C_m{k}_{m(3)}}{\lambda R_m{\mu }_m}\frac{p_{(3)}}{T_{(3)}}$, ${\chi }^{(T)}=\frac{\lambda }{\rho C}$, $k_c=k_0{S}_c^3$, $k_{m(i)}=k_0{S}_{m(i)}^3$ (i = 2, 3). In addition, from (2) and (3) it follows that $S_l=\frac{{\rho }_{hm}(1-G_m)}{{\rho }_l}\nu$, $S_{hc}=\frac{{\rho }_l{S}_l}{{\rho }_{hc}(1-G_c)}$, $S_c=1-S_{hc}$. Hereinafter, the subscripts in brackets i = 1, 2, 3 relate respectively to the indicated area.

Problems (6)–(8) with boundary, initial and on the moving boundaries of phase transitions conditions (2)–(5) are closed. To solve it, the method of catching the front into a grid node is used [38,39]. When using the method of catching the front at the grid point, it is assumed that the boundary of the CO₂ hydrate formation moves along the coordinate grid by exactly one step in one step by time. This time step is calculated by iterations. The distributions of pressure and temperature in the far and intermediate regions, as well as the position of the phase transition boundary x = x_(d), are determined based on the end-to-end counting method.

To test the mathematical model, we used approximate analytical solutions presented in work [24]. These approximate analytical solutions were obtained for the problem of decomposition of methane gas hydrate during the injection of liquid carbon dioxide into a gas hydrate layer based on the method of converting to a self-similar variable. To obtain analytical solutions, a number of simplifying assumptions were used. For example, the self-similar approximation and linearization of equations were used. It was also assumed that the reservoir has a semi-infinite extent. Therefore, the analytical solutions presented in work [24] are valid only for the initial stage of time.

In [24], these values of the parameters were used: φ = 0.2, ν = 0.2, T_e = 282 K, T₀ = 274 K, p₀ = 3.5 MPa, p_e = 4 MPa, k₀ = 10⁻¹⁶ m², ρC = 2 × 10⁶ J/(K∙m³), λ = 2 W/(m∙K). For these parameters, the following values of the self-similar coordinates of the phase transition boundaries were obtained in the work of [24] (p. 744, Figure 5):

$${\xi }_{(n)}=0.65, {\xi }_{(d)}=0.95$$

(9)

where $\xi =\frac{x}{\sqrt{\lambda t/\rho C}}={10}^3\frac{x}{\sqrt{t}}$.

Thus, with the parameters listed above, the results obtained in [24] correspond to the following dependences of the coordinates of the phase transition boundaries on time:

$$x_{(n)}=6.5\times {10}^{-4}\sqrt{t}, x_{(d)}=9.5\times {10}^{-4}\sqrt{t}$$

(10)

We compared our numerical solutions with those of an analytical solution. Figure 3 shows the dependence of the coordinates of the phase transitions boundaries on time. The solid curve corresponds to the numerical solutions obtained from our model. The dashed curve corresponds to the analytical solutions obtained in [24]. Comparison of these solutions shows a fairly good match for small values of time. Note that for large values of time, self-similar analytical solutions do not allow adequately describing the process, as they are obtained for the case of a semi-infinite reservoir. However, any layer has a finite extent. For large time values, the pressure perturbation will reach the right boundary of the reservoir. In this case, the conditions on the right border will have a significant impact on the peculiarities of the process.

3. Calculations, Results and Discussion

The original parameters used in the model are shown in

Table 1. Basic parameters for the model.

Variables	Symbol	Value	Unit
Porosity	φ	0.2	-
Initial hydrate saturation	ν	0.2	-
Permeability	k0	2 × 10−16	m2
Reservoir length	L	100	m
Initial temperature	T0	274	K
Injection temperature	Te	280	K
Specific volumetric heat capacity	ρC	2.0 × 106	J/(K∙m3)
System thermal conductivity coefficient	λ	2	W/(m∙K)
Mass concentrations of carbon dioxide in hydrate	Gc	0.28	-
Mass concentrations of methane in hydrate	Gm	0.13	-
Gas constant of methane	Rm	520	J/(kg∙K)
Density of carbon dioxide hydrate	ρhc	1100	kg/m3
Density of methane hydrate	ρhm	900	kg/m3
Density of water	ρl	1000	kg/m3
Density of carbon dioxide	ρc0	890	kg/m3
Compressibility factor of carbon dioxide	β	10−8	Pa−1
Dynamic viscosity of carbon dioxide	µc	10−4	Pa∙s
Dynamic viscosity of methane	µm	10−5	Pa∙s
Heat of the formation of carbon dioxide hydrate	Lhc	3.51 × 105	J/kg
Heat of the formation of methane hydrate	Lhm	4.48 × 105	J/kg
Specific heat capacity of carbon dioxide	Cc	2600	J/(kg∙K)
Specific heat capacity of methane	Cm	1560	J/(kg∙K)

[1,30].

In Figure 4, for the time t = 20 days, the dependences of pressure at the near boundary of phase transitions, as well as temperatures and coordinates of the near (curve 1) and distant (curve 2) of phase transitions boundaries depending on the injection pressure, are shown. The dashed line corresponds to the equilibrium boiling pressure of liquid CO₂. For the value of the initial pressure of the system, the values p₀ = 3.1 MPa (a) and 2.9 MPa (b) are assumed.

Figure 4 shows a decrease in temperature at the boundary of the CO₂ hydrate formation with increasing injection pressure. It also follows from Figure 4 that with an increase in the injection pressure, the coordinate of the hydrate reservoir boundary also increases, and the coordinate of the dissociation boundary of methane hydrate increases slightly. This is due to the increase in the filtration rate of carbon dioxide with increasing injection pressure. The rate of displacement of methane by carbon dioxide has a major effect on the rate of hydrate formation. An increase in the velocity of this boundary leads to a decrease in the influence on it of a hotter left boundary and, accordingly, to a decrease in its temperature. According to Figure 4, at high pressures, the near boundary of phase transitions can catch up with the far boundary. In this case, methane in the gas hydrate is replaced by carbon dioxide at the only phase transition boundary. In addition, at sufficiently low injection pressures, the pressure at the near boundary may fall below the equilibrium boiling pressure. Therefore, in this case, it is necessary, in addition to the area containing liquid CO₂ and its gas hydrate, to introduce into consideration a region saturated with gaseous CO₂ and its gas hydrate. Thus, at low values of the injection pressure of p_e in the reservoir, an additional region saturated with gaseous carbon dioxide and its hydrate will additionally appear. At high injection pressures, a CO₂ gas hydrate formation will occur in the replacement mode in the absence of a region containing methane and water. For average injection pressures, two different cases are possible, depending on the pressure at the right boundary of the reservoir, p₀. At relatively high values of p₀, the regime is implemented according to the scheme shown in Figure 2. At relatively low values of p₀, the formation of CO₂ hydrate will occur in the replacement mode, but is accompanied by boiling of liquid carbon dioxide.

In Figure 5, for the moment of time t = 20 days, the dependences of pressure at the near boundary of phase transitions, as well as temperatures and coordinates of the near (curve 1) and distant (curve 2) of phase transitions boundaries, depending on the pressure at the right boundary of the reservoir, are shown. The values of injection pressure are p_e = 3.7 MPa for case (a) and 3.64 MPa for case (b). Figure 5 shows the increase in temperature at the boundary of the formation of CO₂ gas hydrate with increasing pressure at the right boundary p₀. Also, according to Figure 5, as the pressure on the right border p₀ decreases, the coordinates of both the near and far boundaries of the phase transition increase. This is due to the fact that the rate of CO₂ hydrate formation boundary is determined by the rate of methane displacement by carbon dioxide. Thus, the filtration rate of carbon dioxide increases with increasing pressure drop in the reservoir. An increase in the velocity of this boundary leads to a decrease in the influence on it of a hotter left boundary and, respectively, to a decrease in its temperature. As a consequence, according to Figure 5, at low values of p₀, it is possible to merge the boundaries of phase transitions and therefore it is also possible to merge the formation of CO₂ hydrate in the replacement mode. Also, in the case of low values of p₀, the pressure at the near phase transition boundary can fall below the equilibrium boiling pressure. Thus, as follows from Figure 5, at low pressures at the right boundary of the reservoir, the formation of CO₂ gas hydrate occurs in the replacement mode with the formation of a region saturated with gaseous CO₂ and its gas hydrate. At high values of p₀, the formation of CO₂ gas hydrate occurs according to the scheme shown in Figure 2.

In Figure 6, for the time of t = 20 days the dependences of pressure at the near boundary of phase transitions, as well as temperatures and coordinates of the near (curve 1) and distant (curve 2) phase transition boundaries from the absolute permeability of the reservoir, are shown. The dashed line corresponds to the equilibrium boiling pressure of liquid CO₂. For the pressure of injection, the values are p_e = 3.75 MPa (a) and 3.65 MPa (b). From here and on, the pressure at the right boundary of the reservoir was assumed to be p₀ = 3 MPa. As follows from Figure 6, with an increase in the permeability of the reservoir, the phase transitions may merge and produce CO₂ gas hydrate in the replacement mode. Also, according to Figure 6, at relatively high injection pressures, the process of forming CO₂ gas hydrate will occur without forming a region saturated with gaseous CO₂ and its gas hydrate. At low injection pressures, the process will be accompanied by boiling of liquid carbon dioxide.

In Figure 7 for time of t = 20 days, the dependences of the limiting values of injection pressure p_*, separating modes with boiling and without boiling of carbon dioxide (dashed line) and modes with and without dissociation of methane gas hydrate (solid line) on the permeability of the porous medium (a), the pressure value at the right boundary of the reservoir (b), from the initial temperature of the reservoir (c) and from the injection temperature (d). The dashed line corresponds to the equilibrium boiling pressure of liquid CO₂. Figure 7 shows four regions. In region I, there is no dissociation of CH₄ hydrate and the CO₂ boiling mode is present. This mode is implemented at high values of injection pressure. In region II, solutions are located without dissociation of CH₄ hydrate and with CO₂ boiling. This mode is typical for highly permeable reservoirs, for reservoirs with low pressure at the right boundary, also when there is a low temperature of injected liquid and low initial reservoir temperature. Region III corresponds to the mode of the process with the dissociation of CH₄ hydrate and without boiling of CO₂. This mode is typical for low-permeable reservoirs and high values of pressure at the right reservoir boundary. This mode is also implemented at high values of the injection temperature and of the initial temperature of the reservoir. In region IV, solutions are located with the dissociation of CH₄ hydrate and with boiling of CO₂. This mode is implemented at low values of injection pressure.

4. Conclusions

The main features of mathematical models are formulated, which provide a consistent description of the process of injection of liquid carbon dioxide into a gas hydrate reservoir. Maps of possible solutions have been built. These maps show in what ranges of parameters certain mathematical models are consistent. Numerical solutions are obtained for the problem of injection of warm liquid CO₂ into a reservoir of finite length, accompanied by the decomposition of CH₄ gas hydrate and the formation of CO₂ gas hydrate. The dependences of the phase transition boundaries coordinates that determine the rate of dissociation of CH₄ gas hydrate and the formation of CO₂ gas hydrate, as well as the pressure and temperature values at these boundaries on the pressure of carbon dioxide injected, as well as the permeability and initial pressure of the reservoir, were obtained. It was established that with increasing injection pressure and decreasing pressure at the right boundary of the reservoir, the temperature decreases at the boundary of carbon dioxide gas hydrate formation and the coordinate of the carbon dioxide gas hydrate formation increases. It is shown that at sufficiently low pressures at the right reservoir boundary and high injection pressures, the formation boundary of carbon dioxide gas hydrate can catch up with the decomposition boundary of methane gas hydrate. This corresponds to the mode of the process with the replacement of CH₄ with CO₂ in hydrate without releasing free water. It was also found that at sufficiently low values of injection pressure and pressure at the right reservoir boundary, the pressure at the boundary of carbon dioxide gas hydrate formation drops below the boiling pressure of carbon dioxide. These values of pressure at the right boundary and injection pressure can correspond both to the existence of a region saturated with the products of decomposition of methane gas hydrate, and its absence. Hydrate decomposition can be accompanied by boiling and occur without it. It has been established that the mode with the dissociation of CH₄ hydrate to water and gas is realized in low-permeable reservoirs, as well as at relatively high values of the initial reservoir temperature and injection temperature. It was established that the mode with boiling of liquid carbon dioxide is characteristic for relatively low values of pressure at the right boundary of the reservoir and CO₂ injection pressure.