Classifications of Canal Surfaces with the Gauss Maps in Minkowski 3-Space

Abstract

In this work, we study the canal surfaces foliated by pseudo spheres ${\mathbb{S}}_1^2$ along a Frenet curve in terms of their Gauss maps in Minkowski 3-space. Such kind of surfaces with pointwise 1-type Gauss maps are classified completely. For example, the canal surface with proper pointwise 1-type Gauss map of the first kind if and only if it is a part of a minimal surface of revolution.

1. Introduction

In the theory of surface, a kind of surface called canal surfaces will shaped by sweeping a family of spheres whose centers lie on a space curve in Euclidean 3-space. The geometric characters of such surfaces have been studied by many experts and geometers [1,2,3]. For example, the authors of [1] investigated the geometric properties of such surfaces, including the Gaussian curvature, the mean curvature and their relationships. As time goes on, the construction idea of canal surfaces in Euclidean 3-space is extended into the spaces with indefinite metric, especially into Lorentz–Minkowski space. In Minkowski 3-space, a canal surface can be formed as the envelope of a family of pseudo-Riemannian space forms, i.e., pseudo spheres ${\mathbb{S}}_1^2$, pseudo hyperbolic spheres ${\mathbb{H}}_0^2$ and lightlike cones ${\mathbb{Q}}^2$ [4,5,6]. According to the classification of curves in Minkowski space, i.e., spacelike curve, timelike curve and lightlike (null) curve, there are nine types of canal surfaces in Minkowski 3-space. The parametric expressions and the fundamental geometric properties are stated by discussing the linear Weingarten canal surfaces in [4,5].

The idea of finite type immersion of Riemannian manifolds into Euclidean space (resp. pseudo Euclidean space) was introduced by B.Y. Chen in the late 1970s, which was extended into the differential maps on the submanifolds such as the Gauss maps. A submanifold $\mathbb{M}$ in Euclidean space (resp. pseudo Euclidean space) whose Gauss map $\mathbb{G}$ satisfies $\Delta \mathbb{G}=f(\mathbb{G}+C)$ is said to have pointwise 1-type Gauss map for a non-zero smooth function f and a constant vector C, where $\Delta$ is the Laplacian defined on $\mathbb{M}$ stated by

$$\Delta =-\frac{1}{\sqrt{\left|det\right(g_{ij}\left)\right|}}\sum _{i,j}\frac{\partial }{\partial x^i}\left(\sqrt{\left|det\right(g_{ij}\left)\right|}{g}^{ij}\frac{\partial }{\partial x^j}\right),$$

(1)

where $g^{ij}$ are the components of the inverse matrix of the first fundamental form of $\mathbb{M}$. In particular, it is said to be of the first kind or the second kind when the vector C is zero or non-zero, respectively. Furthermore, $\mathbb{G}$ is said to be of proper pointwise 1-type if the function f is not constant, then a non-proper pointwise 1-type Gauss map is of ordinary 1-type. When the smooth function f vanishes, $\mathbb{G}$ is said to be harmonic [7,8,9].

Based on the conclusions obtained in [1], the canal surface with pointwise 1-type Gauss map is discussed in [2]. In order to do further and complete geometric investigation for canal surfaces in Minkowski 3-space, the canal surfaces foliated by pseudo spheres ${\mathbb{S}}_1^2$ along Frenet curves to be studied in the present work. In Section 2, some basic facts including the Frenet formulas of Frenet curves, the expression forms, and the relationships between the Gaussian curvatures and the mean curvatures of three types of canal surfaces are recalled. In Section 3, three types of canal surfaces with pointwise 1-type Gauss maps are classified completely.

The surfaces are smooth, regular, topologically connected unless otherwise stated in this paper.

2. Preliminaries

The Minkowski 3-space ${\mathbb{E}}_1^3$ is provided with the standard indefinite flat metric given by

$$⟨·,·⟩=d{x}_1^2+d{x}_2^2-d{x}_3^2$$

in terms of the natural coordinate system $(x_1,x_2,x_3)$. A vector v is called to be spacelike, timelike and lightlike (null), if $⟨v,v⟩>0$ or $v=0$, $⟨v,v⟩<0$ and $⟨v,v⟩=0$, $(v\ne 0)$, respectively. The norm of the vector v is defined by $\parallel v\parallel =\sqrt{|⟨v,v⟩|}$. According to the causal character of the tangent vectors, the curves are divided into spacelike, timelike, or lightlike (null) curves. Furthermore, a spacelike curve is classified into the first kind, the second kind spacelike curve or the null type spacelike curve (the pseudo null curve) when the normal vector is spacelike, timelike or lightlike, separately.

Remark 1

([10]). Timelike curves and spacelike curves with spacelike or timelike normal vectors are called Frenet curves in Minkowski space.

Proposition 1

([4]). Let $c\left(s\right):\mathbf{I}\to {\mathbb{E}}_1^3$ be a Frenet curve parameterized by arc length s with Frenet frame $\{\alpha ,\beta ,\gamma \}$. Then, the following Frenet equations are satisfied:

$$\left\{\begin{array}{c}{\alpha }^{\prime }\left(s\right)=\kappa \left(s\right)\beta \left(s\right),\hfill \\ {\beta }^{\prime }\left(s\right)=-{ϵ}_1\kappa \left(s\right)\alpha \left(s\right)+{ϵ}_2\tau \left(s\right)\gamma \left(s\right),\hfill \\ {\gamma }^{\prime }\left(s\right)=\tau \left(s\right)\beta \left(s\right),\hfill \end{array}\right.$$

where α is the tangent vector, β and γ is the normal vector and the binormal vector of $c\left(s\right)$, respectively. When $c\left(s\right)$ is a timelike curve, ${ϵ}_1={ϵ}_2=-1$; when $c\left(s\right)$ is a spacelike curve of the first kind, ${ϵ}_1={ϵ}_2=1$; when $c\left(s\right)$ is a spacelike curve of the second kind, ${ϵ}_1=-{ϵ}_2=-1$. The function $\kappa \left(s\right)$, $\tau \left(s\right)$ is said to be the curvature and the torsion of $c\left(s\right)$, respectively.

Proposition 2

([4]). Let p be a fixed point, $r>0$ be a constant in ${\mathbb{E}}_1^3$. Then, the pseudo-Riemannian space forms, i.e., the de-Sitter space ${\mathbb{S}}_1^2(p,r)$, the hyperbolic space ${\mathbb{H}}_0^2(p,r)$ and the lightlike cone ${\mathbb{Q}}_1^2\left(p\right)$ are defined by

$${\mathbb{M}}^2\left(ϵ\right)=\{x\in {\mathbb{E}}_1^3:⟨x-p,x-p⟩=ϵr^2\}=\left\{\begin{array}{c}{\mathbb{S}}_1^2(p,r)|ϵ=1;\hfill \\ {\mathbb{H}}_0^2(p,r)|ϵ=-1;\hfill \\ {\mathbb{Q}}_1^2\left(p\right)|ϵ=0.\hfill \end{array}\right.$$

In particular, when $r=1$ and the center p is the origin, we write them by ${\mathbb{S}}_1^2$, ${\mathbb{H}}_0^2$ and ${\mathbb{Q}}^2$ simply.

Definition 1

([6]). A surface $\mathbb{M}$ in ${\mathbb{E}}_1^3$ is called a canal surface which is formed as the envelope of a family of pseudo spheres ${\mathbb{S}}_1^2$(resp. pseudo hyperbolic spheres ${\mathbb{H}}_0^2$ or lightlike cones ${\mathbb{Q}}^2$) whose centers lie on a space curve $c\left(s\right)$ framed by $\{\alpha ,\beta ,\gamma \}$. $\mathbb{M}$ can be parameterized by

$$x(s,\theta )=c\left(s\right)+\lambda (s,\theta )\alpha \left(s\right)+\mu (s,\theta )\beta \left(s\right)+\omega (s,\theta )\gamma \left(s\right),$$

where λ, μ, and ω are differential functions of s and θ, ${\parallel x(s,\theta )-c\left(s\right)\parallel }^2=ϵr^2\left(s\right)$, $(ϵ=\pm 1$ or $0)$. The curve $c\left(s\right)$ is called the center curve, $r\left(s\right)$ is called the radial function of $\mathbb{M}$.

Precisely, if $\mathbb{M}$ is foliated by pseudo spheres ${\mathbb{S}}_1^2$ (resp. pseudo hyperbolic spheres ${\mathbb{H}}_0^2$ or lightlike cones ${\mathbb{Q}}^2$), then $ϵ=1$ (resp. $-1$ or 0) and $\mathbb{M}$ is said to be of type ${\mathbb{M}}_{+}$ (resp. ${\mathbb{M}}_{-}$ or ${\mathbb{M}}_0$). In addition, the canal surface of type ${\mathbb{M}}_{+}$ can be classified into ${\mathbb{M}}_{+}^1$ (resp. ${\mathbb{M}}_{+}^2$ or ${\mathbb{M}}_{+}^3$) when $c\left(s\right)$ is spacelike (resp. timelike or null). Moreover, when $c\left(s\right)$ is the first kind, the second kind spacelike curve and the pseudo null curve, ${\mathbb{M}}_{+}^1$, is denoted by ${\mathbb{M}}_{+}^{11}$, ${\mathbb{M}}_{+}^{12}$ and ${\mathbb{M}}_{+}^{13}$, respectively. Similarly, the canal surfaces ${\mathbb{M}}_{-}$ (resp. ${\mathbb{M}}_0$) can be classified into ${\mathbb{M}}_{-}^1$, ${\mathbb{M}}_{-}^2$ and ${\mathbb{M}}_{-}^3$ (resp. ${\mathbb{M}}_0^1$, ${\mathbb{M}}_0^2$ and ${\mathbb{M}}_0^3$). Naturally, ${\mathbb{M}}_{-}^1$ (resp. ${\mathbb{M}}_0^1$) can be divided into ${\mathbb{M}}_{-}^{11}$, ${\mathbb{M}}_{-}^{12}$ and ${\mathbb{M}}_{-}^{13}$ (resp. ${\mathbb{M}}_0^{11}$, ${\mathbb{M}}_0^{12}$ and ${\mathbb{M}}_0^{13}$) [5].

Remark 2.

In the present work, we consider the canal surfaces foliated by pseudo spheres ${\mathbb{S}}_1^2$ which have Frenet curves as center curves, i.e., the canal surfaces of type ${\mathbb{M}}_{+}^{11}$, ${\mathbb{M}}_{+}^{12}$ and ${\mathbb{M}}_{+}^2$.

In [4], the canal surfaces ${\mathbb{M}}_{+}^{11}$, ${\mathbb{M}}_{+}^{12}$ and ${\mathbb{M}}_{+}^2$ are expressed by

$$\begin{array}{cc}\hfill {\mathbb{M}}_{+}^{11}& :x(s,\theta )=c\left(s\right)+r\left(s\right)\{-r^{\prime }\left(s\right)\alpha +\sqrt{1-r^{\prime 2}\left(s\right)}cosh\theta \beta +\sqrt{1-r^{\prime 2}\left(s\right)}sinh\theta \gamma \};\hfill \\ \hfill {\mathbb{M}}_{+}^{12}& :x(s,\theta )=c\left(s\right)+r\left(s\right)\{-r^{\prime }\left(s\right)\alpha +\sqrt{1-r^{\prime 2}\left(s\right)}sinh\theta \beta +\sqrt{1-r^{\prime 2}\left(s\right)}cosh\theta \gamma \};\hfill \\ \hfill {\mathbb{M}}_{+}^2& :x(s,\theta )=c\left(s\right)+r\left(s\right)\{r^{\prime }\left(s\right)\alpha +\sqrt{1+r^{\prime 2}\left(s\right)}cos\theta \beta +\sqrt{1+r^{\prime 2}\left(s\right)}sin\theta \gamma \}.\hfill \end{array}$$

For convenience, the authors assumed $-r^{\prime }\left(s\right)=cos\phi$ for ${\mathbb{M}}_{+}^{11}$ and ${\mathbb{M}}_{+}^{12}$, $r^{\prime }\left(s\right)=tan\phi$ for ${\mathbb{M}}_{+}^2$, where $\phi =\phi \left(s\right)$ is a smooth function, then the canal surfaces ${\mathbb{M}}_{+}^{11}$, ${\mathbb{M}}_{+}^{12}$ and ${\mathbb{M}}_{+}^2$ are rewritten by

$${\mathbb{M}}_{+}^{11}:x(s,\theta )=c\left(s\right)+r\left(s\right)(cos\phi \left(s\right)\alpha +sin\phi \left(s\right)cosh\theta \beta +sin\phi \left(s\right)sinh\theta \gamma );$$

(2)

$${\mathbb{M}}_{+}^{12}:x(s,\theta )=c\left(s\right)+r\left(s\right)(cos\phi \left(s\right)\alpha +sin\phi \left(s\right)sinh\theta \beta +sin\phi \left(s\right)cosh\theta \gamma );$$

(3)

$${\mathbb{M}}_{+}^2:x(s,\theta )=c\left(s\right)+r\left(s\right)(tan\phi \left(s\right)\alpha +sec\phi \left(s\right)cos\theta \beta +sec\phi \left(s\right)sin\theta \gamma ).$$

(4)

Example 1.

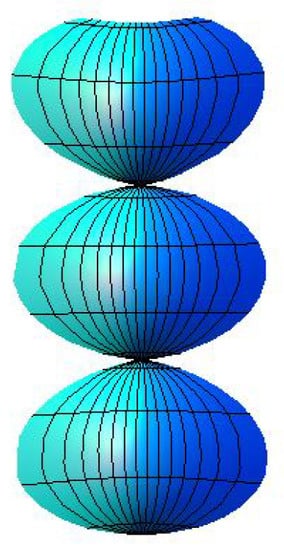
Let $c\left(s\right)=(s,0,0)$ be a spacelike curve, the radial function $r\left(s\right)=sins$, then the canal surface ${\mathbb{M}}_{+}^{11}$$\left({\mathbb{M}}_{+}^{12}\right)$ can be expressed as (see Figure 1)

$$x(s,\theta )=(-sinscoss+s,{sin}^{2}scosh\theta ,{sin}^{2}ssinh\theta ).$$

Figure 1. ${\mathbb{M}}_{+}^{11}$ (${\mathbb{M}}_{+}^{12}$) with $r\left(s\right)=sins$.

Example 2.

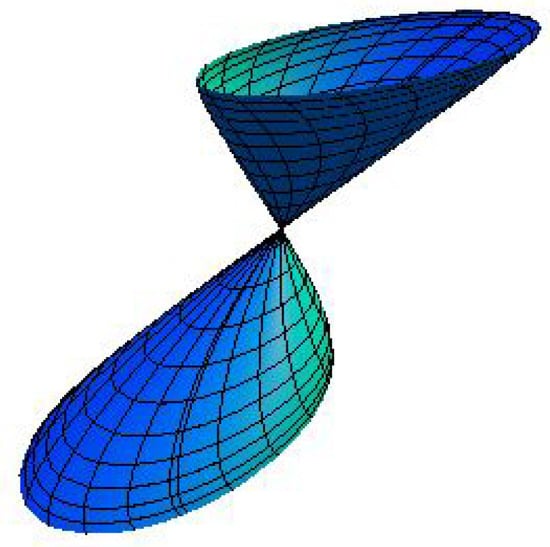
Let $c\left(s\right)=(sin\frac{s}{2},cos\frac{s}{2},\frac{\sqrt{5}}{2}s)$ be a timelike curve, the radial function $r\left(s\right)=sins$, then the canal surface ${\mathbb{M}}_{+}^2$ can be expressed as (see Figure 2)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x(s,\theta )=& \{sin\frac{s}{2}+\frac{1}{4}sin2scos\frac{s}{2}-sins\sqrt{1+{cos}^{2}s}(sin\frac{s}{2}cos\theta -\frac{\sqrt{5}}{2}cos\frac{s}{2}sin\theta ),cos\frac{s}{2}-\frac{1}{4}sin2ssin\frac{s}{2}-\hfill \\ & sins\sqrt{1+{cos}^{2}s}(cos\frac{s}{2}cos\theta +\frac{\sqrt{5}}{2}sin\frac{s}{2}sin\theta ),\frac{\sqrt{5}}{2}s+\frac{\sqrt{5}}{4}sin2s+\frac{1}{2}sins\sqrt{1+{cos}^{2}s}sin\theta \}.\hfill \end{array}\end{array}$$

Figure 2. ${\mathbb{M}}_{+}^2$ with $r\left(s\right)=sins$.

Proposition 3

([4]). For the canal surface ${\mathbb{M}}_{+}^{11}$(resp. ${\mathbb{M}}_{+}^{12},{\mathbb{M}}_{+}^2)$, the Gaussian curvature K and the mean curvature H satisfy

$$H=-\frac{1}{2}(Kr+\frac{1}{r}).$$

Remark 3.

By Proposition 3, the principal curvatures ${\kappa }_1,{\kappa }_2$ of the canal surface ${\mathbb{M}}_{+}^{11}$(resp. ${\mathbb{M}}_{+}^{12},{\mathbb{M}}_{+}^2)$ are given by

$${\kappa }_1=-Kr,{\kappa }_2=-\frac{1}{r}.$$

3. Main Conclusions

In this section, the classifications of three types of canal surfaces are discussed in terms of their Gauss maps. We prove the results for ${\mathbb{M}}_{+}^{11}$ and omit the proofs for ${\mathbb{M}}_{+}^{12}$ and ${\mathbb{M}}_{+}^2$ since they can be similarly done to those of ${\mathbb{M}}_{+}^{11}$ in what follows.

3.1. The Canal Surfaces of Type ${\mathbb{M}}_{+}^{11}$ with Pointwise 1-Type Gauss Maps

From Equation (2), the canal surface ${\mathbb{M}}_{+}^{11}$ is parameterized as

$$x(s,\theta )=c\left(s\right)+r\left(s\right)(cos\phi (s)\alpha +sin\phi (s)cosh\theta \beta +sin\phi (s)sinh\theta \gamma ),$$

where $cos\phi \left(s\right)=-r^{\prime }\left(s\right)$, ($\phi \in [0,\pi )$) is a smooth function.

Through direct calculations, we have initially

$$x_s=x_s^1\alpha +x_s^2\beta +x_s^3\gamma ,x_{\theta }=x_{\theta }^1\beta +x_{\theta }^2\gamma ,$$

where

$$\begin{array}{cc}\hfill & x_s^1=-r{r}^{″}-r\kappa sin\phi cosh\theta +{sin}^2\phi ;\hfill \\ \hfill & x_s^2=r^{\prime }sin\phi cosh\theta -r{r}^{\prime }{\phi }^{\prime }cosh\theta +r\tau sin\phi sinh\theta -r{r}^{\prime }\kappa ;\hfill \\ \hfill & x_s^3=r^{\prime }sin\phi sinh\theta -r{r}^{\prime }{\phi }^{\prime }sinh\theta +r\tau sin\phi cosh\theta ;\hfill \\ \hfill & x_{\theta }^1=rsin\phi sinh\theta ;\hfill \\ \hfill & x_{\theta }^2=rsin\phi cosh\theta .\hfill \end{array}$$

(5)

Thus, the Gauss map $\mathbb{G}$ of ${\mathbb{M}}_{+}^{11}$ is

$$\mathbb{G}=cos\phi \alpha +sin\phi cosh\theta \beta +sin\phi sinh\theta \gamma ,$$

(6)

which points towards ${\mathbb{M}}_{+}^{11}$ inside and $⟨\mathbb{G},\mathbb{G}⟩=1$.

Meanwhile, the quantities of the first fundamental form are obtained as

$$g_{11}=\frac{P_1^2-r^2{R}_1^2}{{sin}^2\phi },g_{12}=-r^2{R}_1,g_{22}=-r^2{sin}^2\phi ,$$

(7)

and the quantities of the second fundamental form are written by

$$h_{11}=\frac{r{R}_1^2-P_1{Q}_1}{{sin}^2\phi },h_{12}=r{R}_1,h_{22}=r{sin}^2\phi ,$$

(8)

where

$$\begin{array}{cc}\hfill & P_1=r{r}^{″}+r\kappa sin\phi cosh\theta -{sin}^2\phi =r{Q}_1-{sin}^2\phi ,\hfill \\ \hfill & Q_1=r^{″}+\kappa sin\phi cosh\theta ,\hfill \\ \hfill & R_1=\tau {sin}^2\phi +r^{\prime }\kappa sin\phi sinh\theta .\hfill \end{array}$$

(9)

From Equations (7) and (8), the Gaussian curvature K and the mean curvature H of ${\mathbb{M}}_{+}^{11}$ are

$$K=\frac{Q_1}{r{P}_1},H=-\frac{2P_1+{sin}^2\phi }{2r{P}_1}.$$

(10)

Remark 4.

From $g_{11}{g}_{22}-g_{12}^2=-r^2{P}_1^2,$ due to regularity, we see that $P_1\ne 0$ everywhere.

Serving the following discussion, the Laplacian of the Gauss map $\mathbb{G}$ of ${\mathbb{M}}_{+}^{11}$ needs to be calculated. First, from the first fundamental form of ${\mathbb{M}}_{+}^{11}$, we have

$$g^{11}=\frac{{sin}^2\phi }{P_1^2},g^{12}=g^{21}=-\frac{R_1}{P_1^2},g^{22}=\frac{r^2{R}_1^2-P_1^2}{r^2{P}_1^2{sin}^2\phi }.$$

(11)

Substituting (6), (7), and (11) into (1), and by putting

$$\begin{array}{c}\hfill \begin{array}{c}\hfill U_1=g_{22}{H}_s-g_{12}{H}_{\theta },V_1=-g_{12}{H}_s+g_{11}{H}_{\theta },\end{array}\end{array}$$

(12)

where

$$\begin{array}{cc}\hfill H_s=& \frac{2r^2{r}^{\prime }{\kappa }^2{sin}^2\phi {cosh}^2\theta -(2r{r}^{\prime }\kappa -r^2{\kappa }^{\prime }){sin}^3\phi cosh\theta +5r^2{r}^{\prime }{r}^{″}\kappa sin\phi cosh\theta }{2r^2{P}_1^2}+\hfill \\ \hfill & \frac{-2r{r}^{\prime }{r}^{″}{sin}^2\phi +r^2{r}^{‴}{sin}^2\phi +4r^2{r}^{\prime }{r}^{″2}+r^{\prime }{sin}^4\phi }{2r^2{P}_1^2},\hfill \\ \hfill H_{\theta }=& \frac{\kappa {sin}^3\phi sinh\theta }{2P_1^2},\hfill \end{array}$$

(13)

after complicated arrangements, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Delta \mathbb{G}=& \frac{1}{r^2{P}_1^2}\{[(r^2{Q}_1^2+P_1^2)cos\phi -2x_s^1{U}_1]\alpha +[(r^2{Q}_1^2+P_1^2)sin\phi cosh\theta -2(x_s^2{U}_1+x_{\theta }^1{V}_1)]\beta +\hfill \\ \hfill & [(r^2{Q}_1^2+P_1^2)sin\phi sinh\theta -2(x_s^3{U}_1+x_{\theta }^2{V}_1)]\gamma \}.\hfill \end{array}\end{array}$$

(14)

Assume that a canal surface ${\mathbb{M}}_{+}^{11}$ satisfies $\Delta \mathbb{G}=f(\mathbb{G}+C)$. Without loss of generality, we may suppose

$$C=C_1\alpha +C_2\beta +C_3\gamma ,$$

(15)

where $C_1=⟨C,\alpha ⟩,C_2=⟨C,\beta ⟩,C_3=-⟨C,\gamma ⟩$.

Substituting (6), (14), and (15) into $\Delta \mathbb{G}=f(\mathbb{G}+C)$, we obtain the following equation system:

$$\left\{\begin{array}{c}(r^2{Q}_1^2+P_1^2)cos\phi -2x_s^1{U}_1=r^2{P}_1^2(cos\phi +C_1)f,\hfill \\ (r^2{Q}_1^2+P_1^2)sin\phi cosh\theta -2(x_s^2{U}_1+x_{\theta }^1{V}_1)=r^2{P}_1^2(sin\phi cosh\theta +C_2)f,\hfill \\ (r^2{Q}_1^2+P_1^2)sin\phi sinh\theta -2(x_s^3{U}_1+x_{\theta }^2{V}_1)=r^2{P}_1^2(sin\phi sinh\theta +C_3)f.\hfill \end{array}\right.$$

(16)

From the last two equations of (16), we have

$$\begin{array}{cc}\hfill & 2U_1(r\tau {sin}^2\phi +r{r}^{\prime }\kappa sin\phi sinh\theta +x_s^3{C}_2-x_s^2{C}_3)+2V_1(r{sin}^2\phi +x_{\theta }^2{C}_2-x_{\theta }^1{C}_3)\hfill \\ \hfill =& sin\phi (2P_1^2+2P_1{sin}^2\phi +{sin}^4\phi )(C_{2}sinh\theta -C_{3}cosh\theta ).\hfill \end{array}$$

(17)

Rearranging (17) with the help of (5), (9), and (12), we get

$$\begin{array}{cc}\hfill & 2(g_{22}{H}_s-g_{12}{H}_{\theta })(r\tau {sin}^2\phi +r{r}^{\prime }\kappa sin\phi sinh\theta +x_s^3{C}_2-x_s^2{C}_3)+2(-g_{12}{H}_s+g_{11}{H}_{\theta })\hfill \\ & (r{sin}^2\phi +rsin\phi cosh\theta C_2-rsin\phi sinh\theta C_3)\hfill \\ \hfill =& sin\phi [{(r\kappa sin\phi cosh\theta +r{r}^{″}-{sin}^2\phi )}^2+{(r\kappa sin\phi cosh\theta +r{r}^{\prime \prime })}^2](C_{2}sinh\theta -C_{3}cosh\theta ).\hfill \end{array}$$

(18)

Since $\{cosh(m\theta ),sinh(m\theta \left)\right|m\in \mathbb{N}\}$ constructs a set of linearly independent functions, in view of the coefficients of $sinh5\theta$ and $cosh5\theta$ in (18) by the aid of (5), (7), and (13), we have

$$\left\{\begin{array}{c}{r}^6{\kappa }^4{sin}^5\phi C_3=0,\hfill \\ r^6{\kappa }^4{sin}^5\phi C_2=0.\hfill \end{array}\right.$$

(19)

From (19), we consider a non-empty open subset $\mathcal{O}=\{p\in {\mathbb{M}}_{+}^{11}\mid \kappa \left(p\right)\ne 0\}$ of ${\mathbb{M}}_{+}^{11}$. Since $r\ne 0$, $sin\phi \ne 0$, then we have $C_2=C_3=0$ on $\mathcal{O}$. However, if $C_2=C_3=0$, (18) gives

$$r^2{R}_1^2+g_{11}{sin}^2\phi =P_1^2=0$$

which contradicts the regularity of ${\mathbb{M}}_{+}^{11}$. Hence, $\kappa \equiv 0$, ${\mathbb{M}}_{+}^{11}$ is a surface of revolution.

Putting $c\left(s\right)=(s,0,0)$ and $\alpha =(1,0,0),\beta =(0,1,0),\gamma =(0,0,1)$, ${\mathbb{M}}_{+}^{11}$ can be represented by

$$x(s,\theta )=(s+r(s)cos\phi ,r(s)sin\phi cosh\theta ,r(s)sin\phi sinh\theta ).$$

Furthermore, when $\kappa =0$, the first equation of (16) gives

$$\begin{array}{c}\hfill f=\frac{(2P_1^2+2P_1{sin}^2\phi +{sin}^4\phi )cos\phi -2r^2{sin}^2\phi P_1{H}_s}{r^2{P}_1^2(cos\phi +C_1)}.\end{array}$$

(20)

Because $P_1,H_s$ are all functions of s when $\kappa =0$, Equation (20) yields $f=f\left(s\right)$. Then, by the last two equations of (16), we obtain

$$\left\{\begin{array}{c}(r^2{Q}_1^2+P_1^2)sin\phi cosh\theta +2r^2{r}^{\prime }{sin}^2\phi H_s(sin\phi -r{\phi }^{\prime })cosh\theta =r^2{P}_1^2(sin\phi cosh\theta +C_2)f,\hfill \\ (r^2{Q}_1^2+P_1^2)sin\phi sinh\theta +2r^2{r}^{\prime }{sin}^2\phi H_s(sin\phi -r{\phi }^{\prime })sinh\theta =r^2{P}_1^2(sin\phi sinh\theta +C_3)f.\hfill \end{array}\right.$$

(21)

Because $r\ne 0$, $P_1\ne 0$ and $f=f\left(s\right)$, Equation system (21) implies $C_2=C_3=0$. In addition,

$$\begin{array}{c}\hfill f\left(s\right)=\frac{2P_1^2+2P_1{sin}^2\phi +{sin}^4\phi +2r^2{H}_s{P}_{1}cos\phi }{r^2{P}_1^2}.\end{array}$$

(22)

Combining (20) and (22), we get

$$\begin{array}{c}\hfill 2r^2{H}_s{P}_1(1-C_1{r}^{\prime })+C_1(2P_1^2+2P_1{sin}^2\phi +{sin}^4\phi )=0.\end{array}$$

(23)

Substituting (23) into (22), we have

$$f\left(s\right)=-\frac{2H_s}{C_1{P}_1}=\frac{P_1^2+r^2{Q}_1^2}{r^2{P}_1^2(1-C_1{r}^{\prime })}=\frac{4H^2-2K}{1-C_1{r}^{\prime }}.$$

(24)

Noticing that the principal curvatures are given by

$${\kappa }_1=-\frac{r^{″}}{r{r}^{″}+r^{\prime 2}-1},{\kappa }_2=-\frac{1}{r}$$

(25)

when $\kappa =0$, and thus the Gaussian curvature K, the mean curvature H can be abbreviated as

$$K=\frac{r^{″}}{r(r{r}^{″}+r^{\prime 2}-1)},H=-\frac{2r{r}^{″}+r^{\prime 2}-1}{2r(r{r}^{″}+r^{\prime 2}-1)}.$$

(26)

Due to $f\ne 0$, the mean curvature cannot be a constant. With the help of (10), Equation (23) can be rewritten as

$$2r^2{H}_s(1+rH)(C_1{r}^{\prime }-1)=C_1(2r^2{H}^2+2rH+1)(r^{\prime 2}-1).$$

(27)

Simplifying (27) with the help of (26), the radial function $r\left(s\right)$ satisfies the following equation:

$${\left[\frac{2r{r}^{″}+r^{\prime 2}-1}{r(r{r}^{″}+r^{\prime 2}-1)}\right]}^{\prime }=\frac{C_1}{1-C_1{r}^{\prime }}\frac{{\left(r{r}^{″}\right)}^2+{(r{r}^{″}+r^{\prime 2}-1)}^2}{r^2(r{r}^{″}+r^{\prime 2}-1)}.$$

(28)

Conversely, if ${\mathbb{M}}_{+}^{11}$ is a surface of revolution which satisfies (28), then $\Delta \mathbb{G}=f(\mathbb{G}+C)$ is satisfied for a non-zero function f as stated by (24) and a constant vector $C=(C_1,0,0)$ in which $C_1$ is a non-zero constant.

Theorem 1.

A canal surface ${\mathbb{M}}_{+}^{11}$ has a proper pointwise 1-type Gauss map of the second kind iff it is a surface of revolution with the following form:

$$x(s,\theta )=(s+r(s)cos\phi ,r(s)sin\phi cosh\theta ,r(s)sin\phi sinh\theta )$$

which satisfies (28).

Corollary 1.

A canal surface ${\mathbb{M}}_{+}^{11}$ with proper pointwise 1-type Gauss map of the second kind satisfies $\Delta \mathbb{G}=f(\mathbb{G}+C)$ for a constant vector $C=(C_1,0,0)$ and non-zero smooth function

$$f\left(s\right)=\frac{4H^2-2K}{1-C_1{r}^{\prime }},$$

where H and K are given by (26), and $C_1$ is a non-zero constant.

Corollary 2.

A canal surface ${\mathbb{M}}_{+}^{11}$ has 1-type Gauss map of the second kind iff it is a surface of revolution represented as

$$x(s,\theta )=(s+r(s)cos\phi ,r(s)sin\phi cosh\theta ,r(s)sin\phi sinh\theta )$$

which satisfies (30).

Proof. 

When a canal surface ${\mathbb{M}}_{+}^{11}$ satisfies $\Delta \mathbb{G}=\lambda (\mathbb{G}+C)$, $(\lambda \in \mathbb{R}-\{0\},C\ne 0)$, by Theorem 1, ${\mathbb{M}}_{+}^{11}$ is a surface of revolution which satisfies (28). By Corollary 1, we get

$${\left[\frac{2r{r}^{″}+r^{\prime 2}-1}{r(r{r}^{″}+r^{\prime 2}-1)}\right]}^{\prime }=\lambda C_1(r{r}^{″}+r^{\prime 2}-1).$$

(29)

From (28) and (29), we get

$${(r{r}^{″}+r^{\prime 2}-1)}^2(\lambda r^2(1-C_1{r}^{\prime })-1)-{\left(r{r}^{″}\right)}^2=0.$$

(30)

The converse is straightforward. □

Theorem 2.

A canal surface ${\mathbb{M}}_{+}^{11}$ has proper pointwise 1-type Gauss map of the first kind iff it is minimal. Precisely, it is a part of a surface of revolution as

$$x(s,\theta )=(s+r(s)cos\phi (s),r(s)sin\phi (s)cosh\theta ,r(s)sin\phi (s)sinh\theta )$$

which satisfies (33).

Proof. 

A canal surface ${\mathbb{M}}_{+}^{11}$ has proper pointwise 1-type Gauss map of the first kind, i.e., $\Delta \mathbb{G}=f\mathbb{G}$ for some smooth function f. From Equation (14), we have

$$\left\{\begin{array}{c}(r^2{Q}_1^2+P_1^2)cos\phi -2x_s^1{U}_1=r^2{P}_1^{2}cos\phi f,\hfill \\ (r^2{Q}_1^2+P_1^2)sin\phi cosh\theta -2(x_s^2{U}_1+x_{\theta }^1{V}_1)=r^2{P}_1^{2}sin\phi cosh\theta f,\hfill \\ (r^2{Q}_1^2+P_1^2)sin\phi sinh\theta -2(x_s^3{U}_1+x_{\theta }^2{V}_1)=r^2{P}_1^{2}sin\phi sinh\theta f.\hfill \end{array}\right.$$

(31)

From the last two equations of (31), we get

$$\begin{array}{c}\hfill (g_{22}{H}_s-g_{12}{H}_{\theta })(\tau {sin}^2\phi +r^{\prime }\kappa sin\phi sinh\theta )+(-g_{12}{H}_s+g_{11}{H}_{\theta }){sin}^2\phi =0,\end{array}$$

(32)

with the help of Equation (7), we obtain $P_1^2{H}_{\theta }=0$. Therefore, $H_{\theta }=0$ due to $P_1\ne 0$. Furthermore, from the first two equations of (31), we get $2r^2{P}_1{H}_s=0$. It is obvious that $H_s=0$. Then, the mean curvature of ${\mathbb{M}}_{+}^{11}$ is constant.

By the Corollary 3.6 of [4], i.e., the canal surface ${\mathbb{M}}_{+}^{11}$ with non-zero constant mean curvature does not exist, thus the canal surface ${\mathbb{M}}_{+}^{11}$ is minimal. From the Theorem 3.8 of [4], it is a part of a surface of revolution with the following form:

$$x(s,\theta )=(s+r(s)cos\phi (s),r(s)sin\phi (s)cosh\theta ,r(s)sin\phi (s)sinh\theta )$$

which satisfies

$$s=c_2\pm \int \sqrt{\frac{r}{r-c_1}}dr,(0<c_1<r,c_2\in \mathbb{R}).$$

(33)

Looking back the Equation (31) with the conclusions obtained above, we have

$$f\left(s\right)=-2K=\frac{2}{r^2}.$$

(34)

Conversely, suppose that ${\mathbb{M}}_{+}^{11}$ is a surface of revolution satisfying (33), ${\mathbb{M}}_{+}^{11}$ is minimal from the Theorem 3.8 of [4] and $\Delta \mathbb{G}=f\mathbb{G}$ is satisfied for some non-zero function f given by (34). □

Corollary 3.

A canal surface ${\mathbb{M}}_{+}^{11}$ with proper pointwise 1-type Gauss map of the first kind satisfies $\Delta \mathbb{G}=\frac{2}{r^2}\mathbb{G}.$

Assume that a canal surface ${\mathbb{M}}_{+}^{11}$ satisfies $\Delta \mathbb{G}=\lambda \mathbb{G}$, $(\lambda \in \mathbb{R}-\{0\left\}\right)$. By Corollary 3, we have $\lambda =\frac{2}{r^2}$ is a constant, i.e., r is a constant. Thus, we have the following result.

Corollary 4.

A canal surface ${\mathbb{M}}_{+}^{11}$ has 1-type Gauss map of the first kind iff it is a circular cylinder.

From Corollary 3, the following conclusion is straightforward since $\frac{2}{r^2}\ne 0$.

Corollary 5.

The canal surface ${\mathbb{M}}_{+}^{11}$ with harmonic Gauss map does not exist.

3.2. The Canal Surfaces of Type ${\mathbb{M}}_{+}^{12}$ with Pointwise 1-Type Gauss Maps

From Equation (3), the canal surface ${\mathbb{M}}_{+}^{12}$ is parameterized as

$$x(s,\theta )=c\left(s\right)+r\left(s\right)(cos\phi (s)\alpha +sin\phi (s)sinh\theta \beta +sin\phi (s)cosh\theta \gamma ),$$

where $cos\phi \left(s\right)=-r^{\prime }\left(s\right)$, $(\phi \in [0,\pi \left)\right)$ is a smooth function.

Through direct calculations, we have initially

$$x_s=x_s^1\alpha +x_s^2\beta +x_s^3\gamma ,x_{\theta }=x_{\theta }^1\beta +x_{\theta }^2\gamma ,$$

where

$$\begin{array}{cc}\hfill & x_s^1=-r{r}^{″}+r\kappa sin\phi sinh\theta +{sin}^2\phi ;\hfill \\ \hfill & x_s^2=r^{\prime }sin\phi sinh\theta -r{r}^{\prime }{\phi }^{\prime }sinh\theta +r\tau sin\phi cosh\theta -r{r}^{\prime }\kappa ;\hfill \\ \hfill & x_s^3=r^{\prime }sin\phi cosh\theta -r{r}^{\prime }{\phi }^{\prime }cosh\theta +r\tau sin\phi sinh\theta ;\hfill \\ \hfill & x_{\theta }^1=rsin\phi cosh\theta ;\hfill \\ \hfill & x_{\theta }^2=rsin\phi sinh\theta .\hfill \end{array}$$

Thus, the Gauss map $\mathbb{G}$ of ${\mathbb{M}}_{+}^{12}$ is

$$\mathbb{G}=-cos\phi \alpha -sin\phi sinh\theta \beta -sin\phi cosh\theta \gamma ,$$

(35)

which points towards ${\mathbb{M}}_{+}^{12}$ inside and $⟨\mathbb{G},\mathbb{G}⟩=1$.

Meanwhile, the quantities of the first fundamental form are obtained as

$$g_{11}=\frac{P_2^2-r^2{R}_2^2}{{sin}^2\phi },g_{12}=r^2{R}_2,g_{22}=-r^2{sin}^2\phi ,$$

(36)

the quantities of the second fundamental form are written by

$$h_{11}=\frac{-r{R}_2^2+P_2{Q}_2}{{sin}^2\phi },h_{12}=r{R}_2,h_{22}=-r{sin}^2\phi ,$$

(37)

where

$$\begin{array}{cc}\hfill & P_2=-r{r}^{″}+r\kappa sin\phi sinh\theta +{sin}^2\phi =r{Q}_2+{sin}^2\phi ,\hfill \\ \hfill & Q_2=-r^{″}+\kappa sin\phi sinh\theta ,\hfill \\ \hfill & R_2=r^{\prime }\kappa sin\phi cosh\theta -\tau {sin}^2\phi .\hfill \end{array}$$

From Equations (36) and (37), the Gaussian curvature K and the mean curvature H of ${\mathbb{M}}_{+}^{12}$ are

$$K=\frac{Q_2}{r{P}_2},H=\frac{2P_2-{sin}^2\phi }{2r{P}_2}.$$

Remark 5.

From $g_{11}{g}_{22}-g_{12}^2=-r^2{P}_2^2,$ due to regularity, we see that $P_2\ne 0$ everywhere.

Next, the Laplacian of the Gauss map $\mathbb{G}$ of ${\mathbb{M}}_{+}^{12}$ is to be calculated. First, from the first fundamental form of ${\mathbb{M}}_{+}^{12}$, we have

$$g^{11}=\frac{{sin}^2\phi }{P_2^2},g^{12}=g^{21}=\frac{R_2}{P_2^2},g^{22}=\frac{r^2{R}_2^2-P_2^2}{r^2{P}_2^2{sin}^2\phi }.$$

(38)

Substituting (35), (36), and (38) into (1), by putting

$$\begin{array}{c}\hfill \begin{array}{c}\hfill U_2=g_{22}{H}_s-g_{12}{H}_{\theta },V_2=-g_{12}{H}_s+g_{11}{H}_{\theta },\end{array}\end{array}$$

where

$$\begin{array}{cc}\hfill H_s=& \frac{-2r^2{r}^{\prime }{\kappa }^2{sin}^2\phi {sinh}^2\theta -(2r{r}^{\prime }\kappa -r^2{\kappa }^{\prime }){sin}^3\phi sinh\theta +5r^2{r}^{\prime }{r}^{″}\kappa sin\phi sinh\theta }{2r^2{P}_2^2}+\hfill \\ \hfill & \frac{2r{r}^{\prime }{r}^{″}{sin}^2\phi -r^2{r}^{‴}{sin}^2\phi -4r^2{r}^{\prime }{r}^{″2}-r^{\prime }{sin}^4\phi }{2r^2{P}_2^2},\hfill \\ \hfill H_{\theta }=& \frac{\kappa {sin}^3\phi cosh\theta }{2P_2^2},\hfill \end{array}$$

after complicated arrangements, we get

$$\begin{array}{cc}\hfill \Delta \mathbb{G}=& -\frac{1}{r^2{P}_2^2}\{[(r^2{Q}_2^2+P_2^2)cos\phi +2x_s^1{U}_2]\alpha +[(r^2{Q}_2^2+P_2^2)sin\phi sinh\theta +2(x_s^2{U}_2+x_{\theta }^1{V}_2)]\beta +\hfill \\ \hfill & [(r^2{Q}_2^2+P_2^2)sin\phi cosh\theta +2(x_s^3{U}_2+x_{\theta }^2{V}_2)]\gamma \}.\hfill \end{array}$$

Due to discussions similar to those of ${\mathbb{M}}_{+}^{11}$, we have the following conclusions directly.

Theorem 3.

A canal surface ${\mathbb{M}}_{+}^{12}$ has proper pointwise 1-type Gauss map of the second kind iff it is a surface of revolution with the following form:

$$x(s,\theta )=(s+r(s)cos\phi ,r(s)sin\phi cosh\theta ,r(s)sin\phi sinh\theta )$$

which satisfies

$${\left[\frac{2r{r}^{″}+r^{\prime 2}-1}{r(r{r}^{″}+r^{\prime 2}-1)}\right]}^{\prime }=\frac{C_1}{1+C_1{r}^{\prime }}\frac{{\left(r{r}^{″}\right)}^2+{(r{r}^{″}+r^{\prime 2}-1)}^2}{r^2(r{r}^{″}+r^{\prime 2}-1)},$$

where $C_1$ is a non-zero constant.

Corollary 6.

A canal surface ${\mathbb{M}}_{+}^{12}$ with proper pointwise 1-type Gauss map of the second kind satisfies $\Delta \mathbb{G}=f(\mathbb{G}+C)$ for a constant vector $C=(C_1,0,0)$ and non-zero smooth function

$$f\left(s\right)=\frac{4H^2-2K}{1+C_1{r}^{\prime }},$$

where $C_1$ is a non-zero constant, H and K are given by

$$K=\frac{r^{″}}{r(r{r}^{″}+r^{\prime 2}-1)},H=\frac{2r{r}^{″}+r^{\prime 2}-1}{2r(r{r}^{″}+r^{\prime 2}-1)}.$$

Corollary 7.

A canal surface ${\mathbb{M}}_{+}^{12}$ has 1-type Gauss map of the second kind iff it is a surface of revolution represented as

$$x(s,\theta )=(s+r(s)cos\phi ,r(s)sin\phi cosh\theta ,r(s)sin\phi sinh\theta )$$

which satisfies

$${(r{r}^{″}+r^{\prime 2}-1)}^2(\lambda r^2(1+C_1{r}^{\prime })+1)+{\left(r{r}^{″}\right)}^2=0.$$

Theorem 4.

A canal surface ${\mathbb{M}}_{+}^{12}$ has proper pointwise 1-type Gauss map of the first kind iff it is minimal. Precisely, it is a part of a surface of revolution as

$$x(s,\theta )=(s+r(s)cos\phi (s),r(s)sin\phi (s)cosh\theta ,r(s)sin\phi (s)sinh\theta )$$

which satisfies

$$s=c_2\pm \int \sqrt{\frac{r}{r-c_1}}dr,(0<c_1<r,c_2\in \mathbb{R}).$$

Corollary 8.

A canal surface ${\mathbb{M}}_{+}^{12}$ with proper pointwise 1-type Gauss map of the first kind satisfies $\Delta \mathbb{G}=\frac{2}{r^2}\mathbb{G}.$

Corollary 9.

A canal surface ${\mathbb{M}}_{+}^{12}$ has 1-type Gauss map of the first kind iff it is a circular cylinder.

Corollary 10.

The canal surface ${\mathbb{M}}_{+}^{12}$ with harmonic Gauss map does not exist.

3.3. The Canal Surfaces of Type ${\mathbb{M}}_{+}^2$ with Pointwise 1-Type Gauss Maps

From Equation (4), the canal surface ${\mathbb{M}}_{+}^2$ is parameterized as

$$x(s,\theta )=c\left(s\right)+r\left(s\right)(tan\phi (s)\alpha +sec\phi (s)cos\theta \beta +sec\phi (s)sin\theta \gamma ),$$

where $tan\phi \left(s\right)=r^{\prime }\left(s\right)$, $(\phi \in (-\frac{\pi }{2},\frac{\pi }{2}))$ is a smooth function.

Through direct calculations, we have initially

$$x_s=x_s^1\alpha +x_s^2\beta +x_s^3\gamma ,x_{\theta }=x_{\theta }^1\beta +x_{\theta }^2\gamma ,$$

where

$$\begin{array}{cc}\hfill & x_s^1=r{r}^{″}+r\kappa sec\phi cos\theta +{sec}^2\phi ;\hfill \\ \hfill & x_s^2=r^{\prime }sec\phi cos\theta +r{r}^{\prime }{\phi }^{\prime }sec\phi cos\theta +r\tau sec\phi sin\theta +r{r}^{\prime }\kappa ;\hfill \\ \hfill & x_s^3=r^{\prime }sec\phi sin\theta +r{r}^{\prime }{\phi }^{\prime }sec\phi sin\theta -r\tau sec\phi cos\theta ;\hfill \\ \hfill & x_{\theta }^1=-rsec\phi sin\theta ;\hfill \\ \hfill & x_{\theta }^2=rsec\phi cos\theta .\hfill \end{array}$$

Thus, the Gauss map $\mathbb{G}$ of ${\mathbb{M}}_{+}^2$ is

$$\mathbb{G}=tan\phi \alpha +sec\phi cos\theta \beta +sec\phi sin\theta \gamma ,$$

(39)

which points towards ${\mathbb{M}}_{+}^2$ inside and $⟨\mathbb{G},\mathbb{G}⟩=1$.

Meanwhile, the quantities of the first fundamental form are obtained as

$$g_{11}=-\frac{P_3^2-r^2{R}_3^2}{{sec}^2\phi },g_{12}=-r^2{R}_3,g_{22}=r^2{sec}^2\phi ,$$

(40)

and the quantities of the second fundamental form are written by

$$h_{11}=\frac{-r{R}_3^2+P_3{Q}_3}{{sec}^2\phi },h_{12}=r{R}_3,h_{22}=-r{sec}^2\phi ,$$

(41)

where

$$\begin{array}{cc}\hfill & P_3=r{r}^{″}+r\kappa sec\phi cos\theta +{sec}^2\phi =r{Q}_3+{sec}^2\phi ,\hfill \\ \hfill & Q_3=r^{″}+\kappa sec\phi cos\theta ,\hfill \\ \hfill & R_3=r^{\prime }\kappa sec\phi sin\theta +\tau {sec}^2\phi .\hfill \end{array}$$

From Equations (40) and (41), the Gaussian curvature K and the mean curvature H of ${\mathbb{M}}_{+}^2$ are

$$K=\frac{Q_3}{r{P}_3},H=\frac{-2P_3+{sec}^2\phi }{2r{P}_3}.$$

(42)

Remark 6.

From $g_{11}{g}_{22}-g_{12}^2=-r^2{P}_3^2,$ due to regularity, we see that $P_3\ne 0$ everywhere.

In the following, the Laplacian of the Gauss map $\mathbb{G}$ of ${\mathbb{M}}_{+}^2$ is to be calculated. First, from the first fundamental form of ${\mathbb{M}}_{+}^2$, we have

$$g^{11}=-\frac{{sec}^2\phi }{P_3^2},g^{12}=g^{21}=-\frac{R_3}{P_3^2},g^{22}=\frac{P_3^2-r^2{R}_3^2}{r^2{P}_3^2{sec}^2\phi }.$$

(43)

Substituting (39), (40), and (43) into (1), by putting

$$\begin{array}{c}\hfill \begin{array}{c}\hfill U_3=g_{22}{H}_s-g_{12}{H}_{\theta },V_3=-g_{12}{H}_s+g_{11}{H}_{\theta },\end{array}\end{array}$$

where

$$\begin{array}{cc}\hfill H_s=& \frac{2r^2{r}^{\prime }{\kappa }^2{sec}^2\phi {cos}^2\theta +(2r{r}^{\prime }\kappa -r^2{\kappa }^{\prime }){sec}^3\phi cos\theta +5r^2{r}^{\prime }{r}^{″}\kappa sec\phi cos\theta }{2r^2{P}_3^2}+\hfill \\ \hfill & \frac{2r{r}^{\prime }{r}^{″}{sec}^2\phi -r^2{r}^{‴}{sec}^2\phi +4r^2{r}^{\prime }{r}^{″2}+r^{\prime }{sec}^4\phi }{2r^2{P}_3^2},\hfill \\ \hfill H_{\theta }=& \frac{\kappa {sec}^3\phi sin\theta }{2P_3^2},\hfill \end{array}$$

through complicated arrangements, we get

$$\begin{array}{cc}\hfill \Delta \mathbb{G}=& \frac{1}{r^2{P}_3^2}\{[(r^2{Q}_3^2+P_3^2)tan\phi -2x_s^1{U}_3]\alpha +[(r^2{Q}_3^2+P_3^2)sec\phi cos\theta -2(x_s^2{U}_3+x_{\theta }^1{V}_3)]\beta +\hfill \\ \hfill & [(r^2{Q}_3^2+P_3^2)sec\phi sin\theta -2(x_s^3{U}_3+x_{\theta }^2{V}_3)]\gamma \}.\hfill \end{array}$$

Due to discussions similar to those of ${\mathbb{M}}_{+}^{11}$ and ${\mathbb{M}}_{+}^{12}$, the following results for ${\mathbb{M}}_{+}^2$ can be given directly.

Theorem 5.

A canal surface ${\mathbb{M}}_{+}^2$ has proper pointwise 1-type Gauss map of the second kind iff it is a surface of revolution with the following form:

$$x(s,\theta )=\left(r\right(s)sec\phi sin\theta ,r(s)sec\phi cos\theta ,s+r(s)tan\phi )$$

which satisfies

$${\left[\frac{2r{r}^{″}+r^{\prime 2}+1}{r(r{r}^{″}+r^{\prime 2}+1)}\right]}^{\prime }=\frac{C_1}{1-C_1{r}^{\prime }}\frac{{\left(r{r}^{″}\right)}^2+{(r{r}^{″}+r^{\prime 2}+1)}^2}{r^2(r{r}^{″}+r^{\prime 2}+1)},$$

where $C_1$ is a non-zero constant.

Corollary 11.

A canal surface ${\mathbb{M}}_{+}^2$ with proper pointwise 1-type Gauss map of the second kind satisfies $\Delta \mathbb{G}=f(\mathbb{G}+C)$ for a constant vector $C=(C_1,0,0)$ and non-zero smooth function

$$f\left(s\right)=\frac{4H^2-2K}{1-C_1{r}^{\prime }},$$

where $C_1$ is a non-zero constant, H and K are given by

$$K=\frac{r^{″}}{r(r{r}^{″}+r^{\prime 2}+1)},H=-\frac{2r{r}^{″}+r^{\prime 2}+1}{2r(r{r}^{″}+r^{\prime 2}+1)}.$$

Corollary 12.

A canal surface ${\mathbb{M}}_{+}^2$ has 1-type Gauss map of the second kind iff it is a surface of revolution represented as

$$x(s,\theta )=\left(r\right(s)sec\phi sin\theta ,r(s)sec\phi cos\theta ,s+r(s)tan\phi )$$

where $r\left(s\right)$ satisfies

$${(r{r}^{″}+r^{\prime 2}+1)}^2(\lambda r^2(1-C_1{r}^{\prime })-1)-{\left(r{r}^{″}\right)}^2=0.$$

Theorem 6.

A canal surface ${\mathbb{M}}_{+}^2$ has proper pointwise 1-type Gauss map of the first kind iff it is minimal. Precisely, it is a part of a surface of revolution as

$$x(s,\theta )=\left(r\right(s)sec\phi sin\theta ,r(s)sec\phi cos\theta ,s+r(s)tan\phi ),$$

which satisfies

$$s=c_2\pm \int \sqrt{\frac{r}{c_1-r}}dr,(c_1>r>0,c_2\in \mathbb{R}).$$

Corollary 13.

A canal surface ${\mathbb{M}}_{+}^2$ with proper pointwise 1-type Gauss map of the first kind satisfies $\Delta \mathbb{G}=\frac{2}{r^2}\mathbb{G}.$

Corollary 14.

A canal surface ${\mathbb{M}}_{+}^2$ has 1-type Gauss map of the first kind iff it is a circular cylinder.

Corollary 15.

The canal surface ${\mathbb{M}}_{+}^2$ with harmonic Gauss map does not exist.

Until now, the canal surfaces foliated by pseudo spheres ${\mathbb{S}}_1^2$ along the Frenet curves, i.e., ${\mathbb{M}}_{+}^{11}$, ${\mathbb{M}}_{+}^{12}$, and ${\mathbb{M}}_{+}^2$ have been classified in terms of their Gauss maps completely. The similar works for the canal surfaces ${\mathbb{M}}_{-}^{11}$, ${\mathbb{M}}_{-}^{12}$ and ${\mathbb{M}}_{-}^2$ will be done in the near future. At the same time, considering that the canal surfaces ${\mathbb{M}}_0$ foliated by lightlike cones ${\mathbb{Q}}^2$ along a space curve are degenerate [4,5], the canal surfaces ${\mathbb{M}}_{+}^{13}$, ${\mathbb{M}}_{+}^3$ (resp. ${\mathbb{M}}_{-}^{13}$, ${\mathbb{M}}_{-}^3$) foliated by pseudo spheres ${\mathbb{S}}_1^2$ (resp. pseudo hyperbolic spheres ${\mathbb{H}}_0^2$) along a pseudo null curve or a null curve, respectively, are to be investigated in our future works.