A Fuzzy-Statistical Tolerance Interval from Residuals of Crisp Linear Regression Models

Abstract

Linear regression is a simple but powerful tool for prediction. However, it still suffers from some deficiencies, which are related to the assumptions made when using a model like normality of residuals, uncorrelated errors, where the mean of residuals should be zero. Sometimes these assumptions are violated or partially violated, thereby leading to uncertainties or unreliability in the predictions. This paper introduces a new method to account for uncertainty in the residuals of a linear regression model. First, the error in the estimation of the dependent variable is calculated and transformed to a fuzzy number, and this fuzzy error is then added to the original crisp prediction, thereby resulting in a fuzzy prediction. The results are compared to a fuzzy linear regression with crisp input and fuzzy output, in terms of their ability to represent uncertainty in prediction.

1. Introduction

In classical linear regression models, assumptions like linearity, fixed independent variables, normality of residuals, uncorrelated errors are made to simplify model estimation procedures. Despite these assumptions, the results are often taken at face value with very little effort, to adequately represent the uncertainty in predictions made by the model. Uncertainties in linear regression models are often represented via confidence and prediction intervals, which may not be adequate, since only one interval is calculated; e.g., 95% confidence or the prediction interval. Fuzzy linear regression with crisp input can be used to better represent uncertainty in prediction. This fuzzy model, first proposed in [1], has been widely used as alternative to classical crisp linear regression models. Since then, there have been various modifications to the model to overcome certain limitations of the original model [2,3,4,5]. Although such fuzzy linear regression models can represent uncertainty, there has always been doubt in terms of their suitability for prediction of future values (see a discussion on this in [6]). The problem is that minimization of fuzziness of the model is done, such that model fits the available sample with a certain h-value. There is no connection with prediction of future values like those of classic regression. Recently, there has been an attempt by [7] to create fuzzy numbers from predictions made by classic linear regression models, without the need of optimization or assuming any fuzzy coefficient, or fuzzy input or output. In their work, confidence and prediction intervals from crisp linear regression are converted to fuzzy numbers, by superimposing intervals and deriving the equivalent membership functions using fuzzy estimators. In this paper, we use the technique that was introduced in [7], and we propose a new approach to fuzzify the outputs of crisp linear regression models, for use in the case of tolerance intervals that are required, instead of prediction intervals. In our proposed approach, we assume that errors are normally distributed and, as such, we can construct a tolerance interval of normal distribution for the errors. This tolerance interval will contain at least a proportion of the errors, both those in the sample and those outside of the sample (future predictions). Using the method proposed in [8], we construct a fuzzy number by superimposing the tolerance intervals up to the mean error. We then use this fuzzy tolerance interval as a fuzzy estimate of the error in our model. This is similar to the error proposed in [9], which uses crisp coefficients, and estimates a fuzzy error using optimization. This is to avoid the issue of the increasing magnitude of spread with an increasing independent variable. To complete the process, we add the fuzzy tolerance error to our crisp estimate, thereby resulting in a fuzzy estimate. The advantage of the proposed approach is that all possible statistical errors in the model are represented in one interval. Statistical tolerance intervals are, by definition, different from prediction intervals, and they serve a different purpose. Tolerance intervals give the percentage of population coverage interval with some confidence level, while a prediction interval will give the coverage interval for a single prediction. The interpretation and calculation of both intervals are also different. This paper thus extends the work in [7,8], to produce fuzzy statistical tolerance intervals. The method proposed here is important for applications where a tolerance interval is needed, instead of a prediction interval. The tolerance interval covers both the confidence interval and the prediction interval. Thus, both in-sample, out-of-sample, and future errors are covered. It also uses the information that model errors are normally distributed, so the better the original crisp model, the better the fuzzy model. Finally, the proposed method produces a fuzzy output with only crisp input, and crisp parameters without the need for optimization.

2. Crisp Linear Regression

A linear regression model with $n$ independent variables and one dependent variable can be written as:

$$Y_k={\alpha }_0+{\alpha }_1{X}_{k1}+{\alpha }_2{X}_{k2}+\dots +{\alpha }_n{X}_{kn}+{\epsilon }_k$$

where $Y_k$ is the dependent variable, $X_{ki},i=1,2,\dots ,n$ are the independent variables, ${\alpha }_0,{\alpha }_1$,…,${\alpha }_n$ are the coefficients which need to be estimated, and ${\epsilon }_k$ is the random error of the model. The linear regression model assumes that errors are normally distributed with zero mean and constant variance, i.e., ${\epsilon }_k\sim N\left(0,\sigma \right)$.

The method of least squares is the most common way of estimating the model parameters. The parameters are calculated as:

$$A={(X^{T}X)}^{-1}{X}^{T}Y$$

where $A$ is a vector of the parameters, $X$ is a matrix of explanatory variables, and $Y$ is a vector of the response variable. A thorough examination of the distribution of errors is usually done after model estimation, to check the validity of the model.

To account for uncertainty in prediction due to random errors, prediction and confidence intervals are easily constructed both for the estimated parameters and for the predicted response. The $(1-\alpha$)% prediction intervals are given as follows:

$$\overline{Y_k}\pm t_{1-\frac{\alpha }{2},K-p}\sqrt{MSE\left(1+h_f\right)}$$

where $X$ is a matrix of explanatory variables, $\overline{Y}$ is the estimated response variable, $K$ is the sample size, $MSE$ is the estimate of the mean-squared error of the model, $t_{1-\frac{\alpha }{2},K-p}$ is a t-distribution with K−p degrees of freedom, and $h_f=x_f{\left(X^{T}X\right)}^{-1}{x}_f$, where $x_f$ is the row-vector of that observation.

3. Fuzzy Linear Regression

The classical fuzzy linear regression model proposed by [1] is similar to the crisp linear regression. The main difference is that the parameters are fuzzy numbers. This results in a fuzzy output for the response variable. The model is given below:

$$\widetilde{Y_k}={\tilde{A}}_0+{\tilde{A}}_1{X}_{k1}+{\tilde{A}}_2{X}_{k2}+\dots +{\tilde{A}}_n{X}_{kn}$$

where $\widetilde{A_i}\left(i=1,2,\dots ,n\right)$ are symmetric triangular fuzzy numbers of the form $\left(c_i,r_i\right)$, $c_i$ is the center of the triangular fuzzy number and $r_i$ is the spread. The objective of the fuzzy linear regression model is to minimize the uncertainty by minimizing the spreads of the fuzzy numbers. This results in the linear optimization problem below [1]:

$$J=m{c}_0+{\displaystyle \sum }_{j=1}^K{\displaystyle \sum }_{i=1}^n{c}_i\left|x_{ij}\right|$$

with the following constraints:

$$y_j\ge r_0+{\displaystyle \sum }_{i=1}^n{r}_i{x}_{ij}-\left(1-h\right)\left(c_0+{\displaystyle \sum }_{i=1}^n{c}_i\left|x_{ij}\right|\right)$$

$$y_j\le r_0+{\displaystyle \sum }_{i=1}^n{r}_i{x}_{ij}+\left(1-h\right)\left(c_0+{\displaystyle \sum }_{i=1}^n{c}_i\left|x_{ij}\right|\right)$$

where $c_i\ge 0,i=1,2,\dots ,n$. The value $0\le h\le 1$ represents the confidence level of the model and the membership value of all all responses in the sample should be at least h i.e., $\mu \left(y_j\right)\ge h$ for $j=1,2,\dots ,K$.

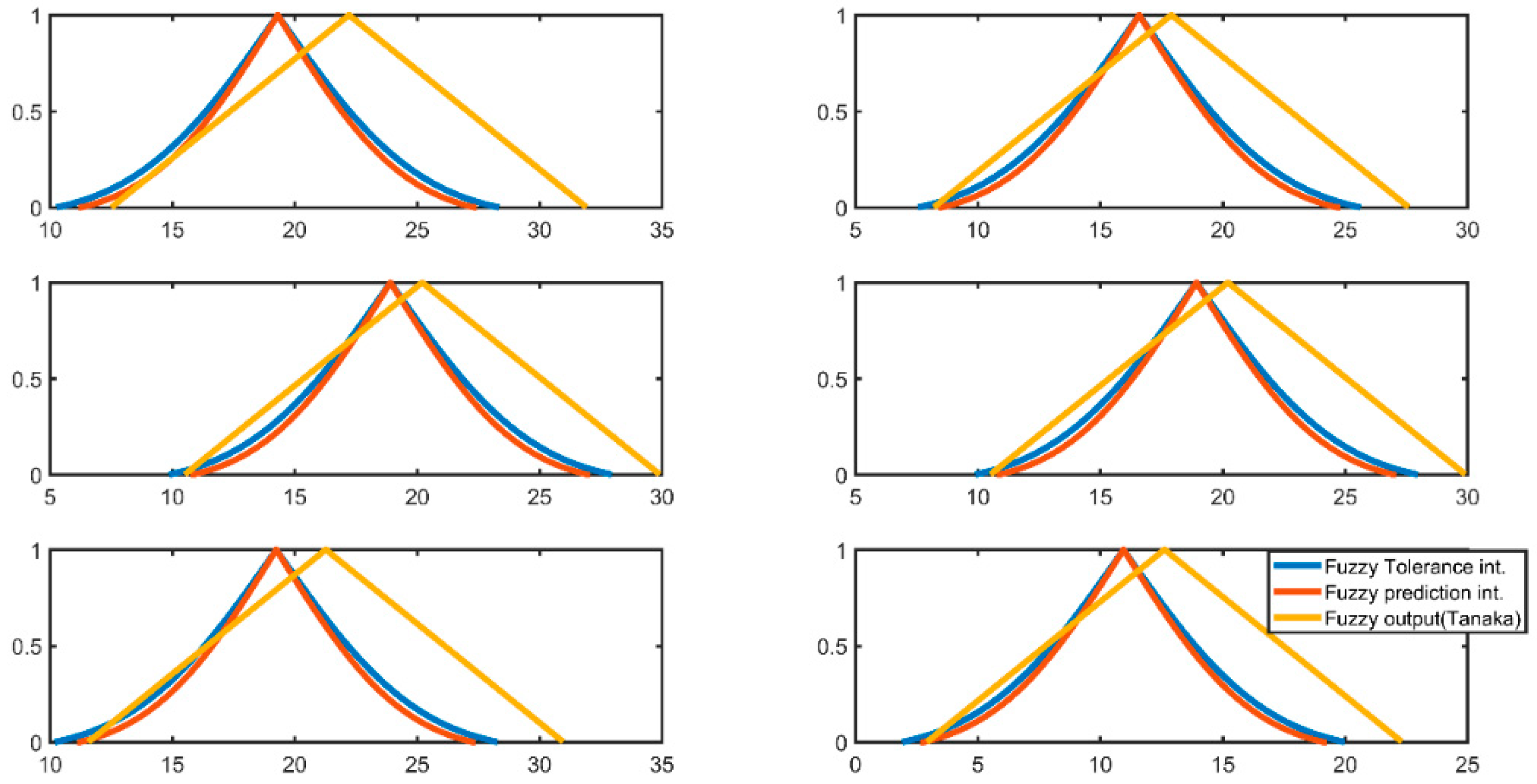
4. Proposed Method

Suppose that we have estimated a linear regression model and checked its validity with the necessary residual plots. That is, we assume that the model is well calibrated, and the distribution of errors are approximately normal. From every observation, our model produces an error:

$${\epsilon }_k=y_k-{\widehat{y}}_k$$

where $y_k$ is the real value of the response variable and ${\widehat{y}}_k$ is the estimate from the model. We assume that all errors in the model come from a normal distribution, with an unknown mean and unknown standard deviation. To accommodate the uncertainty in our errors, we can construct confidence intervals for the mean, or standard deviation of errors. However, this does not give us a bound on all errors that the model can produce, but only a bound for the mean. Additionally, a prediction interval can only hold for a particular prediction and, thus, it is not valid for other predictions. To accommodate both sample errors and future prediction errors, we opt to use a tolerance interval to bound the errors; an interval which contains $p\%$ of all errors with confidence $\gamma \%.$ To simplify calculations, we do not focus on tolerance intervals for $Y$ given a particular $X$ (see for example [10]). Rather, we focus on calculating a general tolerance interval of a random sample originating from a normal distribution. We treat all errors in our model estimation as a random sample and try to find a tolerance interval for such errors. There are various ways to calculate the tolerance interval of a sample from a normal distribution [11,12,13]. For simplicity we choose, the approximation offered by [13]. The tolerance interval is defined below:

$$\overline{x}\pm K_{2}s$$

$$K_2=z_{\frac{1+p}{2}}\sqrt{\frac{\nu \left(1+\frac{1}{N}\right)}{{\chi }_{1-\gamma ,\nu }^2}}$$

where $\overline{x}=\overline{\epsilon }$ is the sample mean of the errors, $s$ the sample standard deviation of the errors, $K_2$ is the tolerance factor, ${\chi }_{1-\gamma ,\nu }^2$ is the critical value of the chi-square distribution with degrees of freedom ν that is exceeded with probability $\gamma$ and $z_{\raisebox{1ex}{$\left(1+p\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ is the critical value of the normal distribution associated with cumulative probability $\frac{1+p}{2}$.

To represent more proportions, we convert this interval to a fuzzy interval by superimposing all proportions up to $p=0\%$, while the confidence level $\gamma \%$ is kept constant. Using the method proposed in [14,15], which was generalized in [8], we convert this interval to a fuzzy number with explicit membership function. In [8], it was shown that any interval of the form $\left[\overline{x}-mf\left(\alpha \right) \overline{x}+mf\left(\alpha \right)\right]$ can be converted to a fuzzy number with explicit membership function if an appropriate function $f\left(\alpha \right)$ is chosen, where $m$ is a constant and $f\left(\alpha \right)$ a function of $\alpha$-cut of the corresponding fuzzy number. It has been shown that the inverse cumulative distribution functions are proper candidates for $\left(\alpha \right)$. Since $z_{\frac{1+p}{2}}$ is an inverse cumulative distribution function, the superimposed intervals can be converted to a fuzzy number.

Now, the tolerance interval $\left[\overline{x}-K_{2}s \overline{x}+K_{2}s\right]$ can be written in the form:

$$\left[\overline{x}-mf\left(\beta \right) \overline{x}+mf\left(\beta \right)\right]$$

where $m=s\sqrt{\frac{\nu \left(1+\frac{1}{N}\right)}{{\chi }_{1-\gamma ,\nu }^2}}$, $f\left(\beta \right)=z_{\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, $z_{\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}={\Phi }^{-1}\left(1-\frac{\beta }{2}\right)$.

Note that we substitute $z_{\raisebox{1ex}{$\left(1+p\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ =$z_{\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ where $\beta =1-p$ for convenience; for example, $p=0.90$ is equivalent to $\beta =0.1$. The tolerance interval is then written as:

$$\left[\overline{x}-K_{2}s \overline{x}+K_{2}s\right]=\left[\overline{x}-m{z}_{\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \overline{x}+m{z}_{\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]$$

The interval above is exactly the $(1-\beta$)% tolerance interval with confidence $\gamma \%$.

With the above substitutions, the following membership function can be derived for the interval:

$$A\left(x\right)=\{\begin{array}{c}\frac{2}{1-\beta }\Phi \left(\frac{x-\overline{x}}{m}\right)-\frac{\beta }{1-\beta },\overline{x}-m{\Phi }^{-1}\left(1-\frac{\beta }{2}\right)\le \overline{x}\\ \frac{2}{1-\beta }\Phi \left(\frac{\overline{x}-x}{m}\right)-\frac{\beta }{1-\beta },\overline{x}\le \overline{x}+m{\Phi }^{-1}\left(1-\frac{\beta }{2}\right)\\ 0,otherwise\end{array}$$

The a-cut of the fuzzy number above is [8]:

$${}^{\alpha }A=\left[\overline{x}-m{z}_{h\left(\alpha \right)} \overline{x}+m{z}_{h\left(\alpha \right)}\right]$$

where $z_{h\left(\alpha \right)}={\Phi }^{-1}\left(1-h\left(\alpha \right)\right)$ is the inverse cumulative distribution function (cdf) of a normal distribution and $h\left(\alpha \right)$ is any monotonic non-decreasing function $h\left(\alpha \right):\left(0,1\right]\to \left[\frac{\beta }{2},0.5\right]$, $\beta \in \left(0,1\right)$, where $h\left(\alpha \right)$=$\left(\frac{1}{2}-\frac{\beta }{2}\right)\alpha +\frac{\beta }{2}$.

Constructing a fuzzy output from the crisp linear regression, using the fuzzy number constructed from the tolerance interval of the errors, a crisp prediction from a linear regression model can be converted to a fuzzy output by adding the fuzzy error. The fuzzy output can be then written as:

$$\widetilde{Y_k}={\alpha }_0+{\alpha }_1{X}_{k1}+{\alpha }_2{X}_{k2}+\dots +{\alpha }_n{X}_{kn}+\tilde{\epsilon }$$

where $\tilde{\epsilon }$ is the fuzzy error constructed from the tolerance interval using the procedure described above. The reason for having only one error and not a prediction specific error is that it considers all errors in the model and, thus, it gives more conservative estimates compared to a prediction interval. Note that this approach is similar to the fuzzy linear regression model proposed in [9] but the error that they propose there is a fuzzy error estimated from an optimization process, and is not based on any statistical interval like the current one. Additionally, our method is similar to the one proposed in [7], but there the authors do not use the tolerance interval for errors like we do here. In their approach they convert well-known confidence and prediction intervals from linear regression to fuzzy numbers, using the same procedure used here. Our model can be viewed as a fuzzy linear regression model with a fuzzy error constructed from a statistical tolerance interval. This can be used in the case where a tolerance interval is of interest, rather than a prediction or confidence interval.

5. Case Study

In order to test the applicability of our fuzzy linear regression model, two datasets from the fuzzy literature are used [16] and two real datasets from the classical linear regression literature (car data, UCI machine learning repository [17], Hald Cement data [18,19]. We compare the results to those of classical linear regression, to fuzzy linear regression of [1] and the fuzzy prediction intervals proposed in [7]. The datasets from the fuzzy literature are shown in the

Table 1. First dataset from Liu and Chen 2013 [16].

$x_1$	29.50	31.30	37.60	39.90	39.90	40.30	41.50	43.60	45.70	47.80	49.50
$x_2$	79.99	75.63	69.25	62.75	64.66	63.09	61.51	60.07	58.22	58.43	60.57
$y$	133.60	137.63	147.86	196.76	220.53	223.25	233.19	265.67	335.16	411.29	460.68

,

Table 2. First dataset from Liu and Chen 2013 [16].

$x_1$	50.10	50.20	49.90	50.00	50.00	50.00	50.90	53.10	55.20
$x_2$	58.23	58.03	57.53	55.68	55.24	54.51	50.08	50.05	49.72
$y$	477.96	474.02	466.80	466.16	469.80	468.95	476.24	499.39	521.20

and

Table 3. Second dataset from Liu and Chen 2013 [16].

$x$	2	4	6	8	10	12	16	18
$y$	14	16	14	18	18	22	18	22

below.

Note that the comparison with a classical fuzzy model, and fuzzy prediction interval proposed in [7] is done for clarity, rather than to compare predictive performance. As it is well-known, tolerance interval, prediction interval, and the spreads from a fuzzy linear regression have different interpretations and are used for different purposes. Therefore, the results are not directly comparable. However, all three models share some similarities. For example, they can measure how close the true value is to our predicted value using the membership function of the predicted value. In addition, they can measure how much uncertainty is in the model, by using the spreads of the predicted values. In [16], the credibility of a predicted value is measured by how close it is to the original value and also how precise it is (i.e., how small the spreads of the value). The credibility of a fuzzy predicted value is defined as [16]:

$$Z_i=\frac{{\mu }_{{\tilde{y}}_i}\left(y_i\right)}{{\Delta }_{{\tilde{y}}_i}}$$

where ${\mu }_{{\tilde{y}}_i}\left(y_i\right)$ is the membership value of the true value, $y_i$ in the fuzzy predicted value ${\tilde{y}}_i$ and ${\Delta }_{{\tilde{y}}_i}$ is the fuzziness of the prediction which is equivalent to the area of the fuzzy number, which is a symmetric triangular fuzzy number with height of 1. The area is just the spread of fuzzy number, i.e., the difference between the central value and the right or left value.

For a model with sample size K, the total credibility of the model is the sum of the credibility of the individual sample predictions. The total credibility is given by:

$$TC={\displaystyle \sum }_{i=1}^K{Z}_i={\displaystyle \sum }_i^K\frac{{\mu }_{{\tilde{y}}_i}\left(y_i\right)}{{\Delta }_{{\tilde{y}}_i}}$$

Table 4. Fuzzy model (data from Liu and Chen, 2013 [16]).

Hvalue	A	Total Credibility
0.3148	y ∗ = (−610.8251, 0.0000) + (19.1484, 0.0000)x1 + (1.4018, 1.2301)x2	0.1371
0	y = (−610.8233, 0.0000) + (19.1484, 0.0000)x1 + (1.4017, 0.8429)x2	0.1082
0.5	y = (−610.8240, 0.0000) + (19.1484, 0.0000)x1 + (1.4017, 1.6857)x2	0.1271

,

Table 5. Linear Model based on the fuzzy prediction intervals (data from Liu and Chen, 2013 [16]).

Confidence Level	Linear Model Based on Fuzzy Prediction Intervals (Data from Liu and Chen, 2013)	Total Credibility	Lowest Membership Value
90%	y = (−1590.9) + (29.6726)x1 + (9.9906)x2	0.2153	0
95%	y = (−1590.9) + (29.6726)x1 + (9.9906)x2	0.2056	0.0169
99%	y = (−1590.9) + (29.6726)x1 + (9.9906)x2	0.1949	0.0566

,

Table 6. Linear model based on the fuzzy tolerance intervals (data from Liu and Chen, 2013 [16]).

Proportion	Linear Model Based on Fuzzy Tolerance Interval (Data from Liu and Chen 2013)	Total Credibility	Lowest Membership Value
90%	y = (−1590.9) + (29.6726)x1 + (9.9906)x2	0.2029	0
95%	y = (−1590.9) + (29.6726)x1 + (9.9906)x2	0.1871	0.0793
99%	y = (−1590.9) + (29.6726)x1 + (9.9906)x2	0.1631	0.1794

,

Table 7. Fuzzy model (Data from Liu and Chen 2013 [16]).

Hvalue	Fuzzy Model (Data from Liu and Chen 2013)	Total Credibility
0.2666	y ∗ = (12.0000, 1.3635) + (0.6250,0.1704)x	1.4960
0	y = (12.0000, 1.000) + (0.6250,0.1300)x	1.2984
0.7	y = (12.0000, 3.330) + (0.6250,0.4200)x	0.9736

,

Table 8. Linear Model based on the fuzzy prediction intervals (Data from Liu and Chen, 2013 [16]).

Confidence Level	Linear Model Based on Fuzzy Prediction Interval (Data from Liu and Chen 2013)	Total Credibility	Lowest Membership Value
90%	y = (12.93) + (0.54)x	1.5612	0.1371
95%	y = (12.93) + (0.54)x	1.4698	0.1825
99%	y = (12.93) + (0.54)x	1.3651	0.2155

,

Table 9. Linear model based on the fuzzy tolerance intervals (data from Liu and Chen, 2013 [16]).

Proportion	Linear Model Based on Fuzzy Tolerance Interval (Data from Liu and Chen 2013)	Total Credibility	Lowest Membership Value
90%	y = (12.93) + (0.54)x	1.3813	0.2921
95%	y = (12.93) + (0.54)x	1.1850	0.4034
99%	y = (12.93) + (0.54)x	0.8866	0.5627

,

Table 10. Fuzzy model (Car data, UCI repository).

Hvalue	Fuzzy Model (Car Data UCI Repository)	Total Credibility
0.3	y = (45.4865, 13.8711) + (−0.0026, 0.0000)x1 + (−1.091, 0.0000)x2	4.4629
0	y * = (45.4865, 9.7097) + (−0.0026, 0.0000)x1 + (−1.091, 0.0000)x2	5.4725
0.5	y = (45.4865, 19.4195) + (−0.0026, 0.0000)x1 + (−1.091, 0.0000)x2	3.7626

,

Table 11. Linear model based on the fuzzy prediction intervals (Car data, UCI Repository).

Confidence Level	Linear Model Based on Fuzzy Prediction Intervals (Car data UCI Repository)	Total Credibility	Lowest Membership Value
90%	y = (47.7694) + (−0.0066)x1 + (−0.0420)x2	7.9395	0
95%	y = (47.7694) + (−0.0066)x1 + (−0.0420)x2	7.6792	0
99%	y = (47.7694) + (−0.0066)x1 + (−0.0420)x2	7.3592	0

,

Table 12. Linear Model based on the fuzzy tolerance intervals (Car data, UCI Repository).

Proportion	Linear Model Based on Fuzzy Tolerance Interval (Car data UCI Repository)	Total Credibility	Lowest Membership Value
90%	y = (47.7694) + (−0.0066)x1 + (−0.0420)x2	7.7065	0
95%	y = (47.7694) + (−0.0066)x1 + (−0.0420)x2	7.4172	0
99%	y = (47.7694) + (−0.0066)x1 + (−0.0420)x2	7.0796	0

,

Table 13. Fuzzy model (Hald Cement dataset [17]).

Hvalue	Fuzzy Model (Hald Cement Dataset [17])	Total Credibility
0.2487	y ∗ = (79.3955, 0.0000) + (1.5212, 0.2474)x1 + (0.3238, 0.0000)x2 + (−0.0839, 0.1453)x3 + (0.3187, 0.0000)x4	1.9208
0	y = (79.3955, 0.0000) + (1.5212, 0.1859)x1 + (0.3238, 0.0000)x2 + (−0.0839, 0.1091)x3 + (0.3187, 0.0000)x4	1.7102
0.5	y ∗ = (79.3955, 0.0000) + (1.5212, 0.3718)x1 + (0.3238, 0.0000)x2 + (−0.0839, 0.2183)x3 + (0.3187, 0.0000)x4	1.7059

,

Table 14. Linear model based on the fuzzy prediction intervals (Hald Cement dataset [17]).

Confidence Level	Linear Model Based on Fuzzy Prediction Intervals (Hald Cement Dataset [17])	Total Credibility	Lowest Membership Value
90%	y = (62.4054) + (1.5511)x1 + (0.5102)x2 + (0.1091)x3 + (−0.1441)x4	1.8326	0.0762
95%	y = (62.4054) + (1.5511)x1 + (0.5102)x2 + (0.1091)x3 + (−0.1441)x4	1.7302	0.1248
99%	y = (62.4054) + (1.5511)x1 + (0.5102)x2 + (0.1091)x3 + (−0.1441)x4	1.6160	0.1602

and

Table 15. Linear model based on the fuzzy tolerance intervals (Hald Cement dataset [17]).

Proportion	Linear Model Based on Fuzzy Tolerance Interval (Hald Cement Dataset [17])	Total Credibility	Lowest Membership Value
90%	y = (62.4054) + (1.5511)x1 + (0.5102)x2 + (0.1091)x3 + (−0.1441)x4	1.7655	0.1870
95%	y = (62.4054) + (1.5511)x1 + (0.5102)x2 + (0.1091)x3 + (−0.1441)x4	1.6683	0.2298
99%	y = (62.4054) + (1.5511)x1 + (0.5102)x2 + (0.1091)x3 + (−0.1441)x4	1.5724	0.2609

below show the total credibility of all three models on all two datasets. The comparison with fuzzy linear regression is made for the h-value with the maximum credibility (indicated with * in the tables). However, since the h-value is not comparable to a statistical confidence level, we also show the lowest membership value of the true value in the fuzzy number, that is produced from both a prediction and tolerance interval. A visual comparison is also shown in Figure 1 and Figure 2. Since every data now belongs to the interval with some membership value, it is possible to calculate the minimum membership value in the dataset; this is what is defined as the lowest membership value, and it gives an indication of how good the coverage interval is. A value of zero indicates that there is at least one data that does not belong to the interval, while a value greater than zero implies that all data belong to the interval.

The credibility of the proposed model for this dataset is slightly higher than that of the classical fuzzy model and lower than that of the fuzzy prediction intervals. As it can be seen, the credibility of all three models is within the same range of values, and this confirms the applicability of the proposed model. As expected, the credibility falls as the coverage probability increases. The 95% coverage seems to be the best coverage, since it contains all true values and a high credibility.

As with the previous dataset, the credibility of the proposed model is within the same range as the classical fuzzy model, and the fuzzy prediction interval further confirms its applicability. However, the values for both 90%, 95% and 99% coverage are slightly lower than the other two models. Again, the credibility falls as the coverage increases. All the three intervals contain the true values and with high membership values. The 90% coverage seems to give the best trade-off between total credibility and lowest membership value of true value.

6. Conclusions

Errors from a linear regression model are assumed to be normally distributed, with a mean of zero and constant standard deviation. In this study, we have shown how to construct a fuzzy error from the tolerance interval of the errors in a linear model. This approach leads to a fuzzy linear regression model with a constant fuzzy error. The fuzzy error is constructed entirely from the observed errors and it does not need to be optimized like the usual fuzzy regression models. The current model is useful for applications where a tolerance interval is needed to bound acceptable errors, in both sample and future predictions of a linear regression model.

For clarification, our method does not remove uncertainties in regression models, however, it gives a better method to use a fuzzy number to represent these uncertainties, instead of a single number or a single interval like it, as is normally done. In addition, choosing only one coverage interval, say 99%, it does not fully represent all the uncertainty in the model. In contrast, the fuzzy number produced contains all the uncertainty from, for example, 99% up to 0%.

In addition, by using a fuzzy number, another level of uncertainty is captured. Whether a number belongs to an interval or not is no longer crisp (0 or 1), but now one can say that a number belongs to the interval with some possibility [20], say 0.7. This captures the uncertainty in the assumptions that the interval will contain, say, 99% of the data. The fuzzy number shows that some data are more likely to be captured in the interval, compared to others.

Unlike crisp predictions, the true values can belong to the fuzzy output with a membership degree. As an added advantage, the total credibility of the model can be used to select among two linear regression models, and to choose the most credible model in terms of tolerance intervals for predictions. Additionally, similar to how h is used in a classical fuzzy model, a decision-maker can choose a linear model whose true value belongs to the fuzzy predicted values, with at least a specified membership degree.

The limitation of the model is that the fuzzy error is constant and is added to all crisp output. So, all outputs are assumed to be affected by the same error. In future research, non-constant tolerance interval could be used, which would depend on the input. The same procedure, for constructing a fuzzy number from a statistical interval, can be used to convert the tolerance intervals to fuzzy numbers. Last, but not least, different approximations exist for tolerance intervals, and they can be used apart from the one used in this paper. It would be worthwhile to extend this method to non-parametric tolerance intervals for solving the problem of assuming a known distribution.