Abstract
A harmony search (HS) algorithm for solving high-dimensional multimodal optimization problems (named DIHS) was proposed in 2015 and showed good performance, in which a dynamic-dimensionality-reduction strategy is employed to maintain a high update success rate of harmony memory (HM). However, an extreme assumption was adopted in the DIHS that is not reasonable, and its analysis for the update success rate is not sufficiently accurate. In this study, we reanalyzed the update success rate of HS and now present a more valid method for analyzing the update success rate of HS. In the new analysis, take-k and take-all strategies that are employed to generate new solutions are compared to the update success rate, and the average convergence rate of algorithms is also analyzed. The experimental results demonstrate that the HS based on the take-k strategy is efficient and effective at solving some complex high-dimensional optimization problems.
1. Introduction
Harmony search (HS) [1,2,3,4,5], which is a meta-heuristic search algorithm that mimics the process of improvising a musical harmony, has been extensively employed in the fields of complex scientific computing and engineering optimization. Deng et al. developed an improved HS algorithm to construct examples for an algebra system in 2015 [6]. Tuo et al. proposed a hybrid algorithm based on HS and teaching-learning-based optimization (TLBO) for solving complex high-dimensional optimization problems; the algorithm showed efficient performance [7]. In the fields of engineering optimization, an enhanced HS was proposed to solve dynamic economic emission dispatch problems; the experimental results indicated better solutions and less computational time [8]. An adaptive dynamic HS is presented for optimizing aircraft panels [9]. Xu and Wang developed a harmony search algorithm for minimizing serve energy by examining information caching and upgrading techniques of the Internet of Things (IoT) [10]. To solve complex engineering design optimization, Yi et al. proposed an online variable-fidelity surrogate-assisted HS with a multi-level screening strategy [11]. In addition, HS has also been applied in manufacturing systems [12], microgrid planning with ESS [13], flow shop scheduling problems [14] etc. [15,16,17].
In recent years, various variants of HS were proposed to improve the performance for solving complex optimization problems [17,18,19,20,21,22,23,24], such as accelerating search speed, enhancing the power of global exploration and balancing the tradeoff between diversification and intensification. Zhang et al. reviewed the HS and its variants with respect to the algorithm structure [23]. D. Manjarres et al. analyzed the main characteristics and application portfolio of HS, and presented future research lines of HS in 2013 [24]. Nasir et al. compared the study of HS in China, Japan and Korea [25]. Although, the HS and its variants have shown strong power for solving some complex optimization problems, they have low-efficiency and low-precision solutions for solving high-dimensional (>=500) multimodal optimization problems. In 2015, an HS algorithm named “A harmony search algorithm for high-dimensional multimodal optimization problems (DIHS) [4]” was proposed. In DIHS, to determine why the standard HS has low efficiency and low precision in solving high-dimensional optimization problems, the take-one search strategy and take-all search strategy were compared to analyze the success rate of newly generated solutions for updating the worst solution in harmony memory (HM). In the comparative analysis, an extreme case of solutions for the HM is adopted assuming that all solutions need only adjust one-dimensional values to achieve the global optimal solution. The analytical results [4] are as follows:
- (1)
- The update success rate (defined as the rate that the new generated harmony is better than the worst harmony in HM.) of the take-one strategy iswhere D is the dimension of the optimization problem and HMS denotes the size of the harmony memory.
- (2)
- The update success rate of the take-all strategy is
In recent research, we identified a key analysis error in the article of DIHS, when the dimension D is larger than the HMS, the update success rate formulas [4] are incorrect. Although the error does not affect the correctness of the final conclusion of the article, it may cause readers to misunderstand and incorrectly apply the DIHS algorithm. To correct the error, in this work, we introduce a new method for analyzing the take-one search and take-all search strategies.
The contributions of this article are listed as follows:
- (1)
- New analysis strategies, namely, the take-k and take-all schemes, are presented. The analysis assumptions used are closer to the conditions in the actual optimization process than are the previous extreme assumptions.
- (2)
- An adaptive take-k strategy is proposed for improving the harmony search algorithm.
The remainder of this paper is organized as follows. HS is introduced in Section 2. Section 3 presents detailed analyses of the take-one strategy and take-all strategy. Section 4 introduces new take-k and take-all strategies. The simulation experiments are performed and the results are analyzed in Section 5. In Section 6, discussions are presented.
2. Standard Harmony Search Algorithm
HS is a very simple real-code optimization algorithm that can be easily used to solve continuous and discrete optimization problems. This algorithm contains three operators:
(1) The combinatorial operator is designed to select values from HM and obtain a new harmony. The objective is to improve the new harmony based on the historical memory of musicians.
(2) The local-adjusting operator fine-tunes the potential solutions near the new harmony with the aim of finding the most precise solution. This approach can aggravate spatial disturbances associated with a large fret width and fine-tune harmonies with a small fret width.
(3) The random search operator is designed to explore unknown search areas and prevent the algorithm from falling to local optima.
The pseudocode of the standard HS algorithm is expressed as algorithm 1:
Algorithm 1. The pseudocode of standard HS algorithm. | |
| Input: MaxT: maximum number of iterations HMCR: harmony memory consideration rate HMS: harmony memory size PAR: pitch-adjusting rate fw: fret width Output: Best harmony Xbest | |
|
3. Take-One Strategy and Take-All Strategy
In the original paper about DIHS, an extreme case of solutions in the HM is adopted assuming that all solutions need only adjust one-dimensional values to achieve the global optimal solution. HM can be converted to the following matrix by swapping rows and columns.
In the HM, indicates that the ith decision variable has an optimal value. are decision variables for which the optimal value has not been obtained.
Under this assumption,
(1) The success rate of update of the take-one strategy should be , not , where indicates the probability of selecting one of the previous HMS columns from HM to be adjusted. represents the probability of obtaining the best value of the ith decision variable.
(2) The success rate of update of the take-all strategy should be , not , because all of the values of decision variables are optimal.
Under this condition, the update success rate of the take-all strategy is independent of the dimension of the problem, which is inconsistent with the results of the previous analysis. If we assume that there is one and only one nonoptimal value in all columns of the matrix HM, formulas (1) and (2) are correct.
However, based on many experimental results, the concept of the DIHS algorithm should be correct, but the premise assumptions were too extreme for this analysis. Therefore, in this work, we employ more realistic hypothetical conditions to reanalyze the dynamic-dimensionality-reduction adjustment (DDRA) strategy using take-k strategy and take-all strategy.
4. Take-K Strategy and Take-All Strategy
4.1. Concepts and Assumptions
The take-k strategy means that k decision variables of are chosen for adjusting. If the adjusted is better than the old , then the in HM is replaced by the adjusted . If the value of k is equal to dimension D, the take-k strategy is referred to as the take-all strategy.
The take-k strategy employs the following step to improvise the harmony (see Algorithm 2).
| Algorithm 2. The Pseudocode for improvising new harmony for the take-k strategy. |
| For i = 1➔D |
| If rand(0,1) < k/D // each dimension has a k/D chance of being adjusted. |
| If rand(0,1) < HMCR |
| //combinatorial operator |
| If rand(0,1) < PAR |
| //local-adjusting operator |
| End |
| Else |
| // random search operator |
| End |
| End |
| End |
Assumption 1.
Suppose that in the ith column of HM, there is only one value that is not equal to . In the jth row of HM, there are D/HMS values that do not reach the optimal value, as follows:
Assumption 2.
Suppose that in generation t, the probability that each dimension in HM is able to obtain a better value by employing three optimal operators (combinatorial operator, local-adjusting operator, and random search operator) than it currently holds is equal to.
In the take-k strategy, first ; then, each dimension (i = 1,2,…,D) has a k/D chance of being updated by the three operators. If k==D, the take-k and take-all strategies are equivalent.
If is chosen from HM for adjustment, the probability of improving is p(t), and the probability of the value worsening is 1 − p(t).
Assumption 3.
Suppose that there are k decision variables in that are selected to be adjusted. If more than 1/2 of the decision variables achieved improved values, a better solution was obtained.
Definition 1.
Gain value. is a new improvised solution in the t-th iteration. The gain value obtained at the t-th iteration is defined as
The gain value after iterations is defined as
where , and denote the best solutions at times and (), respectively.
4.2. Update Success Rate of Take-k and Take-All Strategies
To analyze the update success rate of the take-k and take-all strategies, Figure 1 introduces the judging criteria for generating a better solution, . In the take-k strategy, first, the values of are initialized to the values of the worst harmony in HM. Second, is adjusted according to algorithm 2. If more than 1/2 of the decision variables of have been improved, we think is improved successfully. Otherwise, is considered to be an improvision.
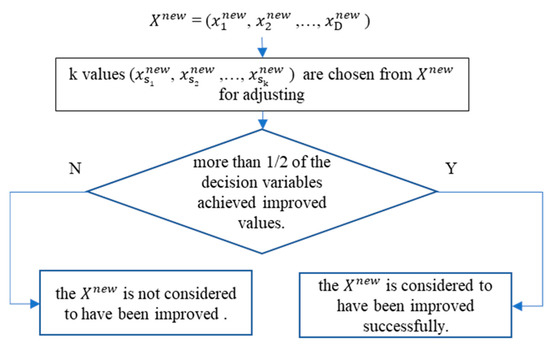
Figure 1.
Flow chart that shows adjustments to .
By assumption 3, the probability that a better solution can be obtained using the take-k strategy is
where i = k/2 + 1 to k, which means that among the k decision variables, more than k/2 decision variables obtain better values.
The take-all strategy is equivalent to the take-D strategy (k = D), and the probability of obtaining a better solution is
From Equation (7), the update success rate is independent of the dimension D. Figure 2 shows the success rate curves of the take-k (k = 0.1D) and take-all strategies as the dimension D changes.
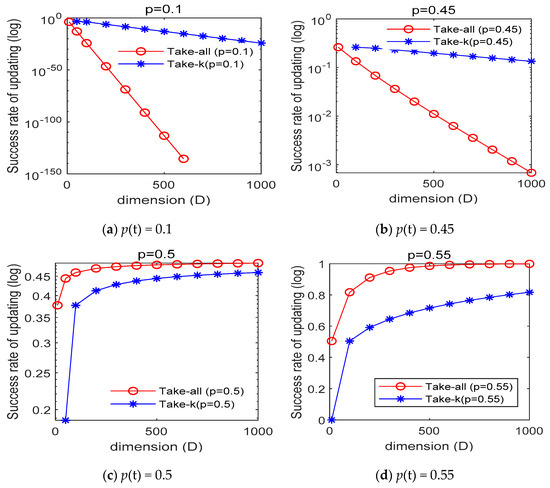
Figure 2.
Comparison of the take-k and take-all strategies (k = 0.1D). (a) p(t) = 0.1; (b) p(t) = 0.45; (c) p(t) = 0.5; (d) p(t) = 0.55.
As shown in Figure 2, when p(t) < 0.5, the update success rate for both strategies decreases with dimension D, but the take-all curve decreases much faster than the take-k curve. When p > 0.5, the update success rate of the take-all strategy is higher than that of the take-k strategy for a high-dimensional optimization problem; moreover, if D > 500, the success rate of the take-all approach is close to 1. However, in practice, the value of p(t) is usually less than 0.5.
Figure 3 shows a comparison of the update success rate of the take-k and take-all strategies when using p(t) ∈ {0.3, 0.25, 0.2, 0.15, 0.1, 0.05}. In Figure 3a,b, the x-axis represents the probability that decision variable in HM can obtain a better value than the current value; the y-axis shows the update success rate. We can see that as D and k increase, the success rate of updating the HM significantly decreases. Moreover, the smaller the value of p(t) is, the smaller the success rate.
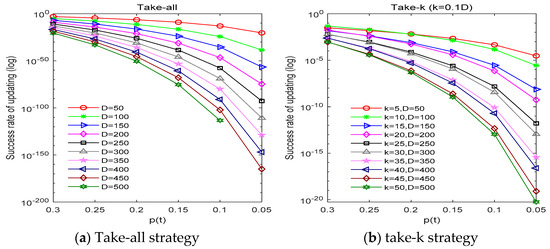
Figure 3.
Update success rate.
Generally, for a complex optimization problem, in the search process of an intelligent optimization algorithm, the population has excellent initial diversity, and each decision variable has a high probability of achieving an improved value. As the search progresses, the diversity of the population decreases, and the probability of finding better individuals decreases. However, if the population is clustered around a local optimal solution (the local optimal solution has not yet been obtained), then the probability of finding a better solution is usually high. However, if the population has converged to a local optimum (the local optimal solution has been found), the probability of finding a better solution is 0.
To adapt to the search process, DIHS adopted a DDRA strategy. An adaptive take-k strategy can be employed in the DIHS algorithm as follows:
where and represent the maximum and minimum values of k, respectively. a is a parameter used to adjust the rate of descent of k, taking a value of 2 in this paper. MaxFEs denotes the Maximum number of function evaluations (FEs).
The parameters PAR and fw are the same as those in the original DIHS method [4].
where and represent the maximum and minimum pitch adjustment rates, respectively; and denote the minimum and maximum fret widths, respectively; and is a value between and .
The parameters PAR and fw are both used to balance the exploration power and exploitation power of DIHS. Equation (9) is equivalent to Equation (1) of literature [4] in which the parameters a, HMS, PAR and fw have been analyzed in detail.
5. Simulation Experiments
5.1. Experimental Environment and Parameter Settings
To investigate the take-k and take-all strategies, six classical benchmark functions [26] (see Table 1) are employed to test the performance of the two strategies. Take-all-based HS, take-k-based HS and take-k-based DIHS are compared based on the six benchmark functions. The dimensions (D) of all functions are equal to 1000 in the experiments. In the take-k-based HS, the value of k is set to 0.01D. In the take-k-based DIHS, parameters are set as follows:

Table 1.
Six classical benchmark functions.
Simulation experiments are performed to compare the update success rate and convergence of the three algorithms. Figure 4 shows the success rate curves and convergence curves. To further investigate the search ability of the three algorithms, we trace the values of the gains obtained during time and the convergence rate.
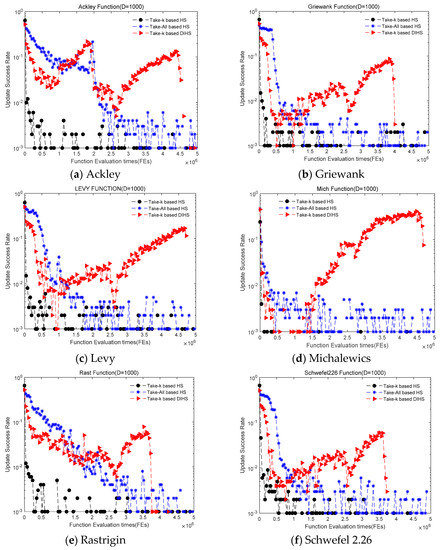
Figure 4.
Update success rate comparisons of the take-all and take-k strategies.
5.2. Update Success Rate and Convergence Speed
As shown in Figure 4, at the beginning of the search process, the take-all-based HS has a higher update success rate than the take-k-based HS. As the search progresses, the update success rate of the take-all-based HS decreases dramatically, and the take-k-based HS and DIHS methods are able to maintain a high update success rate during the search. The take-all-based HS approach can be compared to take-k-based DIHS; the former has a higher success rate at the beginning stage of the search. However, in the mid to late stages of the search, the update success rate for the take-k-based DIHS gradually increases and exceeds the success rate for the take-k-based HS.
From the convergence curves of the algorithms in Figure 5, the take-all-based HS algorithm has the slowest convergence rate among the three compared algorithms. The take-k-based HS has a high convergence rate during the initial stage of the search, but it is much slower than take-k-based DIHS overall. Of the three algorithms, DIHS has the strongest ability to obtain high-precision optimal solutions for all test functions.
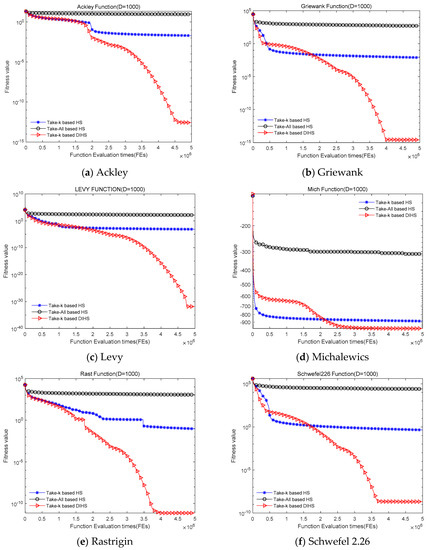
Figure 5.
Convergence curves of the take-all and take-k strategies.
Figure 6 presents the gain values that are traced during the search. Although the take-k strategy has a higher probability of finding an improved solution than the take-all strategy during the search process, the improvement over the best solution of the take-k strategy may be small. As shown in Figure 6, the standard HS algorithms that are based on the take-k and take-all strategies have higher gain values than the take-k-based DIHS at certain times, but they are prone to have zero (less than 1 × 10−30) gain values at points in the search process. The take-k-based DIHS seldom obtains a zero-gain value before the global optimal solution is reached, except for the Michalewics function. The gain values of the take-k-based DIHS become very small late in the search process because the DIHS algorithm has converged to the global optimal solution.
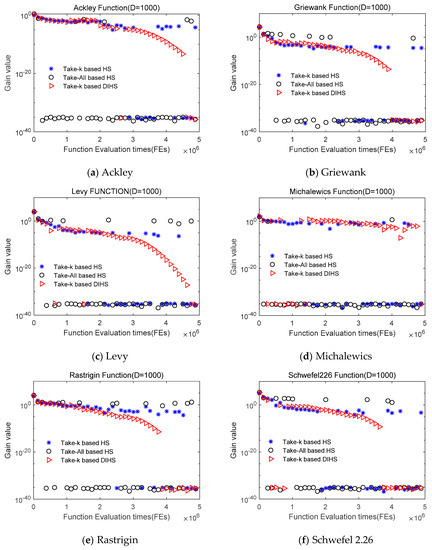
Figure 6.
Gain value of three algorithms during the search process.
To further investigate the performance of the take-k strategy for HS, six classical high-dimensional optimization problems with multimodal functions (sphere shift function, Schwefel shift function, Rastrigin shift function, Ackley shift function, Griewank shift function and fast fractal double dip function) [27,28] are tested. Figure 7 presents the update success rate of three algorithms (take-k-based HS, take-all-based HS and take-k-based DIHS); the results confirm the previous conclusions.
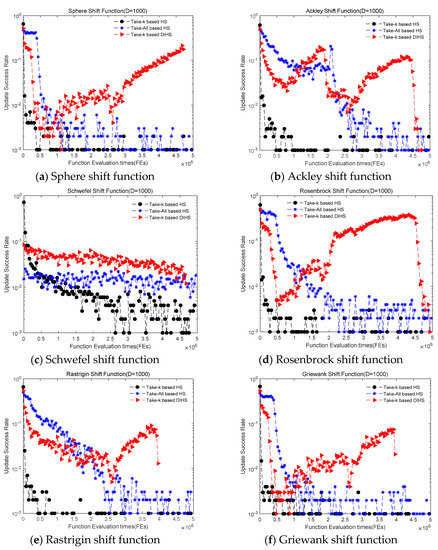
Figure 7.
Update success rate of the algorithms for six classical high-dimensional optimization problems.
Table 2 summarized the test results of six algorithms (take-all-based HS, take-k-based HS, SaDE [29], CoDE [30], CLPSO [31] and take-k-based DIHS) for the six high-dimensional optimization problems.

Table 2.
Comparisons of six algorithms for six high-dimensional optimization problems (D=1000) (Best/Mean/Worst denotes the best/mean/worst fitness values, respectively, obtained in 30 runs).
As shown in Table 2, the best/mean/worst solution of take-k-based DIHS is superior to those of the other algorithms for all functions. The take-k-based HS (k = 0.01D) has the shortest run time. Additionally, take-all-based HS requires more than twice the run time of the take-k-based HS algorithm. The take-k-based DIHS requires a slightly higher run time than the take-k-based HS algorithm. Compared to SaDE, CoDE and CLPSO, the take-k-based DIHS is optimal for all metrics.
5.3. Analysis of the Take-k-Based DIHS Results
As shown in Figure 4 and Figure 7, for most test functions, the update success rate curve of the DIHS algorithm displays an “N-shaped” trajectory. The initial value is close to 50%, and this value then rapidly decreases to between 0.1% and 1%. Next, the curve slowly rises (to approximately 35%), and in the final stage, the success rate suddenly and rapidly drops to a very low value (close to 0).
We believe that this phenomenon is due to the following factors.
- (1)
- The population is randomly initialized, and every individual has a bad fitness value. In this case, DIHS has a higher probability than the other algorithms of finding an improved solution.
- (2)
- In the early stage of the search, the DIHS algorithm perturbs the search space to find the global optimal region with a high perturbation step fw, resulting in a rapid decrease in the probability of finding a better solution than the current solution.
5.4. Convergence Rate
To test the convergence ability of algorithms during the search, we employ the average convergence rate of HS for t generations. The average convergence rate at time t [32] is defined as Formula (12):
where and respectively denote the initial population (harmony memory, HM) and the harmony memory after t generations. represents the best fitness value among the individuals of . denotes the optimal fitness of the problem.
Figure 8 shows the convergence rates of 8 complex benchmark functions by using standard HS (take-all-based HS), take-k-based HS and take-k-based DIHS algorithms. It can be seen from the figure that on all functions, the take-k-based method is superior to the take-all method, and the take-k-based DIHS has a higher convergence rate than other algorithms. At the beginning of the search process, the take-k-based DIHS can maintain a high convergence rate that declines slowly. In the second half of the search, the take-k-based DIHS has a progressively higher convergence rate for most functions (e.g., Ackley, Griewank and so on). In particular, the convergence rate on the Rastrigin shift function grows to 1. The results of this experiment further validate that the take-k strategy and dynamic dimensionality reduction are correct and effective improvement strategies for improving harmony search to solve complex high-dimensional optimization problems.
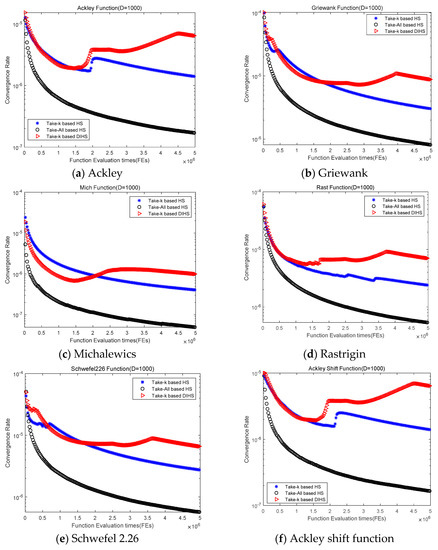
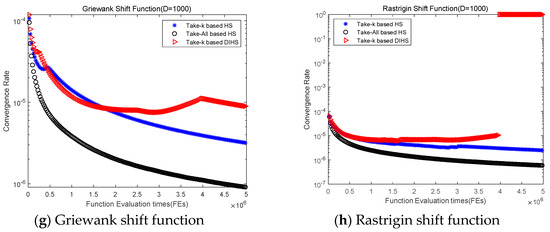
Figure 8.
Convergence rates of 12 test functions by using three algorithms.
6. Discussion
Although many algorithms, such as cooperative coevolution (CC) algorithms [33,34,35,36] (decomposition-based algorithms), have been designed to solve high-dimensional optimization problems and achieved notable progress, they are still ineffective for some complex optimization problems [37]. This work aims to discover why effective HS algorithms that are able to solve small-scale optimization problems are not effective in solving high-dimensional optimization problems. By comparing take-k-based HS with take-all-based HS, it is found that take-all-based HS has a very low update success rate in the later search stage when solving high-dimensional optimization problems.
At the beginning of the search, a large k-value in the take-k-based HS is beneficial for accelerating the exploration process and obtaining a large gain value at each iteration, but the update success rate decreases rapidly as the search progresses. A small k-value is beneficial for achieving a high update success rate, but the obtained gain value at each iteration is small.
To improve the performance of take-k-based HS, DIHS employs the dynamic take-k strategy, dynamic pitch adjustment rate and dynamic fret width. The experimental results demonstrate that the dynamic take-k strategy is very effective for balancing the update success rate and gain value in the search process. However, the take-k-based DIHS is still not effective for obtaining high-precision globally optimal solution for some high-dimensional optimization problems (e.g., Rosenbrock function) in which all decision variables are highly interconnected.
In this work, the goal is to improve the HS algorithm without employing any complex strategies, such as CC and decomposition-based algorithms. The proposed approach can be used in various applications and requires a search algorithm that is as simple as possible. Recently, the HS algorithm and its variants have received considerable attention, such as in portfolio selection [38] and searching for pathogenic sites based on the entire human genome [39,40,41]. For HS, improving the search speed and solving complex high-dimensional optimization problems remain an important focus of future research. The take-k-based strategy is a promising approach for improving the global search power, enhancing the solution quality and accelerating the speed.
Author Contributions
Conceptualization, S.T. and Z.W.G.; methodology, S.T.; formal analysis, S.T.; writing—original draft preparation, S.T.; writing—review and editing, S.T.; supervision, Z.W.G. and J.H.Y.; funding acquisition, S.T. and J.H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Education of Humanities and Social Science project, China under Nos. 19YJCZH148. This work was also supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2020R1A2C1A01011131).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. Harmony search optimization: Application to pipe network design. Int. J. Model. Simul. 2002, 22, 125–133. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Tuo, S.; Yong, L.; Deng, F.; Li, Y.; Lin, Y.; Lu, Q. A harmony search algorithm for high-dimensional multimodal optimization problems. Digit. Sign. Process. 2015, 46, 151–163. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Deng, F.; Tuo, S.; Yong, L.; Zhou, T. Construction example for algebra system using harmony search algorithm. Math. Probl. Eng. 2015, 2015, 15. [Google Scholar] [CrossRef]
- Tuo, S.; Yong, L.; Deng, F.; Li, Y.; Lin, Y.; Lu, Q. HSTLBO: A hybrid algorithm based on Harmony Search and Teaching-Learning-Based Optimization for complex high-dimensional optimization problems. PLoS ONE 2017, 12, e0175114. [Google Scholar] [CrossRef]
- Li, Z.; Zou, D.; Kong, Z. A harmony search variant and a useful constraint handling method for the dynamic economic emission dispatch problems considering transmission loss. Eng. Appl. Artif. Intell. 2019, 84, 18–40. [Google Scholar] [CrossRef]
- Keshtegar, B.; Hao, P.; Wang, Y.; Li, Y. Optimum design of aircraft panels based on adaptive dynamic harmony search. Thin Walled Struct. 2017, 118, 37–45. [Google Scholar] [CrossRef]
- Xu, C.; Wang, X. Transient content caching and updating with modified harmony search for Internet of Things. Digit. Commun. Netw. 2019, 5, 24–33. [Google Scholar] [CrossRef]
- Yi, J.; Gao, L.; Li, X.A.; Shoemaker, C.; Lu, C. An on-line variable-fidelity surrogate-assisted harmony search algorithm with multi-level screening strategy for expensive engineering design optimization. Knowl. Based Syst. 2019, 170, 1–19. [Google Scholar] [CrossRef]
- Li, G.; Zeng, B.; Liao, W.; Li, X.; Gao, L. A new AGV scheduling algorithm based on harmony search for material transfer in a real-world manufacturing system. Adv. Mech. Eng. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Jiao, Y.; Wu, J.; Tan, Q.K.; Tan, Z.F.; Wang, G. An optimization model and modified Harmony Search algorithm for microgrid planning with ESS. Discret. Dyn. Nat. Soc. 2017, 11, 1–11. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, Y.; Zhang, Y.; Ma, W.; Zhang, C. A hybrid harmony search algorithm with efficient job sequence scheme and variable neighborhood search for the permutation flow shop scheduling problems. Eng. Appl. Artif. Intell. 2017, 65, 178–199. [Google Scholar] [CrossRef]
- Saka, M.P.; Hasançebi, O.; Geem, Z.W. Metaheuristics in structural optimization and discussions on harmony search algorithm. Swarm Evolut. Comput. 2016, 28, 88–97. [Google Scholar] [CrossRef]
- Moon, Y.Y.; Geem, Z.W.; Han, G.T. Vanishing point detection for self-driving car using harmony search algorithm. Swarm Evolut. Comput. 2018, 41, 111–119. [Google Scholar] [CrossRef]
- Kim, Y.K.; Yoon, Y.; Geem, Z.W. A comparison study of harmony search and genetic algorithm for the max-cut problem. Swarm Evolut. Comput. 2019, 44, 130–135. [Google Scholar] [CrossRef]
- Das, S.; Mukhopadhyay, A.; Roy, A.; Abraham, A.; Panigrahi, B.K. Exploratory power of the harmony search algorithm: Analysis and improvements for global numerical optimization. IEEE Trans. Syst. Man Cybern. Part B (Cybernetics) 2011, 41, 89–106. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Suganthan, P.N.; Tasgetiren, M.F.; Liang, J.J. A self-adaptive global best harmony search algorithm for continuous optimization problems. Appl. Math. Comput. 2010, 216, 830–848. [Google Scholar] [CrossRef]
- Peraza, C.; Valdez, F.; Garcia, M.; Melin, P.; Castillo, O. A new fuzzy harmony search algorithm using fuzzy logic for dynamic parameter adaptation. Algorithms 2016, 9, 19. [Google Scholar] [CrossRef]
- Kattan, A.; Abdullah, R. A dynamic self-adaptive harmony search algorithm for continuous optimization problems. Appl. Math. Comput. 2013, 219, 8542–8567. [Google Scholar] [CrossRef]
- Assad, A.; Deep, K.A. Hybrid harmony search and simulated annealing algorithm for continuous optimization. Inform. Sci. 2018, 450, 246–326. [Google Scholar] [CrossRef]
- Zhang, T.; Geem, Z.W. Review of harmony search with respect to algorithm structure. Swarm Evolut. Comput. 2019, 48, 31–43. [Google Scholar] [CrossRef]
- Manjarres, D.; Landa-Torres, I.; Gil-Lopez, S.; Del Ser, J.; Bilbao, M.N.; Salcedo-Sanz, S.; Geem, Z.W. A survey on applications of the harmony search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 1818–1831. [Google Scholar] [CrossRef]
- Nasir, M.; Sadollah, A.; Yoon, J.H.; Geem, Z.W. Comparative study of Harmony Search algorithm and its applications in China, Japan and Korea. Appl. Sci. 2020, 10, 3970. [Google Scholar] [CrossRef]
- Fukushima, M. Test Functions for Unconstrained Global Optimization; Springer: New York, NY, USA, 2006; Available online: http://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar_files/TestGO_files/Page364.htm (accessed on 10 June 2018).
- Tang, K.; Yao, X.; Suganthan, P.N.; MacNish, C.; Chen, Y.P.; Chen, C.M.; Yang, Z. Benchmark Functions for the CEC’2008 Special Session and Competition on Large Scale Global Optimization; China & Nanyang Technological University: Singapore, 2008; Available online: http://www.ntu.edu.sg/home/EPNSugan/ (accessed on 10 June 2018).
- Tang, K.; Li, X.; Suganthan, P.N.; Yang, Z.; Weise, T. Benchmark Functions For The CEC’2010 Special Session And Competition On Large Scale Global Optimization; Technical report; Nature Inspired Computation and Applications Laboratory, USTC, China & Nanyang Technological University: Singapore, 2009; Available online: http://nical.ustc.edu.cn/cec10ss.php (accessed on 10 June 2018).
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Potter, M.A.; Jong, K.A.D. Cooperative coevolution: An architecture for evolving coadapted subcomponents. Evolut. Comput. 2000, 8, 1–29. [Google Scholar] [CrossRef]
- He, J.; Lin, G. Average convergence rate of evolutionary algorithms. IEEE Trans. Evol. Comput. 2015, 20, 316–321. [Google Scholar] [CrossRef]
- Omidvar, M.; Li, X.; Mei, Y.; Yao, X. Cooperative co-evolution with differential grouping for large scale optimization. IEEE Trans. Evol. Comput. 2014, 18, 378–393. [Google Scholar] [CrossRef]
- Omidvar, M.N.; Kazimipour, B.; Li, X.; Yao, X. Cbcc3- a contribution-based cooperative co-evolutionary algorithm with improved exploration/exploitation balance. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24 July 2016; Volume 7, pp. 3541–3548. [Google Scholar]
- Omidvar, M.N.; Yang, M.; Mei, Y.; Li, X.; Yao, X. DG2: A faster and more accurate differential grouping for large-scale black-box optimization. IEEE Trans. Evol. Comput. 2017, 21, 929–942. [Google Scholar] [CrossRef]
- Liu, J.; Peng, H.; Wu, Z.; Chen, J.; Deng, C. A hybrid deep grouping algorithm for large scale global optimization. IEEE Trans. Evol. Comput. 2020. [Google Scholar] [CrossRef]
- Tuo, S.H.; He, H. Solving complex cardinality constrained mean-variance portfolio optimization problems using hybrid HS and TLBO algorithm economic computation and economic cybernetics studies and research. Acad. Econ. Stud. 2018, 52, 231–248. [Google Scholar]
- Tuo, S.H.; Zhang, J.; Yuan, X.; He, Z.; Liu, Y.; Liu, Z. Niche harmony search algorithm for detecting complex disease associated high-order SNP combinations. Sci. Rep. 2017, 7, 11529. [Google Scholar] [CrossRef]
- Tuo, S.H.; Zhang, J.; Yuan, X.; Zhang, Y.; Liu, Z. FHSA-SED: Two-locus model detection for genome-wide association study with harmony search algorithm. PLoS ONE 2016, 11, e0150669. [Google Scholar] [CrossRef]
- Tuo, S.H.; Liu, H.; Chen, H. Multi-population harmony search algorithm for the detection of high-order SNP interactions. Bioinformatics 2020. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).