Supplier Selection by Fuzzy Assessment and Testing for Process Quality under Consideration with Data Imprecision

Abstract

Supply chain management models integrate upstream and downstream organizations to enable rapid response to consumer needs. For the manufacturing industry, the process quality of suppliers is thus the foundation of sustainable growth for firms and an important indicator of whether a firm can effectively reduce waste and protect the environment. To this end, this paper proposes a model of supplier selection for manufacturers based on process quality assessment. First of all, Six Sigma quality index $Q_{pk}$ is adopted as the assessment tool to conveniently measure the quality level of process. Practical applications require estimates of $Q_{pk}$ from the data collected to analyze the process quality of each supplier. The fact that uncertainty is unavoidable in the collected data means that using the crisp estimate of $Q_{pk}$ can lead to misjudgment of the process quality. To enhance the reliability of evaluation and reduce the risk of misjudgment, the fuzzy number ${\tilde{\widehat{Q}}}_{pk}$ is proposed to perform the fuzzy testing of two indices $Q_{pk}$ provided by suppliers with the intent of making reliable decisions on supplier selection.

1. Introduction

Due to globalization, firms have been developing technologies and products with large markets and high added value based on industry differences and similarities as well as the potentially massive demands of future markets to satisfy the requirements of various consumers and achieve sustainable development. To maintain industrial competitiveness, firms must continually enhance their technical capabilities, improve product quality, shorten lead time, and cut down costs. They must also maintain flexible production processes and respond quickly to changes in the market. These capabilities are well supported by supply chain management models that integrate upstream and downstream organizations. The growing prevalence of these intercorporation business models have led to the introduction of strategic alliances in which profits are shared with supply chain members so as to enable rapid response to consumer needs.

A good supply chain requires coordination among many cooperating organizations, among which material suppliers or service providers have the closest relationship with firms. When a firm is allied with a good supplier, it can obtain the support of outsourced services and even increase the competitiveness of the entire industry chain. In contrast, working with a supplier performing poorly may result in inconsistent product quality and delayed deliveries, thereby causing the firm to lose its competitive advantage in the market. Current trends in business development have made supplier quality vital to a firm’s operational success. The development of an objective supplier selection model therefore represents a valuable contribution to the field.

As time goes on, changes in corporate competitive models, production strategies, and industry characteristics mean the factors that firms take into consideration in supplier selection and their relevant weights also change. In existing literature regarding supplier selection, the three attributes frequently employed to evaluate suppliers are quality, cost price, and delivery [1,2,3,4,5]. However, as Kellner et al. [6] pointed out, supplier selection usually involves multiple criteria, and criteria often conflict with each other. For instance, lower procurement costs may mean inconsistent quality with respect to components and parts. This may affect the firm’s processing performance and product quality. Chen and Chen [7] indicated that shortening the lead time may also affect product quality. As a result, firms should endeavor to maintain or enhance product quality as their primary objective with the prerequisite of not delaying the lead time. Furthermore, the most important attribute for a firm in evaluating the optimal supplier is to have quality [8,9,10] as their primary consideration in supplier selection. By comparison, high process quality and good service are the most important attributes for strategic partners.

On the other hand, increasing awareness of the need for environmental protection and sustainable development has also placed the environmental impact of products under scrutiny. Many nations and firms have thus been advocating for a circular economy in recent years. This entails dismantling the conventional linear economy in favor of industry models that circulate resources. In the industrial production and consumption system of a linear economy, resources undergo the process of take, make, use, and dispose. This means that many resources are only used once before they are considered devoid of usefulness and value. In contrast, a circular economy emphasizes the full utilization of resources to eliminate waste. This increases resource utilization efficiency and strikes a balance between the needs of the economy and the environment. Clearly, the implementation of a circular economy contributes to minimizing pollution in production and consumption as well as turning waste into resources or nonhazardous waste.

Increasing environmental awareness has solidified the place of the 4Rs in the production and supply systems of firms in pursuit of sustainable development. To attain the production requirements of this trend, increasing the process quality of products is a crucial implementation strategy. Increasing process quality reduces scrap and rework rates of production (reduce), increases product availability and thereby increases the proportion of products that are reused (reuse), and ensures the quality of all product components, which not only enhances their recovery rate (recover) but also increases the likelihood of their transformation into new products (recycle). Thus, quality improvement in processes can effectively assist firms in striking a balance between the needs of the economy and the environment to attain sustainable development. Ahujaet and Khamba [11] and Cornuel [12] also indicated that quality enhancement has become a trend in organizational operation and management as well as a critical factor of sustainable development. From the above, we can see that the process quality of products is the foundation of corporate survival and an important indicator of whether a firm can protect the environment by reducing waste. Thus, this paper proposes a model for optimal supplier selection based on process quality from the perspective of a circular economy.

In view of the fact that the value of Six Sigma quality index (SSQI) $Q_{pk}$ represents the achieved quality level for a process of interest, we used it to assess the process quality provided by suppliers. In practice, the $Q_{pk}$ value must be calculated using the collected sample data. This increases uncertainty assessment due to sampling error. Consequently, using point estimates ${\widehat{Q}}_{pk}$ for index calculation may procure inaccuracy in assessing the process quality provided by a supplier. For this reason, we attempted to derive the $100\left(1-\alpha \right)\%$ confidence interval (CI) of $Q_{pk}$ and applied this in development of a supplier selection model aimed at long-term collaboration. On the other hand, the inherent uncertainty in the collected data is unavoidable. Therefore, the approach with crisp estimate of $Q_{pk}$ is not suitable for use in the quality assessment of a supplier. To enhance the reliability of evaluation and reduce the risk of miscalculation, we proposed a triangular-shaped fuzzy number (TFN) of ${\widehat{Q}}_{pk}$ and further developed a fuzzy model of selecting a supplier with the intent of making reliable selection decisions for optimal supplier selection. Thus, in addition to ensuring that the products produced by firms satisfy the needs of the end customer, the proposed model can also lead firms toward sustainable development.

The structure of this paper is as follows. In Section 2, the SSQI $Q_{pk}$ corresponding to assessing the quality level of each process characteristic is given. Section 3 presents the derivation of $100\left(1-\alpha \right)\%$ confidence intervals for $Q_{pk}$. In Section 4, the fuzzy hypothesis testing for two indices $Q_{pk}$ is proposed to select a supplier with consideration of data imprecision. An illustrative example is conducted in Section 5 to demonstrate the applicability of the proposed fuzzy testing approach for supplier selection. The conclusion and the summary of this paper are drawn in Section 6.

2. SSQI ${\mathit{Q}}_{\mathit{p}\mathit{k}}$

A process capability index (PCI) uses numerical quantification to examine the relationship between process performance and product specification. Many studies have used PCIs to judge whether a given process reaches the ability or quality demanded by customers [13,14,15,16,17,18,19,20]. At present, $C_{pk}$ is the most frequently used PCI for manufacturing industries [21]. A general formula of $C_{pk}$ is as follows:

$$C_{pk}=\min \left\{\frac{USL-\mu }{3\sigma },\frac{\mu -LSL}{3\sigma }\right\}$$

(1)

where $\mu$ and $\sigma$ denote the process mean and standard deviation of the process, respectively, and $USL$ and $LSL$ represent the upper and lower specification limits, respectively. As indicated by Boyles [22], the measurement index $C_{pk}$ is defined by process yield. Under the assumptions that the process data follows $N\left(\mu ,{\sigma }^2\right)$, the relationship between process yield and $C_{pk}$ is $2\mathsf{\Phi }\left(3C_{pk}\right)-1\le Yield\%\le \mathsf{\Phi }\left(3C_{pk}\right)$. Clearly, process yield can be reflected fully by $C_{pk}$.

Six Sigma strategies introduced in the 1980s can identify and eliminate the causes of process defects to enhance the quality of the output of a process [23,24,25]. Linderman et al. [26] observed that the quality of a given process achieves the $6\sigma$ level when $\sigma =d/6$ and $\left|\mu -T\right|\le 1.5\sigma$, where $d=\left(USL-LSL\right)/2$. This means that only when $\sigma =d/k$ and $\left|\mu -T\right|\le 1.5\sigma$ can the quality for a given process in question be claimed to achieve the $k\sigma$ level. Based on the above criteria, numerous researchers have conducted studies on the relationship between quality level in Six Sigma and various PCIs to judge whether the quality of a given process achieves the level required by customers [27,28,29,30,31]. Although these studies effectively evaluated process quality level, their PCI values could only indicate the range of the achieved quality level. To overcome this inconvenience in assessing the quality level, Chen et al. [32] proposed the SSQI $Q_{pk}$ based on the concept of quality level in Six Sigma. A general formula of $Q_{pk}$ is as follows:

$$Q_{pk}=\min \left\{\frac{USL-\mu +1.5\sigma }{\sigma },\frac{\mu -LSL+1.5\sigma }{\sigma }\right\}$$

(2)

Unfortunately, a single index value does not convey sufficient information. In the event that the quality level corresponding to a quality characteristic does not meet the needs of customers, the $Q_{pk}$ value cannot point toward the cause of poor performance or provide the manufacturer with reference for improvement. In view of the fact that $\gamma$ and $\delta$ can analyze the degrees of variance and shift in quality characteristics, respectively, many researchers convert PCIs into both of their functions. This approach can lead manufacturers to formulate targeted improvement measures [33,34,35,36,37]. $\gamma$ and $\delta$ are the precision and accuracy indices [38], respectively, defined as follows:

$$\gamma =\frac{\sigma }{d}\mathrm{and}\delta =\frac{\mu -T}{d}$$

(3)

where $T$ denotes the process target value. Clearly, in case the quality of a given process achieves the $k\sigma$ level, Equation (3) can be re-expressed based on the previous point as follows:

$$\gamma =\frac{\sigma }{d}=\frac{1}{k}\mathrm{and}\left|\delta \right|=\frac{\left|\mu -T\right|}{d}\le \frac{1.5}{k}$$

(4)

Thus, according to Equation (2), $Q_{pk}$ can be written as functions of $\gamma$ and $\delta$ to more accurately indicate the causes of poor process quality level:

$$Q_{pk}=\min \left(\frac{1-\delta }{\gamma }+1.5,\frac{1+\delta }{\gamma }+1.5\right)=\{\begin{array}{l}\frac{1-\delta }{\gamma }+1.5,\mathrm{for}\delta >0\\ \frac{1}{\gamma }+1.5,\mathrm{for}\delta =0\\ \frac{1+\delta }{\gamma }+1.5,\mathrm{for}\delta <0\end{array}$$

(5)

From Equations (4) and (5), $Q_{pk}=k$ can be obtained. This means that the value $k$ of $Q_{pk}$ equals the $k\sigma$ level achieved for the quality of an interested process. Thus, $Q_{pk}$ makes manufacturers conveniently available to analyze the quality level and the cause of poor quality. Furthermore, Chen et al. [32] indicated that $Q_{pk}$ has a one-to-one relationship $Yield\%\ge 2\mathsf{\Phi }\left(Q_{pk}-1.5\right)-1$ with process yield. It is relatively easy to see that a larger $Q_{pk}$ means better process performance and higher process yield.

3. Confidence Interval of ${\mathit{Q}}_{\mathit{p}\mathit{k}}$

In practice, both $\sigma$ and $\mu$ are definitely unknown population parameters. For this reason, manufacturers need to estimate $\sigma$ and $\mu$ from collected sample data and judge whether the quality level corresponding to a quality characteristic achieves the required needs of customers. Without loss of generality, we assumed that the quality characteristic $X$ with two-sided specification limits follows $N\left(\mu ,{\sigma }^2\right)$. We can obtain $n$ sample observations $X_1,X_2,\cdots ,X_n$ via random sampling. Furthermore, let $Y=\left(X-T\right)/d$, then $Y~N\left(\delta ,{\gamma }^2\right)$. The estimate of $Q_{pk}$ can be expressed as follows:

$${\widehat{Q}}_{pk}=\{\begin{array}{l}\frac{1-\widehat{\delta }}{\widehat{\gamma }}+1.5,\mathrm{for}\widehat{\delta }>0\\ \frac{1}{\widehat{\gamma }}+1.5,\mathrm{for}\widehat{\delta }=0\\ \frac{1+\widehat{\delta }}{\widehat{\gamma }}+1.5,\mathrm{for}\widehat{\delta }<0\end{array}$$

(6)

where $\widehat{\delta }=\left(\overline{X}-T\right)/d=\overline{Y}={\displaystyle {\sum }_{i=1}^n{Y}_i}/n$, $\overline{X}={\displaystyle {\sum }_{i=1}^n{X}_i}/n$, $\widehat{\gamma }=s/d=\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}/n}$, $s=\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(X_i-\overline{X}\right)}^2}/n}$. Clearly, ${\widehat{Q}}_{pk}$ is the maximum likelihood estimate (MLE) of $Q_{pk}$ because $s^2$ and $\overline{X}$ are the MLEs of ${\sigma }^2$ and $\mu$, respectively.

However, the structure of the samples may not be exactly the same as that of the population, which means that it is impossible to completely eliminate sampling error. Consequently, the estimated value ${\widehat{Q}}_{pk}$ cannot be expected to be equal to the true value of $Q_{pk}$. It is clear that using ${\widehat{Q}}_{pk}$ to judge the quality level of a given process may lead to misjudgment. In contrast, the CI is a range that estimates where the true population value lies. For this reason, many studies have employed the CI to judge whether the quality of a given process achieves the level required by customers [39,40,41,42,43,44]. In view of this, we derived the $100\left(1-\alpha \right)\%$ CI for $Q_{pk}$ to analyze whether the quality level of an interested process meets the acceptable level. This approach effectively handles the uncertainty involved in process quality assessment. We then used the CI to develop a supplier selection model.

First, let $Z=\sqrt{n}\left(\widehat{\delta }-\delta \right)/\gamma$ and $K=n{\widehat{\gamma }}^2/{\gamma }^2$. Then, $K$ and $Z$ follow ${\chi }_{n-1}^2$ and $N\left(0,1\right)$, respectively, under the assumption of normality. This implies $P\left(K_l\le K\le K_u\right)=1-{\alpha }^{\prime }$ and $P\left\{-Z_u\le Z\le Z_u\right\}=1-{\alpha }^{\prime }$, where $Z_u$ denotes $Z_{{\alpha }^{\prime }/2}$, and $K_l$ and $K_u$ denote ${\chi }_{{\alpha }^{\prime }/2,n-1}^2$ and ${\chi }_{1-\left({\alpha }^{\prime }/2\right),n-1}^2$, respectively. More specifically, ${\chi }_{{\alpha }^{\prime }/2,n-1}^2$ denotes the lower ${\alpha }^{\prime }/2$ quantile of ${\chi }_{n-1}^2$, and $Z_{{\alpha }^{\prime }/2}$ is the upper ${\alpha }^{\prime }/2$ quantile of $N\left(0,1\right)$, where ${\alpha }^{\prime }=1-\sqrt{1-\alpha }$ and $\alpha$ is the significance level. As $\widehat{\delta }$ and ${\widehat{\gamma }}^2$ are mutually independent, so are $Z$ and $K$. Based on this relationship, the following equation can be easily obtained:

$$P\left\{K_l\le K\le K_u,-Z_u\le Z\le Z_u\right\}=1-\alpha$$

(7)

Equivalently,

$$P\left\{\widehat{\gamma }\sqrt{\frac{n}{K_u}}\le \gamma \le \widehat{\gamma }\sqrt{\frac{n}{K_l}},\widehat{\delta }-\frac{\gamma Z_u}{\sqrt{n}}\le \delta \le \widehat{\delta }+\frac{\gamma Z_u}{\sqrt{n}}\right\}=1-\alpha$$

(8)

The interval of $\delta$, $\left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$, may or may not include 0. We examined these two cases. Let straight line $L$ and set $CR$ be as follows:

$$L:\delta =0\mathrm{and}CR=\left\{\left(\gamma ,\delta \right)|\widehat{\gamma }\sqrt{\frac{n}{K_u}}\le \gamma \le \widehat{\gamma }\sqrt{\frac{n}{K_l}},\widehat{\delta }-\frac{\gamma Z_u}{\sqrt{n}}\le \delta \le \widehat{\delta }+\frac{\gamma Z_u}{\sqrt{n}}\right\}$$

(9)

Case 1. 

$0\in \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$

When the intersection between$L$and$CR$is not an empty set (i.e., $L\cap CR\ne \varphi$), $0\in \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$. We can thus infer that $\delta =0$. Thus,$Q_{pk}={\gamma }^{-1}+1.5$. In this case, Equation (8) can be re-expressed as follows:

$$\begin{gathered} P\left\{\widehat{\gamma }\sqrt{\frac{n}{K_u}}\le \gamma \le \widehat{\gamma }\sqrt{\frac{n}{K_l}}\right\}=1-\alpha \\ s \end{gathered}$$

(10)

Clearly, when$0\in \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$, the$100\left(1-\alpha \right)\%$CI of$Q_{pk}$,$\left[L{Q}_{pk},U{Q}_{pk}\right]$, can be written as follows:

$$\left[L{Q}_{pk},U{Q}_{pk}\right]=\left[\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_l}{n}}+1.5,\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_u}{n}}+1.5\right]$$

(11)

Case 2. 

$0\notin \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$

When the intersection between$L$and$CR$is an empty set (i.e.,$L\cap CR=\varphi$),$0\notin \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$. We can infer that$\delta \ne 0$. We can then derive the$100\left(1-\alpha \right)\%$CI of$Q_{pk}$when$\delta >0$and$\delta <0$:

a. 

When$\delta >0$, Equations (5) and (8) indicate that$Q_{pk}=\left(1-\delta \right){\gamma }^{-1}+1.5$and$\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)>0$, so${\widehat{Q}}_{pk}=\left(1-\widehat{\delta }\right){\widehat{\gamma }}^{-1}+1.5$. Equation (8) can therefore be rewritten as follows:

$$\begin{array}{c}P\left\{\frac{1-\widehat{\delta }}{\gamma }-\frac{Z_u}{\sqrt{n}}+1.5\le \frac{1-\delta }{\gamma }+1.5\le \frac{1-\widehat{\delta }}{\gamma }+\frac{Z_u}{\sqrt{n}}+1.5,\widehat{\gamma }\sqrt{\frac{n}{K_u}}\le \gamma \le \widehat{\gamma }\sqrt{\frac{n}{K_l}}\}\right\}=1-\alpha \\ \Rightarrow P\left\{\frac{1-\widehat{\delta }}{\widehat{\gamma }}\left(\sqrt{\frac{K_l}{n}}\right)-\frac{Z_u}{\sqrt{n}}+1.5\le Q_{pk}\le \frac{1-\widehat{\delta }}{\widehat{\gamma }}\left(\sqrt{\frac{K_u}{n}}\right)+\frac{Z_u}{\sqrt{n}}+1.5\right\}=1-\alpha \\ \Rightarrow P\left\{\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_l}{n}}-\frac{Z_u}{\sqrt{n}}+1.5\le Q_{pk}\le \left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_u}{n}}+\frac{Z_u}{\sqrt{n}}+1.5\right\}=1-\alpha \end{array}$$

(12)

Clearly, when$0\notin \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$and$\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)>0$, the$100\left(1-\alpha \right)\%$CI of$Q_{pk}$,$\left[L{Q}_{pk},U{Q}_{pk}\right]$, can be written as follows:

$$\left[L{Q}_{pk},U{Q}_{pk}\right]=\left[\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_l}{n}}-\frac{Z_u}{\sqrt{n}}+1.5,\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_u}{n}}+\frac{Z_u}{\sqrt{n}}+1.5\right]$$

(13)

b. 

Similarly, when$\delta <0$, Equations (5) and (8) indicate that$Q_{pk}=\left(1+\delta \right){\gamma }^{-1}+1.5$and$\widehat{\delta }+Z_u\sqrt{\widehat{\gamma }/K_l}<0$, so${\widehat{Q}}_{pk}=\left(1+\widehat{\delta }\right){\widehat{\gamma }}^{-1}+1.5$. Equation (8) can therefore be rewritten as follows:

$$\begin{array}{c}P\left\{\frac{1+\widehat{\delta }}{\gamma }-\frac{Z_u}{\sqrt{n}}+1.5\le \frac{1+\delta }{\gamma }+1.5\le \frac{1+\widehat{\delta }}{\gamma }+\frac{Z_u}{\sqrt{n}}+1.5,\widehat{\gamma }\sqrt{\frac{n}{K_u}}\le \gamma \le \widehat{\gamma }\sqrt{\frac{n}{K_l}}\}\right\}=1-\alpha \\ \Rightarrow P\left\{\frac{1+\widehat{\delta }}{\widehat{\gamma }}\left(\sqrt{\frac{K_l}{n}}\right)-\frac{Z_u}{\sqrt{n}}+1.5\le Q_{pk}\le \frac{1+\widehat{\delta }}{\widehat{\gamma }}\left(\sqrt{\frac{K_u}{n}}\right)+\frac{Z_u}{\sqrt{n}}+1.5\right\}=1-\alpha \\ \Rightarrow P\left\{\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_l}{n}}-\frac{Z_u}{\sqrt{n}}+1.5\le Q_{pk}\le \left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_u}{n}}+\frac{Z_u}{\sqrt{n}}+1.5\right\}=1-\alpha \end{array}$$

(14)

c. 

Clearly, when$0\notin \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$and$\widehat{\delta }+Z_u\sqrt{\widehat{\gamma }/K_l}<0$, the$100\left(1-\alpha \right)\%$CI of$Q_{pk}$,$\left[L{Q}_{pk},U{Q}_{pk}\right]$, can be written as follows:

$$\left[L{Q}_{pk},U{Q}_{pk}\right]=\left[\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_l}{n}}-\frac{Z_u}{\sqrt{n}}+1.5,\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_u}{n}}+\frac{Z_u}{\sqrt{n}}+1.5\right]$$

(15)

For reasons of convenience, based on Equations (11), (13), and (15), $L{Q}_{pk}$ and $U{Q}_{pk}$ of the $100\left(1-\alpha \right)\%$ CI for $Q_{pk}$ can be expressed as follows:

$$L{Q}_{pk}=\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_l}{n}}-I\times \frac{Z_u}{\sqrt{n}}+1.5$$

(16)

$$U{Q}_{pk}=\left({\widehat{Q}}_{pk}-1.5\right)\sqrt{\frac{K_u}{n}}+I\times \frac{Z_u}{\sqrt{n}}+1.5$$

(17)

where $I=0$ if $0\in \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$, and $I=1$ if $0\notin \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$.

4. A Fuzzy Model of Supplier Selection

4.1. Model of Supplier Selection by General Hypothesis Testing

To effectively construct an objective and scientific supplier selection model, we used statistical hypothesis testing to assist firms in comparing the index $Q_{pk}$ provided from two suppliers and further established criteria for judgment. We let $Q_{pki}$ and $Q_{pkj}$ represent the process quality level of suppliers $i$ and $j$, respectively, where $\forall i\ne j$. The statistical hypothesis testing of the process quality levels between suppliers $i$ and $j$ is as follows:

$$\{\begin{array}{l}{H}_0:Q_{pki}=Q_{pkj}\\ H_1:Q_{pki}\ne Q_{pkj}\end{array}$$

(18)

Using Equations (11), (13) and (15), we can obtain the $100\left(1-\alpha \right)\%$ CIs $D_i=\left[L{Q}_{pki},U{Q}_{pki}\right]$ and $D_j=\left[L{Q}_{pkj},U{Q}_{pkj}\right]$ for $Q_{pki}$ and $Q_{pkj}$, respectively. We thus employed CI to compare the process quality levels between suppliers $i$ and $j$. The recommended selection criteria are as follows:

• If $D_i\cap D_j\ne \varphi$, then $L{Q}_{pki}\le U{Q}_{pkj}\le U{Q}_{pki}$ or $L{Q}_{pki}\le L{Q}_{pkj}\le U{Q}_{pki}$. In this case, we did not reject $H_0$ because of insufficient evidence, which means $Q_{pki}=Q_{pkj}$. The firm can select supplier $i$ or $j$ as a long-term partner.
• If $D_i\cap D_j=\varphi$, then we have sufficient evidence against the null hypothesis $H_0$ to reject it. The supplier the firm should choose as a long-term partner depends on the following conditions:

  (1)

  If $U{Q}_{pkj}<L{Q}_{pki}$, then $Q_{pki}>Q_{pkj}$. The firm should therefore choose supplier $i$ to ensure that their end products offer features required to meet customers’ needs and that they progress toward sustainable development.

  (2)

  Conversely, if $L{Q}_{pkj}>U{Q}_{pki}$, then $Q_{pkj}>Q_{pki}$. This means that the process quality level of supplier $j$ is higher than that of supplier $i$. The firm should therefore choose supplier $j$ as a long-term partner.

4.2. Fuzzy Estimator for $Q_{pkh}$ of Supplier $h$

As mentioned before, fuzziness and stochastic uncertainty exist in data collected from real-world situations. Taking this into account, it is possible for the above hypothesis testing to make a misjudgment. We thus proposed a TFN of ${\widehat{Q}}_{pk}$ and further developed a fuzzy model of selecting a supplier to enhance the reliability of evaluation and reduce the risk of miscalculation. According to Equations (6), (11), (13) and (15), we can obtain the ${\widehat{Q}}_{pk}$ of supplier $h$ as follows:

$${\widehat{Q}}_{pkh}=\{\begin{array}{l}\frac{1-{\widehat{\delta }}_h}{{\widehat{\gamma }}_h}+1.5,\mathrm{for}{\widehat{\delta }}_h-Z_u\left({\widehat{\gamma }}_h/\sqrt{K_l}\right)>0\\ \frac{1}{{\widehat{\gamma }}_h}+1.5,\mathrm{for}0\in \left[{\widehat{\delta }}_h-Z_u\left({\widehat{\gamma }}_h/\sqrt{K_l}\right),{\widehat{\delta }}_h+Z_u\left({\widehat{\gamma }}_h/\sqrt{K_l}\right)\right]\\ \frac{1+{\widehat{\delta }}_h}{{\widehat{\gamma }}_h}+1.5,\mathrm{for}{\widehat{\delta }}_h+Z_u\left({\widehat{\gamma }}_h/\sqrt{K_l}\right)<0\end{array}$$

(19)

By the inspiration of Buckley [45], the $\alpha \text{-}\mathrm{cuts}$ of the TFN ${\tilde{\widehat{Q}}}_{pkh}$ for supplier $h$ can be obtained as follows:

$${\tilde{\widehat{Q}}}_{pkh}\left[\alpha \right]=\{\begin{array}{l}\left[{\widehat{Q}}_{pkh1}\left(\alpha \right),{\widehat{Q}}_{pkh2}\left(\alpha \right)\right],\mathrm{for}0.01\le \alpha \le 1\\ \left[{\widehat{Q}}_{pkh1}\left(0.01\right),{\widehat{Q}}_{pkh2}\left(0.01\right)\right],\mathrm{for}0\le \alpha \le 0.01\end{array}$$

(20)

where ${\widehat{Q}}_{pkh1}\left(\alpha \right)=\left({\widehat{Q}}_{pkh}-1.5\right)\sqrt{\frac{K_l}{n}}-I\times \frac{Z_u}{\sqrt{n}}+1.5$ and ${\widehat{Q}}_{pkh2}\left(\alpha \right)=\left({\widehat{Q}}_{pkh}-1.5\right)\sqrt{\frac{K_u}{n}}+I\times \frac{Z_u}{\sqrt{n}}+1.5$.

For $0.01\le \alpha \le 1$, starting at 0.01 is arbitrary so we can begin at 0.001 or 0.005, etc. When $\alpha =1$, then ${\widehat{Q}}_{pkh1}\left(1\right)=\left[\left({\widehat{Q}}_{pkh}-1.5\right)\sqrt{{\chi }_{0.5,n-1}^2/n}\right]+1.5={\widehat{Q}}_{pkh2}\left(1\right)$. Thus, the TFN ${\tilde{\widehat{Q}}}_{pkh}$ of ${\widehat{Q}}_{pkh}$ can be defined as follows:

$${\tilde{\widehat{Q}}}_{pkh}=\left[{\widehat{Q}}_{pkh1}\left(0.01\right),{\widehat{Q}}_{pkh1}\left(1\right)={\widehat{Q}}_{pkh2}\left(1\right),{\widehat{Q}}_{pkh2}\left(0.01\right)\right]$$

(21)

where

$$\begin{array}{c}{\widehat{Q}}_{pkh1}\left(0.01\right)=\left({\widehat{Q}}_{pkh}-1.5\right)\sqrt{\frac{{\chi }_{0.0025,n-1}^2}{n}}-I\times \frac{Z_{0.0025}}{\sqrt{n}}+1.5,\\ {\widehat{Q}}_{pkh1}\left(1\right)={\widehat{Q}}_{pkh2}\left(1\right)=\left({\widehat{Q}}_{pkh}-1.5\right)\sqrt{\frac{{\chi }_{0.5,n-1}^2}{n}}+1.5,\\ {\widehat{Q}}_{pkh2}\left(0.01\right)=\left({\widehat{Q}}_{pkh}-1.5\right)\sqrt{\frac{{\chi }_{0.9975,n-1}^2}{n}}+I\times \frac{Z_{0.0025}}{\sqrt{n}}+1.5.\end{array}$$

Under the circumstances, the membership function (MF) of ${\tilde{\widehat{Q}}}_{pkh}$ can be presented as follows:

$${\psi }_{{\tilde{\widehat{Q}}}_{pkh}}(x)=\{\begin{array}{l}0,\mathrm{if}x<{\widehat{Q}}_{pkh1}\left(0.01\right)\\ {\alpha }_1,\mathrm{if}{\widehat{Q}}_{pkh1}\left(0.01\right)\le x<{\widehat{Q}}_{pkh1}\left(1\right)\\ 1,\mathrm{if}x={\widehat{Q}}_{pkh1}\left(1\right)={\widehat{Q}}_{pkh2}\left(1\right)\\ {\alpha }_2,\mathrm{if}{\widehat{Q}}_{pkh2}\left(1\right)<x\le {\widehat{Q}}_{pkh2}\left(0.01\right)\\ 0,\mathrm{if}{\widehat{Q}}_{pkh2}\left(0.01\right)<x\end{array}$$

(22)

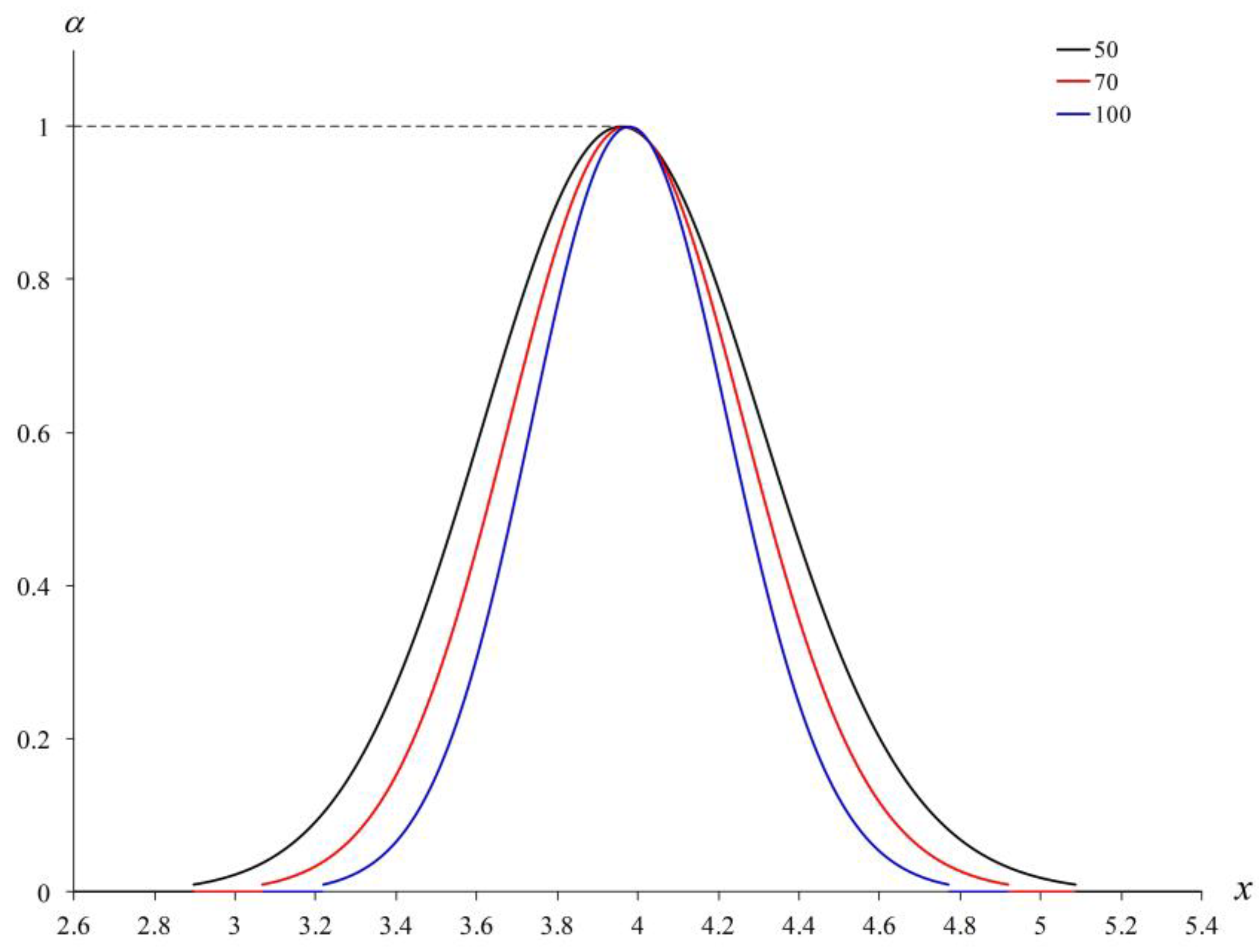
where ${\alpha }_1$ and ${\alpha }_2$ are determined by ${\widehat{Q}}_{pkh1}\left({\alpha }_1\right)=x$ and ${\widehat{Q}}_{pkh2}\left({\alpha }_2\right)=x$, respectively. Figure 1 presents the MF of ${\tilde{\widehat{Q}}}_{pkh}$ with ${\widehat{Q}}_{pkh}=4$, $0\notin \left[{\widehat{\delta }}_h-Z_u\left({\widehat{\gamma }}_h/\sqrt{K_l}\right),{\widehat{\delta }}_h+Z_u\left({\widehat{\gamma }}_h/\sqrt{K_l}\right)\right]$ for $n=50$, 70, and 100.

4.3. Fuzzy Model of Supplier Selection by Fuzzy Hypothesis Testing

We know from Section 4.1 that the quality level of supplier $i$ is better than supplier $j$ when $U{Q}_{pkj}<L{Q}_{pki}$; conversely, the quality level of supplier $j$ is better than supplier $i$ when $U{Q}_{pki}<L{Q}_{pkj}$. As ${\widehat{Q}}_{pkh}$ of supplier $h$ changes into a TFN ${\tilde{\widehat{Q}}}_{pkh}$ with consideration of data uncertainty, the decision rule for fuzzy hypothesis testing of the index ${\widehat{Q}}_{pkh}$ provided from suppliers $i$ and $j$ is based on the relationship between ${\tilde{\widehat{Q}}}_{pki}$ and ${\tilde{\widehat{Q}}}_{pkj}$. 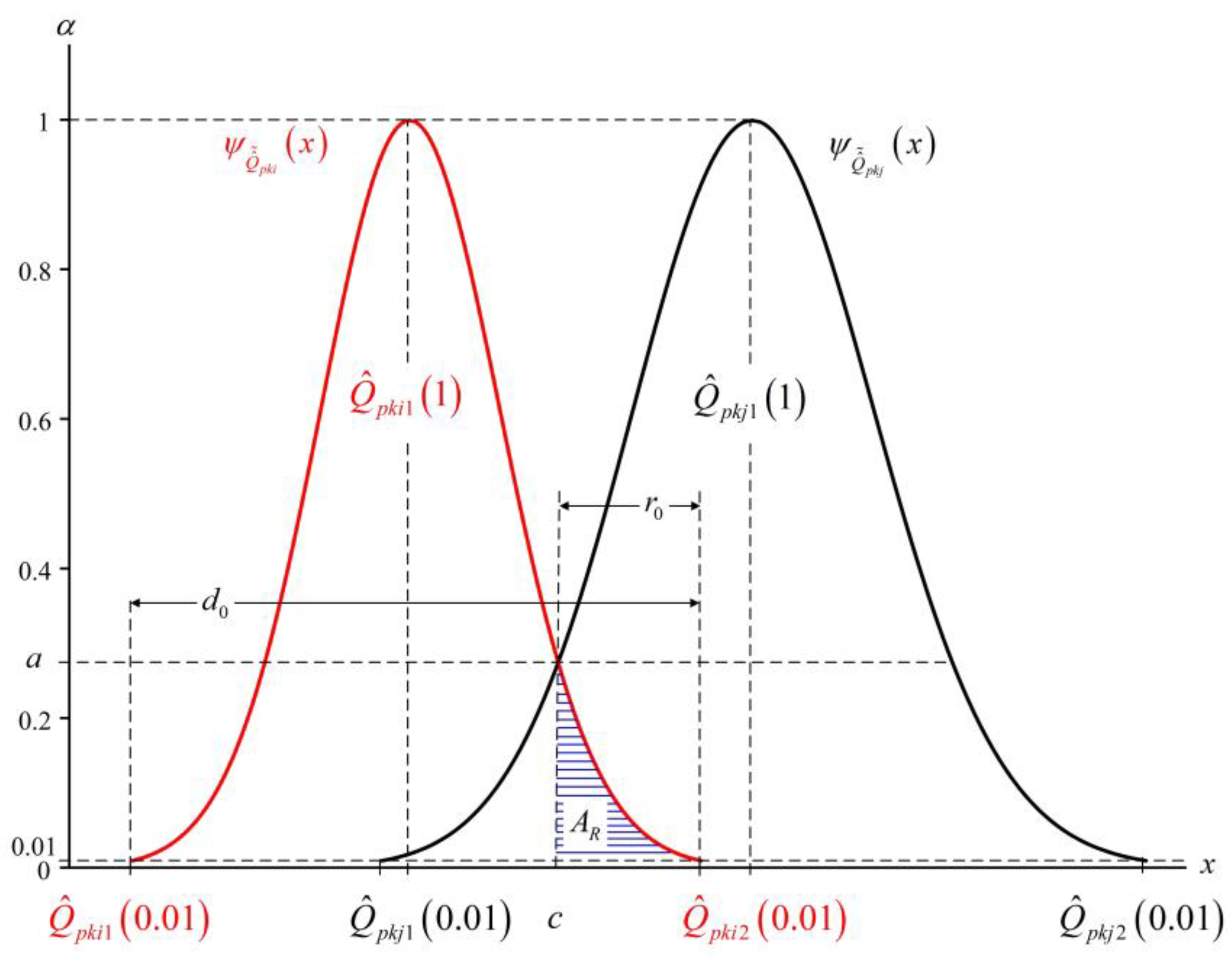Firstly, the situation of ${\widehat{Q}}_{pkj}>{\widehat{Q}}_{pki}$ is discussed to develop the fuzzy hypothesis testing model. With regard to this situation, it can be best explained by studying Figure 2. It is worth mentioning that the individual vertices ${\psi }_{{\tilde{\widehat{Q}}}_{pki}}(x)$ and ${\psi }_{{\tilde{\widehat{Q}}}_{pkj}}(x)$ are at $x={\widehat{Q}}_{pki1}\left(1\right)={\widehat{Q}}_{pki2}\left(1\right)$ and $x={\widehat{Q}}_{pkj1}\left(1\right)={\widehat{Q}}_{pkj2}\left(1\right)$, respectively. If the situation is ${\widehat{Q}}_{pkj}<{\widehat{Q}}_{pki}$, then the same conclusion will be made as soon as these two are swapped.

The ratio of two specific defined areas is used to perform testing with a TFN [45]. In view of this, we defined $A_T$ as the total area under the graph of ${\psi }_{{\tilde{\widehat{Q}}}_{pki}}(x)$ and $A_R$ as the area under the graph of ${\psi }_{{\tilde{\widehat{Q}}}_{pki}}(x)$ but to the right of the vertical line through $c$ (see Figure 2). Unfortunately, the complexity of ${\psi }_{{\tilde{\widehat{Q}}}_{pki}}(x)$ greatly hinders the computing of $A_T$ and $A_R$. Thus, we proposed an approximate approach to compute $A_T$ and $A_R$ for making a final decision in fuzzy hypothesis testing. First, let $l=\lfloor 100\alpha \rfloor$ because of $0.01\le \alpha \le 1$, where $l$ is the greatest integer that is less than or equal to $100\alpha$, then ${\alpha }^{\prime }=1-\sqrt{1-0.01l}$ and $l=1,2,\cdots ,100$. Obviously, $d_l$ can be calculated as follows:

$$d_l=\left({\widehat{Q}}_{pki}-1.5\right)\left(\sqrt{\frac{{\chi }_{1-\left(\left(1-\sqrt{1-0.01l}\right)/2\right),n-1}^2}{n}}-\sqrt{\frac{{\chi }_{\left(1-\sqrt{1-0.01l}\right)/2,n-1}^2}{n}}\right)+I\times \frac{2Z_{\left(1-\sqrt{1-0.01l}\right)/2}}{\sqrt{n}}$$

(23)

It is worth noting that $d_0=d_1$, which can be expressed as follows:

$$d_0=d_1=\left({\widehat{Q}}_{pki}-1.5\right)\left(\sqrt{\frac{{\chi }_{0.9975,n-1}^2}{n}}-\sqrt{\frac{{\chi }_{0.0025,n-1}^2}{n}}\right)+I\times \frac{2Z_{0.0025}}{\sqrt{n}}$$

(24)

Likewise, we let $w=\lfloor 100a\rfloor$ because of $0.01\le \alpha \le a$. That is, $l=1,2,\cdots ,h$. In addition, $c$ can be obtained based on the following Equation (25).

$$\begin{array}{cc}\hfill c& =\left({\widehat{Q}}_{pkj}-1.5\right)\sqrt{\frac{{\chi }_{\left(1-\sqrt{1-0.01w}\right)/2,n-1}^2}{n}}-I\times \frac{Z_{\left(1-\sqrt{1-0.01w}\right)/2}}{\sqrt{n}}+1.5\hfill \\ & =\left({\widehat{Q}}_{pki}-1.5\right)\sqrt{\frac{{\chi }_{\left(1-\sqrt{1-0.01w}\right)/2,n-1}^2}{n}}+I\times \frac{Z_{\left(1-\sqrt{1-0.01w}\right)/2}}{\sqrt{n}}+1.5\hfill \end{array}$$

(25)

Thus, $r_l$ can be expressed as follows:

$$r_l=\left({\widehat{Q}}_{pki}-1.5\right)\sqrt{\frac{{\chi }_{1-\left(\left(1-\sqrt{1-0.01l}\right)/2\right),n-1}^2}{n}}+\frac{Z_{\left(1-\sqrt{1-0.01l}\right)/2}}{\sqrt{n}}+1.5-c,l=1,2,\cdots ,h$$

(26)

In addition, $r_0=r_1$. Therefore, $A_T$ and $A_R$ can be approximately obtained as follows:

$$A_T={\displaystyle \sum _{l=1}^{100}\left(\frac{d_{l-1}+d_l}{2}\right)\times (0.01)}\mathrm{and}{A}_R={\displaystyle \sum _{l=1}^h\left(\frac{r_{l-1}+r_l}{2}\right)\times (0.01)}$$

(27)

In conclusion, we can calculate the ratio of $A_R$ to $A_T$ according to Equation (27) and further make reliable decisions to select the best supplier with our proposed fuzzy estimator ${\tilde{\widehat{Q}}}_{pkh}$. Thus, we chose two numbers ${\varphi }_1$ and ${\varphi }_2$, such as $0<{\varphi }_1<{\varphi }_2<0.5$, and the decision rules are as follows:

(1)

If $A_R/A_T\le {\varphi }_1$, then reject $H_0$ and conclude that $Q_{pki}<Q_{pkj}$.

(2)

For ${\varphi }_1<A_R/A_T<{\varphi }_2$, make no decision on reject/not reject.

(3)

For $A_R/A_T\ge {\varphi }_2$, do not reject $H_0$ and conclude that $Q_{pki}=Q_{pkj}$.

According to the abovementioned evaluation rules, we conducted comparisons and tests on all suppliers one after another so as to find the suppliers with better quality level. Furthermore, the proposed fuzzy model is based on the CI of estimator ${\widehat{Q}}_{pkh}$ provided by supplier $h$. From the perspective of statistical theory, the degree of imprecision can be indicated according to the length of the CI. We can see from Equations (16) and (17) that the length of the confidence interval for $Q_{pkh}$ of supplier $h$ depends on sample size n and confidence level $\alpha$. More specifically, the length of the confidence interval for $Q_{pkh}$ decreases with an increase in $n$ for fixed $\alpha$, whereas the length of the confidence interval for $Q_{pkh}$ decreases with an increase in $\alpha$ for fixed $n$. Obviously, the stability of the proposed fuzzy model depends on $n$ and $\alpha$. Thus, a number of researchers have applied this concept to analyze the sensitivity and stability of the fuzzy model [46,47].

5. Illustrative Example

In order to illustrate how the proposed approach can be utilized in practical applications, we considered a case study involving a gear product. Gears change the direction and speed of power within machines, making them an integral aspect of mechanized industries. In practice, gear manufacturing follows the 4R concept and includes several procedures; grinding is one such important process involving high precision and fairly small grinding surfaces. As grinding is associated with several quality characteristics, we considered only the process quality level of the most crucial quality characteristic, which is the internal diameter. Furthermore, there is no place in the world like Taichung, Taiwan, with the entire machinery industry clustered together. In view of this, we assisted a machine tool factory located in Taichung to select the optimal supplier of gear components. Thus, the specification limits of internal diameter for the gear specified by the factory were set as follows: LSL = 21.8 mm, T = 21.85 mm and USL = 21.9 mm. We applied the proposed approach to compare the process quality offered by two gear suppliers located in Taichung, Taiwan.

For a mass-produced gear product, a process engineer used the simple random sampling to collect 60 samples each of internal diameter from Supplier 1 and Supplier 2 during the month of April 2020 (i.e., $n=60$). However, the proposed supplier selection model in this paper is based on theoretical assumptions of normality for the process data. Thus, we cannot use the proposed approach to select a supplier when the collected data is not normally distributed. For this reason, we employed the Anderson–Darling test to confirm the assumption of normality with p-value > 0.05. Therefore, it is reasonable to assume that the collected data are normally distributed.

Table 1. Statistics of collected samples.

Supplier Code	${\overline{\mathit{X}}}_{\mathit{h}}$	${\mathit{s}}_{\mathit{h}}$	${\widehat{\mathit{\delta }}}_{\mathit{h}}$	${\widehat{\mathit{\gamma }}}_{\mathit{h}}$	${\widehat{\mathit{Q}}}_{\mathit{p}\mathit{k}\mathit{h}}$
$h=1$	21.8804	0.0075	0.608	0.149	4.131
$h=2$	21.8913	0.0024	0.825	0.048	5.146

presents the statistics of the collected samples.

Supposing that significance level $\alpha$ is set to 0.05 (i.e., ${\alpha }^{\prime }=0.025321$), $\left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]=\left[0.57231,0.64369\right]$ for Supplier 1 can be obtained, and it can be further concluded that $0\notin \left[\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right),\widehat{\delta }+Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)\right]$ and $\widehat{\delta }-Z_u\left(\widehat{\gamma }/\sqrt{K_l}\right)>0$, respectively. Therefore, the $95\%$ CI $D_1=\left[3.2887,4.9368\right]$ of $Q_{pk1}$ for Supplier 1 can be obtained from Equation (12). In a manner similar to Supplier 1, we can derive the $95\%$ CI $D_2=\left[4.0901,6.15129\right]$ of $Q_{pk2}$ for Supplier 2. These results indicate that $L{Q}_{pk2}\le U{Q}_{pk1}\le U{Q}_{pk2}$; therefore $D_1\cap D_2\ne \varphi$. As we do not have enough statistical evidence to reject $H_0:Q_{pk1}=Q_{pk2}$, we can conclude that there is no significant difference between the process quality levels of Supplier 1 and Supplier 2.

As mentioned above, we can decide to reject $H_0$ or not by comparing the CIs of $Q_{pk1}$ and $Q_{pk2}$. However, taking into consideration data imprecision, we further employed the decision-making procedure for fuzzy hypothesis testing of $Q_{pkh}$ to assess whether the relationship between the process quality levels of Supplier 1 and Supplier 2 is equal or not. 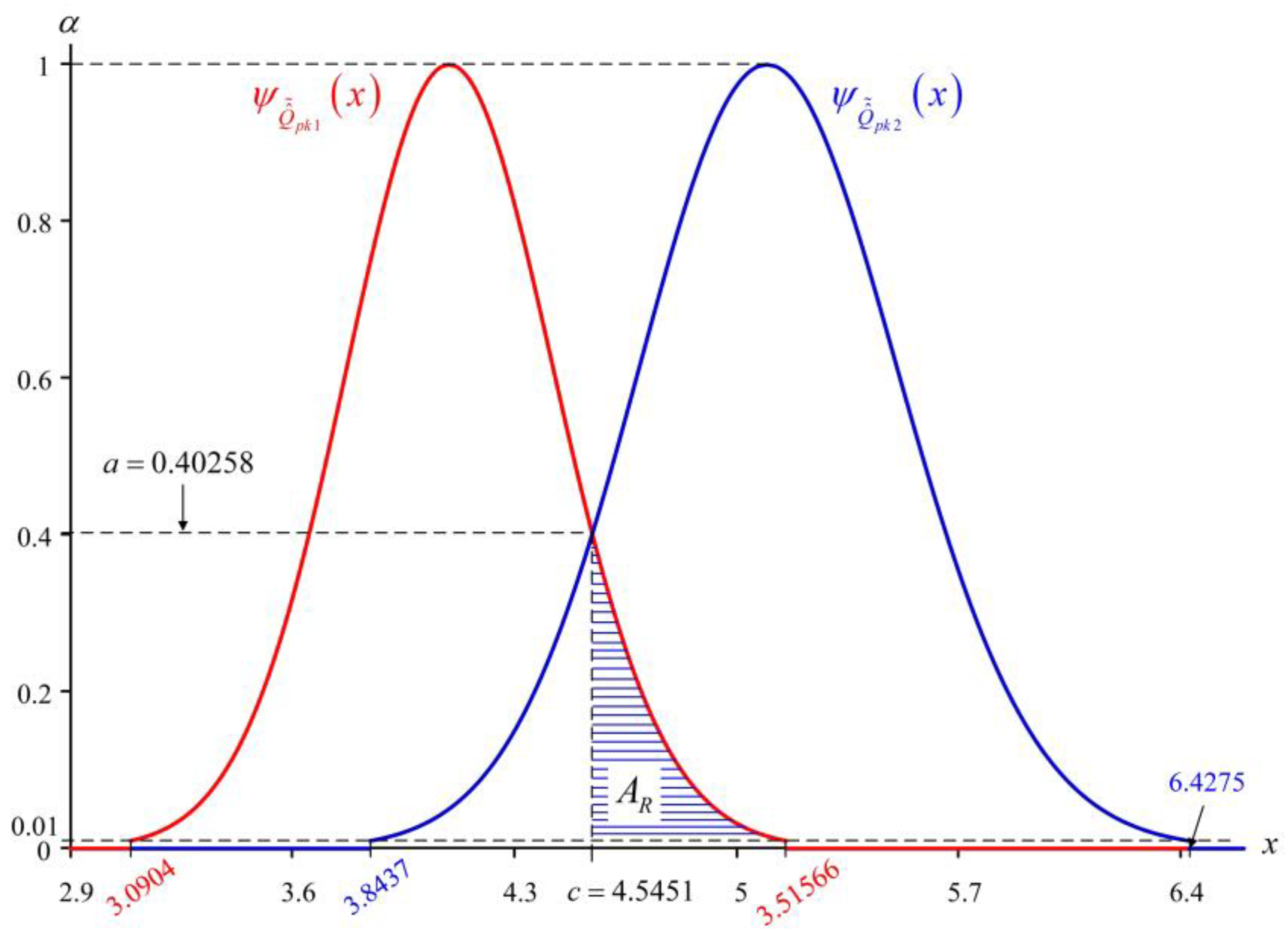Thus, ${\widehat{Q}}_{pk1}$ and ${\widehat{Q}}_{pk2}$ became TFN ${\tilde{\widehat{Q}}}_{pk1}$ and ${\tilde{\widehat{Q}}}_{pk2}$, respectively, with our proposed approach. For the sake of illustration, Figure 3 plots the relationship between ${\tilde{\widehat{Q}}}_{pk1}$ and ${\tilde{\widehat{Q}}}_{pk2}$ as it pertains to this example.

Therefore, Equations (23) and (27) can be used to obtain $A_T=83.0000$. On the other hand, $a=0.40258$ and $w=40$ can be solved with Equation (25). In such a case, $c=4.545096$ and $A_R=7.7737$ are obtained from Equations (25)–(27). Thus, we can further calculate $A_R/A_T=0.0937$. Let the two numbers in the fuzzy testing be ${\varphi }_1=0.2$ and ${\varphi }_2=0.4$, $A_R/A_T\le 0.2$ can be found based on the abovementioned criterion of judgment. Obviously, this result shows that the null hypothesis $H_0$ of the hypothesis testing can be rejected. There is sufficient evidence showing that a difference exists between process quality levels of Supplier 1 and Supplier 2. However, a greater ${\widehat{Q}}_{pk}$ value indicates higher process quality levels and higher process yield. Thus, the buying firm should choose Supplier 2 as a long-term partner due to ${\widehat{Q}}_{pk1}<{\widehat{Q}}_{pk2}$. In this way, buying firms can more effectively ensure the quality levels of their products and increase global competitiveness.

6. Conclusions and Research Limitations

Faced with swift market changes and globalized competition, firms must respond quickly to the varying demands of customers to maintain their own competitive advantages. Supply chain management allows firms to integrate both upstream and downstream. Supplier selection is a vital aspect of a firm’s development and actual gains. In view of this, this study developed a supplier selection model based on process quality from the perspective of a circular economy. We first employed the SSQI $Q_{pk}$, which can directly reflect process quality levels, to evaluate the process quality of suppliers. In practice, process mean $\mu$ and standard deviation $\sigma$ are generally unknown population parameters. This means that $Q_{pk}$ must be estimated based on collected sample data. Using the point estimate ${\widehat{Q}}_{pk}$ to determine the process quality of suppliers may lead to miscalculation. Thus, to enhance the reliability of evaluation, we derived the $100\left(1-\alpha \right)\%$ CI of $Q_{pk}$ for application to a supplier selection model.

The fact that fuzziness and stochastic uncertainty are unavoidable features for collected data has led some researchers to assess process quality by taking into consideration data imprecision. For this reason, this study proposed a TFN of ${\widehat{Q}}_{pk}$ and further developed a fuzzy testing model of selecting a supplier with the intent of reducing the risk of miscalculation and making reliable selection decisions for the evaluation of process quality level. To illustrate the applicability of the proposed approach, we demonstrated its implementation through a case study involving a gear component product. In the general hypothesis testing, the results showed that there was no significant difference between the process quality levels of Supplier 1 and Supplier 2. However, it is worth noting that ${\widehat{Q}}_{pk2}$ was 1.015 higher than ${\widehat{Q}}_{pk1}$. This meant the difference between the process yield of the two was 0.008247 (i.e., 8247.05 defects per million opportunities). In view of this, we were bewildered by the inference results of the general hypothesis testing.

To this end, we further investigated the TFN of ${\widehat{Q}}_{pk1}$ and ${\widehat{Q}}_{pk2}$ and performed the proposed fuzzy hypothesis testing for $H_0:Q_{pk1}=Q_{pk2}$. These results showed that there was sufficient evidence showing that a difference existed between the process quality levels of Supplier 1 and Supplier 2. More specifically, Supplier 2 would be better than Supplier 1 from a strategic perspective for the firm. Thus, the fuzzy model proposed in this study can more reliably assist firms in choosing the optimal supplier for long-term collaborations, thereby leading to a reduction in the amount of scrap and rework and helping firms move toward sustainability and production. In conclusion, the proposed model can help firms make reliable decisions in a fuzzy environment, ensuring that their products meet the needs of the end customer and leading firms toward sustainable development. The limitations in this study, however, is that in order to effectively assess process quality provided by suppliers and select the optimal supplier by the proposed fuzzy model, the collected sample data must come from a stable process and follow a normal distribution.