Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 2: Finite-Core-Vortex Approach and Oceanographic Application
Abstract
1. Introduction
- (1)
- Lagrangian conservation: in unforced, non-dissipative flows, each fluid column conserves its potential vorticity along its motion.
- (2)
- Invertibility: potential vorticity is invertible into stream-function via the inversion of a generalized Laplacian operator. Horizontal velocity derives from stream-function via a skew-symmetric matrix and a gradient operator.
- (3)
- The “impermeability” theorem: in a fluid layer without the time-change of total mass, nor of total momentum, the volume integral of potential vorticity is conserved [18].
2. Model
2.1. Mathematical Model
2.2. Numerical Models
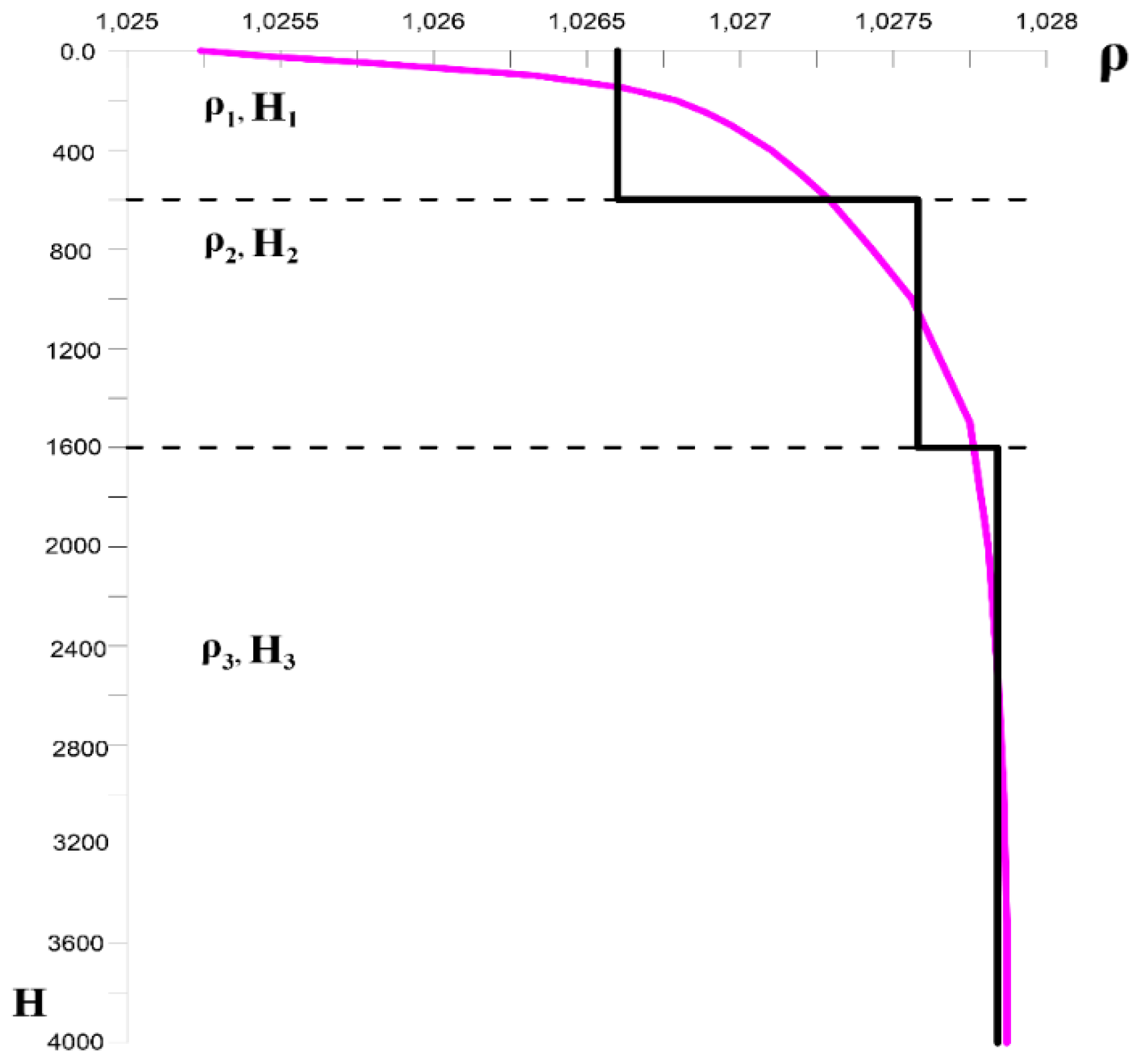
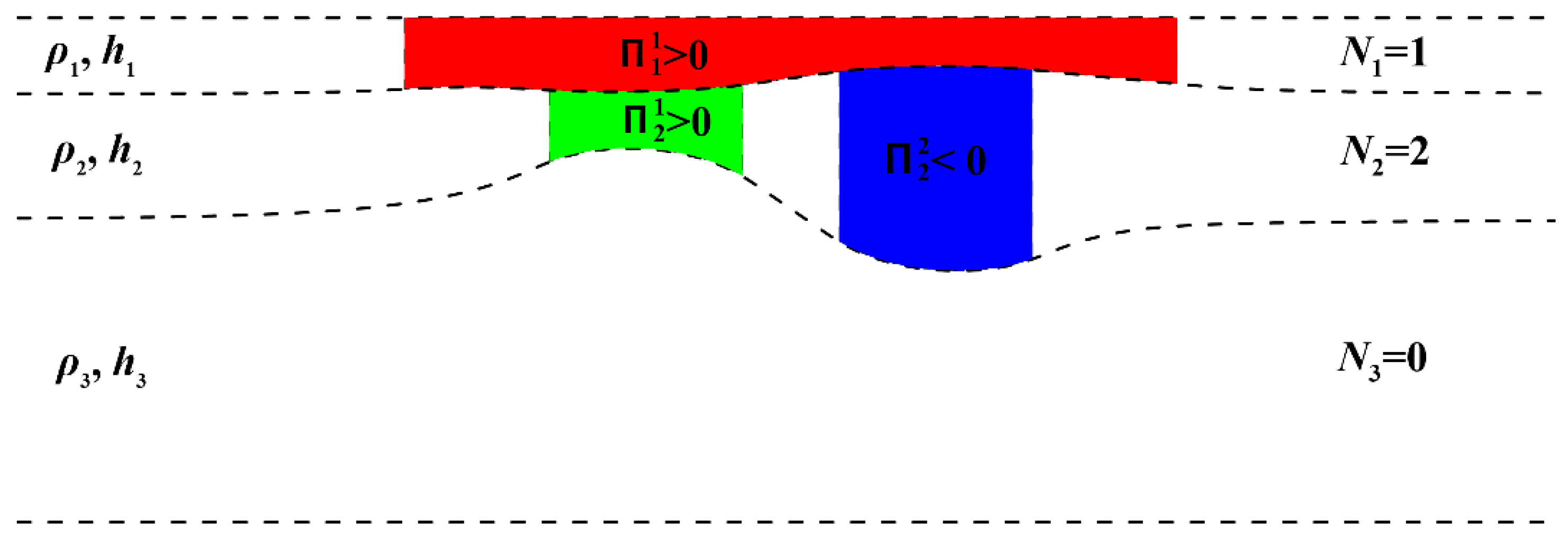
2.3. Physical Model of the Present Problem
- If the surface cyclone over a large intrathermocline vortex forms a stable structure.
- If the surface cyclone remains coherent and/or if it sheds filaments, small eddies, or small eddy pairs.
- The evolution of the intrathermocline vortices and their ability to deform the upper cyclone with a characteristic surface signature.
- If the intra-layer or inter-layer interactions dominate and in particular, if horizontal vortex pairs or vertical vortex pairs (hetons) or the vertical alignment of like-signed vorticity patches, are the prevalent mechanism.
3. Interaction of a Surface Vortex with a Single Intrathermocline Lens
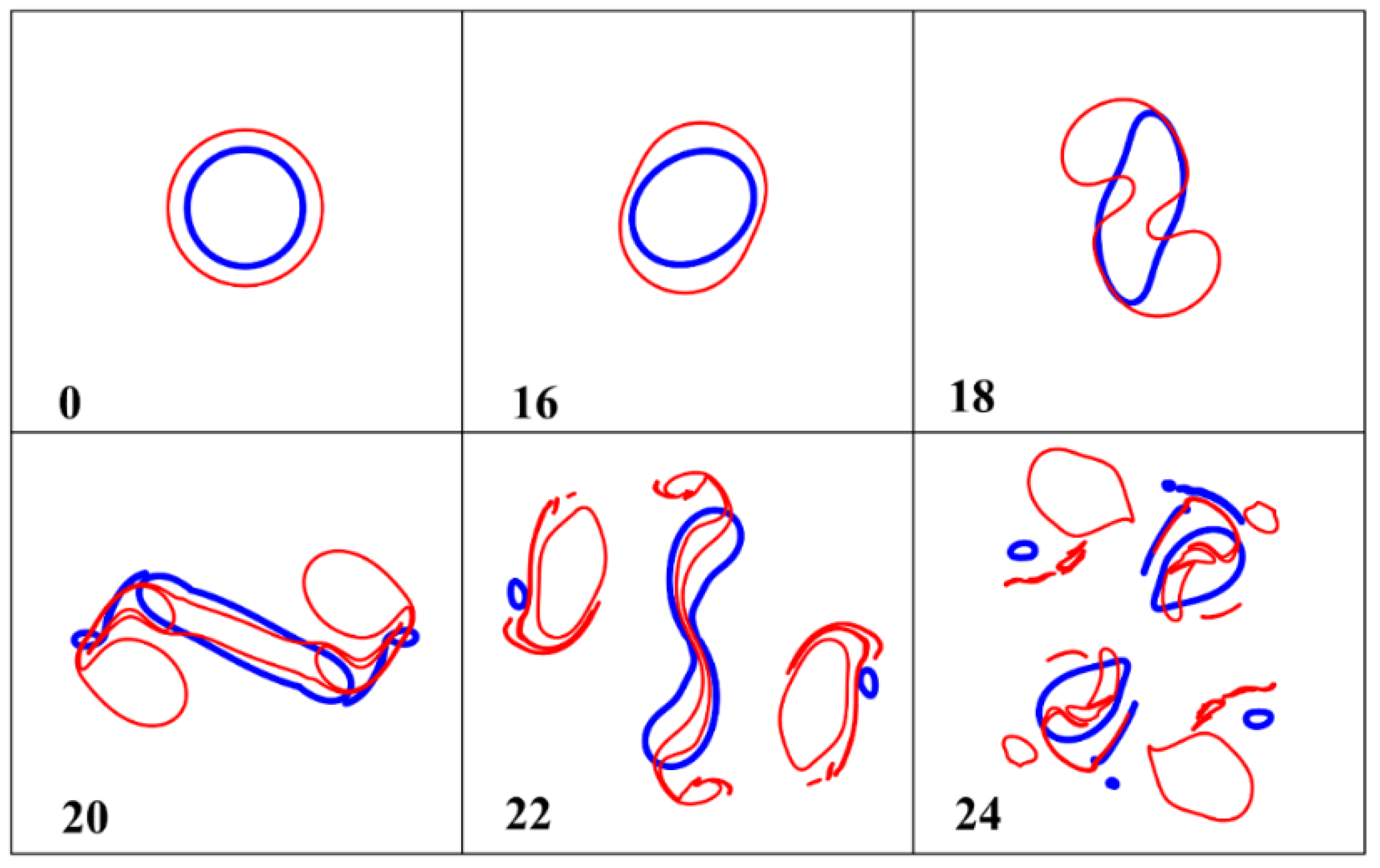
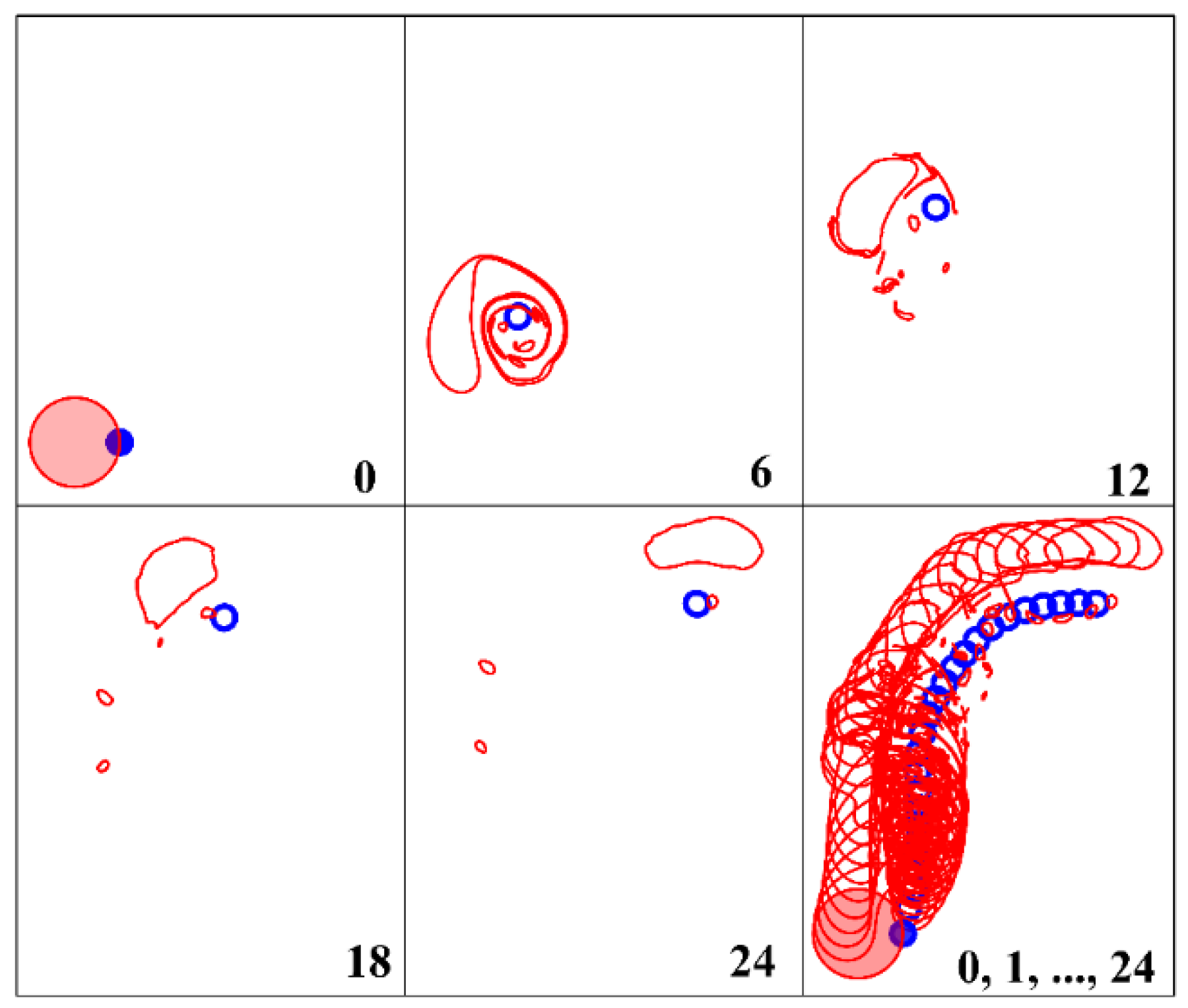
3.1. Vertically Aligned Vortices
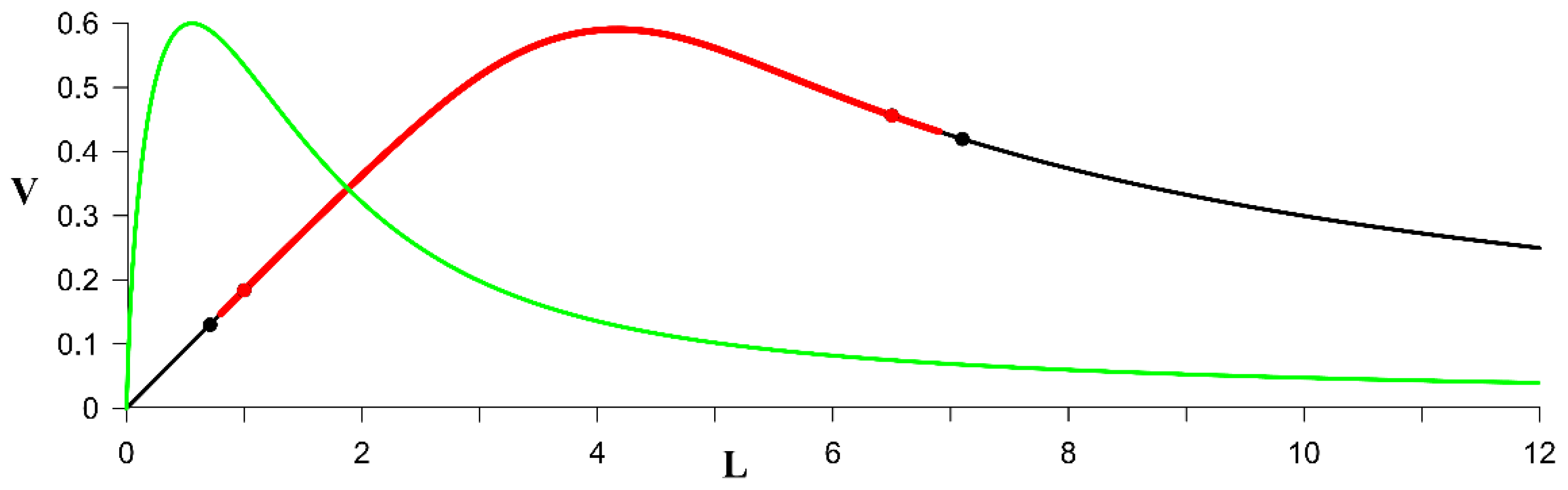
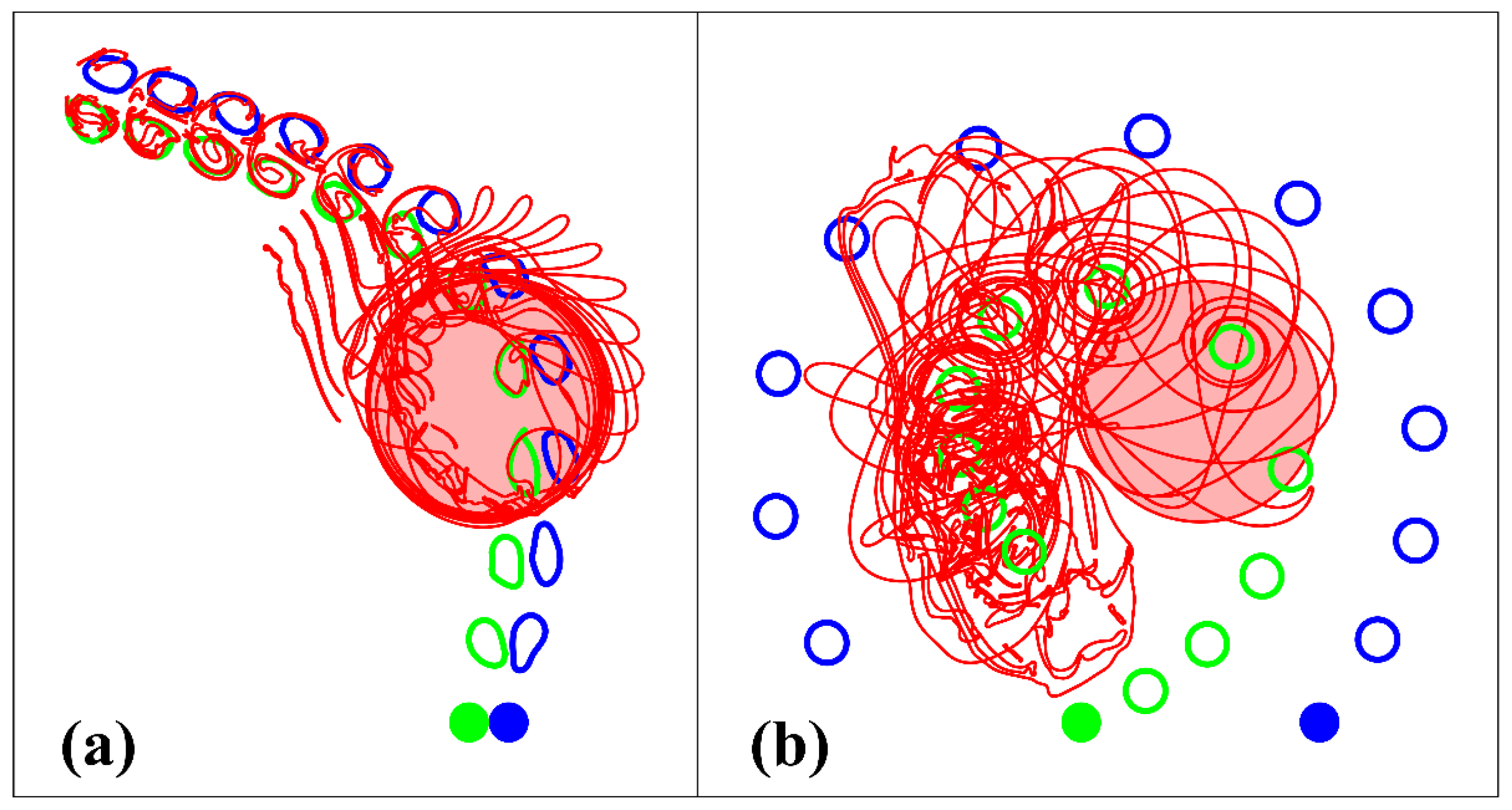
3.2. Vertically Shifted Vortices
4. Interaction of a Surface Vortex with Two Middle Layer Vortices
4.1. Collinear Initial Configuration
4.2. Impact of the Two External Intrathermocline Vortices on the Surface Cyclone
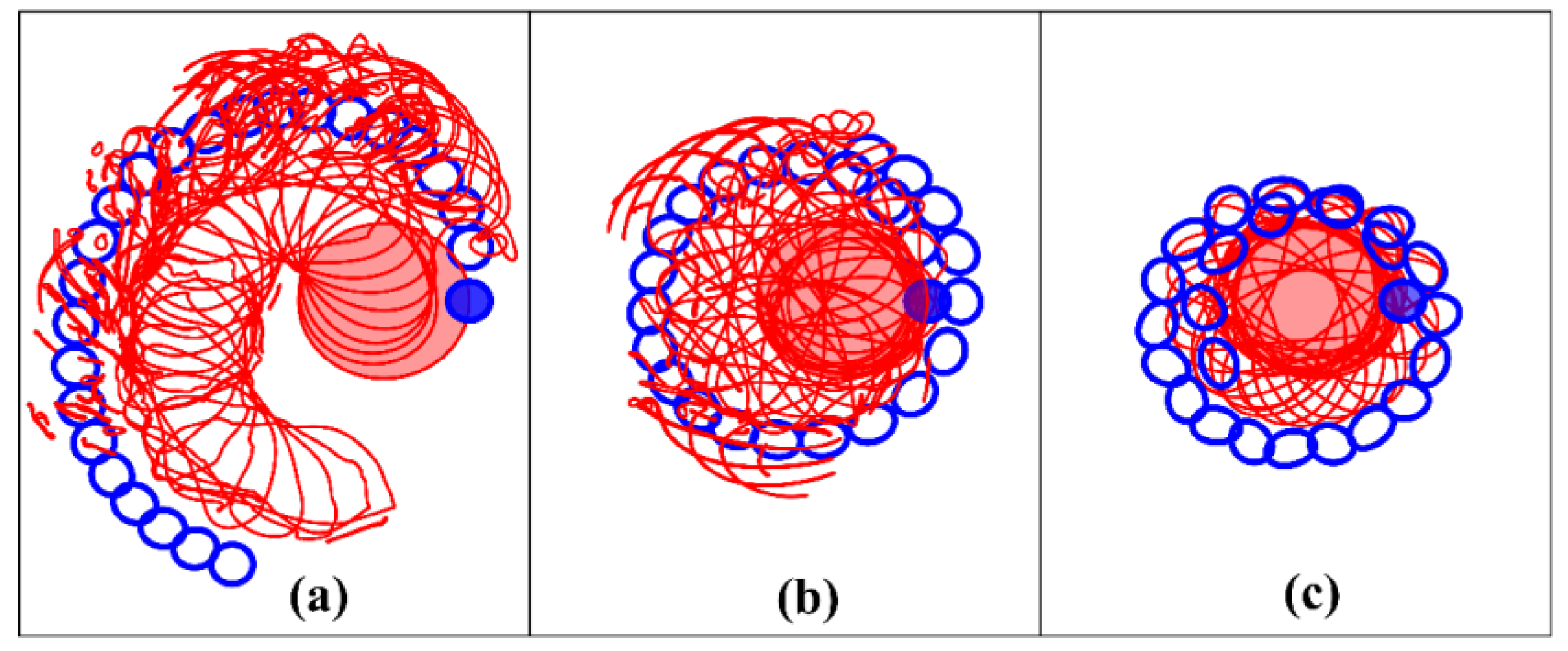
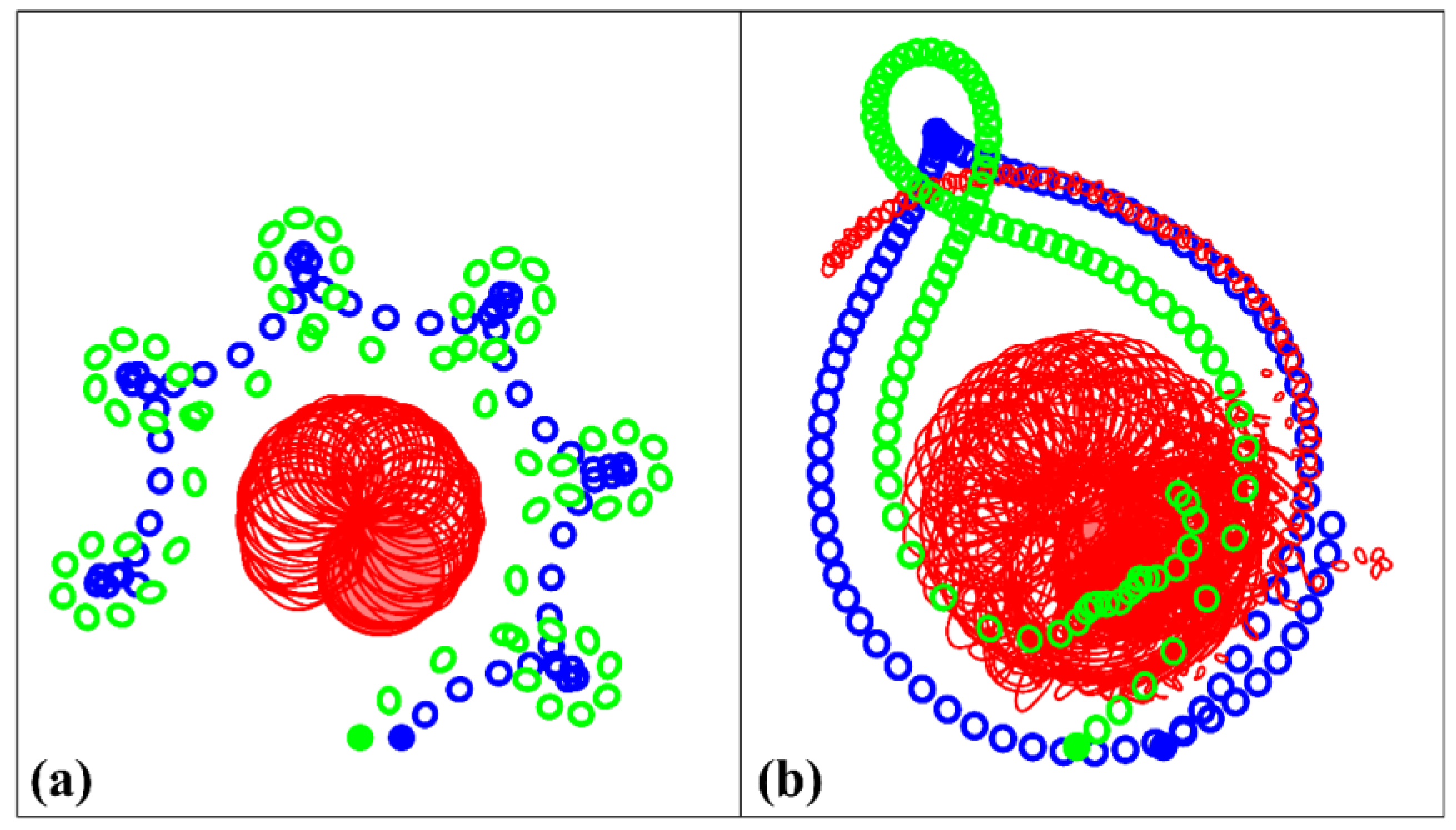
4.2.1. Case of Intrathermocline Dipole
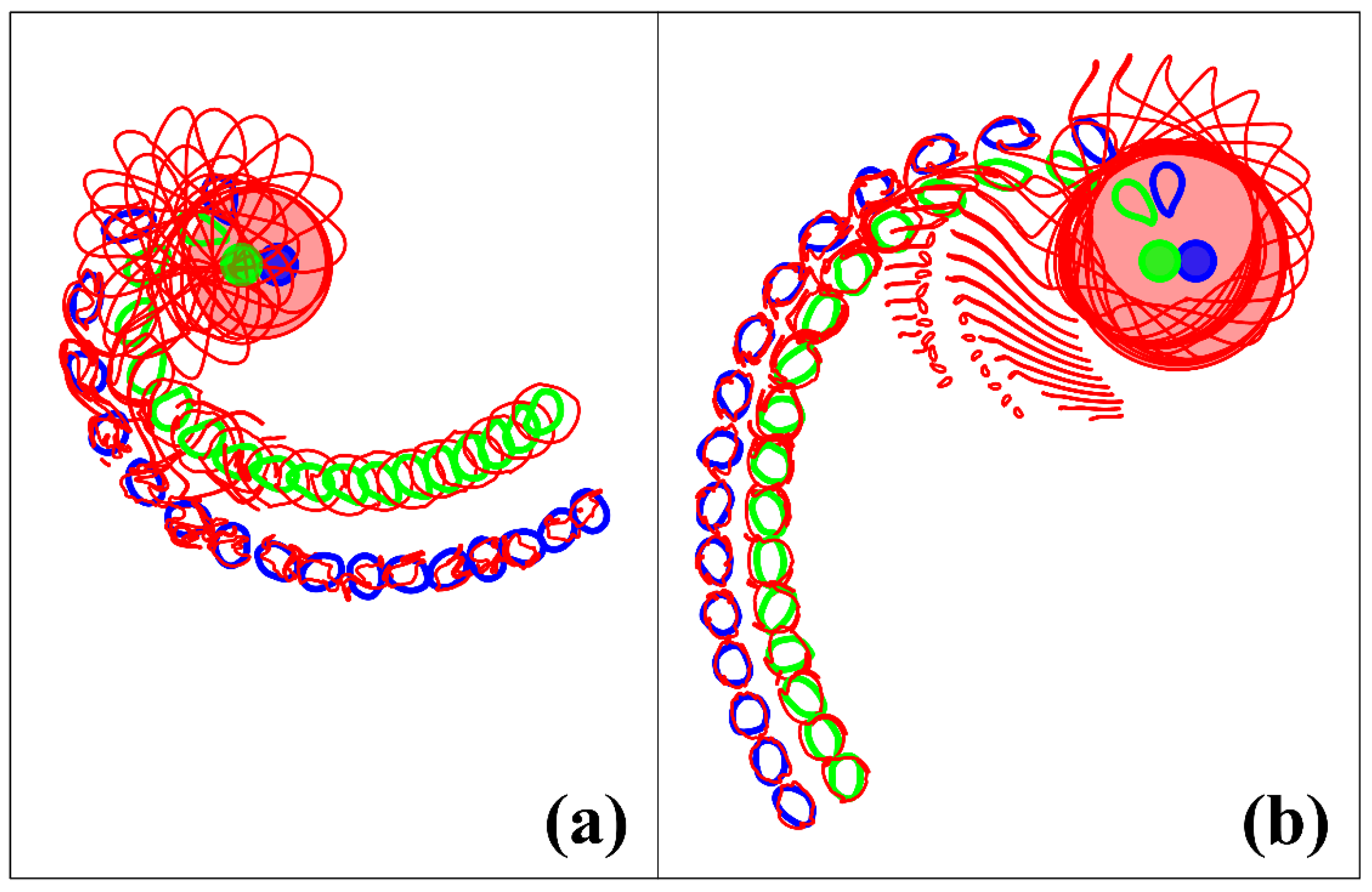
4.2.2. Case of Asymmetric Middle Layer Vortices
5. Discussion and Conclusions
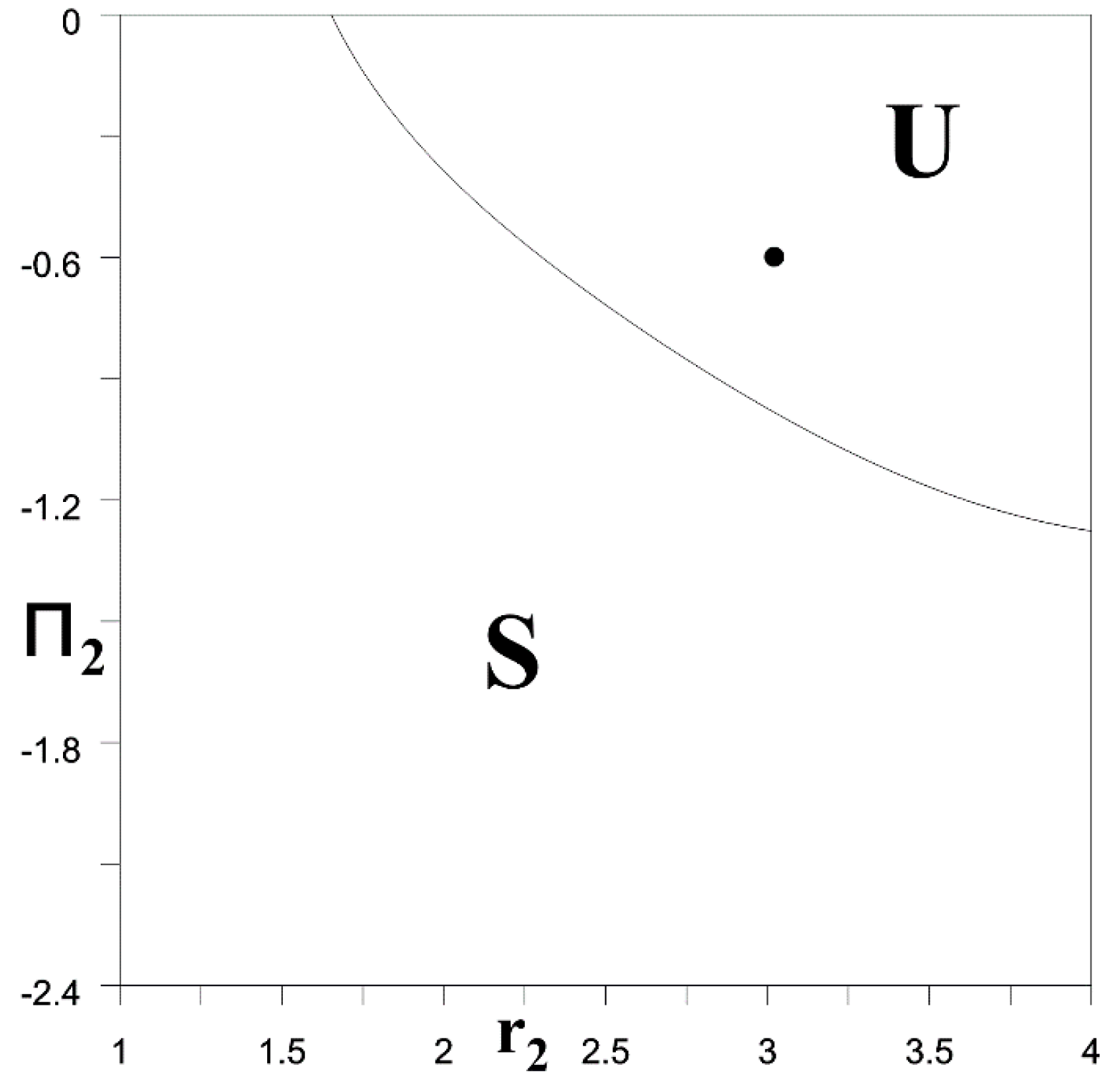
- A two-layer vortex with a vertical axis, consisting of a large-scale cyclone of the upper layer and a sufficiently large anticyclone of the middle layer, can be unstable with respect to small perturbations of the shape of the vortex patches and decompose into smaller two-layer vortex structures. In the case when the intratermocline anticyclone is of the order of Rd1, the two-layer vortex behaves stably (Section 3.1). Note that such a vortex structure consisting of point vortices is also always stable.
- If the centers of the cyclone of the upper layer and the anticyclonic lens of the middle layer are spaced, then such a two-layer vortex can either move forward (when its total effective vorticity is zero) or rotate relative to the center of vorticity (when its total effective vorticity is nonzero). These properties are also characteristic of point vortices. For finite-core vortices, in addition, there is a certain interval of distances between their centers, in which the motion of the vortex patches is accompanied by a partial destruction of the surface cyclone and a deviation from the trajectory predicted by the theory of point vortices occurs (Section 3.2).
- If intrathermocline dipole is initially located below the surface vortex core, the formation of a such new type of vortex structure occurs when most of the surface cyclone core is left behind and two of its fragments pair up with the lenses and drift away. The two-layer structure including the lenses has a complex form: one part consists of two cyclonic vortex patches in the upper and middle layers, and the second part has a hetonic nature (Section 4.1).
- If the intrathermocline dipole is running onto the surface vortex, then (like in the point vortex case [19]) we have two regimes: (a) the pair passes under the surface vortex, changing its direction in its vicinity and capturing part of its mass; (b) the cyclonic vortex of the intrathermocline dipole is captured by the surface cyclone, and the anticyclonic lens rotates at the periphery of the newly formed bilayer cyclonic structure; and, unlike the case of point vortices, the dipole of the middle layer cannot leave the vicinity of the surface cyclone. (Section 4.2.1).
- If an asymmetry in the distribution of potential vorticity is observed in a vortex structure incident on a surface cyclone, then it makes loop-like movements and, at the same time, rotates around the cyclone of the upper layer. It is striking that in the case of finite-core vortices (depending on the initial distance between them), states can be formed that resemble the modal structures obtained for point vortices (19) as quasi-stationary solutions (Section 4.2.2).
Author Contributions
Funding
Conflicts of Interest
References
- Basdevant, C.; Legras, B.; Sadourny, R.; Béland, M. A Study of Barotropic Model Flows: Intermittency, Waves and Predictability. J. Atmos. Sci. 1981, 38, 2305–2326. [Google Scholar] [CrossRef]
- Benzi, R.; Patarnello, S.; Santangelo, P. Self-Similar Coherent Structures in Two-Dimensional Decaying Turbulence. J. Phys. A 1988, 21, 1221–1237. [Google Scholar] [CrossRef]
- Melander, M.V.; Zabusky, N.J.; McWilliams, J.C. Asymmetric Vortex Merger in Two Dimensions: Which Vortex is “Victorious”? Phys. Fluids 1987, 30, 2610–2612. [Google Scholar] [CrossRef]
- Dritschel, D.G.; Waugh, D.W. Quantification of the Inelastic Interaction of Unequal Vortices in Two-Dimensional Vortex Dynamics. Phys. Fluids A 1992, 4, 1737–1744. [Google Scholar] [CrossRef]
- Yasuda, I.; Flierl, G.R. Two-Dimensional Asymmetric Vortex Merger: Contour Dynamics Experiment. J. Oceanogr. 1995, 51, 145–170. [Google Scholar] [CrossRef]
- Trieling, R.R.; Velasco Fuentes, O.U.; van Heijst, G.J.F. Interaction of Two Unequal Corotating Vortices. Phys. Fluids 2005, 17, 087103. [Google Scholar] [CrossRef]
- Brandt, L.K.; Cichocki, T.K.; Nomura, K. Asymmetric Vortex Merger: Mechanism and Criterion. Theor. Comput. Fluid Dyn. 2010, 24, 163–167. [Google Scholar] [CrossRef]
- Brandt, L.K.; Nomura, K. Characterization of the Interactions of Two Unequal Co-Rotating Vortices. J. Fluid Mech. 2010, 646, 233–253. [Google Scholar] [CrossRef]
- Ozugurlu, E.; Reinaud, J.N.; Dritschel, D.G. Interaction between Two Quasi-Geostrophic Vortices of Unequal Potential Vorticity. J. Fluid Mech. 2008, 597, 395–414. [Google Scholar] [CrossRef]
- Charney, J. Geostrophic Turbulence. J. Atmos. Sci. 1971, 28, 1087–1095. [Google Scholar] [CrossRef]
- McWilliams, J.C. Statistical Properties of Decaying Geostrophic Turbulence. J. Fluid Mech. 1989, 198, 199–230. [Google Scholar] [CrossRef]
- McWilliams, J.C. The Vortices of Geostrophic Turbulence. J. Fluid Mech. 1990, 219, 387–404. [Google Scholar] [CrossRef]
- Treguier, A.M.; Hua, B.L. Oceanic Quasi-Geostrophic Turbulence Forced by Stochastic Wind Fluctuations. J. Phys. Oceanogr. 1987, 17, 397–411. [Google Scholar] [CrossRef][Green Version]
- Treguier, A.M.; Hua, B.L. Influence of Bottom Topography on Stratified Quasi-Geostrophic Turbulence in the Ocean. Geophys. Astrophys. Fluid Dyn. 1988, 43, 265–305. [Google Scholar] [CrossRef]
- Carton, X.; Daniault, N.; Alves, J.; Chérubin, L.; Ambar, I. Meddy Dynamics and Interaction with Neighboring Eddies Southwest of Portugal: Observations and Modeling. J. Geophys. Res. 2010, 115, C06017. [Google Scholar] [CrossRef]
- Filyushkin, B.N.; Sokolovskiy, M.A. Modeling the Evolution of Intrathermocline Lenses in the Atlantic Ocean. J. Mar. Res. 2011, 69, 191–220. [Google Scholar] [CrossRef]
- L’Hégaret, P.; Carton, X.; Ambar, I.; Menesguen, C.; Hua, B.L.; Chérubin, L.; Aguiar, A.; Le Cann, B.; Daniault, N.; Serra, N. Evidence of Mediterranean Water Dipole Collision in the Gulf of Cadiz. J. Geophys. Res. Oceans. 2014, 119, 5337–5359. [Google Scholar] [CrossRef]
- Haynes, P.H.; McIntyre, M.E. On the Conservation and Impermeability Theorems for Potential Vorticity. J. Atmos. Sci 1990, 47, 2021–2031. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Carton, X.J.; Filyushkin, B.N. Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 1: Point-Vortex Approach. Mathematics 2020, 8, 1228. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Filyushkin, B.N.; Carton, X.J. Dynamics of Intrathermocline Vortices in a Gyre Flow over a Seamount Chain. Ocean Dyn. 2013, 63, 741–760. [Google Scholar] [CrossRef]
- Kamenkovich, V.M.; Koshlyakov, M.N.; Monin, A.S. Synoptic Eddies in the Ocean; Kamenkovich, V.M., Ed.; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1986; p. 444. [Google Scholar]
- Sokolovskiy, M.A.; Carton, X.J.; Filyushkin, B.N.; Yakovenko, I.O. Interaction between a Surface Jet and Subsurface Vortices in a Three-Layer Quasi-Geostrophic Model. Geophys. Astrophys. Fluid Dyn. 2016, 110, 201–223. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics. In Fundamentals and Large-Scale Circulation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; p. 964. ISBN 9781107065505. [Google Scholar]
- Kamenkovich, V.M.; Larichev, V.D.; Kharkov, B.V. A Numerical Barotropic Model for Analysis of Synoptic Eddies in the Open Ocean. Oceanology 1982, 21, 549–558. [Google Scholar]
- Kozlov, V.F. The Method of Contour Dynamics in Model Problems of the Ocean Topographic Cyclogenesis. Izv. Atmos. Oceanic Phys. 1983, 19, 635–640. [Google Scholar]
- Sokolovskiy, M.A. Modeling Triple-Layer Vortical Motions in the Ocean by the Contour Dynamics Method. Izv. Atmos. Ocean. Phys. 1991, 27, 380–388. [Google Scholar]
- Makarov, V.G. Computational Algorithm of the Contour Dynamics Method with Changeable Topology of Domains under Study. Model. Mekh. 1991, 5, 83–95. [Google Scholar]
- Sokolovskiy, M.A. Stability of an Axisymmetric Three-Layer Vortex. Izv. Atmos. Ocean. Phys. 1997, 33, 16–26. [Google Scholar]
- Sokolovskiy, M.A. Stability Analysis of the Axisymmetric Three-Layered Vortex Using Contour Dynamics Method. Comput. Fluid Dyn. J. 1997, 6, 133–156. [Google Scholar]
- Hogg, N.G.; Stommel, H.M. The heton, an Elementary Interaction Between Discrete Baroclinic Geostrophic Vortices, and its Implications Concerning Eddy Heat-Flow. Proc. R. Soc. Lond. A 1985, 397, 1–20. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolovskiy, M.A.; Carton, X.J.; Filyushkin, B.N. Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 2: Finite-Core-Vortex Approach and Oceanographic Application. Mathematics 2020, 8, 1267. https://doi.org/10.3390/math8081267
Sokolovskiy MA, Carton XJ, Filyushkin BN. Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 2: Finite-Core-Vortex Approach and Oceanographic Application. Mathematics. 2020; 8(8):1267. https://doi.org/10.3390/math8081267
Chicago/Turabian StyleSokolovskiy, Mikhail A., Xavier J. Carton, and Boris N. Filyushkin. 2020. "Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 2: Finite-Core-Vortex Approach and Oceanographic Application" Mathematics 8, no. 8: 1267. https://doi.org/10.3390/math8081267
APA StyleSokolovskiy, M. A., Carton, X. J., & Filyushkin, B. N. (2020). Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 2: Finite-Core-Vortex Approach and Oceanographic Application. Mathematics, 8(8), 1267. https://doi.org/10.3390/math8081267






