Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 1: Point-Vortex Approach
Abstract
:1. Introduction
2. Three-Layer Model
3. Numerical Modeling of Vortex Interaction
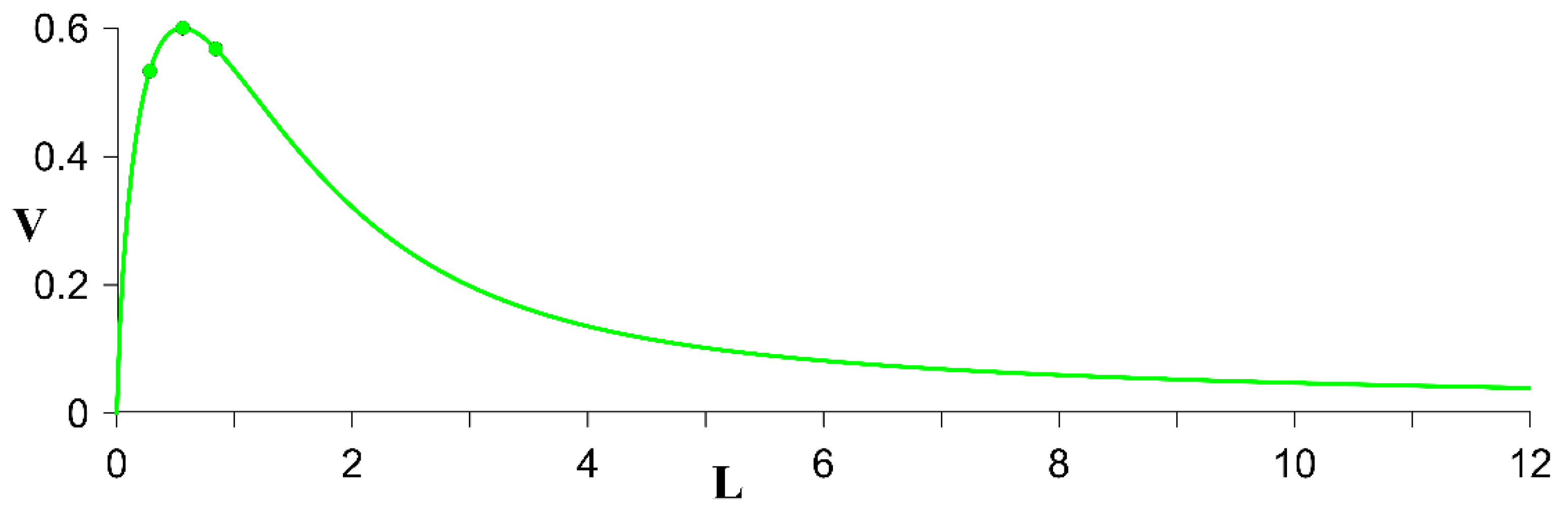
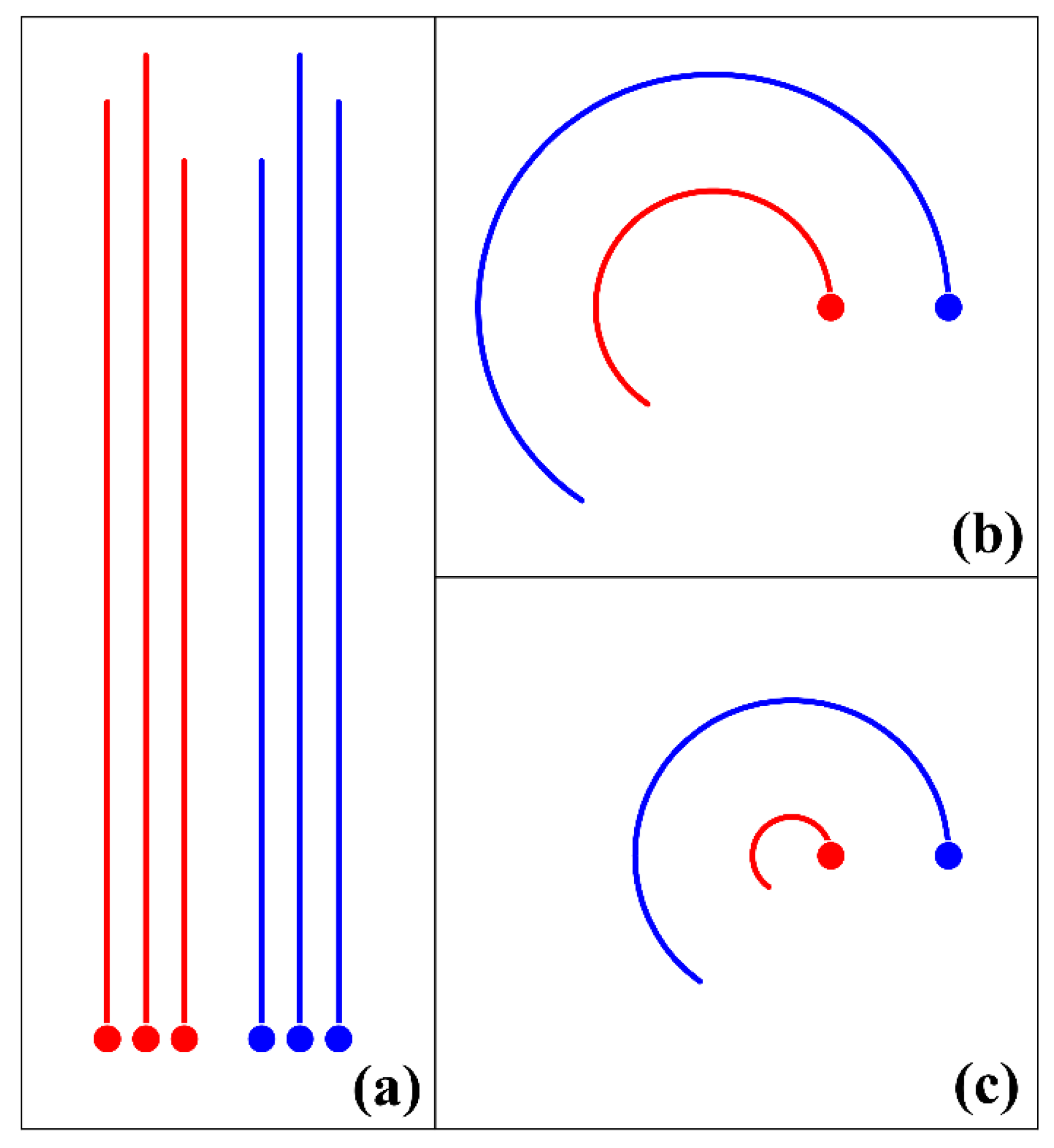
3.1. Cyclonic Surfer Vortex and Anticyclonic Intrathermocline Lenses
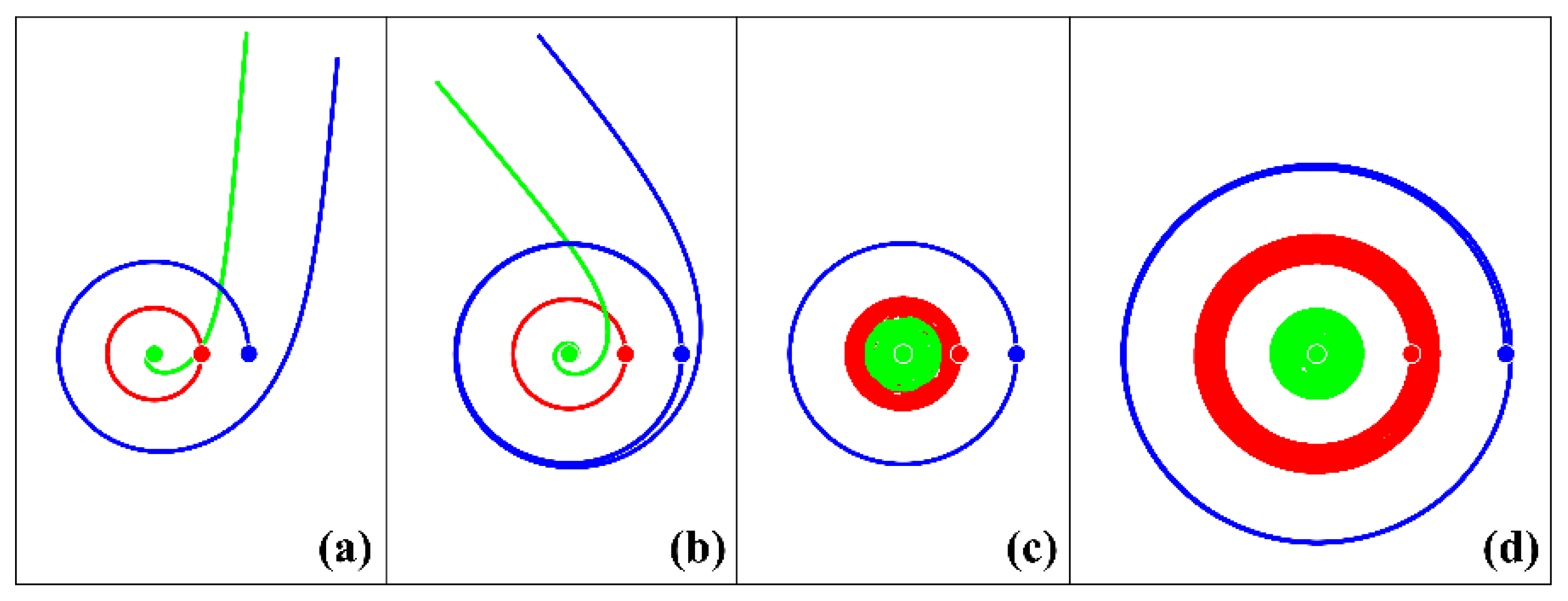
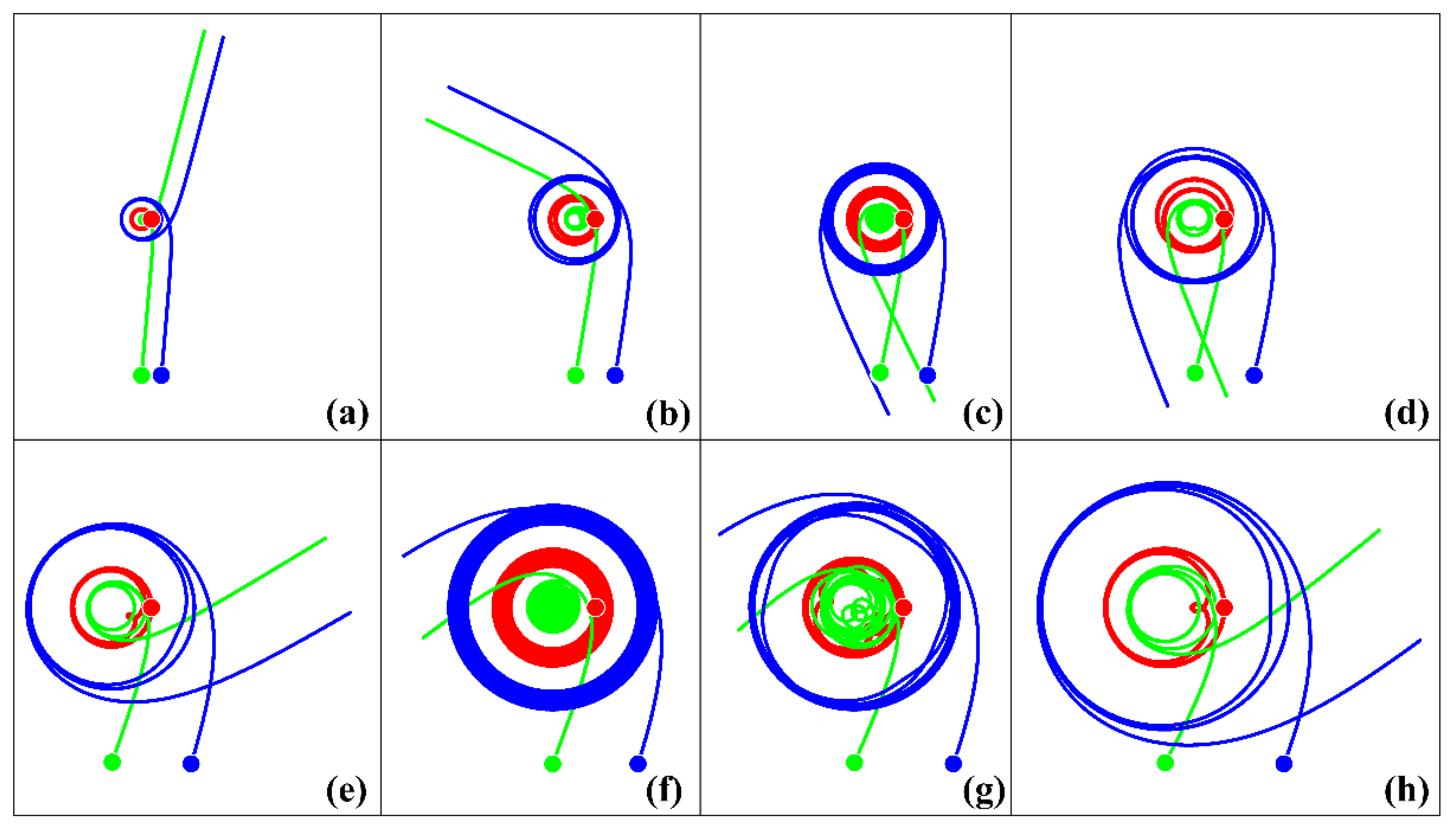
3.2. Interaction of a Surface Vortex with Two Middle Layer Vortices
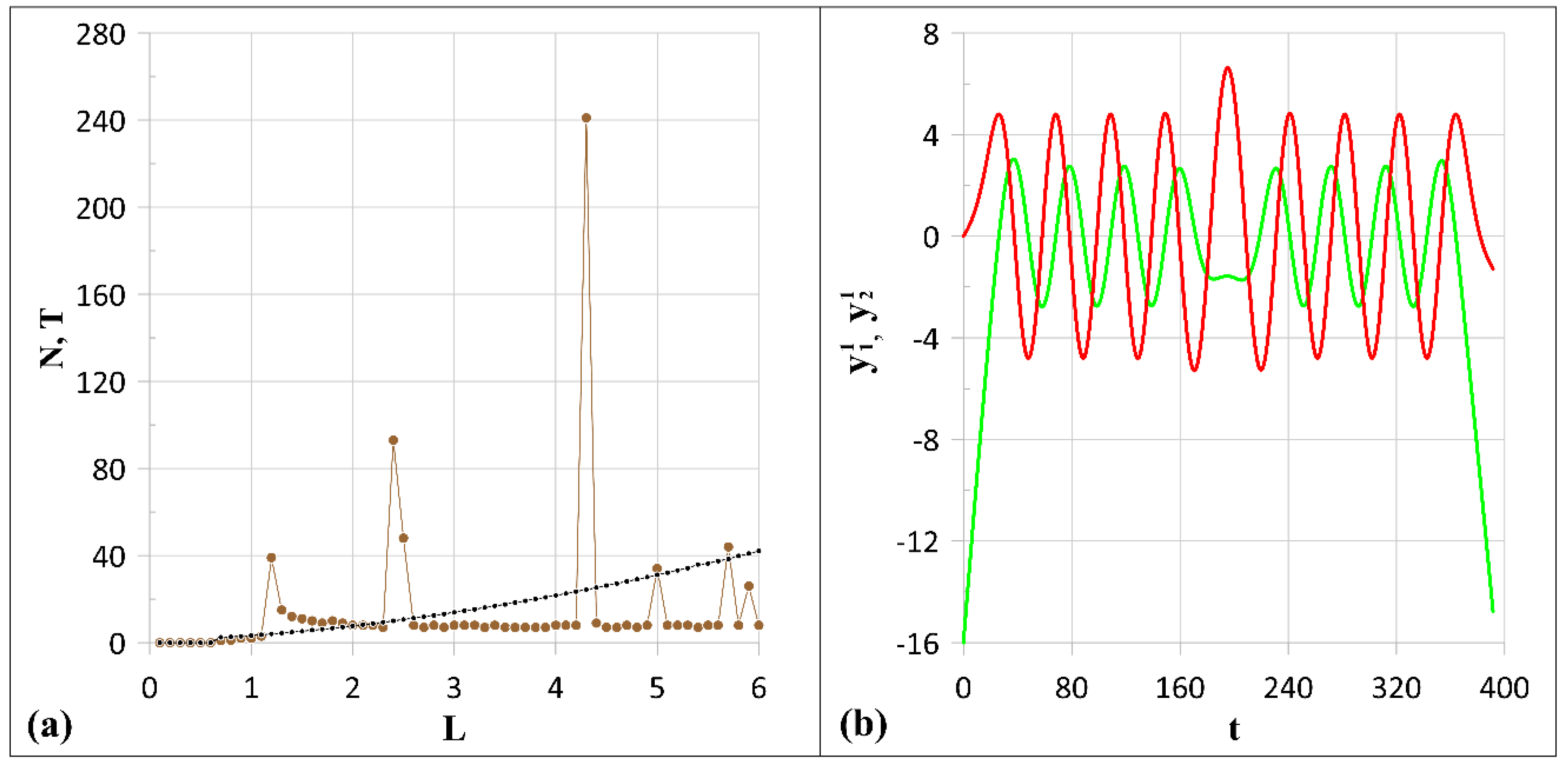
3.2.1. Collinear Initial Configuration
3.2.2. Impact of the Two External Intrathermocline Vortices on the Surface Cyclone
4. Discussion and Conclusions
- If the cyclone of the upper layer and the anticyclonic lens of the middle layer are separated by some distance, then such a two-layer vortex can either move forward (when its total effective vorticity is zero) or rotate relative to the center of vorticity (when its total effective vorticity is nonzero). In any case, both vortices can move far enough from the original location (Section 3.1).
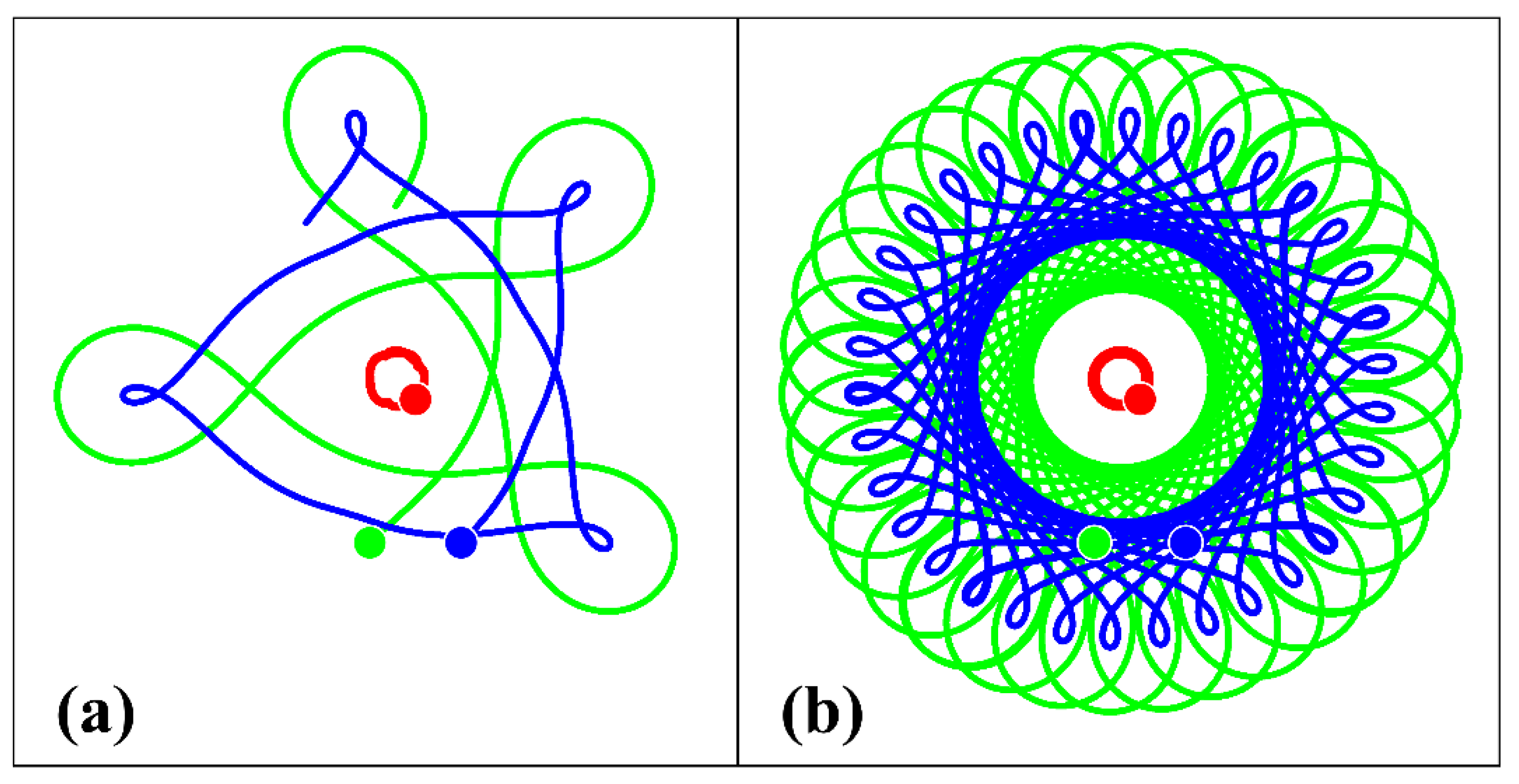
- If two middle layer (intrathermocline) vortices of opposite signs are initially located on different sides relative to the central surface vortex, then (a) if they are separated far enough, all three vortices move inside individual coaxial annular regions; (b) if the distance between them is small, after a temporary bounded stage of movement, they leave the vicinity of the surface vortex (Section 3.2.1).
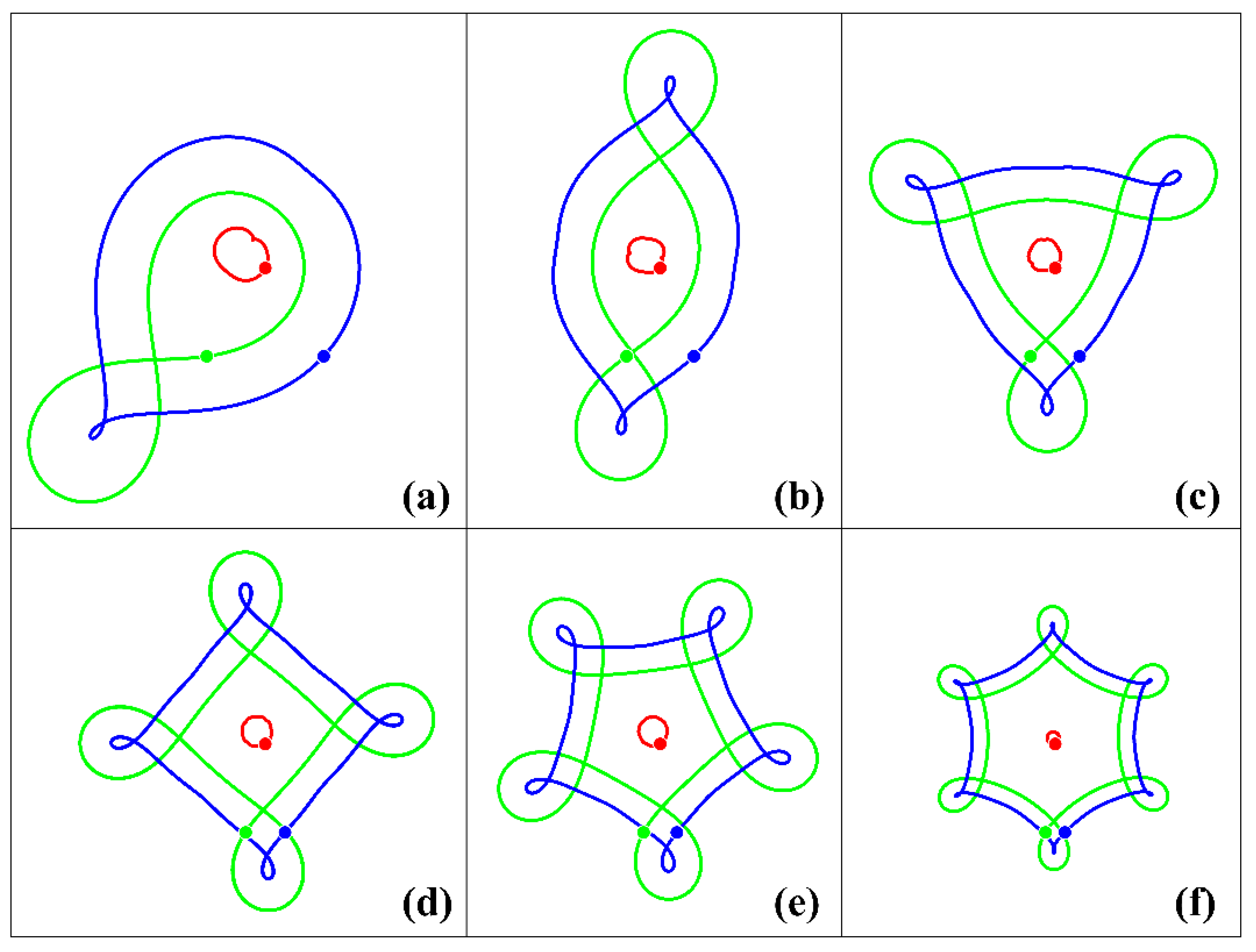
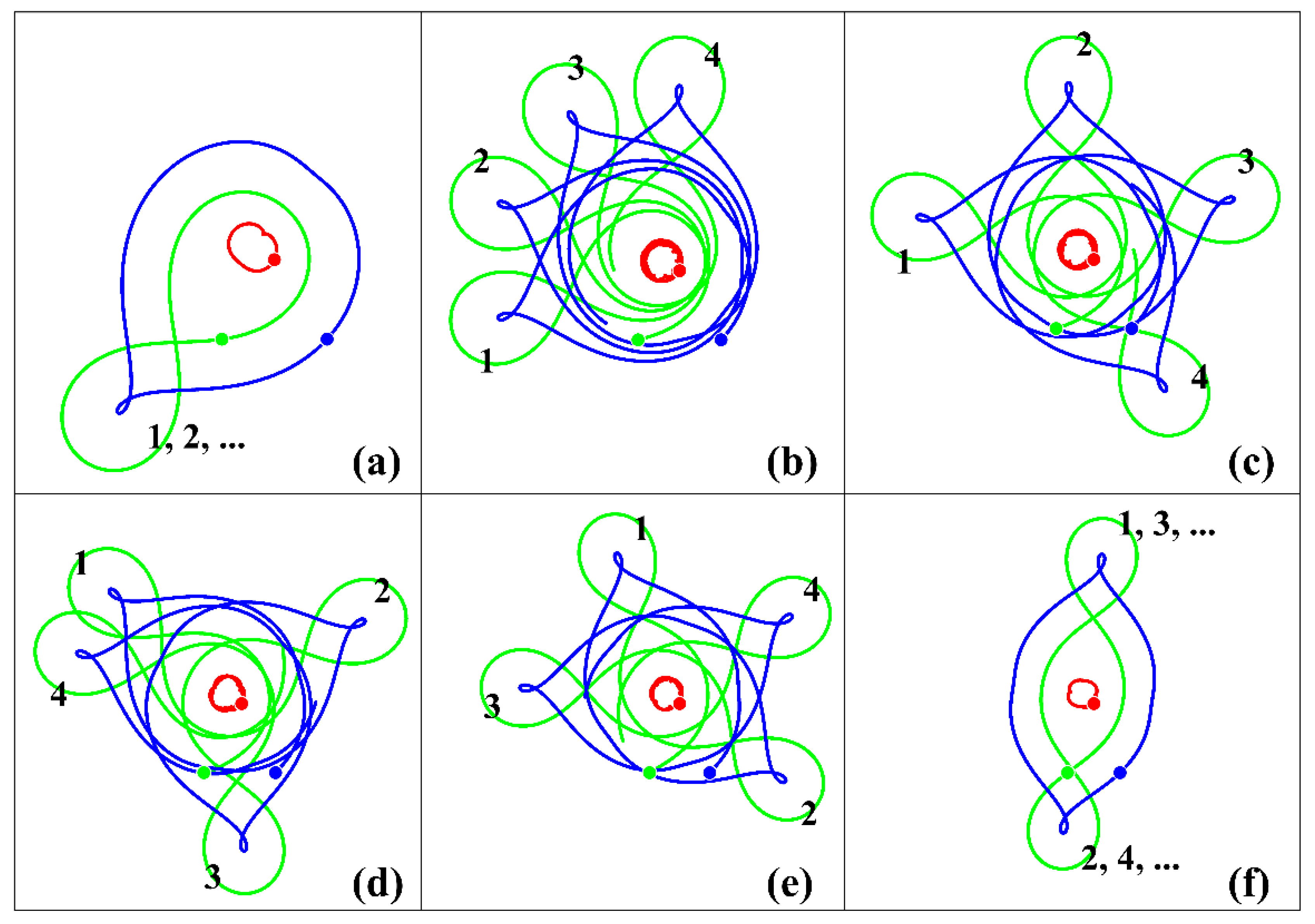
- If the intrathermocline vortices make up a pair running into the surface vortex, then two regimes are possible: (a) the pair passes under the surface vortex, changing its direction in its vicinity; (b) the dipole is delayed in the vicinity of the surface vortex, and at this intermediate stage, all three vortices move within a bounded region, after which it is freed from the influence of the cyclone and carried away from it. Such intermediate stages can have different durations which do not regularly depend on the initial distance between the vortices of the pair (Section 3.2.2).
- If the intrathermocline vortices have different intensities (which is a more realistic situation), then the vortices of the middle layer always move along loop-like trajectories in the vicinity of the surface vortex. For certain initial distances between the intrathermocline vortices, their movements have a periodic character (Section 3.2.2).
Author Contributions
Funding
Conflicts of Interest
References
- Von Helmholtz, H.H. Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen. J. Reine Angew. Math. 1858, 55, 25–55. [Google Scholar] [CrossRef] [Green Version]
- Kirchoff, G. Vorlesungen űber Methamatische Physik; Mechanik: Leipzig, Germany, 1876. [Google Scholar]
- Gröbli, W. Spezielle Probleme über die Bewegung Geradliniger Paralleler Wirbelfäden; Vierteljschr. Naturf. Ges.; Druck von Zürcher und Furrer: Zürich, Switzerland, 1877; Volume 22, pp. 129–165. [Google Scholar]
- Thomson, W. Floating magnets. Nature 1878, 18, 13–14. [Google Scholar] [CrossRef]
- Thomson, W. Vortex statics. Proc. R. Soc. Edinb. 1878, 9, 59–73. [Google Scholar] [CrossRef] [Green Version]
- Poincaré, H. Théorie des Tourbillons; Gauthier-Villars: Paris, France, 1893. [Google Scholar]
- Villat, H. Leçons sur la Théorie des Tourbillons; Gauthier-Villars: Paris, France, 1930. [Google Scholar]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Aref, H.; Kadtke, J.B.; Zawadzki, I.; Campbell, L.J.; Eckhardt, B. Point vortex dynamics: Recent results and open problems. Fluid Dyn. Res. 1988, 3, 63–74. [Google Scholar] [CrossRef] [Green Version]
- Saffman, P.G. Vortex Dynamics; Cambridge Monographs on Mechanics and Applied Mathematics; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Meleshko, V.V.; Konstantinov, M.Y. Dynamics of Vortex Structures; Naukova Dumka: Kiev, Ukraine, 1993. (In Russian) [Google Scholar]
- Carton, X. Hydrodynamical modelling of oceanic vortices. Surv. Geophys. 2001, 22, 179–263. [Google Scholar] [CrossRef]
- Newton, P.K. The N-Vortex Problem: Analytical Techniques; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2001; Volume 145. [Google Scholar]
- Kozlov, V.V. General Theory of Vortices; Dynamical Systems, X, Encyclopaedia Math. Sci.; Springer: Berlin, Germany, 2003; Volume 67. [Google Scholar]
- Borisov, A.V.; Mamaev, I.S. Mathematical Methods in the Dynamics of Vortex Structures; Institute of Computer Sciences: Moscow-Izhevsk, Russia, 2005. (In Russian) [Google Scholar]
- Meleshko, V.V.; Aref, H. A bibliography of vortex dynamics 1858–1956. Adv. Appl. Mech. 2007, 41, 197–292. [Google Scholar] [CrossRef]
- Stewart, H.J. Periodic properties of the semi-permanent atmospheric pressure systems. Q. Appl. Math. 1943, 1, 262–285. Available online: https://www.ams.org/journals/qam/1943-01-03/S0033-569X-1943-09349-4/S0033-569X-1943-09349-4.pdf (accessed on 25 January 2020). [CrossRef] [Green Version]
- Obukhov, A.M. On the question of the geostrophic wind. Izv. AN SSSR Ser. Geograf-Geofiz. 1949, 13, 281–306. [Google Scholar]
- Morikawa, G.K. Geostrophic vortex motion. J. Meteorol. 1960, 17, 148–158. [Google Scholar] [CrossRef] [Green Version]
- Charney, J.G. Numerical experiments in atmospheric hydrodynamics. In Experimental Arithmetic, High Speed Computing and Mathematics, Proceedings of the Symposia in Applied Mathematics, Chicago, IL, USA, 12–14 April 1962; American Mathematical Society: Providence, Rhode Island, 1963; Volume 15, pp. 289–310. [Google Scholar]
- Morikawa, G.K.; Swenson, E.V. Interacting motion of rectilinear geostrophic vortices. Phys. Fluids 1971, 14, 1058–1073. [Google Scholar] [CrossRef]
- Hill, F.M. A numerical study of the descent of a vortex pair in a stably stratified atmosphere. J. Fluid Mech. 1975, 71, 1–13. [Google Scholar] [CrossRef]
- Kuhlbrodt, T.; Névir, P. Low-order point vortex models of atmospheric blocking. Meteorol. Atmos. Phys. 2000, 73, 127–138. [Google Scholar] [CrossRef]
- Zabusky, N.J.; McWilliams, J.C. A modulated point-vortex model for geostrophic, β-plane dynamics. Phys. Fluids 1982, 25, 2175. [Google Scholar] [CrossRef]
- Kono, M.; Horton, W. Point vortex description of drift wave vortices: Dynamics and transport. Phys. Fluids B Plasma Phys. 1991, 3, 3255. [Google Scholar] [CrossRef]
- Reznik, G.M.; Kravtsov, S. Dynamics of a barotropic singular monopole on the beta-plane. Izv. Atmos. Ocean. Phys. 1995, 32, 762–769. [Google Scholar]
- Velasco Fuentes, O.U.; van Heijst, G.J.F. Collision of dipolar vortices on a β -plane. Phys. Fluids 1995, 7, 2735–2750. [Google Scholar] [CrossRef] [Green Version]
- Velasco Fuentes, O.U.; van Heijst, G.J.F.; van Lipzing, N.P.M. Unsteady behaviour of a topography-modulated tripole. J. Fluid Mech. 1996, 307, 11–41. [Google Scholar] [CrossRef]
- Dunn, D.C.; McDonald, N.D.; Johnson, E.R. The motion of a singular vortex near an escarpment. J. Fluid Mech. 2001, 448, 335–365. [Google Scholar] [CrossRef] [Green Version]
- Drótos, G.; Tél, T. On the validity of the β-plane approximation in the dynamics and the chaotic advection of a point vortex pair model on a rotating sphere. J. Atmos. Sci. 2015, 72, 415–429. [Google Scholar] [CrossRef]
- Gryanik, V.M. Dynamics of singular geostrophic vortices in a two-level model of atmosphere (ocean). Izv. Atmos. Ocean. Phys. 1983, 19, 171–179. [Google Scholar]
- Gryanik, V.M. Dynamics of singular geostrophic vortices near critical points of currents in a N-layer model of the atmosphere (ocean). Izv. Atmos. Ocean. Phys. 1991, 27, 517–526. [Google Scholar]
- Hogg, N.G.; Stommel, H.M. The heton, an elementary interaction between discrete baroclinic geostrophic vortices, and its implications concerning eddy heat-flow. Proc. R. Soc. London A 1985, 397, 1–20. [Google Scholar]
- Hogg, N.G.; Stommel, H.M. Hetonic explosions: The breakup and spread of warm pools as explained by baroclinic point vortices. J. Atmos. Sci. 1985, 42, 1465–1476. [Google Scholar] [CrossRef] [Green Version]
- Young, W.R. Some interactions between small numbers of baroclinic, geostrophic vortices. Geophys. Astrophys. Fluid Dyn. 1985, 33, 35–61. [Google Scholar] [CrossRef]
- Gryanik, V.M.; Tevs, M.V. Dynamics of singular geostrophic vortices in an N-layer model of atmosphere (ocean). Izv. Atmos. Ocean. Phys. 1989, 25, 179–188. [Google Scholar]
- Hogg, N.G.; Stommel, H.M. How currents in the upper thermocline could advect meddies deeper down. Deep Sea Res. 1990, 37, 613–623. [Google Scholar] [CrossRef]
- Reznik, G.M. Dynamics of singular vortices on a β-plane. J. Fluid Mech. 1992, 240, 405–432. [Google Scholar] [CrossRef]
- Gryanik, V.M. Radiation of Rossby waves and adaptation of potential vorticity fields in the atmosphere (ocean). Trans. (Doklady) RAS Earth Sci. Sect. 1992, 326, 976–979. [Google Scholar]
- Legg, S.; Marshall, J. A heton model of the spreading phase of open-ocean deep convection. J. Phys. Oceanogr. 1993, 23, 1040–1056. [Google Scholar] [CrossRef] [Green Version]
- Marshall, J.S. Chaotic oscillations and breakup of quasigeostrophic vortices in the N-layer approximation. Phys. Fluids 1995, 7, 983–992. [Google Scholar] [CrossRef]
- Reznik, G.M.; Grimshaw, R.H.J.; Sriskandarajah, K. On basic mechanisms governing two-layer vortices on a beta-plane. Geophys. Astrophys. Fluid. Dyn. 1997, 86, 1–42. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Four-vortex motion in the two layer approximation: Integrable case. Reg. Chaotic Dyn. 2000, 5, 414–436. [Google Scholar] [CrossRef]
- Reznik, G.M.; Grimshaw, R.H.J. Ageostrophic dynamics of an intense localized vortex on a β-plane. J. Fluid Mech. 2001, 443, 351–376. [Google Scholar] [CrossRef]
- Danilov, S.; Gryanik, V.; Olbers, D. Equilibration and lateral spreading of a strip-shaped convection region. J. Phys. Oceanogr. 2001, 31, 1075–1087. [Google Scholar] [CrossRef]
- White, A.J.; McDonald, N.R. The motion of a point vortex near large-amplitude topography in a two-layer fluid. J. Phys. Oceanogr. 2004, 34, 2808–2824. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Dynamics of three vortices in a two-layer rotating fluid. Reg. Chaotic Dyn. 2004, 9, 417–438. [Google Scholar] [CrossRef]
- Gryanik, V.M.; Sokolovskiy, M.A.; Verron, J. Dynamics of heton-like vortices. Reg. Chaotic Dyn. 2006, 11, 383–434. [Google Scholar] [CrossRef]
- Kizner, Z. Stability and transitions of hetonic quartets and baroclinic modons. Phys. Fluids 2006, 18, 056601. [Google Scholar] [CrossRef]
- Reznik, G.M.; Kizner, Z. Two-layer quasi-geostrophic singular vortices embedded in a regular flow. Part 1. Invariants of motion and stability of vortex pairs. J. Fluid Mech. 2007, 584, 185–202. [Google Scholar] [CrossRef]
- Reznik, G.M.; Kizner, Z. Two-layer quasigeostrophic singular vortices embedded in a regular flow. Part 2. Steady and unsteady drift of individual vortices on a beta-plane. J. Fluid Mech. 2007, 584, 203–223. [Google Scholar] [CrossRef]
- Reznik, G.M.; Kizner, Z. Singular vortices in regular flows. Theor. Comput. Fluid Dyn. 2010, 24, 65–75. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Carton, X.J. Baroclinic multipole formation from heton interaction. Fluid Dyn. Res. 2010, 42, 045501. [Google Scholar] [CrossRef] [Green Version]
- Kizner, Z. Stability of point-vortex multipoles revisited. Phys. Fluids 2011, 23, 064104. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Koshel, K.V.; Verron, J. Three-vortex quasi-geostrophic dynamics in a two-layer fluid. Part 1. Analysis of relative and absolute motions. J. Fluid Mech. 2013, 717, 232–254. [Google Scholar] [CrossRef]
- Koshel, K.V.; Sokolovskiy, M.A.; Verron, J. Three-vortex quasi-geostrophic dynamics in a two-layer fluid. Part 2. Regular and chaotic advection around the perturbed steady states. J. Fluid Mech. 2013, 717, 255–280. [Google Scholar] [CrossRef]
- Kizner, Z. On the stability of two-layer geostrophic point-vortex multipoles. Phys. Fluids 2014, 26, 046602. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V. Resonance phenomena in a two-layer two-vortex shear flow. Chaos 2016, 26, 113116. [Google Scholar] [CrossRef]
- Kurakin, L.G.; Ostrovskaya, I.V.; Sokolovskiy, M.A. On the stability of discrete tripole, quadrupole, Thomson’ vortex triangle and square in a two-layer/homogeneous rotating fluid. Reg. Chaotic Dyn. 2016, 21, 291–334. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V.; Sokolovskiy, M.A.; Carton, X. Interaction of an along-shore propagating vortex with a vortex enclosed in a circular bay. Phys. Fluids 2018, 30, 016602. [Google Scholar] [CrossRef]
- Koshel, K.V.; Reinaud, J.N.; Riccardi, G.; Ryzhov, E.A. Entrapping of a vortex pair interacting with a fixed point vortex revisited. I. Point vortices. Phys. Fluids 2018, 30, 096603. [Google Scholar] [CrossRef] [Green Version]
- Koshel, K.V.; Ryzhov, E.A.; Carton, X.J. Vortex interactions subjected to deformation flows: A review. Fluids 2019, 4, 14. [Google Scholar] [CrossRef] [Green Version]
- Kurakin, L.G.; Lysenko, I.A.; Ostrovskaya, I.V.; Sokolovskiy, M.A. On stability of the Thomson’s vortex N-gon in the geostrophic model of the point vortices in two-layer fluid. J. Nonlinear Sci. 2019, 29, 1659–1700. [Google Scholar] [CrossRef]
- Bashmachnikov, I.; Machín, F.; Mendonc, A.; Martins, A. In situ and remote sensing signature of meddies east of the mid-Atlantic ridge. J. Geophys. Res. 2009, 114, C05018. [Google Scholar] [CrossRef] [Green Version]
- Filyushkin, B.A.; Sokolovskiy, M.A. Modeling the evolution of intrathermocline lenses in the Atlantic Ocean. J. Mar. Res. 2011, 69, 191–220. [Google Scholar] [CrossRef]
- Carton, X.; Daniault, N.; Alves, J.; Chérubin, L.; Ambar, I. Meddy dynamics and interaction with neighboring eddies southwest of Portugal: Observations and modeling. J. Geophys. Res. 2010, 115, C06017. [Google Scholar] [CrossRef] [Green Version]
- L’Hégaret, P.; Carton, X.; Ambar, I.; Menesguen, C.; Hua, B.L.; Chérubin, L.; Aguiar, A.; Le Cann, B.; Daniault, N.; Serra, N. Evidence of Mediterranean Water dipole collision in the Gulf of Cadiz. J. Geophys. Res. Oceans 2014, 119, 5337–5359. [Google Scholar] [CrossRef] [Green Version]
- Ryzhov, E.A.; Sokolovskiy, M.A. Interaction of two-layer vortex pair with a submerged cylindrical obstacle in a two-layer rotating fluid. Phys. Fluids 2016, 28, 056602. [Google Scholar] [CrossRef]
- Simó, C. New families of solutions to the N-body problems. In Proceedings of the European Congress of Mathematics, Barcelona, Spain, 10–14 July 2000; Progress in Mathematics. Casacuberta, C., Miró-Roig, R.M., Verdera, J., Xambó-Descamps, S., Eds.; Birkhäuser: Basel, Switzerland, 2001; Volume 201. [Google Scholar] [CrossRef]
- Richardson, P.L.; Tychensky, A. Meddy trajectories in the Canary Basin measured during the SEMAPHORE experiment 1993–1995. J. Geophys. Res. 1998, 103, 25029–25045. [Google Scholar] [CrossRef]
- Armi, L.; Hebert, D.; Oakey, N.; Price, J.; Richardson, P.L.; Rossby, T.; Ruddick, B. The history and decay of a Mediterranean salt lens. Nature 1998, 333, 649–651. [Google Scholar] [CrossRef]
- Aguiar, A.C.B.; Peliz, Á.; Carton, X. A census of meddies in a long-term high-resolution simulation. Progr. Oceanogr. 2013, 116, 80–94. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolovskiy, M.A.; Carton, X.J.; Filyushkin, B.N. Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 1: Point-Vortex Approach. Mathematics 2020, 8, 1228. https://doi.org/10.3390/math8081228
Sokolovskiy MA, Carton XJ, Filyushkin BN. Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 1: Point-Vortex Approach. Mathematics. 2020; 8(8):1228. https://doi.org/10.3390/math8081228
Chicago/Turabian StyleSokolovskiy, Mikhail A., Xavier J. Carton, and Boris N. Filyushkin. 2020. "Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 1: Point-Vortex Approach" Mathematics 8, no. 8: 1228. https://doi.org/10.3390/math8081228
APA StyleSokolovskiy, M. A., Carton, X. J., & Filyushkin, B. N. (2020). Mathematical Modeling of Vortex Interaction Using a Three-Layer Quasigeostrophic Model. Part 1: Point-Vortex Approach. Mathematics, 8(8), 1228. https://doi.org/10.3390/math8081228





