Deep Learning Methods for Modeling Bitcoin Price
Abstract
1. Introduction
2. Deep Learning Methods
2.1. Deep Recurrent Convolution Neural Network (DRCNN)
2.2. Deep Neural Decision Trees (DNDT)
2.3. Deep Learning Linear Support Vector Machines (DSVR)
2.4. Sensitivity Analysis
3. Data and Variables
4. Results
4.1. Descriptive Statistics
4.2. Empirical Results
4.3. Post-Estimations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kristoufek, L. What Are the Main Drivers of the Bitcoin Price? Evidence from Wavelet Coherence Analysis. PLoS ONE 2015, 10, e0123923. [Google Scholar] [CrossRef]
- Wamba, S.F.; Kamdjoug, J.R.K.; Bawack, R.E.; Keogh, J.G. Bitcoin, Blockchain and Fintech: A systematic review and case studies in the supply chain. Prod. Plan. Control Manag. Oper. 2019, 31, 115–142. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, Z.; Ma, M.; Wu, J.; Zhou, Y.; Yao, J. Dependence structure between bitcoin price and its influence factors. Int. J. Comput. Sci. Eng. 2020, 21, 334–345. [Google Scholar] [CrossRef]
- Balcilar, M.; Bouri, E.; Gupta, R.; Roubaud, D. Can volume predict bitcoin returns and volatility? A quantiles-based approach. Econ. Model. 2017, 64, 74–81. [Google Scholar] [CrossRef]
- Ciaian, P.; Rajcaniova, M.; Artis Kancs, D. The economics of BitCoin price formation. Appl. Econ. 2016, 48, 1799–1815. [Google Scholar] [CrossRef]
- Schmidt, R.; Möhring, M.; Glück, D.; Haerting, R.; Keller, B.; Reichstein, C. Benefits from Using Bitcoin: Empirical Evidence from a European Country. Int. J. Serv. Sci. Manag. Eng. Technol. 2016, 7, 48–62. [Google Scholar] [CrossRef]
- Velankar, S.; Valecha, S.; Maji, S. Bitcoin Price Prediction using Machine Learning. In Proceedings of the 20th International Conference on Advanced Communications Technology (ICACT), Chuncheon-si, Korea, 11–14 February 2018. [Google Scholar]
- McNally, S.; Roche, J.; Caton, S. Predicting the Price of Bitcoin Using Machine Learning. In Proceedings of the 26th Euromicro International Conference on Parallel, Distributed, and Network-Based Processing, Cambridge, UK, 21–23 March 2018. [Google Scholar]
- Yogeshwaran, S.; Kaur, M.J.; Maheshwari, P. Project Based Learning: Predicting Bitcoin Prices using Deep Learning. In Proceedings of the 2019 IEEE Global Engineering Education Conference (EDUCON), Dubai, UAE, 9–11 April 2019. [Google Scholar]
- Demir, A.; Akılotu, B.N.; Kadiroğlu, Z.; Şengür, A. Bitcoin Price Prediction Using Machine Learning Methods. In Proceedings of the 2019 1st International Informatics and Software Engineering Conference (UBMYK), Ankara, Turkey, 6–7 November 2019. [Google Scholar]
- Rizwan, M.; Narejo, S.; Javed, M. Bitcoin price prediction using Deep Learning Algorithm. In Proceedings of the 13th International Conference on Mathematics, Actuarial Science, Computer Science and Statistics (MACS), Karachi, Pakistan, 14–15 December 2019. [Google Scholar]
- Linardatos, P.; Kotsiantis, S. Bitcoin Price Prediction Combining Data and Text Mining. In Advances in Integrations of Intelligent Methods. Smart Innovation, Systems and Technologies; Hatzilygeroudis, I., Perikos, I., Grivokostopoulou, F., Eds.; Springer: Singapore, 2020. [Google Scholar]
- Felizardo, L.; Oliveira, R.; Del-Moral-Hernández, E.; Cozman, F. Comparative study of Bitcoin price prediction using WaveNets, Recurrent Neural Networks and other Machine Learning Methods. In Proceedings of the 6th International Conference on Behavioral, Economic and Socio-Cultural Computing (BESC), Beijing, China, 28–30 October 2019. [Google Scholar]
- Dutta, A.; Kumar, S.; Basu, M. A Gated Recurrent Unit Approach to Bitcoin Price Prediction. J. Risk Financ. Manag. 2020, 13, 23. [Google Scholar] [CrossRef]
- Ji, S.; Kim, J.; Im, H. A Comparative Study of Bitcoin Price Prediction Using Deep Learning. Mathematics 2019, 7, 898. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Tong, C.; Zhao, Z. Matching Synchrosqueezing Wavelet Transform and Application to Aeroengine Vibration Monitoring. IEEE Trans. Instrum. Meas. 2017, 66, 360–372. [Google Scholar] [CrossRef]
- Huang, C.-W.; Narayanan, S.S. Deep convolutional recurrent neural network with attention mechanism for robust speech emotion recognition. In Proceedings of the 2017 IEEE International Conference on Multimedia and Expo, Hong Kong, China, 10–14 July 2017; pp. 583–588. [Google Scholar]
- Ran, X.; Xue, L.; Zhang, Y.; Liu, Z.; Sang, X.; Xe, J. Rock Classification from Field Image Patches Analyzed Using a Deep Convolutional Neural Network. Mathematics 2019, 7, 755. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep Recurrent Convolutional Neural Network for Remaining Useful Life Prediction. In Proceedings of the 2019 IEEE International Conference on Prognostics and Health Management (ICPHM), San Francisco, CA, USA, 17–20 June 2019; pp. 1–4. [Google Scholar]
- Yang, Y.; Garcia-Morillo, I.; Hospedales, T.M. Deep Neural Decision Trees. In Proceedings of the 2018 ICML Workshop on Human Interpretability in Machine Learning (WHI 2018), Stockholm, Sweden, 14 July 2018. [Google Scholar]
- Norouzi, M.; Collins, M.D.; Johnson, M.; Fleet, D.J.; Kohli, P. Efficient non-greedy optimization of decision trees. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2015; pp. 1729–1737. [Google Scholar]
- Dougherty, J.; Kohavi, R.; Sahami, M. Supervised and unsupervised discretization of continuous features. In Proceedings of the 12th International Conference on Machine Learning (ICML), Tahoe City, CA, USA, 9–12 July 1995. [Google Scholar]
- Jang, E.; Gu, S.; Poole, B. Categorical reparameterization with Gumbel-Softmax. arXiv 2017, arXiv:1611.01144. [Google Scholar]
- Tang, Y. Categorical reparameterization with Gumbel-Softmax. arXiv 2013, arXiv:1306.0239. [Google Scholar]
- Delen, D.; Kuzey, C.; Uyar, A. Measuring firm performance using financial ratios: A decision tree approach. Expert Syst. Appl. 2013, 40, 3970–3983. [Google Scholar] [CrossRef]
- Efimov, D.; Sulieman, H. Sobol Sensitivity: A Strategy for Feature Selection. In Mathematics Across Contemporary Sciences. AUS-ICMS 2015; Springer Proceedings in Mathematics & Statistics: Cham, Switzerland, 2017; Volume 190. [Google Scholar]
- Alaminos, D.; Fernández, S.M.; García, F.; Fernández, M.A. Data Mining for Municipal Financial Distress Prediction, Advances in Data Mining, Applications and Theoretical Aspects. Lect. Notes Comput. Sci. 2018, 10933, 296–308. [Google Scholar]
- Zhang, G.P.; Qi, M. Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Polasik, M.; Piotrowska, A.I.; Wisniewski, T.P.; Kotkowski, R.; Lightfoot, G. Price fluctuations and the use of Bitcoin: An empirical inquiry. Int. J. Electron. Commer. 2015, 20, 9–49. [Google Scholar] [CrossRef]
- Al-Khazali, O.; Bouri, E.; Roubaud, D. The impact of positive and negative macroeconomic news surprises: Gold versus Bitcoin. Econ. Bull. 2018, 38, 373–382. [Google Scholar]
- Koprinska, I.; Rana, M.; Rahman, A. Dynamic ensemble using previous and predicted future performance for Multi-step-ahead solar power forecasting. In Proceedings of the ICANN 2019: Artificial Neural Networks and Machine Learning, Munich, Germany, 17–19 September 2019; pp. 436–449. [Google Scholar]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef] [PubMed]



| Variables | Description |
|---|---|
| (a) Demand and Supply | |
| Transaction value | Value of daily transactions |
| Number of Bitcoins | Number of mined Bitcoins currently circulating on the network |
| Bitcoins addresses | Number of unique Bitcoin addresses used per day |
| Transaction volume | Number of transactions per day |
| Unspent transactions | Number of valid unspent transactions |
| Blockchain transactions | Number of transactions on blockchain |
| Blockchain addresses | Number of unique addresses used in blockchain |
| Block size | Average block size expressed in megabytes |
| Miners reward | Block rewards paid to miners |
| Mining commissions | Average transaction fees (in USD) |
| Cost per transaction | Miners’ income divided by the number of transactions |
| Difficulty | Difficulty mining a new blockchain block |
| Hash | Times a hash function can be calculated per second |
| Halving | Process of reducing the emission rate of new units |
| (b) Attractive | |
| Forum posts | Number of new members in online Bitcoin forums |
| Forum members | New posts in online Bitcoin forums |
| (c) Macroeconomic and Financial | |
| Texas oil | Oil Price (West Texas) |
| Brent oil | Oil Price (Brent, London) |
| Dollar exchange rate | Exchange rate between the US dollar and the euro |
| Dow Jones | Dow Jones Index of the New York Stock Exchange |
| Gold | Gold price in US dollars per troy ounce |
| Variables | Obs | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| Transaction value | 112 | 342,460,106,866,711.0000 | 143,084,554,727,531.0000 | 59,238,547,391,199.6000 | 735,905,260,141,564.0000 |
| Number of bitcoins | 112 | 13,634,297.4824 | 3,709,010.0736 | 5,235,454.5455 | 18,311,982.5000 |
| Bitcoins addresses | 112 | 285,034.2515 | 219,406.3874 | 1576.8333 | 849,668.1000 |
| Transaction volume | 112 | 154,548.8041 | 117,104.3686 | 1105.5000 | 373,845.6000 |
| Unspent transactions | 112 | 28,581,914.9054 | 22,987,595.3012 | 78,469.7273 | 66,688,779.9000 |
| Blockchain transactions | 112 | 156,444,312.9120 | 161,252,448.1997 | 237,174.8889 | 520,792,976.5000 |
| Blockchain addresses | 112 | 4,812,692.05 | 13,735,245.35 | −14,437,299.03 | 117,863,226.2 |
| Block size | 112 | 0.4956 | 0.3638 | 0.0022 | 0.9875 |
| Miners reward | 112 | 420,160,582,581,028.0000 | 174,396,895,338,462.0000 | 101,244,436,734,897.0000 | 796,533,076,376,536.0000 |
| Mining commissions | 112 | 9,581,973,325,205.4400 | 42,699,799,790,392.8000 | 0.2591 | 315,387,506,596,395.0000 |
| Cost per transaction | 112 | 155,354,364,458,705.0000 | 156,696,788,525,225.0000 | 0.1179 | 757,049,771,708,905.0000 |
| Difficulty | 112 | 187,513,499,336,866.0000 | 195,421,886,528,251.0000 | 212,295,141,771.2000 | 836,728,509,520,663.0000 |
| Hash | 112 | 110,434,372.2765 | 154,717,725.3881 | 0.5705 | 516,395,703.4338 |
| Halving | 112 | 279,853,454,485,387.0000 | 162,806,469,642,875.0000 | 6,473,142,955,255.1700 | 804,437,327,302,638.0000 |
| Forum posts | 112 | 9279.8844 | 8585.0583 | 455.0000 | 53132.0000 |
| Forum members | 112 | 2432.2545 | 3394.4635 | 30.6364 | 14,833.3409 |
| Texas Oil | 112 | 72.4878 | 23.7311 | 21.1230 | 135.6700 |
| Brent Oil | 112 | 78.4964 | 26.5819 | 19.1900 | 139.3800 |
| Dollar exchange rate | 112 | 1.3767 | 0.9604 | 1.0494 | 8.7912 |
| Dow Jones | 112 | 15,926.7161 | 3324.8875 | 11,602.5212 | 22,044.8627 |
| Gold | 112 | 1329.400847 | 244.4099259 | 739.15 | 1846.75 |
| Sample | DRCNN | DNDT | DSVR | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Acc. (%) | RMSE | MAPE | Acc. (%) | RMSE | MAPE | Acc. (%) | RMSE | MAPE | |
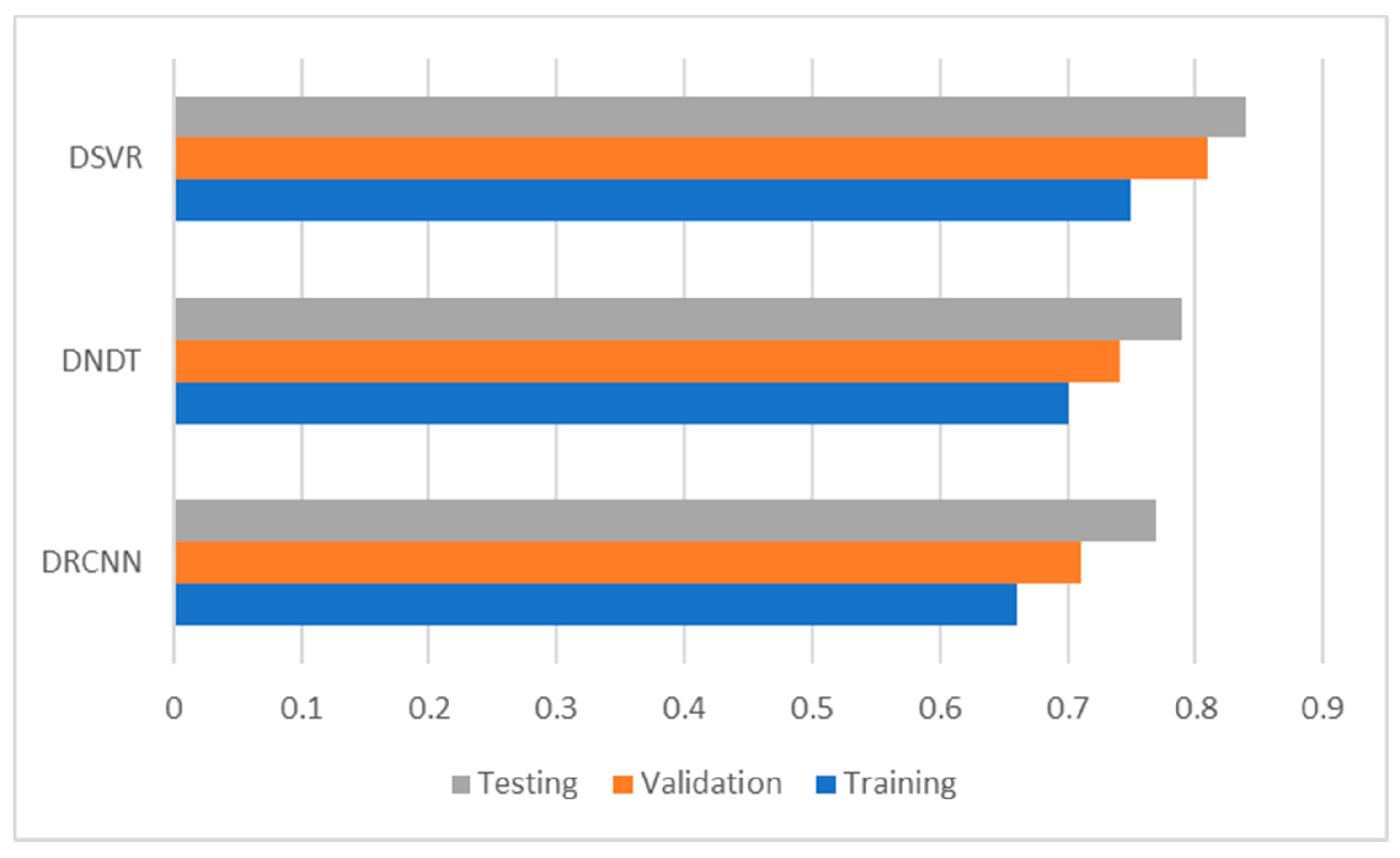
| Training | 97.34 | 0.66 | 0.29 | 95.86 | 0.70 | 0.33 | 94.49 | 0.75 | 0.38 |
| Validation | 96.18 | 0.71 | 0.34 | 95.07 | 0.74 | 0.37 | 93.18 | 0.81 | 0.43 |
| Testing | 95.27 | 0.77 | 0.40 | 94.42 | 0.79 | 0.42 | 92.61 | 0.84 | 0.47 |
| DRCNN | DNDT | DSVR |
|---|---|---|
| Transaction value | Transaction volume | Transaction value |
| Transaction volume | Block size | Block size |
| Block size | Blockchain transactions | Blockchain transactions |
| Cost per transaction | Cost per transaction | Cost per transaction |
| Difficulty | Difficulty | Difficulty |
| Dollar exchange rate | Forum posts | Forum posts |
| Dow Jones | Dow Jones | Dollar exchange rate |
| Gold | Gold | Dow Jones |
| Gold |
| Horizon | DRCNN | DNDT | DSVR | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Acc. (%) | RMSE | MAPE | Acc. (%) | RMSE | MAPE | Acc. (%) | RMSE | MAPE | |
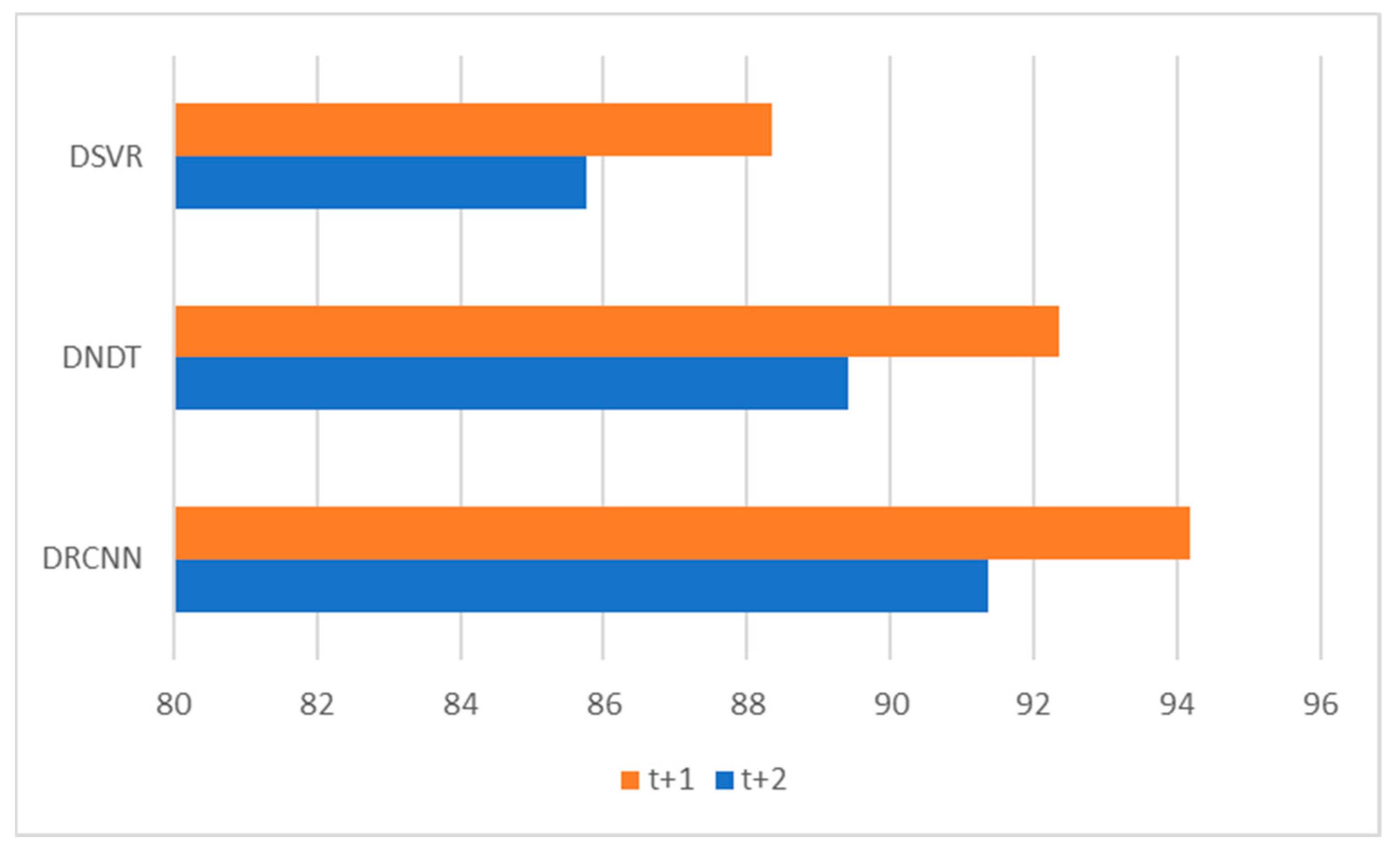
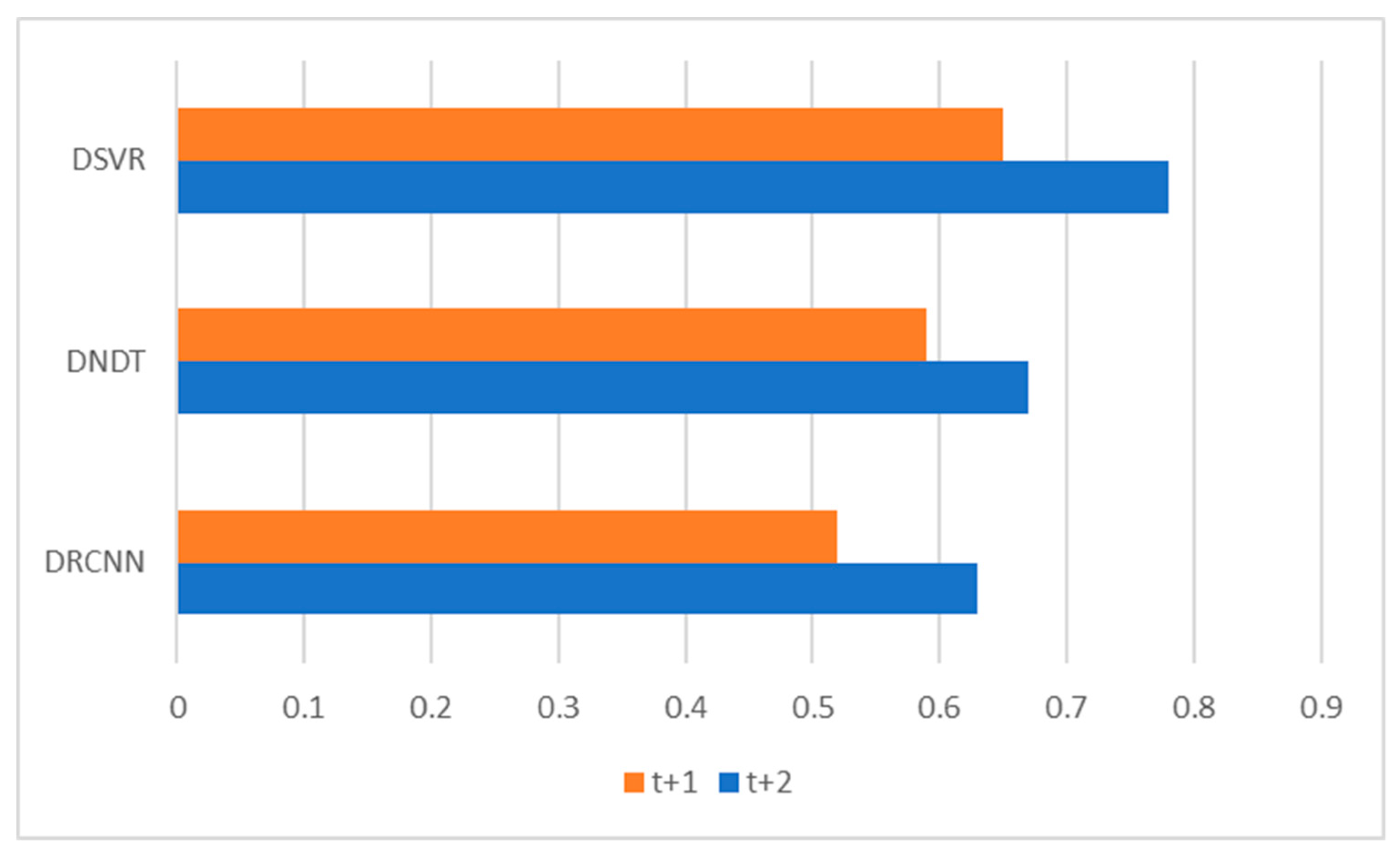
| t + 1 | 94.19 | 0.81 | 0.52 | 92.35 | 0.87 | 0.59 | 88.34 | 0.97 | 0.65 |
| t + 2 | 91.37 | 0.92 | 0.63 | 89.41 | 1.03 | 0.67 | 85.76 | 1.10 | 0.78 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamothe-Fernández, P.; Alaminos, D.; Lamothe-López, P.; Fernández-Gámez, M.A. Deep Learning Methods for Modeling Bitcoin Price. Mathematics 2020, 8, 1245. https://doi.org/10.3390/math8081245
Lamothe-Fernández P, Alaminos D, Lamothe-López P, Fernández-Gámez MA. Deep Learning Methods for Modeling Bitcoin Price. Mathematics. 2020; 8(8):1245. https://doi.org/10.3390/math8081245
Chicago/Turabian StyleLamothe-Fernández, Prosper, David Alaminos, Prosper Lamothe-López, and Manuel A. Fernández-Gámez. 2020. "Deep Learning Methods for Modeling Bitcoin Price" Mathematics 8, no. 8: 1245. https://doi.org/10.3390/math8081245
APA StyleLamothe-Fernández, P., Alaminos, D., Lamothe-López, P., & Fernández-Gámez, M. A. (2020). Deep Learning Methods for Modeling Bitcoin Price. Mathematics, 8(8), 1245. https://doi.org/10.3390/math8081245





