Application of the Kernel Density Function for the Analysis of Regional Growth and Convergence in the Service Sector through Productivity
Abstract
:1. Introduction
2. Theoretical Framework
2.1. Dispersion and Distribution Measures to Address Convergence
2.2. Economic Growth and Convergence
2.3. Subsection
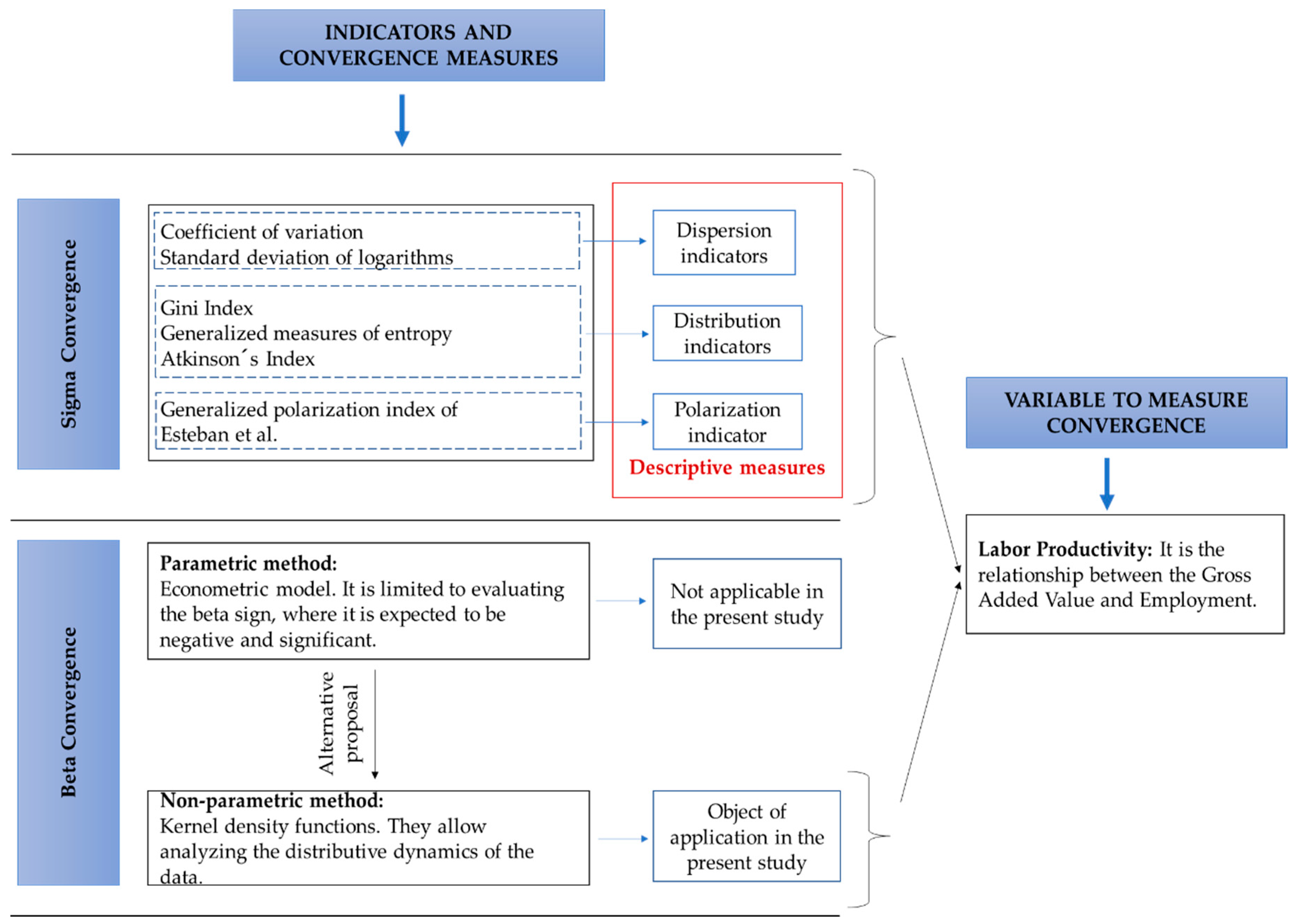
3. Methodology
3.1. Sigma Convergence (σ)
3.2. Beta Convergence (β)
4. Data Analysis and Results
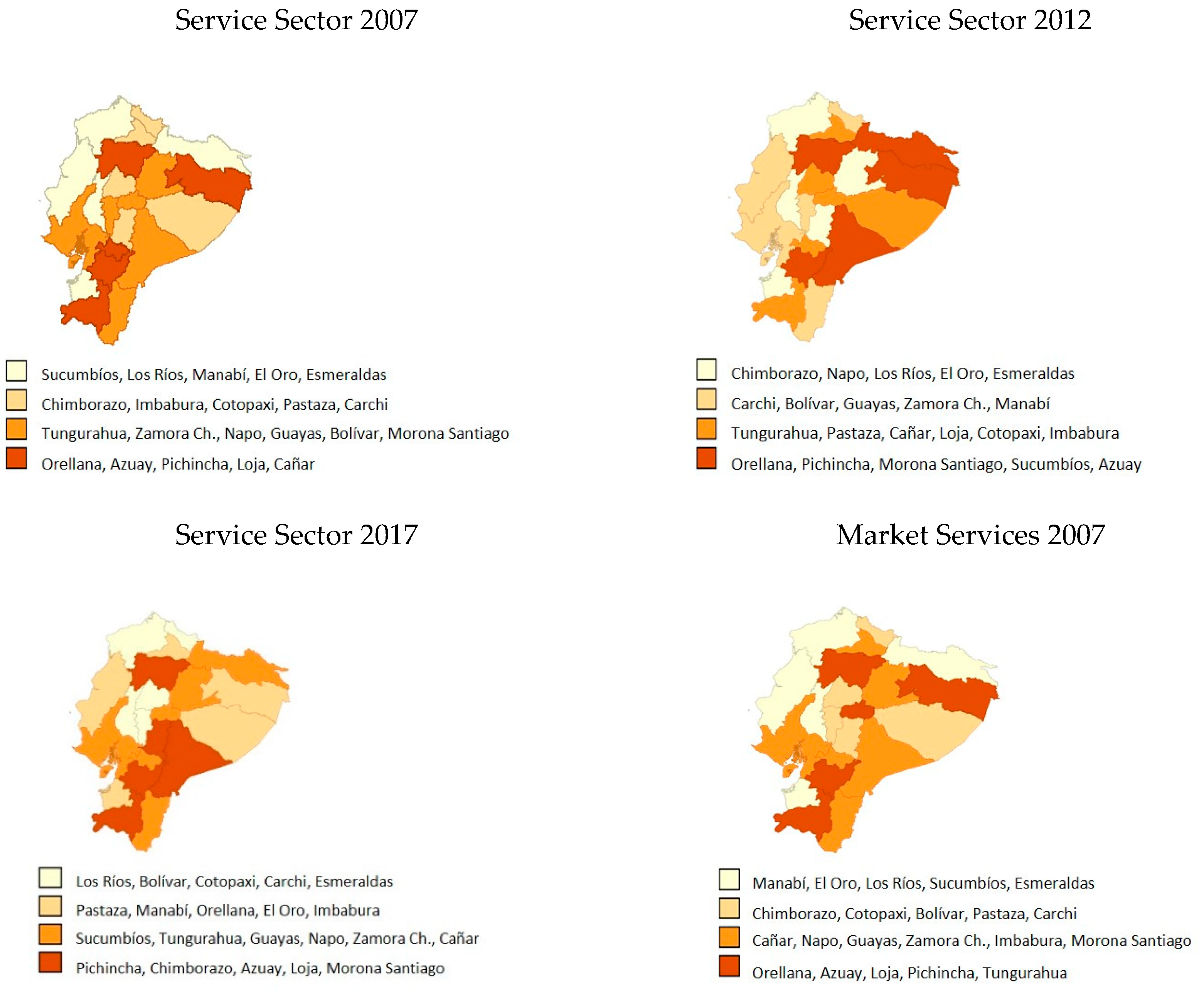
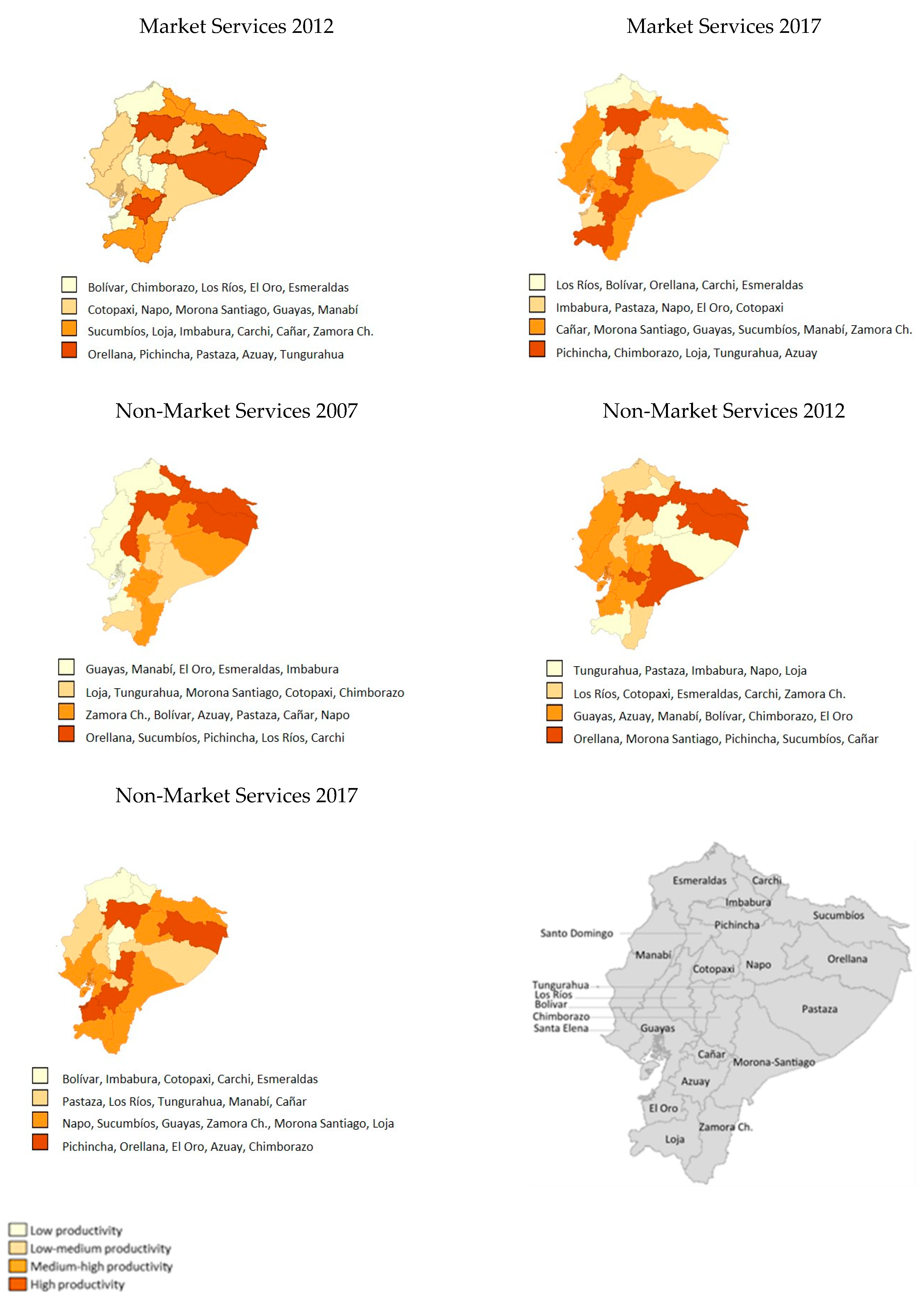
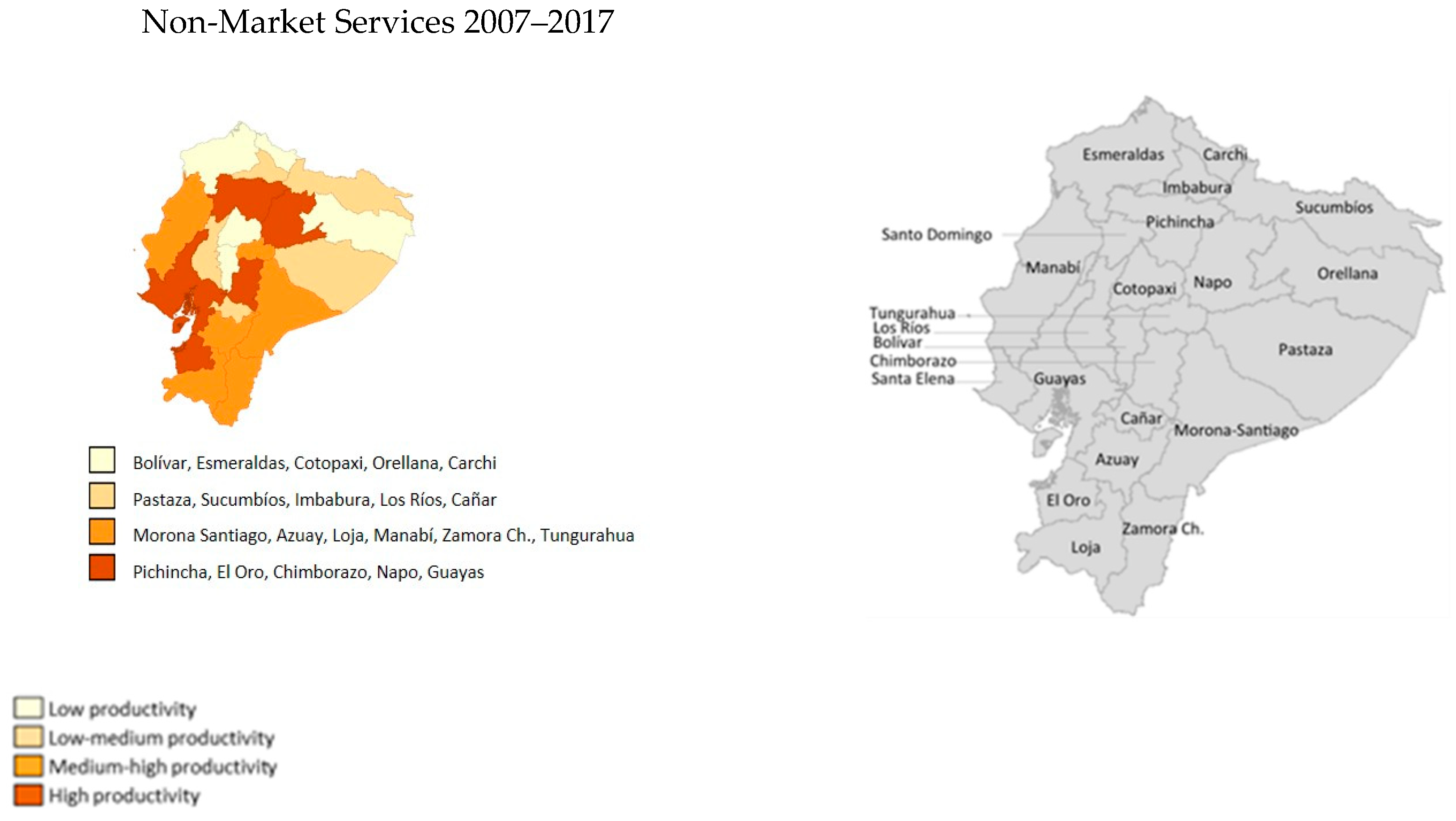
4.1. Sectoral Evolution of Regional Productivity
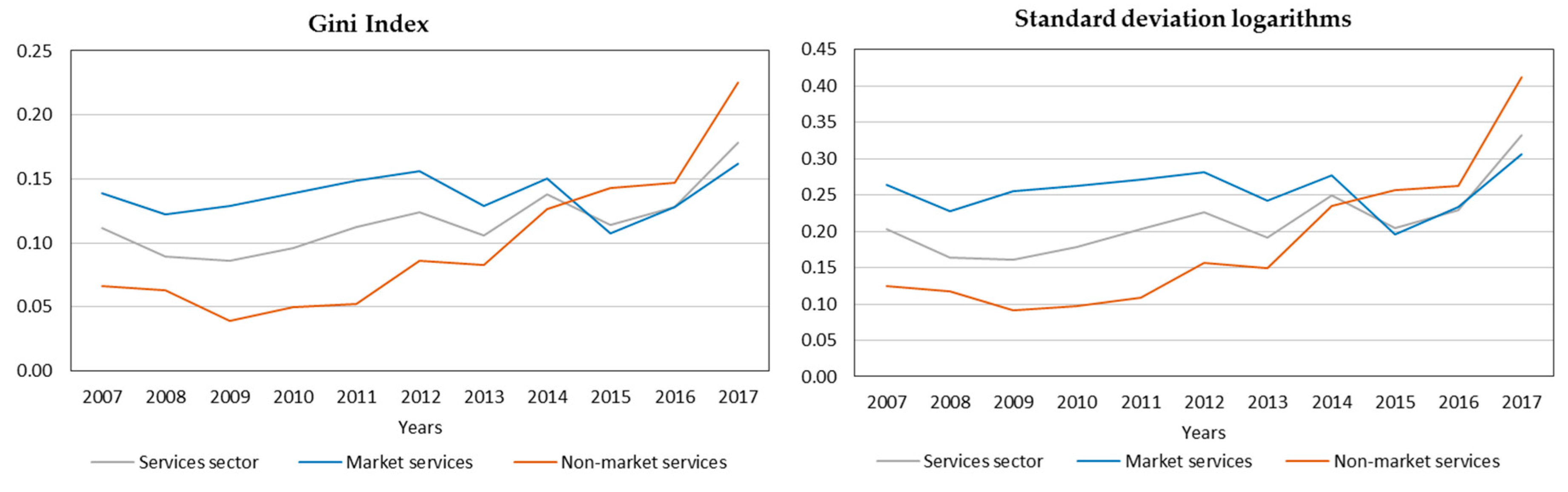
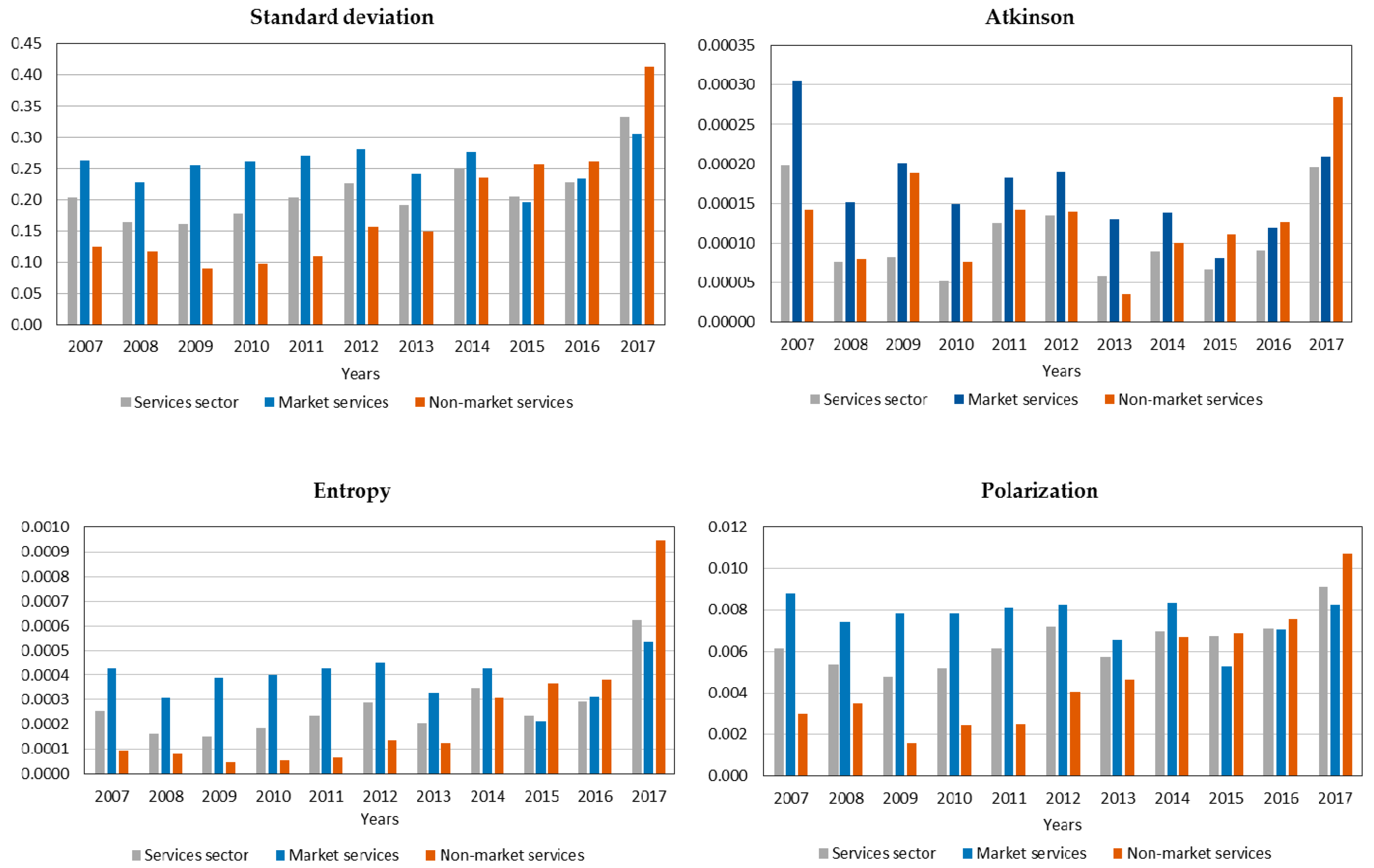
4.2. Gini Index and Sigma Convergence
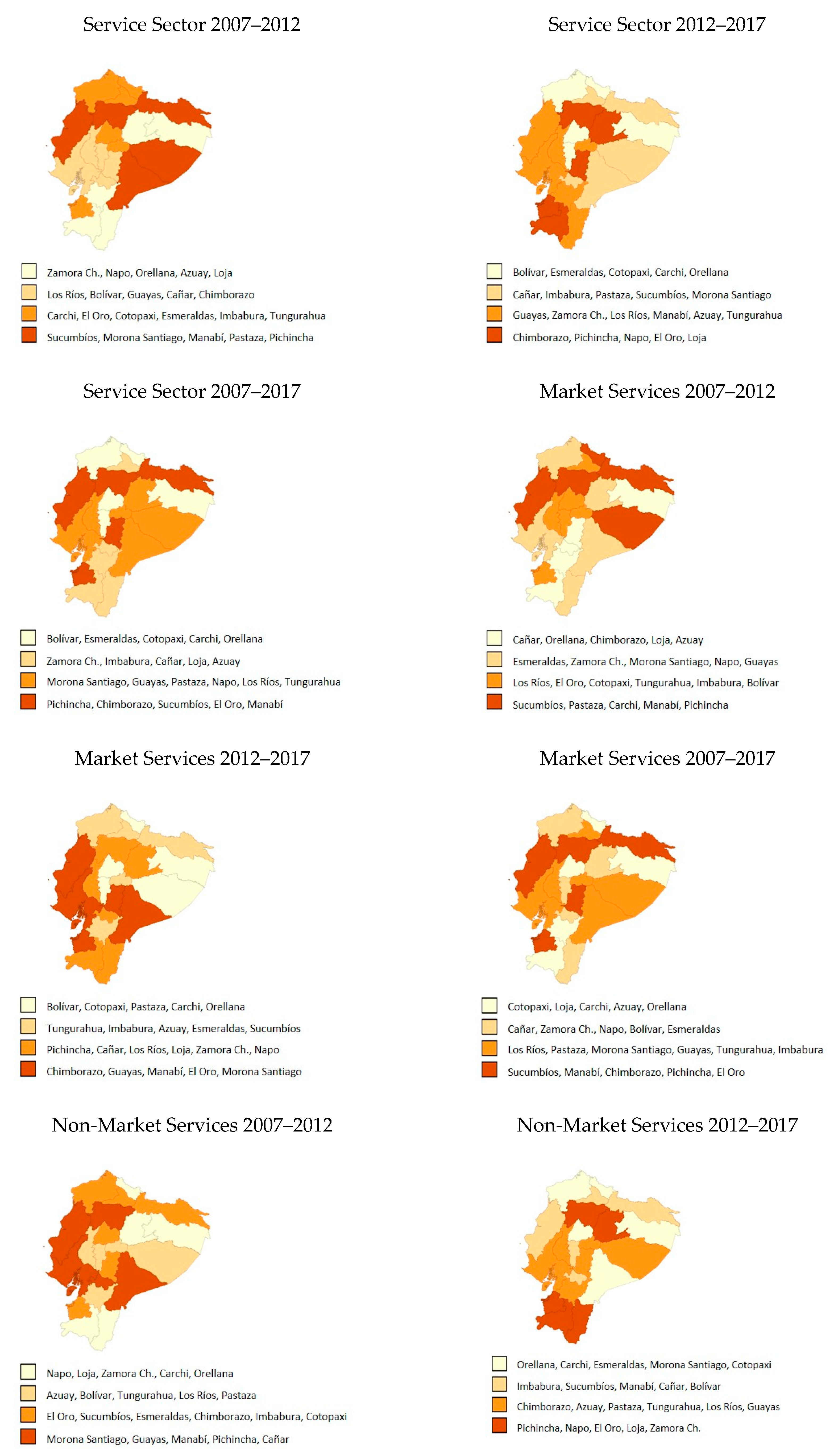
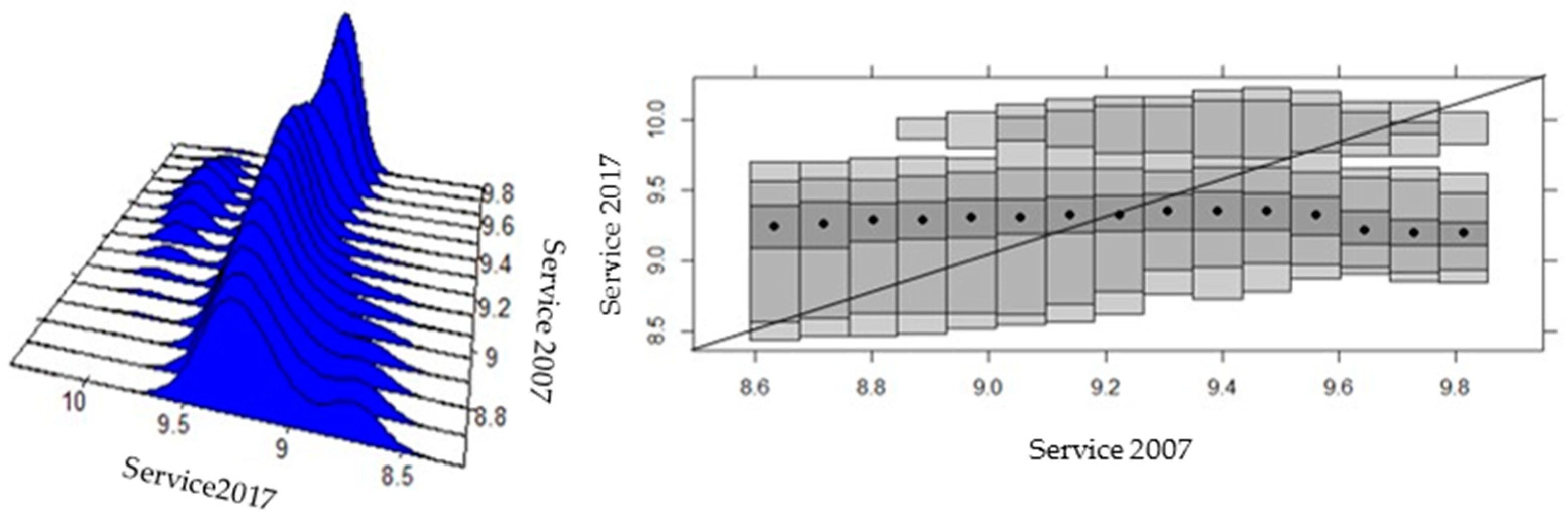
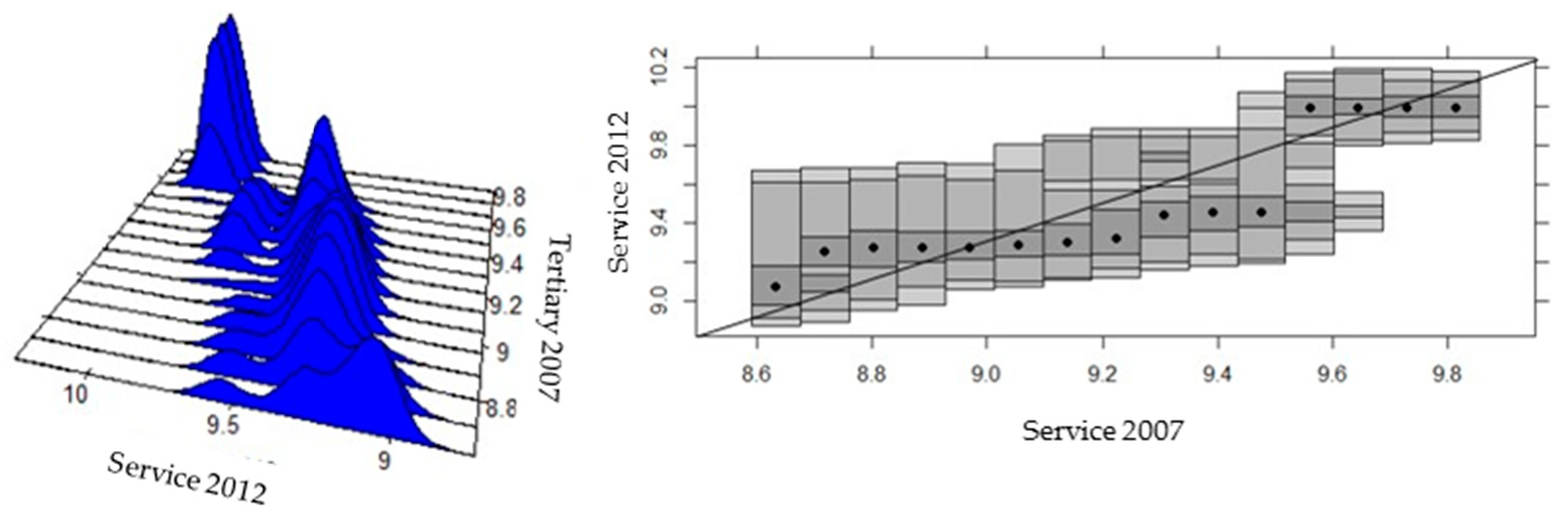
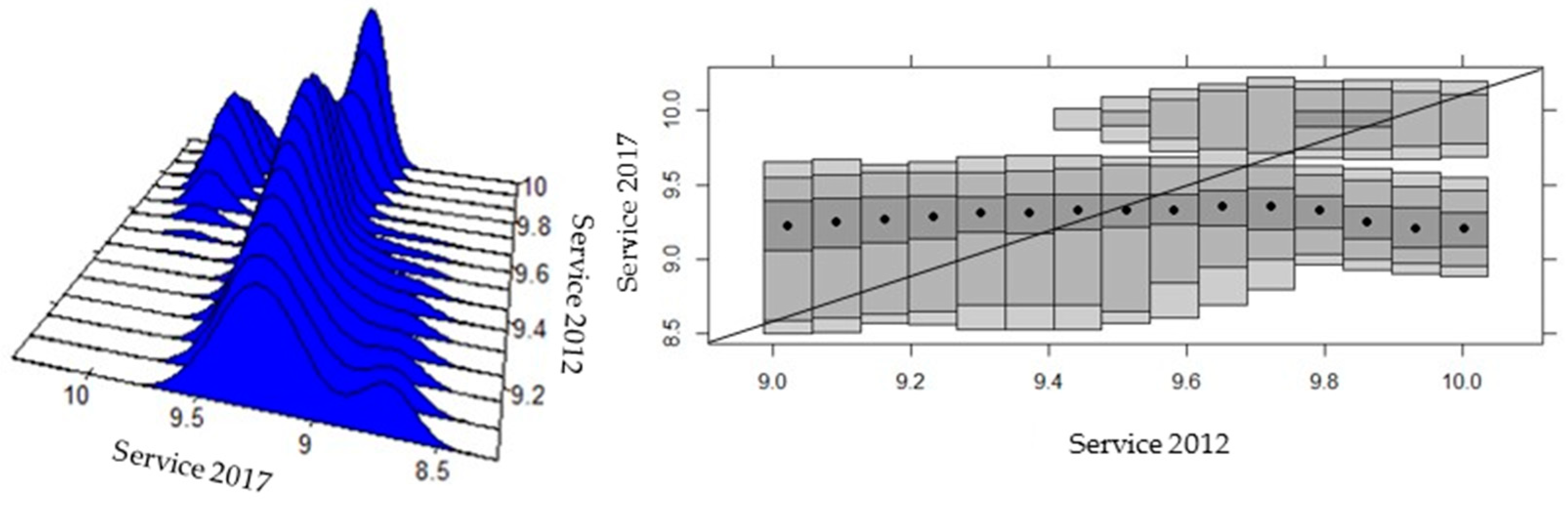
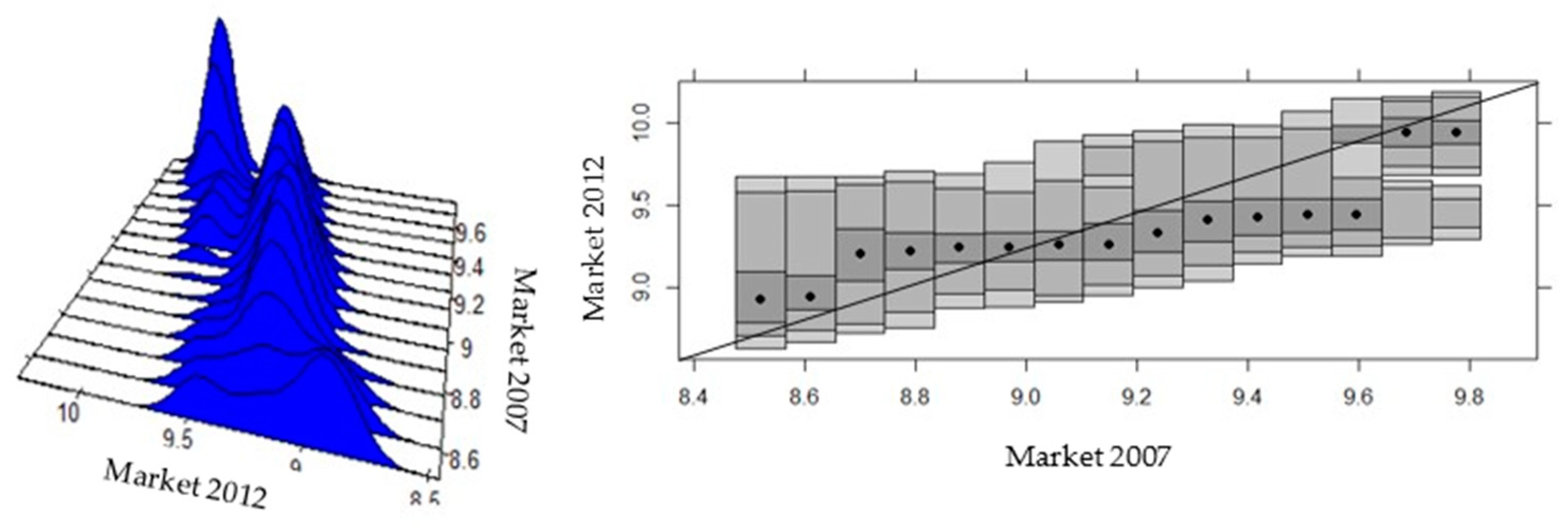
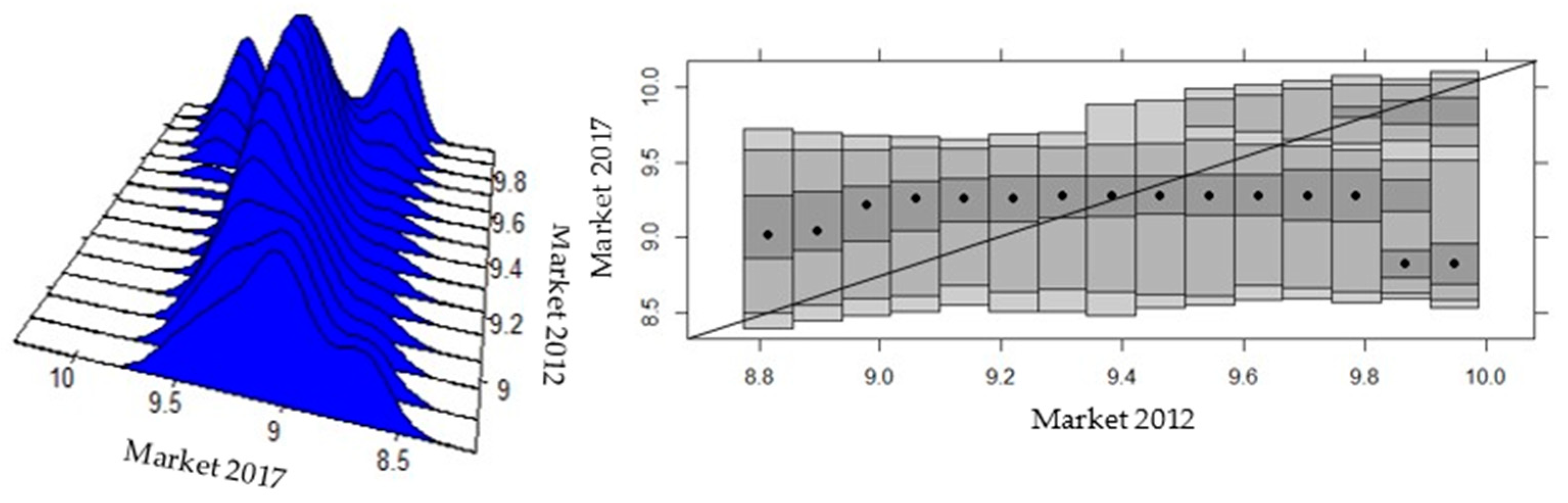
4.3. Beta Convergence and Analysis of Sectoral Intra-Distributive Dynamics in Ecuadorian Provinces
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bastos, S.Q.D.A.; Perobelli, F.S.; Souza, K.B.D. Analysis of the productive structure of the service sector in countries with different levels of development/Análisis de la estructura productiva del sector servicios en países con diferentes niveles de desarrollo. Rev. CEPAL 2012, 108, 91–113. [Google Scholar]
- Flores Sánchez, C.A.; Castillo Ponce, R.A.; Rodríguez Espinosa, M.D.L. The importance of the service sector in the Mexican economy: An analysis of time series/La importancia del sector servicios en la economía mexicana: Un análisis de series de tiempo. Paradig. Econ. 2013, 5, 5–27. [Google Scholar]
- Maroto, A. Productivity in the Services Sector. An Applied Economic Analysis /La Productividad en el Sector Servicios. Un Análisis Económico Aplicado (Tesis Doctoral). Ph.D. Thesis, Universidad de Alcalá, Fort Henares, Spain, 2007. [Google Scholar]
- Maroto-Sánchez, A. Productivity in the services sector: Conventional and current explanations. Serv. Ind. J. 2012, 32, 719–746. [Google Scholar] [CrossRef]
- Bonet, J. The outsourcing of regional economic structures in Colombia/La terciarización de las estructuras económicas regionales en Colombia. Rev. Econ. Rosario 2007, 10, 1–19. [Google Scholar]
- World Bank (WB). World Development Indicators. Available online: https://datos.bancomundial.org/ (accessed on 5 April 2020).
- Kinfemichael, B.; Morshed, A.M. Unconditional convergence of labor productivity in the service sector. J. Macroecon. 2019, 59, 217–229. [Google Scholar] [CrossRef]
- Rabanal, C. Hypothesis on economic convergence: A review of the approaches used/Hipótesis sobre la convergencia económica: Una revisión de los enfoques utilizados. Econ. Adm. 2017, 7, 113–132. [Google Scholar] [CrossRef] [Green Version]
- Quah, D. Galton’s fallacy and tests of the convergence hypothesis. Scand. J. Econ. 1993, 552, 427–443. [Google Scholar] [CrossRef]
- Quah, D. Empirics for economic growth and convergence. Eur. Econ. Rev. 1996, 40, 1353–1375. [Google Scholar] [CrossRef]
- González, M.; Del Río Gómez, C.; Domínguez, J.M. The services: Concept, classification and measurement problems/Los servicios: Concepto, clasificación y problemas de medición. Ekon. Rev. Vasca Econ. 1989, 13, 10–19. [Google Scholar]
- Solow, R. A contribution to the theory of economic growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Swan, T.W. Economic growth and capital accumulation. Econ. Rec. 1956, 32, 334–361. [Google Scholar] [CrossRef]
- Romer, P.M. Increasing returns and long-run growth. J. Political Econ. 1986, 94, 1002–1037. [Google Scholar] [CrossRef] [Green Version]
- Lucas, R.E., Jr. On the mechanics of economic development. J. Monet. Econ. 1988, 22, 3–42. [Google Scholar] [CrossRef]
- Carrillo Huerta, M.M.; Ceron Vargas, J.A.; Reyes Hernández, M.S. Analysis of Economic Growth/Análisis del Crecimiento Económico (No. 3 330); e-libro Corp.: Madrid, Spain, 2007. [Google Scholar]
- Barro, R.J.; Sala-i-Martin, X. Economic Growth; McGraw-Hill: Santa Fe, CDMX, Mexico, 1995. [Google Scholar]
- Galor, O. Convergence? Inferences from theoretical models. Econ. J. 1996, 106, 1056–1069. [Google Scholar] [CrossRef]
- Esquivel, G. Regional convergence in Mexico, 1940–1995/Convergencia regional en México, 1940–1995. El Trimest. Econ. 1999, 264, 725–761. [Google Scholar]
- Mankiw, N.G.; Romer, D.; Weil, D.N. A contribution to the empirics of economic growth. Q. J. Econ. 1992, 107, 407–437. [Google Scholar] [CrossRef]
- Barro, R.J.; Sala-i-Martin, X.; Robinson, R.A.; de Espinoza, J.R. Economic Growth/Crecimiento Económico; Reverté: Barcelona, Spain, 2009. [Google Scholar]
- Abramovitz, M. Catching up, forging ahead, and falling behind. J. Econ. Hist. 1986, 46, 385–406. [Google Scholar] [CrossRef]
- Baumol, W. Productivity growth, convergence and welfare: What the long-run data show. Am. Econ. Rev. 1986, 76, 1072–1085. [Google Scholar]
- Barro, R.J.; Sala-i-Martin, X.; Blanchard, O.J.; Hall, R.E. Convergence across states and regions. Brook. Pap. Econ. Act. 1991, 107–182. [Google Scholar] [CrossRef] [Green Version]
- Quintana-Romero, L.; Correa-Quezada, R.; Ramón-Mendieta, M.G.; Álvarez-García, J. Sectoral regional growth and convergence in Ecuador: An analysis of the intra-distributive dynamics of productivity. Symmetry 2019, 11, 461. [Google Scholar] [CrossRef] [Green Version]
- Barro, R.J. Economic growth and convergence, applied to China. China World Econ. 2016, 24, 5–19. [Google Scholar] [CrossRef]
- Ahmad, M.; Hall, S.G. Economic growth and convergence: Do institutional proximity and spillovers matter? J. Policy Model. 2017, 39, 1065–1085. [Google Scholar] [CrossRef] [Green Version]
- Borozan, D. Internal migration, regional economic convergence, and growth in Croatia. Int. Reg. Sci. Rev. 2017, 40, 141–163. [Google Scholar] [CrossRef]
- Jiang, L.I.U.; Yang, S.H.E.N. Industrial convergence, market segmentation and economic growth. J. Lanzhou Univ. Financ. Econ. 2017, 6, 7–15. [Google Scholar]
- Jianyu, C.H.I.; Enshu, G.U. Intellectual property rights protection, economic growth and economic convergence: An empirical study based on panel threshold model. Rev. Econ. Manag. 2017, 4, 2–18. [Google Scholar]
- Juknys, R.; Liobikienė, G.; Dagiliūtė, R. Sustainability of economic growth and convergence in regions of different developmental stages. Sustain. Dev. 2017, 25, 276–287. [Google Scholar] [CrossRef]
- Åslund, A. What happened to the economic convergence of central and eastern europe after the global financial crisis? Comp. Econ. Stud. 2018, 60, 254–270. [Google Scholar] [CrossRef]
- Labella, Á.; Rodríguez-Cohard, J.C.; Sánchez-Martínez, J.D.; Martínez, L. An AHPSort II Based Analysis of the Inequality Reduction within European Union. Mathematics 2020, 8, 646. [Google Scholar] [CrossRef]
- Szkutnik, W.; Szkutnik, W. Socio-economic convergence in models of endogeneous economic growth. Ekon. Manaz. Spectr. 2018, 12, 1–14. [Google Scholar]
- Vâlsan, C.; Druică, E. Corporate performance and economic convergence between europe and the us: A cluster analysis along industry lines. Mathematics 2020, 8, 451. [Google Scholar] [CrossRef] [Green Version]
- Willington, M. An Empirical Analysis of Regional Economic Growth in Argentina/Un Análisis Empírico del Crecimiento Económico Regional en Argentina; Working Document nº14; IERAL, Fundación Mediterránea: Córdoba, Argentina, 1998; pp. 1–54. [Google Scholar]
- Cuervo, L.M. Regional convergence and divergence studies in Latin America: Balance and perspectives/Estudios de convergencia y divergencia regional en América Latina: Balance y perspectivas. Investig. Reg. J. Reg. Res. 2004, 5, 29–66. [Google Scholar]
- Quintana-Romero, L.; Mendoza, M.A.; Correa-Quezada, R. Ecuadorian regions in the Latin American context/Las regiones ecuatorianas en el contexto Latinoamericano. In Regions and Economy in Ecuador: Growth, Industry, Migration and Employment/Regiones y Economía en el Ecuador: Crecimiento, Industria, Migración y Empleo; Quintana, L., Mendoza, M.A., Correa-Quezada, R., Eds.; In Abya Yala: Quito, Ecuador, 2014; pp. 13–27. [Google Scholar]
- Ramón-Mendieta, M.G.; Ochoa-Moreno, W.S.; Ochoa-Jiménez, D.A. Growth, Clusters, and Convergence in Ecuador: 1993–2011. In Regional Problems and Policies in Latin America; Cuadrado-Roura y P. Aroca, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 323–337. [Google Scholar]
- Ramón-Mendieta, M.; Quintana-Romero, L. Regional convergence and divergence in Ecuador/Convergencia y divergencia regional en Ecuador. In Regions and Economy in Ecuador: Growth, Industry, Migration and Employment/Regiones y Economía en el Ecuador: Crecimiento, Industria, Migración y Empleo; Quintana, L., Mendoza, M.A., Correa-Quezada, R., Eds.; In Abya Yala: Quito, Ecuador, 2014; pp. 85–105. [Google Scholar]
- Szeles, M.R.; Muñoz, R.M. Analyzing the regional economic convergence in Ecuador. Insights from parametric and nonparametric models. Rom. J. Econ. Forecast. 2016, 19, 43–65. [Google Scholar]
- Arias, T. Structural Change and Regional Inequalities in Ecuador: 1993–2014/El Cambio Estructural y las Desigualdades Regionales en el Ecuador: 1993–2014. Ph.D. Thesis, University of Alcala, Alcalá de Henares, Spain, 2017. [Google Scholar]
- Flores-Chamba, J.; Correa-Quezada, R.; Álvarez-García, J.; del Río-Rama, M.D.L. Spatial Economic Convergence and Public Expenditure in Ecuador. Symmetry 2019, 11, 130. [Google Scholar] [CrossRef] [Green Version]
- Mendieta Muñoz, R.M. The Conditional Convergence Hypothesis in Ecuador: An Analysis at the Cantonal Level/La hipótesis de la convergencia condicional en Ecuador: Un análisis a nivel cantonal. Retos Rev. Ciencias Adm. Econ. 2015, 5, 13–25. [Google Scholar]
- Mendieta Muñoz, R.; Pontarollo, N. Cantonal convergence in ecuador: A spatial econometric perspective. J. Appl. Econ. Sci. 2016, XI, 107–126. [Google Scholar]
- Central Bank of Ecuador (BCE). Regional National Accounts/Cuentas Nacionales Regionales. Available online: https://www.bce.fin.ec/index.php/component/k2/item/293-cuentas-provinciales/ (accessed on 5 April 2020).
- National Institute of Statistics and Censuses (INEC). Employment, Unemployment and Underemployment Surveys/Encuestas de Empleo, Desempleo y Subempleo (ENEMDU). Available online: http://www.ecuadorencifras.gob.ec/informacion-historica-de-empleo/ (accessed on 5 April 2020).
- Ezcurra, R.; Rodríguez-Pose, A. Measuring the regional divide. In Handbook of Regional Growth and development Theories; Capello, R., Nijkamp, P., Eds.; Edward Elgar Publishing: Cheltenham, UK, 2009; pp. 329–353. [Google Scholar]
- Quintana, L.; Asuad, N. Growth, Concentration, Inequality and Regional Policy in Mexico. In Regional Problems and Policies in Latin America; Cuadrado-Roura, J., Aroca, P., Eds.; Springer: London, UK, 2013; pp. 165–195. [Google Scholar]
- Quintana, L.; Prudencio, J.; Salas, C. Inequality and Spatial Convergence in the Mexico City Metropolitan Area, 1989-2010. J. Rev. Glob. Econ. 2016, 5, 69–83. [Google Scholar] [CrossRef]
- Esteban, J.; Gradín, C.; Ray, D. An extension of a measure of polarization, with an application to the income distribution of five OECD countries. J. Econ. Inequal. 2007, 5, 1–19. [Google Scholar] [CrossRef]
- Barro, R.J.; Sala-i-Martin, X. Economic Growth and Convergence Across the United States; Working Paper no. 3419; National Bureau of Economic Research: Cambridge, UK, 1990. [Google Scholar]
- Barro, R.J. Economic Growth in a Cross Section of Countries. Q. J. Econ. 1991, 106, 407–443. [Google Scholar] [CrossRef] [Green Version]
- Sala-i-Martin, X. The classical approach to convergence analysis. Econ. J. 1996, 1019–1036. [Google Scholar] [CrossRef]
- Sala-i-Martin, X. Notes of Economic Growth/Apuntes de Crecimiento Económico; Antoni Bosch Editor: Barcelona, Spain, 2000. [Google Scholar]
- Bickenbach, F.; Eckhardt, B. Evaluating the markov property in studies of economic convergence. Int. Reg. Sci. Rev. 2003, 26, 363–392. [Google Scholar] [CrossRef]
- Magrini, S. Analysing Convergence Through the Distribution Dynamics Approach: Why and How? In Working Paper Department of Economics; Num. 13 /wp/2007; Ca’ Foscari University of Venice: Venezia, Italy, 2007. [Google Scholar]
- Hyndman, R. Computing and graphing highest density regions. Am. Stat. 1996, 50, 120–126. [Google Scholar]
- Hyndman, R.; Bashtannyk, D.; Grunwald, G. Estimating and visualizing conditional densities. J. Comput. Gr. Stat. 1996, 5, 315–336. [Google Scholar]
- Borrayo López, R.; Castañeda Arriaga, J.M. Dynamic transition analysis: A non-parametric approach applied to the central region of Mexico (1988–2003)/Análisis de transición dinámica: Un enfoque no paramétrico aplicado a la región centro de México (1988–2003). Probl. Desarro. 2011, 42, 7–44. [Google Scholar]
- Arbia, G.; Basile, R.; Piras, G. Analyzing intra-distribution dynamics: A reappraisal. In ERSA Conference Papers; (No. ersa06p262); European Regional Science Association: Louvain-la-Neuve, Belgium, 2006. [Google Scholar]
- Hyndman, R.J. Hdrcde: Highest Density Regions and Conditional Density Estimation. R Package Version 3.4. Available online: http://pkg.robjhyndman.com/hdrcde (accessed on 5 March 2020).

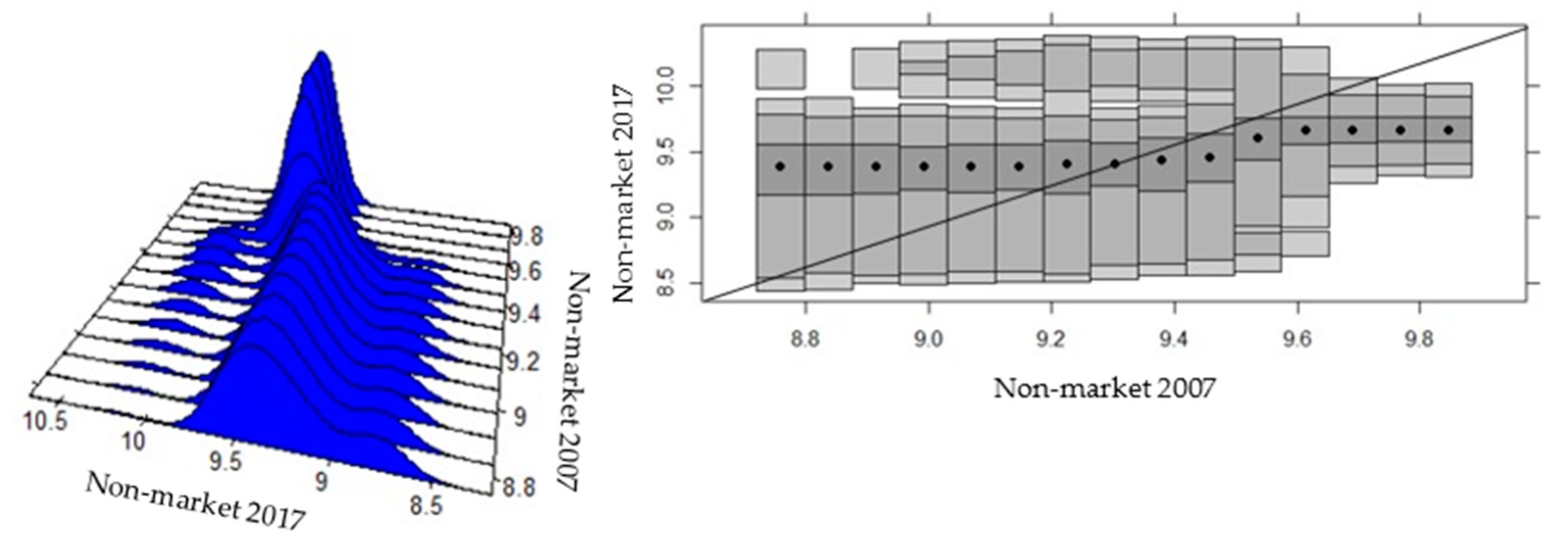

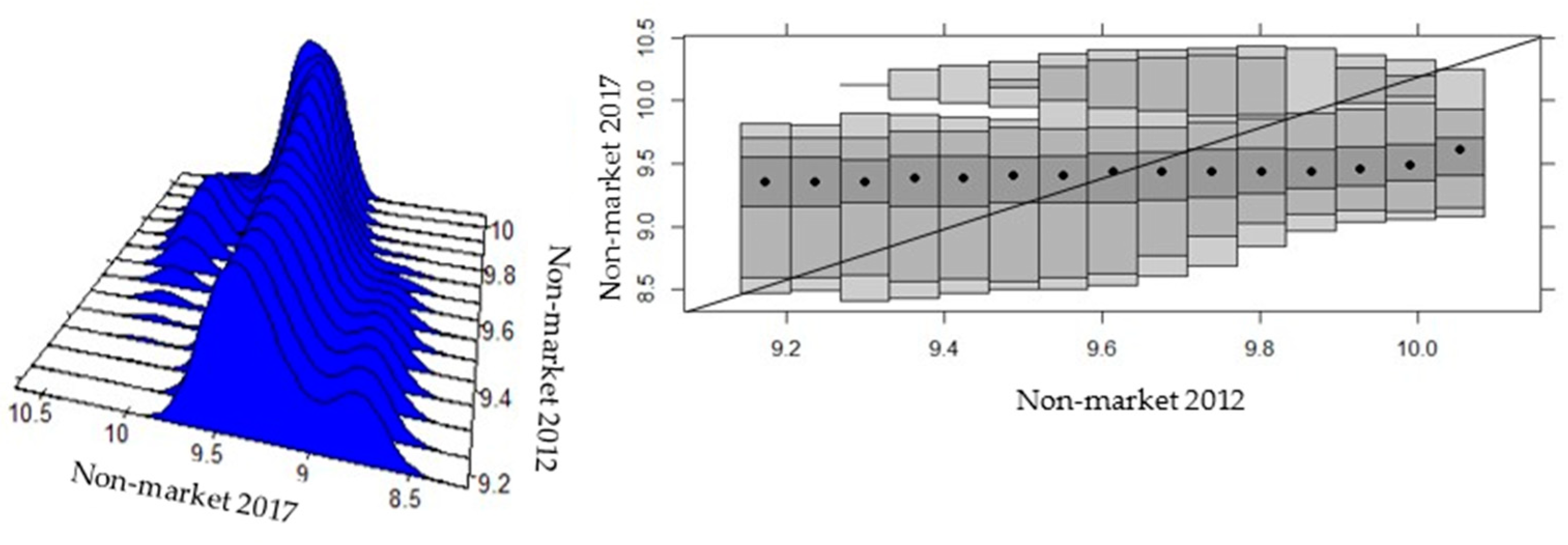
| Descriptive Measures | 2007 | 2017 | ||||
|---|---|---|---|---|---|---|
| Total Services | Market Services | Non-Market Services | Total Services | Market Services | Non-Market Services | |
| Maximum | 18.3 | 17.6 | 18.9 | 20.8 | 18.7 | 25.3 |
| Minimum | 5.6 | 5.0 | 6.4 | 6.0 | 5.8 | 6.4 |
| Mean | 8.1 | 8.1 | 8.1 | 10.6 | 10.1 | 11.7 |
| Standard deviation | 2.7 | 3.0 | 2.6 | 3.0 | 2.8 | 4.1 |
| Coefficient of variation * | 33.3 | 36.8 | 31.6 | 28.2 | 28.0 | 34.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Correa-Quezada, R.; Cueva-Rodríguez, L.; Álvarez-García, J.; del Río-Rama, M.d.l.C. Application of the Kernel Density Function for the Analysis of Regional Growth and Convergence in the Service Sector through Productivity. Mathematics 2020, 8, 1234. https://doi.org/10.3390/math8081234
Correa-Quezada R, Cueva-Rodríguez L, Álvarez-García J, del Río-Rama MdlC. Application of the Kernel Density Function for the Analysis of Regional Growth and Convergence in the Service Sector through Productivity. Mathematics. 2020; 8(8):1234. https://doi.org/10.3390/math8081234
Chicago/Turabian StyleCorrea-Quezada, Ronny, Lucía Cueva-Rodríguez, José Álvarez-García, and María de la Cruz del Río-Rama. 2020. "Application of the Kernel Density Function for the Analysis of Regional Growth and Convergence in the Service Sector through Productivity" Mathematics 8, no. 8: 1234. https://doi.org/10.3390/math8081234
APA StyleCorrea-Quezada, R., Cueva-Rodríguez, L., Álvarez-García, J., & del Río-Rama, M. d. l. C. (2020). Application of the Kernel Density Function for the Analysis of Regional Growth and Convergence in the Service Sector through Productivity. Mathematics, 8(8), 1234. https://doi.org/10.3390/math8081234








