The Global Well-Posedness for Large Amplitude Smooth Solutions for 3D Incompressible Navier–Stokes and Euler Equations Based on a Class of Variant Spherical Coordinates
Abstract
1. Introduction
1.1. Background
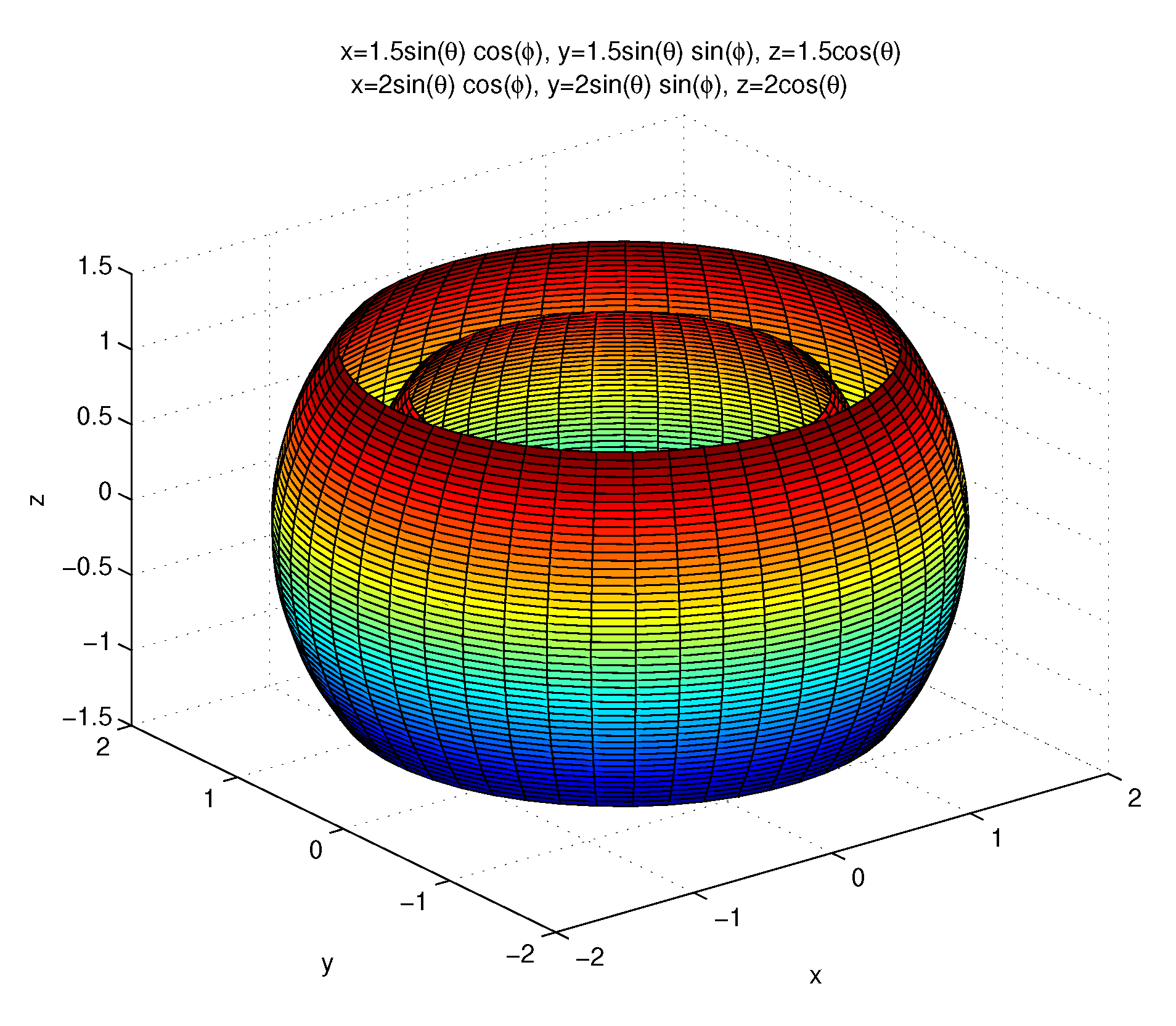
1.2. A Class of Variant Spherical Coordinates
1.3. Research Model
1.4. Preliminaries
2. Main Results
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hopf, E. Über die Anfangswertaufgabe für die hydrodynamischen Grundgleichungen. Math. Nachr. 1951, 4, 213–231. [Google Scholar] [CrossRef]
- Leray, J. Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 1934, 63, 193–248. [Google Scholar] [CrossRef]
- Cafferalli, L.; Kohn, R.; Nirenberg, L. Partial regularity of suitable weak solutions of the Navier–Stokes equations. Commun. Pure Appl. Math. 1982, 35, 771–831. [Google Scholar] [CrossRef]
- Lin, F. A new proof of the Caffarelli-Kohn-Nirenberg theorem. Commun. Pure Appl. Math. 1998, 51, 241–257. [Google Scholar] [CrossRef]
- Majda, A.; Bertozzi, A. Vorticity and incompressible flow. In Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Prodi, G. Un teorema di unicità per le equazioni di Navier–Stokes. Ann. Mat. Pura Appl. 1959, 48, 173–182. [Google Scholar] [CrossRef]
- Serrin, J. On the interior regularity of weak solutions of the Navier–Stokes equations. Arch. Rat. Mech. Anal. 1962, 9, 187–195. [Google Scholar] [CrossRef]
- Beale, J.T.; Kato, T.; Majda, T.A. Remarks on the breakdown of smooth solutions for the 3-D Euler equations. Commun. Math. Phys. 1984, 94, 61–66. [Google Scholar] [CrossRef]
- Constantin, P. On the Euler equations of incompressible fluids. Bull. Am. Math. Soc. 2007, 44, 603–621. [Google Scholar] [CrossRef]
- Escauriaza, L.; Serëgin, G.A.; Šverák, V. L3−∞-solutions of Navier–Stokes equations and backward uniqueness. Rus. Math. Surv. 2003, 58, 211–250. [Google Scholar] [CrossRef]
- Cao, C.; Titi, E.S. Regularity criteria for the three dimensional Navier–Stokes equations. Indiana Univ. Math. J. 2008, 57, 2643–2661. [Google Scholar] [CrossRef]
- Kukavica, I.; Ziane, M. One component regularity for the Navier–Stokes equations. Nonlinearity 2006, 19, 453–469. [Google Scholar] [CrossRef]
- Miller, E. A regularity criterion for the Navier–Stokes equation involving only the middle eigenvalue of the strain tensor. Arch. Ration. Mech. Anal. 2020, 235, 99–139. [Google Scholar] [CrossRef]
- Neustupa, J.; Novotný, A.; Penel, P. An interior regularity of a weak solution to the Navier–Stokes equations in dependence on one component of velocity. Top. Math. Fluid Mech. Quad. Mat. 2002, 10, 163–183. [Google Scholar]
- Zhou, Y.; Pokorný, M. On the regularity of the solutions of the Navier–Stokes equations via one velocity component. Nonlinearity 2010, 23, 1097–1107. [Google Scholar] [CrossRef]
- Cheskidov, A.; Shvydkoy, R. A unified approach to regularity problems for the 3D Navier–Stokes and Euler equations: The use of Kolmogorov’s dissipation range. J. Math. Fluid Mech. 2014, 16, 263–273. [Google Scholar] [CrossRef]
- Chen, H.; Fang, D.; Zhang, T. Regularity of 3D axisymmetric Navier–Stokes equations. Discrete Contin. Dyn. Syst. 2017, 37, 1923–1939. [Google Scholar] [CrossRef]
- Hou, T.Y.; Shi, Z.; Wang, S. On singularity formation of a 3D model for incompressible Navier–Stokes equations. Adv. Math. 2012, 230, 607–641. [Google Scholar] [CrossRef][Green Version]
- Hou, T.Y.; Lei, Z.; Luo, G.; Wang, S.; Zou, C. On finite time singularity and global regularity of an axisymmetric model for the 3D Euler equations. Arch. Ration. Mech. Anal. 2014, 212, 683–706. [Google Scholar] [CrossRef][Green Version]
- Leonardi, S.; Málek, J.; Nečas, J.; Pokorný, M. On axially symmetric flows in ℝ3. Z. Anal. Anwendungrn. 1999, 18, 639–649. [Google Scholar] [CrossRef]
- Ukhovskii, M.R.; Iudovich, V.I. Axially symmetric flows of ideal and viscous fluids filling the whole space. J. Appl. Math. Mech. 1968, 32, 52–61. [Google Scholar] [CrossRef]
- Wei, D. Regularity criterion to the axially symmetric Navier–Stokes equations. J. Math. Anal. Appl. 2016, 435, 402–413. [Google Scholar] [CrossRef]
- Zajączkowski, W.M. A regularity criterion for axially symmetric solutions to the Navier–Stokes equations. J. Math. Sci. 2011, 178, 265–273. [Google Scholar] [CrossRef]
- Zhang, Z. A pointwise regularity criterion for axisymmetric Navier–Stokes system. J. Math. Anal. Appl. 2018, 461, 1–6. [Google Scholar] [CrossRef]
- Zhang, Z. On weighted regularity criteria for the axisymmetric Navier–Stokes equations. Appl. Math. Comput. 2017, 296, 18–22. [Google Scholar] [CrossRef]
- Zhang, Z. Remarks on the regularity criteria for the Navier–Stokes equations with axisymmetric data. Ann. Pol. Math. 2016, 117, 181–196. [Google Scholar] [CrossRef]
- Zhang, Z.; Ouyang, X.; Yang, X. Refined a priori estimates for the axisymmetric Navier–Stokes equations. J. Appl. Anal. Comput. 2017, 7, 554–558. [Google Scholar]
- Zhang, Z.; Wang, S. Weighted a priori estimates for the swirl component of the vorticity of the axisymmetric Navier–Stokes system. Appl. Math. Lett. 2020, 104, 106275. [Google Scholar] [CrossRef]
- Ladyžhenskaya, O.A. Unique global solvability of the three-dimensional Cauchy problem for the Navier–Stokes equations in the presence of axial symmetry. Zap. Naučn. Sem. Leningrad. Otdel. Math. Inst. Steklov. (LOMI) 1968, 7, 155–177. (In Russian) [Google Scholar]
- Ladyžhenskaya, O.A. The Mathematical Theory of Viscous Incompressible Flow, 2nd ed.; Translated from the Russian by Richard A. Silverman and John Chu; Mathematics and Its Applications; Gordon and Breach, Science Publishers: New York, NY, USA; London, UK; Paris, France, 1969; Volume 2. [Google Scholar]
- Serfati, P. Régularité stratifiée et équation d’Euler 3D à temps grand. C. R. Acad. Sci. Paris Sér. I Math. 1994, 318, 925–928. [Google Scholar]
- Moschandreou, T.E.; Afas, K.C. Compressible Navier–Stokes Equations in Cylindrical Passages and General Dynamics of Surfaces-(I)-Flow Structures and (II)-Analyzing Biomembranes under Static and Dynamic Conditions. Mathematics 2019, 7, 1060. [Google Scholar] [CrossRef]
- Moschandreou, T.E. A Method of Solving Compressible Navier Stokes Equations in Cylindrical Coordinates Using Geometric Algebra. Mathematics 2019, 7, 126. [Google Scholar] [CrossRef]
- Mahalov, A.; Titi, E.S.; Leibovich, S. Invariant helical subspaces for the Navier–Stokes equations. Arch. Ration. Mech. Anal. 1990, 112, 193–222. [Google Scholar] [CrossRef]
- Diego, C.G. Absence of Simple Hyperbolic Blow-Up for the Quasi-Geostrophic and Euler Equations. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1998; 61p. [Google Scholar]
- Chae, D.; Kim, N. Axisymmetric weak solutions of the 3-D Euler equations for incompressible fluid flows. Nonlinear Anal. 1997, 29, 1393–1404. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wang, Y. The Global Well-Posedness for Large Amplitude Smooth Solutions for 3D Incompressible Navier–Stokes and Euler Equations Based on a Class of Variant Spherical Coordinates. Mathematics 2020, 8, 1195. https://doi.org/10.3390/math8071195
Wang S, Wang Y. The Global Well-Posedness for Large Amplitude Smooth Solutions for 3D Incompressible Navier–Stokes and Euler Equations Based on a Class of Variant Spherical Coordinates. Mathematics. 2020; 8(7):1195. https://doi.org/10.3390/math8071195
Chicago/Turabian StyleWang, Shu, and Yongxin Wang. 2020. "The Global Well-Posedness for Large Amplitude Smooth Solutions for 3D Incompressible Navier–Stokes and Euler Equations Based on a Class of Variant Spherical Coordinates" Mathematics 8, no. 7: 1195. https://doi.org/10.3390/math8071195
APA StyleWang, S., & Wang, Y. (2020). The Global Well-Posedness for Large Amplitude Smooth Solutions for 3D Incompressible Navier–Stokes and Euler Equations Based on a Class of Variant Spherical Coordinates. Mathematics, 8(7), 1195. https://doi.org/10.3390/math8071195





