On Generalized Fourier’s and Fick’s Laws in Bio-Convection Flow of Magnetized Burgers’ Nanofluid Utilizing Motile Microorganisms
Abstract
1. Introduction
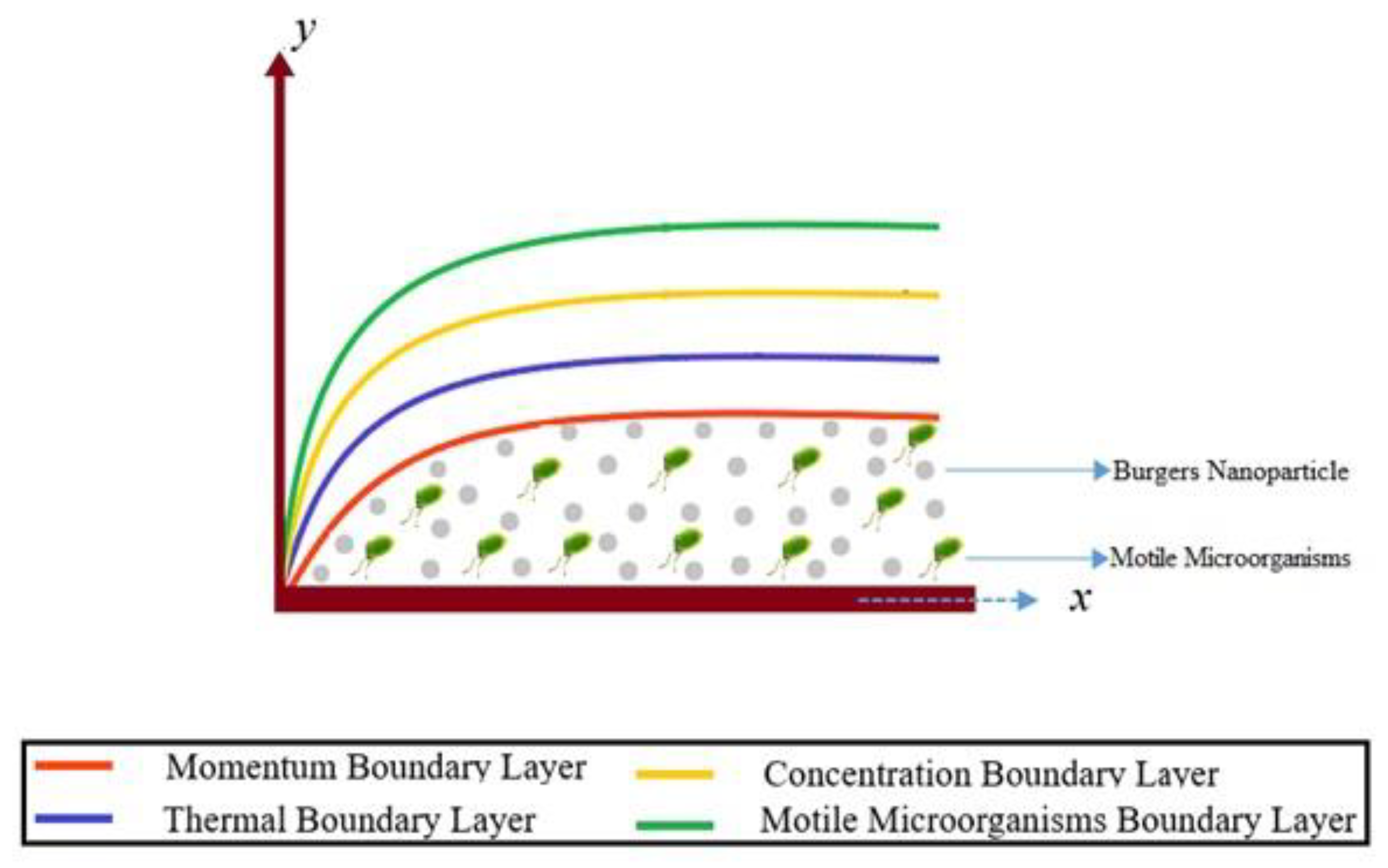
2. Mathematical Formulation
3. Numerical Approach
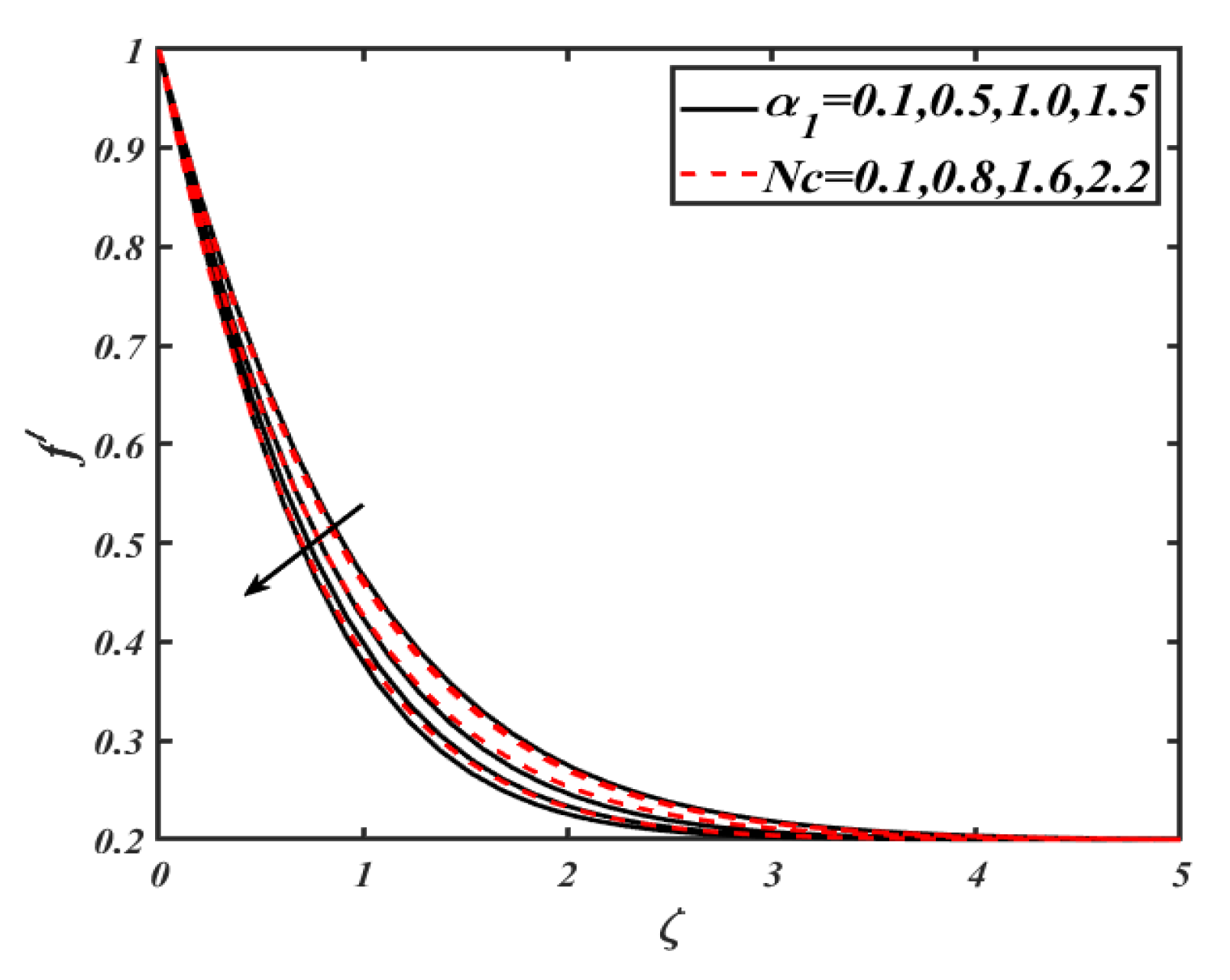
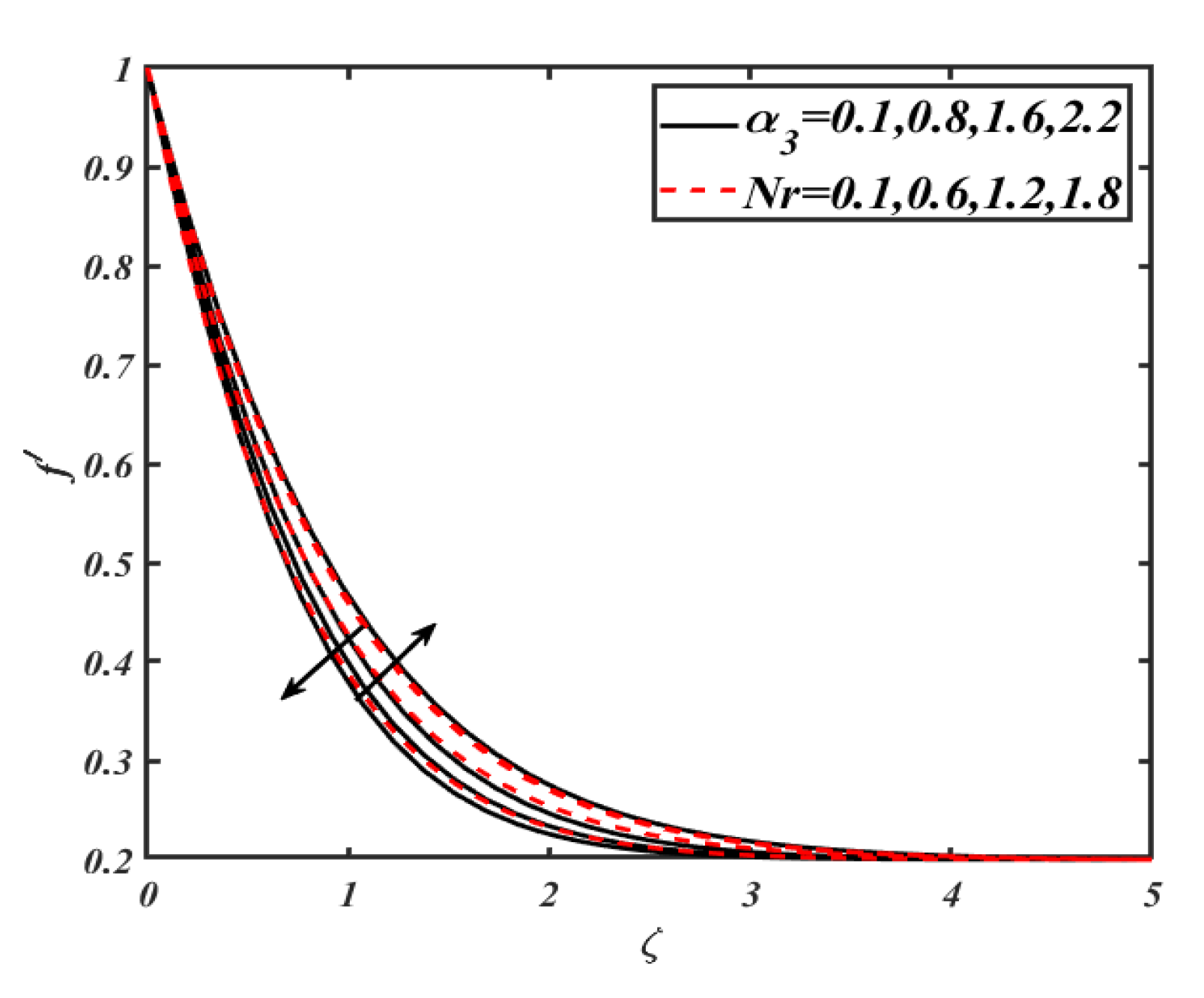
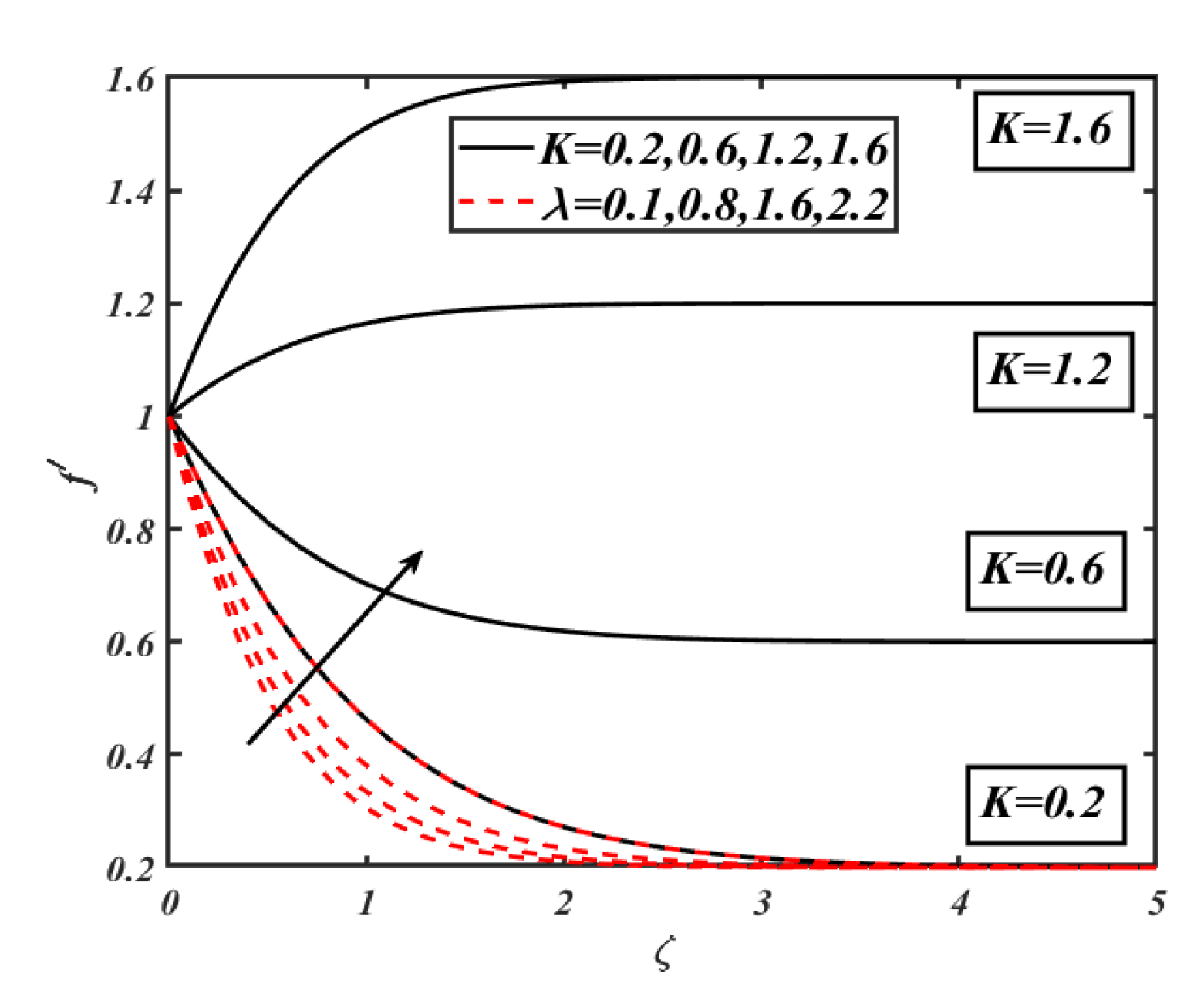
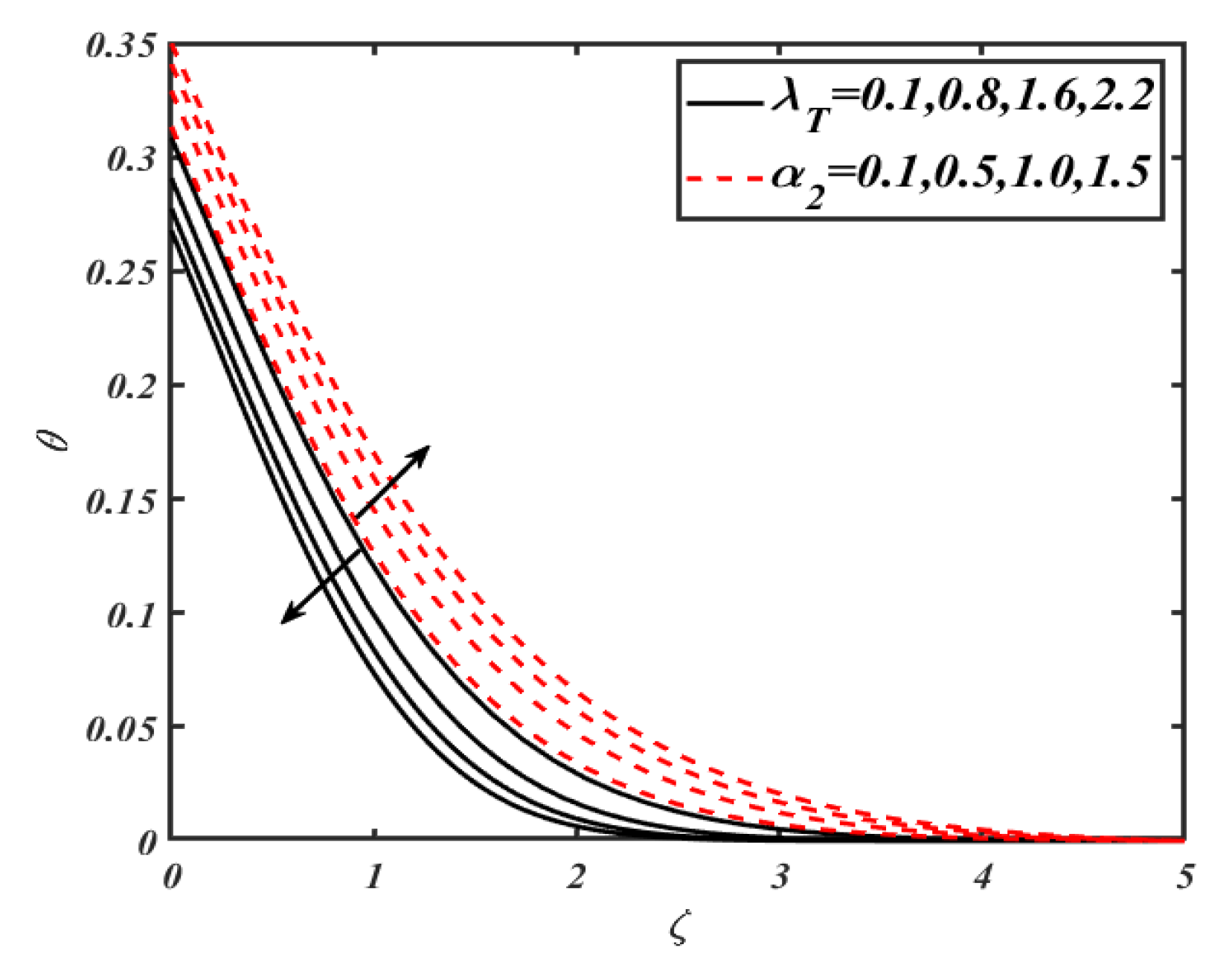
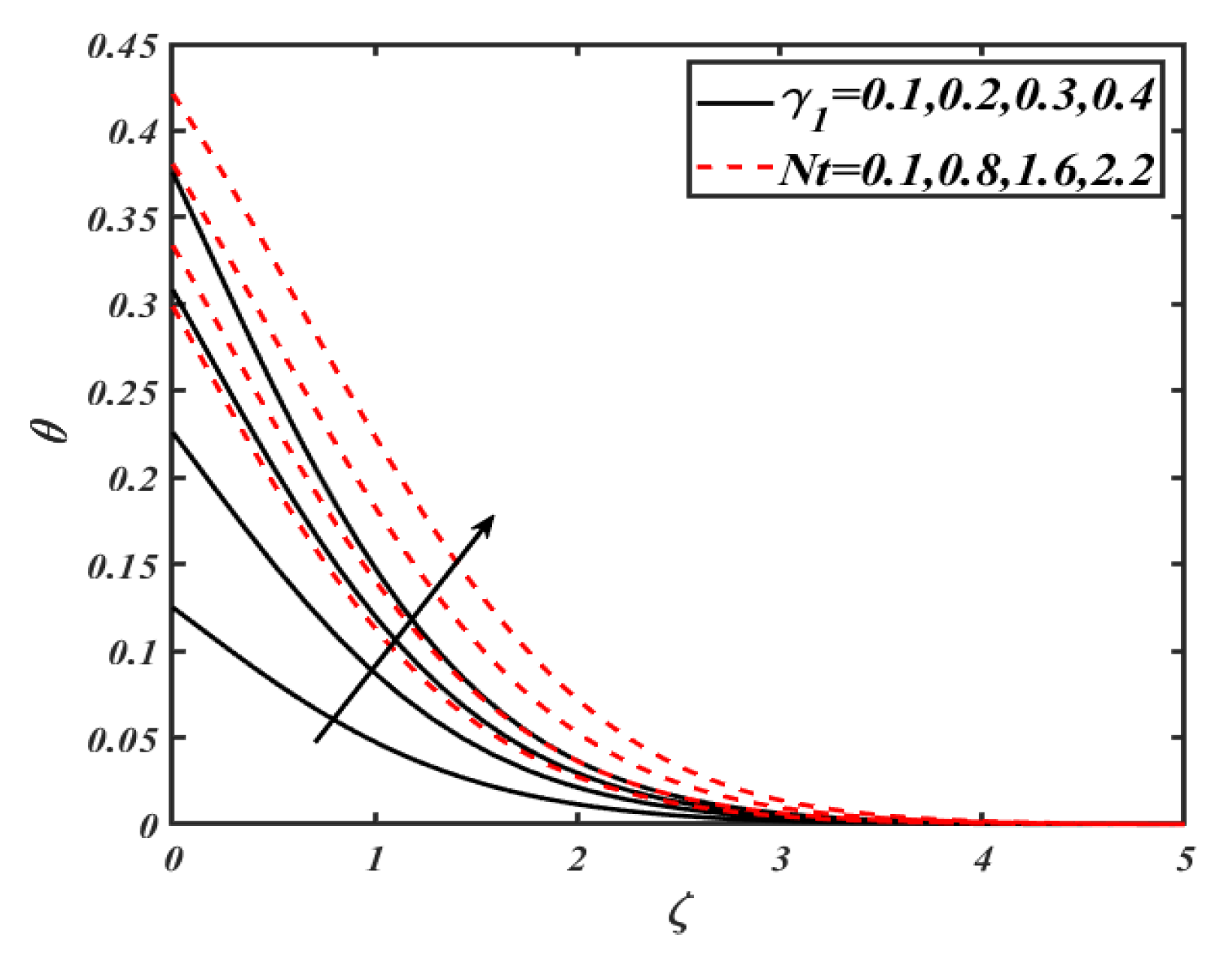
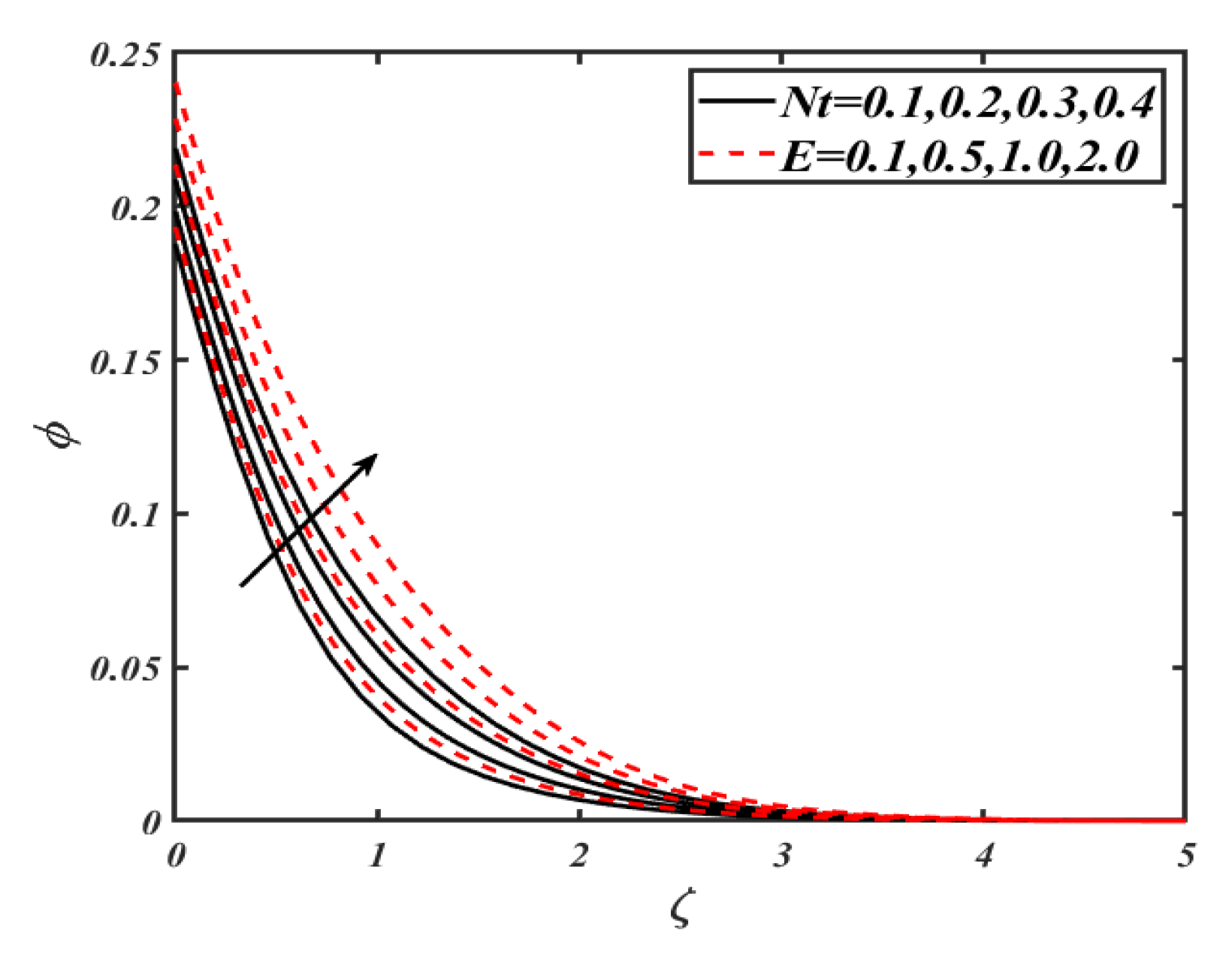
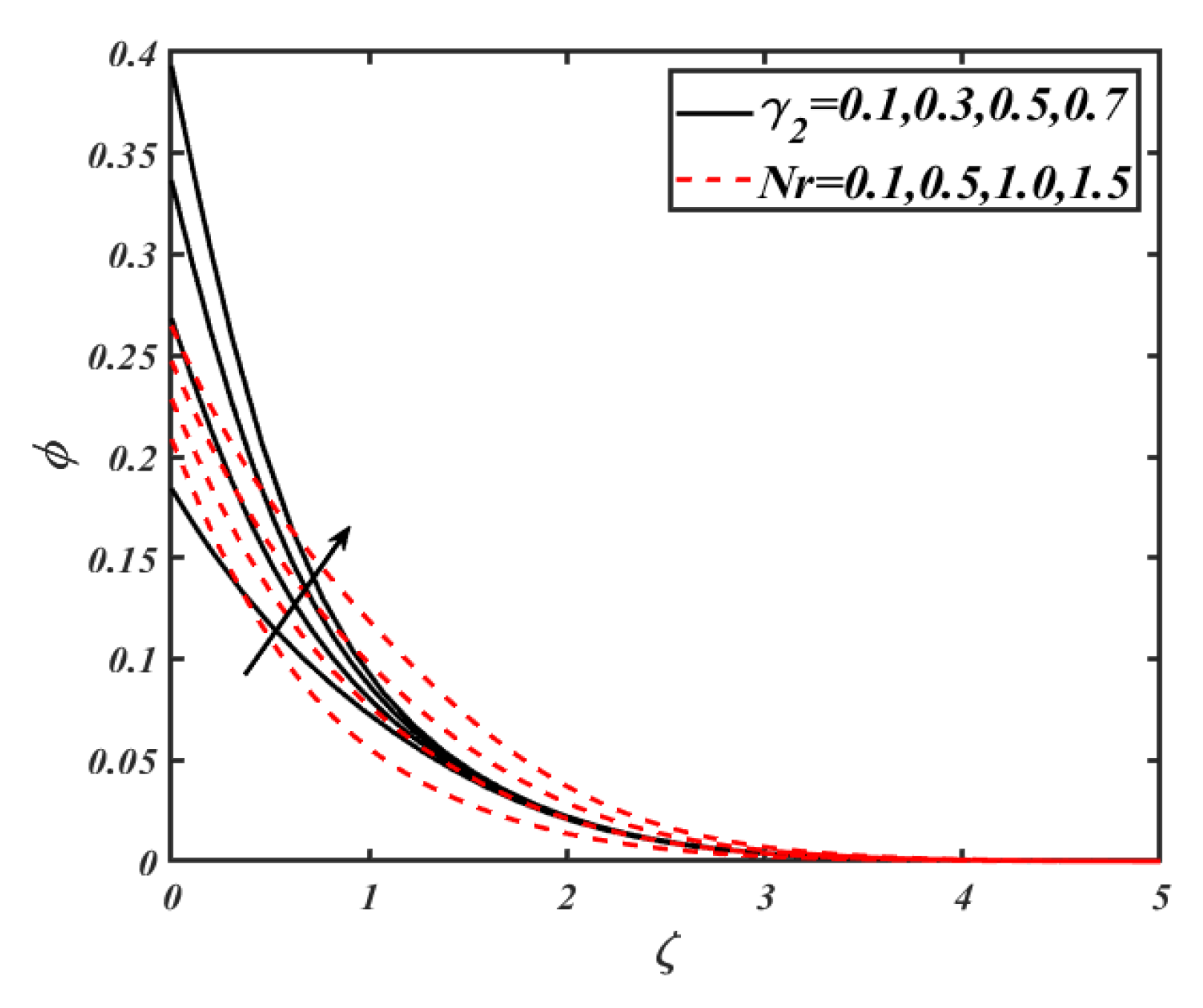
4. Results and Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles; FED 231/MD; ASME: New York, NY, USA, 1995; pp. 99–105. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Single phase nanofluids in fluid mechanics and their hydrodynamic linear stability analysis. Comput. Methods Programs Biomed. 2020, 187, 105171. [Google Scholar] [CrossRef]
- Ellahi, R.; Hussain, F.; Abbas, S.A.; Sarafraz, M.M.; Goodarzi, M.; Shadloo, M.S. Study of two-phase Newtonian nanofluid flow hybrid with Hafnium particles under the effects of slip. Inventions 2020, 5, 6. [Google Scholar] [CrossRef]
- Alamri, S.Z.; Ellahi, R.; Shehzad, N.; Zeeshan, A. Convective radiative plane Poiseuille flow of nanofluid through porous medium with slip: An application of Stefan blowing. J. Mol. Liq. 2019, 273, 292–304. [Google Scholar] [CrossRef]
- Khan, A.M.; Jamil, M.; Mia, M.; He, N.; Zhao, W.; Gong, L. Sustainability-based performance evaluation of hybrid nanofluid assisted machining. J. Clean. Prod. 2020, 257, 120541. [Google Scholar] [CrossRef]
- Irfan, M.; Farooq, M.A.; Iqra, T. A new computational technique design for EMHD nanofluid flow over a variable thickness surface with variable liquid characteristics. Front. Phys. 2020, 8, 66. [Google Scholar] [CrossRef]
- Reddy, S.R.R.; Reddy, P.B.A.; Rashad, A.M. Activation energy impact on chemically reacting Eyring--Powell nanofluid flow over a stretching cylinder. Arab. J. Sci. Eng. 2020, 45, 5227–5242. [Google Scholar] [CrossRef]
- Khan, S.U.; Tlili, I.; Waqas, H.; Imran, M. Effects of nonlinear thermal radiation and activation energy on modified second-grade nanofluid with Cattaneo-Christov expressions. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Alghamdi, M. On magnetohydrodynamic flow of viscoelastic nanofluids with homogeneous-heterogeneous reactions. Coatings 2020, 10, 55. [Google Scholar] [CrossRef]
- Uddin, S.; Mohamad, M.; Rahimi-Gorji, M.; Roslan, R.; Alarifi, I.M. Fractional electro-magneto transport of blood modeled with magnetic particles in cylindrical tube without singular kernel. Microsyst. Technol. 2020, 26, 405–414. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bhatti, M.M.; Sheikholeslami, M. Peristaltic propulsion of Jeffrey nanofluid with thermal radiation and chemical reaction effects. Inventions 2019, 4, 68. [Google Scholar] [CrossRef]
- Babazadeh, H.; Muhammad, T.; Shakeriaski, F.; Ramzan, M.; Hajizadeh, M.R. Nanomaterial between two plates which are squeezed with impose magnetic force. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Balankin, A.S.; Golmankhaneh, A.K.; Patiño-Ortiz, J.; Patiño-Ortiz, M. Noteworthy fractal features and transport properties of Cantor tartans. Phys. Lett. A 2018, 382, 1534–1539. [Google Scholar] [CrossRef]
- Niazmand, A.; Sola, J.F.; Alinejad, F.; Dehgolan, F.R. Investigation of mixed convection in a cylindrical lid driven cavity filled with water-Cu nanofluid. Inventions 2019, 4, 60. [Google Scholar] [CrossRef]
- Mondal, H.; Das, S.; Kundu, P.K. Influence of an inclined stretching cylinder over MHD mixed convective nanofluid flow due to chemical reaction and viscous dissipation. Heat Transf. 2020, 49, 2183–2193. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Michaelides, E.E. Study of Arrhenius activation energy on the thermo-bioconvection nanofluid flow over a Riga plate. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Abdulrazzaq, T.; Togun, H.; Goodarzi, M.; Kazi, S.N.; Ariffin, M.K.A.; Adam, N.M.; Hooman, K. Turbulent heat transfer and nanofluid flow in an annular cylinder with sudden reduction. J. Therm. Anal. Calorim. 2020, 141, 373–385. [Google Scholar] [CrossRef]
- Saeed, A.; Tassaddiq, A.; Khan, A.; Jawad, M.; Deebani, W.; Shah, Z.; Islam, S. Darcy-Forchheimer MHD hybrid nanofluid flow and heat transfer analysis over a porous stretching cylinder. Coatings 2020, 10, 391. [Google Scholar] [CrossRef]
- Souayeh, B.; Kumar, K.G.; Reddy, M.G.; Rani, S.; Hdhiri, N.; Alfannakh, H.; Rahimi-Gorji, M. Slip flow and radiative heat transfer behavior of Titanium alloy and ferromagnetic nanoparticles along with suspension of dusty fluid. J. Mol. Liq. 2019, 290, 111223. [Google Scholar] [CrossRef]
- Tlili, I.; Hamadneh, N.N.; Khan, W.A. Thermodynamic analysis of MHD heat and mass transfer of nanofluids past a static wedge with Navier slip and convective boundary conditions. Arab. J. Sci. Eng. 2019, 44, 1255–1267. [Google Scholar] [CrossRef]
- Farhangmehr, V.; Moghadasi, H.; Asiaei, S. A nanofluid MHD flow with heat and mass transfers over a sheet by nonlinear boundary conditions: Heat and mass transfers enhancement. J. Cent. South Univ. 2019, 26, 1205–1217. [Google Scholar] [CrossRef]
- Khan, M.; Irfan, M.; Khan, W.A. Impact of nonlinear thermal radiation and gyrotactic microorganisms on the Magneto-Burgers nanofluid. Int. J. Mech. Sci. 2017, 130, 375–382. [Google Scholar] [CrossRef]
- Khan, M.; Khan, W.A.; Alshomrani, A.S. Non-linear radiative flow of three-dimensional Burgers nanofluid with new mass flux effect. Int. J. Heat Mass Transf. 2016, 101, 570–576. [Google Scholar] [CrossRef]
- Khan, M.; Khan, W.A. Forced convection analysis for generalized Burgers nanofluid flow over a stretching sheet. AIP Adv. 2015, 5, 107138. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Shehzad, S.A.; Alsaedi, A. Mixed convection flow of a Burgers nanofluid in the presence of stratifications and heat generation/absorption. Eur. Phys. J. Plus 2016, 131, 253. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. On model for flow of Burgers nanofluid with Cattaneo—Christov double diffusion. Chin. J. Phys. 2017, 55, 916–929. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Shehzad, S.A.; Alsaedi, A. On model of Burgers fluid subject to magneto nanoparticles and convective conditions. J. Mol. Liq. 2016, 222, 181–187. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Yang, Z.; Awais, M.; Nawaz, M.; Hayat, T. Generalized magnetic field effects in Burgers’ nanofluid model. PLoS ONE 2017, 12, e0168923. [Google Scholar] [CrossRef]
- Iqbal, Z.; Khan, M.; Ahmed, J.; Hafeez, A. Thermal energy transport in Burgers nanofluid flow featuring the Cattaneo-Christov double diffusion theory. Appl. Nanosci. 2020. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Avramenko, A.A. Effect of small particles on this stability of bioconvection in a suspension of gyrotactic microorganisms in a layer of finite depth. Int. Commun. Heat Mass Transf. 2004, 31, 1–10. [Google Scholar] [CrossRef]
- Ghorai, S.; Hill, N.A. Wavelengths of gyrotactic plumes in bioconvection. Bull. Math. Biol. 2000, 62, 429–450. [Google Scholar] [CrossRef] [PubMed]
- Atif, S.M.; Hussain, S.; Sagheer, M. Magnetohydrodynamic stratified bioconvective flow of micropolar nanofluid due to gyrotactic microorganisms. AIP Adv. 2019, 9, 025208. [Google Scholar] [CrossRef]
- Khan, S.U.; Waqas, H.; Bhatti, M.M.; Imran, M. Bioconvection in the rheology of magnetized couple stress nanofluid featuring activation energy and Wu’s slip. J. Non Equilib. Thermodyn. 2020, 45, 81–95. [Google Scholar] [CrossRef]
- Amirsom, N.A.; Uddin, M.J.; Basir, M.F.M.; Ismail, A.I.M.; Beg, O.A.; Kadir, A. Three-dimensional bioconvection nanofluid flow from a bi-axial stretching sheet with anisotropic slip. Sains Malays. 2019, 48, 1137–1149. [Google Scholar] [CrossRef]
- Zhang, T.; Khan, S.U.; Imran, M.; Tlili, I.; Waqas, H.; Ali, N. Activation energy and thermal radiation aspects in bioconvection flow of rate-type nanoparticles configured by a stretching/shrinking disk. J. Energy Resour. Technol. 2020, 142, 112102. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Rashidi, M.M. Gegenbauer wavelets collocation-based scheme to explore the solution of free bio-convection of nanofluid in 3D nearby stagnation point. Neural Comput. Appl. 2019, 31, 8003–8019. [Google Scholar] [CrossRef]
- Basir, M.F.M.; Uddin, M.J.; Ismail, A.I.M. Scaling group analysis of mixed bioconvective flow in nanofluid with presence of slips, MHD and chemical reactions. Preprints 2018. [Google Scholar] [CrossRef]
- Muhammad, T.; Alamri, S.Z.; Waqas, H.; Habib, D.; Ellahi, R. Bioconvection flow of magnetized Carreau nanofluid under the influence of slip over a wedge with motile microorganisms. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Mansour, M.A.; Rashad, A.M.; Mallikarjuna, B.; Hussein, A.K.; Aichouni, M.; Kolsi, L. MHD mixed bioconvection in a square porous cavity filled by gyrotactic microorganisms. Int. J. Heat Technol. 2019, 37, 433–445. [Google Scholar] [CrossRef]
- Li, Y.; Waqas, H.; Imran, M.; Farooq, U.; Mallawi, F.; Tlili, I. A numerical exploration of modified second-grade nanofluid with motile microorganisms, thermal radiation, and Wu’s slip. Symmetry 2020, 12, 393. [Google Scholar] [CrossRef]
- Waqas, H.; Imran, M.; Muhammad, T.; Sait, S.M.; Ellahi, R. Numerical investigation on bioconvection flow of Oldroyd B nanofluid with nonlinear thermal radiation and motile microorganisms over rotating disk. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Imran, M.; Bhatti, M.M. Thermally developed Falkner-Skan bioconvection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno’s nanofluid model. Phys. Scr. 2019, 94, 115304. [Google Scholar] [CrossRef]
- Alwatban, A.M.; Khan, S.U.; Waqas, H.; Tlili, I. Interaction of Wu’s slip features in bioconvection of Eyring Powell nanoparticles with activation energy. Processes 2019, 7, 859. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Hassan, M.; Bhatti, M.M.; Imran, M. Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. J. Mol. Liq. 2019, 291, 111231. [Google Scholar] [CrossRef]
- Waqas, H.; Shehzad, S.A.; Khan, S.U.; Imran, M. Novel numerical computations on flow of nanoparticles in porous rotating disk with multiple slip effects and microorganisms. J. Nanofluids 2019, 8, 1423–1432. [Google Scholar] [CrossRef]
- Wang, Y.; Waqas, H.; Tahir, M.; Imran, M.; Jung, C.Y. Effective Prandtl aspects on bio-convective thermally developed magnetized tangent hyperbolic nanoliquid with gyrotactic microorganisms and second order velocity slip. IEEE Access 2019, 7, 130008–130023. [Google Scholar] [CrossRef]
- Tlili, I.; Waqas, H.; Almaneea, A.; Khan, S.U.; Imran, M. Activation energy and second order slip in bioconvection of Oldroyd-B nanofluid over a stretching cylinder: A proposed mathematical model. Processes 2019, 7, 914. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Jang, T.S. An efficient numerical scheme for analyzing bioconvection in von-Kármán flow of third-grade nanofluid with motile microorganisms. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Shahid, A.; Huang, H.; Bhatti, M.M.; Zhang, L.; Ellahi, R. Numerical investigation on the swimming of gyrotactic microorganisms in nanofluids through porous medium over a stretched surface. Mathematics 2020, 8, 380. [Google Scholar] [CrossRef]
- Asma, M.; Othman, W.A.M.; Muhammad, T. Numerical study for Darcy-Forchheimer flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius activation energy. Mathematics 2019, 7, 921. [Google Scholar] [CrossRef]
- Zhu, J.; Xu, Y.; Han, X. A non-Newtonian magnetohydrodynamics (MHD) nanofluid flow and heat transfer with nonlinear slip and temperature jump. Mathematics 2019, 7, 1199. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Squeezed hybrid nanofluid flow over a permeable sensor surface. Mathematics 2020, 8, 898. [Google Scholar] [CrossRef]



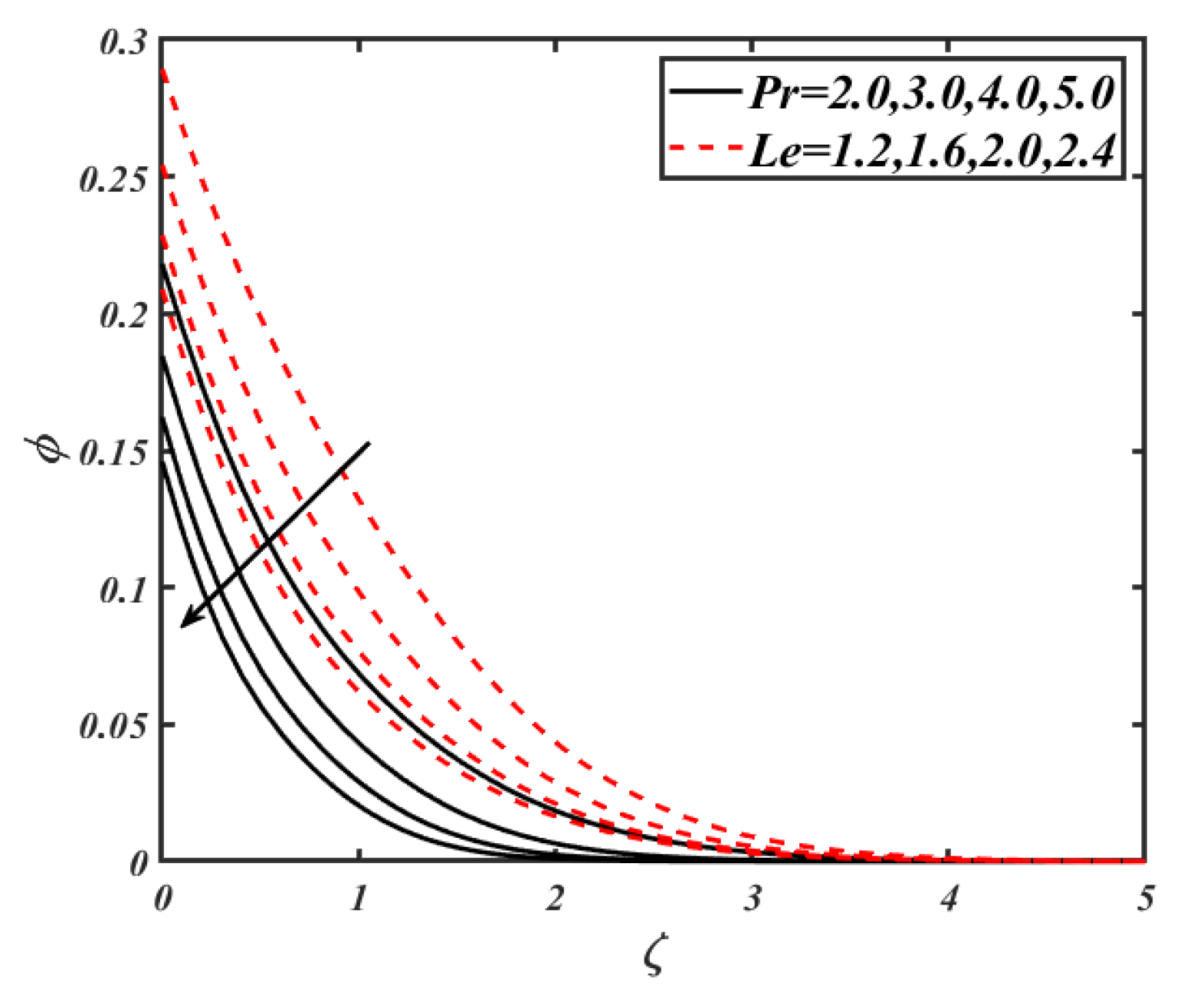
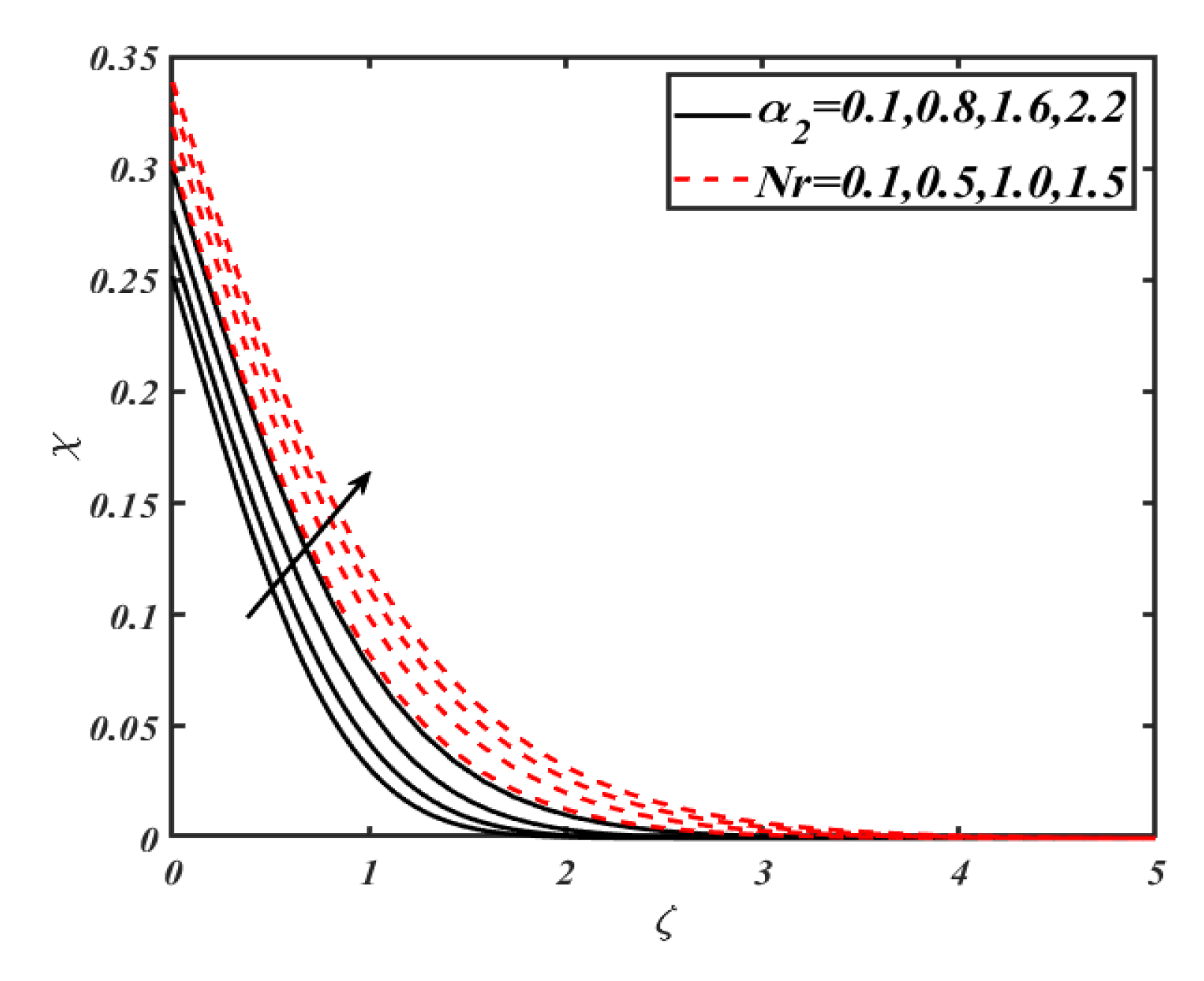

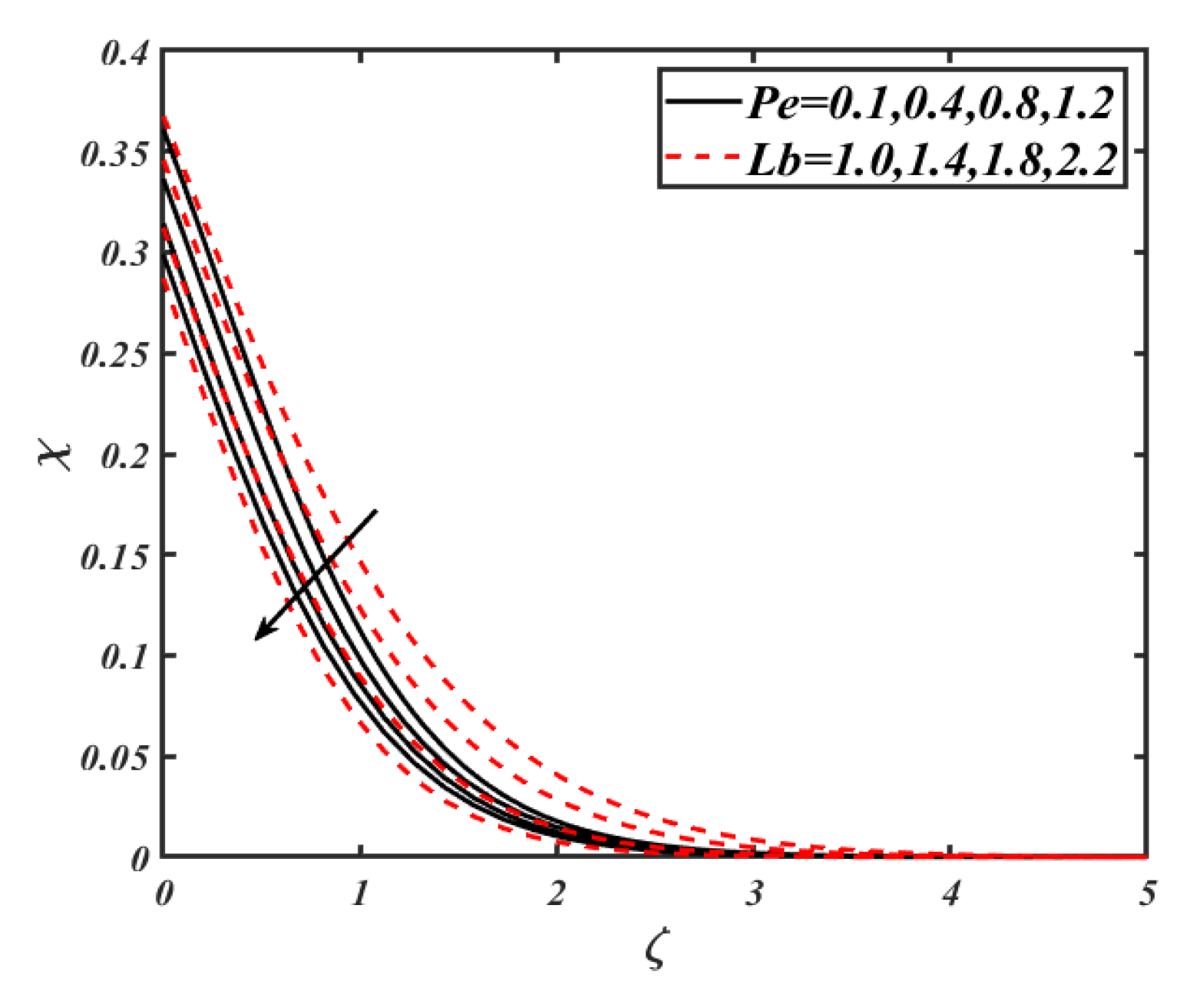
| 0.1 0.5 1.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.2867 0.9398 1.0320 |
| 0.4 | 0.2 0.5 0.8 | 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.8569 0.6030 0.2641 |
| 0.4 | 0.1 | 0.2 0.8 1.6 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.9142 0.8803 0.8365 |
| 0.4 | 0.1 | 0.1 | 0.2 1.0 2.0 | 0.1 | 0.2 | 0.2 | 0.2 | 0.9203 0.9239 0.9284 |
| 0.4 | 0.1 | 0.1 | 0.1 | 0.2 1.0 2.0 | 0.2 | 0.2 | 0.2 | 0.9204 0.9242 0.9291 |
| 0.4 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 0.5 1.0 | 0.2 | 0.2 | 0.9158 0.9112 0.9591 |
| 0.4 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.1 0.5 1.0 | 0.2 | 0.9090 0.9506 0.9991 |
| 0.4 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | 0.1 0.5 1.0 | 0.9463 0.9112 0.8681 |
| 0.1 0.5 1.0 | 0.1 | 0.3 | 0.2 | 0.4 | 0.3 | 0.2060 0.2048 0.2035 |
| 0.4 | 0.2 0.5 0.8 | 0.3 | 0.2 | 0.4 | 0.3 | 0.2068 0.2114 0.2149 |
| 0.4 | 0.1 | 0.1 0.4 0.8 | 0.2 | 0.4 | 0.3 | 0.2059 0.2026 0.1982 |
| 0.4 | 0.1 | 0.3 | 0.1 0.4 0.8 | 0.4 | 0.3 | 0.2078 0.2033 0.1968 |
| 0.4 | 0.1 | 0.3 | 0.2 | 0.1 0.8 1.6 | 0.3 | 0.3130 0.1961 0.1824 |
| 0.4 | 0.1 | 0.3 | 0.2 | 0.4 | 0.1 0.5 1.0 | 0.0871 0.2791 0.3787 |
| 0.1 0.5 1.0 | 0.1 | 0.3 | 0.2 | 0.4 | 0.3 | 0.2303 0.2295 0.2287 |
| 0.4 | 0.2 0.5 0.8 | 0.3 | 0.2 | 0.4 | 0.3 | 0.2310 0.2377 0.2346 |
| 0.4 | 0.1 | 0.1 0.4 0.8 | 0.2 | 0.4 | 0.3 | 0.2087 0.2399 0.2451 |
| 0.4 | 0.1 | 0.3 | 0.1 0.4 0.8 | 0.4 | 0.3 | 0.2424 0.2236 0.2033 |
| 0.4 | 0.1 | 0.3 | 0.2 | 0.1 0.8 1.6 | 0.3 | 0.2278 0.2316 0.2346 |
| 0.4 | 0.1 | 0.3 | 0.2 | 0.4 | 0.1 0.8 1.6 | 0.0860 0.4802 0.7137 |
| 0.1 0.5 1.0 | 0.1 | 0.1 | 0.1 | 0.3 | 0.1 | 0.1 | 0.2786 0.2771 0.2755 |
| 0.4 | 0.2 0.5 0.8 | 0.1 | 0.1 | 0.3 | 0.1 | 0.1 | 0.2796 0.2855 0.2907 |
| 0.4 | 0.1 | 0.2 0.8 1.6 | 0.1 | 0.3 | 0.1 | 0.1 | 0.2776 0.2781 0.2788 |
| 0.4 | 0.1 | 0.1 | 0.2 1.0 2.0 | 0.3 | 0.1 | 0.1 | 0.2775 0.2774 0.2773 |
| 0.4 | 0.1 | 0.1 | 0.1 | 0.1 0.8 1.6 | 0.1 | 0.1 | 0.0900 0.4251 0.5793 |
| 0.4 | 0.1 | 0.1 | 0.1 | 0.3 | 0.2 0.5 1.0 | 0.1 | 0.2757 0.2565 0.2265 |
| 0.4 | 0.1 | 0.1 | 0.1 | 0.3 | 0.1 | 1.0 2.0 3.0 | 0.2373 0.2973 0.3184 |
| Pr | Iqbal et al. [30] | Present Results |
|---|---|---|
| 0.7 | 0.45312 | 0.45312 |
| 2.0 | 0.90894 | 0.90894 |
| 7.0 | 1.88986 | 1.88985 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshomrani, A.S. On Generalized Fourier’s and Fick’s Laws in Bio-Convection Flow of Magnetized Burgers’ Nanofluid Utilizing Motile Microorganisms. Mathematics 2020, 8, 1186. https://doi.org/10.3390/math8071186
Alshomrani AS. On Generalized Fourier’s and Fick’s Laws in Bio-Convection Flow of Magnetized Burgers’ Nanofluid Utilizing Motile Microorganisms. Mathematics. 2020; 8(7):1186. https://doi.org/10.3390/math8071186
Chicago/Turabian StyleAlshomrani, Ali Saleh. 2020. "On Generalized Fourier’s and Fick’s Laws in Bio-Convection Flow of Magnetized Burgers’ Nanofluid Utilizing Motile Microorganisms" Mathematics 8, no. 7: 1186. https://doi.org/10.3390/math8071186
APA StyleAlshomrani, A. S. (2020). On Generalized Fourier’s and Fick’s Laws in Bio-Convection Flow of Magnetized Burgers’ Nanofluid Utilizing Motile Microorganisms. Mathematics, 8(7), 1186. https://doi.org/10.3390/math8071186




