Abstract
The minimum weight vertex independent dominating set (MWVIDS) problem is an important version of the minimum independent dominating set. The MWVIDS problem has a number of applications in many fields. However, the MWVIDS problem is known to be NP-hard and thus computationally challenging. In this work, we present the improved memetic algorithm called MSSAS for solving the MWVIDS problem. The proposed MSSAS algorithm combines probability-based dynamic optimization (PDO) (to generate good and diverse offspring solutions by assembling elements of existing good solutions) as well as a local search phase named C_LS (to seek high-quality local optima by combining the idea of constrained-based two-level configuration checking strategy and tabu mechanism). The extensive results on popular DIMACS and BHOLIB benchmarks demonstrate that MSSAS competes favorably with the state-of-the-art algorithms. In addition, we analyze the benefits of the newly raised components including two above proposed ideas with our memetic framework. It is worth mentioning that the combination of both components has excellent effects for the MWVIDS problem.
1. Introduction
Given an undirected graph G, an independent dominating set (IDS) is a subset of vertices D such that every vertex that is not in D is adjacent to a vertex that is in D and there are no pairs of adjacent vertices in D. The minimum independent dominating set (MIDS) problem consists in finding an independent dominating set with the minimum size. There are many variants of MIDS, consisting of minimum weight independent dominating set (MWIDS), minimum weight vertex independent dominating set (MWVIDS) and minimum weight edge independent dominating set (MWEIDS). Among these different versions of MIDS, MWIDS considers both vertex and edge weights, while MWEIDS only considers the weight of edge. Similarly, MWVIDS only considers vertex weight and ignores edge weight, i.e., each vertex has a positive weight. The aim of MWVIDS is to identify the minimum weight of IDS in the given graph. To greatly illustrate these problems, an example is shown in Figure 1. MIDS and its variants are NP-hard (non-deterministic polynomial hard) problems [1], which means that, there are no polynomial-time algorithms for these problems unless P = NP.
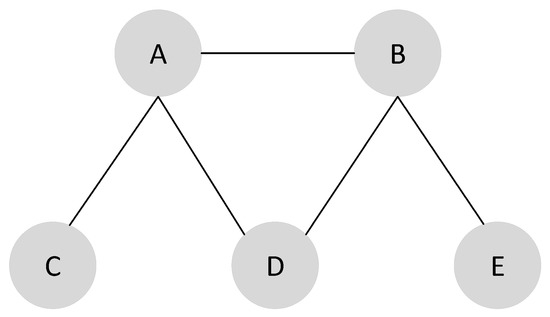
Figure 1.
An illustration of the relation between four IDS related problems. Given a graph where : (a) assuming that the weight values of all vertices is 1, then is one MIDS solution of this given graph; (b) assuming each vertex has weight value such that , , , , and each edge has a weight value such that , , , , , then the one MWIDS solution is and its total weight is 11; (c) if the weight value of each vertex has still followed by (b) and each edge’s weight is 0, then the MWVIDS solution is with the total weight value of 4; and (d) when only considering the weight of edges, the solution MWEIDS value is and the sum of its weight value is 7.
Its extended versions are combinatorial optimization problems, which are widely used in many fields, such as wireless network [2], warehouse location [3] and virtual machine integration [4]. In practice, the majority of them have to consider vertex weights, which belongs to MWVIDS. In this way, we choose MWVIDS as the object of our study because of its great significance.
An important problem in wireless sensor networks [5,6] is the deployment of the sink vertex. The problem is to find the appropriate location of the sink vertex to minimize the network maintenance cost. The sensor vertex is used to monitor the situation in the surrounding area, while the sink vertex is responsible for receiving and processing information from the surrounding sensor vertices. If the network is modeled as a graph, the maintenance cost of the vertex can be regarded as the vertex weight, and the cost of communication between vertices is considered as the weight of the edge. In large-scale wireless sensor network environment nowadays, multi-sink vertex [7] is adopted to improve the accuracy and efficiency of information collection; however, compared with the traditional single sink vertex, it also increases the cost of network maintenance. The maintenance cost of the vertex is far greater than the communication cost between vertices, so this problem can be regarded as MWVIDS.
The layout of the city express station [8] can also make use of the MWVIDS idea. Each city will set up a courier station, responsible for distributing delivery into the surrounding area. How to arrange the courier station reasonably is the key to achieve high efficiency and save money. When modeling the delivery process of a city, the cost of express warehouse management is regarded as vertex weight and the cost of express distribution is regarded as edge weight. Compared with the express delivery process, the warehouse management cost is much more expensive; in other words, the edge weight can be ignored, so the essence of this problem is also to find MWVIDS to some degree.
For MIDS and its variants, many algorithms have been proposed to solve the related problems. A branch-and-reduce MIDS algorithm based on some well-designed branching rules was offered by Gaspers and Liedloff [9], as well as it can reach a very close lower bound on running time. According to Wang et al. [10], a greedy randomized adaptive search procedure (GRASP) combined with tabu strategy was proposed for MIDS, which can find a better solution based on the information of path cost. Subsequently, Wang et al. introduced a tabu search-based memetic MIDS algorithm [11], in which tabu method was used to prevent cycling problems and a repairing-based crossover strategy was added to compensate for infeasible solutions. For MWIDS, Davidson et al. [12] built three different integer linear programming (ILP) models. At the same time, they put forward two different greedy heuristics, where one does not consider the weight of the edge and the other considers the weight of the edge. A biased random key genetic algorithm is proposed for MWIDS [13]. The decoder in the algorithm can transform any real value vector into an effective solution to the problem. Recently, a local search algorithm with a reinforcement learning-based repair procedure was designed [14], which combines the idea of reinforcement learning, local search and repair process to improve the solution of the MWIDS.
For MWVIDS, we designed a memetic algorithm to solve it. Memetic algorithm (MA) is formally proposed in [15] and used to solve the TSP problem. The framework of memetic algorithm is described as follows: the outstanding offspring is selected from the parent solutions through performing a series of optimizations to obtain a higher quality solution. Recently, memetic algorithms have been widely used in optimization problems [16,17,18,19]. For example, the dynamic optimization problems are proposed to combine an adaptive hill climbing method as the local search technique [16]. An improved MA for the partial vertex cover problem is designed [17], in which adaptive mutation and crossover strategies skip local optima. A MA for solving the problem of graph coloring is provided in [18], where a distance-and-quality based replacement criterion is used for pool updating. In [11], a tabu search-based MA is proposed to solve MIDS, in which a repairing-based crossover strategy is added to compensate for the infeasible solutions. A MA is proposed for a vehicle routing problem in [19], which uses different local search algorithms to solve it.
The contributions of the work are highlighted as follows.
Firstly, we propose an improved memetic algorithm called sequential self-adaptive search (MSSAS) for solving the MWVIDS problem, which explores the synergy between the process of local search process (C_LS) and a combination operator (PDO). The algorithm also integrates the construction of initial solutions generated by a kind of greedy randomized construction heuristic and an effective pool updating procedure.
Secondly, in the stage of local search improvement, we adapt the constrained-CC strategy for MWVIDS problem based on CC [20] to prevent from the cycling problem. In addition, each choice of removal vertices is accompanied by tabu restriction [21,22] to refrain from exploring visited solutions. Furthermore, our scoring function takes the frequency of vertices into consideration for searching for high-quality solutions. With strategies above, we get an improved vertex selection strategy for evaluating which vertex to be added or removed in this process. Then, we develop a procedure called C_LS which combines constrained-based CC, scoring function and tabu strategy with local search.
Thirdly, we propose a combination operator called probability-based dynamic optimization (PDO) to generate offspring solutions by combining vertices of existing good solutions. The PDO process is accompanied by a pool updating dynamically to maintain a space of optimal solutions. In this way, the diversity of our solutions would be effectively increased.
Finally, we carried out extensive experiments to evaluate the performance of our proposed MSSAS algorithm on two benchmarks DIMACS [23] and BHOLIB [24]. The results show that MSSAS performs better than competitors for almost all instances.
The rest of the paper is organized as follows. Some definitions and notations are introduced in Section 2. The general framework of our algorithm is proposed in Section 3.1. The construction phase is described in Section 3.2. Then, we put forward local search procedure in Section 3.3. We elaborate the process of probability-based dynamic optimization (PDO) in Section 3.4. After that, we recommend our pool updating strategy in Section 3.5. In Section 4, our experiment results compared with two competitors are displayed and analyzed. Finally, the conclusions and acknowledgment are shown.
2. Preliminaries
At first, we list some necessary notations for MWVIDS. An undirected graph comprises a vertex set of n vertices together with a set of m edges, where each edge connects two vertices u and v, and these two vertices are called the endpoints of edge e. If there is an edge between two vertices, these two vertices are defined as neighbors. The distance between two vertices u and v is expressed as , which means the number of edges in the shortest path from u to v. For a vertex v, we define its ith level neighborhood as . We use to denote a collection of vertices with = 1, i.e., . In addition, . For a broader definition, we define as an assemble of neighbors of vertices in S, where . For a vertex set , a vertex v is dominated by if: (1) ; and (2) , but there exists with .
A dominating set of G is a subset such that every vertex in G either belongs to D or is adjacent to a vertex in D, while an independent set of G is a subset where no two vertices in are adjacent. Thus, a subset of V is called as an independent dominating set, if is both a dominating set and an independent set. In a graph G, when each vertex v is associated with a positive weight , G is called an undirected weight graph. The task of minimum weight vertex independent dominating set (MWVIDS) problem is to find an independent dominating set , which minimizes the total weight of vertices in .
3. The Improved Memetic Algorithm for MWVIDS
3.1. Discussion of the Capabilities of Some Previous Evolutionary-Based Metaheuristics
Recently, there are various evolutionary-based metaheuristics to solve some hard optimization problems. We can learn from the paper [25] that, to reduce the amount of data, it is an efficient idea to choose swarm intelligence (SI) for feature selection process of data. This is proved as a technique for solving NP-hard computational problems. In addition, a multiple swarm intelligence optimization algorithm is used for effectively addressing the wind speed data, obtaining an optimal forecasting performance in paper [26]. While in paper [27] the particle swarm optimization (PSO) algorithm and the ant colony optimization (ACO) method act as the representatives of the SI approach. Afterwards, the proposed technique SCH-SpecPSO justifies the data communication for making dynamic network handover decisions through machine learning methods in [28]. The usage of bio-inspired swarm intelligence provides more ideas for robust communication networks. When it comes to the question of truck scheduling at cross-docking terminals, on the one hand, it is proved efficient to combine the strong mutation, which is dedicated to altering solutions in searching process, with the weak mutation, which has little ground of concrete strategies in [29]. On the other hand, a novel delayed start parallel evolutionary algorithm is proposed in paper [30], which executes separate evolutionary algorithms exchanging the promising solutions for an excellent result. The memetic algorithm, which is introduced below, is very suitable for our problem. Thus, we choose MAs as our framework.
3.2. General Approach
In our paper, we propose an algorithm for MWVIDS based on MA. Memetic algorithms (MAs) are hybrid search methods that combine the population-based search framework and local search framework. In the context of combinatorial optimization, Cowling et al. introduced the term “hyperheuristic” as a strategy that views the process of searching as an evolution, which needs to make choices which elements could be added in the result set [31]. In this way, we consider population-based search more as a container for our search with better performance. The basic implementation of initial construct is memoryless, since computations in a construct iteration do not make use of information collected in previous iterations. The idea of population-based search is based on memory structures, such as path relinking [32], which is an intensification strategy that can be applied to introduce memory structures to solution construction [33,34].
Generally speaking, MAs maintain a search space of candidate solutions, make great use of solutions and explore better components of solutions step by step with designed operators such as combination and improvement. In addition, it is always followed with an evaluation function for choosing suitable components. We put forward our sequential self-adaptive search called MSSAS, which is a constantly sequential process with an evolving solution. In detail, our improvement process is a sequential iteration by combing probability-based dynamic optimization namely PDO which works as a constructor to generate superior solution at a particular rate as well as a local search phase to seek high-quality local optima with ideas of constrained-based CC and tabu mechanism. With the group of combination operator and improvement operator taking into account the solution structure, our algorithm definitely achieves a high performance in quality and diversity compared with other algorithms.
First, we present the general framework of our algorithm in Algorithm 1 as follows.
| Algorithm 1: MSSAS(G) |
 |
In the beginning, the algorithm starts with an initial population set P. In our work, the size of P is set to 10. All of the elite solutions are generated by the construct procedure, which is a greedy randomized construction heuristic (Line 3) and the following improved function local search (Line 4). In this loop (Line 2–7), with times, we generate an initial population set P. During each iteration, we add the local best solution into P (Line 5), along with updating the global best solution (Line 6–7). Afterwards, two solutions are randomly selected from the P, and then recombined by the PDO, which is described in Section 3.4 to generate a new offspring solution (Lines 8–9). The loop on Lines 10–16 persistently executes until the total time of the process reaches a given time limit. By using the local search process to improve the solution, we would obtain a local best solution . If is better than , then should be updated accordingly (Lines 12–13). Meanwhile, the algorithm uses to update the population P (Line 14). At the end of loop, we use PDO like a constructor to build a new initial solution by modifying the structure of solutions provided by a random solution from P and when the local search procedure finds a better solution than . Otherwise, the PDO process will use two random solutions and from population P as the input parameters. This new generated solution in the current loop will be the inception of the next local search repeatedly for better performance.
3.3. Construction Phase
The construction phase is similar to the semi-greedy heuristic proposed by Hart and Shogan [35]. For implementing this phase, we constantly maintain the candidate set with a particular order called restricted candidate list (RCL), which is measured by the benefit of adding the next vertex. During each selection process, we choose to pick vertices with more benefits in RCL list for better solution composition.
In this section, we propose the covering cardinality to measure which vertex will be picked as the next element. For and a current candidate solution , the covering cardinality is defined as the number of vertices not yet dominated by that will become domination if is added into . Meanwhile, each vertex has a property, i.e., a ratio = / between its weight and covering cardinality. Obviously, a vertex with a smaller value of is more likely to have more neighbors, with a lower weight value.
We present the pseudo-code of the construction phase in Algorithm 2. At first, the algorithm initializes the candidate list L, covering cardinality and ratio accordingly (Line 1). During each loop of Lines 2–8, the algorithm adds one vertex into , until becomes an independent dominating set. The minimum and maximum greedy function values of the candidate vertices are computed (Lines 3–4), respectively. The restricted candidate list (RCL), formed by all candidate vertices whose greedy function value is less than or equal to + , is built (Line 5), where is a real-valued parameter between 0 and 1. A vertex e is chosen at random from the RCL (Line 6) and then is added to (Line 7). At the end of each loop (Line 8), the covering cardinalities are recomputed and the greedy function values are updated for all candidate vertices for the next iteration.
| Algorithm 2: Construct() |
 |
3.4. Local Search Procedure
Local search shows great performance on seeking good solutions. By exploring the neighborhood structure, the searching process is accomplished by allowing one vertex to move from one solution to a better one intelligently. Based on the idea that better neighboring solutions are usually accepted, while much worse neighboring solutions are accepted with a low probability. Especially, we combine local search process with a corresponding population solution pool which acts as a container of excellent solutions to recompose newly better solutions. We introduce the principle of population solution pool below. In the case of circulation problem, the constrained-CC strategy based on CC [20] is proposed to improve the efficiency of the local search. Meanwhile, each iteration is attached with tabu restriction [21] to avoid exploring visited solutions.
3.4.1. Scoring Function
Based on the limited local information, the evaluation function greatly influences the quality of the solution. Some vertices are selected by following vertex selection strategy rule, which combines the proposed constrained-based CC with our scoring function here. We take the frequency of each vertex into account referring to the idea in [20]. At the start, each vertex v initializes the frequency variable . After each iteration, for all vertices still not be dominated by the candidate solution, the corresponding will be increased by 1. On this account, we encourage the algorithm to dominate those undominated vertices in the next time. Based on this idea, we propose our scoring function as below.
Considering a graph and a candidate solution S, for each vertex v, we express the value of score by . is a positive value indicating the weight of v. We use a list to identify if v is independent. indicates v is independent, which means none of v’s neighbors is in S. On the contrary, means v is not independent.
where is denoted as the number of vertices in which are in S, and . Indeed, is a set of vertices which are the neighbors of v, under the constraint that they have not been dominated by S but would be dominated by adding v. is a set of vertices which are the neighbors of v, along with the constraint that they have been dominated by S and would be undominated by removing v.
3.4.2. Constrained-Based CC and Vertex Selection Strategy
During the process of searching, we choose a vertex by assessment of configuration and score value. It is more likely to have a circulation problem in the searching process of local search. The phenomenon often manifests as visiting one solution repeatedly, or even caught in a poor local result. In consideration of this cause, the two-level configuration checking (CC for short) strategy [20] was proposed to handle this problem in local search. Therefore, we adapt this strategy to constrained-CC for MWIDS problem during the local search process. We choose a vertex by checking the configuration, which means, when adding a vertex without changing the configuration compared with before, there is no need to append it. At the same time, we need to check respectively to guarantee every vertex is independent. In detail, we implement with a boolean array , which indicates whether a vertex can be chosen. means v is a configuration changed vertex and is allowed to be added to the candidate solution S. On the contrary, we cannot add a vertex with . At the beginning, we initialize as 1 for all the vertex in S. When is changed, the value of its neighbors will be adjusted as well. In this process, the configuration changing should take both its state and its neighbors’ states into consideration.
The quality of candidate solutions largely depends on the evaluation function. We choose which vertices to add or remove on the basis of limited local information each time. Here, we evaluate vertices by scoring function, constrained-based CC and tabu strategy. The tabu strategy [21,22] aims to avoid visiting previous solutions. It is implemented by a list named to prevent adding the vertex which has just been removed. In other words, we use the state of vertex about whether in to mark which one can be picked up. Further, we tend to choose a vertex older with more steps since the last time it changes its state (be removed from or added into the candidate solution). Thus, we give priority to the oldest one while picking a vertex. We define some rules for different situations as below.
- Remove-Rule1: Choose the vertex with the highest score value, then remove the oldest one by breaking ties randomly and update the configuration accordingly.
- Remove-Rule2: Choose the vertex not in with the highest score value, then remove the oldest one by breaking ties randomly and update the configuration accordingly.
- Add-Rule: Choose a vertex v which could be allowed to add into the solution with and the highest score value and update the configuration accordingly.
3.4.3. The Main Procedure of the Local Search
We develop a procedure called C_LS (Algorithm 3) which combines constrained-based CC and tabu strategy with local search. At first, we should initialize , , , weight and score values for all vertices (Line 1). Then, candidate solution and local best solution are both set to an empty set (Line 2).
While the non-improvement number of iteration is not reached, the search process works for a dominating set and then swaps some vertices for the final best solution (Lines 3–20). Then, if the algorithm gets to an IDS in which all vertices are dominated (Lines 4–9), then we update the local best solution by using (Lines 5–6). We select a vertex v, and then remove it from according to Remove-Rule1 (Lines 7). Then, the algorithm updates the configuration of its neighbors by constrained-based CC (Line 8).
The algorithm removes a vertex not in the according to Remove-Rule2 (Line 10). Afterwards, the configuration is updated accordingly (Line 11). The should be cleared up in order that the forbidden vertices would be available for the next circulation (Line 12). The aim of the following loop on Lines 13–19 is to add vertices into the candidate set until there are no undominated vertices. A vertex is selected according to Add-Rule and the algorithm makes sure the vertex is independent (Line 14). Here, if the weight of plus the just selected added vertex is larger than the global best solution (Lines 15–16), the algorithm obviously abandons this vertex and then breaks this adding process. Otherwise, the suitable vertex is added in the candidate solution and the value is updated according to constrained-based CC (Line 17). The current added vertex will be put into the as well (Line 18). For each undominated vertex v, the frequency value is increased by 1 (Line 19). Finally, when reaching , the local best solution of the problem will be returned.
| Algorithm 3: C_LS() |
 |
3.5. Probability-Based Dynamic Optimization
Our combination operator is particularly designed based on probability, which elevates the property of offspring acceptation with more possibility of exploring new promising solutions. From a general perspective, our proposed algorithm is composed of a number of basic components: a pool of candidate solutions which is effective to maintain a search space and a combination operator called the process of probability-based dynamic optimization (PDO) to generate better solutions by combining vertices of existing good solutions.
In this section, we take both the quality and the diversity of population P into account. When selecting the parents for recombination, we tend to consider the quality of the candidate solutions as a crucial factor. It is based on an idea that the shared vertices contained in both good parent solutions are more likely to exist in an optimal solution. The recombination mechanism can make great use of the good properties from parents to offspring. Our mechanism named PDO (Algorithm 4) is a kind of algorithm to recompose existing solutions with a certain probability, with the process of checking the composition of the existing good solutions. The vertices concluded in both parent solutions will be chosen at a bigger rate , while vertices concluded in one parent solution will be picked up at a lower rate .
In addition, considering the parents selection may make a difference to the diversity of population. Exploring more new search areas in a diverse and random way for seeking promising solutions is vital. More specifically, to ensure the heritage of good properties from parents to offspring, we generate a circulation that begins with a local search process and is followed by PDO to combine two solutions and randomly, which may be from solution pool or from the improved solution from local search. If a vertex v which is assumed to be independent is concluded in both and , we add v into at rate (Lines 2–3). On the other hand, if v is concluded in or , we add v in at rate ; at the same time, we need to assure v is independent (Line 5–6). Otherwise, if the vertex v is not independent, we remove all neighbors of v in at a rate of and then add v into (Lines 8–11). We come up with this idea to add as many independent vertices as possible instead of skipping this possibility.
| Algorithm 4: PDO(,) |
 |
After offspring elements selection, we recompose current solution by the construction procedure until all vertices are dominated, which is very similar to the construction process (Lines 12–18). In addition, there are some adjustments following the birth of offspring. If the returned solution is already an IDS, we find a better solution (Line 19). Otherwise, which is not a feasible solution will be returned (Line 17), i.e., failing to obtain a better solution, compared with . In addition, the offspring obtained would be the inception of the next local search procedure repeatedly for a better performance. At the same time, updating the composition of population with local optimal solutions accordingly, we also propose a technique to clear or exchange the worst elements of population P to keep high-quality solution set.
3.6. Population Updating Strategy
Our population updating strategy is shown here, which is proved to conduct well for maintaining top solutions. Population updating is a crucial factor for exploring a promising, high-quality solution area. First, we combine local search process with population updating for improving the solution quality as much as possible. Local search is used to pursue high-quality results by exploring the neighbor structure, while population provides a container to maintain optimal solutions. Population updating is used to decide whether a solution could be a member of it and which one would be replaced. Moreover, considering a poor diversity may attribute to situations such as repetitions of solution components or stopping with poor local optima [36]. Thus, we need to manage population diversity by the offspring acceptance and replacement strategies.
In this section, we introduce our pool updating strategy, namely PoolUpdate, that manages the composition of pool and decides which existing solution should be replaced. At the very beginning, we initiate preferable solutions of population by random generation construction followed with local search improvement. Along with the search process, the pool constantly maintains the top optimal solutions. It is realized according to the idea of basic quality-based pool updating [36]; we come up with the mechanism that replaces the worst solution of the pool for a better population structure. In detail, in each circulation, if the weight of local optimal solution from improvement of local search is lower than the worst one in the pool, we replace the worst one with . When the weight value of is equivalent to the worst one in the pool, we execute replacement at a rate of 50%. In short, the population quality is increased by the dynamic replacement strategy above.
3.7. Discussion of MSSAS’s Complexity
In this subsection, we discuss the complexity of each component of MSSAS, including the construct, local search and population updating procedures. The complexity of the construct procedure is O(). The complexity of one iteration in local search procedure is O(). The complexity of population updating procedure is O().
4. Experimental Results
In this section, to verify the effectiveness of our proposed algorithm, we compare MSSAS with two algorithms: CCFS [20] and CPLEX. Specially, CCFS is an efficient algorithm for the minimum weight dominating set problem. The authors of the improved CCFS [20] provided us with their source code, which had been modified for greatly solving MWIDS problem. In addition, we compare solution values with those of CPLEX, which is a high-performance mathematical programming solver for linear programming, mixed-integer programming and quadratic programming. In our work, the version of CPLEX that we used is CPLEX 12.6.
Our proposed algorithm was implemented in C++ and compiled by g++ with option -O3 in Intel Xeon E5-2640 v4 @ 2.40GHz CPU with 128GB RAM under CentOS 7.5. Many previous works use the time limit as the stopping criterion of tested algorithms [37,38,39]. For the MSSAS and competitors, the time limit was set to 100 s. All algorithms were executed 10 times under the same time limit. The MIN column is denoted as the minimal solution values, while the AVG column is denoted as the average solution value over 10 run times. The bold values of the following tables indicate the best values in the comparison of other algorithms.
We evaluated the performance of our proposed algorithm on two sets of benchmarks, namely DIMACS [23] and BHOLIB [24], where DIMACS has already used for testing several graph problems, such as vertex cover [40], dominating set [20] and clique [39], while BHOSLIB is the famous benchmark for graph problems which has many crafted hard instances with hidden optimum solutions. For generating the corresponding weighting instances, we used the same weighting function as the authors of [20,39], i.e., mod 200) + 1, for each vertex .
4.1. Parameter Settings
To obtain the suitable parameter settings of our proposed algorithm, the automatic configuration tool irace [41] was applied for , , , and . We restricted the training set to include 20 training instances chosen from DIMACS and BHOLIB benchmarks. The tuning process was given a budget of 9000 runs of the proposed algorithm. For each execution, the time limit was set to 100 s. Table 1 represents the values tuning of parameters.

Table 1.
The parameter settings of our proposed algorithm.
4.2. Experimental Evaluation of MSSAS on DIMACS and BHOLIB Benchmarks
Table 2 and Table 3 show that the results obtained by CCFS can match with the results of MSSAS for only three instances, but the run time of CCFS is always slower than MSSAS. Except for these three instances, MSSAS can steadily find better solutions than CCFS. For all tested instances, the average number of MSSAS iterations is 6,011,056.71, while the average number of CCFS iterations is 6,916,590.65. Because our proposed MSSAS needs to maintain some candidate solutions during the search process, it is obvious that the average iteration number of MSSAS is larger than that of CCFS. Now, we focus on the comparison between CPLEX and MSSAS. For 12 instances, MSSAS obtains better solution values than CPLEX, while, for the remaining instances, both of them can obtain the same solution quality. From the analysis of Table 2 and Table 3, we can draw a conclusion that for DIMACS Benchmark the quality of solution found by MSSAS is always better than those of the other algorithms.

Table 2.
Experimental results of CPLEX, CCFS and MSSAS I.

Table 3.
Experimental results of CPLEX, CCFS and MSSAS II.
The experiment results of BHOSLIB Benchmarks are shown in Table 4. It is obvious that MSSAS has outstanding performance than other algorithms in comparison. Only the results of frb30-15-3 and frb30-15-5 are equivalent to those of CPLEX. Therefore, MSSAS performed the best.

Table 4.
Experimental results of CPLEX, CCFS and MSSAS III.
4.3. The Effectiveness of the Components of MSSAS
To show the effectiveness of two components of MSSAS including our local search procedure and probability-based dynamic optimization, we designed two alternative algorithms, i.e., MSSAS1 and MSSAS2. To be specific, when adding vertices into the candidate solution, MSSAS1 adopts tabu mechanism (in our work, the added forbidden length esd set to 7 based on preliminary experiments) without using the constrained CC. MSSAS2 uses a simple strategy, i.e., randomly selecting a random solution from population and then removing some vertices from this solution as the input of local search, making sure the weight of input solution is always smaller than that of the global best solution, rather than our probability-based dynamic optimization.
The time-to-target plot [42] was used to compare MSSAS with MSSAS1 and MSSAS2 on four instances and their respective targets. To get the time-to-target plots, we performed 200 independent runs of MSSAS, MSSAS1 and MSSAS2 on these four instances. Figure 2 and Figure 3 illustrate the efficiency contribution of our two proposed components. Figure 2 shows that the probabilities of obtaining a solution of the target value by MSSAS are approximately 10% and 30% in at most 0.22 and 0.89 s, respectively, whereas the probabilities of obtaining a solution of the target value are approximately 10% and 30% in almost 32.46 and 98.28 s by MSSAS1, as well as at least 0.35 and 1.04 s by MSSAS2, which are considerably more than MSSAS.
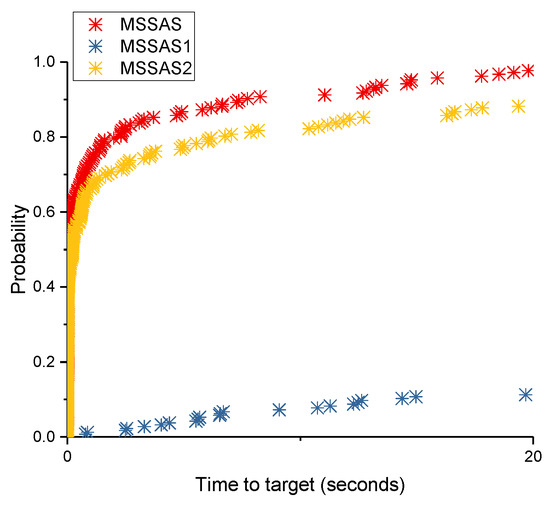
Figure 2.
Time-to-target plot comparing MSSAS with MSSAS1 and MSSAS2 on instance C125.9 and its target 512.
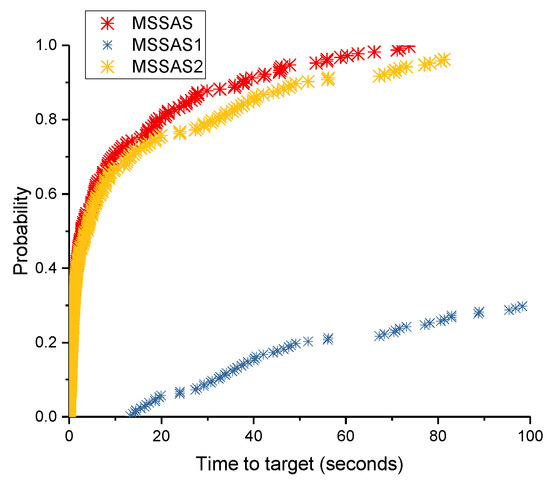
Figure 3.
Time-to-target plot comparing MSSAS with MSSAS1 and MSSAS2 on instance frb30-15-1 and its target 500.
5. Conclusions and Future Work
In this work, we introduced a novel algorithm for solving the NP-hard minimum weight vertex independent dominating set problem. Firstly, an improved mimetic algorithm called sequential self-adaptive search is proposed for solving the denoted problem, which explores the synergy between the process of local search process and a combination operator. The algorithm also integrates the construction of initial solutions generated by a kind of greedy randomized construction heuristic and an effective pool updating procedure. Secondly, in the stage of local search improvement, the constrained-CC strategy for MWVIDS problem based on CC is adapted to prevent from the cycling problem. In addition, each choice of removal vertices is accompanied by tabu restriction to refrain from exploring visited solutions. Furthermore, the proposed scoring function takes the frequency of vertices into consideration for searching high-quality solutions. With the strategies above, an improved vertex selection strategy for evaluating which vertex to be added or removed in this process is obtained. Then, a procedure called C_LS is developed which combines constrained-based CC, scoring function and tabu strategy with local search. Thirdly, the research indicates a combination operator called probability-based dynamic optimization (PDO) to generate offspring solutions by combining vertices of existing good solutions. The PDO process is accompanied by a pool updating dynamically to maintain a space of optimal solutions. In this way, the diversity of solutions can be effectively increased. Extensive experiments were carried out to evaluate the performance of proposed MSSAS algorithm on two benchmarks DIMACS and BHOLIB. The results show that MSSAS performs better than competitors for almost all instances.
In the future, we will focus on improving the performance of our algorithm on solving massive graphs regarding some real applications, because, with the increase of instance scale, our proposed method may not scale very well. In addition, we would find some other important properties and improve scoring function. In addition, we may explore a better way [43,44] to estimate the size of the search space and improve corresponding strategies in our algorithm with more creative ideas.
Author Contributions
Conceptualization, Y.Z. and Y.L. (Yong Lai); methodology, J.L. and Y.L. (Yang Liu); validation, S.L. and J.W.; writing-original draft preparation, S.L., J.W., and Y.L. (Yong Lai); writing-review and editing, Y.Z., J.L., Y.L. (Yang Liu), and Y.L. (Yong Lai). All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Fundamental Research Funds for the Central Universities 2412020FZ030 and 2412018ZD017, project of Jilin Provincial Science and Technology Department under Grant No. 20190302109GX, Jilin Province Natural Science Foundation under grant 20190103005JH and NSFC (under grant nos. 61806050, 61972063, 61976050, 61972384).
Conflicts of Interest
The authors declare that they have no conflicts of interest to this work. We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
References
- Hartmanis, J. Computers and intractability: A guide to the theory of NP-completeness (michael r. garey and david s. johnson). Siam Rev. 1982, 24, 90. [Google Scholar] [CrossRef]
- Lin, C.R.; Gerla, M. Adaptive clustering for mobile wireless networks. IEEE J. Sel. Areas Commun. 1997, 15, 1265–1275. [Google Scholar] [CrossRef]
- Khumawala, B.M. An efficient branch and bound algorithm for the warehouse location problem. Manag. Sci. 1972, 18, B-718. [Google Scholar] [CrossRef]
- Terra-Neves, M.; Lynce, I.; Manquinho, V. Virtual machine consolidation using constraint-based multi-objective optimization. J. Heuristics 2019, 25, 339–375. [Google Scholar] [CrossRef]
- Nocetti, F.G.; Gonzalez, J.S.; Stojmenovic, I. Connectivity based k-hop clustering in wireless networks. Telecommun. Syst. 2003, 22, 205–220. [Google Scholar] [CrossRef]
- Tree, S. Wireless sensor networks. Self 2014, 1, C0. [Google Scholar]
- Dai, S.; Tang, C.; Qiao, S.; Xu, K.; Li, H.; Zhu, J. Optimal multiple sink nodes deployment in wireless sensor networks based on gene expression programming. In Proceedings of the 2010 Second International Conference on Communication Software and Networks, Singapore, 26–28 February 2010; pp. 355–359. [Google Scholar]
- Ji, Y.; Yang, H.; Zhang, Y.; Zhong, W. Location optimization model of regional express distribution center. Procedia-Soc. Behav. Sci. 2013, 96, 1008–1013. [Google Scholar] [CrossRef][Green Version]
- Gaspers, S.; Liedloff, M. A branch-and-reduce algorithm for finding a minimum independent dominating set in graphs. In International Workshop on Graph-Theoretic Concepts in Computer Science; Springer: Berlin, Germany, 2006; pp. 78–89. [Google Scholar]
- Wang, Y.; Li, R.; Zhou, Y.; Yin, M. A path cost-based GRASP for minimum independent dominating set problem. Neural Comput. Appl. 2017, 28, 143–151. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Sun, H.; Yin, M. A memetic algorithm for minimum independent dominating set problem. Neural Comput. Appl. 2018, 30, 2519–2529. [Google Scholar] [CrossRef]
- Davidson, P.P.; Blum, C.; Lozano, J.A. The weighted independent domination problem: Integer linear programming models and metaheuristic approaches. Eur. J. Oper. Res. 2018, 265, 860–871. [Google Scholar] [CrossRef]
- Corominas, G.R.; Blum, C.; Blesa, M.J. A biased random key genetic algorithm for the weighted independent domination problem. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 2052–2055. [Google Scholar]
- Wang, Y.; Pan, S.; Li, C.; Yin, M. A local search algorithm with reinforcement learning based repair procedure for minimum weight independent dominating set. Inf. Sci. 2020, 512, 533–548. [Google Scholar] [CrossRef]
- Moscato, P.; Norman, M.G. A memetic approach for the traveling salesman problem implementation of a computational ecology for combinatorial optimization on message-passing systems. Parallel Comput. Transput. Appl. 1992, 1, 177–186. [Google Scholar]
- Wang, H.; Wang, D.; Yang, S. A memetic algorithm with adaptive hill climbing strategy for dynamic optimization problems. Soft Comput. 2009, 13, 763–780. [Google Scholar] [CrossRef]
- Zhou, Y.; Qiu, C.; Wang, Y.; Fan, M.; Yin, M. An improved memetic algorithm for the partial vertex cover problem. IEEE Access 2019, 7, 17389–17402. [Google Scholar] [CrossRef]
- Lü, Z.; Hao, J.K. A memetic algorithm for graph coloring. Eur. J. Oper. Res. 2010, 203, 241–250. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Saremi, A.; Ziaee, M. A memetic algorithm for a vehicle routing problem with backhauls. Appl. Math. Comput. 2006, 181, 1049–1060. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, S.; Yin, M. Local search for minimum weight dominating set with two-level configuration checking and frequency based scoring function. J. Artif. Intell. Res. 2017, 58, 267–295. [Google Scholar] [CrossRef]
- Dawei, L.; Li, W.; Mengguang, W. Genetic algorithm and tabu search: A hybrid strategy. J. Syst. Eng. 1998, 13, 28–34. [Google Scholar]
- Glover, F.W.; Kochenberger, G.A. Handbook of Metaheuristics; Springer Science & Business Media: Berlin, Germany, 2006; Volume 57. [Google Scholar]
- Johnson, D.S. Cliques, coloring, and satisfiability: Second DIMACS implementation challenge. DIMACS Ser. Discret. Math. Theor. Comput. Sci. 1993, 26, 11–13. [Google Scholar]
- Xu, K.; Boussemart, F.e.e.; Hemery, F.; Lecoutre, C. A simple model to generate hard satisfiable instances. In Proceedings of the 19th International Joint Conference on Artificial Intelligence, Jeju Island, Korea, 11–13 October 2005; pp. 337–342. [Google Scholar]
- Brezočnik, L.; Fister, I.; Podgorelec, V. Swarm Intelligence Algorithms for Feature Selection: A Review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.; Su, J.; Wang, J. Research and Application Based on the Swarm Intelligence Algorithm and Artificial Intelligence for Wind Farm Decision System. Renew. Energy 2018, 134, 681–697. [Google Scholar] [CrossRef]
- Slowik, A.; Kwasnicka, H. Nature Inspired Methods and Their Industry Applications - Swarm Intelligence Algorithms. IEEE Trans. Ind. Inform. 2018, 14, 1004–1015. [Google Scholar] [CrossRef]
- Anandakumar, H.; Umamaheswari, K. A bio-inspired swarm intelligence technique for social aware cognitive radio handovers. Comput. Electr. Eng. 2017, 71, 925–937. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Comprehensive Evaluation of Weak and Strong Mutation Mechanisms in Evolutionary Algorithms for Truck Scheduling at Cross-Docking Terminals. IEEE Access 2018, 6, 65635–65650. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Delayed Start Parallel Evolutionary Algorithm for just-in-time truck scheduling at a cross-docking facility. Int. J. Prod. Econ. 2019, 212, 236–258. [Google Scholar] [CrossRef]
- Cowling, P.; Kendall, G.; Soubeiga, E. A hyperheuristic approach to scheduling a sales summit. In Practice and Theory of Automated Timetabling III, Proceedings of the International Conference on the Practice and Theory of Automated Timetabling, Konstanz, Germany, 16–18 August 2000; Springer: Berlin, Germany, 2000; pp. 176–190. [Google Scholar]
- Pessoa, L.S.; Resende, M.G.C.; Ribeiro, C.C. A hybrid Lagrangean heuristic with GRASP and path-relinking for set k-covering. Comput. Oper. Res. 2013, 40, 3132–3146. [Google Scholar] [CrossRef]
- Resendel, M.G.; Ribeiro, C.C. GRASP with path-relinking: Recent advances and applications. In Metaheuristics: Progress as Real Problem Solvers; Springer: Berlin, Germany, 2005; pp. 29–63. [Google Scholar]
- Resende, M.G.; Ribeiro, C.C. Greedy randomized adaptive search procedures: Advances and applications. Handbook Metaheuristics 2010, 146, 281–317. [Google Scholar]
- Shogan, A.W. Semi-greedy heuristics: An empirical study. Oper. Res. Lett. 1987, 6, 107–114. [Google Scholar]
- Hao, J.K. Memetic algorithms in discrete optimization. In Handbook of Memetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2012; pp. 73–94. [Google Scholar]
- Wang, Y.; Li, C.; Yin, M. A two phase removing algorithm for minimum independent dominating set problem. Appl. Soft Comput. 2020, 88, 105949. [Google Scholar] [CrossRef]
- Cai, S.; Li, Y.; Hou, W.; Wang, H. Towards faster local search for minimum weight vertex cover on massive graphs. Inf. Sci. 2019, 471, 64–79. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, S.; Chen, J.; Yin, M. SCCWalk: An efficient local search algorithm and its improvements for maximum weight clique problem. Artif. Intell. 2020, 280, 103230. [Google Scholar] [CrossRef]
- Cai, S.; Su, K.; Luo, C.; Sattar, A. NuMVC: An efficient local search algorithm for minimum vertex cover. J. Artif. Intell. Res. 2013, 46, 687–716. [Google Scholar] [CrossRef]
- López-Ibá nez, M.; Dubois-Lacoste, J.; Cáceres, L.P.; Birattari, M.; Stützle, T. The irace package: Iterated racing for automatic algorithm configuration. Oper. Res. Perspect. 2016, 3, 43–58. [Google Scholar] [CrossRef]
- Aiex, R.M.; Resende, M.G.C.; Ribeiro, C.C. TTT plots: A perl program to create time-to-target plots. Optim. Lett. 2007, 1, 355–366. [Google Scholar] [CrossRef]
- Abdelmaguid, T.F. An Efficient Mixed Integer Linear Programming Model for the Minimum Spanning Tree Problem. Mathematics 2018, 6, 183. [Google Scholar] [CrossRef]
- Yuan, F.; Li, C.; Gao, X.; Yin, M.; Wang, Y. A novel hybrid algorithm for minimum total dominating set problem. Mathematics 2019, 7, 222. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).