Finite-Time Mittag–Leffler Synchronization of Neutral-Type Fractional-Order Neural Networks with Leakage Delay and Time-Varying Delays
Abstract
1. Introduction
2. Preliminaries
3. Main Results
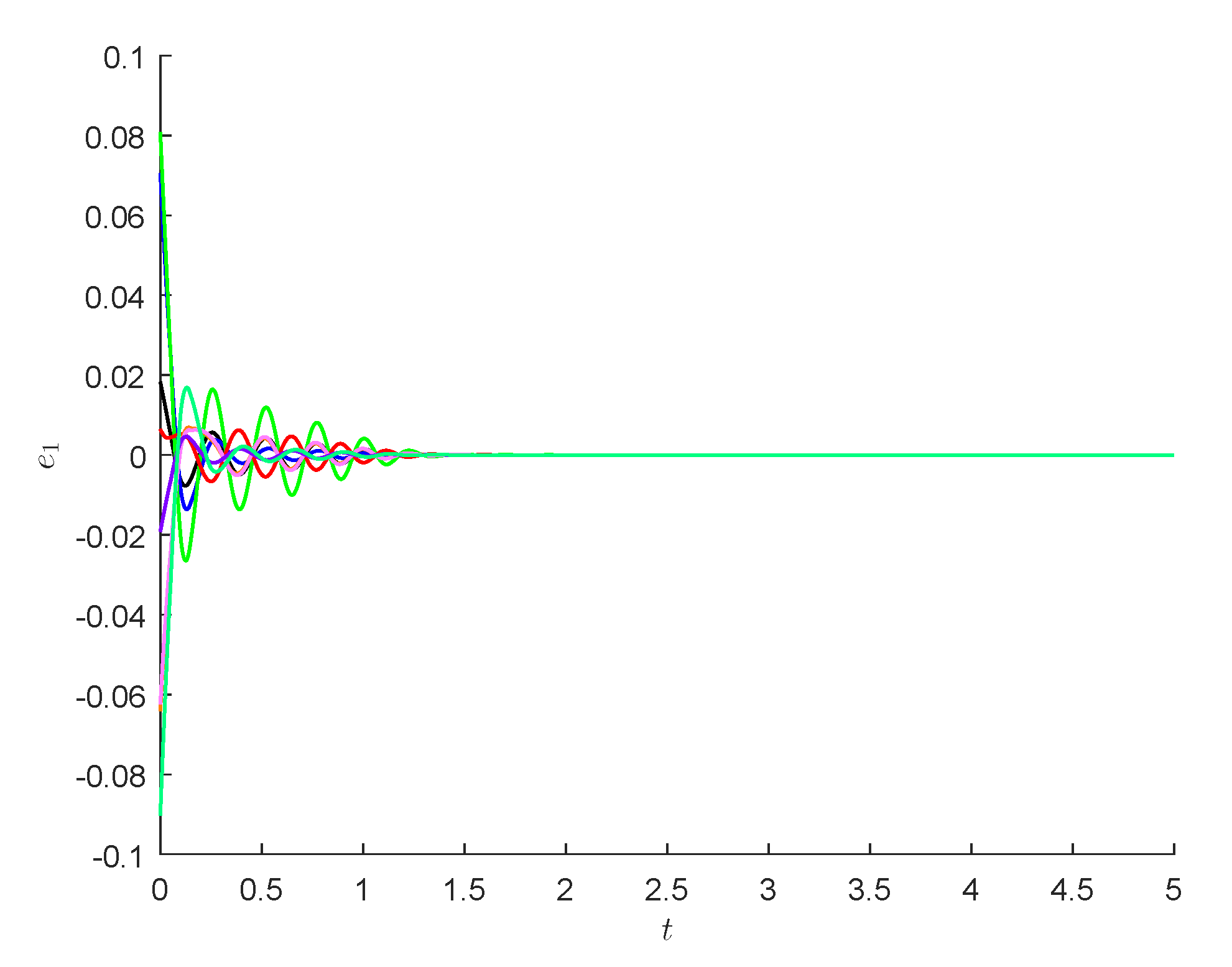
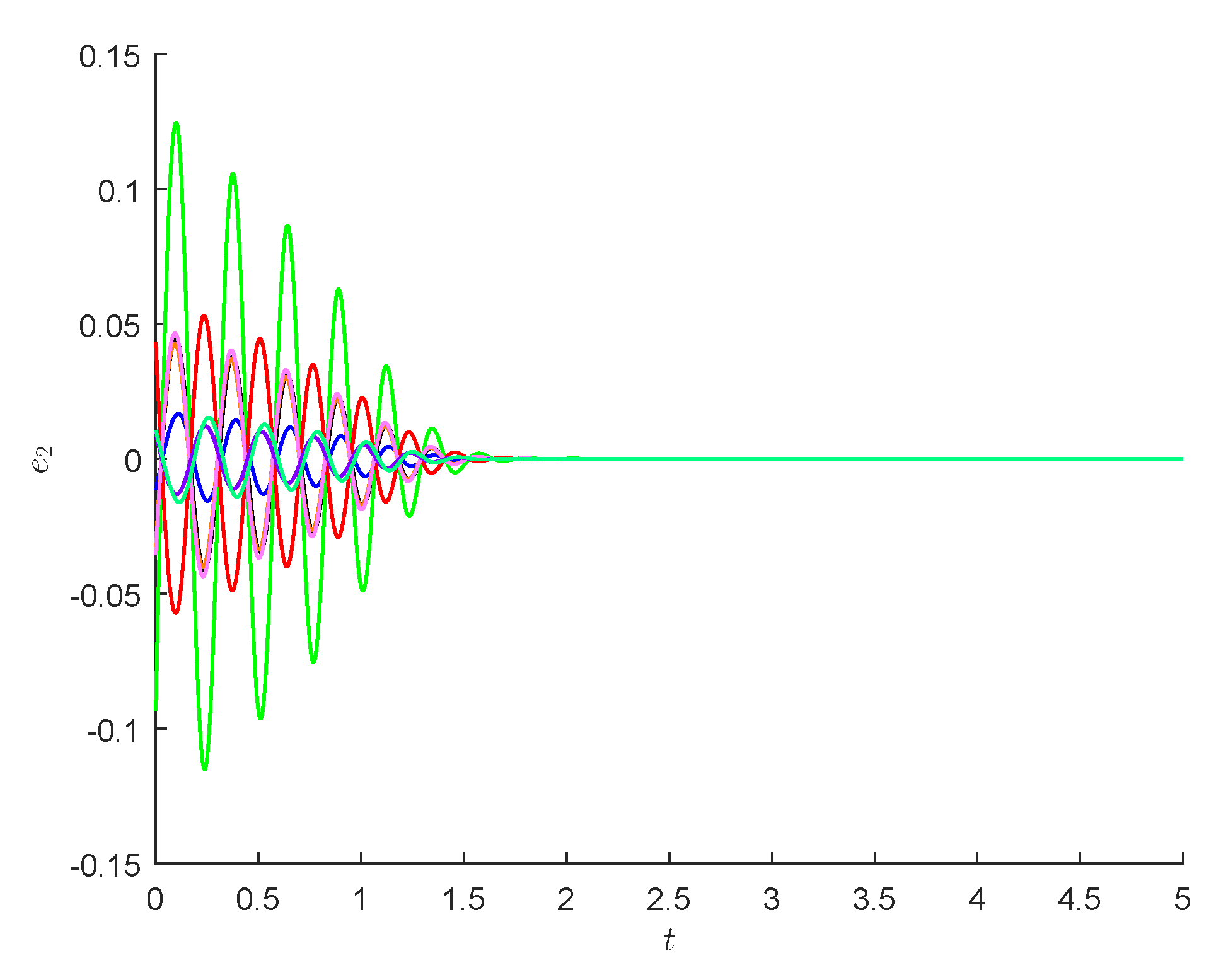
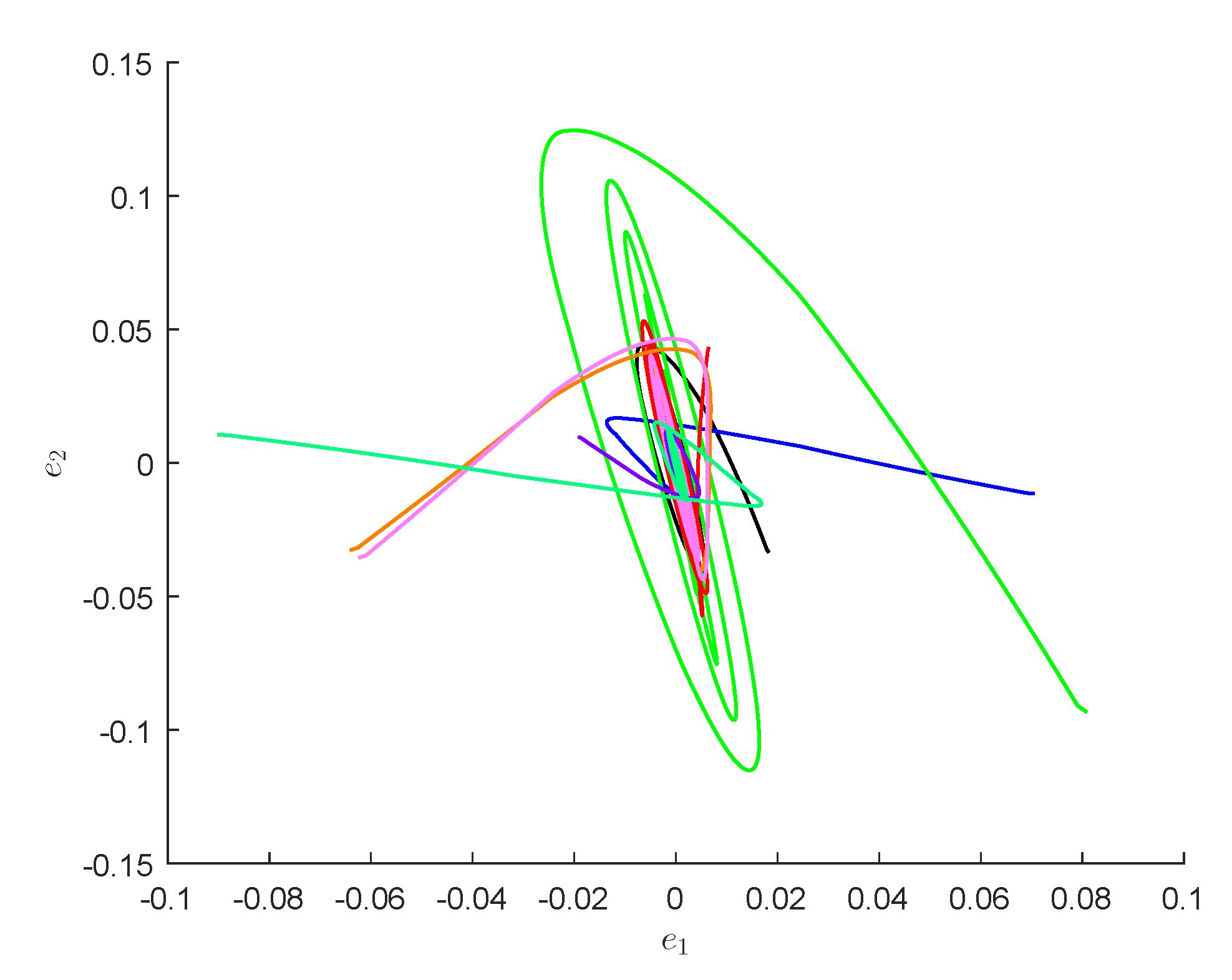
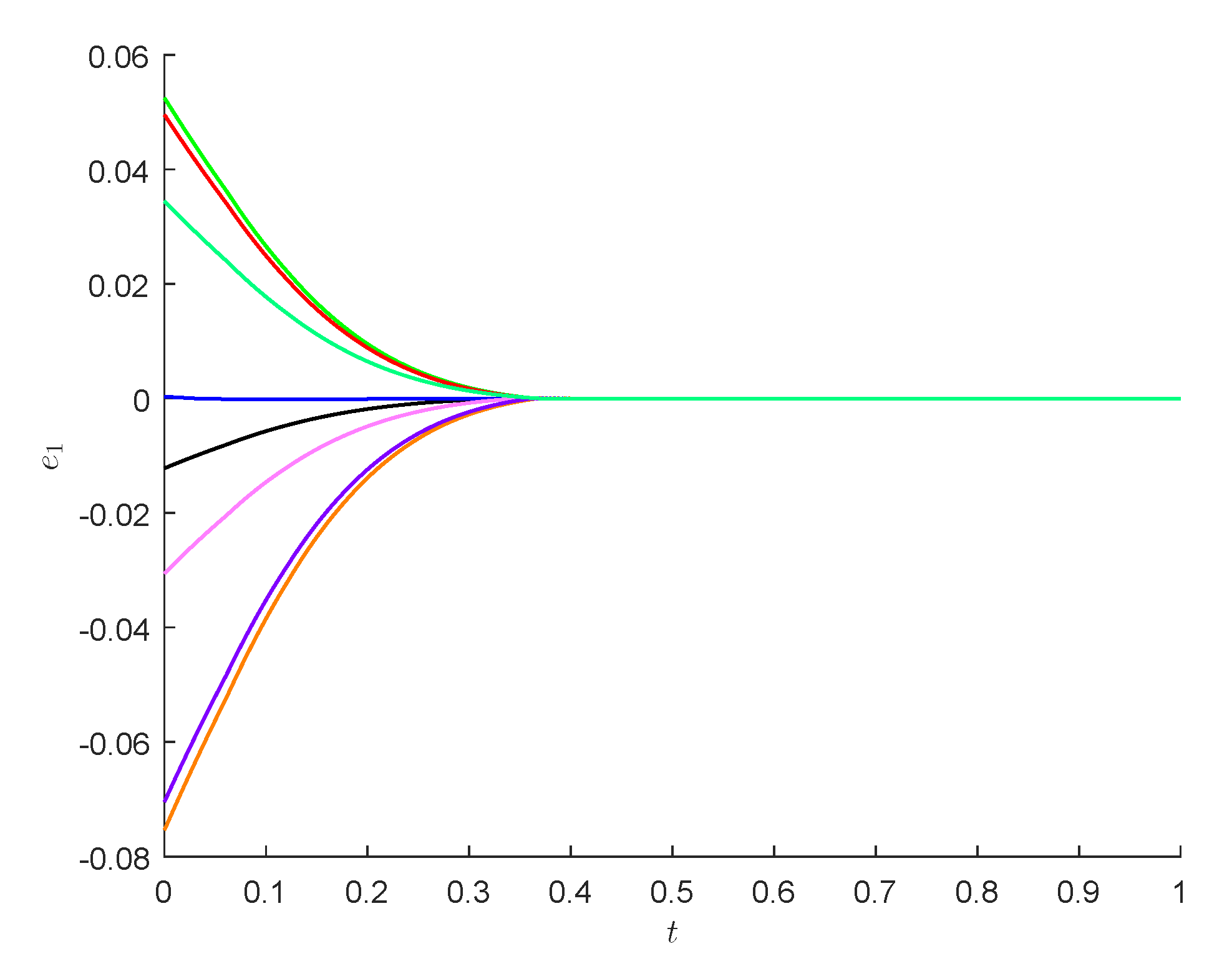
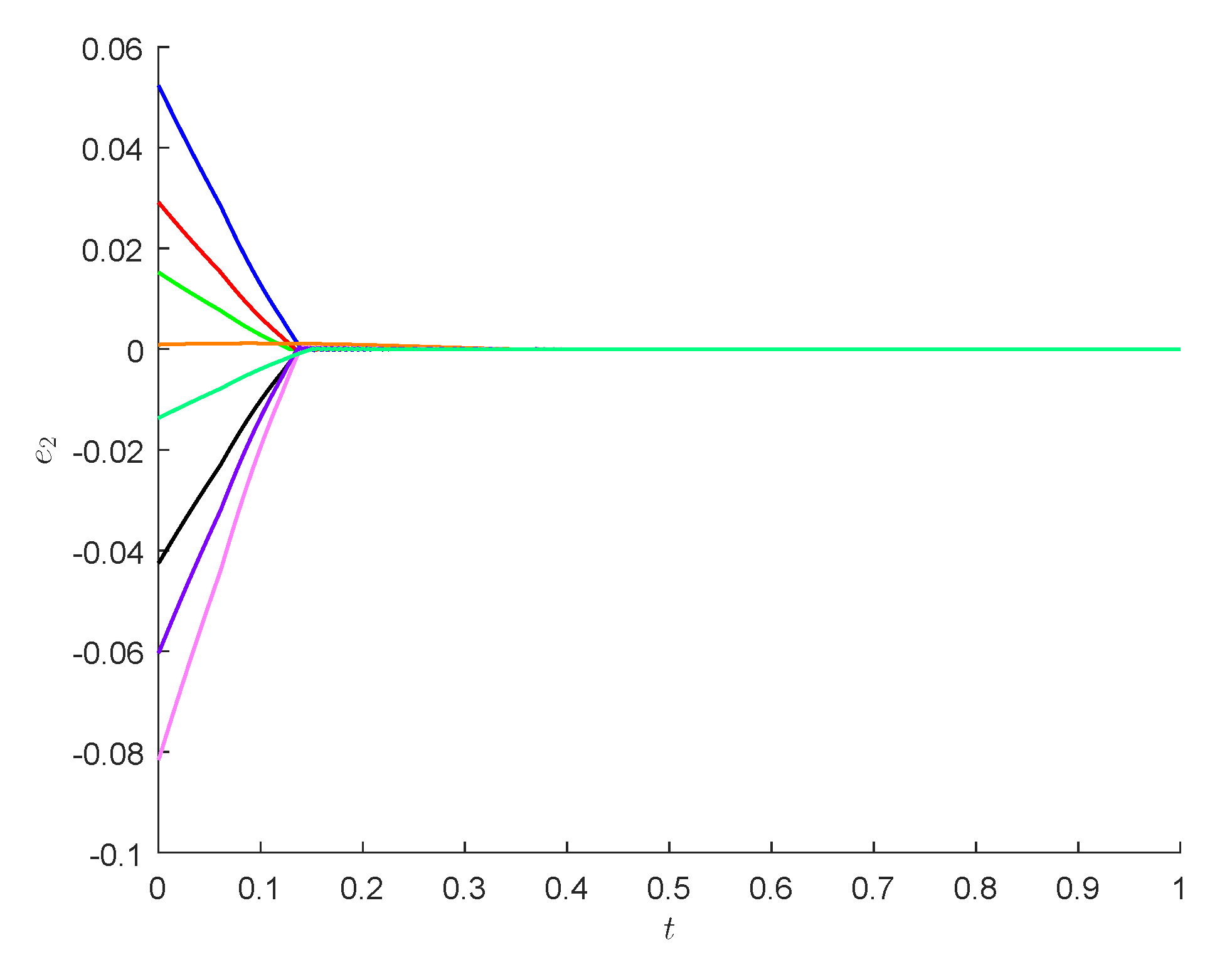
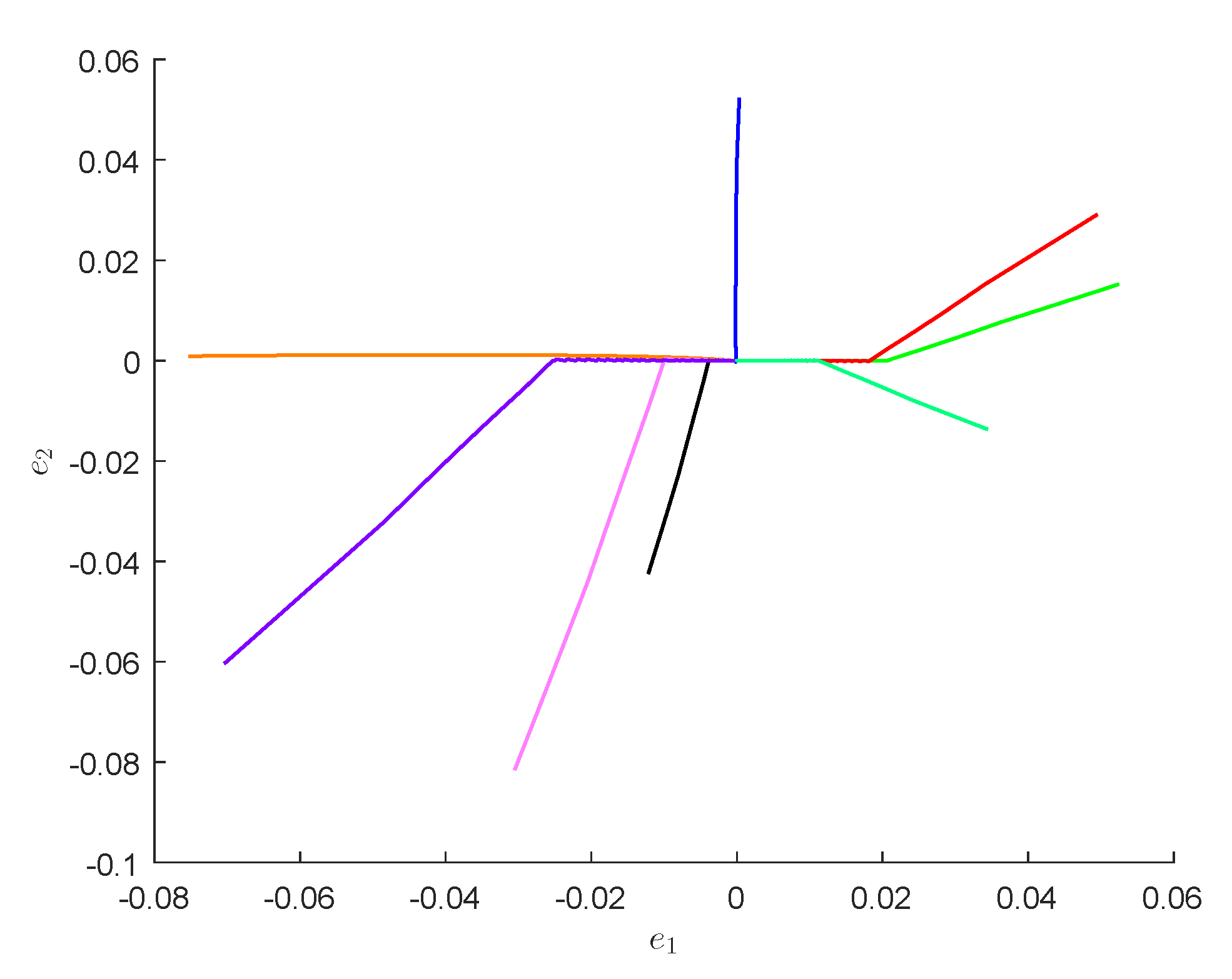
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar] [CrossRef]
- Wang, L.; Song, Q.; Liu, Y.; Zhao, Z.; Alsaadi, F.E. Global asymptotic stability of impulsive fractional-order complex-valued neural networks with time delay. Neurocomputing 2017, 243, 49–59. [Google Scholar] [CrossRef]
- Chen, J.; Chen, B.; Zeng, Z. Global asymptotic stability and adaptive ultimate Mittag–Leffler synchronization for a fractional-order complex-valued memristive neural networks with delays. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2519–2535. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, X.; Zhong, S. Global asymptotic synchronization of nonidentical fractional-order neural networks. Neurocomputing 2018, 313, 39–46. [Google Scholar] [CrossRef]
- Chen, J.; Li, C.; Yang, X. Asymptotic stability of delayed fractional-order fuzzy neural networks with impulse effects. J. Frankl. Inst. 2018, 355, 7595–7608. [Google Scholar] [CrossRef]
- Chen, L.; Huang, T.; Machado, J.T.; Lopes, A.M.; Chai, Y.; Wu, R. Delay-dependent criterion for asymptotic stability of a class of fractional-order memristive neural networks with time-varying delays. Neural Netw. 2019, 118, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.S.; Hymavathi, M.; Senan, S.; Shekher, V.; Arik, S. Global asymptotic synchronization of impulsive fractional-order complex-valued memristor-based neural networks with time varying delays. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 1–21. [Google Scholar] [CrossRef]
- Chen, J.; Chen, B.; Zeng, Z. O(t−α)-synchronization and Mittag–Leffler synchronization for the fractional-order memristive neural networks with delays and discontinuous neuron activations. Neural Netw. 2018, 100, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Pratap, A.; Raja, R.; Sowmiya, C.; Bagdasar, O.; Cao, J.; Rajchakit, G. Robust generalized Mittag–Leffler synchronization of fractional order neural networks with discontinuous activation and impulses. Neural Netw. 2018, 103, 128–141. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Song, Q.; Chen, J.; Huang, J. Global Mittag–Leffler stability and synchronization analysis of fractional-order quaternion-valued neural networks with linear threshold neurons. Neural Netw. 2018, 105, 88–103. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.F.; Wu, H.; Liu, D.Y.; Boutat, D.; Chen, Y.M. Lur’e Postnikov Lyapunov functional technique to global Mittag–Leffler stability of fractional-order neural networks with piecewise constant argument. Neurocomputing 2018, 302, 23–32. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Zhao, Z. Global Mittag–Leffler stability and synchronization of discrete-time fractional-order complex-valued neural networks with time delay. Neural Netw. 2020, 122, 382–394. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.S.; Narayanan, G.; Shekher, V.; Alsaedi, A.; Ahmad, B. Global Mittag–Leffler stability analysis of impulsive fractional-order complex-valued BAM neural networks with time varying delays. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 1–22. [Google Scholar] [CrossRef]
- Ding, Z.; Shen, Y. Global dissipativity of fractional-order neural networks with time delays and discontinuous activations. Neurocomputing 2016, 196, 159–166. [Google Scholar] [CrossRef]
- Velmurugan, G.; Rakkiyappan, R.; Vembarasan, V.; Cao, J.; Alsaedi, A. Dissipativity and stability analysis of fractional-order complex-valued neural networks with time delay. Neural Netw. 2017, 86, 42–53. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Huang, X.; Wang, Z.; Li, Y. Global dissipativity and quasi-synchronization of asynchronous updating fractional-order memristor-based neural networks via interval matrix method. J. Frankl. Inst. 2018, 355, 5998–6025. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Velmurugan, G.; Cao, J. Finite-time stability analysis of fractional-order complex-valued memristor-based neural networks with time delays. Nonlinear Dyn. 2014, 78, 2823–2836. [Google Scholar] [CrossRef]
- Wu, R.; Lu, Y.; Chen, L. Finite-time stability of fractional delayed neural networks. Neurocomputing 2015, 149, 700–707. [Google Scholar] [CrossRef]
- Yang, X.; Song, Q.; Liu, Y.; Zhao, Z. Finite-time stability analysis of fractional-order neural networks with delay. Neurocomputing 2015, 152, 19–26. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Wu, R.; He, Y.; Chai, Y. Finite-time stability criteria for a class of fractional-order neural networks with delay. Neural Comput. Appl. 2015, 27, 549–556. [Google Scholar] [CrossRef]
- Rajivganthi, C.; Rihan, F.A.; Lakshmanan, S.; Muthukumar, P. Finite-time stability analysis for fractional-order Cohen–Grossberg BAM neural networks with time delays. Neural Comput. Appl. 2018, 29, 1309–1320. [Google Scholar] [CrossRef]
- Wang, L.; Song, Q.; Liu, Y.; Zhao, Z.; Alsaadi, F.E. Finite-time stability analysis of fractional-order complex-valued memristor-based neural networks with both leakage and time-varying delays. Neurocomputing 2017, 245, 86–101. [Google Scholar] [CrossRef]
- Ding, X.; Cao, J.; Zhao, X.; Alsaadi, F.E. Finite-time stability of fractional-order complex-valued neural networks with time delays. Neural Process. Lett. 2017, 46, 561–580. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, S.; Wei, Y.; Yang, C. Finite-time stability of delayed memristor-based fractional-order neural networks. IEEE Trans. Cybern. 2018, 50, 1607–1616. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, S.; Martha, S. Finite-time stability for a class of fractional-order fuzzy neural networks with proportional delay. Fuzzy Sets Syst. 2020, 381, 68–77. [Google Scholar] [CrossRef]
- Hu, T.; He, Z.; Zhang, X.; Zhong, S. Finite-time stability for fractional-order complex-valued neural networks with time delay. Appl. Math. Comput. 2020, 365, 1–17. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Zhao, Z. Existence and finite-time stability of discrete fractional-order complex-valued neural networks with time delays. Neural Netw. 2020, 123, 248–260. [Google Scholar] [CrossRef]
- Velmurugan, G.; Rakkiyappan, R.; Cao, J. Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw. 2016, 73, 36–46. [Google Scholar] [CrossRef]
- Zheng, M.; Li, L.; Peng, H.; Xiao, J.; Yang, Y.; Zhao, H. Finite-time projective synchronization of memristor-based delay fractional-order neural networks. Nonlinear Dyn. 2017, 89, 2641–2655. [Google Scholar] [CrossRef]
- Li, X.; Fang, J.; Zhang, W.; Li, H. Finite-time synchronization of fractional-order memristive recurrent neural networks with discontinuous activation functions. Neurocomputing 2018, 316, 284–293. [Google Scholar] [CrossRef]
- Zheng, M.; Li, L.; Peng, H.; Xiao, J.; Yang, Y.; Zhang, Y.; Zhao, H. Finite-time stability and synchronization of memristor-based fractional-order fuzzy cellular neural networks. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 272–291. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Rajchakit, G.; Alsaadi, F.E. Further synchronization in finite time analysis for time-varying delayed fractional order memristive competitive neural networks with leakage delay. Neurocomputing 2018, 317, 110–126. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, S. Finite-time projective synchronization of fractional-order complex-valued memristor-based neural networks with delay. Chaos Solitons Fractals 2019, 128, 176–190. [Google Scholar] [CrossRef]
- Zheng, B.; Hu, C.; Yu, J.; Jiang, H. Finite-time synchronization of fully complex-valued neural networks with fractional-order. Neurocomputing 2020, 373, 70–80. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y. Finite time impulsive synchronization of fractional order memristive BAM neural networks. Neurocomputing 2020, 384, 213–224. [Google Scholar] [CrossRef]
- Xiao, J.; Zhong, S.; Li, Y.; Xu, F. Finite-time Mittag–Leffler synchronization of fractional-order memristive BAM neural networks with time delays. Neurocomputing 2017, 219, 431–439. [Google Scholar] [CrossRef]
- Xiao, J.; Cao, J.; Cheng, J.; Zhong, S.; Wen, S. Novel methods to finite-time Mittag–Leffler synchronization problem of fractional-order quaternion-valued neural networks. Inf. Sci. 2020, 526, 221–244. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, R.; Cao, J.; Alsaedi, A. Delay-independent stability of Riemann–Liouville fractional neutral-type delayed neural networks. Neural Process. Lett. 2018, 47, 427–442. [Google Scholar] [CrossRef]
- Pahnehkolaei, S.M.A.; Alfi, A.; Machado, J.T. Delay-dependent stability analysis of the QUAD vector field fractional order quaternion-valued memristive uncertain neutral type leaky integrator echo state neural networks. Neural Netw. 2019, 117, 307–327. [Google Scholar] [CrossRef]
- Zhang, L.; Song, Q.; Zhao, Z. Stability analysis of fractional-order complex-valued neural networks with both leakage and discrete delays. Appl. Math. Comput. 2017, 298, 296–309. [Google Scholar] [CrossRef]
- Huang, C.; Meng, Y.; Cao, J.; Alsaedi, A.; Alsaadi, F.E. New bifurcation results for fractional BAM neural network with leakage delay. Chaos Solitons Fractals 2017, 100, 31–44. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J. Impact of leakage delay on bifurcation in high-order fractional BAM neural networks. Neural Netw. 2018, 98, 223–235. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Zhao, L.; Huang, C.; Xiao, M. Novel results on bifurcation for a fractional-order complex-valued neural network with leakage delay. Phys. A Stat. Mech. Its Appl. 2019, 514, 868–883. [Google Scholar] [CrossRef]
- Ali, M.S.; Narayanan, G.; Shekher, V.; Alsulami, H.; Saeed, T. Dynamic stability analysis of stochastic fractional-order memristor fuzzy BAM neural networks with delay and leakage terms. Appl. Math. Comput. 2019, 369, 1–23. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Ye, H.; Gao, J.; Ding, Y. A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popa, C.-A.; Kaslik, E. Finite-Time Mittag–Leffler Synchronization of Neutral-Type Fractional-Order Neural Networks with Leakage Delay and Time-Varying Delays. Mathematics 2020, 8, 1146. https://doi.org/10.3390/math8071146
Popa C-A, Kaslik E. Finite-Time Mittag–Leffler Synchronization of Neutral-Type Fractional-Order Neural Networks with Leakage Delay and Time-Varying Delays. Mathematics. 2020; 8(7):1146. https://doi.org/10.3390/math8071146
Chicago/Turabian StylePopa, Călin-Adrian, and Eva Kaslik. 2020. "Finite-Time Mittag–Leffler Synchronization of Neutral-Type Fractional-Order Neural Networks with Leakage Delay and Time-Varying Delays" Mathematics 8, no. 7: 1146. https://doi.org/10.3390/math8071146
APA StylePopa, C.-A., & Kaslik, E. (2020). Finite-Time Mittag–Leffler Synchronization of Neutral-Type Fractional-Order Neural Networks with Leakage Delay and Time-Varying Delays. Mathematics, 8(7), 1146. https://doi.org/10.3390/math8071146





