Analysis of the Thermoelastic Damping Effect in Electrostatically Actuated MEMS Resonators

Abstract

An important aspect that must be considered when designing micro-electro-mechanical systems (MEMS) for all domains, including robotics, is the thermoelastic damping which occurs when the MEMS material is subjected to cyclic stress. This paper is focused on a model for the thermoelastic damping developed based on the generalized thermoelastic theory with the non-Fourier thermal conduction equation. The model was implemented in MATLAB and several simulations were performed. The theoretical results show a decrease in the deflection amplitude with the increase in time. The deflection amplitude decrease was validated by the experimental investigations, consisting of measuring the loss in amplitude and velocity of oscillations as a function of time. Moreover, this paper also presents the influence of the geometric dimensions on the mentioned decrease, as well as on the initial and final values of the amplitude for several polysilicon resonators investigated in this paper.

1. Introduction

Robotics is one of the fields that has been greatly impacted by the miniaturization trend of the last few decades. If the research conducted in this domain was only theoretical in the 1960s and 1970s, at the end of the 1980s, miniature robots started to emerge [1]. The main reasons for this change are the development of micro-electro-mechanical systems (MEMS) and the substantial industrial attention that they receive.

MEMS have the ability to bring innovation in many fields of engineering, not only robotics, due to their small size and high reliability. MEMS, as well as nano-electro-mechanical systems (NEMS), are an essential discovery for how materials, devices, and systems are perceived, designed, and manufactured in general [2]. Today, they are found in devices and even robots used in many real-world applications from domains such as terrestrial transportation, wearable devices, medicine, metrology, inspection and maintenance, micro-optics, and so on [1,2,3]. Particularly for robotics, the influence of MEMS is well presented in [4], where it is summarized as a threefold impact: “(1) providing sensors and actuators, (2) introducing a new intelligent system concept, such as autonomous distributed systems, and (3) realizing micro robots”.

In particular, MEMS resonators have been widely used in several sensing and wireless applications, such as accelerometers, gyroscopes, oscillators, electrical filters, switches, seismic sensors, and mass detectors in biological and environmental applications. Due to their low-cost fabrication and high level of integration potential, they are used, for example, as a desirable alternative to quartz resonators in real-time clock applications [5,6]. Additionally, they are necessary for radio frequency communication systems and sensory systems [7,8].

Due to the fact that MEMS resonators can provide enhanced performance and more functionality to the systems in which they are integrated, the research regarding aspects such as their optimal design or failure mechanisms has intensified. One situation that presents interest to researchers is reducing the problems caused by thermoelastic damping in MEMS resonators [9,10,11,12]. A well designed and manufactured resonator is characterized by minimum energy loss, because it influences the frequency response and the quality factor of a micro-beam resonator. Several energy dissipation causes have been identified and studied, amongst which thermoelastic damping is considered a significant loss mechanism in MEMS resonators at room temperature [11].

This paper is focused on presenting an analytical model for thermoelastic damping in micro-bridges. The model was validated by experimental measurements, and then it was used to determine the influence of the micro-beam’s geometric dimensions on the decrease in deflection amplitude and on the initial and final amplitude value. This presents interest, for example, for applications where the detection technique is based on laser beam resonators.

2. Theoretical Approach for Thermoelastic Damping

Whenever a MEMS structure is subjected to cyclic motion, the energy dissipation phenomenon occurs due to the material energy loss mechanism [13]. The temperature fluctuation that develops induces heat currents which lead to an increase in the beam resonator entropy, finally causing the energy dissipation process, also known as thermoelastic damping. This process is firstly influenced by the resonator’s material properties but also by the beam geometry and temperature, and it is known to be a serious loss mechanism in MEMS devices [9,11,12].

Pioneer studies in thermoelastic damping were conducted by Zener [14,15,16]. They indicate that a temperature gradient is generated when finite thermal expansion occurs, and this temperature gradient leads to energy dissipation due to the heat currents that it produces. The temperature differences across the beam equalize in a characteristic time ${\tau }_R$ given by [11]:

$${\tau }_R\left(T\right)={\left(\frac{h}{\pi }\right)}^2{D}^{-1}\left(T\right)$$

(1)

where h is the beam thickness, T is the beam temperature, and D is the thermal diffusion coefficient. The beam vibration frequency is [11]:

$$\omega =\frac{q^{2}h}{L^2}\sqrt{\frac{E}{12\rho }}$$

(2)

where $\rho$ is the density, E is the modulus of elasticity, L is the beam length, and $q=\pi$ for beams simply supported at both ends, and $q=4.73$ for beams clamped at both ends.

Zener developed a model based on the classical Fourier thermal conduction theory, according to which there is no temperature gradient across the beam, and he defined the internal friction as the inverse of the quality factor [11]:

$$Q^{-1}=\frac{{\alpha }_T^{2}TE}{C_P}\frac{\omega {\tau }_R}{1+{\omega }^2{\tau }_R^2}$$

(3)

where ${\alpha }_T$ is the linear thermal expansion coefficient and $C_P$ is the specific heat at constant pressure. A more recent approach to the thermoelastic damping theory can be found in [10].

For this paper, Zener’s theory was modified according to [11] by using the generalized thermoelastic theory with the non-Fourier thermal conduction equation and then applied for MEMS micro-bridges, thus eliminating the assumption of infinite speed of heat transportation from the classical thermoelastic theory.

3. Basic Equations Regarding the Thermoelastic Damping Effect

Vibrating micro-electro-mechanical structures are usually prismatic elastic beams with both ends clamped (micro-bridges) or only one of the ends clamped (micro-cantilevers). Furthermore, the study of the basic equations regarding the thermoelastic damping effect of an elastic beam whose dimensions are denoted as L (length), b (width), and h (thickness) is presented. The beam is placed so that the x axis is along the beam axis, while the y axis is along the beam width, and the z axis is along the beam thickness. Before starting to vibrate, the beam is in equilibrium at a temperature of $T_0$ and there is no heat flowing along the upper and lower beam surfaces.

If the Euler–Bernoulli assumption is made, namely that during the bending process the beam cross-sections continue to be perpendicular to the neutral plane, the displacements can be expressed as follows [11]:

$$u=-z\frac{dw}{dx},v=0,w(x,y,z,t)=w(x,t)$$

(4)

where t is time. The cross-section flexure moment is given by [11]:

$$M(x,t)=EI\frac{{\partial }^{2}w}{\partial x^2}+b\beta {\displaystyle \underset{-\frac{h}{2}}{\overset{\frac{h}{2}}{\int }}\theta zdz}$$

(5)

where $\theta =T-T_0$ is the resonator temperature increment, I is the cross-section inertia moment, and $\beta =E{\alpha }_T/(1-2\upsilon )$ is the thermal modulus in which $\upsilon$ is Poisson’s ratio.

By denoting by $M_T$ the last term from the sum given in (5) and by substituting the cross-flexure moment in the traverse motion equation for a beam, the following expression is obtained [11]:

$$EI\frac{{\partial }^{4}w}{\partial x^4}+\frac{{\partial }^2{M}_T}{\partial x^2}+\rho A\frac{{\partial }^{2}w}{\partial t^2}=0$$

(6)

where $\rho$ is the density and $A=bh$ is the cross-section area.

The non-Fourier thermal conduction equation containing the thermoelastic coupling term is [11]:

$$k{\theta }_{i,i}=\rho c_{\upsilon }\frac{\partial \theta }{\partial t}+\beta T_0\frac{\partial u_{i,i}}{\partial t}+{\tau }_0\rho c_{\upsilon }\frac{{\partial }^2\theta }{\partial t^2}+{\tau }_0\beta T_0\frac{{\partial }^2{u}_{i,i}}{\partial t^2}$$

(7)

By substituting (4) in (7), the thermal conduction equation for the beam is obtained as follows [11]:

$$k\frac{{\partial }^2\theta }{\partial x^2}+k\frac{{\partial }^2\theta }{\partial z^2}=c_{\upsilon }\rho \frac{\partial \theta }{\partial t}-T_0\beta z\frac{{\partial }^{3}w}{\partial x^2\partial t}+{\tau }_0{c}_{\upsilon }\rho \frac{{\partial }^2\theta }{\partial t^2}-{\tau }_0{T}_0\beta z\frac{{\partial }^{4}w}{\partial x^2\partial t^2}$$

(8)

After a few transformations and after substituting the value of $M_T$ for a temperature variation given by the $\sin (pz)$ function along the beam thickness, Equation (8) can be rewritten as [11]:

$$k\frac{{\partial }^2{M}_T}{\partial x^2}-k{p}^2{M}_T-c_{\upsilon }\rho \frac{\partial M_T}{\partial t}+T_0{\beta }^{2}I\frac{{\partial }^{3}w}{\partial x^2\partial t}-{\tau }_0{c}_{\upsilon }\rho \frac{{\partial }^2{M}_T}{\partial t^2}+{\tau }_0{T}_0{\beta }^{2}I\frac{{\partial }^{4}w}{\partial x^2\partial t^2}=0$$

(9)

where $p=\frac{\pi }{h}$.

Using the following notations [11]:

$$\xi =\frac{x}{L},W=\frac{w}{h},\tau =\frac{t\epsilon }{L},\epsilon =\sqrt{\frac{E}{\rho }},\Theta =\frac{M_T}{EAh}$$

(10)

the governing equations for the coupled thermoelastic problem can be written in a non-dimensional form as follows [11]:

$$\{\begin{array}{l}\frac{{\partial }^{2}W}{\partial {\tau }^2}+A_1\frac{{\partial }^{4}W}{\partial {\xi }^4}+\frac{{\partial }^2\Theta }{\partial {\xi }^2}=0\\ \frac{{\partial }^2\Theta }{\partial {\xi }^2}-A_2\Theta -A_3\frac{\partial \Theta }{\partial \tau }+A_4\frac{{\partial }^{3}W}{\partial {\xi }^2\partial \tau }-A_5\frac{{\partial }^2\Theta }{\partial {\tau }^2}+A_6\frac{{\partial }^{4}W}{\partial {\xi }^2\partial {\tau }^2}=0\end{array}$$

(11)

where the six coefficients are [11]:

$$\begin{gathered} A_1=\frac{h^2}{12L^2},A_2=p^2{L}^2,A_3=\frac{c_{\upsilon }\rho \epsilon L}{k},A_4=\frac{T_0{\beta }^2{h}^2\epsilon }{12kEL},A_5=\frac{{\tau }_0{c}_{\upsilon }E}{k}, \\ {A}_6=\frac{{\tau }_0{T}_0{\beta }^2{h}^2}{12\rho k{L}^2} \end{gathered}$$

(12)

4. Analytical Solution

The analysis of the thermoelastic coupling effect in MEMS resonators is conducted using the integration transformation method. First, the equations given by (11) are solved for the particular case of micro-bridges with their ends held at a constant temperature, and then the damping effect of the deflection is studied.

For the case considered above, the boundary conditions are [11]:

$$\{\begin{array}{l}{W|}_{{}_{\xi =0}}={W|}_{\xi =1}=0\\ {\frac{{\partial }^{2}W}{\partial {\xi }^2}|}_{\xi =0}={\frac{{\partial }^{2}W}{\partial {\xi }^2}|}_{\xi =1}=0\\ {\Theta |}_{{}_{\xi =0}}={\Theta |}_{\xi =1}=0\end{array}$$

(13)

The following sine Fourier transformation can be used in order to solve (11) [11]:

$$\{\begin{array}{l}{W}_m\left(m,\tau \right)={\displaystyle {\int }_0^{1}W\left(\xi ,\tau \right)\sin \left(r_m\xi \right)d\xi }\\ {\Theta }_m\left(m,\tau \right)={\displaystyle {\int }_0^1\Theta \left(\xi ,\tau \right)\sin \left(r_m\xi \right)d\xi }\end{array}$$

(14)

where $r_m=m\pi ,m=1,3,5,\dots$ and its solutions satisfy the boundary conditions given by (13).

After applying the finite sine transformation to the system given by (11) and to the initial conditions written for the case when a concentrated force is applied to the middle of the beam, the following equations are obtained:

$$\{\begin{array}{l}\frac{{\partial }^2{W}_m}{\partial {\tau }^2}+A_1{r}_m^4{W}_m-r_m^2{\Theta }_m=0\\ \left(r_m^2+A_2\right){\Theta }_m+A_3\frac{\partial {\Theta }_m}{\partial \tau }+A_4{r}_m^2\frac{\partial W_m}{\partial \tau }+A_5\frac{{\partial }^2{\Theta }_m}{\partial {\tau }^2}+A_6{r}_m^2\frac{{\partial }^2{W}_m}{\partial {\tau }^2}=0\end{array}$$

(15)

$$\{\begin{array}{l}{W_m|}_{\tau =0}=\frac{M\left(12-{\pi }^2\right)}{r_m^3}\\ {\frac{\partial W_m}{\partial \tau }|}_{\tau =0}=0\\ {{\Theta }_m|}_{\tau =0}=0\\ {\frac{\partial {\Theta }_m}{\partial \tau }|}_{\tau =0}=0\end{array}$$

(16)

where the relevant constant of the force F is $M=\frac{F{L}^3}{48E{I}_y}$

By applying the Laplace transformation to (15) with respect the initial conditions (16) and then performing the inverse Laplace transform, the obtained solution is:

$$W_m\left(m,\tau \right)=\frac{M\left(12-{\pi }^2\right)}{r_m^3}{\displaystyle \sum _{\alpha }\frac{\left(b_0+b_1\alpha +b_2{\alpha }^2+b_3{\alpha }^3\right)e^{\alpha \tau }}{c_1+2c_2\alpha +3c_3{\alpha }^2+4c_4{\alpha }^3}}$$

(17)

where $b_0=A_4{r}_m^4,$ $b_1=(A_6+1)r_m^2+A_2,$ $b_2=A_3,$ $b_3=A_5,$ $c_0=A_1{r}_m^6+A_1{A}_2{r}_m^4,$ $c_1=\left(A_4+A_1{A}_3\right)r_m^4,$ $c_2=\left(A_6+A_1{A}_5\right)r_m^4+r_m^2+A_2,$ $c_3=A_3,$ $c_4=A_5,$ and $\alpha$ represents the four solutions of the equation $c_0+c_1\alpha +c_2{\alpha }^2+c_3{\alpha }^3+c_4{\alpha }^4=0$.

Then, based on the Fourier series theory, the deflection is given by:

$$W\left(\xi ,\tau \right)=2M\left(12-{\pi }^2\right){\displaystyle \sum _{m=1,3,\dots }^{\infty }\frac{1}{r_m^3}{\displaystyle \sum _{\alpha }\frac{\left(b_0+b_1\alpha +b_2{\alpha }^2+b_3{\alpha }^3\right)e^{\alpha \tau }}{c_1+2c_2\alpha +3c_3{\alpha }^2+4c_4{\alpha }^3}\sin \left(r_m\xi \right)}}$$

(18)

5. Results and Discussions

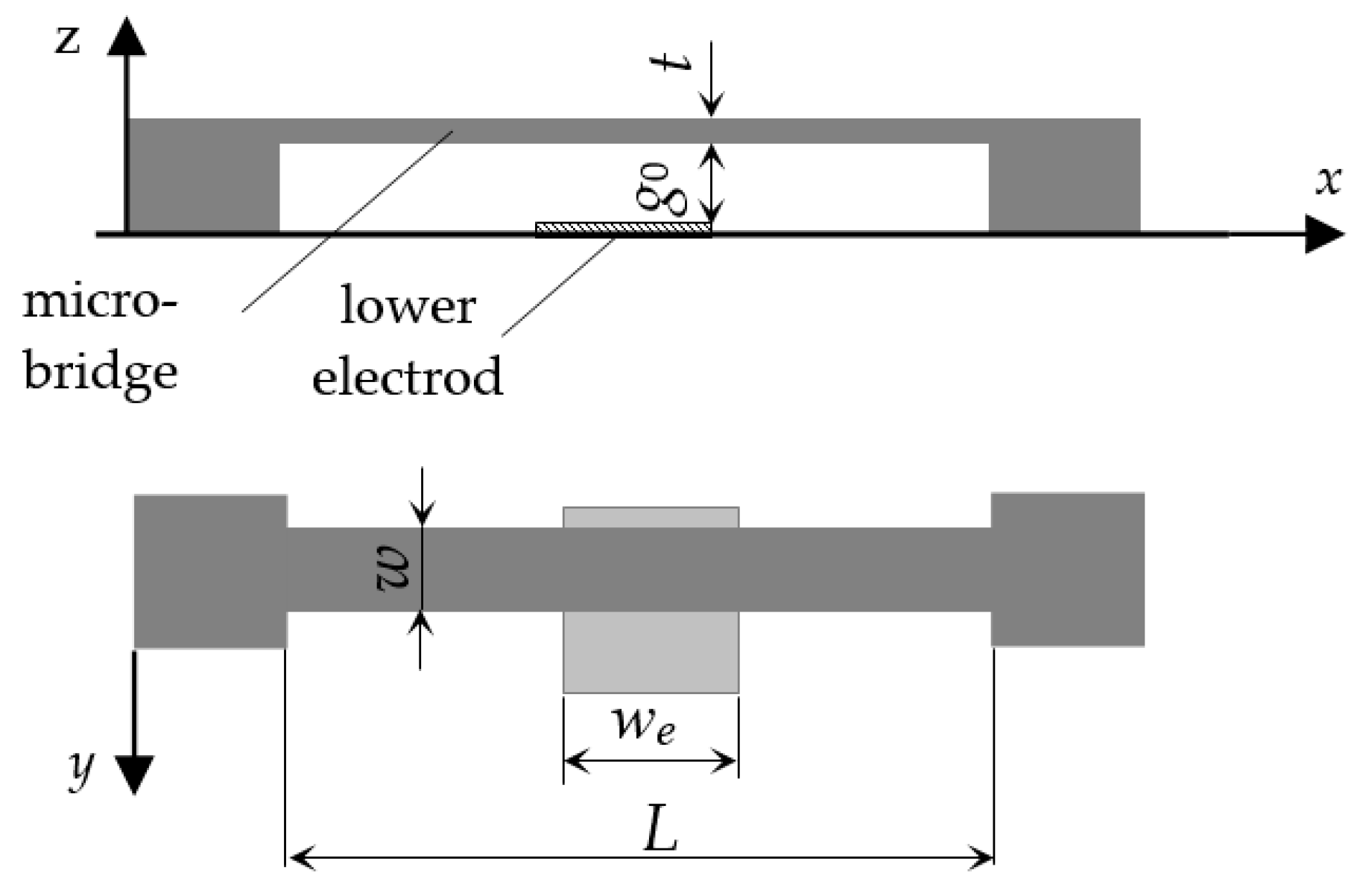
The analytical solution presented above was implemented using MATLAB and was first tested for a polysilicon micro-bridge, whose physical properties are presented in

Table 1. Polysilicon micro-bridge physical properties.

Property	Value
Young’s modulus, E (GPa)	150
Density, $\rho$ (kg/m3)	2330
Specific heat capacity, $c_{\upsilon }$ ($\mathrm{J}/\mathrm{kg}/\mathrm{K}$)	699
Coefficient of thermal expansion, ${\alpha }_T$ (${\mathrm{K}}^{-1}$)	$21.6\cdot {10}^{-6}$
Poisson’s ratio, $\upsilon$ (-)	0.22
Thermal conductivity, k (K)	90
Reference temperature, T0 (K)	293

. The chosen micro-bridge has a reference temperature T₀ = 293 K, length L = 124 µm, width w = 30 µm, and thickness t = 1.9 µm. The gap between the flexible plate and substrate is g₀ = 2 µm and the width of the lower electrode is w_e = 50 µm (Figure 1).

An experimental analysis of the thermo-mechanical behavior was performed on an actual micro-resonator with the properties and dimensions presented above. The experiments were performed using a Vibrometer Analyzer Mechanical Vibrations at the LTAS Laboratory from the University of Liege. During the tests, a DC offset signal of 5 V and a peak amplitude of 5 V of the driving signal were applied in order to bend and oscillate the micro-bridge. The frequency response, the amplitude, and the velocity of oscillations were measured under continuous electrostatic actuation. The tests were performed under ambient conditions. The obtained experimental results regarding the attenuation of the velocity and displacement as a function of the oscillating time were encompassed in [12], where the experimental results regarding the resonant frequency and the quality factor in air and vacuum, together with a validation using finite element prestressed modal analysis, are also presented. For this reason, this micro-resonator was the first chosen to test the analytical model presented in this paper and to validate it. As can be seen in

Table 2. Comparison between analytical and experimental results.

Oscillating Time (h)	Analytical Displacement Attenuation (%)	Experimental Displacement Attenuation (%)
1	33	27
2	55	45
3	69	63
4	79	73

, the theoretical results are in good agreement with the experimental ones. The experimental displacement attenuation is a little smaller due to the fact that the tested micro-bridge had small orifices that were not encompassed in the mathematical model and which slightly reduced the effect of the thermoelastic damping.

After validating the mathematical model, its implementation was included in the MiNaS Toolbox for the thermoelastic analysis of MEMS, which provides a friendly graphical user interface (GUI). Then, it was used to estimate the displacement attenuation after 4 h for several polysilicon micro-bridges of different lengths. The results are included in

Table 3. Analytical results for the investigated micro-bridges.

Length (µm)	Initial Amplitude (m)	Final Amplitude (m)	Displacement Attenuation (%)
124	5.50·10−9	1.14·10−9	79
149	9.54·10−9	4.55·10−9	52
174	15.20·10−9	10.17·10−9	34
199	22.73·10−9	16.36·10−9	28
224	32.42·10−9	28.05·10−9	13

and an example of the toolbox GUI used for the shortest beam is presented in Figure 2.

As can be observed in Table 3, the beam length has a significant influence on the displacement attenuation. The initial and the final amplitude increase with respect to the increase in the micro-bridge length, while the displacement attenuation decreases with the increase in the beam length. Analyzing the values, it can also be seen that for a length increase of 100 µm, the displacement attenuation drops from 79% to 13%.

The influence of the other geometric dimensions was also investigated, considering a total oscillation time of four hours. First, the thickness was varied, while the other dimensions were kept constant (L = 124 µm and w = 30 µm). The displacement attenuation was estimated using the analytical model presented in this paper, and the results are illustrated in Figure 3. The graph shows an almost linear increasing trend of the displacement attenuation with the increase in the beam thickness, reaching a maximum value of 86% for a thickness of 2 µm. However, when studying the influence of the third geometric dimension of the beam while keeping the other two constant (L = 124 µm and t = 1.9 µm), it was noticed that the displacement attenuation remained stable regardless of the variation of the beam width values.

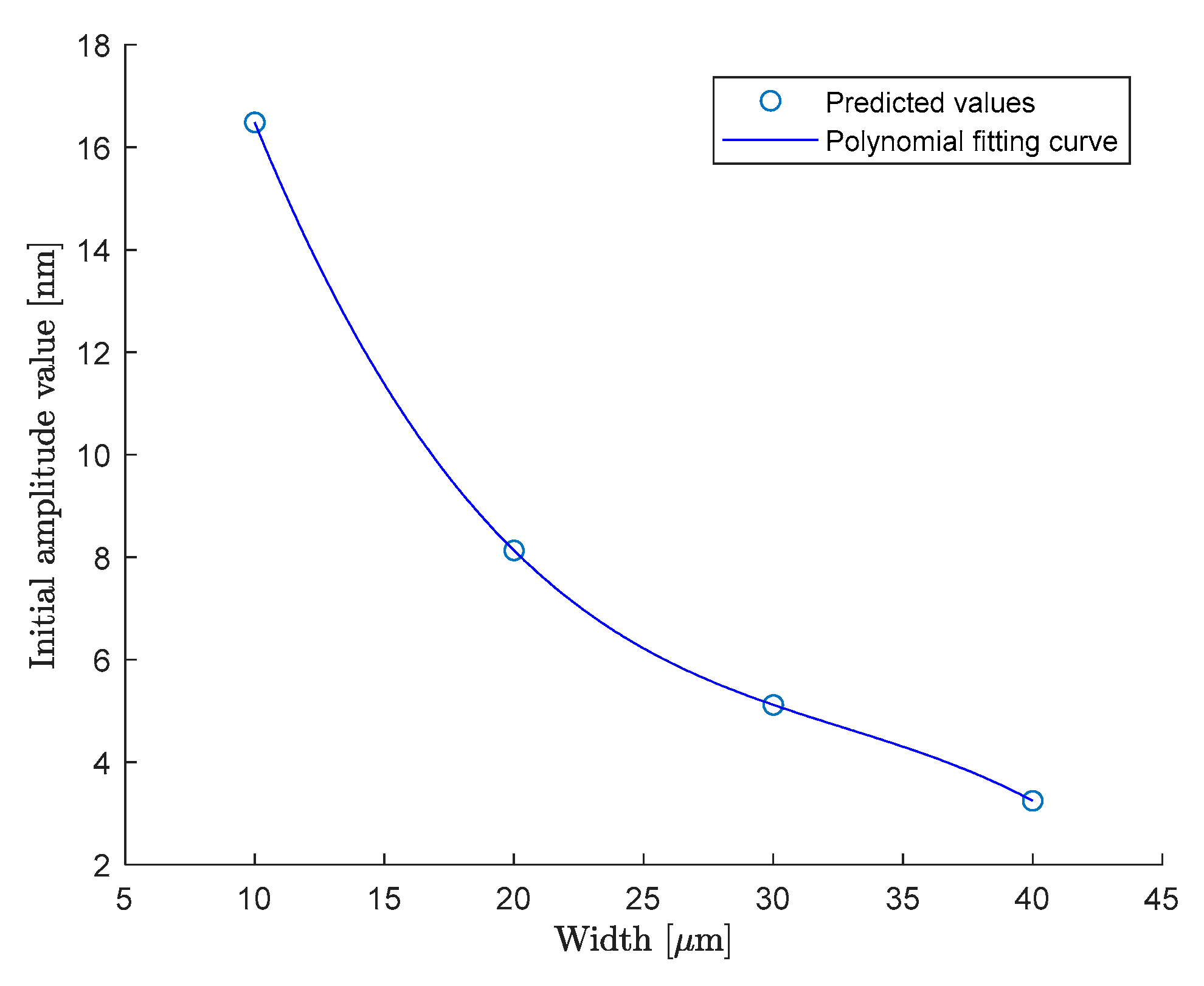
The influence of the geometric dimensions on the initial amplitude value was also investigated by varying just one dimension while keeping the other constant at the same values, as when investigating the influence on the displacement attenuation. The considered time of oscillation was four hours. The obtained results are presented in Figure 4 and Figure 5, together with a third-degree polynomial fitting curve to facilitate the extrapolation of these results. As can be seen, both graphs show convex curvilinear trends and depict an approximately 80% decrease in the initial amplitude value. However, in Figure 4, the decrease in the initial value of the amplitude is obtained for an increase of four times the values of the beam width, while in Figure 5, the same percentage decrease is more dramatic because it was obtained for an increase of approximately two times the value of the beam thickness.

6. Conclusions

Robotics is one of the engineering fields that has been impacted by the development of MEMS and the research surrounding them. In order to have high reliability (micro-)robots, it is required that the MEMS resonators used in the robot design do not fail during the operation.

The energy dissipation process, also known as thermoelastic damping, that occurs when a MEMS structure is subjected to cyclic motion is one of the most significant loss mechanisms in MEMS devices. Therefore, micro-resonators should ensure by design a minimum loss of energy in order to reduce its influence on the amplitude, velocity, and resonant frequency of the beam.

This paper presents an analytical model for thermoelastic damping in micro-bridges derived from an existing one. After validation, the presented model was applied to several micro-bridges with different dimensions in order to study the influence of the geometric dimensions on the deflection amplitude decrease and on the initial and final amplitude values.

It was determined that the displacement amplitude attenuation after four hours increases almost linearly with the increase in the beam thickness, and it decreases with the increase in the beam length, but it is not affected by the increase in the beam width. The initial and final amplitude values decrease with the increase in the width and thickness of the beam, while they increase with the increase in the beam length.

The analytical model presented in this paper, as well as the simulations performed based on it, allow for the determination of an optimal design of MEMS resonators for each specific application. Characteristics like the geometric dimensions of the micro-beams could be established faster and cheaper than using other methods, such as trial and error.