Probabilistic Study of the Effect of Anti-Epileptic Drugs Under Uncertainty: Cost-Effectiveness Analysis
Abstract
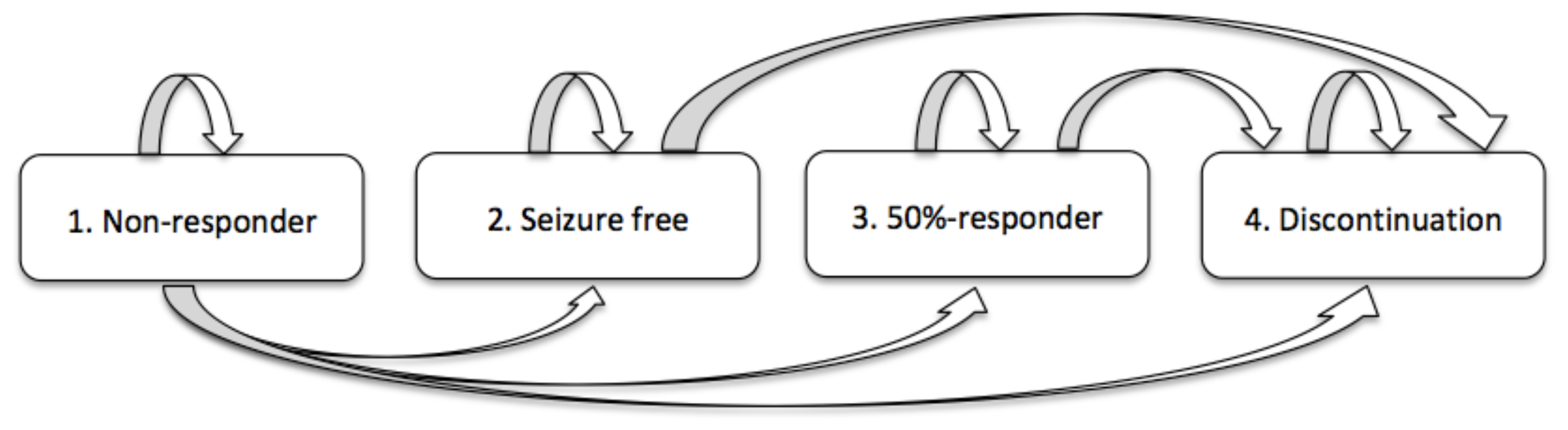
1. Motivation and Preliminaries
2. Solving the Randomized Model
2.1. Computing the 1-PDF of
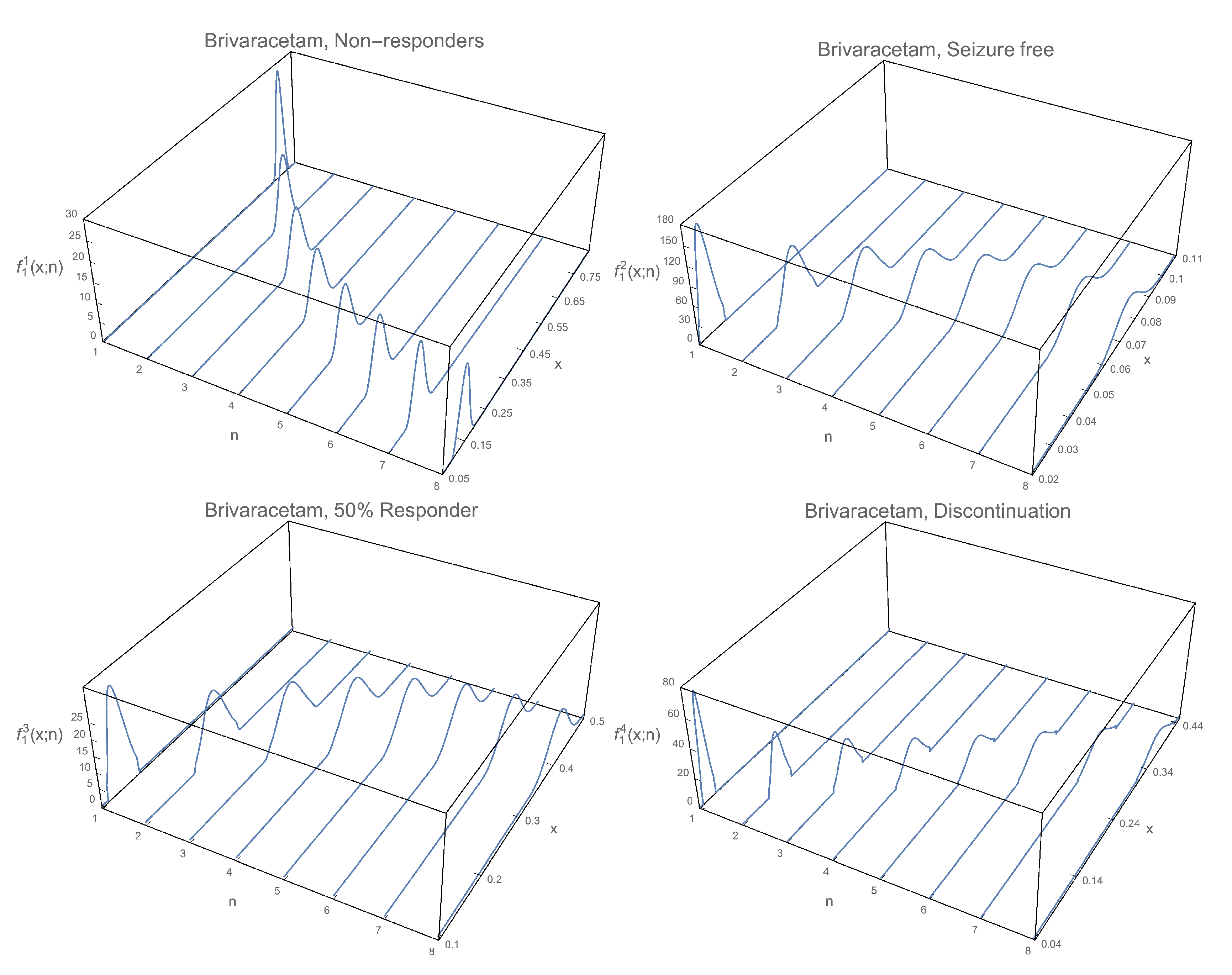
2.1.1. 1-PDF of
2.1.2. 1-PDF of
2.1.3. 1-PDF of
2.1.4. 1-PDF of
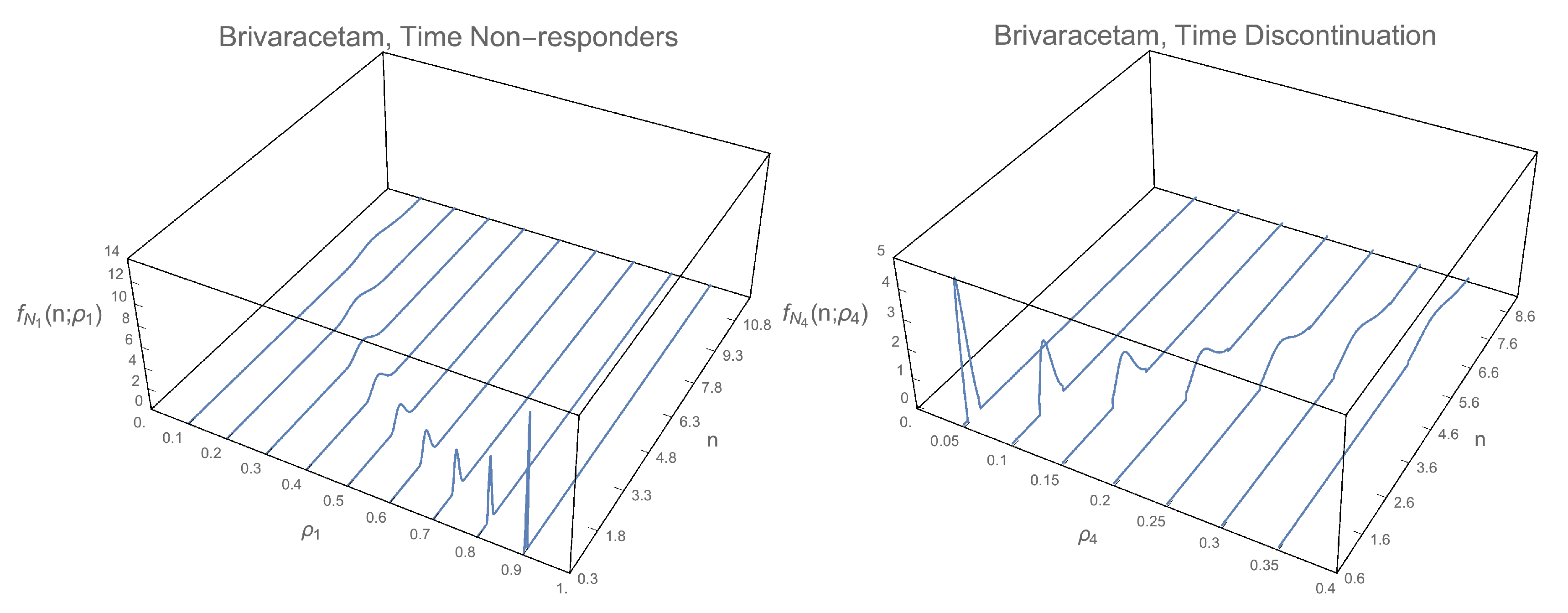
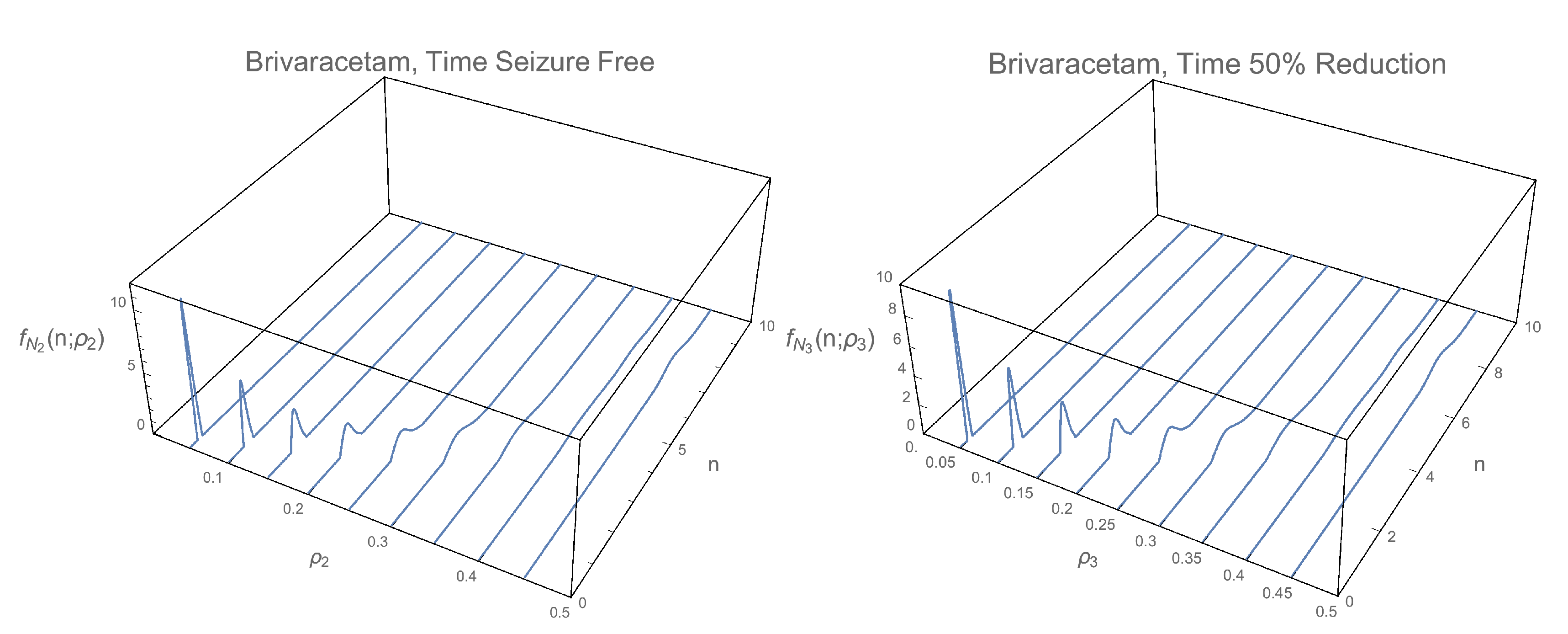
2.2. Computing the Pdf of the Time
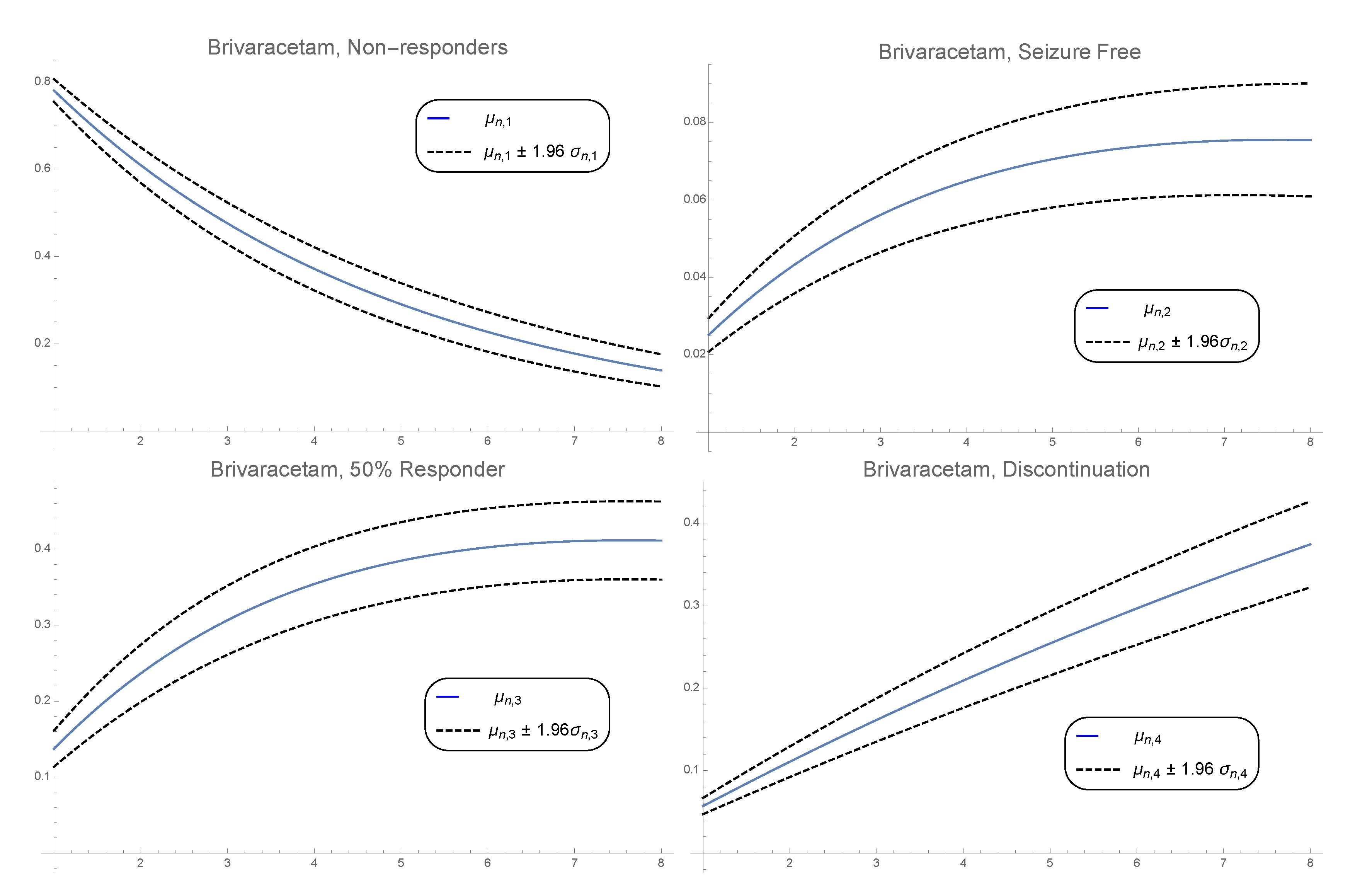
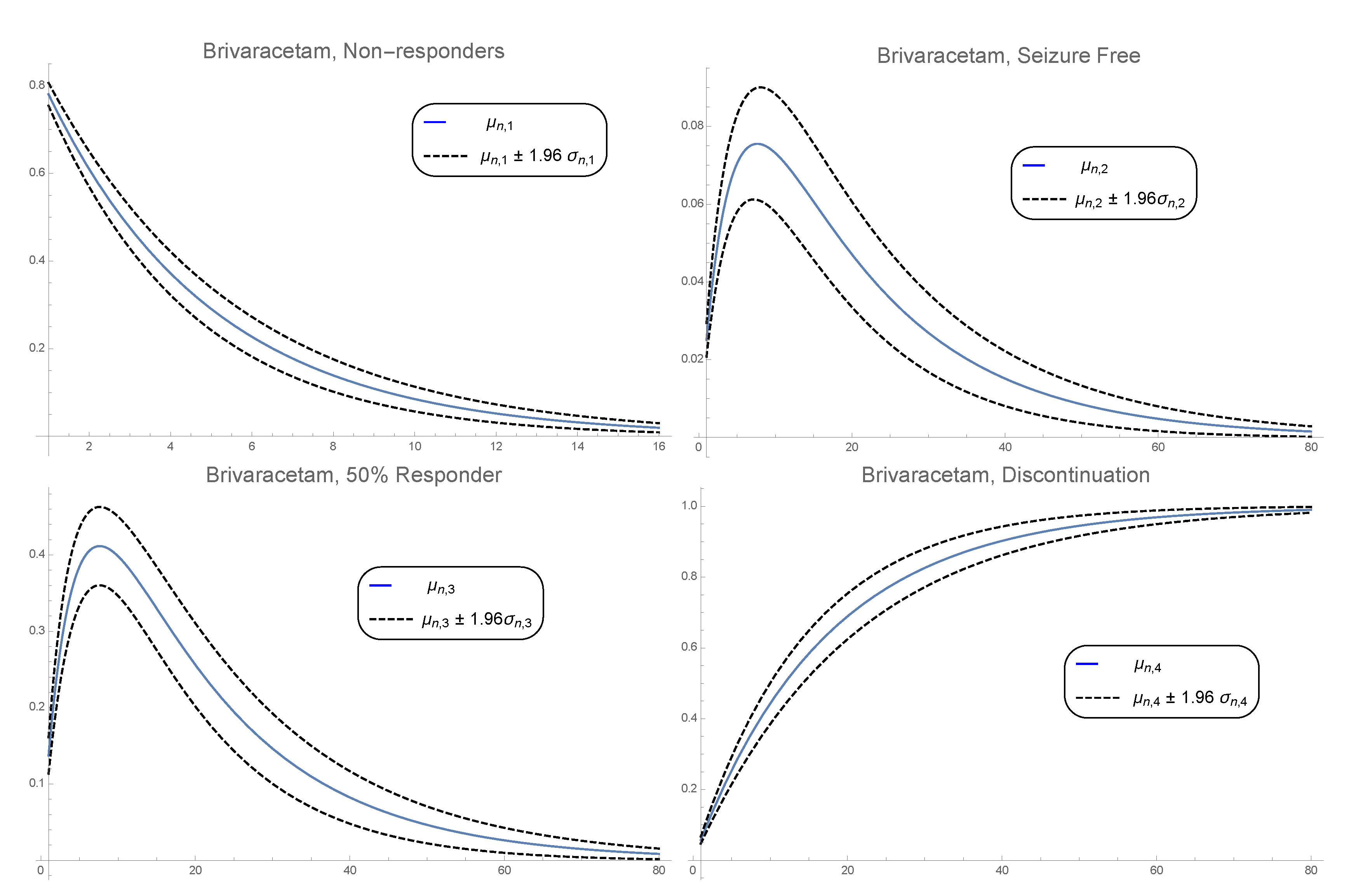
2.2.1. PDF of
2.2.2. PDF of
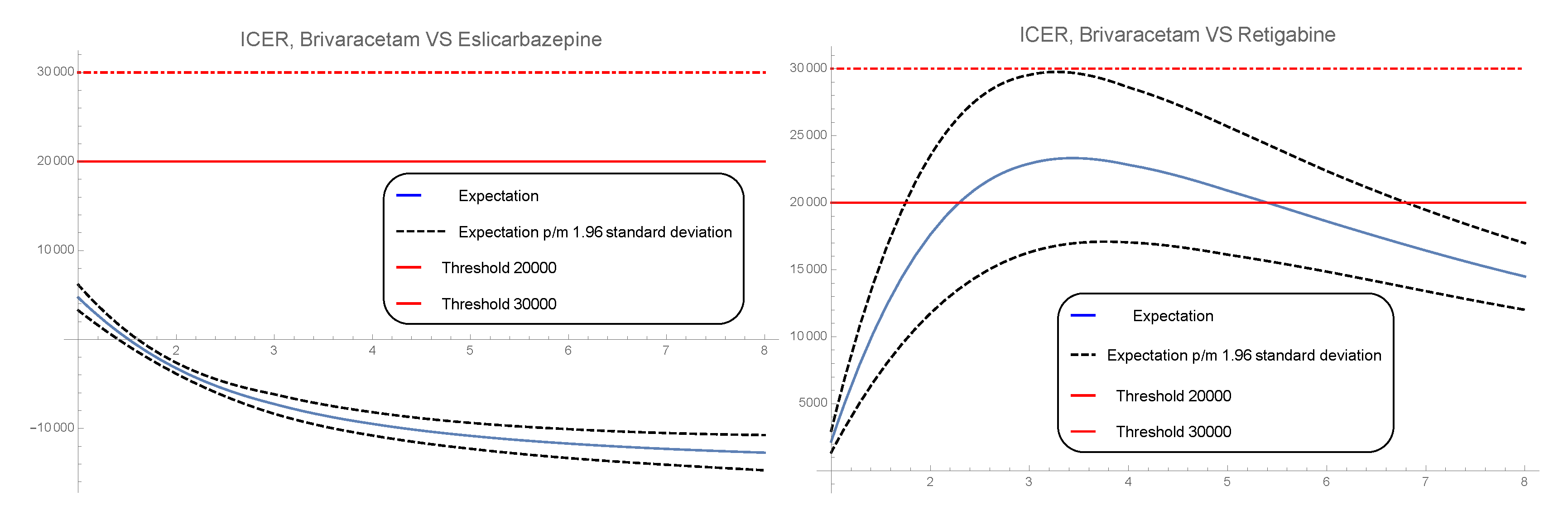
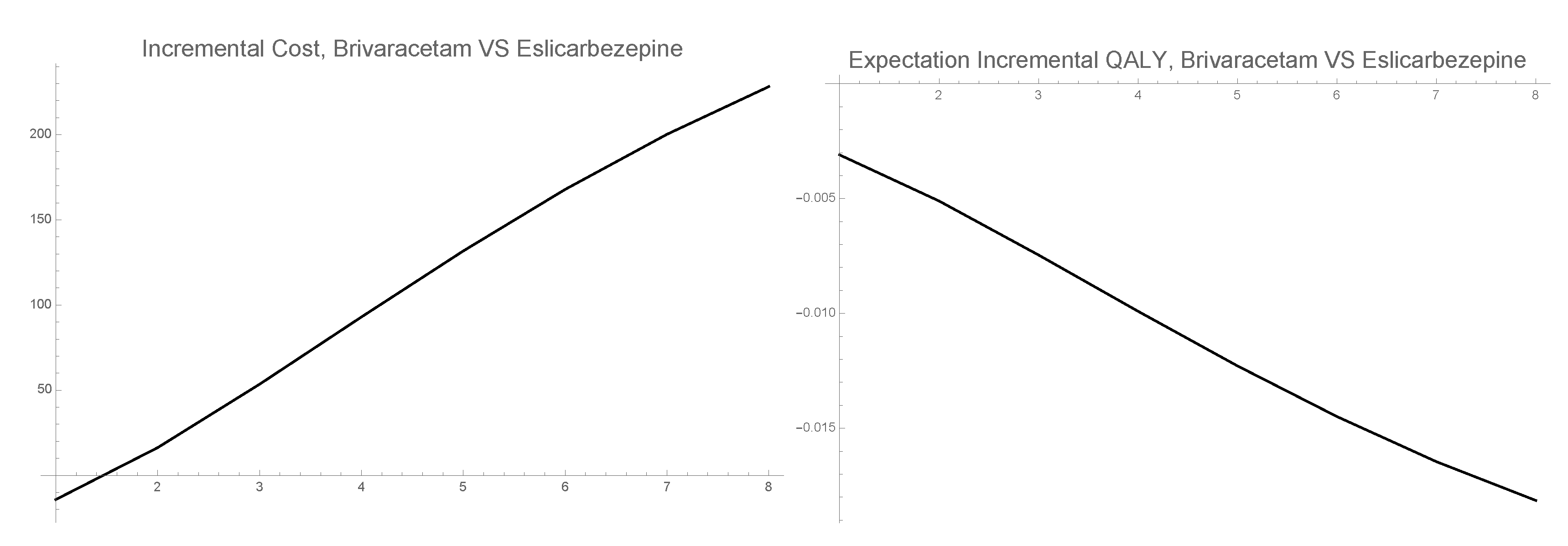
2.3. Computing the Approximated Pdf of the Incremental Cost-Effectiveness Ratio (Icer)
- is the daily AEDs cost.
- is the average cost of concomitant Monotherapy.
- is the Titration total cost.
3. Numerical Example
3.1. 1-Pdf of the Solution Sp
3.2. Pdf of the Time
- Step 1: To sample 500,000 values of the form , according with the distributions assumed for RVs , and .
- Step 2: For each sample in Step 1 we solve the non-linear equationto calculate the values n of , using Newton-Raphson method. From these values, in the subsequent development, the minimum n is selected.
- Step 3: To plot the histogram with the 500,000 values of n. An approximation of the PDF of is obtained by normalizing this histogram.
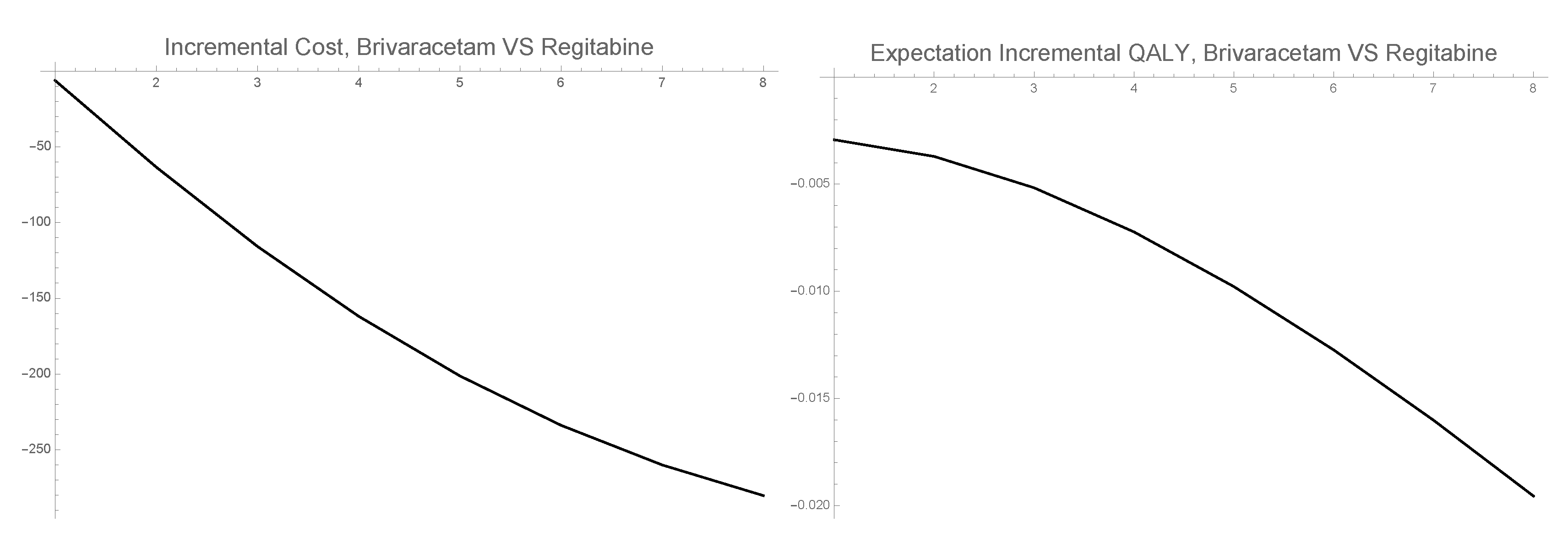
3.3. 1-PDF of ICER
- Probabilities of response, partial response and discontinuation [21]. Brivaracetam: , , . Eslicarbazepine: , , . Retigabine: , , . These quantities will be used to calculate the different expectation in the cost and the effectiveness formulas, , where is the solution SP in cycle j of the state i given in Formula (6).
- Probabilities of adverse events, Ataxia, Dizziness, Fatigue, Nausea and Somnolence [23] As previously, these probabilities will be considered independent absolutely continuous RVs. We choose for each RV a Beta distribution with parameters a and b calculated as before considering the following mean . Brivaracetam: , , , , . Eslicarbazepine: , , , , . Retigabine: , , , , .
- Titration cost (Total cost) [26]. Brivaracetam: . Eslicarbazepine: . Retigabine: .
- Utility of each state in all treatments: , , , .
- Utilities of adverse events [23]: , , , and .
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Magiorkinis, E.; Sidiropoulou, K.; Diamantis, A. Hallmarks in the History of Epilepsy: From Antiquity Till the Twentieth Century; Novel Aspects on Epilepsy; IntechOpen: London, UK, 2011; pp. 131–394. ISBN 978-953-307-678-2. [Google Scholar]
- García Ramos, R.; Pastor, A.; Masjuan, J.; Sánchez, C.; Gil, A. FEEN report on epilepsy in Spain. Neurología 2011, 26, 548–555. [Google Scholar] [CrossRef] [PubMed]
- WHO. Epilepsy. Available online: http://www.who.int/mediacentre/factsheets/fs999/en/ (accessed on 8 July 2020).
- Instituto Nacional de Estadística (INE). Población Estimada en España. Available online: http://www.ine.es/inebaseDYN/cp30321 (accessed on 15 January 2015).
- Trescher, W.; Lesser, R. Epilepsias. In Neurología Clínica; Bradley, W., Daroff, R., Fenichel, G., Jankovic, J., Eds.; Elsevier Dorma SL: Barcelona, Spain, 2005; pp. 1929–1977. [Google Scholar]
- Epilepsy Overview. Encyclopedia of the Neurological Sciences; Academic Press: Cambridge, MA, USA, 2003.
- Duncan, J.; Sander, J.; Sisodiya, S.; Walker, M. Adult epilepsy. Lancet 2006, 367, 1087–1100. [Google Scholar] [CrossRef]
- Brodie, M. Practical use of newer antiepileptic drugs as adjunctive therapy in focal epilepsy. CNS Drugs 2015, 29, 893–904. [Google Scholar] [CrossRef] [PubMed]
- European Medicines Agency (EMA). EPARs for Authorised Medicinal Products for Human Use Stelara. Available online: http://www.emea.europa.eu/humandocs/Humans/EPAR/stelara/stelara.htm (accessed on 10 January 2016).
- Kristian, B.; Wachtmeister, K.; Stefan, F.; Forsgren, L. Retigabine as add-on treatment of refractory epilepsy—A cost-utility study in a Swedish setting. Acta Neurol. Scand. 2013, 127, 419–426. [Google Scholar] [CrossRef] [PubMed]
- Martyn-St James, M.; Glanville, J.; McCool, R.; Duffy, S.; Cooper, J.; Hugel, P.; Lane, P.W. The efficacy and safety of retigabine and other adjunctive treatments for refractory partial epilepsy: A systematic review and indirect comparison. Seizure 2012, 21, 665–678. [Google Scholar] [CrossRef] [PubMed]
- Cortés, J.; Navarro-Quiles, A.; Romero, J.; Roselló, M. Randomizing the parameters of a Markov chain to model the stroke disease: A technical generalization of established computational methodologies towards improving real applications. J. Comput. Appl. Math. 2017, 324, 225–240. [Google Scholar] [CrossRef]
- Sonnenberg, F.A.; Beck, J.R. Markov Models in Medical Decision Making: A Practical Guide. Med. Decis. Mak. 1993, 13, 322–338. [Google Scholar] [CrossRef]
- Markov, A. Rasprostranenie zakona bol’shih chisel na velichiny, zavisyaschie drug ot druga. Izvestiya Fiziko-Matematicheskogo Obschestva Kazan. Univ. 1906, 15, 135–156. [Google Scholar]
- Barrachina-Martínez, I.; Vivas-Consuelo, D.; Piera-Barbastre, A. Budget Impact Analysis of Brivaracetam Adjunctive Therapy for Partial-Onset Epileptic Seizures in Valencia Community, Spain. Clin. Drug Investig. 2018, 38, 353–363. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, S.; Mauskopf, J.; Augustovski, F.; Caro, J.; Lee, K.; Minchin, M.; Orlewska, E.; Penna, P.; Rodriguez Barrios, J.; Shau, W. Budget Impact Analysis Principles of Good Practice: Report of the ISPOR 2012 Budget Impact Analysis Good Practice II Task Force. Value Health 2014, 17, 5–14. [Google Scholar] [CrossRef] [PubMed]
- Cortés, J.; Navarro-Quiles, A.; Romero, J.; Roselló, M. Some results about randomized binary Markov chains: Theory, computing and applications. Int. J. Comput. Math. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Soong, T. Random Differential Equations in Science and Engineering; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Prieto, L.; Sacristán, J.; Antoñanzas, F.; Rubio-Terrés, C.; Pinto, J.; Rovira, J. Análisis coste-efectividad en la evaluación económica de intervenciones sanitarias. Med. Clin. 2004, 122, 505–510. [Google Scholar] [CrossRef]
- Karlsson, G.; Johannesson, M. The decision rule of cost-effectiveness analysis. PharmacoEconomics 1996, 9, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Borghs, S. Brivaracetam-Network Meta-Analysis of Branded AEDs; UCB BresMed: Brussels, Belgium, 2015. [Google Scholar]
- Chhatwal, J.; Jayasuriya, S.; Elbasha, E. Changing Cycle Lengths State-Transition Models: Doing it the Right Way. ISPOR Connect. 2014, 20, 12–14. [Google Scholar]
- Mulhern, B.; Rowen, D.; Snape, D.; Jacoby, A.; Marson, T.; Hughes, D.; Baker, D.; Brazier, J. Valuations of epilepsy-specific health states: A comparison of patients with epilepsy and the general population. Epilepsy Behav. 2014, 36, 12–17. [Google Scholar] [CrossRef]
- BOE. Real Decreto-Ley 8/2010, de 20 de Mayo, Por el Que se Adoptan Medidas Extraordinarias Para la Reducción del Déficit Público. Boletín Oficial del Estado, 20 May 2010.
- de CO de BOTfarma, F.C. BOT Base de Datos del Medicamento. Available online: https://botplusweb.portalfarma.com/ (accessed on 8 July 2020).
- AEMPS. Informe de Posicionamiento Terapéutico de Brivaracetam (Briviact) en Epilepsia. Available online: https://www.aemps.gob.es/medicamentosUsoHumano/informesPublicos/docs/IPTbrivaracetam-Briviact-epilepsia.pdf (accessed on 17 January 2017).
- Sacristán, J.; Oliva, J.; Del Llano, J.; Prieto, L.; Pinto, J. ¿Qué es una tecnología sanitaria eficiente en España? Gac. Sanit. 2002, 4, 334–343. [Google Scholar] [CrossRef]
- Bertram, Y.; Lauer, J.; Joncheere, K.; Edejer, T.; Hutubessy, R.; Kieny, M.; Hill, S. Cost-effectiveness thresholds: Pros and cons. Bull. World Health Organ. 2016, 94, 925–930. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrachina-Martínez, I.; Navarro-Quiles, A.; Ramos, M.; Romero, J.-V.; Roselló, M.-D.; Vivas-Consuelo, D. Probabilistic Study of the Effect of Anti-Epileptic Drugs Under Uncertainty: Cost-Effectiveness Analysis. Mathematics 2020, 8, 1120. https://doi.org/10.3390/math8071120
Barrachina-Martínez I, Navarro-Quiles A, Ramos M, Romero J-V, Roselló M-D, Vivas-Consuelo D. Probabilistic Study of the Effect of Anti-Epileptic Drugs Under Uncertainty: Cost-Effectiveness Analysis. Mathematics. 2020; 8(7):1120. https://doi.org/10.3390/math8071120
Chicago/Turabian StyleBarrachina-Martínez, Isabel, Ana Navarro-Quiles, Marta Ramos, José-Vicente Romero, María-Dolores Roselló, and David Vivas-Consuelo. 2020. "Probabilistic Study of the Effect of Anti-Epileptic Drugs Under Uncertainty: Cost-Effectiveness Analysis" Mathematics 8, no. 7: 1120. https://doi.org/10.3390/math8071120
APA StyleBarrachina-Martínez, I., Navarro-Quiles, A., Ramos, M., Romero, J.-V., Roselló, M.-D., & Vivas-Consuelo, D. (2020). Probabilistic Study of the Effect of Anti-Epileptic Drugs Under Uncertainty: Cost-Effectiveness Analysis. Mathematics, 8(7), 1120. https://doi.org/10.3390/math8071120






