1. Introduction
Finding root of a nonlinear equation
is a very important and interesting problem in many branches of science and engineering. In this work, we examine derivative-free numerical methods to find a multiple root (say,
) with multiplicity
of the equation
that means
and
. Newton’s method [
1] is the most widely used basic method for finding multiple roots, which is given by
A number of modified methods, with or without the base of Newton’s method, have been elaborated and analyzed in literature, see [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14]. These methods use derivatives of either first order or both first and second order in the iterative scheme. Contrary to this, higher order methods without derivatives to calculate multiple roots are yet to be examined. These methods are very useful in the problems where the derivative
is cumbersome to evaluate or is costly to compute. The derivative-free counterpart of classical Newton method (
1) is the Traub–Steffensen method [
15]. The method uses the approximation
or
for the derivative
in the Newton method (
1). Here,
and
is a first order divided difference. Thereby, the method (
1) takes the form of the Traub–Steffensen scheme defined as
The Traub–Steffensen method (
2) is a prominent improvement of the Newton method because it maintains the quadratic convergence without adding any derivative.
Unlike Newton-like methods, the Traub–Steffensen-like methods are difficult to construct. Recently, a family of two-step Traub–Steffensen-like methods with fourth order convergence has been proposed in [
16]. In terms of computational cost, the methods of [
16] use three function evaluations per iteration and thus possess optimal fourth order convergence according to Kung–Traub conjecture (see [
17]). This hypothesis states that multi-point methods without memory requiring
m functional evaluations can attain the convergence order
called optimal order. Such methods are usually known as optimal methods. Our aim in this work is to develop derivative-free multiple root methods of good computational efficiency, which is to say, the methods of higher convergence order with the amount of computational work as small as we please. Consequently, we introduce a class of Traub–Steffensen-like derivative-free fourth order methods that require three new pieces of information of the function
and therefore have optimal fourth order convergence according to Kung–Traub conjecture. The iterative formula consists of two steps with Traub–Steffensen iteration (
2) in the first step, whereas there is Traub–Steffensen-like iteration in the second step. Performance is tested numerically on many problems of different kinds. Moreover, comparison of performance with existing modified Newton-like methods verifies the robust and efficient nature of the proposed methods.
We summarize the contents of paper. In
Section 2, the scheme of fourth order iteration is formulated and convergence order is studied separately for different cases. The main result, showing the unification of different cases, is studied in
Section 3.
Section 4 contains the basins of attractors drawn to assess the convergence domains of new methods. In
Section 5, numerical experiments are performed on different problems to demonstrate accuracy and efficiency of the methods. Concluding remarks about the work are reported in
Section 6.
2. Development of a Novel Scheme
Researchers have used different approaches to develop higher order iterative methods for solving nonlinear equations. Some of them are: Interpolation approach, Sampling approach, Composition approach, Geometrical approach, Adomian approach, and Weight-function approach. Of these, the Weight-function approach has been most popular in recent times; see, for example, Refs. [
10,
13,
14,
18,
19] and references therein. Using this approach, we consider the following two-step iterative scheme for finding multiple root with multiplicity
:
where
,
,
and
is analytic in the neighborhood of zero. This iterative scheme is weighted by the factors
and
, hence the name weight-factor or weight-function technique.
Note that
and
are one-to-
multi-valued functions, so we consider their principal analytic branches [
18]. Hence, it is convenient to treat them as the principal root. For example, let us consider the case of
. The principal root is given by
, with
for
; this convention of
for
agrees with that of
command of Mathematica [
20] to be employed later in the sections of basins of attraction and numerical experiments. Similarly, we treat for
.
In the sequel, we prove fourth order of convergence of the proposed iterative scheme (
3). For simplicity, the results are obtained separately for the cases depending upon the multiplicity
. Firstly, we consider the case
.
Theorem 1.
Assume that is a zero with multiplicity of the function , where is sufficiently differentiable in a domain containing α. Suppose that the initial point is closer to α; then, the order of convergence of the scheme (3) is at least four, provided that the weight-function satisfies the conditions , , and . Proof. Assume that
is the error at the
k-th stage. Expanding
about
using the Taylor series keeping in mind that
,
and
, we have that
where
for
.
Similarly, Taylor series expansion of
is
where
By using (
4) and (
5) in the first step of (
3), we obtain
In addition, we have that
Using (
4), (
5) and (
7), we further obtain
and
Taylor expansion of the weight function
in the neighborhood of origin up to third-order terms is given by
Using (
4)–(
11) in the last step of (
3), we have
where
,
The expressions of
and
being very lengthy have not been produced explicitly.
We can obtain at least fourth order convergence if we set coefficients of
,
and
simultaneously equal to zero. Then, some simple calculations yield
Using (
13) in (
12), we will obtain final error equation
Thus, the theorem is proved. □
Next, we prove the following theorem for case .
Theorem 2.
Using assumptions of Theorem 1, the convergence order of scheme (3) for the case is at least 4, if , , and . Proof. Taking into account that
,
,
and
, the Taylor series development of
about
gives
where
for
.
Expanding
about
where
Then, using (
15) and (
16) in the first step of (
3), we obtain
Expansion of
about
yields
Then, from (
15), (
16), and (
18), it follows that
and
Developing weight function
about origin by the Taylor series expansion,
By using (
15)–(
22) in the last step of (
3), we have
where
,
To obtain fourth order convergence, it is sufficient to set coefficients of
,
, and
simultaneously equal to zero. This process will yield
Then, error equation (
23) is given by
Hence, the result is proved. □
Remark 1.
We can observe from the above results that the number of conditions on is 3 corresponding to the cases to attain the fourth order convergence of the method (3). These cases also satisfy common conditions: , , . Their error equations also contain the term involving the parameter β. However, for the cases , it has been seen that the error equation in each such case does not contain β term. We shall prove this fact in the next section. 4. Basins of Attraction
In this section, we present complex geometry of the above considered method with a tool, namely basin of attraction, by applying the method to some complex polynomials
. Basin of attraction of the root is an important geometrical tool for comparing convergence regions of the iterative methods [
21,
22,
23]. To start with, let us recall some basic ideas concerned with this graphical tool.
Let
be a rational mapping on the Riemann sphere. We define orbit of a point
as the set
. A point
is a fixed point of the rational function
R if it satisfies the equation
. A point
is said to be periodic with period
if
, where
m is the smallest such integer. A point
is called attracting if
, repelling if
, neutral if
and super attracting if
. Assume that
is an attracting fixed point of the rational map
R. Then, the basin of attraction of
is defined as
The set of points whose orbits tend to an attracting fixed point is called the Fatou set. The complementary set, called the Julia set, is the closure of the set of repelling fixed points, which establishes the boundaries between the basins of the roots. Attraction basins allow us to assess those starting points which converge to the concerned root of a polynomial when we apply an iterative method, so we can visualize which points are good options as starting points and which are not.
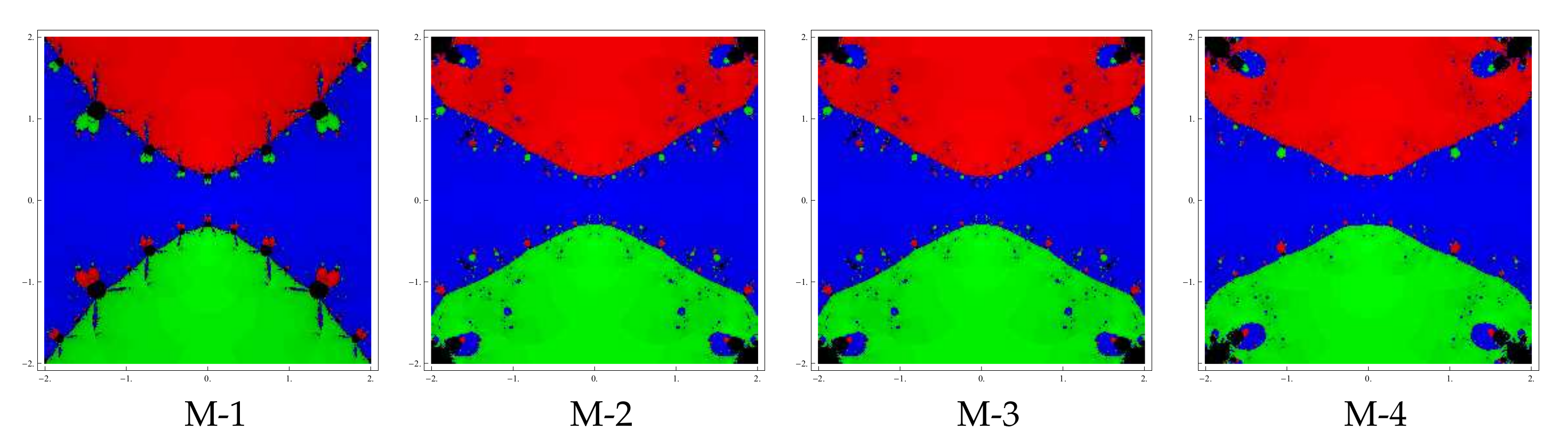
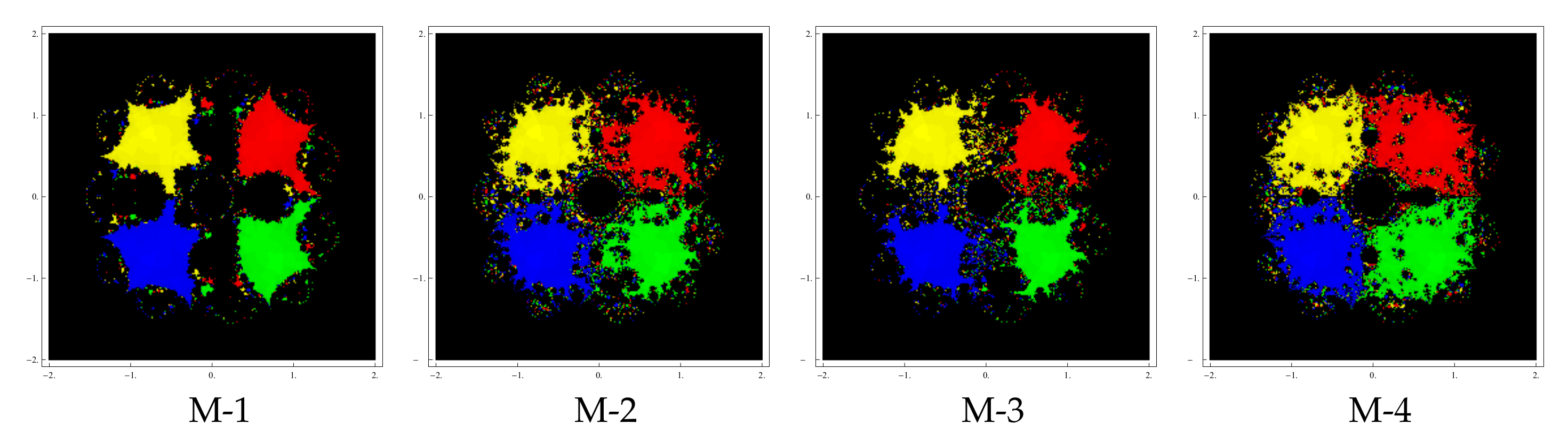
We select as the initial point belonging to D, where D is a rectangular region in containing all the roots of the equation An iterative method starting with a point may converge to the zero of the function or may diverge. To assess the basins, we consider as the stopping criterion for convergence restricted to 25 iterations. If this tolerance is not achieved in the required iterations, the procedure is dismissed with the result showing the divergence of the iteration function started from . While drawing the basins, the following criterion is adopted: A color is allotted to every initial guess in the attraction basin of a zero. If the iterative formula that begins at point converges, then it forms the basins of attraction with that assigned color and, if the formula fails to converge in the required number of iterations, then it is painted black.
To view the complex dynamics, the proposed methods are applied on the following three problems:
Test problem 1. Consider the polynomial
having two zeros
with multiplicity
. The attraction basins for this polynomial are shown in
Figure 1,
Figure 2 and
Figure 3 corresponding to the choices
of parameter
. A color is assigned to each basin of attraction of a zero. In particular, red and green colors have been allocated to the basins of attraction of the zeros
and
, respectively.
Test problem 2. Consider the polynomial
which has three zeros
with multiplicities
. Basins of attractors assessed by methods for this polynomial are drawn in
Figure 4,
Figure 5 and
Figure 6 corresponding to choices
The corresponding basin of a zero is identified by a color assigned to it. For example, green, red, and blue colors have been assigned corresponding to
,
, and 0.
Test problem 3. Next, let us consider the polynomial
that has four zeros
with multiplicity
. The basins of attractors of zeros are shown in
Figure 7,
Figure 8 and
Figure 9, for choices of the parameter
A color is assigned to each basin of attraction of a zero. In particular, we assign yellow, blue, red, and green colors to
,
,
and
, respectively.
Estimation of
values plays an important role in the selection of those members of family (
3) which possess good convergence behavior. This is also the reason why different values of
have been chosen to assess the basins. The above graphics clearly indicate that basins are becoming wider with the smaller values of parameter
. Moreover, the black zones (used to indicate divergence zones) are also diminishing as
assumes small values. Thus, we conclude this section with a remark that the convergence of proposed methods is better for smaller values of parameter
.
5. Numerical Results
In order to validate of theoretical results that have been shown in previous sections, the new methods M1, M2, M3, and M4 are tested numerically by implementing them on some nonlinear equations. Moreover, these are compared with some existing optimal fourth order Newton-like methods. For example, we consider the methods by Li–Liao–Cheng [
7], Li–Cheng–Neta [
8], Sharma–Sharma [
9], Zhou–Chen–Song [
10], Soleymani–Babajee–Lotfi [
12], and Kansal–Kanwar–Bhatia [
14]. The methods are expressed as follows:
Li–Liao–Cheng method (LLCM):
Li–Cheng–Neta method (LCNM):
where
Sharma–Sharma method (SSM):
Zhou–Chen–Song method (ZCSM):
Soleymani–Babajee–Lotfi method (SBLM):
where
.
Kansal–Kanwar–Bhatia method (KKBM):
where
Computations are performed in the programming package of Mathematica software [
20] in a PC with specifications: Intel(R) Pentium(R) CPU B960 @ 2.20 GHz, 2.20 GHz (32-bit Operating System) Microsoft Windows 7 Professional and 4 GB RAM. Numerical tests are performed by choosing the value
for parameter
in new methods. The tabulated results of the methods displayed in
Table 1 include: (i) iteration number
required to obtain the desired solution satisfying the condition
, (ii) estimated error
in the consecutive first three iterations, (iii) calculated convergence order (CCO), and (iv) time consumed (CPU time in seconds) in execution of a program, which is measured by the command “TimeUsed[ ]”. The calculated convergence order (CCO) is computed by the well-known formula (see [
24])
The problems considered for numerical testing are shown in
Table 2.
From the computed results in
Table 1, we can observe the good convergence behavior of the proposed methods. The reason for good convergence is the increase in accuracy of the successive approximations as is evident from values of the differences
. This also implies to stable nature of the methods. Moreover, the approximations to solutions computed by the proposed methods have either greater or equal accuracy than those computed by existing counterparts. The value 0 of
indicates that the stopping criterion
has been satisfied at this stage. From the calculation of calculated convergence order as shown in the second last column in each table, we have verified the theoretical fourth order of convergence. The robustness of new algorithms can also be judged by the fact that the used CPU time is less than that of the CPU time by the existing techniques. This conclusion is also confirmed by similar numerical experiments on many other different problems.