Construction of Different Types Analytic Solutions for the Zhiber-Shabat Equation
Abstract
:1. Introduction
2. -Expansion Method
3. -Expansion Method
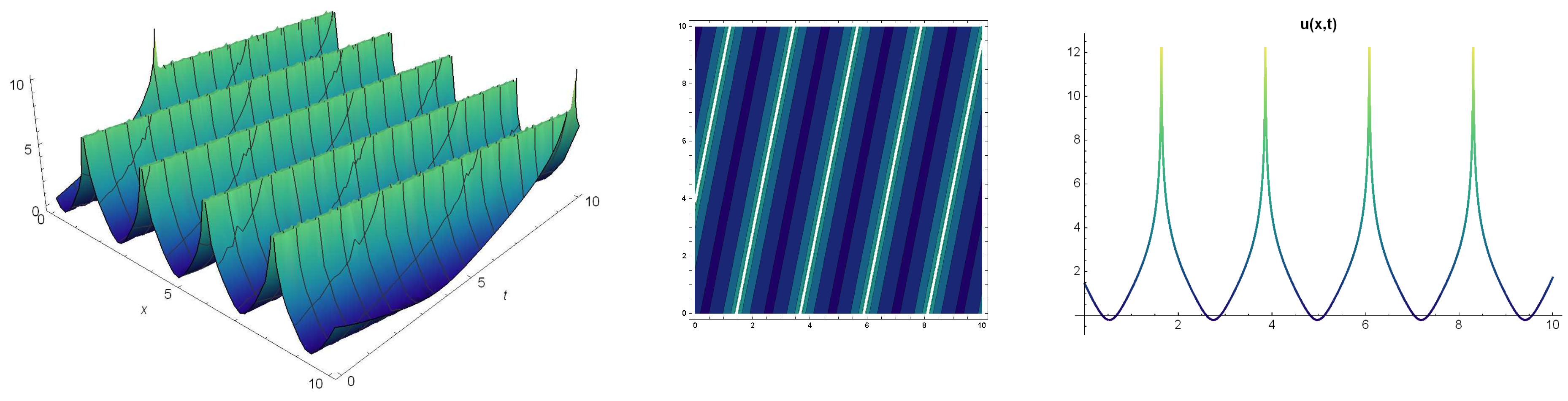
4. Solutions of the (Z-S) Equation Using -Expansion Method
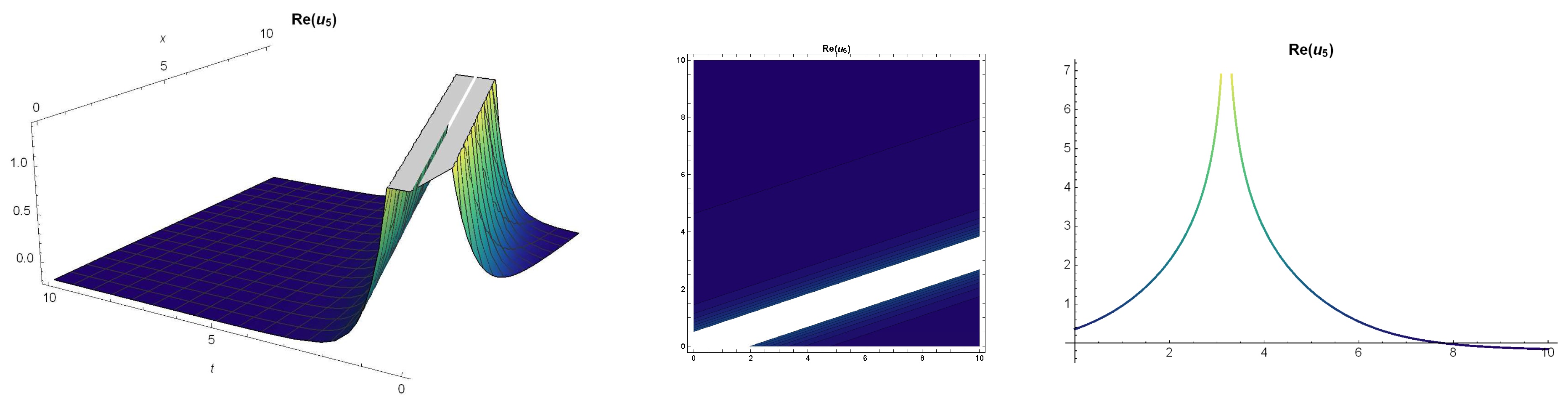
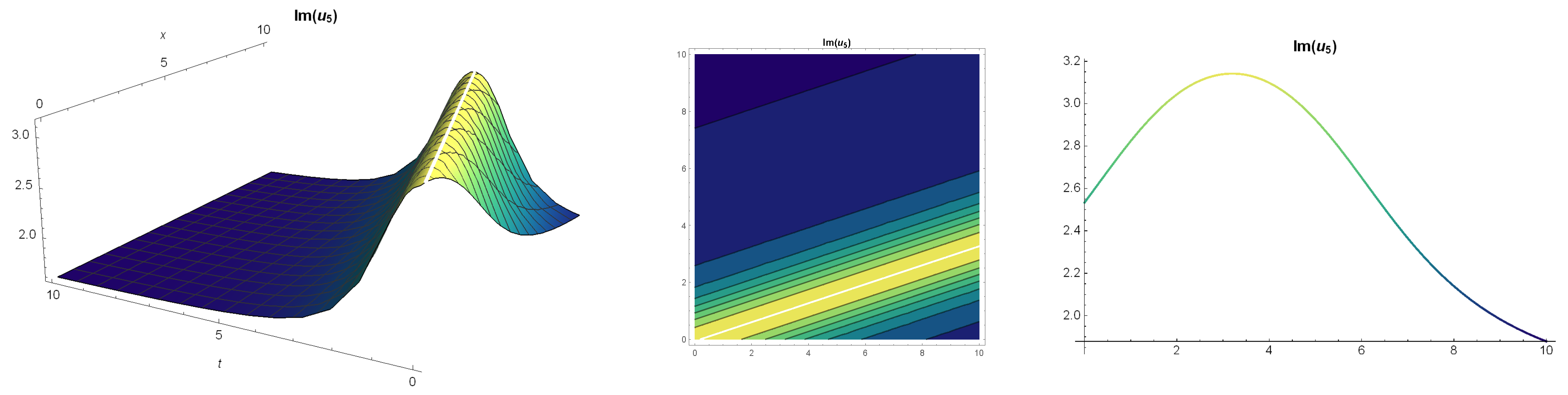
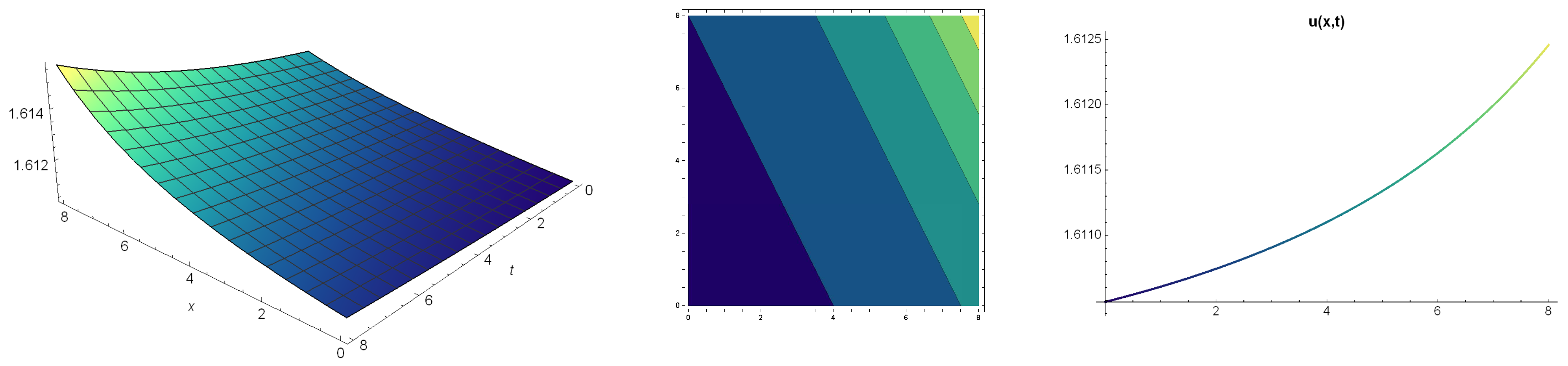
5. Solutions of the (Z-S) Equation Using -Expansion Method
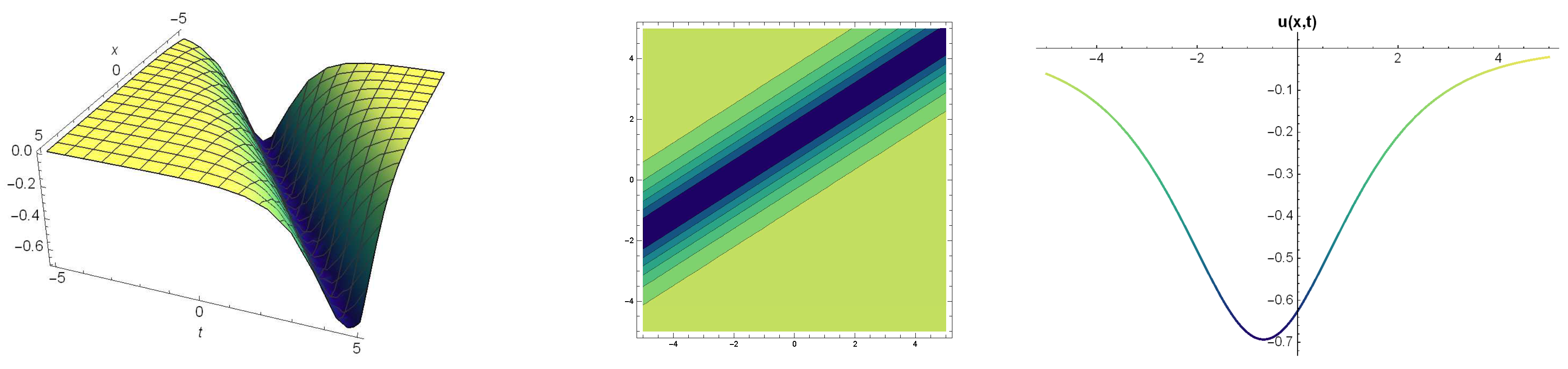
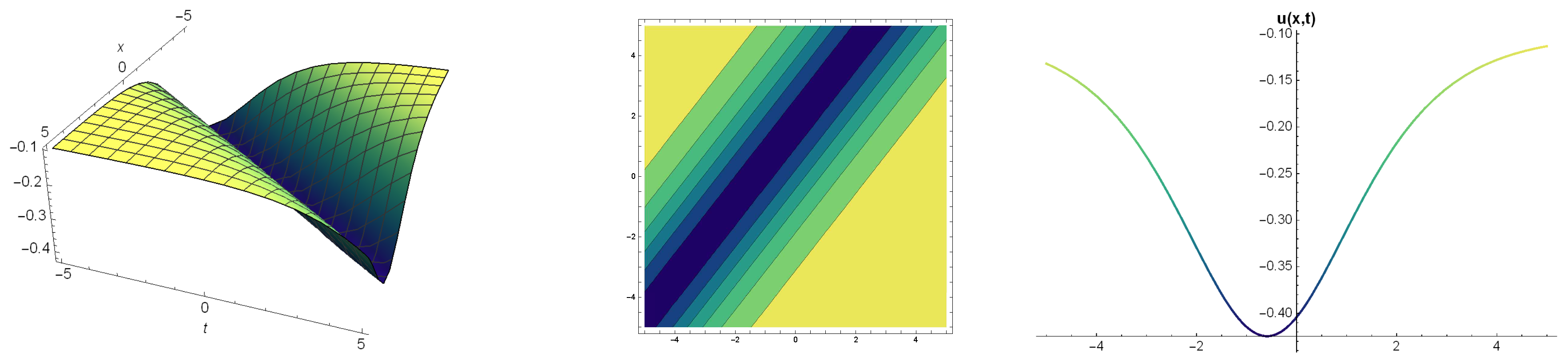
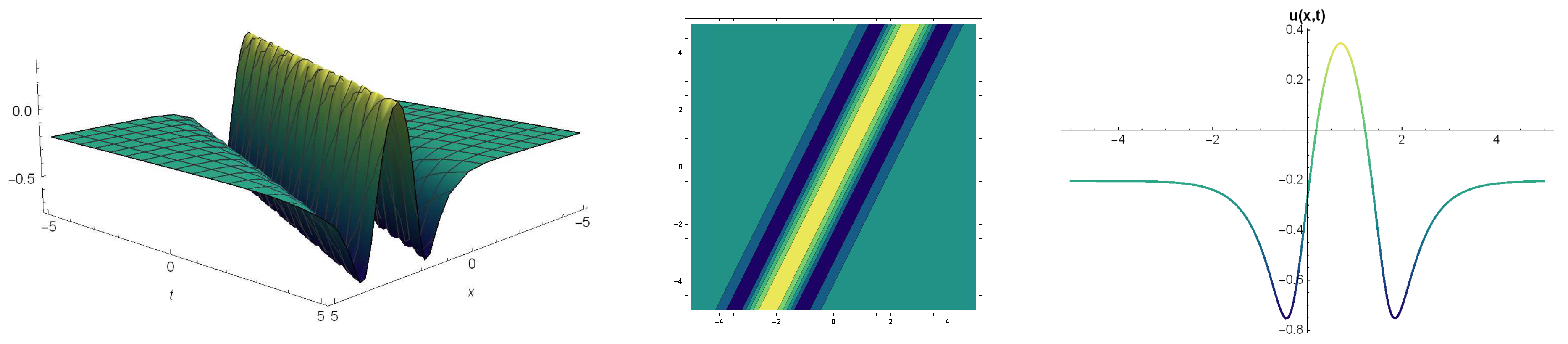
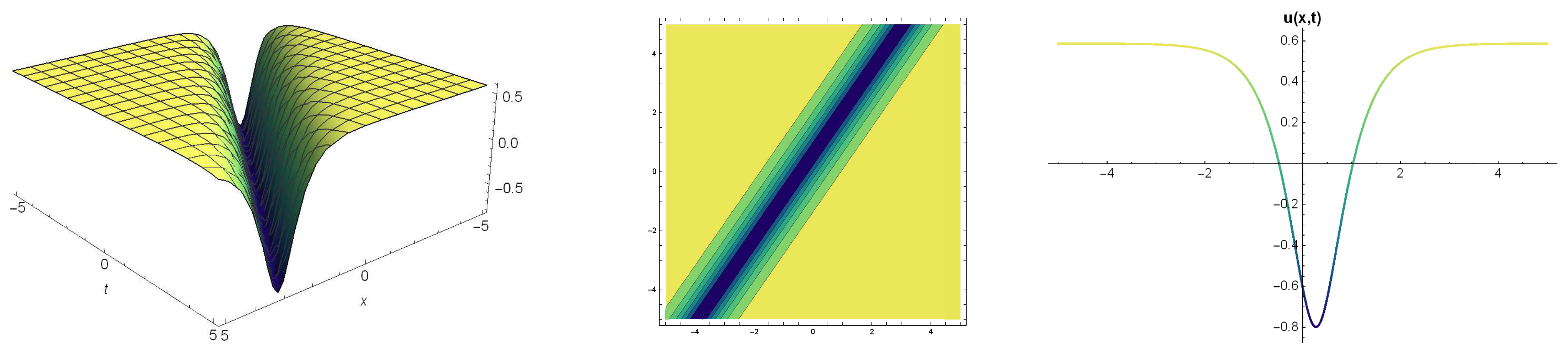
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wazwaz, A.M. A sine-cosine method for handlingnonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H.; Aktürk, T. Investigations of dark, bright, combined dark-bright optical and other soliton solutions in the complex cubic nonlinear Schrödinger equation with δ-potential. Superlattices Microstruct. 2018, 115, 19–29. [Google Scholar] [CrossRef]
- Cattani, C.; Sulaiman, T.A.; Baskonus, H.M.; Bulut, H. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems. Opt. Quantum Electron. 2018, 50. [Google Scholar] [CrossRef]
- Yokuş, A.; Kaya, D. Traveling wave solutions of some nonlinear partial differential equations by using extended-expansion method. İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi 2015, 28, 85–92. [Google Scholar]
- Durur, H. Different types analytic solutions of the (1+1)-dimensional resonant nonlinear Schrödinger’s equation using (G′/G)-expansion method. Mod. Phys. Lett. B 2020, 34. [Google Scholar] [CrossRef]
- Bulut, H.; Yel, G.; Başkonuş, H.M. An application of improved Bernoulli sub-equation function method to the nonlinear time-fractional burgers equation. Turk. J. Math. Comput. Sci. 2016, 5, 1–7. [Google Scholar]
- Ahmad, H.; Seadawy, A.R.; Khan, T.A. Numerical solution of Korteweg-de Vries-Burgers equation by the modified variational Iteration algorithm-II arising in shallow water waves. Phys. Scr. 2020. [Google Scholar] [CrossRef]
- Ahmad, H.; Seadawy, A.R.; Khan, T.A. Study on Numerical Solution of Dispersive Water Wave Phenomena by Using a Reliable Modification of Variational Iteration Algorithm. Math. Comput. Simul. 2020. [Google Scholar] [CrossRef]
- Ahmad, H.; Khan, T.A.; Cesarano, C. Numerical Solutions of Coupled Burgers’ Equations. Axioms 2019, 8, 119. [Google Scholar] [CrossRef] [Green Version]
- Durur, H.; Taşbozan, O.; Kurt, A.; Şenol, M. New Wave Solutions of Time Fractional Kadomtsev-Petviashvili Equation Arising In the Evolution of Nonlinear Long Waves of Small Amplitude. Erzincan Univ. J. Inst. Sci. Technol. 2019, 12, 807–815. [Google Scholar] [CrossRef] [Green Version]
- Aziz, I.; Šarler, B. The numerical solution of second-order boundary-value problems by collocation method with the Haar wavelets. Math. Comput. Model. 2010, 52, 1577–1590. [Google Scholar]
- Nawaz, M.; Ahmad, I.; Ahmad, H. A radial basis function collocation method for space-dependent inverse heat problems. J. Appl. Comput. Mech. 2020. [Google Scholar] [CrossRef]
- Yokuş, A.; Durur, H. Complex hyperbolic traveling wave solutions of Kuramoto-Sivashinsky equation using (1/G′) expansion method for nonlinear dynamic theory. J. BalıKesir Univ. Inst. Sci. Technol. 2010, 21, 590–599. [Google Scholar]
- Durur, H.; Yokuş, A. Analytical solutions of Kolmogorov–Petrovskii–Piskunov equation. Balıkesir Üniversitesi Fen Bilimleri Enstitüsü Dergisi 2020, 22, 628–636. [Google Scholar] [CrossRef]
- Yokuş, A.; Durur, H.; Ahmad, H. Hyperbolic type solutions for the couple Boiti-Leon-Pempinelli system. Facta Univ. Ser. Math. Inform. 2020, 35, 523–531. [Google Scholar]
- Darvishi, M.; Arbabi, S.; Najafi, M.; Wazwaz, A. Traveling wave solutions of a (2 + 1)-dimensional Zakharov-like equation by the first integral method and the tanh method. Optik 2016, 127, 6312–6321. [Google Scholar] [CrossRef]
- Kaya, D.; Yokus, A. A numerical comparison of partial solutions in the decomposition method for linear and nonlinear partial differential equations. Math. Comput. Simul. 2002, 60, 507–512. [Google Scholar] [CrossRef]
- Kaya, D.; Yokus, A. A decomposition method for finding solitary and periodic solutions for a coupled higher-dimensional Burgers equations. Appl. Math. Comput. 2005, 164, 857–864. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A quantitative approach to fractional option pricing problems with decomposition series. Konuralp J. Math. 2018, 6, 102–109. [Google Scholar]
- Jin-Ming, Z.; Yao-Ming, Z. The Hirota bilinear method for the coupled Burgers equation and the high-order Boussinesq—Burgers equation. Chin. Phys. B 2011, 20. [Google Scholar] [CrossRef]
- Ahmad, H. Variational iteration method with an auxiliary parameter for solving differential equations of the fifth order. Nonlinear Sci. Lett. A 2018, 9, 27–35. [Google Scholar]
- Ahmad, H.; Khan, T.A. Variational iteration algorithm-I with an auxiliary parameter for wave-like vibration equations. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1113–1124. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, H.; Khan, T.A. Variational iteration algorithm I with an auxiliary parameter for the solution of differential equations of motion for simple and damped mass–spring systems. Noise Vib. Worldw. 2020, 51, 12–20. [Google Scholar] [CrossRef]
- Ahmad, H.; Seadawy, A.R.; Khan, T.A.; Thounthong, P. Analytic Approximate Solutions for Some Nonlinear Parabolic Dynamical Wave Equations. J. Taibah Univ. Sci. 2020, 14, 346–358. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J.; Srivastava, H.M.; Cattani, C. Local fractional homotopy perturbation method for solving fractal partial differential equations arising in mathematical physics. Rom. Rep. Phys. 2015, 67, 752–761. [Google Scholar]
- Durur, H.; Şenol, M.; Kurt, A.; Taşbozan, O. Zaman-Kesirli Kadomtsev-Petviashvili Denkleminin Conformable Türev ile Yaklaşık Çözümleri. Erzincan Univ. J. Inst. Sci. Technol. 2019, 12, 796–806. [Google Scholar]
- Yokus, A.; Kuzu, B.; Demiroğlu, U. Investigation of solitary wave solutions for the (3 + 1)-dimensional Zakharov–Kuznetsov equation. Int. J. Mod. Phys. B 2019, 33. [Google Scholar] [CrossRef]
- Ricceri, B. A Class of Equations with Three Solutions. Mathematics 2020, 8, 478. [Google Scholar] [CrossRef] [Green Version]
- Treanţă, S. On the Kernel of a Polynomial of Scalar Derivations. Mathematics 2020, 8, 515. [Google Scholar] [CrossRef] [Green Version]
- Treanţă, S.; Vârsan, C. Weak small controls and approximations associated with controllable affine control systems. J. Differ. Equ. 2013, 255, 1867–1882. [Google Scholar] [CrossRef]
- Ahmad, H.; Khan, T.; Stanimirovic, P.; Ahmad, I. Modified Variational Iteration Technique for the Numerical Solution of Fifth Order KdV Type Equations. J. Appl. Comput. Mech. 2020. [Google Scholar] [CrossRef]
- Doroftei, M.; Treanta, S. Higher order hyperbolic equations involving a finite set of derivations. Balk. J. Geom. Its Appl. 2012, 17, 22–33. [Google Scholar]
- Treanţă, S. Gradient Structures Associated with a Polynomial Differential Equation. Mathematics 2020, 8, 535. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, H.; Khan, T.A.; Yao, S. Numerical solution of second order Painlevé differential equation. J. Math. Comput. Sci. 2020, 21, 150–157. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, H.; Rafiq, M.; Cesarano, C.; Durur, H. Variational Iteration Algorithm-I with an Auxiliary Parameter for Solving Boundary Value Problems. Earthline J. Math. Sci. 2020, 3, 229–247. [Google Scholar] [CrossRef] [Green Version]
- Kaya, D.; Yokuş, A.; Demiroğlu, U. Comparison of Exact and Numerical Solutions for the Sharma–Tasso–Olver Equation. In Numerical Solutions of Realistic Nonlinear Phenomena; Springer: Cham, Switzerland, 2020; pp. 53–65. [Google Scholar]
- Kurt, A.; Tasbozan, O.; Durur, H. The Exact Solutions of Conformable Fractional Partial Differential Equations Using New Sub Equation Method. Fundam. J. Math. Appl. 2019, 2, 173–179. [Google Scholar] [CrossRef]
- Ali, K.K.; Yilmazer, R.; Yokus, A.; Bulut, H. Analytical solutions for the (3 + 1)-dimensional nonlinear extended quantum Zakharov–Kuznetsov equation in plasma physics. Phys. A Stat. Mech. Its Appl. 2020, 548. [Google Scholar] [CrossRef]
- Borhanifar, A.; Moghanlu, A.Z. Application of the (G′/G)-expansion method for the Zhiber-Shabat equation and other related equations. Math. Comput. Model. 2011, 54, 2109–2116. [Google Scholar] [CrossRef]
- Tang, Y.; Xu, W.; Shen, J.; Gao, L. Bifurcations of traveling wave solutions for Zhiber-Shabat equation. Nonlinear Anal. Theory Methods Appl. 2007, 67, 648–656. [Google Scholar] [CrossRef]
- Chen, A.; Huang, W.; Li, J. Qualitative behavior and exact travelling wave solutions of the Zhiber-Shabat equation. J. Comput. Appl. Math. 2009, 230, 559–569. [Google Scholar] [CrossRef] [Green Version]
- Hafez, M.G.; Kauser, M.A.; Akter, M.T. Some New Exact Traveling Wave Solutions for the Zhiber-Shabat Equation. J. Adv. Math. Comput. Sci. 2014, 2582–2593. [Google Scholar] [CrossRef]
- Tala-Tebue, E.; Djoufack, Z.I.; Tsobgni-Fozap, D.C.; Kenfack-Jiotsa, A.; Kapche-Tagne, F.; Kofané, T.C. Traveling wave solutions along microtubules and in the Zhiber-Shabat equation. Chin. J. Phys. 2017, 55, 939–946. [Google Scholar] [CrossRef]
- He, B.; Long, Y.; Rui, W. New exact bounded travelling wave solutions for the Zhiber-Shabat equation. Nonlinear Anal. Theory Methods Appl. 2009, 71, 1636–1648. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokus, A.; Durur, H.; Ahmad, H.; Yao, S.-W. Construction of Different Types Analytic Solutions for the Zhiber-Shabat Equation. Mathematics 2020, 8, 908. https://doi.org/10.3390/math8060908
Yokus A, Durur H, Ahmad H, Yao S-W. Construction of Different Types Analytic Solutions for the Zhiber-Shabat Equation. Mathematics. 2020; 8(6):908. https://doi.org/10.3390/math8060908
Chicago/Turabian StyleYokus, Asıf, Hülya Durur, Hijaz Ahmad, and Shao-Wen Yao. 2020. "Construction of Different Types Analytic Solutions for the Zhiber-Shabat Equation" Mathematics 8, no. 6: 908. https://doi.org/10.3390/math8060908
APA StyleYokus, A., Durur, H., Ahmad, H., & Yao, S.-W. (2020). Construction of Different Types Analytic Solutions for the Zhiber-Shabat Equation. Mathematics, 8(6), 908. https://doi.org/10.3390/math8060908




