Application of Functional Data Analysis and FTIR-ATR Spectroscopy to Discriminate Wine Spirits Ageing Technologies
Abstract
1. Introduction
2. Materials and Methods
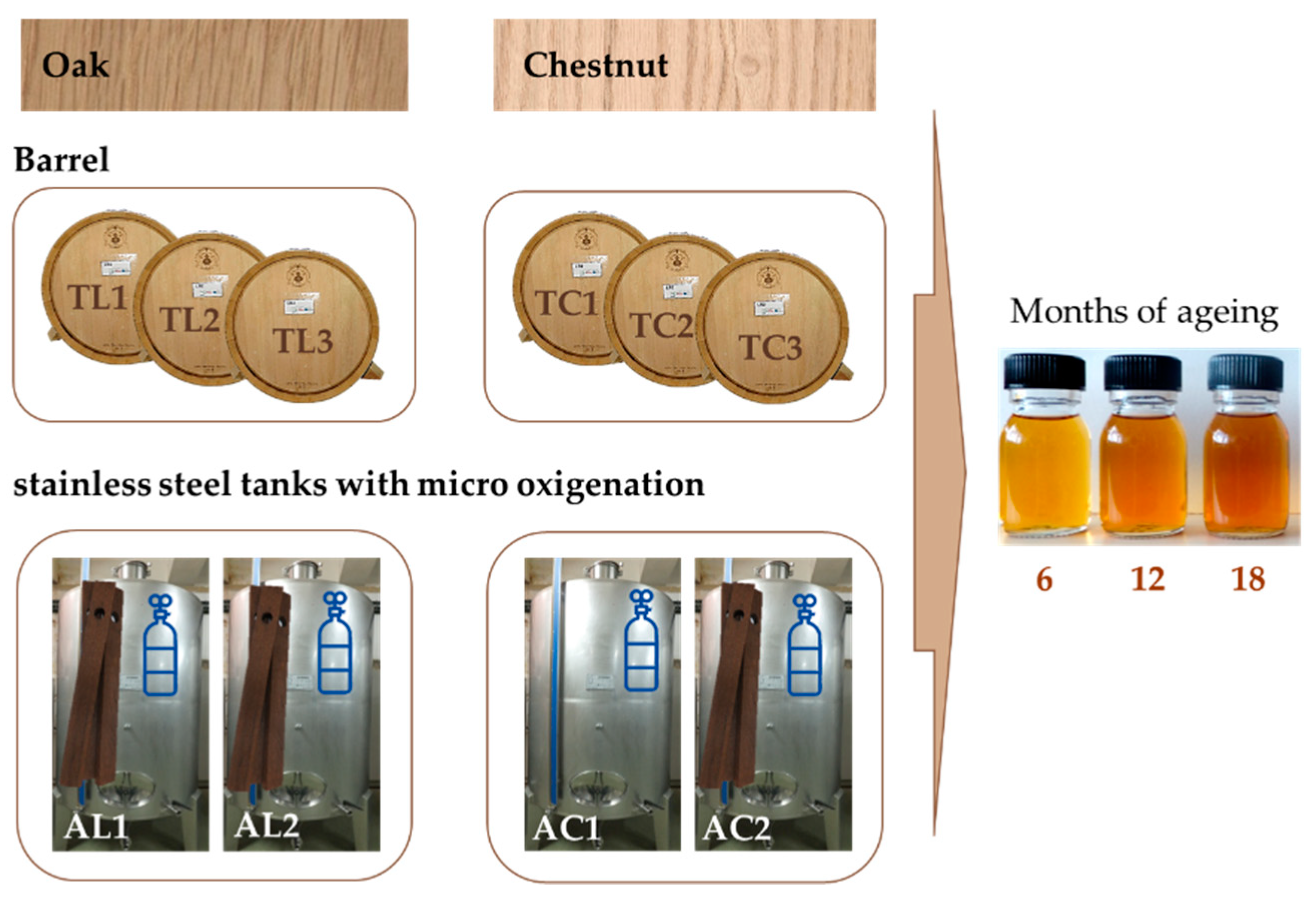
2.1. Samples
- TL—aged in 250 L new oak wooden barrels;
- TC—aged in 250 L new chestnut wooden barrels;
- AL—aged in 1000 L stainless steel tanks with oak wood staves and micro-oxygenation;
- AC—aged in 1000 L stainless steel tanks with chestnut wood staves and micro-oxygenation.
2.2. Analytical Procedures
2.2.1. Analysis of Chromatic Characteristics
2.2.2. Determination of the Total Phenolic Index
2.2.3. Analysis of Low Molecular Weight Compounds
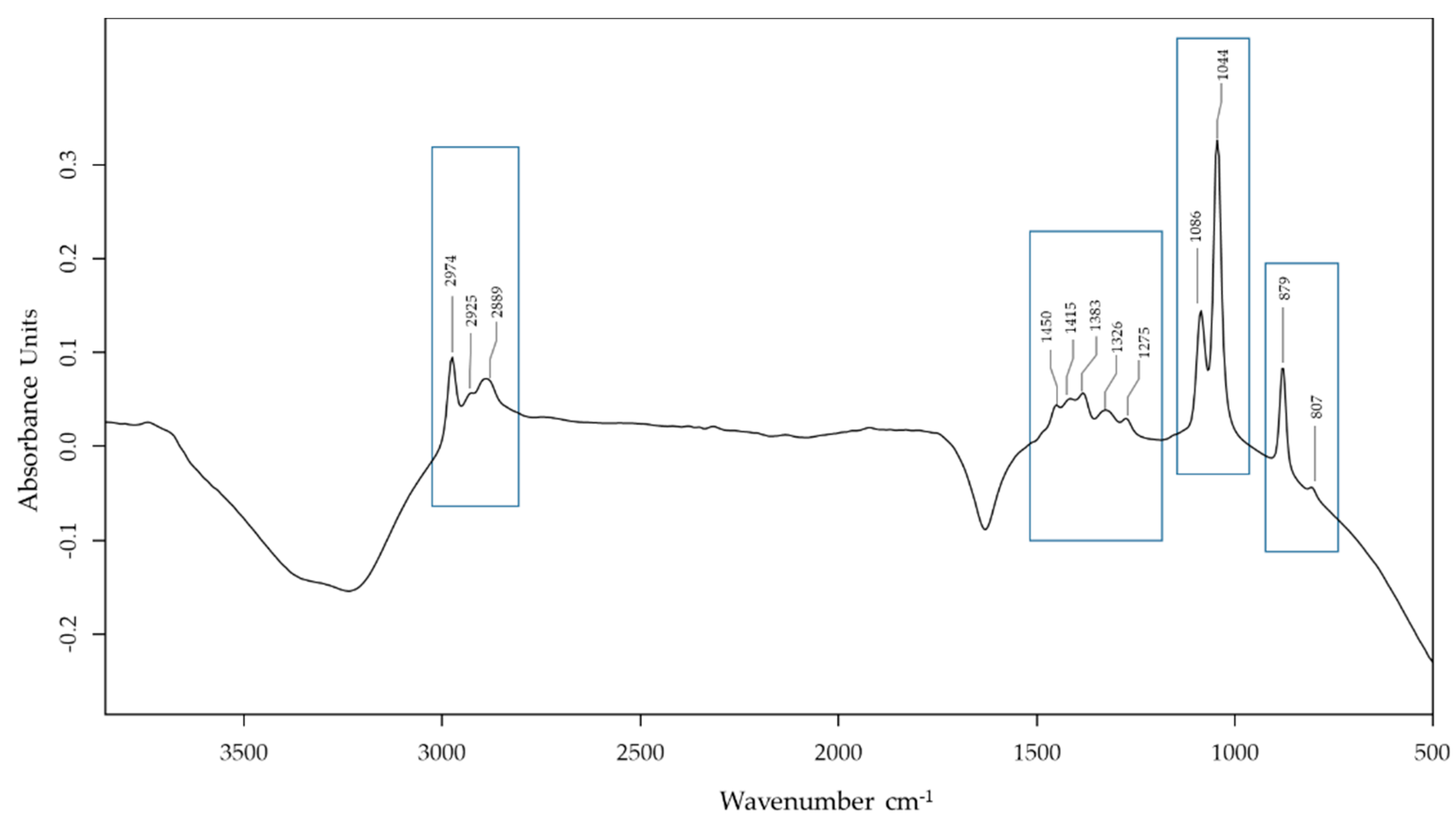
2.2.4. Spectroscopic Analyses
2.3. Statistical Analysis
2.3.1. Statistical Treatment of Analytical Data
2.3.2. Functional Analysis
Functional Data Analysis (FDA)
Functional Depths
Functional ANOVA (FANOVA)
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Canas, S. Phenolic Composition and Related Properties of Aged Wine Spirits: Influence of Barrel Characteristics. A Review. Beverages 2017, 3, 55. [Google Scholar] [CrossRef]
- García-Moreno, M.V.; Sánchez-Guillén, M.M.; Mier, M.R.D.; Delgado-González, M.J.; Rodríguez-Dodero, M.C.; García-Barroso, C.; Guillén-Sánchez, D.A. Use of Alternative Wood for the Ageing of Brandy de Jerez. Foods 2020, 9, 250. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, M.; Rodríguez-Dodero, C.M.; Jurado, S.M.; Puertas, B.G.; Barroso, C.; Guillén, A.D. Analytical Characterization and Sensory Analysis of Distillates of Different Varieties of Grapes Aged by an Accelerated Method. Foods 2020, 9, 277. [Google Scholar] [CrossRef] [PubMed]
- Canas, S.; Caldeira, I.; Belchior, A.P. Extraction/oxidation kinetics of low molecular weight compounds in wine brandy resulting from different ageing technologies. Food Chem. 2013, 138, 2460–2467. [Google Scholar] [CrossRef]
- Caldeira, I.; Santos, R.; Ricardo-da-Silva, J.M.; Anjos, O.; Mira, H.; Belchior, A.P.; Canas, S. Kinetics of odorant compounds in wine brandies aged in different systems. Food Chem. 2016, 211, 937–946. [Google Scholar] [CrossRef]
- Rodríguez-Solana, R.; Rodríguez-Freigedo, S.; Salgado, J.M.; Domínguez, J.M.; Cortés-Diéguez, S. Optimisation of accelerated ageing of grape marc distillate on a micro-scale process using a Box–Benhken design: Influence of oak origin, fragment size and toast level on the composition of the final product. Aust. J. Grape Wine Res. 2017, 23, 5–14. [Google Scholar] [CrossRef]
- Gómez-Plaza, E.; Bautista-Ortín, A.B. Chapter 10—Emerging Technologies for Aging Wines: Use of Chips and Micro-Oxygenation. In Red Wine Technology; Morata, A., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 149–162. [Google Scholar] [CrossRef]
- Canas, S.; Caldeira, I.; Anjos, O.; Belchior, A. Phenolic profile and colour acquired by the wine spirit in the beginning of ageing: Alternative technology using micro-oxygenation vs traditional technology. LWT Food Sci. Technol. 2019, 111, 260–269. [Google Scholar] [CrossRef]
- Llario, R.; Iñón, F.A.; Garrigues, S.; de la Guardia, M. Determination of quality parameters of beers by the use of attenuated total reflectance-Fourier transform infrared spectroscopy. Talanta 2006, 69, 469–480. [Google Scholar] [CrossRef]
- Yadav, P.K.; Sharma, R.M. Classification of illicit liquors based on their geographic origin using Attenuated total reflectance (ATR)—Fourier transform infrared (FT-IR) spectroscopy and chemometrics. Forensic Sci. Int. 2019, 295, e1–e5. [Google Scholar] [CrossRef]
- Nagarajan, R.; Mehrotra, R.; Bajaj, M.M. Quantitative analysis of methanol, an adulterant in alcoholic beverages, using attenuated total reflectance spectroscopy. J. Sci. Ind. Res. 2006, 65, 416–419. [Google Scholar]
- Teodora Emilia, C.; Carmen, S.; Florinela, F.; Floricuţa, R.; Raluca Maria, P.O.P.; Mira, F. Rapid Quantitative Analysis of Ethanol and Prediction of Methanol Content in Traditional Fruit Brandies from Romania, using FTIR Spectroscopy and Chemometrics. Not. Bot. Horti Agrobot. Cluj-Napoca 2013, 41. [Google Scholar] [CrossRef]
- Wiśniewska, P.; Boqué, R.; Borràs, E.; Busto, O.; Wardencki, W.; Namieśnik, J.; Dymerski, T. Authentication of whisky due to its botanical origin and way of production by instrumental analysis and multivariate classification methods. Spectrochim. Acta. Part A Mol. Biomol. Spectrosc. 2017, 173, 849–853. [Google Scholar] [CrossRef] [PubMed]
- Anjos, O.; Santos, A.J.A.; Estevinho, L.M.; Caldeira, I. FTIR–ATR spectroscopy applied to quality control of grape-derived spirits. Food Chem. 2016, 205, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Martínez Comesaña, M.; Martínez Mariño, S.; Eguía Oller, P.; Granada Álvarez, E.; Erkoreka González, A. A Functional Data Analysis for Assessing the Impact of a Retrofitting in the Energy Performance of a Building. Mathematics 2020, 8, 547. [Google Scholar] [CrossRef]
- Martínez, J.; Ordoñez, C.; Matìas, J.M.; Taboada, J. Determining noise in an aggregates plant using functional statistics. Hum. Ecol. Risk Assess. 2011, 17, 521–533. [Google Scholar] [CrossRef]
- Müller, H.-G.; Sen, R.; Stadtmüller, U. Functional data analysis for volatility. J. Econom. 2011, 165, 233–245. [Google Scholar] [CrossRef]
- López, M.; Martínez, J.; Matías, J.M.; Taboada, J.; Vilán, J.A. Shape functional optimization with restrictions boosted with machine learning techniques. J. Comput. Appl. Math. 2010, 234, 2609–2615. [Google Scholar] [CrossRef]
- Sancho, J.; Pastor, J.J.; Martínez, J.; García, M.A. Evaluation of Harmonic Variability in Electrical Power Systems through Statistical Control of Quality and Functional Data Analysis. Procedia Eng. 2013, 63, 295–302. [Google Scholar] [CrossRef]
- Martínez, J.; Pastor, J.; Sancho, J.; McNabola, A.; Martínez, M.; Gallagher, J. A functional data analysis approach for the detection of air pollution episodes and outliers: A case study in Dublin, Ireland. Mathematics 2020, 8, 225. [Google Scholar] [CrossRef]
- Di Battista, T.; Fortuna, F. Functional confidence bands for lichen biodiversity profiles: A case study in Tuscany region (central Italy). Stat. Anal. Data Min. ASA Data Sci. J. 2017, 10, 21–28. [Google Scholar] [CrossRef]
- Ruiz-Bellido, M.A.; Romero-Gil, V.; García-García, P.; Rodríguez-Gómez, F.; Arroyo-López, F.N.; Garrido-Fernández, A. Data on the application of Functional Data Analysis in food fermentations. Data Brief 2016, 9, 401–412. [Google Scholar] [CrossRef] [PubMed]
- Ordoñez, C.; Martínez, J.; Matías, J.M.; Reyes, A.N.; Rodríguez-Pérez, J.R. Functional statistical techniques applied to vine leaf water content determination. Math. Comput. Model. 2010, 52, 1116–1122. [Google Scholar] [CrossRef]
- Crawley, M.J. The R Book; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Ostertagová, E.; Ostertag, O.; Kovác, J. Methodology and application of the Kruskal-Wallis test. Appl. Mech. Mater. 2014, 611, 115–120. [Google Scholar] [CrossRef]
- Cetó, X.; Gutiérrez, J.M.; Gutiérrez, M.; Céspedes, F.; Capdevila, J.; Mínguez, S.; Jiménez-Jorquera, C.; del Valle, M. Determination of total polyphenol index in wines employing a voltammetric electronic tongue. Anal. Chim. Acta 2012, 732, 172–179. [Google Scholar] [CrossRef]
- Canas, S.; Belchior, A.; Spranger, M.; Sousa, R. High-performance liquid chromatography method for analysis of phenolic acids, phenolic aldehydes, and furanic derivatives in brandies. Development and validation. J. Sep. Sci. 2003, 26, 496–502. [Google Scholar] [CrossRef]
- Martínez, J.; Saavedra, Á.; García, P.J.; Piñeiro, J.I.; Iglesias, C.; Taboada, J.; Sancho, J.; Pastor, J. Air quality parameters outliers detection using functional data analysis in the Langreo urban area (Northern Spain). Appl. Math. Comput. 2014, 241, 1–10. [Google Scholar] [CrossRef]
- Wang, J.L.; Chiou, J.M.; Müller, H.G. Functional Data Analysis. Annu. Rev. Stat. Appl. 2016, 3, 257–295. [Google Scholar] [CrossRef]
- Kramosil, I.; Michálek, J. Fuzzy metrics and statistical metric spaces. Kybernetika 1975, 11, 336–344. [Google Scholar]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Cormier, E.; Genest, C.; Nešlehová, J.G. Using B-splines for nonparametric inference on bivariate extreme-value copulas. Extremes 2014, 17, 633–659. [Google Scholar] [CrossRef]
- Kwok, W.Y.; Moser, R.D.; Jiménez, J. A Critical Evaluation of the Resolution Properties of B-Spline and Compact Finite Difference Methods. J. Comput. Phys. 2001, 174, 510–551. [Google Scholar] [CrossRef]
- Piñeiro, J.I.; Torres, J.M.; García, P.J.; Alonso, J.R.; Muñiz, C.D.; Taboada, J. Analysis and detection of functional outliers in waterquality parameters from different automated monitoring stationsin the Nalón River Basin (Northern Spain). Environ. Sci. Pollut. Res. Int. 2015, 22, 387–396. [Google Scholar] [CrossRef] [PubMed]
- Febrero, M.; Galeano, P.; Wenceslao, G.M. Outlier detection in functional data by depth measures, with application to identify abnormal NOx levels. Environmetrics 2008, 19, 331–345. [Google Scholar] [CrossRef]
- Fraiman, R.; Muniz, G. Trimmed means for functional data. TEST 2001, 10, 419–440. [Google Scholar] [CrossRef]
- Cuevas, A.; Febrero, M.; Fraiman, R. Robust estimation and classification for functional data via projection-based notions. Comput. Stat. 2007, 22, 481–496. [Google Scholar] [CrossRef]
- Cuevas, A.; Febrero, M.; Fraiman, R. On the use of bootstrap for estimating functions with functional data. Comput. Stat. Data Anal. 2006, 51, 1063–1074. [Google Scholar] [CrossRef]
- Millán-Roures, L.; Epifanio, I.; Martínez, V. Detection of Anomalies in Water Networks by Functional Data Analysis. Math. Probl. Eng. 2018, 2018, 13. [Google Scholar] [CrossRef]
- Maturo, F.; Battista, T.; Fortuna, F. Parametric functional analysis of variance for fish biodiversity assessment. J. Environ. Inform. 2016, 28, 101–109. [Google Scholar] [CrossRef][Green Version]
- Cuesta-Albertos, J.A.; Febrero, M. A simple multiway ANOVA for functional data. TEST 2010, 19, 537–557. [Google Scholar] [CrossRef]
- Zhang, J.-T. Analysis of Variance for Functional Data. In A Chapman & Hall Book; Press, C.R.C., Ed.; Taylor & Francis Group: Abingdon, UK, 2013; p. 412. [Google Scholar]
- Aguilera, A.; Fortuna, F.; Escabias, M.; Battista, T. Assessing Social Interest in Burnout Using Google Trends Data. Soc. Indic. Res. 2019, 1–13. [Google Scholar] [CrossRef]
- Górecki, T.; Smaga, Ł. fdANOVA: An R software package for analysis of variance for univariate and multivariate functional data. Comput. Stat. 2019, 34, 571–597. [Google Scholar] [CrossRef]
- Zhang, J.-T. Statistical inferences for linear models with functional responses. Stat. Sin. 2011, 21, 1431–1451. [Google Scholar] [CrossRef]
- Górecki, T.; Smaga, Ł. A comparison of tests for the one-way ANOVA problem for functional data. Comput. Stat. 2015, 30, 987–1010. [Google Scholar] [CrossRef]
- Moreira, J.; Santos, L. Spectroscopic interferences in Fourier transform infrared wine analysis. Anal. Chim. Acta 2003, 513, 263–268. [Google Scholar] [CrossRef]
- Shurvell, H.F. Spectra—Structure Correlations in the Mid- and Far-Infrared. In Handbook of Vibrational Spectroscopy; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Tarantilis, P.A.; Troianou, V.E.; Pappas, C.S.; Kotseridis, Y.S.; Polissiou, M.G. Differentiation of Greek red wines on the basis of grape variety using attenuated total reflectance Fourier transform infrared spectroscopy. Food Chem. 2008, 111, 192–196. [Google Scholar] [CrossRef]
- Öztürk, B.; Yucesoy, D.; Ozen, B. Application of Mid-infrared Spectroscopy for the Measurement of Several Quality Parameters of Alcoholic Beverages, Wineand Raki. Food Anal. Methods 2012, 5, 1435–1442. [Google Scholar] [CrossRef]
- Fujieda, M.; Tanaka, T.; Suwa, Y.; Koshimizu, S.; Kouno, I. Isolation and Structure of Whiskey Polyphenols Produced by Oxidation of Oak Wood Ellagitannins. J. Agric. Food. Chem. 2008, 56, 7305–7310. [Google Scholar] [CrossRef]
- Carvalho, A. Identificação anatómica e caracterização física e mecânica das madeiras utilizadas no fabrico de quartolas para produção de aguardentes velhas de qualidade—Denominação Lourinhã. Ciência Técnica Vitivinícola 1998, 13, 71–105. [Google Scholar]
- Martínez-Gil, A.; del Alamo-Sanza, M.; Sánchez-Gómez, R.; Nevares, I. Alternative Woods in Enology: Characterization of Tannin and Low Molecular Weight Phenol Compounds with Respect to Traditional Oak Woods. A Review. Molecules 2020, 25, 1474. [Google Scholar] [CrossRef]
- Oberholster, A.; Elmendorf, B.L.; Lerno, L.A.; King, E.S.; Heymann, H.; Brenneman, C.E.; Boulton, R.B. Barrel maturation, oak alternatives and micro-oxygenation: Influence on red wine aging and quality. Food Chem. 2015, 173, 1250–1258. [Google Scholar] [CrossRef]
- Laqui-Estaña, J.; López-Solís, R.; Peña-Neira, Á.; Medel-Marabolí, M.; Obreque-Slier, E. Wines in contact with oak wood: The impact of the variety (Carménère and Cabernet Sauvignon), format (barrels, chips and staves), and aging time on the phenolic composition. J. Sci. Food Agric. 2019, 99, 436–448. [Google Scholar] [CrossRef]
- Karvela, E.; Makris, D.P.; Kefalas, P.; Moutounet, M. Extraction of phenolics in liquid model matrices containing oak chips: Kinetics, liquid chromatography-mass spectroscopy characterisation and association with in vitro antiradical activity. Food Chem. 2008, 110, 263–272. [Google Scholar] [CrossRef] [PubMed]
- García-Estévez, I.; Alcalde-Eon, C.; Martínez-Gil, A.M.; Rivas-Gonzalo, J.C.; Escribano-Bailón, M.T.; Nevares, I.; del Alamo-Sanza, M. An Approach to the Study of the Interactions between Ellagitannins and Oxygen during Oak Wood Aging. J. Agric. Food. Chem. 2017, 65, 6369–6378. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Gil, A.; Cadahía, E.; Fernández de Simón, B.; Gutiérrez-Gamboa, G.; Nevares, I.; del Álamo-Sanza, M. Phenolic and volatile compounds in Quercus humboldtii Bonpl. wood: Effect of toasting with respect to oaks traditionally used in cooperage. J. Sci. Food Agric. 2019, 99, 315–324. [Google Scholar] [CrossRef] [PubMed]
- Anjos, O.; Carmona, C.; Caldeira, I.; Canas, S. Variation of Extractable Compounds and Lignin Contents in Wood Fragments Used in the Aging of Wine Brandies. BioResources 2013, 8, 4484–4496. [Google Scholar] [CrossRef]
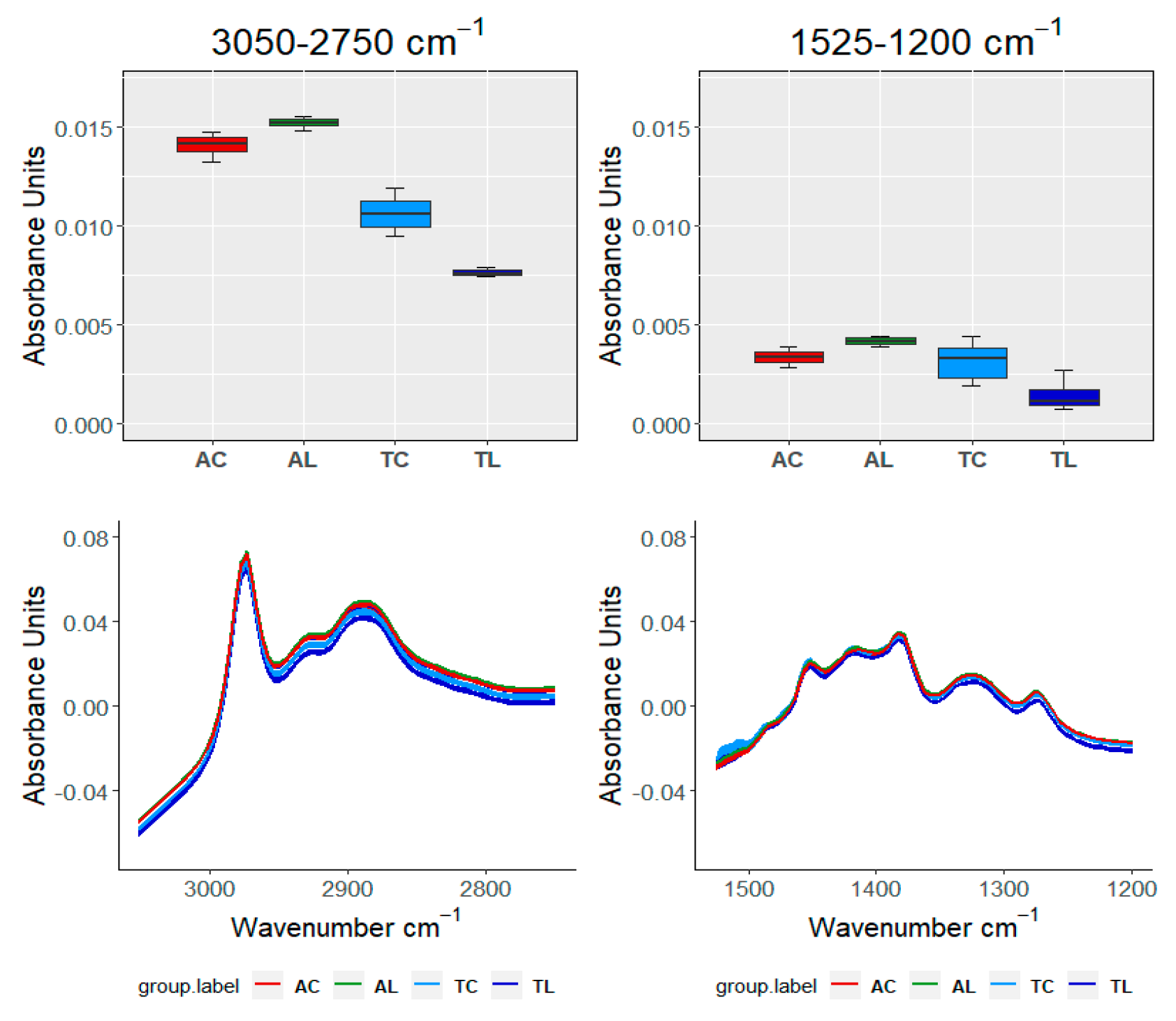
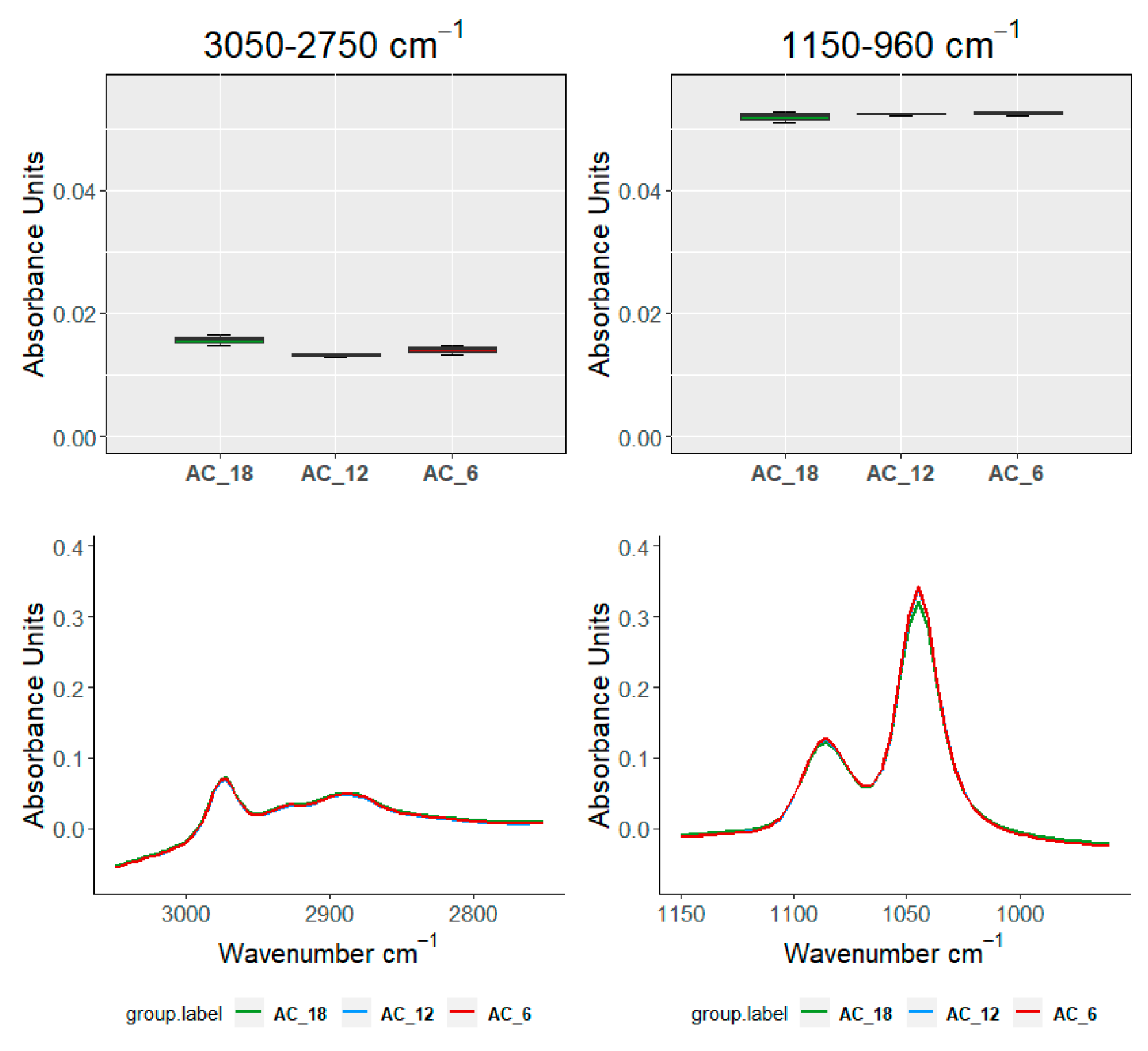
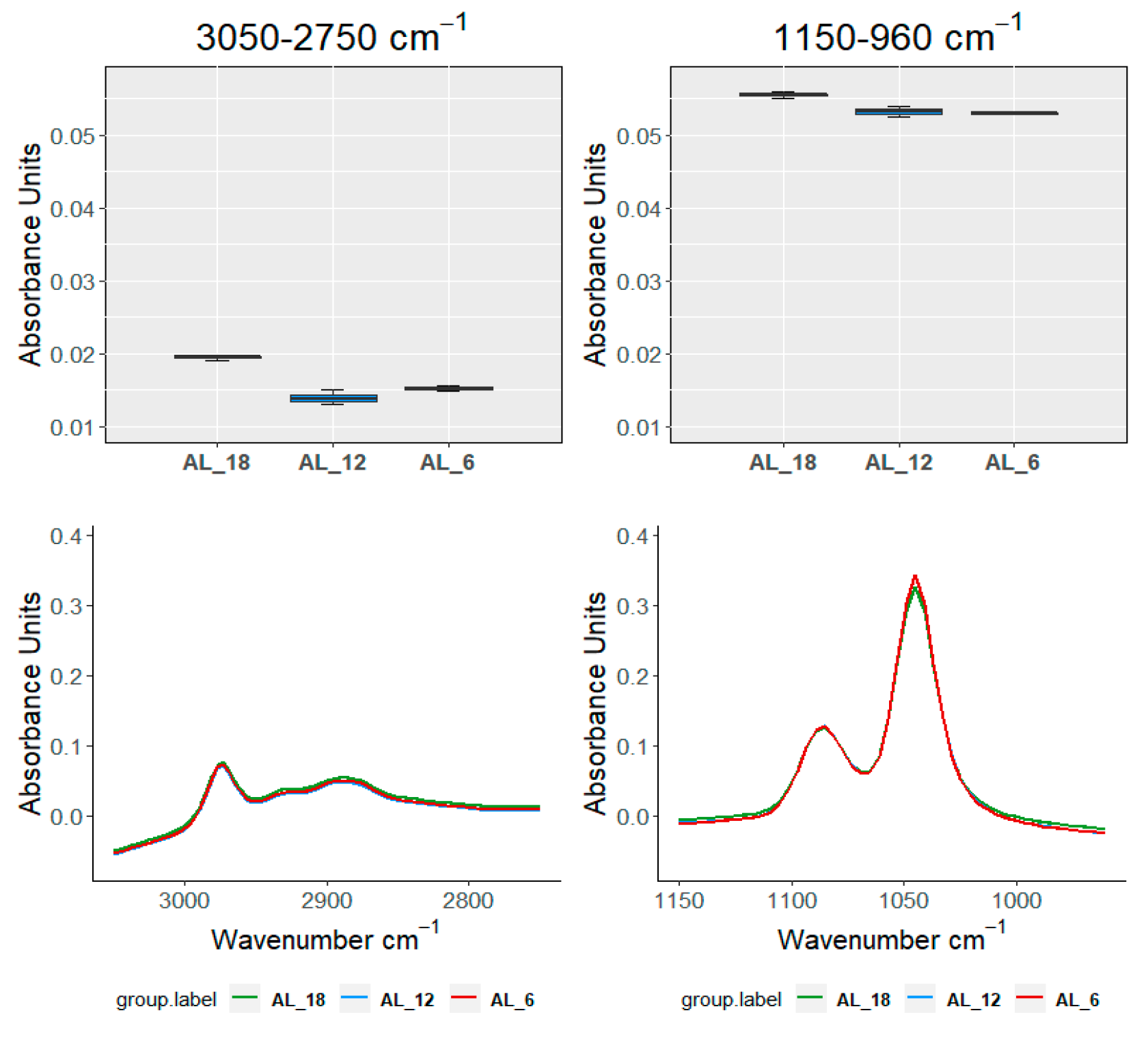
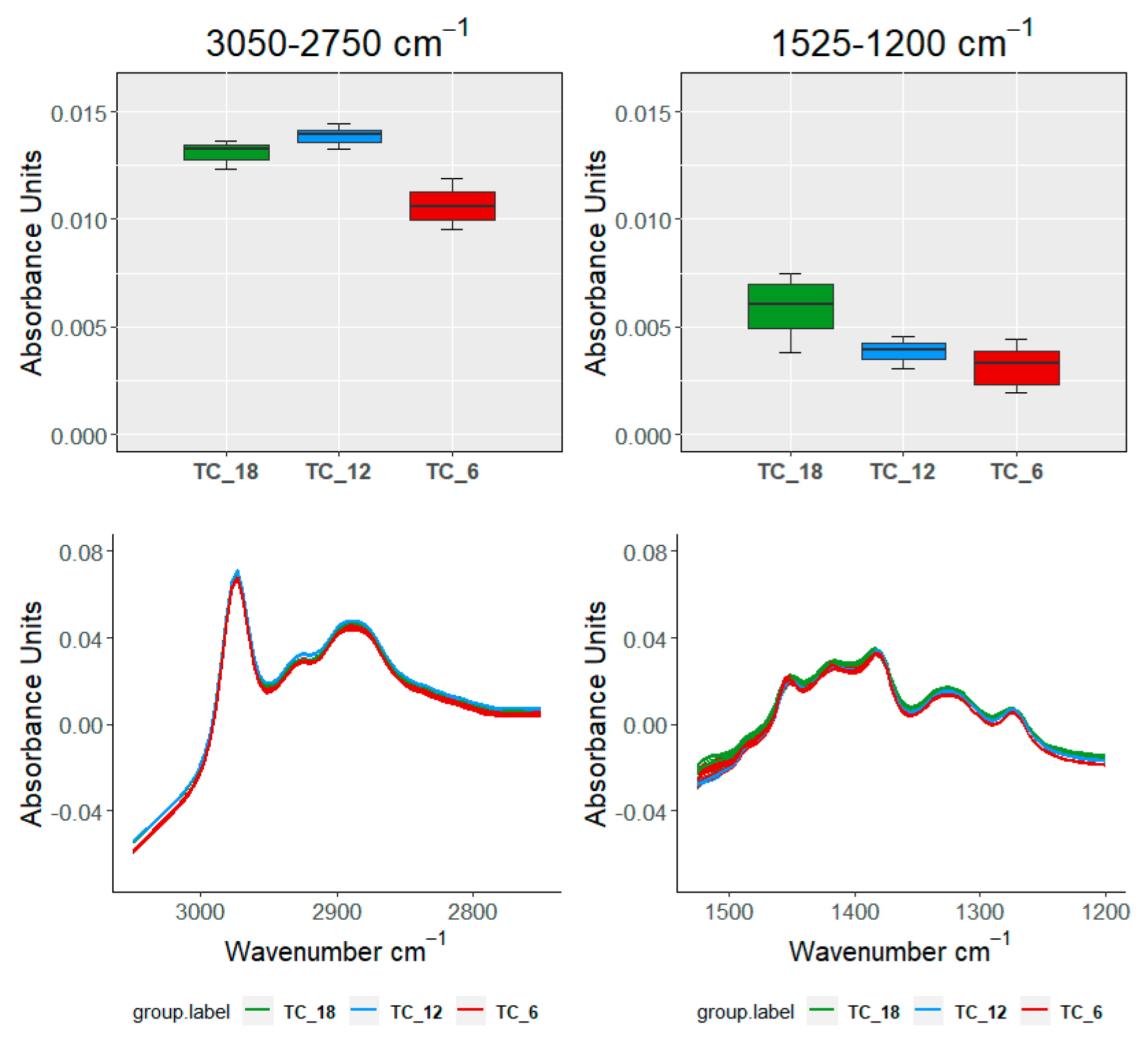
| Ageing Months | Code | L *(%) | A * | B * | C * | TPI |
|---|---|---|---|---|---|---|
| 6 | TC | 85.41 ± 1.41 b | 3.37 ± 1.08 b | 50.96 ± 2.68 b | 51.08 ± 2.74 b | 24.94 ± 1.98 b |
| TL | 93.73 ± 0.42 c | −1.25 ± 0.17 a | 26.76 ± 2.21 a | 26.79 ± 2.20 a | 11.99 ± 1.18 a | |
| AC | 77.14 ± 1.26 a | 11.79 ± 1.22 c | 70.00 ± 1.59 c | 70.99 ± 1.77 c | 47.79 ± 3.80 c | |
| AL | 87.55 ± 0.23 b | 1.75 ± 0.14 b | 46.24 ± 0.14 b | 46.27 ± 0.15 b | 26.88 ± 0.87 b | |
| Variance origin | Technology (S) | 61.9 *** | 52.7 *** | 60.2 *** | 60.2 *** | 42.1 *** |
| Wood (W) | 36.7 *** | 31.9 *** | 38.8 *** | 38.8 *** | 52.4 *** | |
| SxW | NS | 14.0 ** | NS | NS | 4.2 * | |
| Residual | 1.5 | 1.3 | 1.0 | 1.0 | 1.3 | |
| 12 | TC | 79.11 ± 1.38 b | 9.89 ± 1.31 b | 69.41 ± 1.64 b | 70.11 ± 1.80 b | 37.90 ± 1.94 b |
| TL | 90.62 ± 1.04 c | −0.49 ± 0.65 a | 40.66 ± 3.4 a | 40.67 ± 3.40 a | 17.55 ± 1.81 a | |
| AC | 65.58 ± 1.97 a | 25.63 ± 1.78 c | 87.25 ± 0.56 c | 90.95 ± 1.04 c | 65.72 ± 1.37 c | |
| AL | 79.17 ± 0.60 b | 10.38 ± 0.53 b | 70.87 ± 0.61 b | 71.63 ± 0.68 b | 37.86 ± 0.23 b | |
| Variance origin | Technology (S) | 49.2 *** | 49.9 *** | 49.4 *** | 50.7 *** | 48.6 *** |
| Wood (W) | 49.7 *** | 46.3 *** | 43.5 *** | 44.9 *** | 48.8 *** | |
| SxW | NS | 3.1 * | 6.2 *** | 3.6 * | 2.2 * | |
| Residual | 1.1 | 0.8 | 0.9 | 0.8 | 0.5 | |
| 18 | TC | 77.33 ± 1.25 b | 12.06 ± 1.24 b | 73.97 ± 1.22 b | 74.95 ± 1.40 b | 40.98 ± 2.46 b |
| TL | 89.61 ± 1.17 c | −0.02 ± 0.84 a | 44.35 ± 3.74 a | 44.36 ± 3.74 a | 18.15 ± 1.63 a | |
| AC | 62.29 ± 1.94 a | 28.97 ± 1.62 c | 89.27 ± 0.12 c | 93.86 ± 0.61 c | 71.60 ± 2.50 c | |
| AL | 76.59 ± 0.52 b | 13.19 ± 0.45 b | 75.87 ± 0.44 b | 77.01 ± 0.51 b | 40.55 ± 1.25 b | |
| Variance origin | Technology (S) | 52.2 *** | 52.9*** | 47.7 *** | 50.0 *** | 47.9 *** |
| Wood (W) | 46.9 *** | 45.2*** | 40.2 *** | 42.3 *** | 49.5 *** | |
| SxW | NS | 1.4* | 11.1 ** | 6.8 *** | 2.1 * | |
| Residual | 0.9 | 0.6 | 0.9 | 0.9 | 0.6 |
| Ageing Months | Code | Furfural | Ellagic Acid | Vanillin | Coniferaldehyde | sumHPLC |
|---|---|---|---|---|---|---|
| 6 | TC | 38.31 ± 6.90 a | 8.12 ± 1.41 b | 2.03 ± 0.01 b | 6.17 ± 0.63 a | 163.10 ± 24.08 b |
| TL | 31.73 ± 6.38 a | 3.43 ± 0.20 a | 1.49 ± 0.08 a | 5.21 ± 0.04 a | 78.99 ± 9.71 a | |
| AC | 127.05 ± 5.07 c | 15.35 ± 0.38 c | 4.62 ± 0.20 d | 10.60 ± 0.65 b | 296.05 ± 15.91 c | |
| AL | 87.74 ± 4.11 b | 6.28 ± 0.70 a,b | 3.26 ± 0.16 c | 12.20 ± 0.52 b | 195.23 ± 3.04 b | |
| Variance origin | Technology(S) | 82.7 *** | 30.4 *** | 79.1 *** | 98.5 *** | 63.1 *** |
| Wood(W) | 8.1 ** | 56.9 *** | 15.1 *** | NS | 34.6 *** | |
| SxW | 8.0 *** | 10.8 *** | 5.3 ** | NS | NS | |
| Residual | 1.2 | 2.0 | 0.5 | 1.5 | 2.3 | |
| 12 | TC | 35.85 ± 6.03 a | 12.86 ± 1.16 b | 3.61 ± 0.22 b | 7.00 ± 0.57 a | 231.68 ± 26.34 b |
| TL | 31.36 ± 5.80 a | 5.64 ± 0.34 a | 2.66 ± 0.23 a | 6.49 ± 0.58 a | 95.09 ± 13.67 a | |
| AC | 131.17 ± 4.91 c | 24.89 ± 1.26 c | 8.68 ± 0.02 d | 13.97 ± 0.17 b | 369.24 ± 8.57 d | |
| AL | 96.08 ± 1.93 b | 11.94 ± 0.88 b | 6.77 ± 0.09 c | 19.61 ± 0.41 c | 275.32 ± 4.56 c | |
| Variance origin | Technology(S) | 87.9 *** | 41.3 *** | 89.2 *** | 79.7 *** | 64.5 *** |
| Wood(W) | 5.2 ** | 50.0 *** | 8.6 *** | 5.1 *** | 33.8 *** | |
| SxW | 6.1 *** | 7.8 *** | 1.8 *** | 14.8 *** | NS | |
| Residual | 0.8 | 0.9 | 0.3 | 0.4 | 1.7 | |
| 18 | TC | 36.55 ± 7.28 a | 15.48 ± 1.41 b | 4.43 ± 0.34 b | 6.85 ± 0.75 a | 271.85 ± 38.84 b |
| TL | 31.63 ± 6.26 a | 6.81 ± 0.49 a | 3.13 ± 0.23 a | 6.41 ± 0.60 a | 104.10 ± 16.10 a | |
| AC | 113.35 ± 4.27 c | 28.17 ± 1.15 c | 8.61 ± 0.07 d | 11.16 ± 0.15 b | 347.46 ± 4.33 c | |
| AL | 86.72 ± 0.21 b | 13.81 ± 0.23 b | 7.49 ± 0.24 c | 17.93 ± 0.07 c | 275.63 ± 4.79 b | |
| Variance origin | Technology(S) | 89.4 *** | 39.1 *** | 92.0 *** | 63.3 *** | 43.6 *** |
| Wood(W) | 4.8 *** | 53.7 *** | 7.2 *** | 10.0 *** | 40.9 *** | |
| SxW | 4.3 * | 6.2 *** | NS | 26.0 *** | 11.9 * | |
| Residual | 1.5 | 0.8 | 0.7 | 0.7 | 3.6 |
| TC | TL | AC | AL | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 12 | 18 | 6 | 12 | 18 | 6 | 12 | 18 | 6 | 12 | 18 | |
| L *(%) | b | a | a | b | a | a | b | a | a | c | b | a |
| a * | a | b | b | a | a | a | a | b | b | a | b | c |
| b * | a | b | c | a | b | b | a | b | b | a | b | c |
| C * | a | b | c | a | b | b | a | b | b | a | b | c |
| TPI | a | b | b | a | b | b | a | b | b | a | b | b |
| Furf | a | a | a | a | a | a | a | ab | b | a | ab | b |
| Ellag | a | b | b | a | b | c | a | b | b | a | b | c |
| Vanil | a | b | c | a | b | c | a | b | b | a | b | c |
| Cofde | a | a | a | a | b | b | a | b | a | a | b | c |
| sumHPLC | a | b | b | a | a | a | a | b | b | a | b | b |
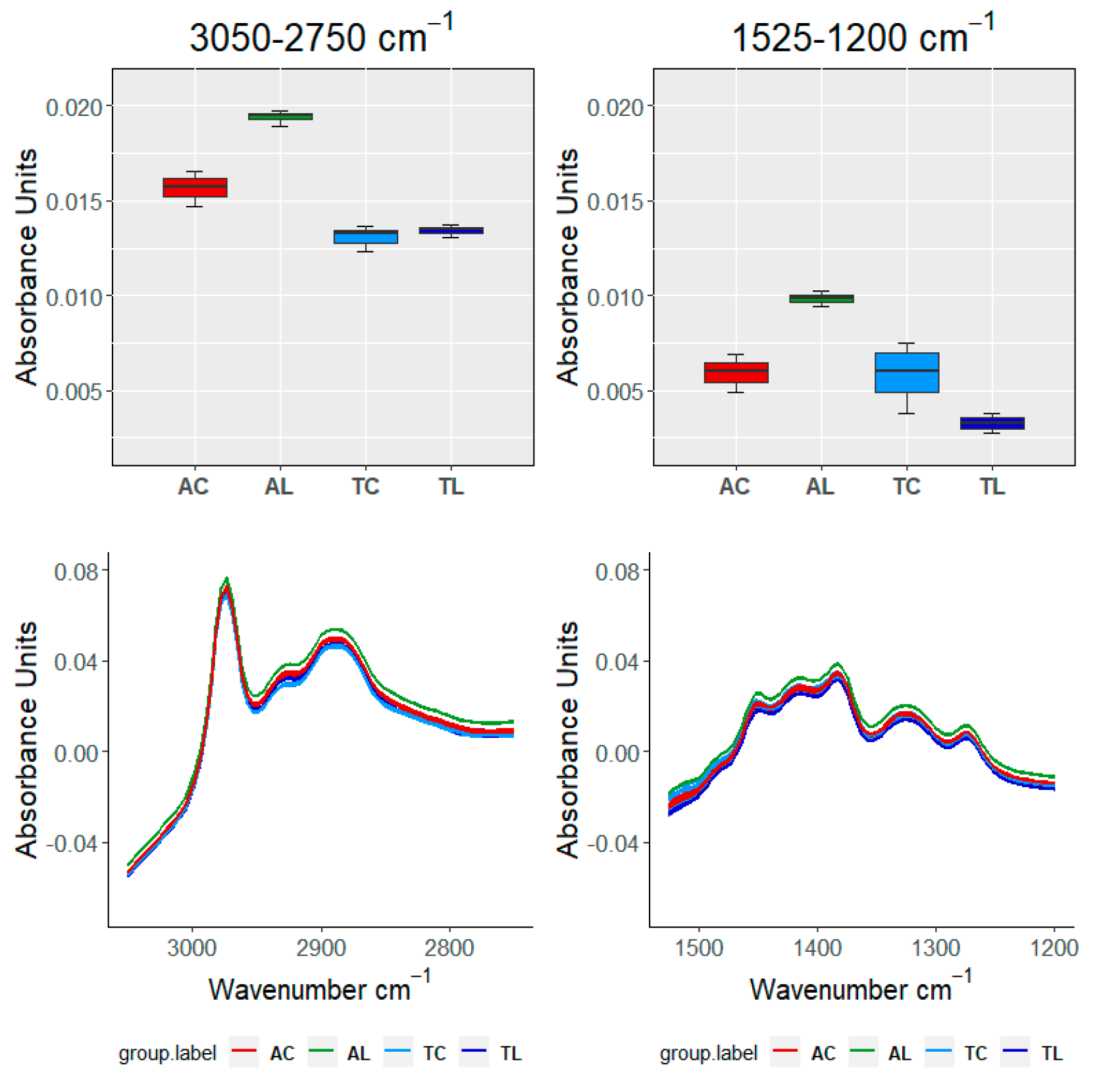
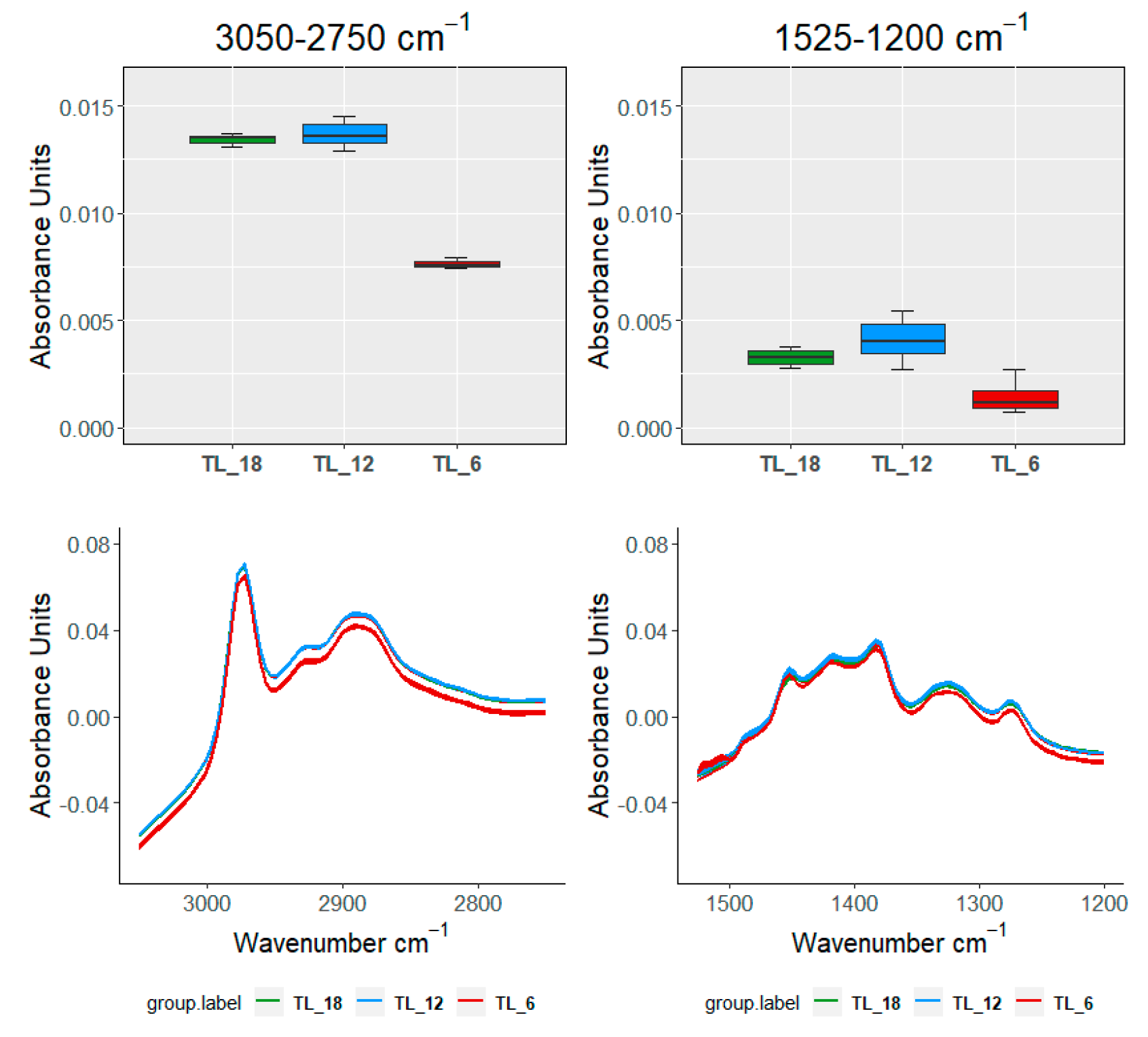
| TEST\SAMPLE | 3050–2750 cm−1 | 1525–120 cm−1 | 1150–960 cm−1 | 910–750 cm−1 | ||
|---|---|---|---|---|---|---|
| 18 months | ||||||
| FDA | FANOVA | FP | ≈0 | ≈0 | ≈0 | ≈0 |
| FB | ≈0 | ≈0 | ≈0 | ≈0 | ||
| VA | ANOVA | ≈0 | ≈0 | ≈0 | ≈0 | |
| Kruskal | ≈0 | ≈0 | ≈0 | ≈0 | ||
| 12 months | ||||||
| FDA | FANOVA | FP | 0.001 | ≈0 | ≈0 | ≈0 |
| FB | 0.003 | ≈0 | 1.31 × 10−5 | ≈0 | ||
| VA | ANOVA | 0.007 | ≈0 | 0.003 | ≈0 | |
| Kruskal | 0.008 | 2.23 × 10−6 | 0.003 | ≈0 | ||
| 6 months | ||||||
| FDA | FANOVA | FP | ≈0 | ≈0 | ≈0 | ≈0 |
| FB | ≈0 | ≈0 | ≈0 | 1 × 10−4 | ||
| VA | ANOVA | ≈0 | ≈0 | ≈0 | ≈0 | |
| Kruskal | ≈0 | ≈0 | ≈0 | ≈0 | ||
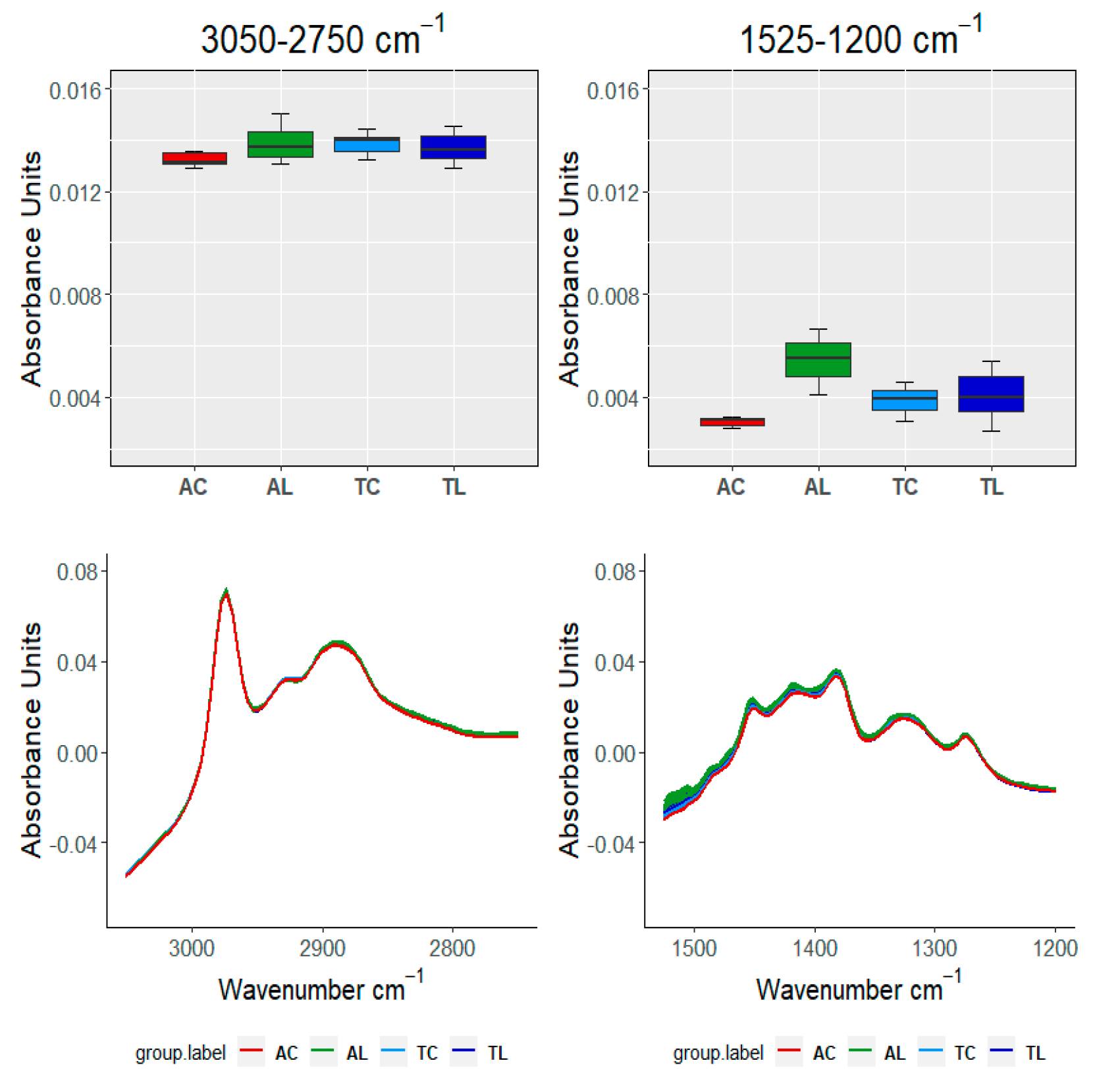
| TEST\SAMPLE | 3050–2750 cm−1 | 1525–120 cm−1 | 1150–960 cm−1 | 910–750 cm−1 | ||
|---|---|---|---|---|---|---|
| Groups within AC | ||||||
| FDA | FANOVA | FP | ≈0 | ≈0 | ≈0 | ≈0 |
| FB | ≈0 | ≈0 | ≈0 | ≈0 | ||
| VA | ANOVA | ≈0 | ≈0 | 0.032 | ≈0 | |
| Kruskal | ≈0 | 6.72 × 10−5 | 0.214 | 1 × 10−4 | ||
| Groups within AL | ||||||
| FDA | FANOVA | FP | ≈0 | ≈0 | ≈0 | ≈0 |
| FB | ≈0 | ≈0 | ≈0 | ≈0 | ||
| VA | ANOVA | ≈0 | ≈0 | ≈0 | ≈0 | |
| Kruskal | 2.07e-06 | 4.14 × 10−6 | 3.34 × 10−5 | 3.71 × 10−6 | ||
| Groups within TC | ||||||
| FDA | FANOVA | FP | ≈0 | ≈0 | ≈0 | ≈0 |
| FB | ≈0 | ≈0 | ≈0 | ≈0 | ||
| VA | ANOVA | ≈0 | ≈0 | ≈0 | ≈0 | |
| Kruskal | ≈0 | 7.32 × 10−6 | ≈0 | ≈0 | ||
| Groups within TL | ||||||
| FDA | FANOVA | FP | ≈0 | ≈0 | ≈0 | ≈0 |
| FB | ≈0 | ≈0 | ≈0 | ≈0 | ||
| VA | ANOVA | ≈0 | ≈0 | ≈0 | ≈0 | |
| Kruskal | 1 × 10−4 | 1.95 × 10−6 | ≈0 | ≈0 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anjos, O.; Martínez Comesaña, M.; Caldeira, I.; Pedro, S.I.; Eguía Oller, P.; Canas, S. Application of Functional Data Analysis and FTIR-ATR Spectroscopy to Discriminate Wine Spirits Ageing Technologies. Mathematics 2020, 8, 896. https://doi.org/10.3390/math8060896
Anjos O, Martínez Comesaña M, Caldeira I, Pedro SI, Eguía Oller P, Canas S. Application of Functional Data Analysis and FTIR-ATR Spectroscopy to Discriminate Wine Spirits Ageing Technologies. Mathematics. 2020; 8(6):896. https://doi.org/10.3390/math8060896
Chicago/Turabian StyleAnjos, Ofélia, Miguel Martínez Comesaña, Ilda Caldeira, Soraia Inês Pedro, Pablo Eguía Oller, and Sara Canas. 2020. "Application of Functional Data Analysis and FTIR-ATR Spectroscopy to Discriminate Wine Spirits Ageing Technologies" Mathematics 8, no. 6: 896. https://doi.org/10.3390/math8060896
APA StyleAnjos, O., Martínez Comesaña, M., Caldeira, I., Pedro, S. I., Eguía Oller, P., & Canas, S. (2020). Application of Functional Data Analysis and FTIR-ATR Spectroscopy to Discriminate Wine Spirits Ageing Technologies. Mathematics, 8(6), 896. https://doi.org/10.3390/math8060896








